MAMGN-HTI: A Graph Neural Network Model with Metapath and Attention Mechanisms for Hyperthyroidism Herb–Target Interaction Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation
2.1.1. Heterogeneous Graph
2.1.2. Metapath
2.1.3. Metapath Instance
2.1.4. Metapath Neighbor Node
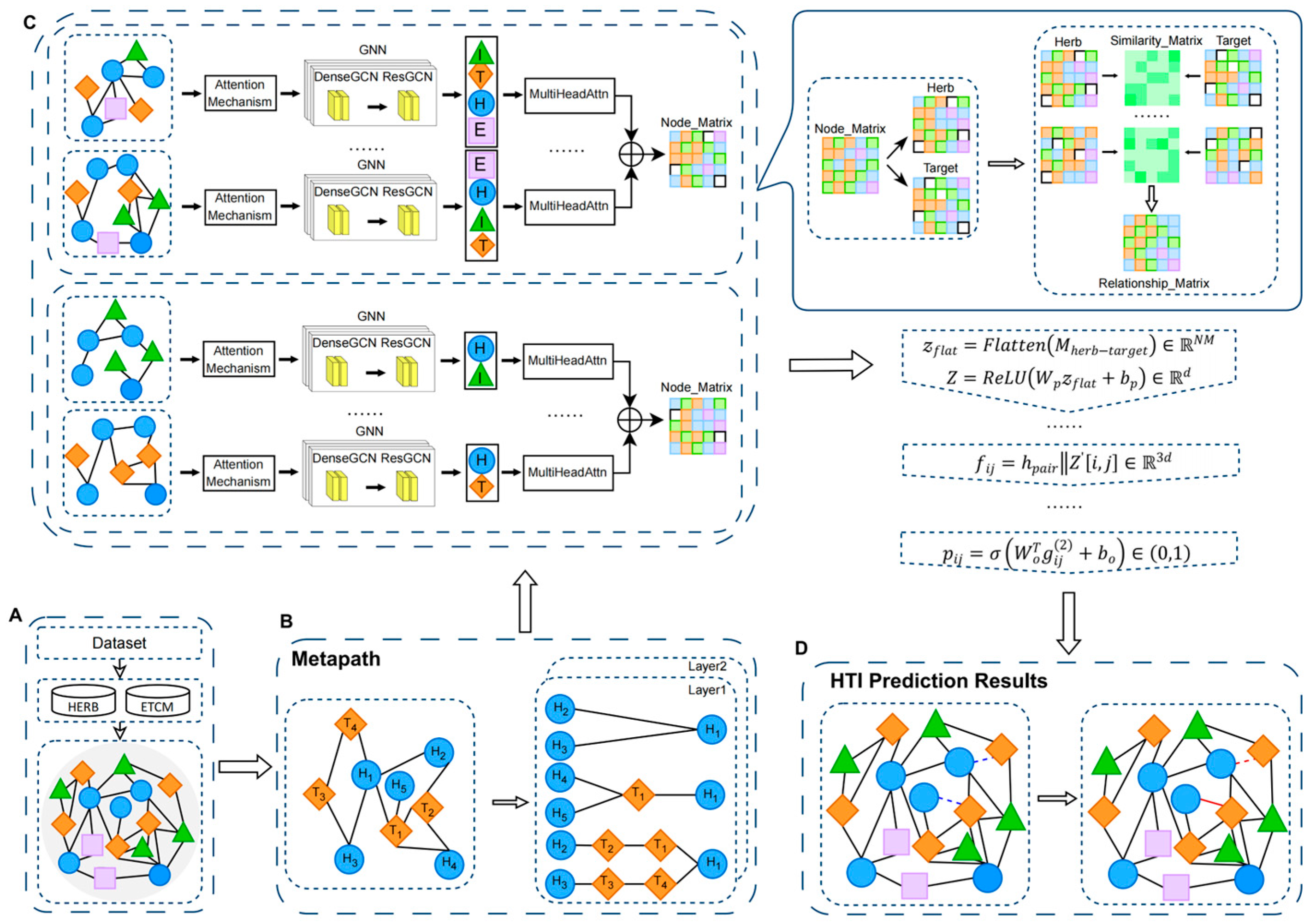
2.2. Methods
2.2.1. Metapath Construction
2.2.2. Herb–Target Representation Learning Module
2.2.3. HTI Prediction Module
2.3. Experiment
2.3.1. Dataset
2.3.2. Evaluation Metrics
2.3.3. Data Processing
2.3.4. Parameter Settings
2.3.5. Baselines
3. Results
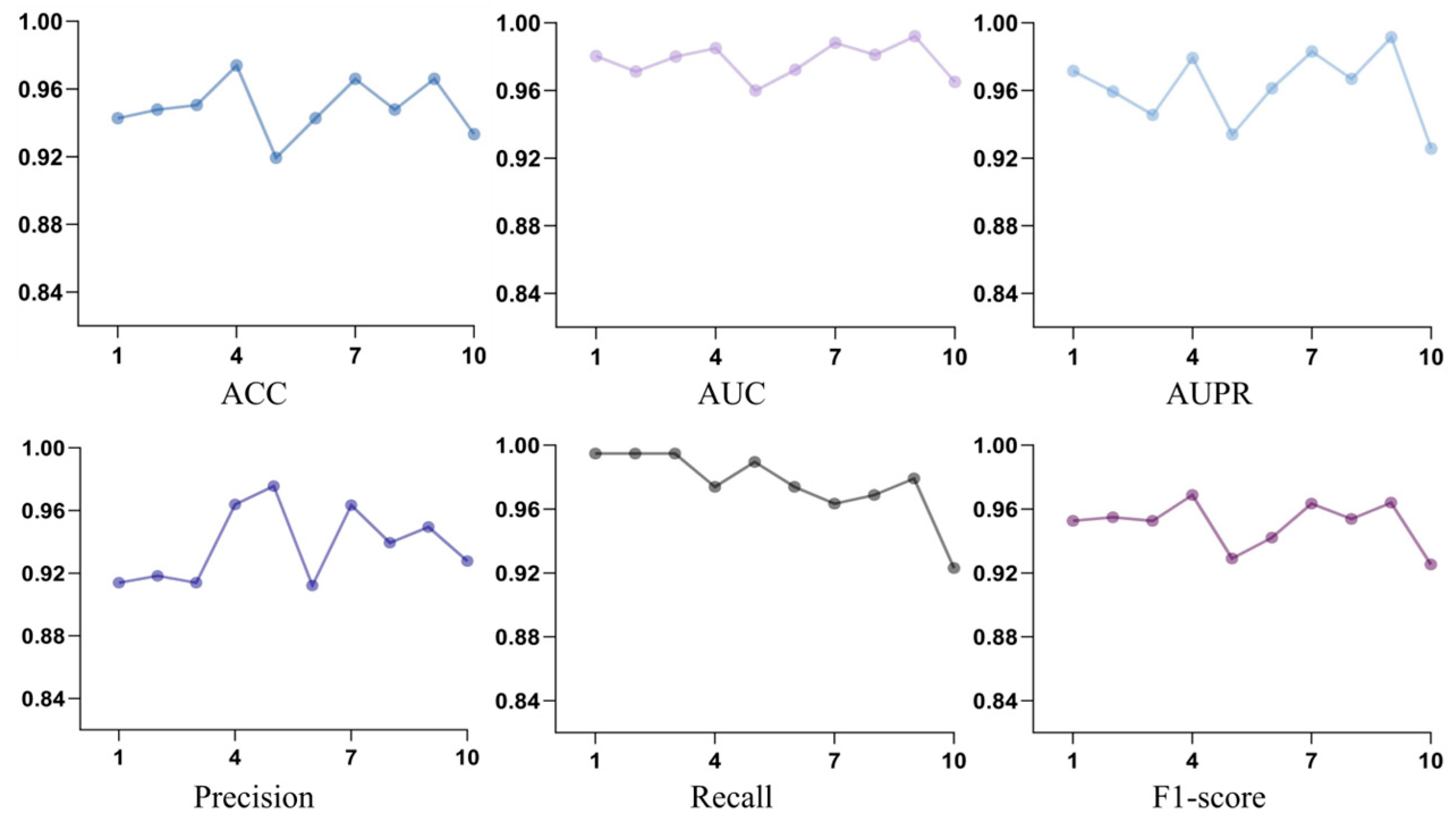
3.1. Experimental Results
3.2. Baseline Comparison Experiments
3.3. Ablation Experiment
3.4. Generalization Ability Validation
3.5. GO Enrichment Analysis
3.6. Prediction Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TCM | Traditional Chinese Medicine |
| GNNs | Graph Neural Networks |
| HTI | Herb–Target Interaction |
| ResGCN | Residual Graph Convolutional Network |
| DenseGCN | Densely Connected Graph Convolutional Network |
| ACC | Accuracy |
| AUC | Area Under the Receiver Operating Characteristic Curve |
| AUPR | Area Under the Precision-Recall Curve |
| SGD | Stochastic Gradient Descent |
| GO | Gene Ontology |
| PPI | Protein–Protein Interaction |
| TSI | Thyroid-Stimulating Immunoglobulin |
| TPO | Thyroid Peroxidase |
| Tg | Thyroglobulin |
| NF-κB | Nuclear Factor kappa-light-chain-enhancer of activated B cells |
| mTORC1 | Mechanistic Target of Rapamycin Complex 1 |
References
- Jin, M.; Liu, L.; Dou, D. Quantitative Analysis of Steroid Hormones to Explore the Effects of Ginseng Medicines Base on UPLC-QqQ-MS/MS. J. Chin. Mass Spectrom. Soc. 2024, 45, 540–551. [Google Scholar] [CrossRef]
- Wu, M.; Li, W. Prevention and Treatment of Radiation Damage After Tumor Radiotherapy with Traditional Chinese Medicine. Jiangsu J. Tradit. Chin. Med. 2023, 55, 1–5. [Google Scholar] [CrossRef]
- Ye, F.; Wu, M.; Zhou, X.; Cheng, H.; Li, L.; Feng, Z.; Jin, L.; Zhu, Y.; Guo, L.; Zhao, Z.; et al. Summary of the Academic Thought of TCM Master Zhou Zhongying on Integrating the Ancient and Modern to Create a New System of Pathogenesis Theory. J. Nanjing Univ. Tradit. Chin. Med. 2024, 40, 1071–1079. [Google Scholar] [CrossRef]
- Yang, X.; Zhu, Y.; Xing, X.; Zhou, Z.; She, K. Research on A TabNet-Based Predictive Model and Medication Patterns in the Diagnosis and Treatment of Hyperthyroidism by Professor Zhou Zhongying. J. Nanjing Univ. Tradit. Chin. Med. 2024, 40, 534–542. [Google Scholar] [CrossRef]
- Gan, X.; Shu, Z.; Wang, X.; Yan, D.; Li, J.; Ofaim, S.; Albert, R.; Li, X.; Liu, B.; Zhou, X. Network medicine framework reveals generic herb-symptom effectiveness of traditional Chinese medicine. Sci. Adv. 2023, 9, eadh0215. [Google Scholar] [CrossRef]
- Wang, H.; Xu, M.; Guo, Z.; You, G.; Wang, G.; Cao, C.; Hu, X. DTI-BGCGCN: A Novel Bipartite Graph-based Cluster Graph Convolutional Network for Drug-Target Interaction Prediction in Modern and Traditional Chinese Medicine. Comput. Biol. Chem. 2025, 117, 108410. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Zhang, M.; Hu, P.; Zhang, J.; Niu, C.; Lu, X.; Jiang, X.; Ma, Y. Dual-channel hypergraph convolutional network for predicting herb–disease associations. Brief. Bioinform. 2024, 25, bbae067. [Google Scholar] [CrossRef]
- Qiu, W.; Liang, Q.; Yu, L.; Xiao, X.; Qiu, W.; Lin, W. LSTM-SAGDTA: Predicting Drug-target Binding Affinity with an Attention Graph Neural Network and LSTM Approach. Curr. Pharm. Des. 2024, 30, 468–476. [Google Scholar] [CrossRef] [PubMed]
- Qu, X.; Du, G.; Hu, J.; Cai, Y. Graph-DTI: A new model for drug-target interaction prediction based on heterogenous network graph embedding. Curr. Comput.-Aided Drug Des. 2024, 20, 1013–1024. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, Y.; Zhao, D.; Xu, J.; Wang, L. HiGNN: A hierarchical informative graph neural network for molecular property prediction equipped with feature-wise attention. J. Chem. Inf. Model. 2022, 63, 43–55. [Google Scholar] [CrossRef]
- Yang, W.; Li, L.; Bai, S.; Ma, Z. IS-GNN: Graph neural network enhanced by aggregating influential and structurally similar nodes. Knowl. -Based Syst. 2024, 301, 112282. [Google Scholar] [CrossRef]
- Wang, S.; Cao, G.; Cao, W.; Li, Y. NLA-GNN: Non-local information aggregated graph neural network for heterogeneous graph embedding. Pattern Recognit. 2025, 158, 110940. [Google Scholar] [CrossRef]
- Li, L.; Yang, W.; Bai, S.; Ma, Z. KNN-GNN: A powerful graph neural network enhanced by aggregating K-nearest neighbors in common subspace. Expert Syst. Appl. 2024, 253, 124217. [Google Scholar] [CrossRef]
- Park, J.; Jeong, S.; Lee, B.S.; Lim, S. MIGTNet: Metapath Instance-based Graph Transformation Network for heterogeneous graph embedding. Future Gener. Comput. Syst. 2023, 149, 390–401. [Google Scholar] [CrossRef]
- Ma, S.; Liu, J.-w.; Zuo, X. Self-supervised learning for heterogeneous graph via structure information based on metapath. Appl. Soft Comput. 2023, 143, 110388. [Google Scholar] [CrossRef]
- Lai, P.; Dai, Q.; Lu, Y.; Wang, Z.; Chen, M.; Wang, C. MIGP: Metapath Integrated Graph Prompt Neural Network. Neural Netw. 2024, 179, 106595. [Google Scholar] [CrossRef]
- Wu, Z.; Guo, M.; Jin, X.; Chen, J.; Liu, B. CFAGO: Cross-fusion of network and attributes based on attention mechanism for protein function prediction. Bioinformatics 2023, 39, btad123. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, M.; Song, Y.; Wang, L.; Lu, Y.; Wang, H.; Chen, X. BAB-GSL: Using Bayesian influence with attention mechanism to optimize graph structure in basic views. Neural Netw. 2025, 181, 106785. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Zhu, Y.; Teng, F.; Li, T. Temporal knowledge graph reasoning based on relation graphs and time-guided attention mechanism. Knowl. -Based Syst. 2024, 301, 112280. [Google Scholar] [CrossRef]
- Fang, S.; Dong, L.; Liu, L.; Guo, J.; Zhao, L.; Zhang, J.; Bu, D.; Liu, X.; Huo, P.; Cao, W. HERB: A high-throughput experiment-and reference-guided database of traditional Chinese medicine. Nucleic Acids Res. 2021, 49, D1197–D1206. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, Y.; Liu, Z.; Chen, T.; Lv, C.; Tang, S.; Zhang, X.; Zhang, W.; Li, Z.; Zhou, R. ETCM: An encyclopaedia of traditional Chinese medicine. Nucleic Acids Res. 2019, 47, D976–D982. [Google Scholar] [CrossRef]
- Li, M.; Liu, H.; Kong, F.; Lv, P. DTRE: A model for predicting drug-target interactions of endometrial cancer based on heterogeneous graph. Future Gener. Comput. Syst. 2024, 161, 478–486. [Google Scholar] [CrossRef]
- Shao, K.; Zhang, Y.; Wen, Y.; Zhang, Z.; He, S.; Bo, X. DTI-HETA: Prediction of drug–target interactions based on GCN and GAT on heterogeneous graph. Brief. Bioinform. 2022, 23, bbac109. [Google Scholar] [CrossRef]
- Hou, Z.; Xu, Z.; Yan, C.; Luo, H.; Luo, J. CPI-GGS: A deep learning model for predicting compound-protein interaction based on graphs and sequences. Comput. Biol. Chem. 2025, 115, 108326. [Google Scholar] [CrossRef] [PubMed]
- An, Q.; Yu, L. A heterogeneous network embedding framework for predicting similarity-based drug-target interactions. Brief. Bioinform. 2021, 22, bbab275. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; Xu, Z.; Li, W.; Xie, X.; Peng, S. MultiDTI: Drug–target interaction prediction based on multi-modal representation learning to bridge the gap between new chemical entities and known heterogeneous network. Bioinformatics 2021, 37, 4485–4492. [Google Scholar] [CrossRef] [PubMed]
- Wan, F.; Hong, L.; Xiao, A.; Jiang, T.; Zeng, J. NeoDTI: Neural integration of neighbor information from a heterogeneous network for discovering new drug–target interactions. Bioinformatics 2019, 35, 104–111. [Google Scholar] [CrossRef]
- Li, J.; Wang, J.; Lv, H.; Zhang, Z.; Wang, Z. IMCHGAN: Inductive matrix completion with heterogeneous graph attention networks for drug-target interactions prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 19, 655–665. [Google Scholar] [CrossRef]
- Li, Y.; Qiao, G.; Gao, X.; Wang, G. Supervised graph co-contrastive learning for drug–target interaction prediction. Bioinformatics 2022, 38, 2847–2854. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Y.; Guan, J.; Li, J.; Han, R.; Hao, J.; Wei, Z.; Shang, X. An end-to-end heterogeneous graph representation learning-based framework for drug–target interaction prediction. Brief. Bioinform. 2021, 22, bbaa430. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, X.; Shi, Y.; Chen, T.; Xu, Z.; Wang, P.; Yu, M.; Chen, W.; Li, B.; Jing, Z. ETCM v2. 0: An update with comprehensive resource and rich annotations for traditional Chinese medicine. Acta Pharm. Sin. B 2023, 13, 2559–2571. [Google Scholar] [CrossRef]
- Gao, K.; Liu, L.; Lei, S.; Li, Z.; Huo, P.; Wang, Z.; Dong, L.; Deng, W.; Bu, D.; Zeng, X. HERB 2.0: An updated database integrating clinical and experimental evidence for traditional Chinese medicine. Nucleic Acids Res. 2025, 53, D1404–D1414. [Google Scholar] [CrossRef]
- Ru, J.; Li, P.; Wang, J.; Zhou, W.; Li, B.; Huang, C.; Li, P.; Guo, Z.; Tao, W.; Yang, Y. TCMSP: A database of systems pharmacology for drug discovery from herbal medicines. J. Cheminform. 2014, 6, 13. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Yu, G.; Tong, J. The pharmacological mechanism of Tangerine peel was analyzed based on network pharmacology. Chin. Tradit. Pat. Med. 2019, 41, 3038–3045. [Google Scholar] [CrossRef]
- Li, J. Based on Data Mining to Explore the Medication Rules of Traditional Chinese Medicine for the Treatment of Yin Deficiency Type Hyperthyroidism. Master’s Thesis, Guangxi University of Chinese Medicine, Nanning, China, 2023. [Google Scholar]
- Li, S.; Fu, Y.; Wei, D.; Wang, F.; Xu, M.; Wang, T.; Yan, S. Research progress on the clinical and mechanism of Xiaoyao Powder and its active ingredients in the treatment of thyroid diseases. Chin. J. Exp. Tradit. Med. Formulae 2025, 31, 302–310. [Google Scholar] [CrossRef]
- Qin, L.; Yang, F.; An, M.; Wei, M.; Shi, Y. To explore the mechanism of algae-Prunella in the treatment of hyperthyroidism based on network pharmacology and molecular docking. J. North Pharm. 2024, 21, 113–116+119. [Google Scholar]
- Sheng, M.; Peng, D.; Peng, H.; Zhang, Y.; Xiao, L.; Zhang, M.; Wang, S.; Zhao, C.; Zhu, S.; Lu, J. Effective substances and molecular mechanisms guided by network pharmacology: An example study of Scrophulariae Radix treatment of hyperthyroidism and thyroid hormone-induced liver and kidney injuries. J. Ethnopharmacol. 2024, 326, 117965. [Google Scholar] [CrossRef]
- Wang, X. Study on the Grouping Pattern and Mechanism of Cooling Blood and Draining Liver Herbs in the Reatment of 200 Patients with Hyperthyroidism. Master’s Thesis, Shandong University of Traditional Chinese Medicine, Jinan, China, 2023. [Google Scholar]
- Stelzer, G.; Rosen, N.; Plaschkes, I.; Zimmerman, S.; Twik, M.; Fishilevich, S.; Stein, T.I.; Nudel, R.; Lieder, I.; Mazor, Y. The GeneCards suite: From gene data mining to disease genome sequence analyses. Curr. Protoc. Bioinform. 2016, 54, 1.30.1–1.30.33. [Google Scholar] [CrossRef]
- Suárez-Varela, J.; Almasan, P.; Ferriol-Galmés, M.; Rusek, K.; Geyer, F.; Cheng, X.; Shi, X.; Xiao, S.; Scarselli, F.; Cabellos-Aparicio, A. Graph neural networks for communication networks: Context, use cases and opportunities. IEEE Netw. 2022, 37, 146–153. [Google Scholar] [CrossRef]
- Solovyev, R.A.; Mkrtchan, I.A.; Telpukhov, D.V.; Shafeev, I.I.; Romanov, A.Y.; Stolbikov, Y.V.; Stempkovsky, A.L. PAGR: Accelerating Global Routing for VLSI Design Flow. IEEE Access 2025, 13, 6440–6450. [Google Scholar] [CrossRef]
- Kumar, S.; Mallik, A.; Khetarpal, A.; Panda, B.S. Influence maximization in social networks using graph embedding and graph neural network. Inf. Sci. 2022, 607, 1617–1636. [Google Scholar] [CrossRef]


| Model | AUC | AUPR | Precision | F1-Score | |
|---|---|---|---|---|---|
| Similarity-based | NEDTP | 0.9227 (±0.0153) | 0.9612 (±0.0227) | 0.8928 (±0.0354) | 0.8618 (±0.0259) |
| MultiDTI | 0.9590 (±0.0126) | 0.9460 (±0.0253) | 0.9263 (±0.0287) | 0.8178 (±0.0304) | |
| GNN-based | NeoDTI | 0.9582 (±0.0149) | 0.8745 (±0.0406) | 0.8609 (±0.0423) | 0.8218 (±0.0281) |
| IMCHGAN | 0.9705 (±0.0107) | 0.8988 (±0.0352) | 0.8974 (±0.0226) | 0.8252 (±0.0273) | |
| SGCL-DTI | 0.9240 (±0.0162) | 0.9551 (±0.0218) | 0.9185 (±0.0309) | 0.9354 (±0.0156) | |
| EEG-DTI | 0.9545 (±0.0134) | 0.9641 (±0.0185) | 0.9162 (±0.0293) | 0.8265 (±0.0277) | |
| / | MAMGN-HTI | 0.9776 (±0.0096) | 0.9618 (±0.0202) | 0.9278 (±0.0257) | 0.9507 (±0.0137) |
| Methods | AUC | AUPR | Precision | F1-Score | |
|---|---|---|---|---|---|
| Metapath | HH | 0.9621 (±0.0123) | 0.9435 (±0.0235) | 0.9012 (±0.0312) | 0.9273 (±0.0187) |
| HIH | 0.9518 (±0.0137) | 0.9304 (±0.0251) | 0.8889 (±0.0330) | 0.9124 (±0.0205) | |
| HTTH | 0.9285 (±0.0162) | 0.9012 (±0.0295) | 0.8623 (±0.0367) | 0.8856 (±0.0231) | |
| HTITH | 0.9157 (±0.0175) | 0.8826 (±0.0322) | 0.8431 (±0.0385) | 0.8682 (±0.0246) | |
| Network | Herb–Target | 0.9064 (±0.0181) | 0.8723 (±0.0340) | 0.8327 (±0.0410) | 0.8589 (±0.0265) |
| Herb–Ingredient | 0.9639 (±0.0118) | 0.9481 (±0.0228) | 0.9127 (±0.0305) | 0.9372 (±0.0178) | |
| Herb–Efficacy | 0.9685 (±0.0109) | 0.9532 (±0.0219) | 0.9201 (±0.0280) | 0.9445 (±0.0165) | |
| Target–Target | 0.9352 (±0.0148) | 0.9108 (±0.0275) | 0.8745 (±0.0355) | 0.8996 (±0.0212) | |
| Skip_Connection | ResGCN | 0.9283 (±0.0160) | 0.9021 (±0.0298) | 0.8614 (±0.0372) | 0.8847 (±0.0230) |
| DenseGCN | 0.9527 (±0.0129) | 0.9316 (±0.0249) | 0.8912 (±0.0321) | 0.9158 (±0.0192) | |
| ResGCN + DenseGCN | 0.8992 (±0.0195) | 0.8614 (±0.0360) | 0.8216 (±0.0415) | 0.8483 (±0.0280) | |
| / | MAMGN-HTI_all | 0.9776 (±0.0096) | 0.9618 (±0.0202) | 0.9278 (±0.0257) | 0.9507 (±0.0137) |
| Herb | Rank | Target | Result | Rank | Target | Result |
|---|---|---|---|---|---|---|
| Salvia miltiorrhiza | 1 | ACHE | T | 6 | EIF6 | T |
| 2 | CCND1 | T | 7 | CES2 | F | |
| 3 | CASP3 | T | 8 | HERC5 | T | |
| 4 | ADRB3 | T | 9 | MAOB | T | |
| 5 | CYP1A2 | T | 10 | CASP8 | T | |
| Glehnia littoralis | 1 | ASIC2 | T | 6 | HIF1A | T |
| 2 | ASIC1 | T | 7 | ADK | F | |
| 3 | ACTB | T | 8 | AHCY | T | |
| 4 | ADA | T | 9 | PTGS2 | T | |
| 5 | ADAR | T | 10 | PTGS1 | T | |
| Coptis chinensis | 1 | ADRA2A | T | 6 | CCND1 | T |
| 2 | ADRB1 | T | 7 | PRSS1 | T | |
| 3 | ADRB3 | T | 8 | MAOB | T | |
| 4 | PTGS2 | T | 9 | TNF | T | |
| 5 | PM20D2 | T | 10 | TP53COR1 | T | |
| Astragalus membranaceus | 1 | PTGS1 | T | 6 | KSR2 | T |
| 2 | RTP1 | T | 7 | F8A1 | T | |
| 3 | PRSS1 | T | 8 | Topbp1-ps1 | T | |
| 4 | RXRA | T | 9 | ICAM1 | T | |
| 5 | ACP4 | T | 10 | Ccpg1os | T | |
| Agastache rugosa | 1 | CHRM1 | T | 6 | PM20D2 | T |
| 2 | PTGS2 | T | 7 | PTGS1 | T | |
| 3 | SLC6A2 | T | 8 | RXRA | T | |
| 4 | DHTKD1 | T | 9 | BCL2 | T | |
| 5 | ACP4 | T | 10 | BAX | T |
| Herb | Rank | Target | Verify_source | Evidence |
|---|---|---|---|---|
| Vinegar-processed Bupleuri Radix | 1 | P2RY12 | Li et al. [36] | — |
| 2 | SRD5A2 | ETCM (V2.0) | — | |
| 3 | CASP3 | Herb (V2.0) | — | |
| Prunellae Spica | 1 | HIF1A | ETCM (V2.0) | GeneCards |
| 2 | IL6 | Qin et al. [37] | GeneCards | |
| 3 | CCND1 | Herb (V2.0) | — | |
| Processed Cyperi Rhizoma | 1 | NOS2 | TCMSP | — |
| 2 | SOD1 | Herb (V2.0) | GeneCards | |
| 3 | FABP1 | ETCM (V2.0) | — | |
| Citrus Reticulata Pericarpium | 1 | TP53 | Huang et al. [34] | GeneCards |
| 2 | TNF | Herb (V2.0) | GeneCards | |
| 3 | CNR2 | ETCM (V2.0) | — | |
| Ophiopogonis Radix | 1 | ADA | ETCM (V2.0) | GeneCards |
| 2 | STAT3 | Li et al. [35] | GeneCards | |
| 3 | TP53 | — | GeneCards | |
| Scrophulariae Radix | 1 | AKT1 | Sheng et al. [38] | GeneCards |
| 2 | PRKAA1 | Herb (V2.0) | — | |
| 3 | TRPV1 | ETCM (V2.0) | — | |
| Moutan Cortex | 1 | CYP1B1 | ETCM (V2.0) | — |
| 2 | IL6 | Herb (V2.0) | GeneCards | |
| 3 | CD14 | — | — | |
| Rehmanniae Radix | 1 | IL6 | Herb (V2.0) | GeneCards |
| 2 | VCP | — | — | |
| 3 | PLA2G1B | ETCM (V2.0) | — |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Yang, X.; Lv, R.; Lang, X.; Zhu, Y.; Zhou, Z.; She, K. MAMGN-HTI: A Graph Neural Network Model with Metapath and Attention Mechanisms for Hyperthyroidism Herb–Target Interaction Prediction. Bioengineering 2025, 12, 1085. https://doi.org/10.3390/bioengineering12101085
Zhou Y, Yang X, Lv R, Lang X, Zhu Y, Zhou Z, She K. MAMGN-HTI: A Graph Neural Network Model with Metapath and Attention Mechanisms for Hyperthyroidism Herb–Target Interaction Prediction. Bioengineering. 2025; 12(10):1085. https://doi.org/10.3390/bioengineering12101085
Chicago/Turabian StyleZhou, Yanqin, Xiaona Yang, Ru Lv, Xufeng Lang, Yao Zhu, Zuojian Zhou, and Kankan She. 2025. "MAMGN-HTI: A Graph Neural Network Model with Metapath and Attention Mechanisms for Hyperthyroidism Herb–Target Interaction Prediction" Bioengineering 12, no. 10: 1085. https://doi.org/10.3390/bioengineering12101085
APA StyleZhou, Y., Yang, X., Lv, R., Lang, X., Zhu, Y., Zhou, Z., & She, K. (2025). MAMGN-HTI: A Graph Neural Network Model with Metapath and Attention Mechanisms for Hyperthyroidism Herb–Target Interaction Prediction. Bioengineering, 12(10), 1085. https://doi.org/10.3390/bioengineering12101085






