The Optimal Fibular Strut Bone Graft Fixation Angle for Unstable Proximal Humerus Fractures: A Finite Element Analysis
Abstract
1. Introduction
2. Materials and Methods
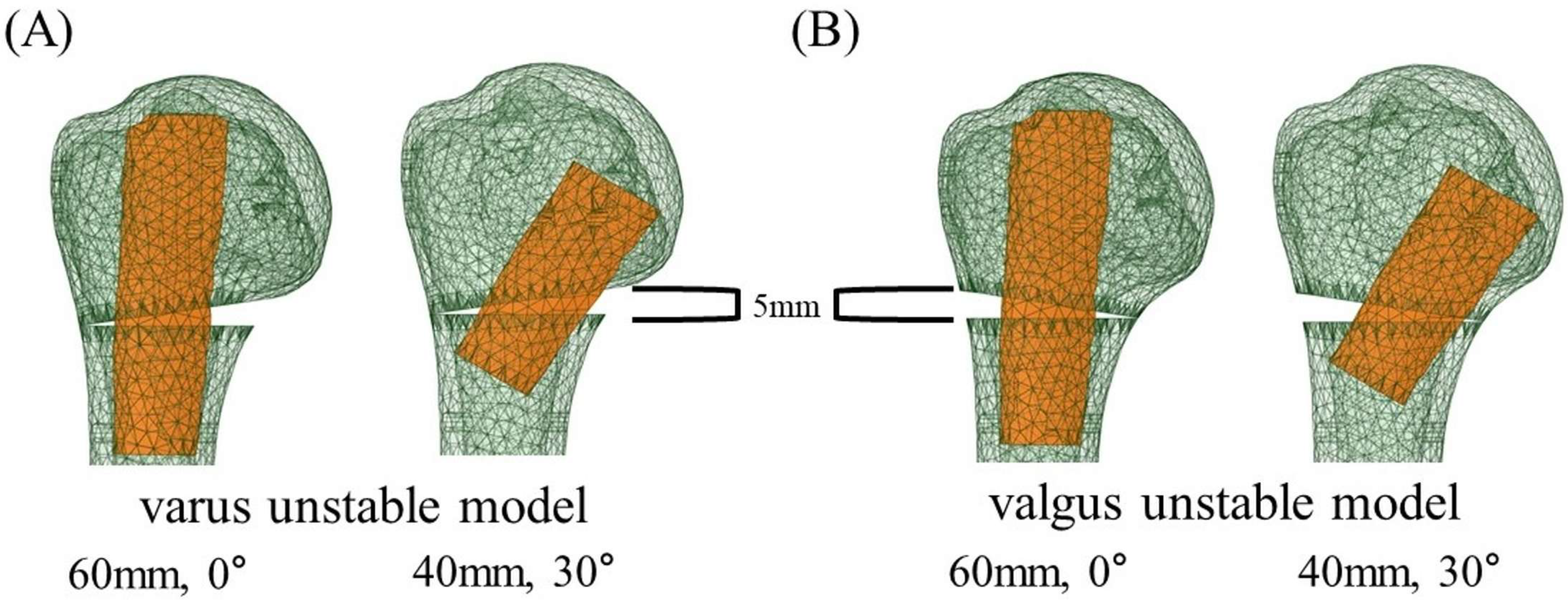
2.1. Finite Element Models (FEM)
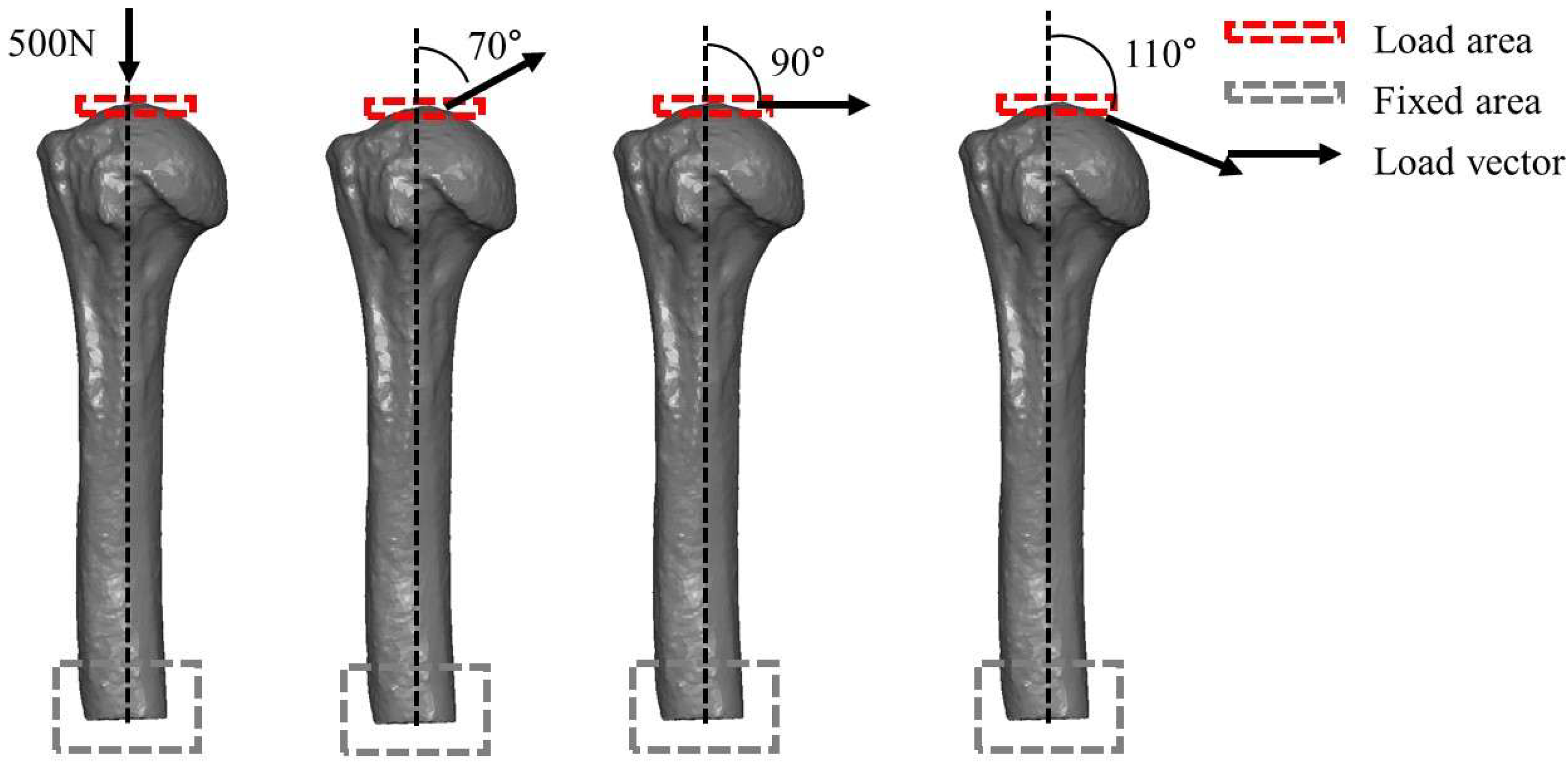
2.2. Finite Element Assessment (FEA)
3. Results
3.1. Von Mises Stress in the Plate and Maximum Principal Stress in the Fibular Graft in the Varus Unstable (Medial Wedge-Out) Model
3.2. Von Mises Stress in the Plate and Maximum Principal Stress in the Fibular Graft in the Valgus Unstable (Lateral Wedge-Out) Model
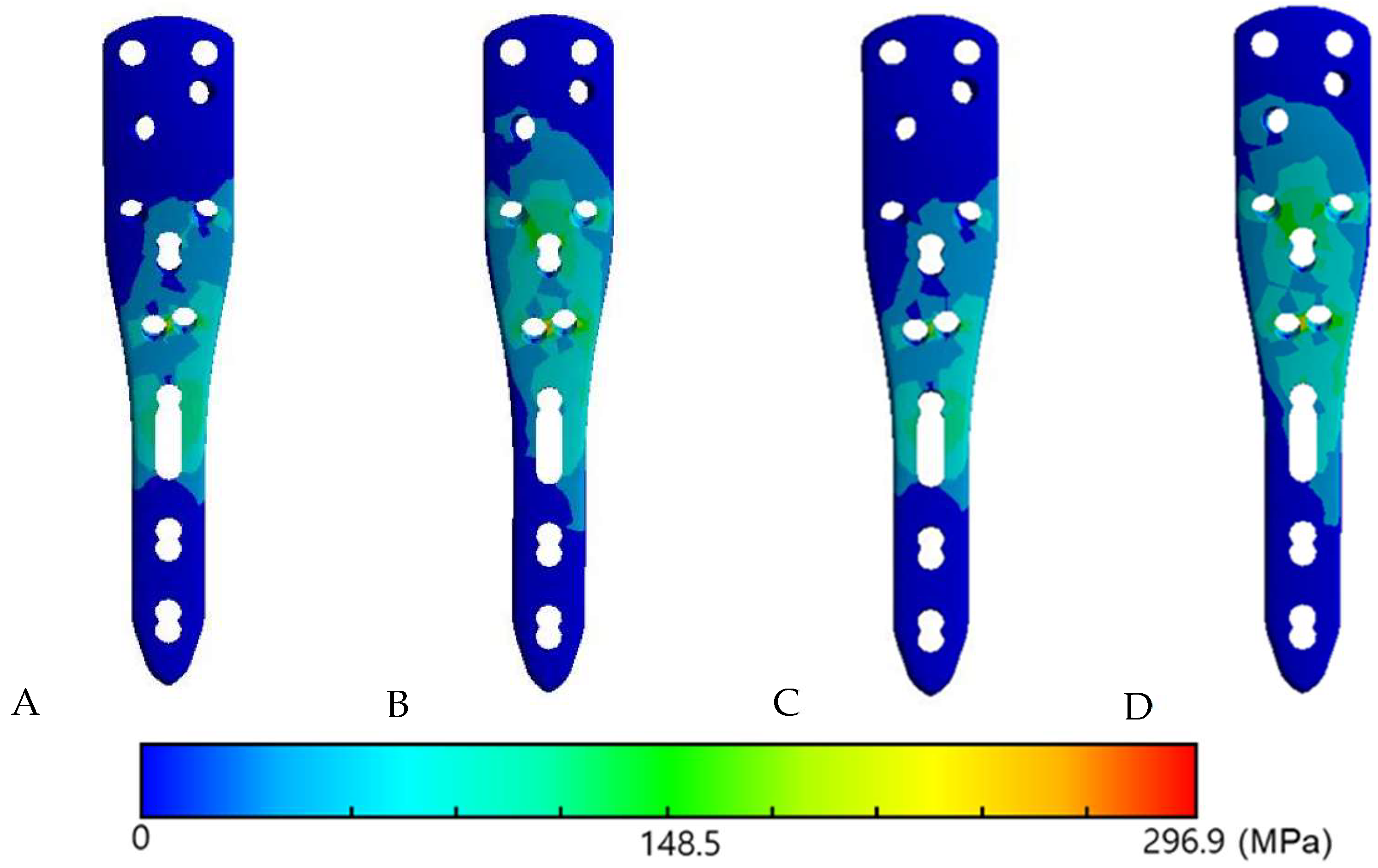
3.3. The Von Mises Stress Distribution on Contact Surface
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Handoll, H.H.; Brorson, S. Interventions for treating proximal humeral fractures in adults. Cochrane Database Syst. Rev. 2015, 11, CD000434. [Google Scholar] [CrossRef]
- Koa, J.; Fares, M.Y.; Daher, M.; Abboud, J.A. Assessment of therapeutic clinical trials for proximal humeral fractures. Clin. Shoulder Elb. 2024, 27, 237–246. [Google Scholar] [CrossRef]
- Kim, D.Y.; Kim, T.Y.; Hwang, J.T. PHILOS plate fixation with polymethyl methacrylate cement augmentation of an osteoporotic proximal humerus fracture. Clin. Shoulder Elb. 2020, 23, 156–158. [Google Scholar] [CrossRef]
- Kim, J.Y.; Lee, J.; Kim, S.H. Comparison between MIPO and the deltopectoral approach with allogenous fibular bone graft in proximal humeral fractures. Clin. Shoulder Elb. 2020, 23, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Claro, R.; Barros, B.; Ferreira, C.; Ribau, A.; Barros, L.H. Comparative analysis of proximal humerus fracture management in elderly patients: Complications of open reduction and internal fixation by shoulder surgeons and non-shoulder surgeons-a retrospective study. Clin. Shoulder Elb. 2024, 27, 32–38. [Google Scholar] [CrossRef] [PubMed]
- Baron, J.A.; Barrett, J.A.; Karagas, M.R. The epidemiology of peripheral fractures. Bone 1996, 18, 209S–213S. [Google Scholar] [CrossRef]
- Kim, S.C.; Yoo, J.C.; Park, J.H.; Bukhary, H.; Choi, Y.S.; Kang, K.T.; Kim, C.H. Changes in Shoulder Trauma during the COVID-19 Pandemic: A South Korean Survey. Clin. Orthop. Surg. 2023, 15, 300–307. [Google Scholar] [CrossRef]
- Patel, A.H.; Wilder, J.H.; Ofa, S.A.; Lee, O.C.; Iloanya, M.C.; Savoie, F.H., 3rd; Sherman, W.F. How age and gender influence proximal humerus fracture management in patients older than fifty years. JSES Int. 2022, 6, 253–258. [Google Scholar] [CrossRef]
- Iglesias-Rodriguez, S.; Dominguez-Prado, D.M.; Garcia-Reza, A.; Fernandez-Fernandez, D.; Perez-Alfonso, E.; Garcia-Pineiro, J.; Castro-Menendez, M. Epidemiology of proximal humerus fractures. J. Orthop. Surg. Res. 2021, 16, 402. [Google Scholar] [CrossRef]
- Konrad, G.; Bayer, J.; Hepp, P.; Voigt, C.; Oestern, H.; Kaab, M.; Luo, C.; Plecko, M.; Wendt, K.; Kostler, W.; et al. Open reduction and internal fixation of proximal humeral fractures with use of the locking proximal humerus plate. Surgical technique. J. Bone Jt. Surg. Am. 2010, 92 Pt 1 (Suppl. S1), 85–95. [Google Scholar] [CrossRef] [PubMed]
- Solberg, B.D.; Moon, C.N.; Franco, D.P.; Paiement, G.D. Locked plating of 3- and 4-part proximal humerus fractures in older patients: The effect of initial fracture pattern on outcome. J. Orthop. Trauma 2009, 23, 113–119. [Google Scholar] [CrossRef]
- Hardeman, F.; Bollars, P.; Donnelly, M.; Bellemans, J.; Nijs, S. Predictive factors for functional outcome and failure in angular stable osteosynthesis of the proximal humerus. Injury 2012, 43, 153–158. [Google Scholar] [CrossRef]
- Gardner, M.J.; Boraiah, S.; Helfet, D.L.; Lorich, D.G. Indirect medial reduction and strut support of proximal humerus fractures using an endosteal implant. J. Orthop. Trauma 2008, 22, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Bae, J.H.; Oh, J.K.; Chon, C.S.; Oh, C.W.; Hwang, J.H.; Yoon, Y.C. The biomechanical performance of locking plate fixation with intramedullary fibular strut graft augmentation in the treatment of unstable fractures of the proximal humerus. J. Bone Jt. Surg. Br. 2011, 93, 937–941. [Google Scholar] [CrossRef]
- Osterhoff, G.; Baumgartner, D.; Favre, P.; Wanner, G.A.; Gerber, H.; Simmen, H.P.; Werner, C.M. Medial support by fibula bone graft in angular stable plate fixation of proximal humeral fractures: An in vitro study with synthetic bone. J. Shoulder Elb. Surg. 2011, 20, 740–746. [Google Scholar] [CrossRef]
- Hinds, R.M.; Garner, M.R.; Tran, W.H.; Lazaro, L.E.; Dines, J.S.; Lorich, D.G. Geriatric proximal humeral fracture patients show similar clinical outcomes to non-geriatric patients after osteosynthesis with endosteal fibular strut allograft augmentation. J. Shoulder Elb. Surg. 2015, 24, 889–896. [Google Scholar] [CrossRef]
- Little, M.T.; Berkes, M.B.; Schottel, P.C.; Lazaro, L.E.; LaMont, L.E.; Pardee, N.C.; Nguyen, J.T.; Helfet, D.L.; Lorich, D.G. The impact of preoperative coronal plane deformity on proximal humerus fixation with endosteal augmentation. J. Orthop. Trauma 2014, 28, 338–347. [Google Scholar] [CrossRef] [PubMed]
- Matassi, F.; Angeloni, R.; Carulli, C.; Civinini, R.; Di Bella, L.; Redl, B.; Innocenti, M. Locking plate and fibular allograft augmentation in unstable fractures of proximal humerus. Injury 2012, 43, 1939–1942. [Google Scholar] [CrossRef] [PubMed]
- Neviaser, A.S.; Hettrich, C.M.; Beamer, B.S.; Dines, J.S.; Lorich, D.G. Endosteal strut augment reduces complications associated with proximal humeral locking plates. Clin. Orthop. Relat. Res. 2011, 469, 3300–3306. [Google Scholar] [CrossRef]
- Tan, E.; Lie, D.; Wong, M.K. Early outcomes of proximal humerus fracture fixation with locking plate and intramedullary fibular strut graft. Orthopedics 2014, 37, e822–e827. [Google Scholar] [CrossRef]
- Kim, D.S.; Lee, D.H.; Chun, Y.M.; Shin, S.J. Which additional augmented fixation procedure decreases surgical failure after proximal humeral fracture with medial comminution: Fibular allograft or inferomedial screws? J. Shoulder Elb. Surg. 2018, 27, 1852–1858. [Google Scholar] [CrossRef]
- Lee, J.W.; Song, M.J.; Lee, S.J.; Song, H.S.; Jung, Y.S.; Kim, H. Biomechanical comparison between low profile 2.7 mm distal locking hook plate and 3.5 mm distal locking hook plate for acromioclavicular joint injury: A finite element analysis. Injury 2024, 55, 111657. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Chung, Y.G.; Jang, J.S.; Kim, Y.; Park, S.B.; Song, H.S. Why locking plates for the proximal humerus do not fit well. Arch. Orthop. Trauma Surg. 2022, 142, 219–226. [Google Scholar] [CrossRef]
- Hosoyama, T.; Kaku, N.; Pramudita, J.A.; Shibuta, Y. Comparison of Early Postoperative Stress Distribution around Short and Tapered Wedge Stems in Femurs with Different Femoral Marrow Cavity Geometries Using Finite Element Analysis. Clin. Orthop. Surg. 2024, 16, 724–732. [Google Scholar] [CrossRef]
- Tseng, J.; Huang, B.; Liang, S.; Yen, K.; Tsai, Y.; Tseng, J. Normal mode analysis of a human fibula. Life Sci. J. 2014, 11, 711–718. [Google Scholar]
- Zhang, Q.H.; Tan, S.H.; Chou, S.M. Effects of bone materials on the screw pull-out strength in human spine. Med. Eng. Phys. 2006, 28, 795–801. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.-H.; Chen, W.-C.; Lin, K.-J.; Lin, K.-P.; Tsai, C.-L.; Wei, H.-W. Effect of semi-rigid locking screws on the stiffness of a fracture-fixation construct: A conceptual finite-element study. Adv. Mech. Eng. 2019, 11, 1687814019854577. [Google Scholar] [CrossRef]
- Yang, P.; Zhang, Y.; Liu, J.; Xiao, J.; Ma, L.M.; Zhu, C.R. Biomechanical effect of medial cortical support and medial screw support on locking plate fixation in proximal humeral fractures with a medial gap: A finite element analysis. Acta Orthop. Traumatol. Turc. 2015, 49, 203–209. [Google Scholar] [CrossRef]
- Fletcher, J.W.A.; Windolf, M.; Richards, R.G.; Gueorguiev, B.; Varga, P. Screw configuration in proximal humerus plating has a significant impact on fixation failure risk predicted by finite element models. J. Shoulder Elb. Surg. 2019, 28, 1816–1823. [Google Scholar] [CrossRef]
- Hirschmann, M.T.; Fallegger, B.; Amsler, F.; Regazzoni, P.; Gross, T. Clinical longer-term results after internal fixation of proximal humerus fractures with a locking compression plate (PHILOS). J. Orthop. Trauma 2011, 25, 286–293. [Google Scholar] [CrossRef]
- Launonen, A.P.; Lepola, V.; Flinkkila, T.; Laitinen, M.; Paavola, M.; Malmivaara, A. Treatment of proximal humerus fractures in the elderly: A systemic review of 409 patients. Acta Orthop. 2015, 86, 280–285. [Google Scholar] [CrossRef]
- Fares, M.Y.; Singh, J.; Boufadel, P.; Cohn, M.R.; Abboud, J.A. Pyrocarbon hemiarthroplasty and the shoulder: Biomechanical and clinical results of an emerging treatment option. Clin. Shoulder Elb. 2024, 27, 117–125. [Google Scholar] [CrossRef]
- Haikal, E.R.; Fares, M.Y.; Abboud, J.A. Patient-specific implants in reverse shoulder arthroplasty. Clin. Shoulder Elb. 2024, 27, 108–116. [Google Scholar] [CrossRef]
- Gardner, M.J.; Weil, Y.; Barker, J.U.; Kelly, B.T.; Helfet, D.L.; Lorich, D.G. The importance of medial support in locked plating of proximal humerus fractures. J. Orthop. Trauma 2007, 21, 185–191. [Google Scholar] [CrossRef]
- Bai, L.; Fu, Z.; An, S.; Zhang, P.; Zhang, D.; Jiang, B. Effect of Calcar Screw Use in Surgical Neck Fractures of the Proximal Humerus With Unstable Medial Support: A Biomechanical Study. J. Orthop. Trauma 2014, 28, 452–457. [Google Scholar] [CrossRef] [PubMed]
- Jung, W.B.; Moon, E.S.; Kim, S.K.; Kovacevic, D.; Kim, M.S. Does medial support decrease major complications of unstable proximal humerus fractures treated with locking plate? BMC Musculoskelet. Disord. 2013, 14, 102. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zheng, J.; Wang, W.; Lin, G.; Huang, Y.; Zheng, J.; Edem Prince, G.A.; Yang, G. The clinical benefit of medial support screws in locking plating of proximal humerus fractures: A prospective randomized study. Int. Orthop. 2011, 35, 1655–1661. [Google Scholar] [CrossRef]
- Zhang, W.; Zeng, L.; Liu, Y.; Pan, Y.; Zhang, W.; Zhang, C.; Zeng, B.; Chen, Y. The mechanical benefit of medial support screws in locking plating of proximal humerus fractures. PLoS ONE 2014, 9, e103297. [Google Scholar] [CrossRef] [PubMed]
- Robinson, C.M.; Page, R.S. Severely impacted valgus proximal humeral fractures. J. Bone Jt. Surg. Am. 2004, 86 (Suppl. S1), 143–155. [Google Scholar] [CrossRef]
- Scheidt, M.D.; Aiyash, S.; Salazar, D.; Garbis, N. Core decompression for early-stage avascular necrosis of the humeral head: Current concepts and techniques. Clin. Shoulder Elb. 2023, 26, 191–204. [Google Scholar] [CrossRef]
- DeFranco, M.J.; Brems, J.J.; Williams, G.R., Jr.; Iannotti, J.P. Evaluation and management of valgus impacted four-part proximal humerus fractures. Clin. Orthop. Relat. Res. 2006, 442, 109–114. [Google Scholar] [CrossRef]
- Walch, G.; Badet, R.; Nove-Josserand, L.; Levigne, C. Nonunions of the surgical neck of the humerus: Surgical treatment with an intramedullary bone peg, internal fixation, and cancellous bone grafting. J. Shoulder Elb. Surg. 1996, 5, 161–168. [Google Scholar] [CrossRef]
- Lee, S.J.; Hyun, Y.S.; Baek, S.H. Strut Support with Tricortical Iliac Allografts in Unstable Proximal Humerus Fractures: Surgical Indication and New Definition of Poor Medial Column Support. Clin. Shoulder Elb. 2019, 22, 29–36. [Google Scholar] [CrossRef]
- Myers, D.M.; Triplet, J.J.; Warmoth, P.J.; Passias, B.J.; McGowan, S.P.; Taylor, B.C. Improved Outcomes Using a Fibular Strut in Proximal Humerus Fracture Fixation. Orthopedics 2020, 43, 262–268. [Google Scholar] [CrossRef]
- Tuerxun, M.; Tuxun, A.; Zeng, L.; Wang, Q.; Chen, Y. Locking Plate Combined With Endosteal Fibular Allograft Augmentation for Medial Column Comminuted Proximal Humeral Fracture. Orthopedics 2020, 43, 367–372. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Wei, H.W.; Lin, K.P.; Chen, W.C.; Tsai, C.L.; Lin, K.J. Biomechanical effect of the configuration of screw hole style on locking plate fixation in proximal humerus fracture with a simulated gap: A finite element analysis. Injury 2016, 47, 1191–1195. [Google Scholar] [CrossRef]
- Kim, H.; Lee, W.; Choi, S.; Kholinne, E.; Lee, E.; Alzahrani, W.M.; Koh, K.H.; Jeon, I.H.; Kim, S. Role of Additional Inferomedial Supporting Screws in Osteoporotic 3-Part Proximal Humerus Fracture: Finite Element Analysis. Geriatr. Orthop. Surg. Rehabil. 2020, 11, 2151459320956958. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhu, Z.G.; Li, J.T.; Chang, Z.H.; Tang, P.F. Finite element analysis of an intramedulary anatomical strut for proximal humeral fractures with disrupted medial column instability: A cohort study. Int. J. Surg. 2020, 73, 50–56. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Zhang, Y.; Wang, Y.; Zhou, D.; Wang, F. Biomechanical evaluation of a novel dualplate fixation method for proximal humeral fractures without medial support. J. Orthop. Surg. Res. 2017, 12, 72. [Google Scholar] [CrossRef]
- Chow, R.M.; Begum, F.; Beaupre, L.A.; Carey, J.P.; Adeeb, S.; Bouliane, M.J. Proximal humeral fracture fixation: Locking plate construct +/− intramedullary fibular allograft. J. Shoulder Elb. Surg. 2012, 21, 894–901. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, J.W.A.; Windolf, M.; Grunwald, L.; Richards, R.G.; Gueorguiev, B.; Varga, P. The influence of screw length on predicted cut-out failures for proximal humeral fracture fixations predicted by finite element simulations. Arch. Orthop. Trauma Surg. 2019, 139, 1069–1074. [Google Scholar] [CrossRef] [PubMed]

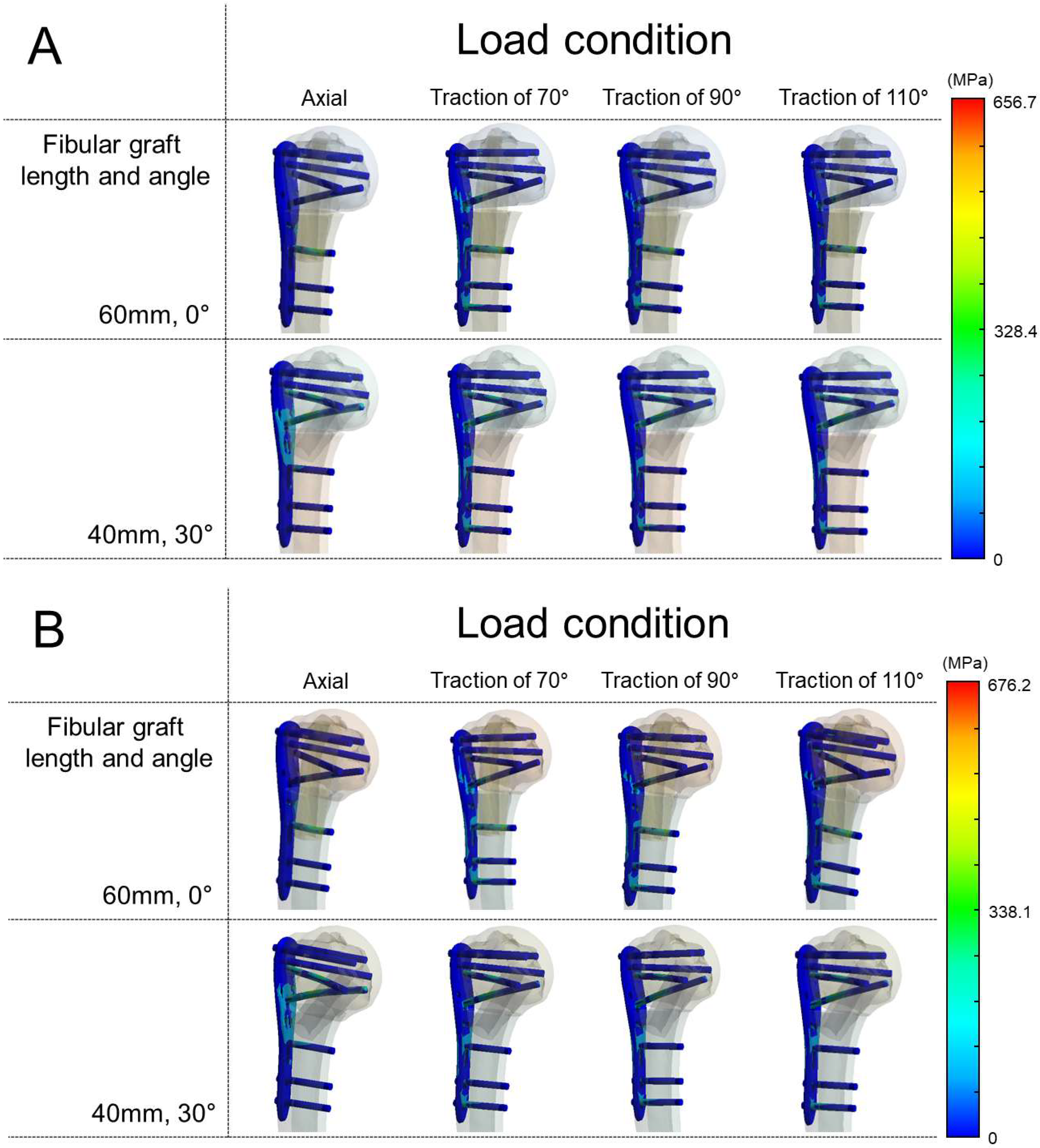
| Axial Load | Traction at 70° | Traction at 90° | Traction at 110° | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plate | Screw | Humerus | Fibula | Plate | Screw | Humerus | Fibula | Plate | Screw | Humerus | Fibula | Plate | Screw | Humerus | Fibula | |
| Vertical | 48.1 | 148.9 | 40.6 | 28.5 | 268.6 | 516.5 | 159.4 | 121.0 | 295.8 | 622.4 | 187.7 | 150.7 | 294.6 | 656.7 | 198.1 | 160.0 |
| Oblique | 60.7 | 134.0 | 136.6 | 91.7 | 26.8 | 540.6 | 260.9 | 186.0 | 59.4 | 611.0 | 322.0 | 67.5 | 287.1 | 618.9 | 346.6 | 68.5 |
| Axial load | Traction at 70° | Traction at 90° | Traction at 110° | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plate | Screw | Humerus | Fibula | Plate | Screw | Humerus | Fibula | Plate | Screw | Humerus | Fibula | Plate | Screw | Humerus | Fibula | |
| Vertical | 44.6 | 145.4 | 47.2 | 37.0 | 270.3 | 494.6 | 182.8 | 140.0 | 296.9 | 591.5 | 216.3 | 175.6 | 290.8 | 623.8 | 221.51 | 185.1 |
| Oblique | 66.9 | 165.5 | 174.5 | 30.5 | 259.0 | 589.4 | 284.1 | 68.8 | 289.2 | 671.3 | 366.7 | 79.1 | 285.1 | 676.2 | 369.4 | 80.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.S.; Gong, H.-G.; Lee, H.-J.; Kim, H.; Tae, K.-S. The Optimal Fibular Strut Bone Graft Fixation Angle for Unstable Proximal Humerus Fractures: A Finite Element Analysis. Bioengineering 2025, 12, 1078. https://doi.org/10.3390/bioengineering12101078
Song HS, Gong H-G, Lee H-J, Kim H, Tae K-S. The Optimal Fibular Strut Bone Graft Fixation Angle for Unstable Proximal Humerus Fractures: A Finite Element Analysis. Bioengineering. 2025; 12(10):1078. https://doi.org/10.3390/bioengineering12101078
Chicago/Turabian StyleSong, Hyun Seok, Hui-Gyeong Gong, Hyun-Ju Lee, Hyungsuk Kim, and Ki-Sik Tae. 2025. "The Optimal Fibular Strut Bone Graft Fixation Angle for Unstable Proximal Humerus Fractures: A Finite Element Analysis" Bioengineering 12, no. 10: 1078. https://doi.org/10.3390/bioengineering12101078
APA StyleSong, H. S., Gong, H.-G., Lee, H.-J., Kim, H., & Tae, K.-S. (2025). The Optimal Fibular Strut Bone Graft Fixation Angle for Unstable Proximal Humerus Fractures: A Finite Element Analysis. Bioengineering, 12(10), 1078. https://doi.org/10.3390/bioengineering12101078







