Attention-Fusion-Based Two-Stream Vision Transformer for Heart Sound Classification
Abstract
1. Introduction
- We propose an efficient AFTViT architecture that effectively learns signal representations from features at different resolutions. By leveraging multi-resolution features, the proposed approach addresses the limitations of single-scale representations, thereby improving the accuracy of HSC.
- A distinctive attention fusion block (AFB) is introduced to integrate the feature representations derived from the small-patch ViT branch and the large-patch ViT branch. Additionally, we evaluate the importance of the proposed AFB by evaluating it against traditional techniques, demonstrating its superiority in achieving robust classification performance.
- We assess the performance of our proposed method on two widely used datasets to validate the effectiveness of the dual-branch approach. The results reveal that the proposed AFTViT outperforms the baseline CNN models and state-of-the-art approaches while maintaining significantly lower parameters because of its efficient design.
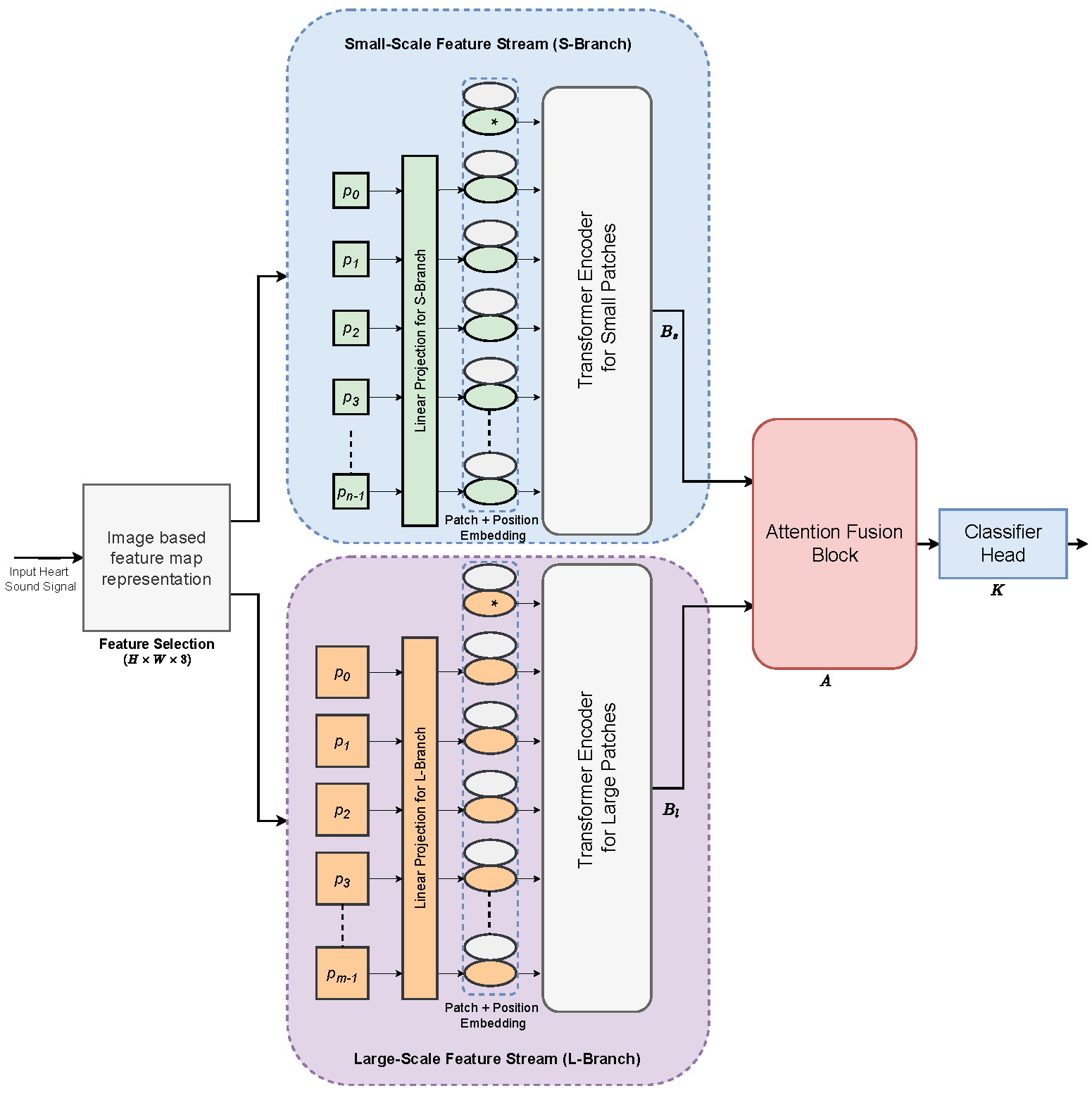
2. Proposed AFTViT Architecture
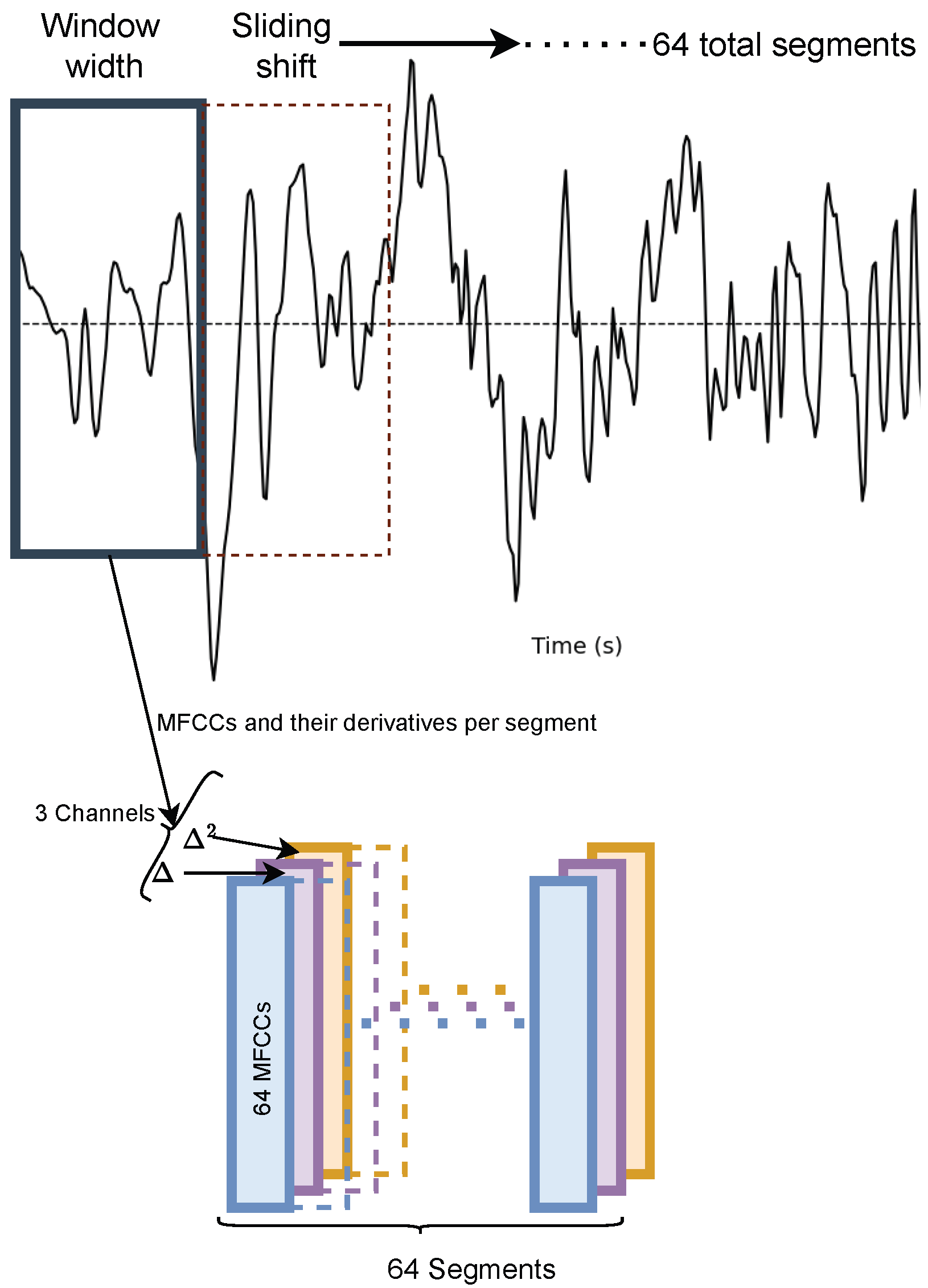
2.1. Feature Selection
2.2. Two-Stream Vision Transformers Framework
2.2.1. Patch Embedding and Positional Encoding
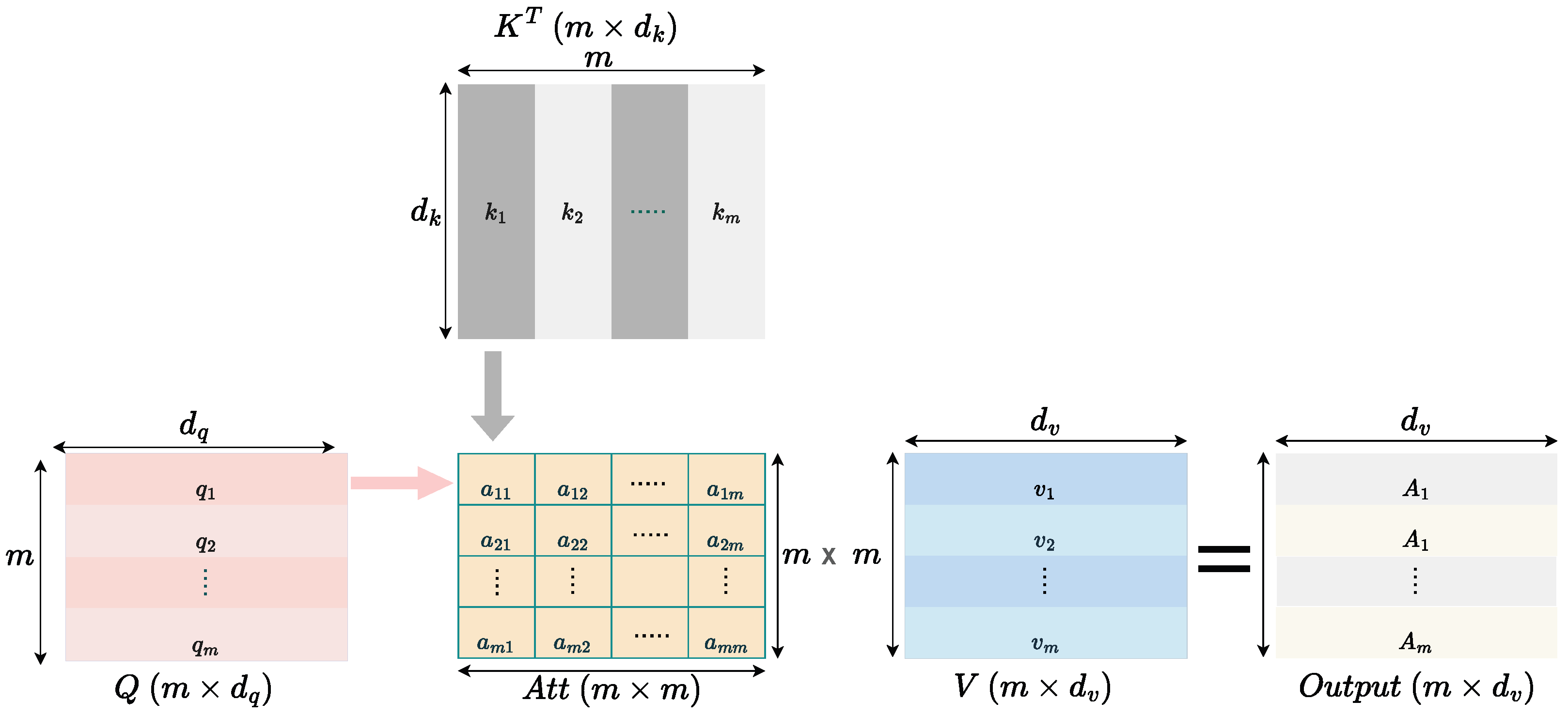
2.2.2. Understanding Self-Attention
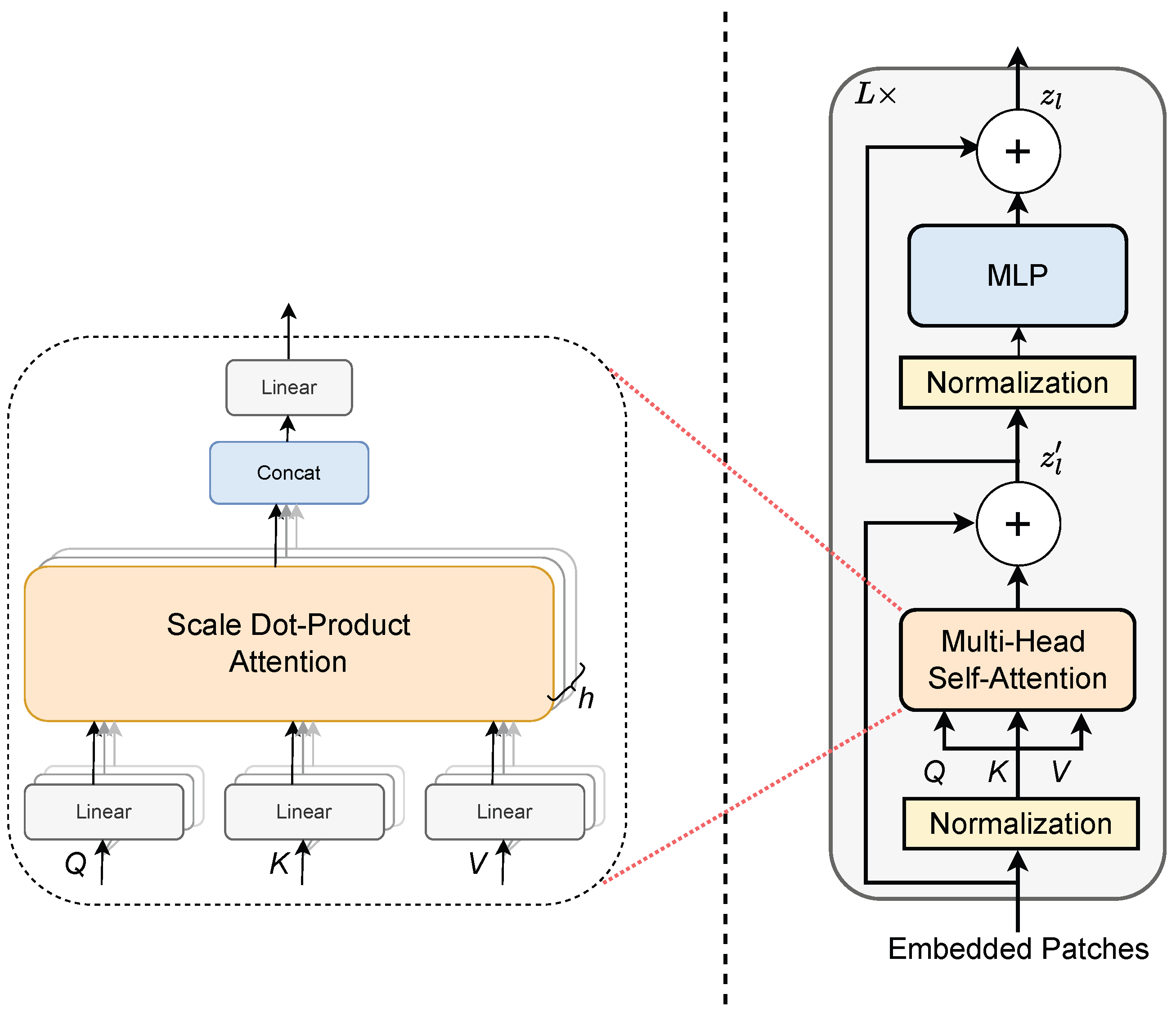
2.2.3. Transformer Encoder
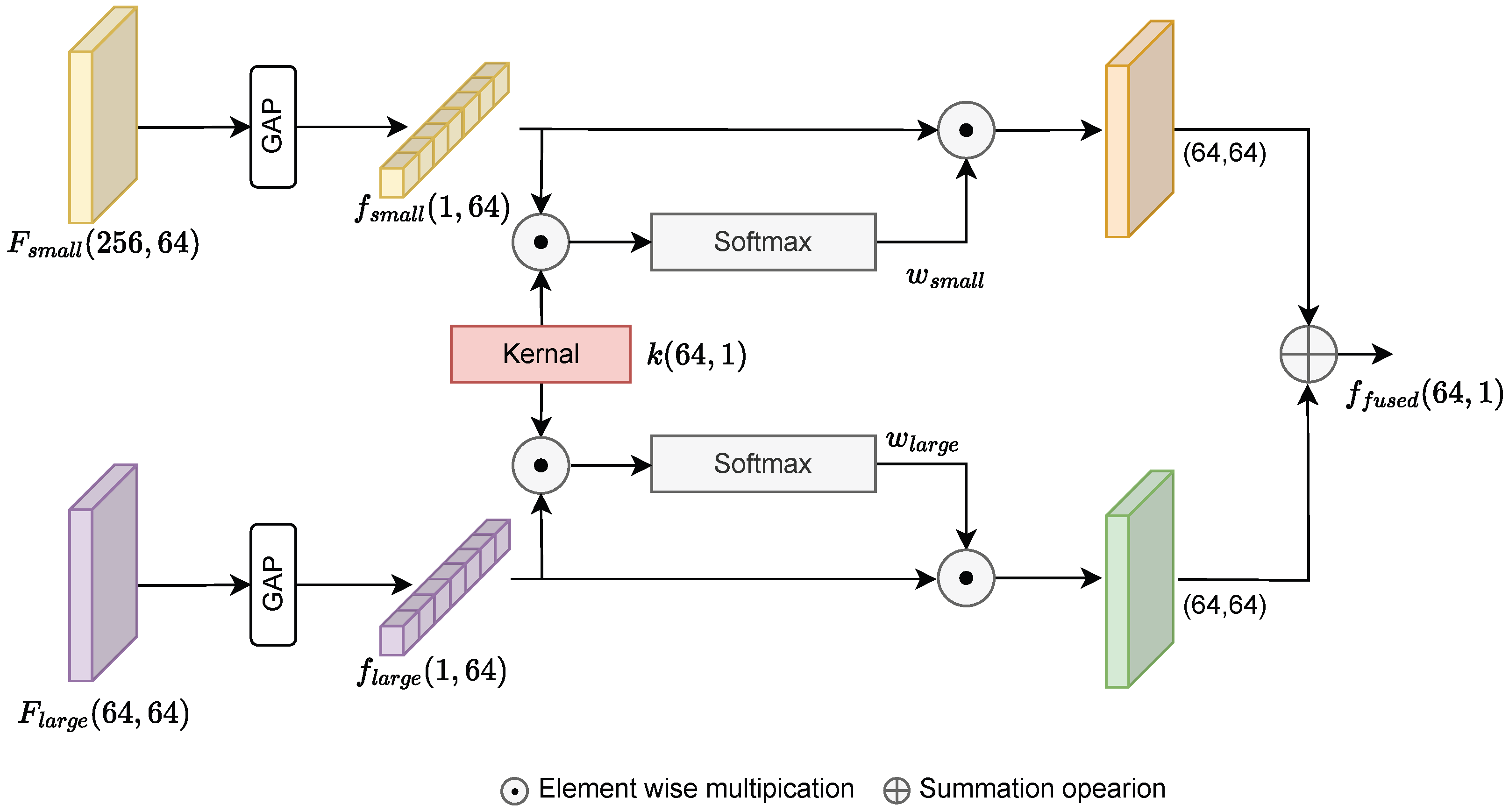
2.3. Attention Fusion Block for Feature Integration
3. Results and Discussion
3.1. Experimental Setup and Evaluation Metrics
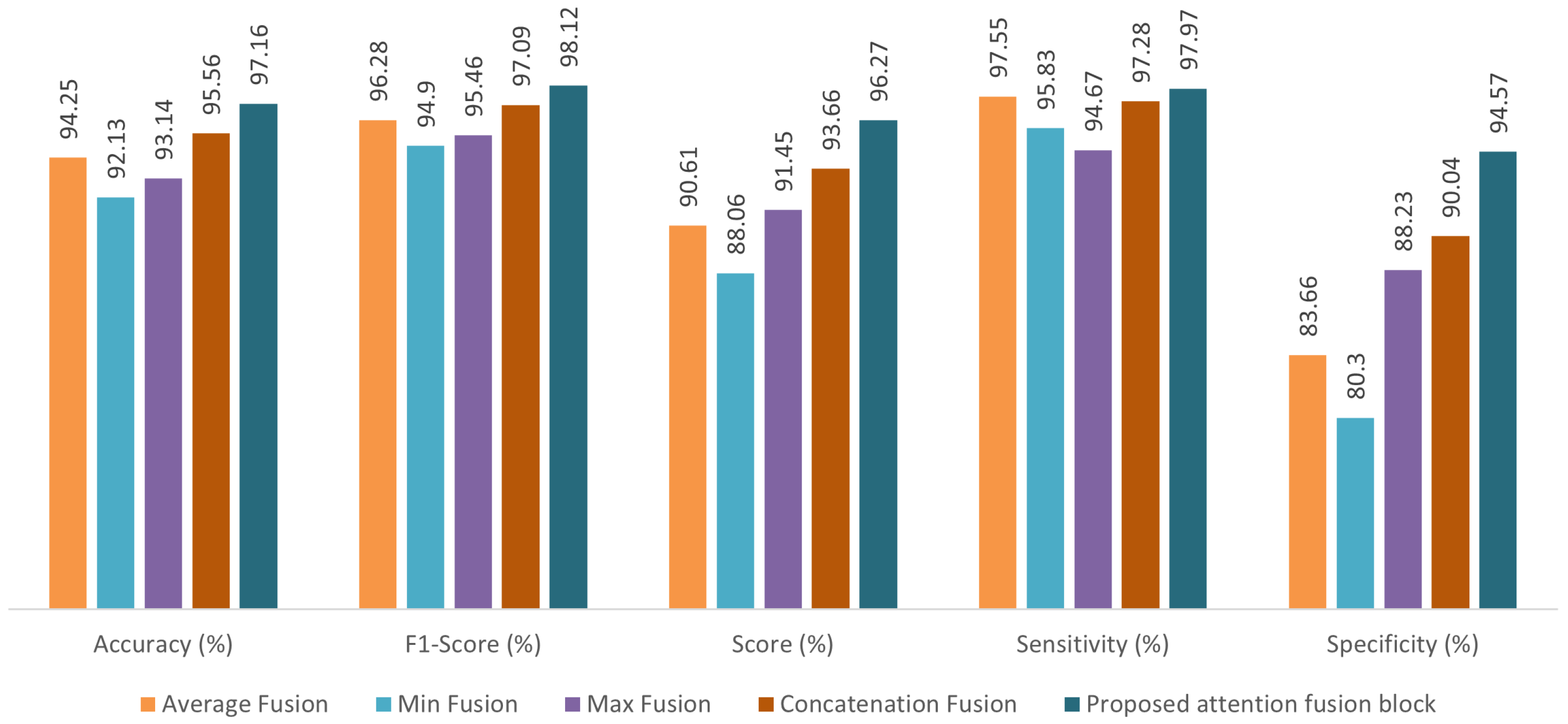
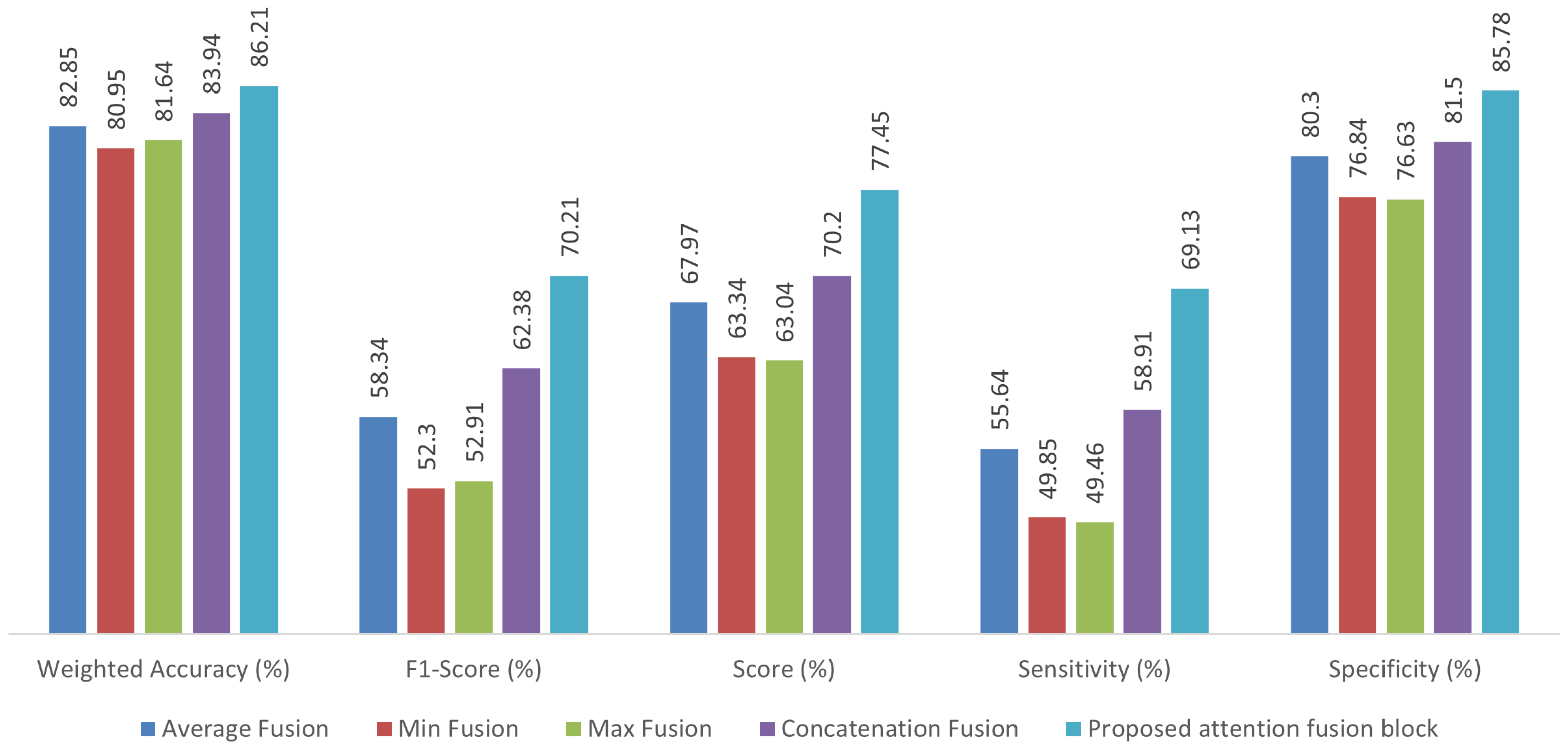
3.2. Comparison of Fusion Methods
3.3. Performance Against Other CNN Approaches
3.4. Performance Against State-of-the-Art Approaches
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Cardiovascular Diseases. 2025. Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 1 January 2025).
- Lam, M.; Lee, T.; Boey, P.; Ng, W.; Hey, H.; Ho, K.; Cheong, P. Factors influencing cardiac auscultation proficiency in physician trainees. Singap. Med. J. 2005, 46, 11. [Google Scholar]
- Kumar, K.; Thompson, W.R. Evaluation of cardiac auscultation skills in pediatric residents. Clin. Pediatr. 2013, 52, 66–73. [Google Scholar] [CrossRef]
- Guven, M.; Uysal, F. A New Method for Heart Disease Detection: Long Short-Term Feature Extraction from Heart Sound Data. Sensors 2023, 23, 5835. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, P.T.; Balasubramanian, P.; Umapathy, S. Automated heart sound classification system from unsegmented phonocardiogram (PCG) using deep neural network. Phys. Eng. Sci. Med. 2020, 43, 505–515. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Zhou, Z.; Bao, J.; Wang, C.; Chen, H.; Xu, C.; Xie, G.; Shen, H.; Wu, H. Classifying heart-sound signals based on cnn trained on melspectrum and log-melspectrum features. Bioengineering 2023, 10, 645. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Lin, W.W.; Huang, J.H. Heart sound classification using deep learning techniques based on log-mel spectrogram. Circuits Syst. Signal Process. 2023, 42, 344–360. [Google Scholar]
- Alkhodari, M.; Fraiwan, L. Convolutional and recurrent neural networks for the detection of valvular heart diseases in phonocardiogram recordings. Comput. Methods Programs Biomed. 2021, 200, 105940. [Google Scholar] [CrossRef]
- Zhou, X.; Guo, X.; Zheng, Y.; Zhao, Y. Detection of coronary heart disease based on MFCC characteristics of heart sound. Appl. Acoust. 2023, 212, 109583. [Google Scholar] [CrossRef]
- Harimi, A.; Majd, Y.; Gharahbagh, A.A.; Hajihashemi, V.; Esmaileyan, Z.; Machado, J.J.; Tavares, J.M.R. Classification of heart sounds using chaogram transform and deep convolutional neural network transfer learning. Sensors 2022, 22, 9569. [Google Scholar] [CrossRef]
- Almanifi, O.R.A.; Ab Nasir, A.F.; Razman, M.A.M.; Musa, R.M.; Majeed, A.P.A. Heartbeat murmurs detection in phonocardiogram recordings via transfer learning. Alex. Eng. J. 2022, 61, 10995–11002. [Google Scholar] [CrossRef]
- Xiang, M.; Zang, J.; Wang, J.; Wang, H.; Zhou, C.; Bi, R.; Zhang, Z.; Xue, C. Research of heart sound classification using two-dimensional features. Biomed. Signal Process. Control 2023, 79, 104190. [Google Scholar] [CrossRef]
- Torre-Cruz, J.; Canadas-Quesada, F.; Ruiz-Reyes, N.; Vera-Candeas, P.; Garcia-Galan, S.; Carabias-Orti, J.; Ranilla, J. Detection of valvular heart diseases combining orthogonal non-negative matrix factorization and convolutional neural networks in PCG signals. J. Biomed. Inform. 2023, 145, 104475. [Google Scholar] [CrossRef]
- Antoni, L.; Bruoth, E.; Bugata, P.; Gajdoš, D.; Hudák, D.; Kmečová, V.; Staňková, M.; Szabari, A.; Vozáriková, G. Murmur identification using supervised contrastive learning. In Proceedings of the 2022 Computing in Cardiology (CinC), Tampere, Finland, 4–7 September 2022; IEEE: New York, NY, USA, 2022; Volume 498, pp. 1–4. [Google Scholar]
- Panah, D.S.; Hines, A.; McKeever, S. Exploring wav2vec 2.0 model for heart murmur detection. In Proceedings of the 2023 31st European Signal Processing Conference (EUSIPCO), Helsinki, Finland, 4–8 September 2023; IEEE: New York, NY, USA, 2023; pp. 1010–1014. [Google Scholar]
- Iqtidar, K.; Qamar, U.; Aziz, S.; Khan, M.U. Phonocardiogram signal analysis for classification of Coronary Artery Diseases using MFCC and 1D adaptive local ternary patterns. Comput. Biol. Med. 2021, 138, 104926. [Google Scholar] [CrossRef]
- Yaseen; Son, G.Y.; Kwon, S. Classification of heart sound signal using multiple features. Appl. Sci. 2018, 8, 2344. [Google Scholar] [CrossRef]
- Aziz, S.; Khan, M.U.; Alhaisoni, M.; Akram, T.; Altaf, M. Phonocardiogram signal processing for automatic diagnosis of congenital heart disorders through fusion of temporal and cepstral features. Sensors 2020, 20, 3790. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, S.K.; Tripathy, R.K.; Ponnalagu, R.; Pachori, R.B. Automated detection of heart valve disorders from the pcg signal using time-frequency magnitude and phase features. IEEE Sens. Lett. 2019, 3, 1–4. [Google Scholar] [CrossRef]
- Azam, F.B.; Ansari, M.I.; Mclane, I.; Hasan, T. Heart sound classification considering additive noise and convolutional distortion. arXiv 2021, arXiv:2106.01865. [Google Scholar]
- Xu, C.; Li, X.; Zhang, X.; Wu, R.; Zhou, Y.; Zhao, Q.; Zhang, Y.; Geng, S.; Gu, Y.; Hong, S. Cardiac murmur grading and risk analysis of cardiac diseases based on adaptable heterogeneous-modality multi-task learning. Health Inf. Sci. Syst. 2023, 12, 2. [Google Scholar]
- Nehary, E.A.; Rajan, S. Phonocardiogram Classification by Learning From Positive and Unlabeled Examples. IEEE Trans. Instrum. Meas. 2024, 73, 1–14. [Google Scholar] [CrossRef]
- Zang, J.; Lian, C.; Xu, B.; Zhang, Z.; Su, Y.; Xue, C. AmtNet: Attentional multi-scale temporal network for phonocardiogram signal classification. Biomed. Signal Process. Control 2023, 85, 104934. [Google Scholar] [CrossRef]
- Koike, T.; Qian, K.; Kong, Q.; Plumbley, M.D.; Schuller, B.W.; Yamamoto, Y. Audio for audio is better? An investigation on transfer learning models for heart sound classification. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; IEEE: New York, NY, USA, 2020; pp. 74–77. [Google Scholar]
- Ranipa, K.; Zhu, W.P.; Swamy, M. Multimodal CNN Fusion Architecture With Multi-features for Heart Sound Classification. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 22–28 May 2021; IEEE: New York, NY, USA, 2021; pp. 1–5. [Google Scholar]
- Guo, Z.; Chen, J.; He, T.; Wang, W.; Abbas, H.; Lv, Z. DS-CNN: Dual-stream convolutional neural networks-based heart sound classification for wearable devices. IEEE Trans. Consum. Electron. 2023, 69, 1186–1194. [Google Scholar] [CrossRef]
- Wang, R.; Duan, Y.; Li, Y.; Zheng, D.; Liu, X.; Lam, C.T.; Tan, T. PCTMF-Net: Heart sound classification with parallel CNNs-transformer and second-order spectral analysis. Vis. Comput. 2023, 39, 3811–3822. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv 2019, arXiv:1810.04805. [Google Scholar]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training; Technical Report; OpenAI: San Francisco, CA, USA, 2018. [Google Scholar]
- Lou, M.; Yu, Y. OverLoCK: An Overview-first-Look-Closely-next ConvNet with Context-Mixing Dynamic Kernels. In Proceedings of the Computer Vision and Pattern Recognition Conference, Nashville, TN, USA, 11–15 June 2025; pp. 128–138. [Google Scholar]
- Ding, X.; Zhang, Y.; Ge, Y.; Zhao, S.; Song, L.; Yue, X.; Shan, Y. Unireplknet: A universal perception large-kernel convnet for audio video point cloud time-series and image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 5513–5524. [Google Scholar]
- Shi, Y.; Dong, M.; Li, M.; Xu, C. Vssd: Vision mamba with non-causal state space duality. arXiv 2024, arXiv:2407.18559. [Google Scholar]
- Shi, Y.; Dong, M.; Xu, C. Multi-scale vmamba: Hierarchy in hierarchy visual state space model. Adv. Neural Inf. Process. Syst. 2024, 37, 25687–25708. [Google Scholar]
- Lou, M.; Fu, Y.; Yu, Y. Sparx: A sparse cross-layer connection mechanism for hierarchical vision mamba and transformer networks. In Proceedings of the AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February–4 March 2025; Volume 39, pp. 19104–19114. [Google Scholar]
- Yang, D.; Lin, Y.; Wei, J.; Lin, X.; Zhao, X.; Yao, Y.; Tao, T.; Liang, B.; Lu, S.G. Assisting heart valve diseases diagnosis via transformer-based classification of heart sound signals. Electronics 2023, 12, 2221. [Google Scholar] [CrossRef]
- Alkhodari, M.; Hadjileontiadis, L.J.; Khandoker, A.H. Identification of congenital valvular murmurs in young patients using deep learning-based attention transformers and phonocardiograms. IEEE J. Biomed. Health Inform. 2024, 28, 1803–1814. [Google Scholar] [CrossRef]
- Jumphoo, T.; Phapatanaburi, K.; Pathonsuwan, W.; Anchuen, P.; Uthansakul, M.; Uthansakul, P. Exploiting Data-Efficient Image Transformer-based Transfer Learning for Valvular Heart Diseases Detection. IEEE Access 2024, 12, 15845–15855. [Google Scholar] [CrossRef]
- Graves, A. Neural Turing Machines. arXiv 2014, arXiv:1410.5401. [Google Scholar]
- Lou, M.; Zhang, S.; Zhou, H.Y.; Yang, S.; Wu, C.; Yu, Y. TransXNet: Learning Both Global and Local Dynamics With a Dual Dynamic Token Mixer for Visual Recognition. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 11534–11547. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Springer, D.; Li, Q.; Moody, B.; Juan, R.A.; Chorro, F.J.; Castells, F.; Roig, J.M.; Silva, I.; Johnson, A.E.; et al. An open access database for the evaluation of heart sound algorithms. Physiol. Meas. 2016, 37, 2181. [Google Scholar] [CrossRef]
- Reyna, M.A.; Kiarashi, Y.; Elola, A.; Oliveira, J.; Renna, F.; Gu, A.; Perez Alday, E.A.; Sadr, N.; Sharma, A.; Kpodonu, J.; et al. Heart murmur detection from phonocardiogram recordings: The george b. moody physionet challenge 2022. PLoS Digit. Health 2023, 2, e0000324. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 11–15 June 2016; pp. 770–778. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 11–15 June 2016; pp. 2818–2826. [Google Scholar]
- Chollet, F. Xception: Deep learning with depthwise separable convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1251–1258. [Google Scholar]


| Baseline Network | Accuracy (%) | F1-Score (%) | Score (%) | Sensitivity (%) | Specificity (%) | Parameters (M) |
|---|---|---|---|---|---|---|
| VGG19 | 89.97 | 93.62 | 83.95 | 95.44 | 72.46 | 20.06 |
| ResNet50 | 91.08 | 94.18 | 87.13 | 94.66 | 79.61 | 23.72 |
| Inception-v3 | 91.41 | 94.38 | 87.92 | 94.59 | 81.25 | 21.94 |
| Xception | 93.36 | 95.62 | 90.78 | 95.71 | 85.86 | 20.99 |
| Proposed AFTViT | 97.16 | 98.12 | 96.27 | 97.97 | 94.57 | 0.86 |
| Model | Weighted Accuracy (%) | F1-Score (%) | Score (%) | Sensitivity (%) | Specificity (%) | Parameters (M) |
|---|---|---|---|---|---|---|
| VGG19 | 77.92 | 41.29 | 56.19 | 40.55 | 71.84 | 20.06 |
| ResNet50 | 79.17 | 45.39 | 58.42 | 43.44 | 73.40 | 23.72 |
| Inception-v3 | 82.42 | 57.49 | 66.91 | 54.73 | 79.08 | 21.94 |
| Xception | 81.24 | 52.11 | 63.11 | 49.25 | 76.97 | 20.99 |
| Proposed AFTViT | 86.21 | 70.21 | 69.13 | 85.78 | 77.45 | 0.86 |
| Network | Features | Configuration | Accuracy | Number of Parameters |
|---|---|---|---|---|
| ResNet152 [20]—2022 | Fbank & MFCCs | early fusion, two branch | 86.20 | 138.85 M |
| AlexNet [10]—2022 | chaogram features | single branch | 89.68 | 61 M |
| PANNs [24] | raw signal | feature-level fusion, two branch | 89.7 | 80.7 M |
| VGG16 [10]—2022 | chaogram features | single branch | 90.05 | 138 M |
| Inception-v3 [10]—2022 | chaogram features | single branch | 90.36 | 23.9M |
| Proposed AFTViT | MFCCs | feature-level fusion, two branch | 97.16 | 0.86 M |
| Network | Features | Configuration | Weighted Accuracy | Number of Parameters |
|---|---|---|---|---|
| ResNet50 [14] | raw signal | single branch | 75.6 | 14.7 M |
| HMT [21] | log-mel spectrogram | late fusion, three branch | 78.3 | 204 M |
| wav2vec model [15] | raw signal | single branch | 80 | 317 M |
| Proposed AFTViT | MFCCs | feature-level fusion, two branch | 86.21 | 0.86 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranipa, K.; Zhu, W.-P.; Swamy, M.N.S. Attention-Fusion-Based Two-Stream Vision Transformer for Heart Sound Classification. Bioengineering 2025, 12, 1033. https://doi.org/10.3390/bioengineering12101033
Ranipa K, Zhu W-P, Swamy MNS. Attention-Fusion-Based Two-Stream Vision Transformer for Heart Sound Classification. Bioengineering. 2025; 12(10):1033. https://doi.org/10.3390/bioengineering12101033
Chicago/Turabian StyleRanipa, Kalpeshkumar, Wei-Ping Zhu, and M. N. S. Swamy. 2025. "Attention-Fusion-Based Two-Stream Vision Transformer for Heart Sound Classification" Bioengineering 12, no. 10: 1033. https://doi.org/10.3390/bioengineering12101033
APA StyleRanipa, K., Zhu, W.-P., & Swamy, M. N. S. (2025). Attention-Fusion-Based Two-Stream Vision Transformer for Heart Sound Classification. Bioengineering, 12(10), 1033. https://doi.org/10.3390/bioengineering12101033






