Trans-cVAE-GAN: Transformer-Based cVAE-GAN for High-Fidelity EEG Signal Generation
Abstract
1. Introduction
- (1)
- Traditional VAE architectures can model latent distributions but often produce blurry samples with structural distortion;
- (2)
- Classical GANs have limited temporal modeling capability, making it difficult to capture the dynamic features and spectral structures of EEG signals;
- (3)
- Most existing models lack effective emotion label conditioning mechanisms, hindering their ability to generate EEG data under specific semantic guidance and thereby limiting their usability in practical scenarios such as emotion regulation and cognitive intervention.
- (1)
- Incorporation of emotion label conditioning to enhance semantic controllability of generated signals
- (2)
- Integration of a Transformer encoder to improve temporal dependency modeling
- (3)
- Joint multi-dimensional structure-aware loss to improve multi-modal fidelity of generated samples
2. Related Work
2.1. VAE-Based Methods for EEG Signal Generation
2.2. GAN-Based Methods for EEG Signal Generation
- (1)
- Lack of temporal modeling capability—Most EEG GAN models rely on one-dimensional convolutional architectures, which are inadequate for capturing long-range dependencies or rhythmically structured temporal patterns, impairing the accurate reconstruction of key frequency bands;
- (2)
- Absence of label-conditioned control mechanisms—The original GAN framework is inherently unconditional, making it difficult to generate EEG samples with semantic attributes corresponding to specific emotional states or cognitive tasks;
- (3)
- Neglect of structural loss constraints—GAN models typically optimize solely based on discriminator feedback and often omit explicit modeling of structural consistency in terms of temporal smoothness or spectral fidelity, resulting in waveform distortion or spectral drift in generated signals;
- (4)
- Susceptibility to mode collapse—In multi-class emotion generation tasks, GANs often struggle to adequately cover the full data distribution across multiple emotional labels, leading to insufficient sample diversity.
3. Materials and Methods
3.1. Dataset
3.2. Preprocessing
3.3. Model
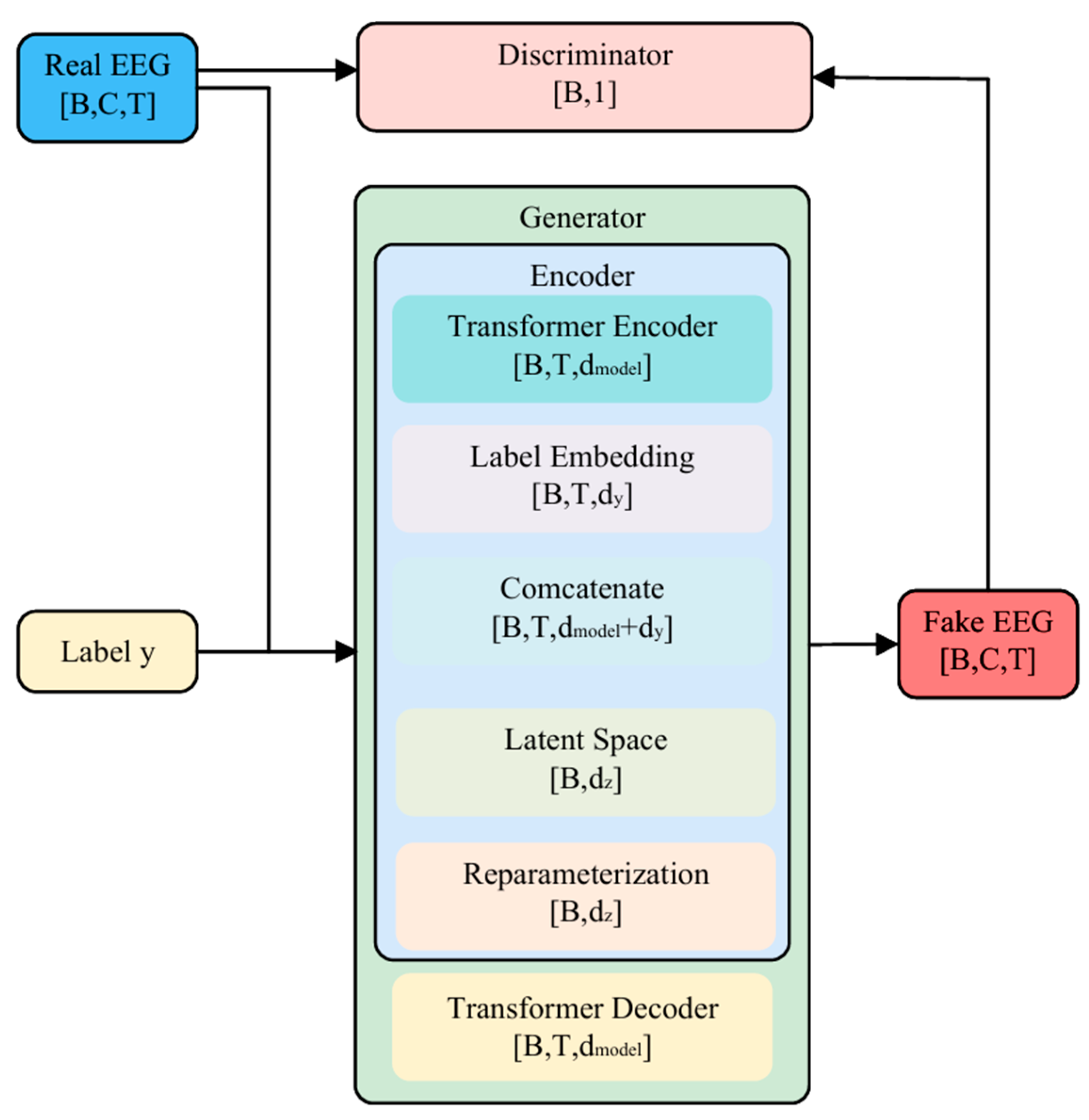
3.3.1. Overall Architecture
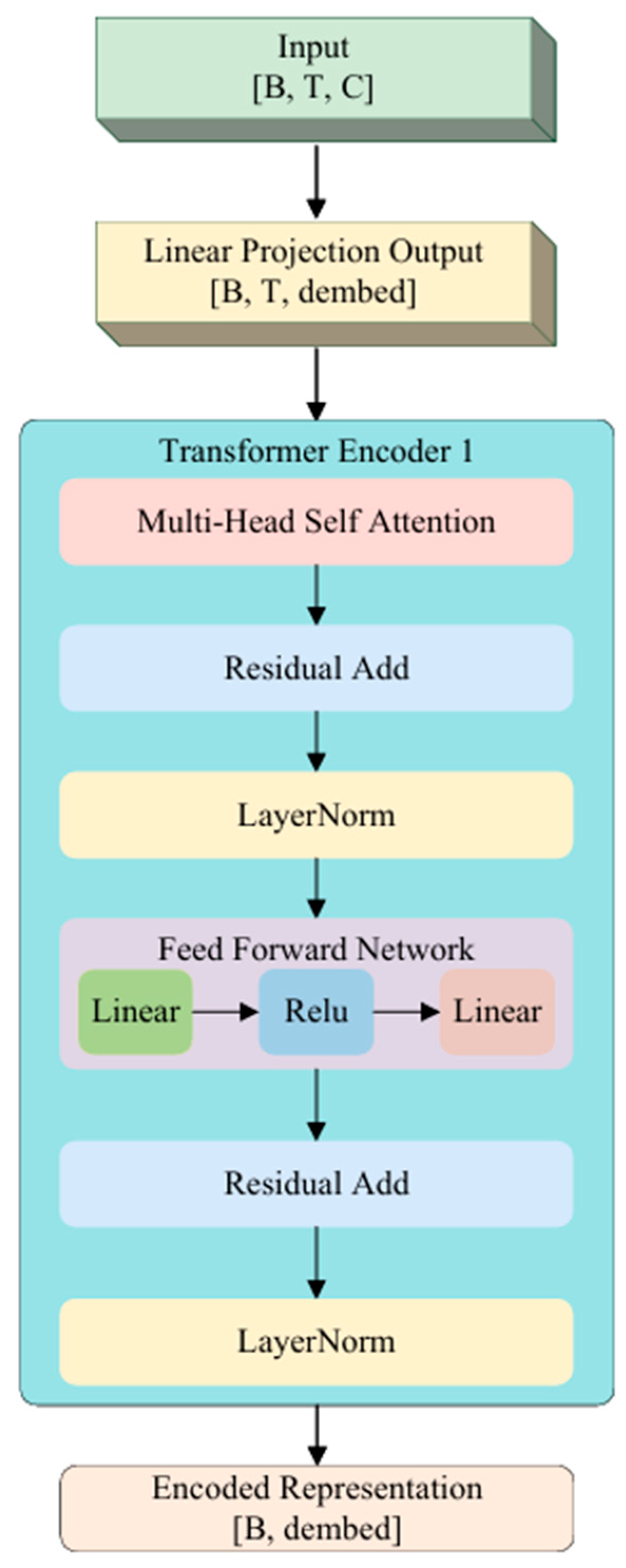
3.3.2. Transformer Encoder
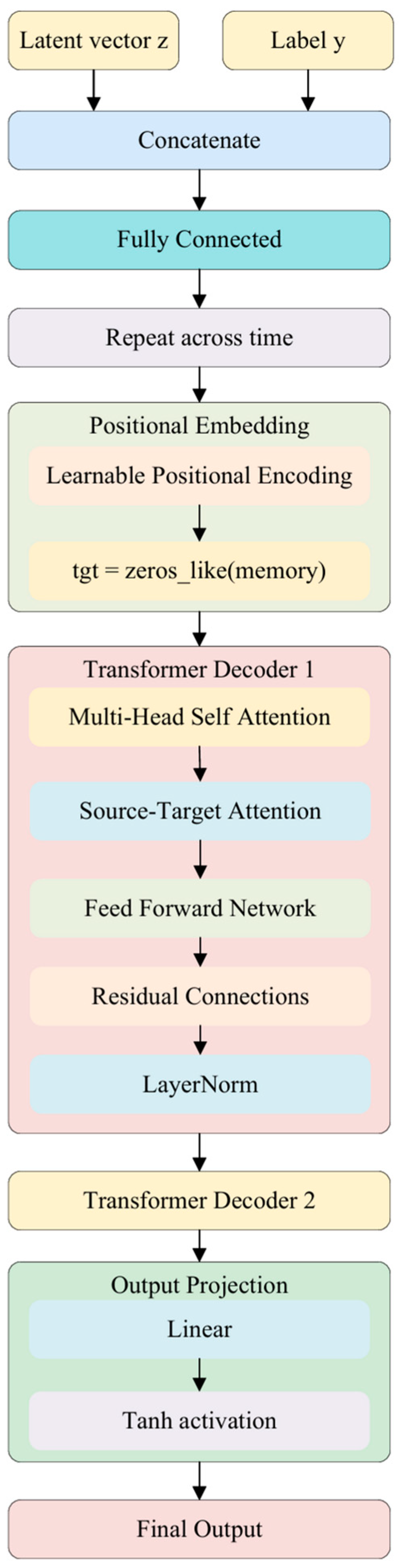
3.3.3. Latent Space Modeling and Label Embedding
3.4. Transformer Conditional Decoder
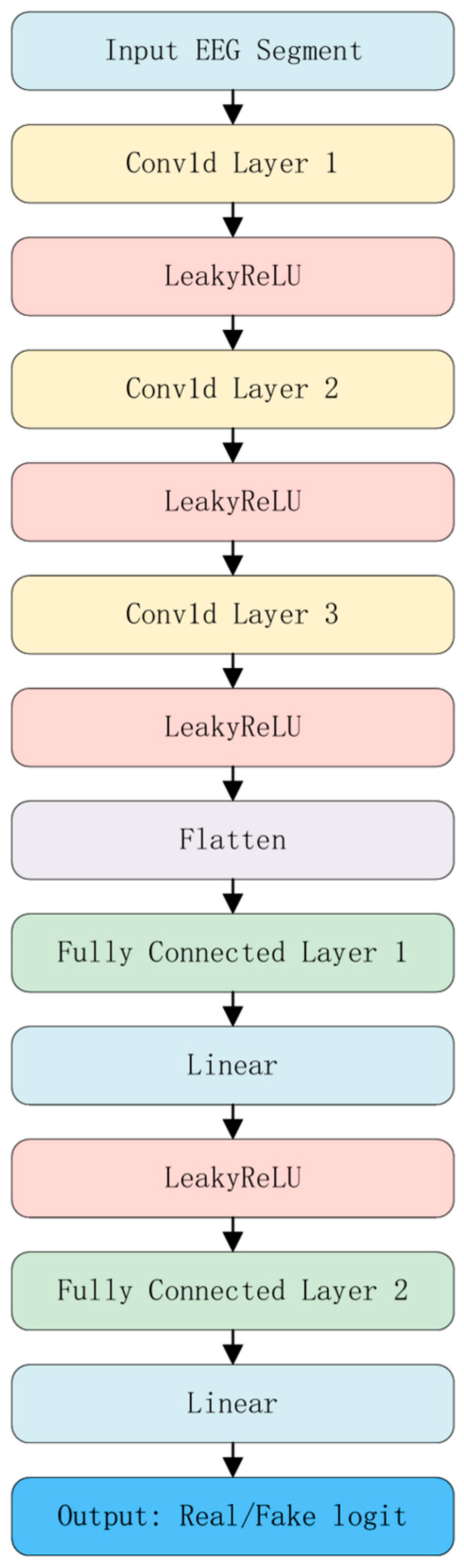
3.5. Discriminator Network
3.6. Loss Function and Joint Optimization Strategy
- (1)
- Reconstruction Loss
- (2)
- KL Divergence Loss
- (3)
- Adversarial Loss
- (4)
- Pearson Correlation Loss
- (5)
- Smoothness Loss
- (6)
- Power Spectrum Consistency Loss
4. Experimental Design and Results Analysis
4.1. Experimental Environment
4.2. Implementation Details and Hyperparameters
4.3. Evaluation Metrics
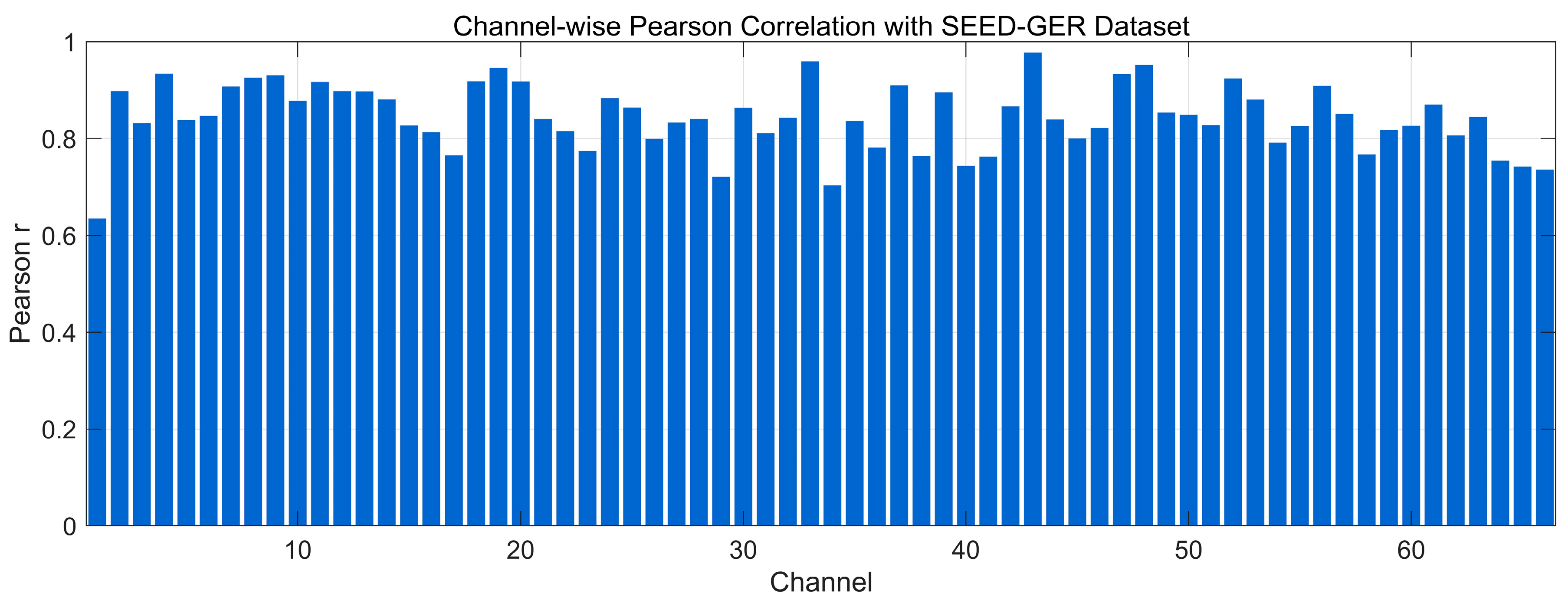
4.3.1. Pearson Correlation Coefficient
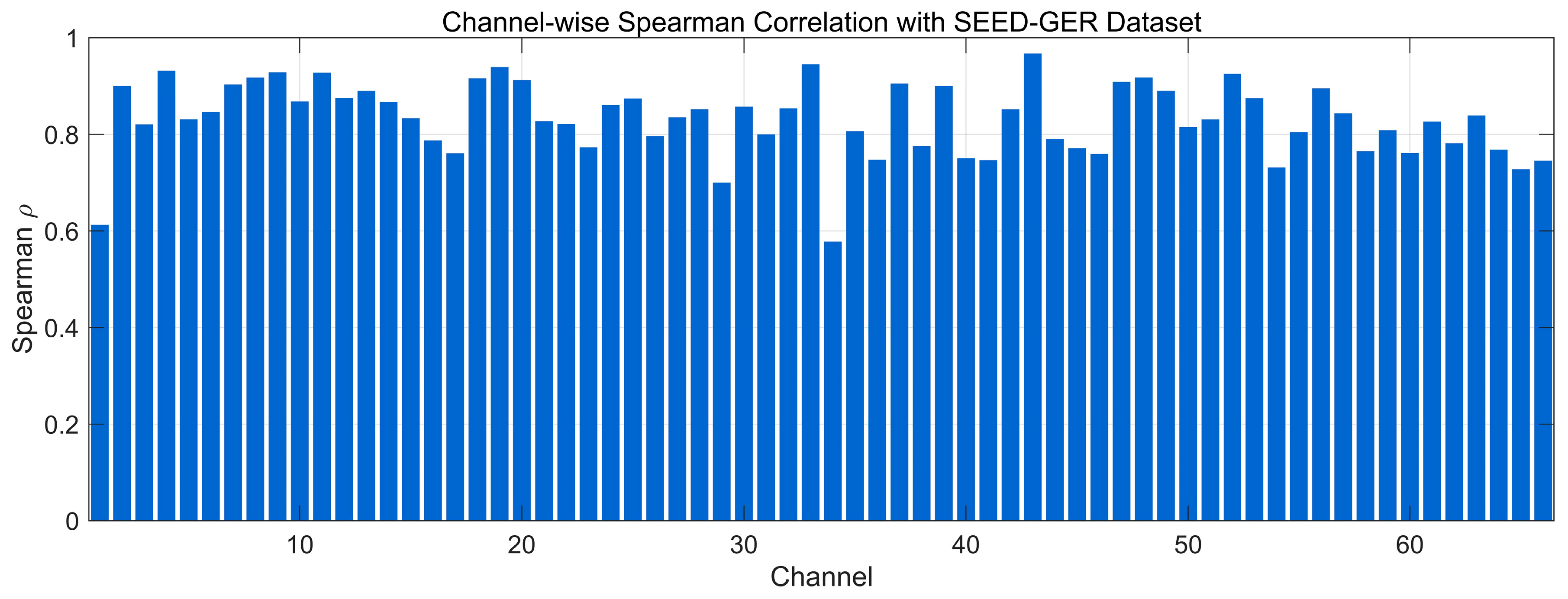
4.3.2. Spearman’s Rank Correlation Coefficient
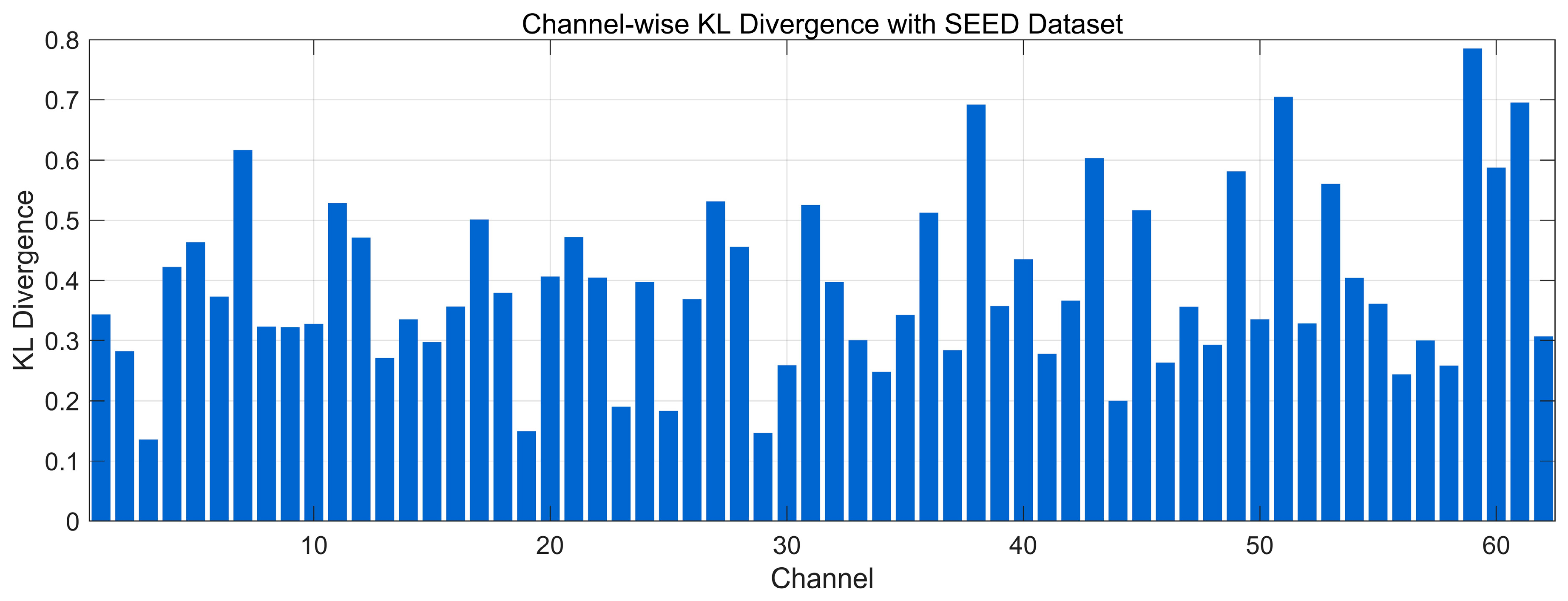
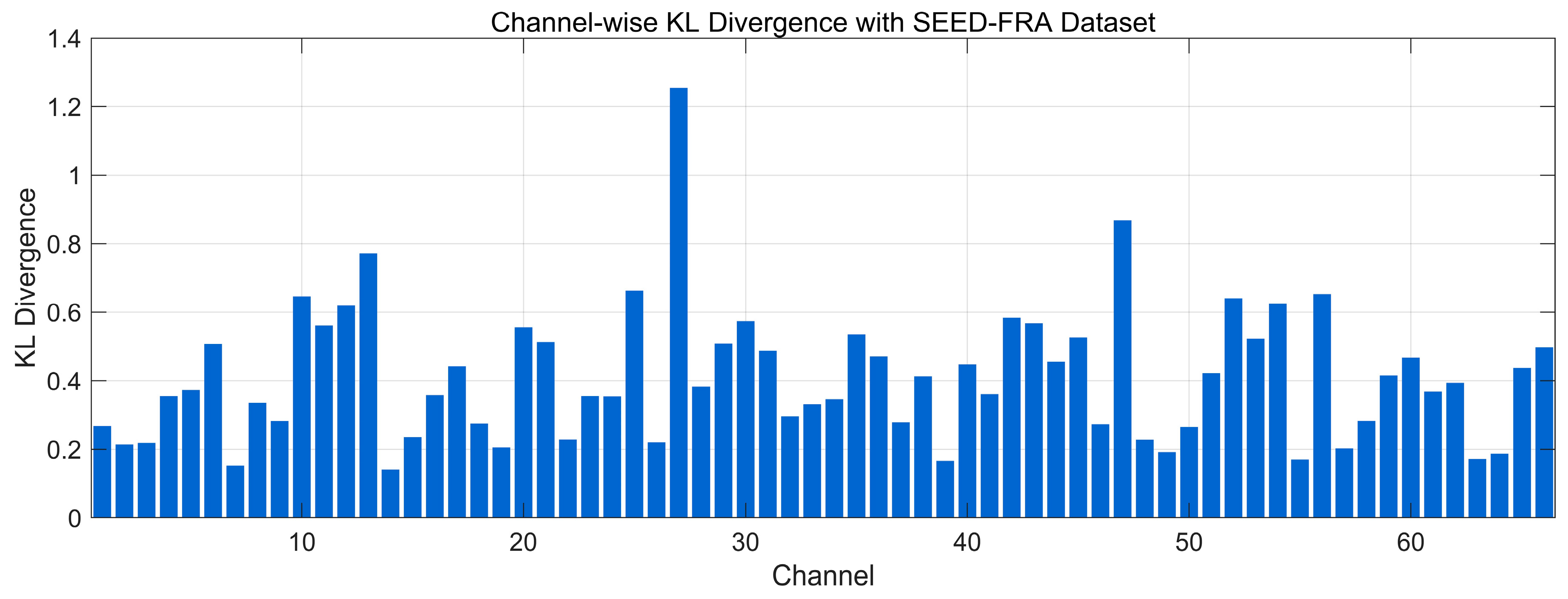
4.3.3. Kullback–Leibler Divergence
4.3.4. Fréchet Distance
4.3.5. Mean Squared Error
4.3.6. Earth Mover’s Distance
4.3.7. Classification Consistency
4.4. Experimental Results and Analysis
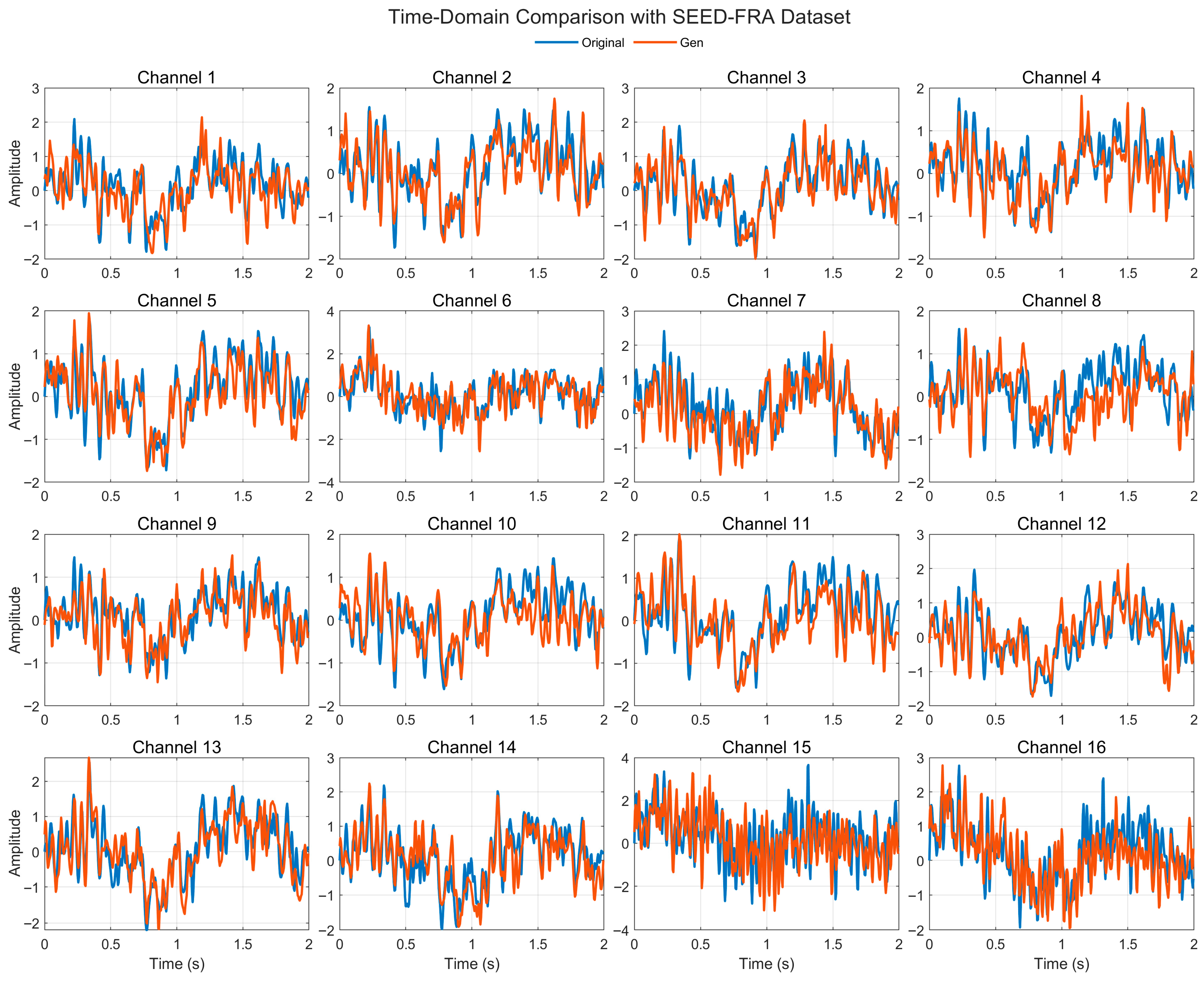
4.4.1. Time-Domain Comparison
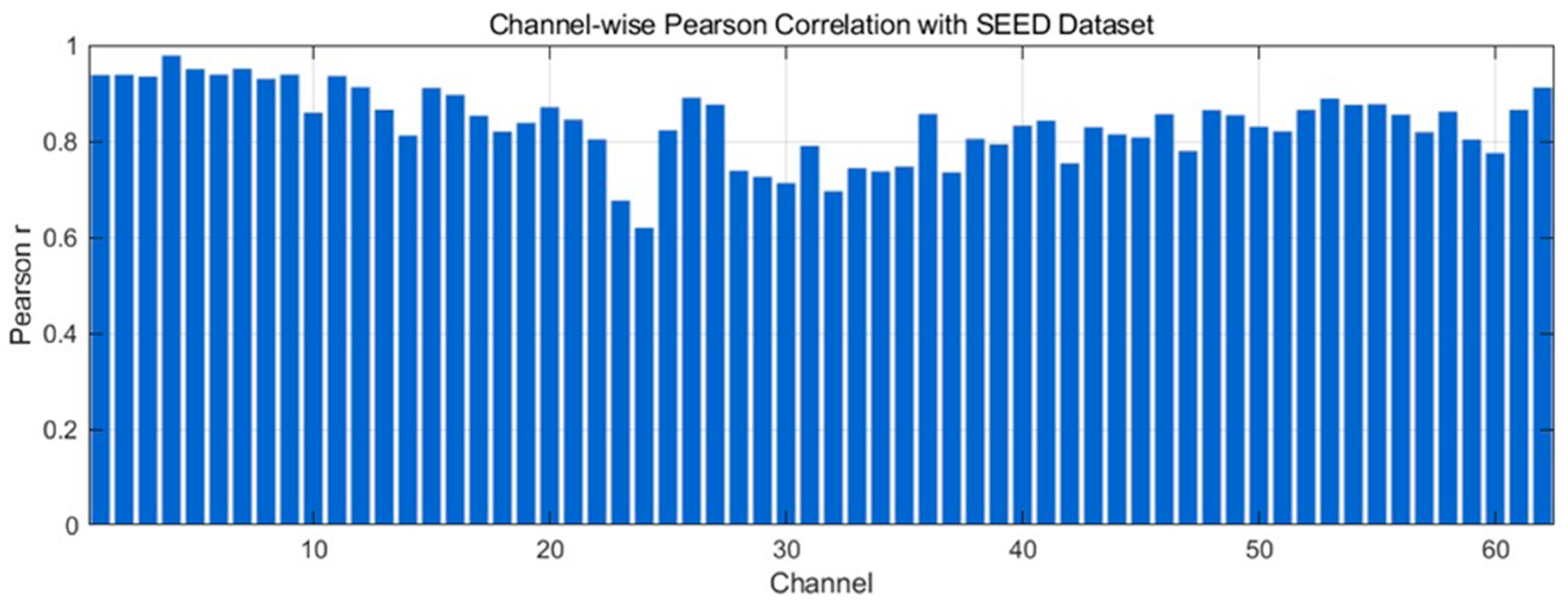
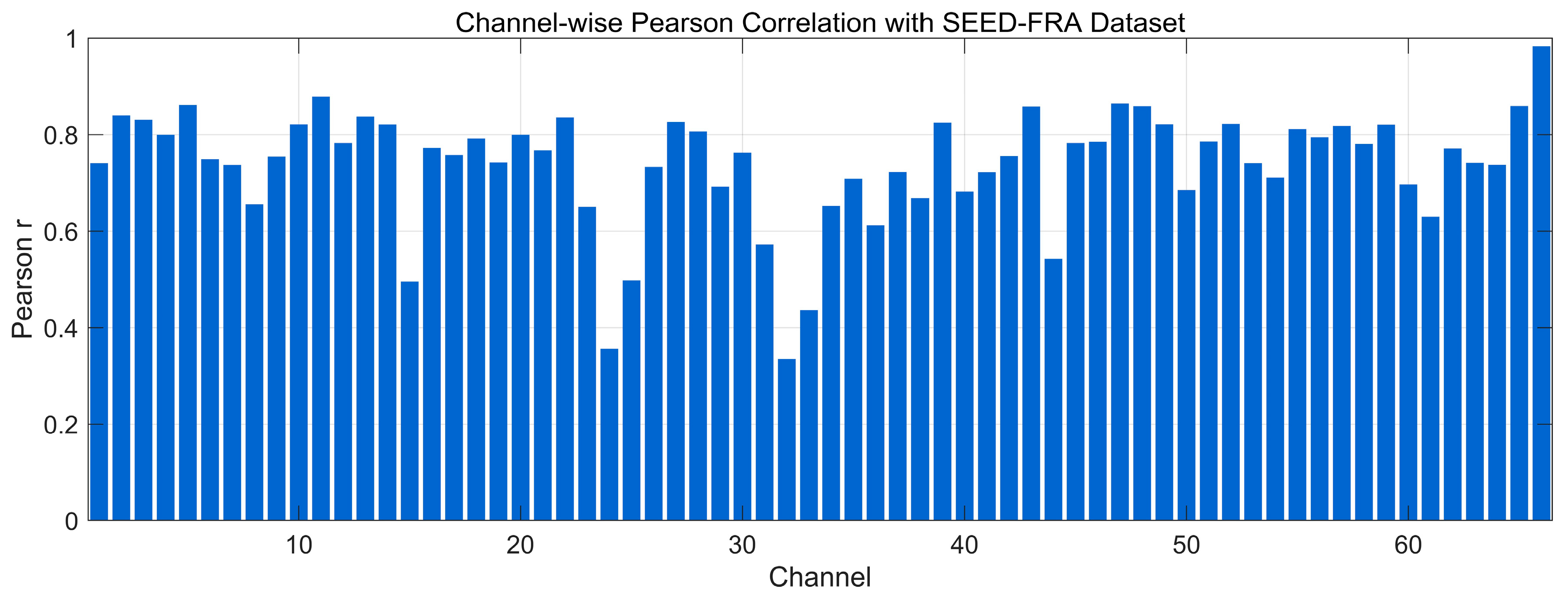
4.4.2. Pearson Correlation Analysis
4.4.3. Spearman Correlation Analysis
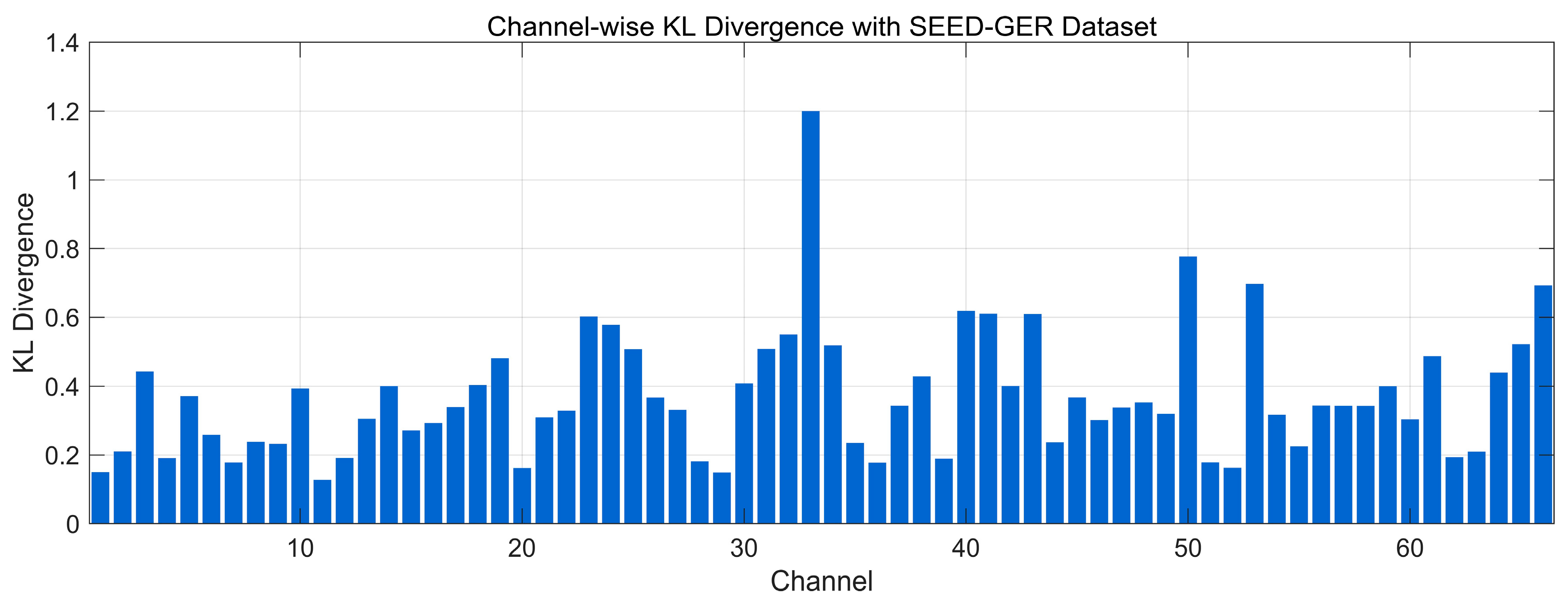
4.4.4. Spectral Distribution Information Divergence Analysis
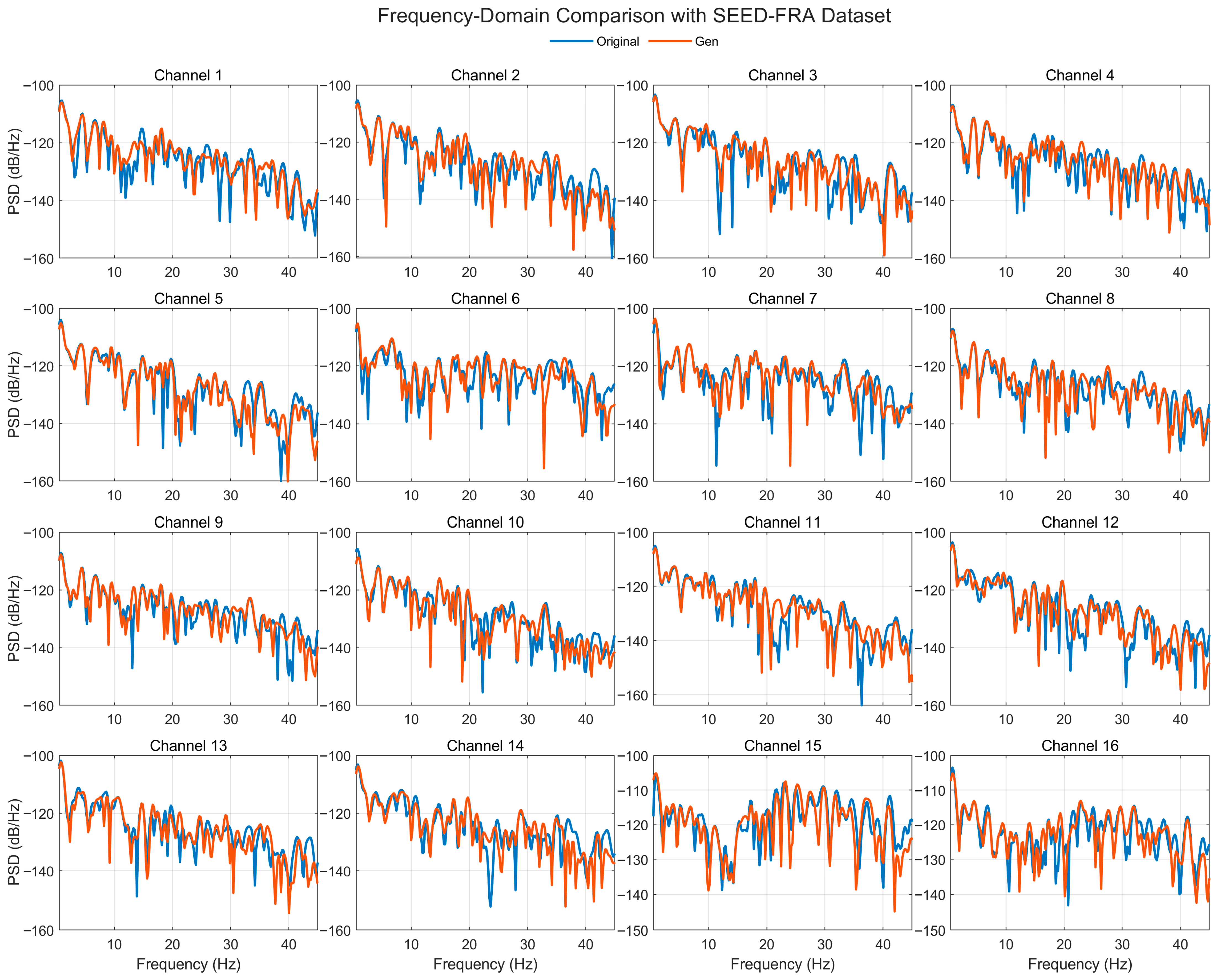
4.4.5. Frequency-Domain Consistency Analysis
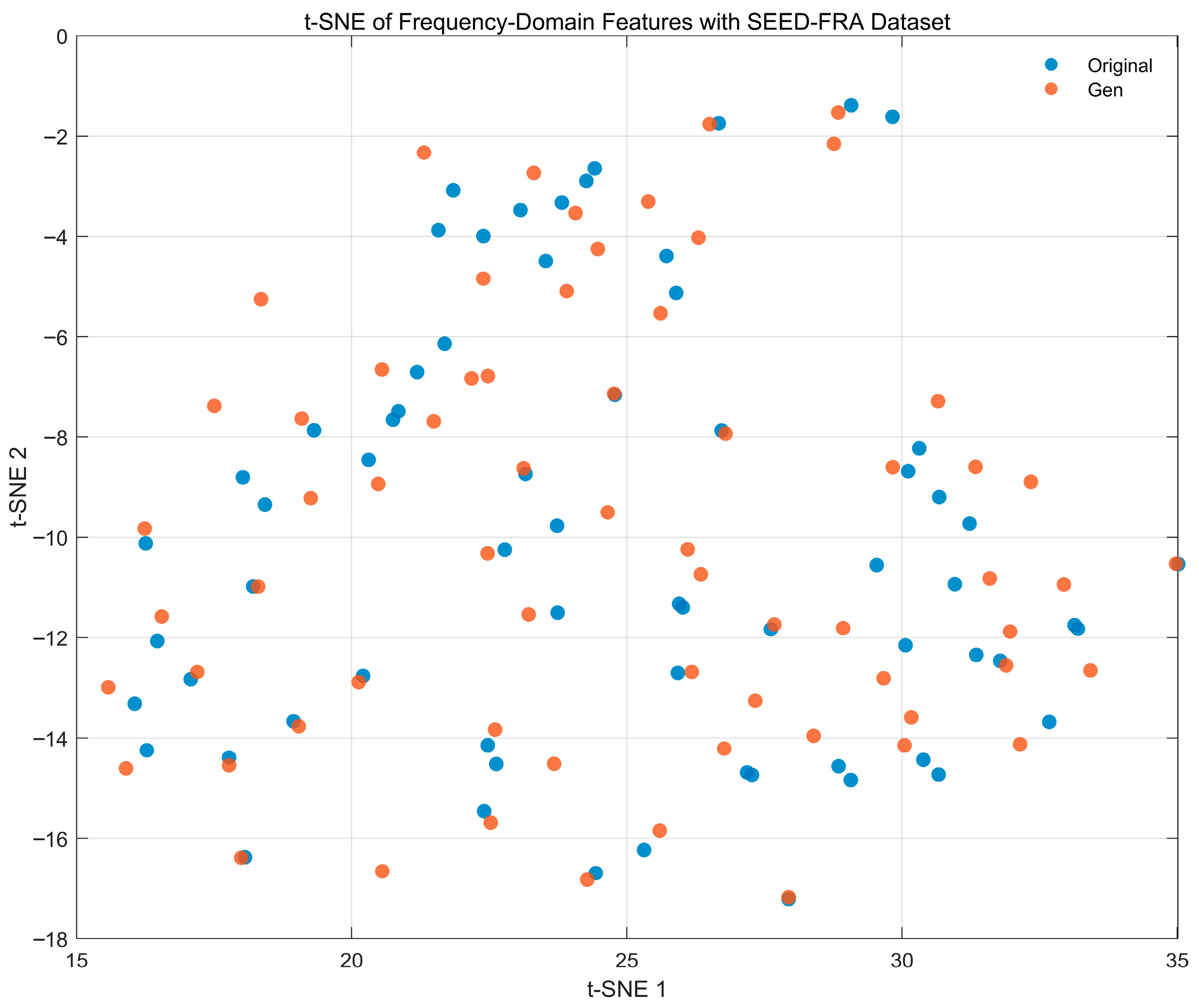
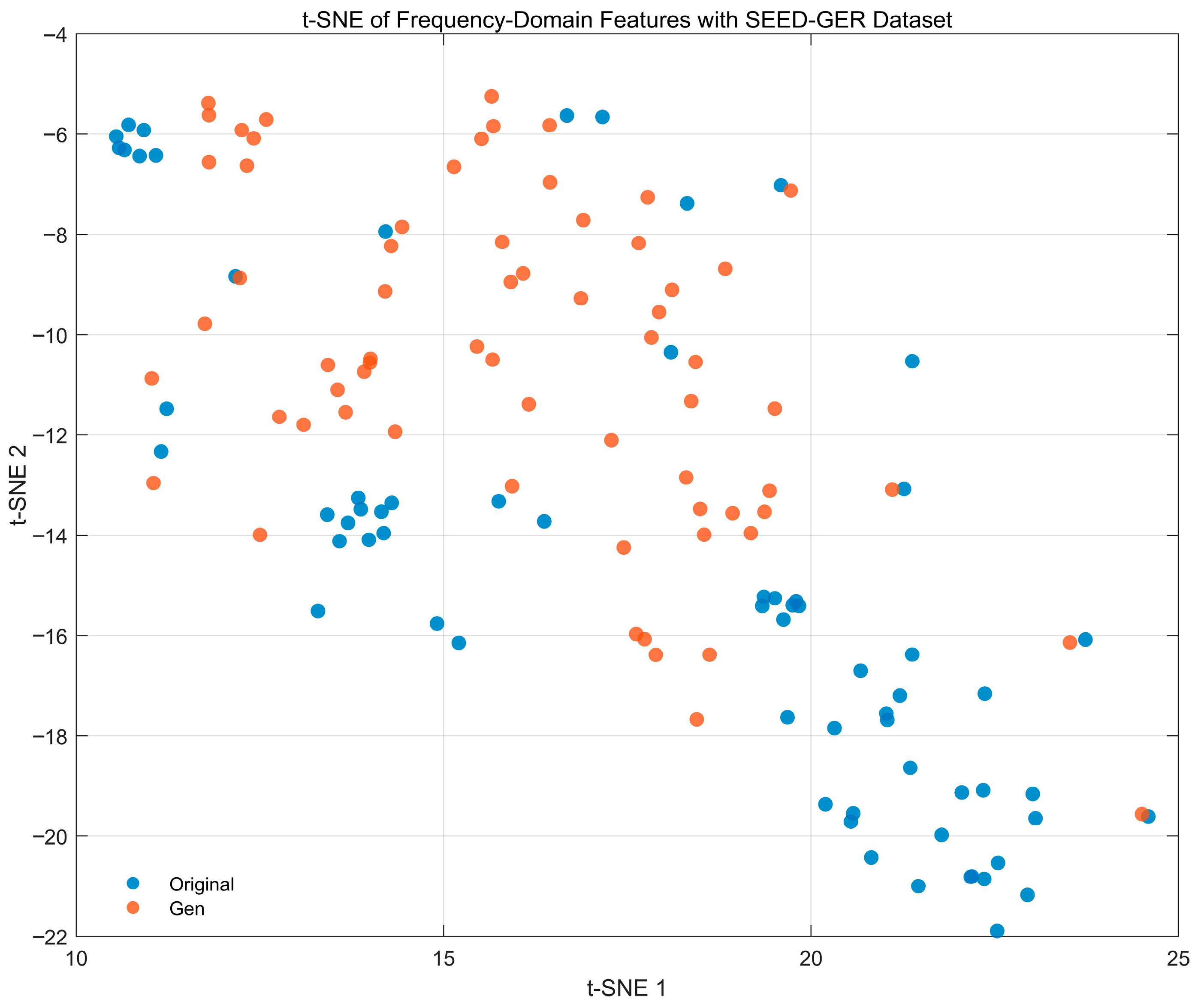
4.4.6. Feature-Space Distribution Visualization Analysis
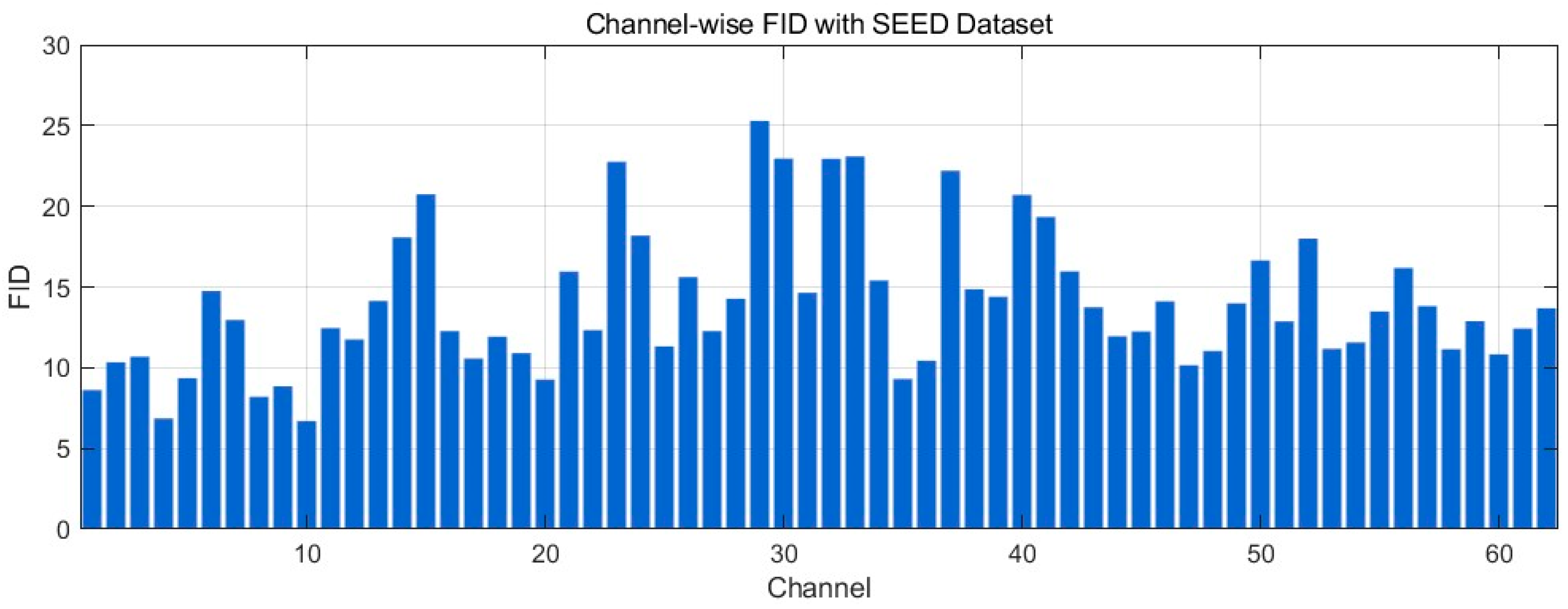
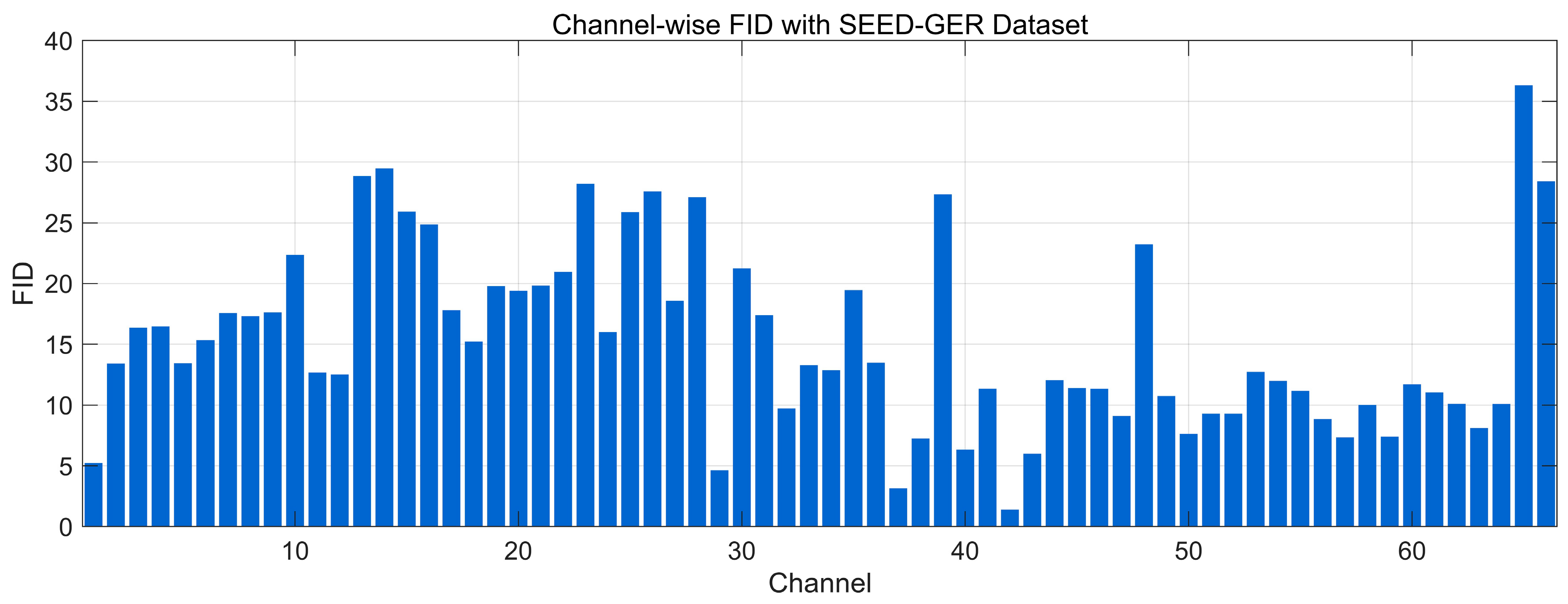
4.4.7. Fréchet Distance Analysis
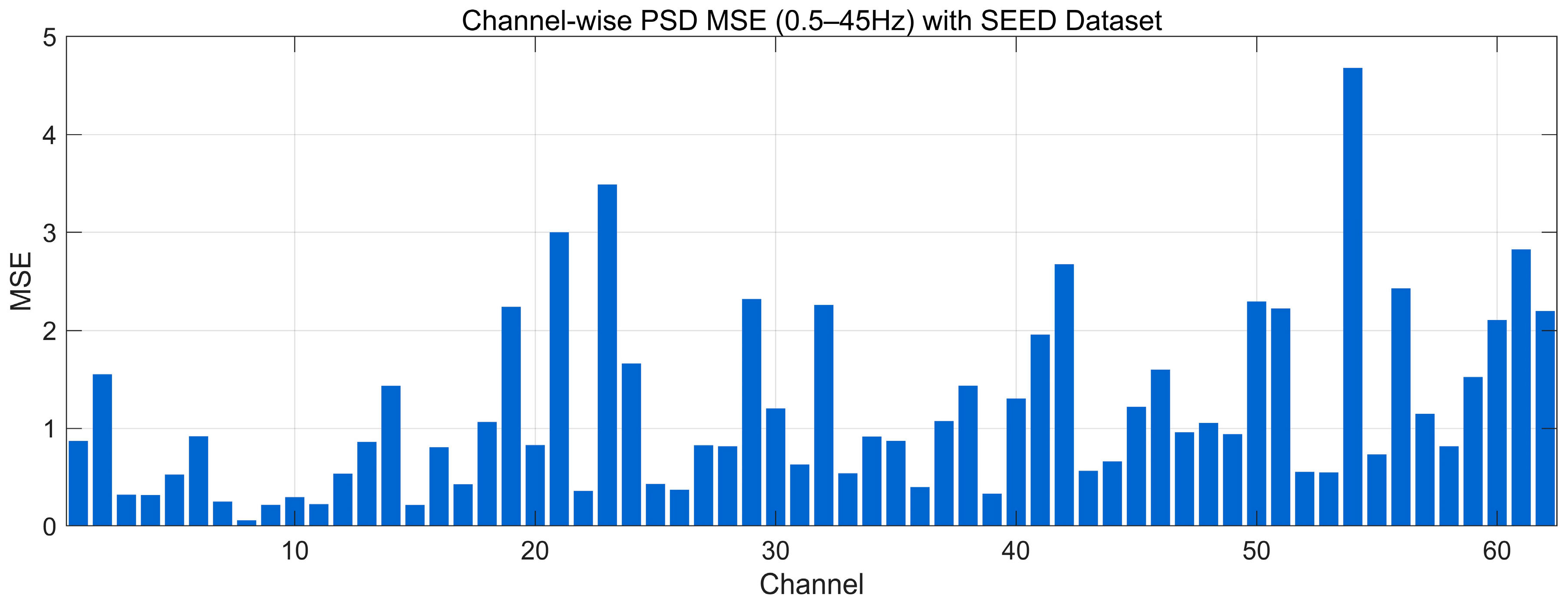
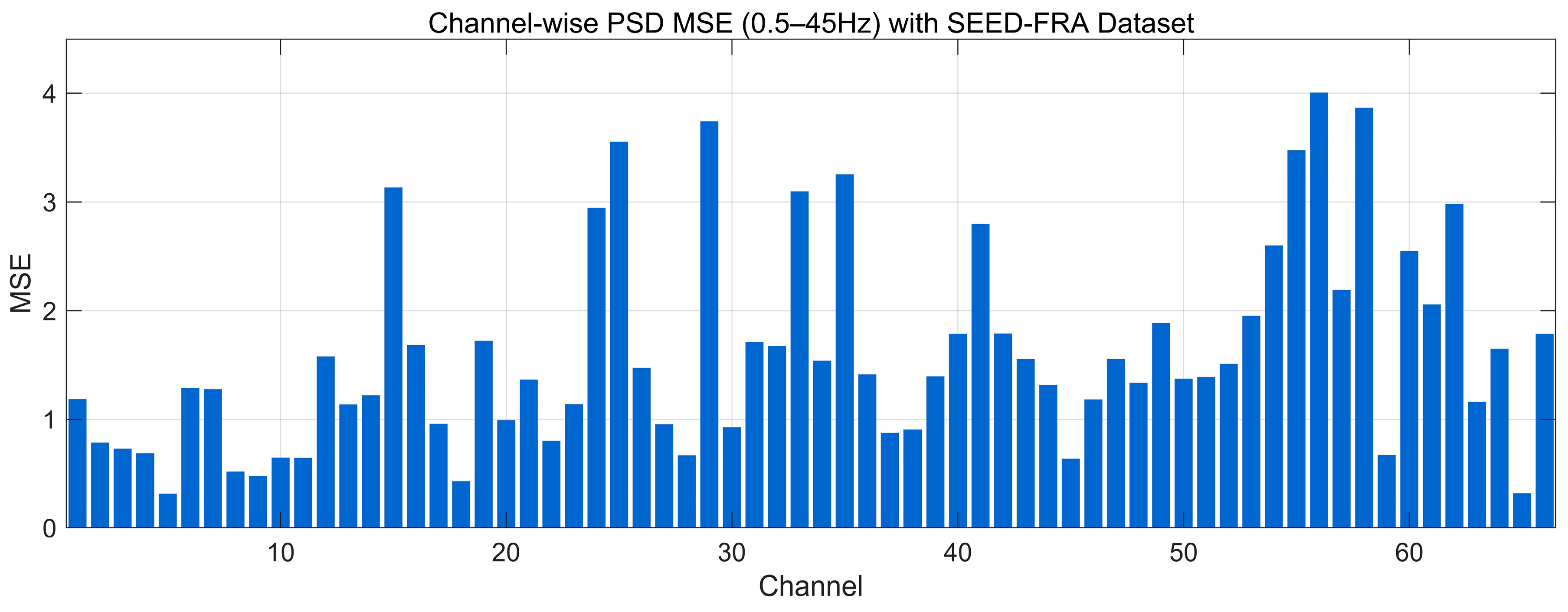
4.4.8. MSE Analysis
4.4.9. Earth Mover’s Distance Analysis
4.4.10. Classification Consistency Analysis
4.5. Ablation Study
4.5.1. Experimental Setup
4.5.2. Results and Analysis
4.6. Comparative Experiments
4.6.1. Experimental Setup
4.6.2. Results and Analysis
5. Discussion
5.1. Challenges of EEG Signal Structural Characteristics for Generative Modeling
5.2. Applicability and Complementarity of Multi-Dimensional Evaluation Metrics
5.3. Challenges in the Interpretability of Generative Models
5.4. Loss Design Under Non-Stationary EEG
5.5. Practical Fidelity for Classification
6. Limitations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, M.; Chen, J.; Hua, C.; Wen, G.; Fu, R. EEG emotion recognition using EEG-SWTNS neural network through EEG spectral image. Inf. Sci. 2024, 680, 121198. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.P.; Zhang, T. GDDN: Graph domain disentanglement network for generalizable EEG emotion recognition. IEEE Trans. Affect. Comput. 2024, 15, 1739–1753. [Google Scholar] [CrossRef]
- Fan, C.; Wang, J.; Huang, W.; Yang, X.; Pei, G.; Li, T.; Lv, Z. Light-weight residual convolution-based capsule network for EEG emotion recognition. Adv. Eng. Inform. 2024, 61, 102522. [Google Scholar] [CrossRef]
- Krothapalli, M.; Buddendorff, L.; Yadav, H.; Schilaty, N.D.; Jain, S. From gut microbiota to brain waves: The potential of the microbiome and EEG as biomarkers for cognitive impairment. Int. J. Mol. Sci. 2024, 25, 6678. [Google Scholar] [CrossRef]
- Xue, C.; Li, A.; Wu, R.; Chai, J.; Qiang, Y.; Zhao, J.; Yang, Q. VRNPT: A neuropsychological test tool for diagnosing mild cognitive impairment using virtual reality and EEG signals. Int. J. Hum.-Comput. Interact. 2024, 40, 6268–6286. [Google Scholar] [CrossRef]
- You, Z.; Guo, Y.; Zhang, X.; Zhao, Y. Virtual Electroencephalogram Acquisition: A Review on Electroencephalogram Generative Methods. Sensors 2025, 25, 3178. [Google Scholar] [CrossRef]
- Pan, Y.; Li, N.; Zhang, Y.; Xu, P.; Yao, D. Short-length SSVEP data extension by a novel generative adversarial networks based framework. Cogn. Neurodynamics 2024, 18, 2925–2945. [Google Scholar] [CrossRef]
- Panwar, S.; Rad, P.; Quarles, J.; Huang, Y. Generating EEG signals of an RSVP experiment by a class conditioned wasserstein generative adversarial network. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1304–1310. [Google Scholar]
- Yin, X.; Han, Y.; Sun, H.; Xu, Z.; Yu, H.; Duan, X. Multi-attention generative adversarial network for multivariate time series prediction. IEEE Access 2021, 9, 57351–57363. [Google Scholar] [CrossRef]
- Krishna, G.; Tran, C.; Carnahan, M.; Tewfik, A. Constrained variational autoencoder for improving EEG based speech recognition systems. arXiv 2020, arXiv:2006.02902. [Google Scholar] [CrossRef]
- Luo, Y.; Zhu, L.-Z.; Wan, Z.-Y.; Lu, B.-L. Data augmentation for enhancing EEG-based emotion recognition with deep generative models. J. Neural Eng. 2020, 17, 056021. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, X.; Tan, F.; Li, Q.; Wang, Y.; Zhang, H.; Xie, J.; Liang, W.; Li, G.; Fang, P. An approach for EEG data augmentation based on deep convolutional generative adversarial network. In Proceedings of the 2022 IEEE International Conference on Cyborg and Bionic Systems (CBS), Wuhan, China, 24–26 March 2023; pp. 347–351. [Google Scholar]
- Zhang, Q.; Liu, Y. Improving brain computer interface performance by data augmentation with conditional deep convolutional generative adversarial networks. arXiv 2018, arXiv:1806.07108. [Google Scholar] [CrossRef]
- Liu, Q.; Hao, J.; Guo, Y. EEG data augmentation for emotion recognition with a task-driven GAN. Algorithms 2023, 16, 118. [Google Scholar] [CrossRef]
- Zhang, A.; Su, L.; Zhang, Y.; Fu, Y.; Wu, L.; Liang, S. EEG data augmentation for emotion recognition with a multiple generator conditional Wasserstein GAN. Complex Intell. Syst. 2022, 8, 3059–3071. [Google Scholar] [CrossRef]
- Xu, M.; Chen, Y.; Wang, Y.; Wang, D.; Liu, Z.; Zhang, L. BWGAN-GP: An EEG data generation method for class imbalance problem in RSVP tasks. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 251–263. [Google Scholar] [CrossRef] [PubMed]
- Aznan, N.K.N.; Atapour-Abarghouei, A.; Bonner, S.; Connolly, J.D.; Al Moubayed, N.; Breckon, T.P. Simulating brain signals: Creating synthetic eeg data via neural-based generative models for improved ssvep classification. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Cisotto, G.; Zancanaro, A.; Zoppis, I.F.; Manzoni, S.L. hvEEGNet: A novel deep learning model for high-fidelity EEG reconstruction. Front. Neuroinform. 2024, 18, 1459970. [Google Scholar] [CrossRef] [PubMed]
- Bethge, D.; Hallgarten, P.; Grosse-Puppendahl, T.; Kari, M.; Chuang, L.L.; Özdenizci, O.; Schmidt, A. EEG2Vec: Learning affective EEG representations via variational autoencoders. In Proceedings of the 2022 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, 9–12 October 2022; pp. 3150–3157. [Google Scholar]
- Li, H.; Yu, S.; Principe, J. Causal recurrent variational autoencoder for medical time series generation. In Proceedings of the AAAI Conference on Artificial Intelligence, Washington, DC, USA, 7–14 February 2023; pp. 8562–8570. [Google Scholar]
- Tian, C.; Ma, Y.; Cammon, J.; Fang, F.; Zhang, Y.; Meng, M. Dual-encoder VAE-GAN with spatiotemporal features for emotional EEG data augmentation. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 2018–2027. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the 28th International Conference on Neural Information Processing Systems, Montreal, Canada, 8–13 December 2014. [Google Scholar]
- Abdelfattah, S.M.; Abdelrahman, G.M.; Wang, M. Augmenting the size of EEG datasets using generative adversarial networks. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar]
- Fahimi, F.; Dosen, S.; Ang, K.K.; Mrachacz-Kersting, N.; Guan, C. Generative adversarial networks-based data augmentation for brain–computer interface. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 4039–4051. [Google Scholar] [CrossRef]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 214–223. [Google Scholar]
- Panwar, S.; Rad, P.; Jung, T.-P.; Huang, Y. Modeling EEG data distribution with a Wasserstein generative adversarial network to predict RSVP events. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1720–1730. [Google Scholar] [CrossRef]
- Smith, K.E.; Smith, A.O. Conditional GAN for timeseries generation. arXiv 2020, arXiv:2006.16477. [Google Scholar] [CrossRef]
- Duan, R.-N.; Zhu, J.-Y.; Lu, B.-L. Differential entropy feature for EEG-based emotion classification. In Proceedings of the 2013 6th international IEEE/EMBS conference on neural engineering (NER), San Diego, CA, USA, 6–8 November 2013; pp. 81–84. [Google Scholar]
- Zheng, W.-L.; Lu, B.-L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks. IEEE Trans. Auton. Ment. Dev. 2015, 7, 162–175. [Google Scholar] [CrossRef]
- Liu, W.; Zheng, W.-L.; Li, Z.; Wu, S.-Y.; Gan, L.; Lu, B.-L. Identifying similarities and differences in emotion recognition with EEG and eye movements among Chinese, German, and French People. J. Neural Eng. 2022, 19, 026012. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, A.; Nils, F.; Sanchez, X.; Philippot, P. Assessing the effectiveness of a large database of emotion-eliciting films: A new tool for emotion researchers. Cogn. Emot. 2010, 24, 1153–1172. [Google Scholar] [CrossRef]
- Ramponi, G.; Protopapas, P.; Brambilla, M.; Janssen, R. T-cgan: Conditional generative adversarial network for data augmentation in noisy time series with irregular sampling. arXiv 2018, arXiv:1811.08295. [Google Scholar]







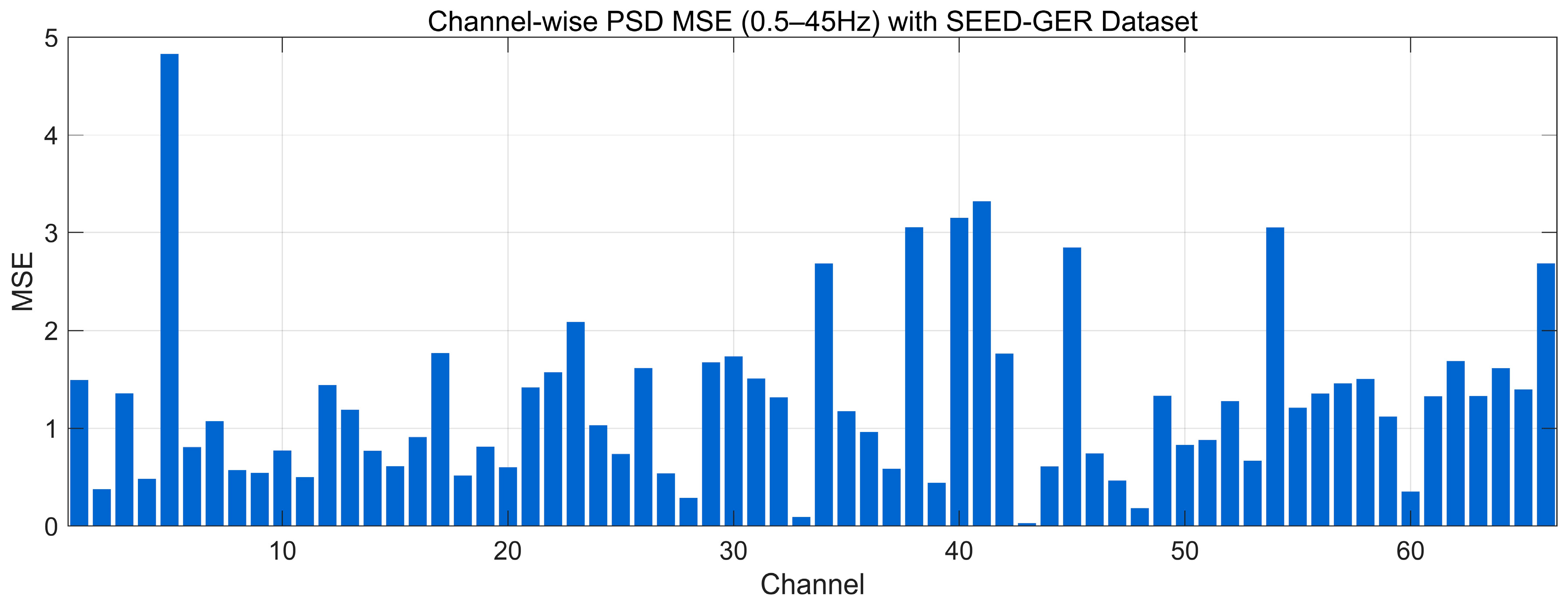
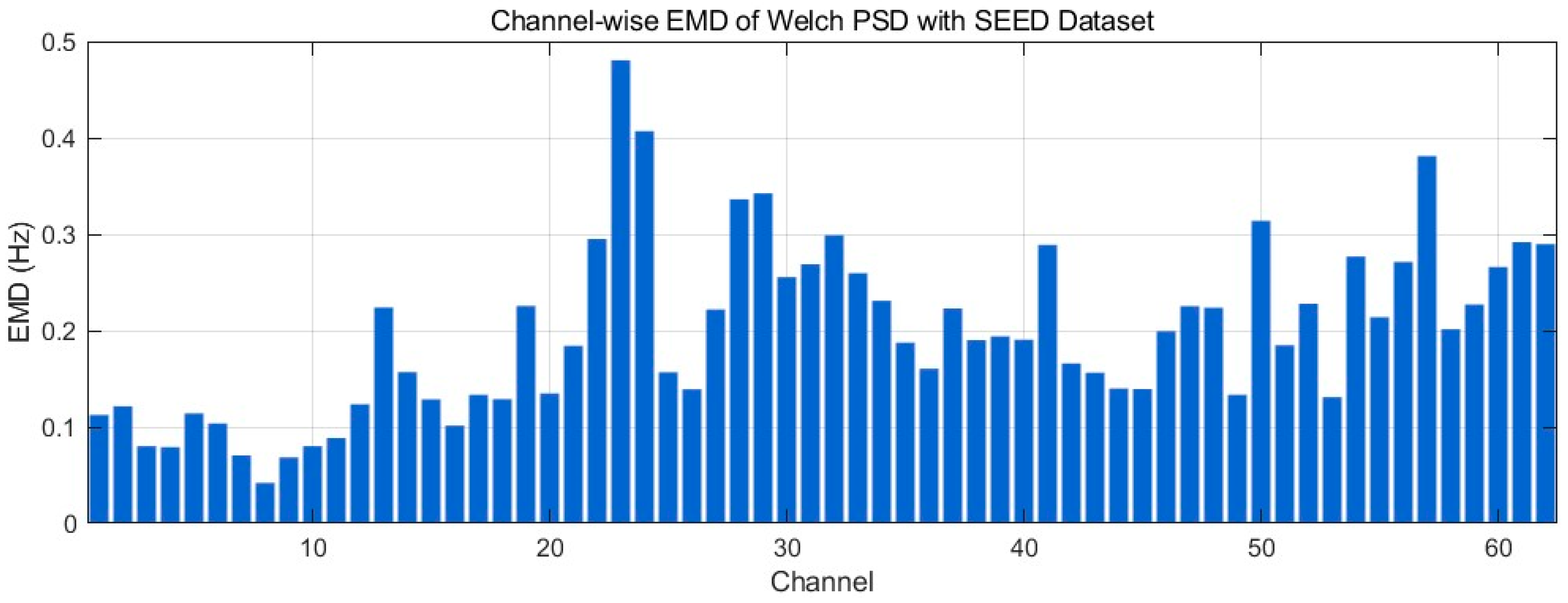
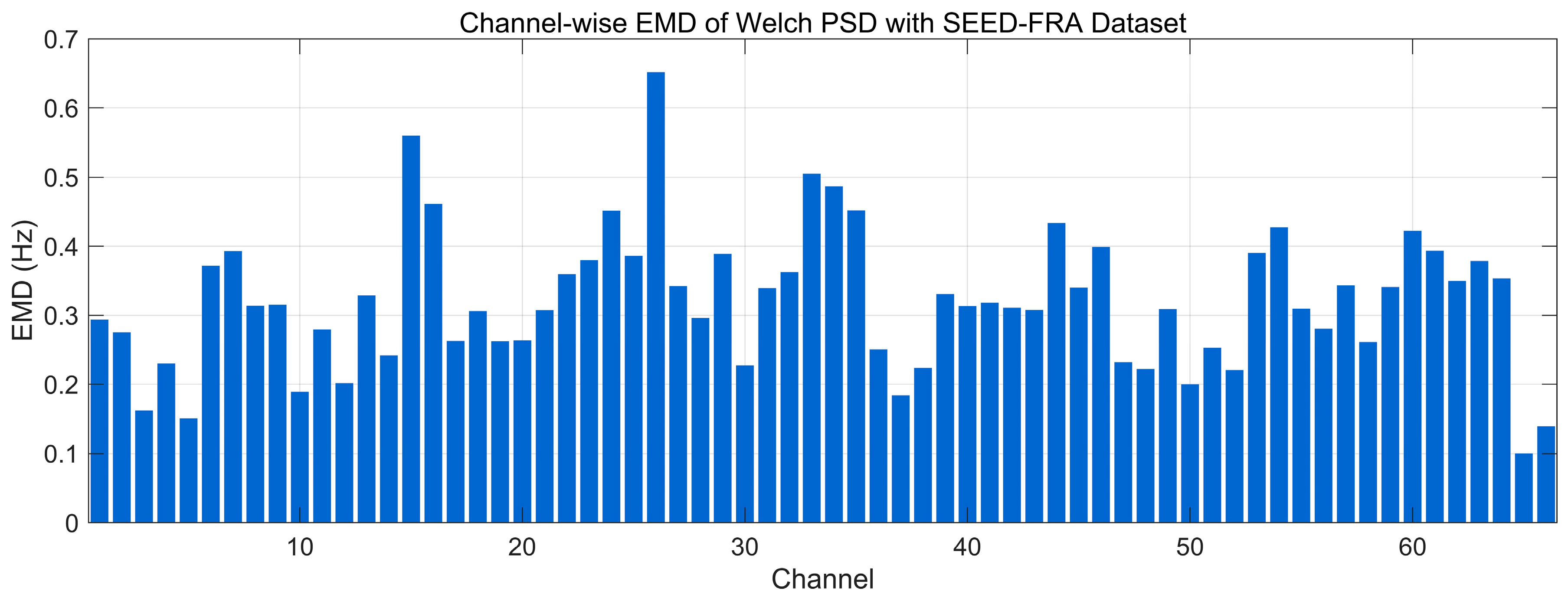
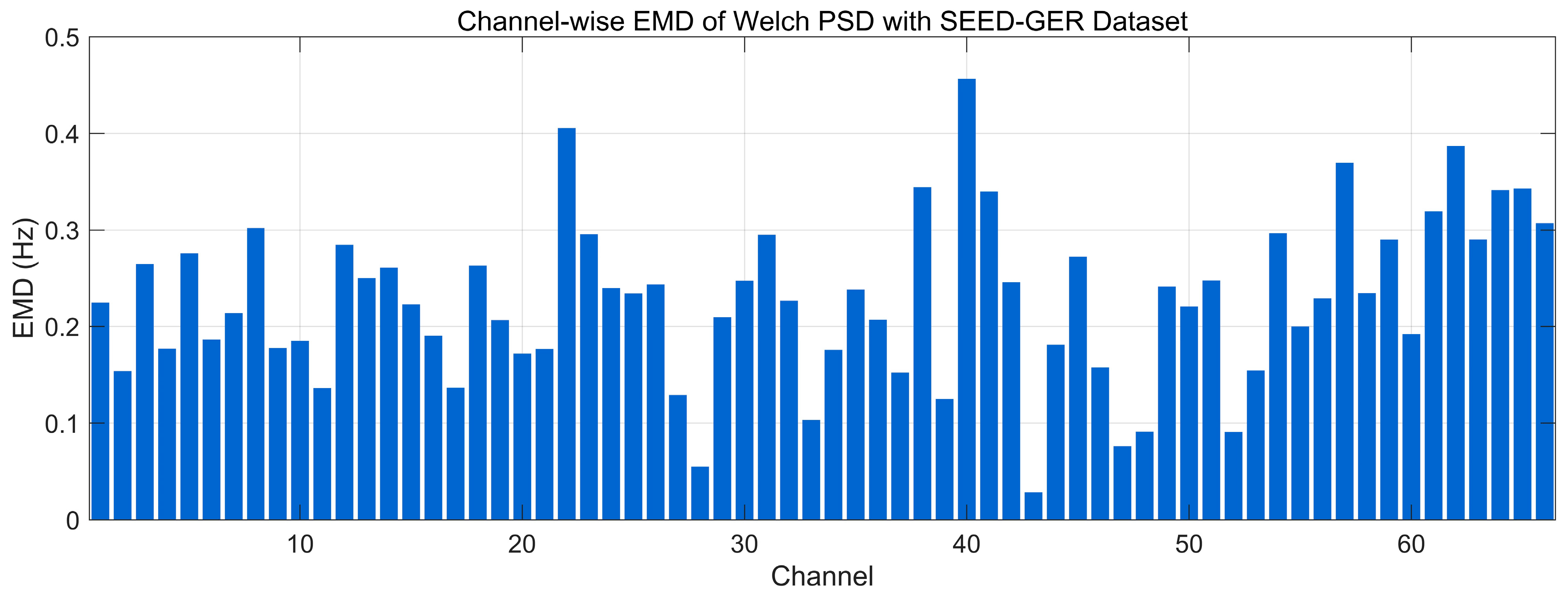
| Data Regime | Train Set | Validation/Test | Accuracy (Mean ± SD) | Precision (Mean ± SD) | Recall (Mean ± SD) | F1-Score (Mean ± SD) | AUC (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| Real EEG | Real | Real | 0.869 ± 0.102 | 0.863 ± 0.114 | 0.859 ± 0.132 | 0.860 ± 0.126 | 0.857 ± 0.107 |
| Generated EEG | Generated | Real | 0.823 ± 0.186 | 0.831 ± 0.194 | 0.834 ± 0.176 | 0.836 ± 0.182 | 0.832 ± 0.190 |
| Real + Generated EEG | Real + Generated | Real | 0.918 ± 0.094 | 0.921 ± 0.087 | 0.918 ± 0.096 | 0.903 ± 0.077 | 0.917 ± 0.084 |
| Data Regime | Train Set | Validation/Test | Accuracy (Mean ± SD) | Precision (Mean ± SD) | Recall (Mean ± SD) | F1-Score (Mean ± SD) | AUC (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| Real EEG | Real | Real | 0.835 ± 0.112 | 0.831 ± 0.121 | 0.839 ± 0.117 | 0.836 ± 0.124 | 0.826 ± 0.124 |
| Generated EEG | Generated | Real | 0.793 ± 0.176 | 0.784 ± 0.176 | 0.795 ± 0.169 | 0.782 ± 0.180 | 0.787 ± 0.173 |
| Real + Generated EEG | Real + Generated | Real | 0.884 ± 0.089 | 0.881 ± 0.073 | 0.878 ± 0.082 | 0.876 ± 0.074 | 0.881 ± 0.081 |
| Data Regime | Train Set | Validation/Test | Accuracy (Mean ± SD) | Precision (Mean ± SD) | Recall (Mean ± SD) | F1-Score (Mean ± SD) | AUC (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| Real EEG | Real | Real | 0.849 ± 0.113 | 0.854 ± 0.115 | 0.846 ± 0.121 | 0.853 ± 0.117 | 0.853 ± 0.119 |
| Generated EEG | Generated | Real | 0.809 ± 0.204 | 0.812 ± 0.210 | 0.808 ± 0.198 | 0.812 ± 0.202 | 0.814 ± 0.213 |
| Real + Generated EEG | Real + Generated | Real | 0.894 ± 0.102 | 0.892 ± 0.107 | 0.901 ± 0.113 | 0.903 ± 0.097 | 0.896 ± 0.104 |
| Model | Pearson (Mean ± SD) | Spearman (Mean ± SD) | KL Divergence (Mean ± SD) | FID (Mean ± SD) | EMD (Mean ± SD) |
|---|---|---|---|---|---|
| Baseline | 0.838 ± 0.075 | 0.819 ± 0.068 | 0.389 ± 0.145 | 13.962 ± 4.293 | 0.198 ± 0.089 |
| Without cVAE | 0.512 ± 0.104 | 0.516 ± 0.122 | 1.476 ± 0.254 | 18.894 ± 8.058 | 0.454 ± 0.243 |
| Without GAN | 0.521 ± 0.131 | 0.504 ± 0.132 | 1.545 ± 0.247 | 20.156 ± 8.156 | 0.584 ± 0.215 |
| Without Label Conditioning | 0.634 ± 0.086 | 0.621 ± 0.107 | 0.843 ± 0.176 | 16.453 ± 7.534 | 0.345 ± 0.156 |
| Without Positional Embedding | 0.612 ± 0.073 | 0.635 ± 0.096 | 0.957 ± 0.169 | 15.346 ± 6.453 | 0.376 ± 0.175 |
| Without Pearson Loss | 0.454 ± 0.156 | 0.476 ± 0.185 | 1.735 ± 0.243 | 21.445 ± 8.475 | 0.635 ± 0.234 |
| Without Transformer Encoder | 0.505 ± 0.116 | 0.543 ± 0.121 | 1.246 ± 0.028 | 19.473 ± 8.456 | 0.548 ± 0.164 |
| Transformer → CNN | 0.673 ± 0.145 | 0.667 ± 0.175 | 1.333 ± 0.168 | 18.437 ± 8.045 | 0.534 ± 0.237 |
| Model | Pearson (Mean ± SD) | Spearman (Mean ± SD) | KL Divergence (Mean ± SD) | FID (Mean ± SD) | EMD (Mean ± SD) |
|---|---|---|---|---|---|
| Baseline | 0.739 ± 0.120 | 0.721 ± 0.117 | 0.411 ± 0.195 | 5.275 ± 2.906 | 0.320 ± 0.100 |
| Without cVAE | 0.438 ± 0.183 | 0.413 ± 0.197 | 1.537 ± 0.354 | 9.453 ± 5.234 | 0.731 ± 0.315 |
| Without GAN | 0.427 ± 0.197 | 0.454 ± 0.204 | 1.678 ± 0.423 | 10.049 ± 4.456 | 0.794 ± 0.434 |
| Without Label Conditioning | 0.579 ± 0.164 | 0.543 ± 0.172 | 1.435 ± 0.275 | 8.134 ± 4.435 | 0.683 ± 0.286 |
| Without Positional Embedding | 0.516 ± 0.157 | 0.523 ± 0.184 | 1.535 ± 0.434 | 7.464 ± 3.537 | 0.647 ± 0.307 |
| Without Pearson Loss | 0.554 ± 0.146 | 0.549 ± 0.135 | 1.835 ± 0.354 | 7.587 ± 4.241 | 0.681 ± 0.314 |
| Without Transformer Encoder | 0.419 ± 0.201 | 0.425 ± 0.201 | 2.154 ± 0.546 | 11.946 ± 6.028 | 0.754 ± 0.412 |
| Transformer → CNN | 0.584 ± 0.175 | 0.548 ± 0.186 | 1.945 ± 0.712 | 7.944 ± 5.453 | 0.657 ± 0.284 |
| Model | Pearson (Mean ± SD) | Spearman (Mean ± SD) | KL Divergence (Mean ± SD) | FID (Mean ± SD) | EMD (Mean ± SD) |
|---|---|---|---|---|---|
| Baseline | 0.844 ± 0.068 | 0.831 ± 0.076 | 0.368 ± 0.184 | 15.308 ± 7.523 | 0.227 ± 0.084 |
| Without cVAE | 0.575 ± 0.172 | 0.548 ± 0.134 | 0.745 ± 0.542 | 18.453 ± 6.457 | 0.646 ± 0.143 |
| Without GAN | 0.546 ± 0.195 | 0.512 ± 0.143 | 0.764 ± 0.459 | 19.378 ± 8.435 | 0.682 ± 0.187 |
| Without Label Conditioning | 0.437 ± 0.176 | 0.487 ± 0.154 | 0.845 ± 0.453 | 19.547 ± 7.945 | 0.721 ± 0.195 |
| Without Positional Embedding | 0.543 ± 0.201 | 0.537 ± 0.194 | 0.794 ± 0.494 | 18.647 ± 7.547 | 0.675 ± 0.157 |
| Without Pearson Loss | 0.538 ± 0.168 | 0.546 ± 0.168 | 0.735 ± 0.427 | 17.287 ± 7.684 | 0.587 ± 0.135 |
| Without Transformer Encoder | 0.517 ± 0.157 | 0.508 ± 0.121 | 0.935 ± 0.543 | 17.548 ± 8.054 | 0.594 ± 0.154 |
| Transformer → CNN | 0.681 ± 0.167 | 0.654 ± 0.135 | 0.673 ± 0.354 | 18.387 ± 8.154 | 0.543 ± 0.123 |
| Model | Pearson (Mean ± SD) | Spearman (Mean ± SD) | KL Divergence (Mean ± SD) | FID (Mean ± SD) | EMD (Mean ± SD) |
|---|---|---|---|---|---|
| Baseline | 0.838 ± 0.075 | 0.819 ± 0.068 | 0.389 ± 0.145 | 13.962 ± 4.293 | 0.198 ± 0.089 |
| DCGAN | 0.543 ± 0.096 | 0.576 ± 0.105 | 0.635 ± 0.234 | 15.436 ± 3.957 | 0.323 ± 0.153 |
| WGAN | 0.567 ± 0.126 | 0.586 ± 0.135 | 0.536 ± 0.142 | 14.954 ± 4.982 | 0.424 ± 0.183 |
| WGAN-GP | 0.629 ± 0.084 | 0.694 ± 0.121 | 0.459 ± 0.139 | 14.532 ± 4.531 | 0.257 ± 0.136 |
| T-CGAN | 0.624 ± 0.093 | 0.657 ± 0.119 | 0.546 ± 0.176 | 15.168 ± 4.587 | 0.275 ± 0.149 |
| Model | Train Set | Validation/Test | Accuracy (Mean ± SD) | Precision (Mean ± SD) | Recall (Mean ± SD) | F1-Score (Mean ± SD) | AUC (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| Baseline | Real | Real | 0.869 ± 0.102 | 0.863 ± 0.114 | 0.859 ± 0.132 | 0.860 ± 0.126 | 0.857 ± 0.107 |
| Generated | Real | 0.823 ± 0.186 | 0.831 ± 0.194 | 0.834 ± 0.176 | 0.836 ± 0.182 | 0.832 ± 0.190 | |
| Real + Generated | Real | 0.918 ± 0.094 | 0.921 ± 0.087 | 0.918 ± 0.096 | 0.903 ± 0.077 | 0.917 ± 0.084 | |
| DCGAN | Real | Real | 0.869 ± 0.102 | 0.863 ± 0.114 | 0.859 ± 0.132 | 0.860 ± 0.126 | 0.857 ± 0.107 |
| Generated | Real | 0.803 ± 0.167 | 0.809 ± 0.186 | 0.806 ± 0.172 | 0.798 ± 0.163 | 0.796 ± 0.171 | |
| Real + Generated | Real | 0.881 ± 0.096 | 0.878 ± 0.102 | 0.876 ± 0.109 | 0.874 ± 0.104 | 0.877 ± 0.098 | |
| WGAN | Real | Real | 0.869 ± 0.102 | 0.863 ± 0.114 | 0.859 ± 0.132 | 0.860 ± 0.126 | 0.857 ± 0.107 |
| Generated | Real | 0.817 ± 0.169 | 0.821 ± 0.173 | 0.819 ± 0.176 | 0.820 ± 0.167 | 0.823 ± 0.162 | |
| Real + Generated | Real | 0.891 ± 0.104 | 0.889 ± 0.106 | 0.893 ± 0.097 | 0.892 ± 0.101 | 0.891 ± 0.106 | |
| WGAN-GP | Real | Real | 0.869 ± 0.102 | 0.863 ± 0.114 | 0.859 ± 0.132 | 0.860 ± 0.126 | 0.857 ± 0.107 |
| Generated | Real | 0.821 ± 0.186 | 0.818 ± 0.176 | 0.823 ± 0.168 | 0.819 ± 0.173 | 0.820 ± 0.157 | |
| Real + Generated | Real | 0.904 ± 0.099 | 0.901 ± 0.103 | 0.897 ± 0.101 | 0.903 ± 0.096 | 0.899 ± 0.093 | |
| T-CGAN | Real | Real | 0.869 ± 0.102 | 0.863 ± 0.114 | 0.859 ± 0.132 | 0.860 ± 0.126 | 0.857 ± 0.107 |
| Generated | Real | 0.812 ± 0.168 | 0.807 ± 0.159 | 0.809 ± 0.172 | 0.813 ± 0.163 | 0.811 ± 0.159 | |
| Real + Generated | Real | 0.886 ± 0.102 | 0.883 ± 0.106 | 0.878 ± 0.096 | 0.886 ± 0.093 | 0.879 ± 0.104 |
| Model | Pearson (Mean ± SD) | Spearman (Mean ± SD) | KL Divergence (Mean ± SD) | FID (Mean ± SD) | EMD (Mean ± SD) |
|---|---|---|---|---|---|
| Baseline | 0.739 ± 0.120 | 0.721 ± 0.117 | 0.411 ± 0.195 | 5.275 ± 2.906 | 0.320 ± 0.100 |
| DCGAN | 0.496 ± 0.103 | 0.481 ± 0.138 | 0.589 ± 0.261 | 8.354 ± 3.984 | 0.631 ± 0.203 |
| WGAN | 0.547 ± 0.135 | 0.537 ± 0.186 | 0.573 ± 0.234 | 7.545 ± 3.533 | 0.538 ± 0.251 |
| WGAN-GP | 0.603 ± 0.129 | 0.684 ± 0.139 | 0.510 ± 0.211 | 7.371 ± 2.574 | 0.357 ± 0.086 |
| T-CGAN | 0.594 ± 0.096 | 0.583 ± 0.126 | 0.476 ± 0.186 | 8.163 ± 3.896 | 0.376 ± 0.168 |
| Model | Train Set | Validation/Test | Accuracy (Mean ± SD) | Precision (Mean ± SD) | Recall (Mean ± SD) | F1-Score (Mean ± SD) | AUC (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| Baseline | Real | Real | 0.835 ± 0.112 | 0.831 ± 0.121 | 0.839 ± 0.117 | 0.836 ± 0.124 | 0.826 ± 0.124 |
| Generated | Real | 0.793 ± 0.176 | 0.784 ± 0.176 | 0.795 ± 0.169 | 0.782 ± 0.180 | 0.787 ± 0.173 | |
| Real + Generated | Real | 0.884 ± 0.089 | 0.881 ± 0.073 | 0.878 ± 0.082 | 0.876 ± 0.074 | 0.881 ± 0.081 | |
| DCGAN | Real | Real | 0.835 ± 0.112 | 0.831 ± 0.121 | 0.839 ± 0.117 | 0.836 ± 0.124 | 0.826 ± 0.124 |
| Generated | Real | 0.773 ± 0.201 | 0.770 ± 0.197 | 0.768 ± 0.194 | 0.776 ± 0.193 | 0.774 ± 0.213 | |
| Real + Generated | Real | 0.851 ± 0.124 | 0.853 ± 0.138 | 0.849 ± 0.132 | 0.852 ± 0.135 | 0.847 ± 0.129 | |
| WGAN | Real | Real | 0.835 ± 0.112 | 0.831 ± 0.121 | 0.839 ± 0.117 | 0.836 ± 0.124 | 0.826 ± 0.124 |
| Generated | Real | 0.776 ± 0.186 | 0.779 ± 0.173 | 0.784 ± 0.174 | 0.777 ± 0.182 | 0.782 ± 0.179 | |
| Real + Generated | Real | 0.861 ± 0.116 | 0.863 ± 0.106 | 0.859 ± 0.124 | 0.868 ± 0.097 | 0.864 ± 0.107 | |
| WGAN-GP | Real | Real | 0.835 ± 0.112 | 0.831 ± 0.121 | 0.839 ± 0.117 | 0.836 ± 0.124 | 0.826 ± 0.124 |
| Generated | Real | 0.781 ± 0.163 | 0.776 ± 0.159 | 0.778 ± 0.168 | 0.783 ± 0.135 | 0.778 ± 0.143 | |
| Real + Generated | Real | 0.867 ± 0.102 | 0.871 ± 0.093 | 0.873 ± 0.086 | 0.869 ± 0.106 | 0.870 ± 0.112 | |
| T-CGAN | Real | Real | 0.835 ± 0.112 | 0.831 ± 0.121 | 0.839 ± 0.117 | 0.836 ± 0.124 | 0.826 ± 0.124 |
| Generated | Real | 0.773 ± 0.172 | 0.771 ± 0.176 | 0.768 ± 0.196 | 0.762 ± 0.189 | 0.776 ± 0.168 | |
| Real + Generated | Real | 0.849 ± 0.084 | 0.847 ± 0.086 | 0.851 ± 0.076 | 0.849 ± 0.081 | 0.850 ± 0.093 |
| Model | Pearson (Mean ± SD) | Spearman (Mean ± SD) | KL Divergence (Mean ± SD) | FID (Mean ± SD) | EMD (Mean ± SD) |
|---|---|---|---|---|---|
| Baseline | 0.844 ± 0.068 | 0.831 ± 0.076 | 0.368 ± 0.184 | 15.308 ± 7.523 | 0.227 ± 0.084 |
| DCGAN | 0.568 ± 0.168 | 0.594 ± 0.172 | 0.531 ± 0.306 | 18.354 ± 8.461 | 0.513 ± 0.197 |
| WGAN | 0.506 ± 0.206 | 0.524 ± 0.234 | 0.608 ± 0.259 | 18.891 ± 8.648 | 0.672 ± 0.216 |
| WGAN-GP | 0.623 ± 0.106 | 0.648 ± 0.269 | 0.514 ± 0.183 | 17.541 ± 6.984 | 0.435 ± 0.105 |
| T-CGAN | 0.618 ± 0.083 | 0.615 ± 0.091 | 0.481 ± 0.241 | 17.764 ± 7.948 | 0.437 ± 0.117 |
| Model | Train Set | Validation/Test | Accuracy (Mean ± SD) | Precision (Mean ± SD) | Recall (Mean ± SD) | F1-Score (Mean ± SD) | AUC (Mean ± SD) |
|---|---|---|---|---|---|---|---|
| Baseline | Real | Real | 0.849 ± 0.113 | 0.854 ± 0.115 | 0.846 ± 0.121 | 0.853 ± 0.117 | 0.853 ± 0.119 |
| Generated | Real | 0.809 ± 0.204 | 0.812 ± 0.210 | 0.808 ± 0.198 | 0.812 ± 0.202 | 0.814 ± 0.213 | |
| Real + Generated | Real | 0.894 ± 0.102 | 0.892 ± 0.107 | 0.901 ± 0.113 | 0.903 ± 0.097 | 0.896 ± 0.104 | |
| DCGAN | Real | Real | 0.849 ± 0.113 | 0.854 ± 0.115 | 0.846 ± 0.121 | 0.853 ± 0.117 | 0.853 ± 0.119 |
| Generated | Real | 0.768 ± 0.189 | 0.772 ± 0.176 | 0.767 ± 0.184 | 0.756 ± 0.167 | 0.761 ± 0.172 | |
| Real + Generated | Real | 0.867 ± 0.119 | 0.863 ± 0.123 | 0.861 ± 0.117 | 0.867 ± 0.120 | 0.862 ± 0.131 | |
| WGAN | Real | Real | 0.849 ± 0.113 | 0.854 ± 0.115 | 0.846 ± 0.121 | 0.853 ± 0.117 | 0.853 ± 0.119 |
| Generated | Real | 0.773 ± 0.173 | 0.772 ± 0.154 | 0.768 ± 0.168 | 0.764 ± 0.171 | 0.774 ± 0.169 | |
| Real + Generated | Real | 0.872 ± 0.083 | 0.869 ± 0.094 | 0.873 ± 0.102 | 0.864 ± 0.099 | 0.871 ± 0.082 | |
| WGAN-GP | Real | Real | 0.849 ± 0.113 | 0.854 ± 0.115 | 0.846 ± 0.121 | 0.853 ± 0.117 | 0.853 ± 0.119 |
| Generated | Real | 0.791 ± 0.110 | 0.793 ± 0.103 | 0.801 ± 0.109 | 0.796 ± 0.104 | 0.794 ± 0.096 | |
| Real + Generated | Real | 0.883 ± 0.106 | 0.886 ± 0.092 | 0.879 ± 0.109 | 0.881 ± 0.086 | 0.884 ± 0.093 | |
| T-CGAN | Real | Real | 0.849 ± 0.113 | 0.854 ± 0.115 | 0.846 ± 0.121 | 0.853 ± 0.117 | 0.853 ± 0.119 |
| Generated | Real | 0.763 ± 0.194 | 0.772 ± 0.183 | 0.768 ± 0.173 | 0.765 ± 0.169 | 0.772 ± 0.164 | |
| Real + Generated | Real | 0.863 ± 0.112 | 0.861 ± 0.094 | 0.869 ± 0.106 | 0.871 ± 0.109 | 0.873 ± 0.097 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, Y.; Wang, X.; Hao, X.; Sun, H.; Dong, R.; Li, Y. Trans-cVAE-GAN: Transformer-Based cVAE-GAN for High-Fidelity EEG Signal Generation. Bioengineering 2025, 12, 1028. https://doi.org/10.3390/bioengineering12101028
Yao Y, Wang X, Hao X, Sun H, Dong R, Li Y. Trans-cVAE-GAN: Transformer-Based cVAE-GAN for High-Fidelity EEG Signal Generation. Bioengineering. 2025; 12(10):1028. https://doi.org/10.3390/bioengineering12101028
Chicago/Turabian StyleYao, Yiduo, Xiao Wang, Xudong Hao, Hongyu Sun, Ruixin Dong, and Yansheng Li. 2025. "Trans-cVAE-GAN: Transformer-Based cVAE-GAN for High-Fidelity EEG Signal Generation" Bioengineering 12, no. 10: 1028. https://doi.org/10.3390/bioengineering12101028
APA StyleYao, Y., Wang, X., Hao, X., Sun, H., Dong, R., & Li, Y. (2025). Trans-cVAE-GAN: Transformer-Based cVAE-GAN for High-Fidelity EEG Signal Generation. Bioengineering, 12(10), 1028. https://doi.org/10.3390/bioengineering12101028





