Anterior Cruciate Ligament Tear Detection Based on T-Distribution Slice Attention Framework with Penalty Weight Loss Optimisation
Abstract
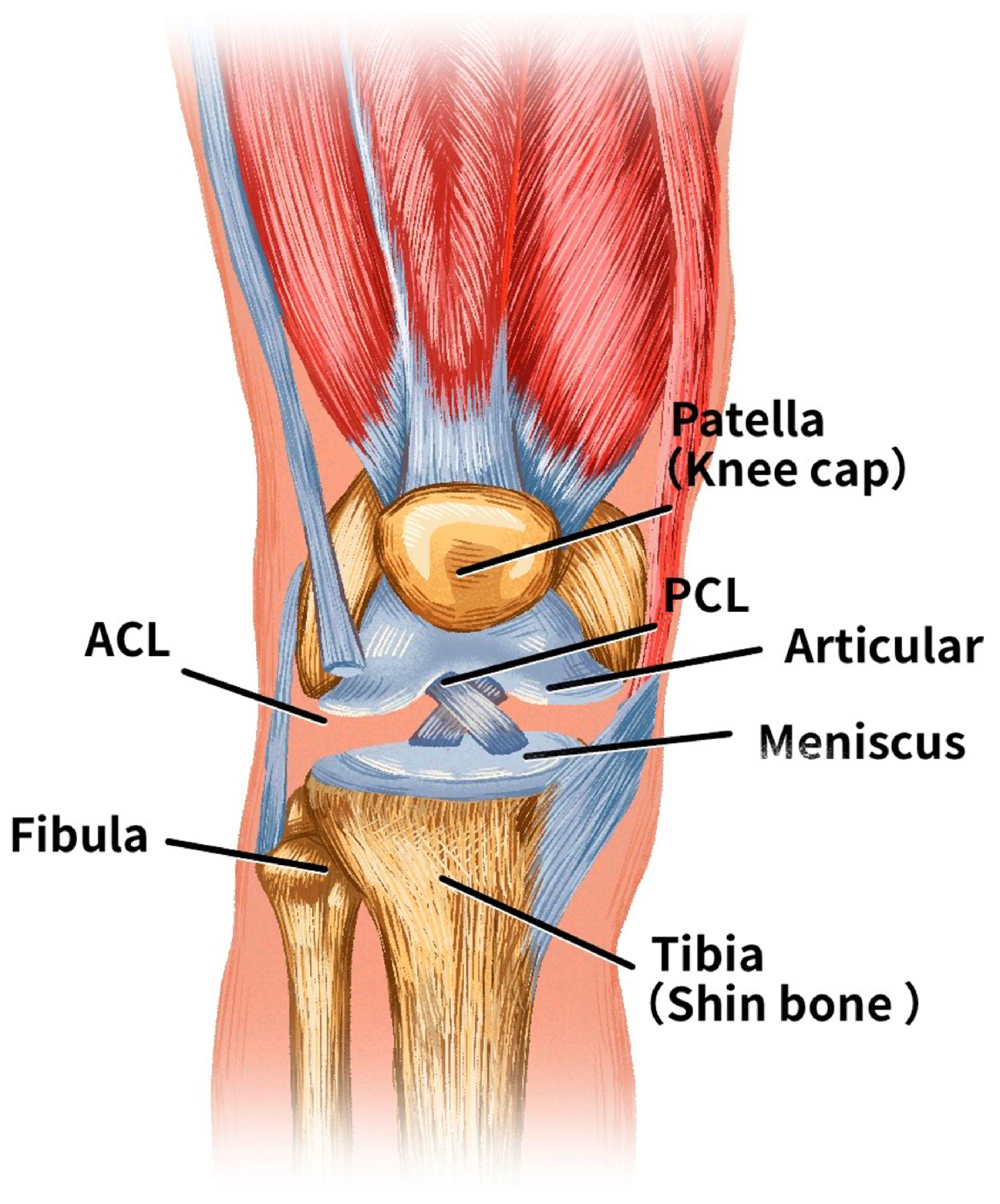
1. Introduction
- Development of a T-distribution slice filter: A T-distribution slice filter model was trained on the MRNet dataset to optimise slice selection for anterior cruciate ligament (ACL) imaging.
- Advanced loss function: Traditional cross-entropy loss was improved by integrating a penalty weight loss function. This modification accounts for previously unrecognised relationships between ACL categories, thereby improving the diagnostic performance of the model.
- Validation and performance: Experimental results using different backbone networks showed significant improvements with the proposed diagnostic framework. This framework provides an effective tool for ACL diagnosis to assist various clinicians in clinical settings.
2. Previous Related Works
2.1. ACL Diagnosis Model
2.2. Attention Mechanism
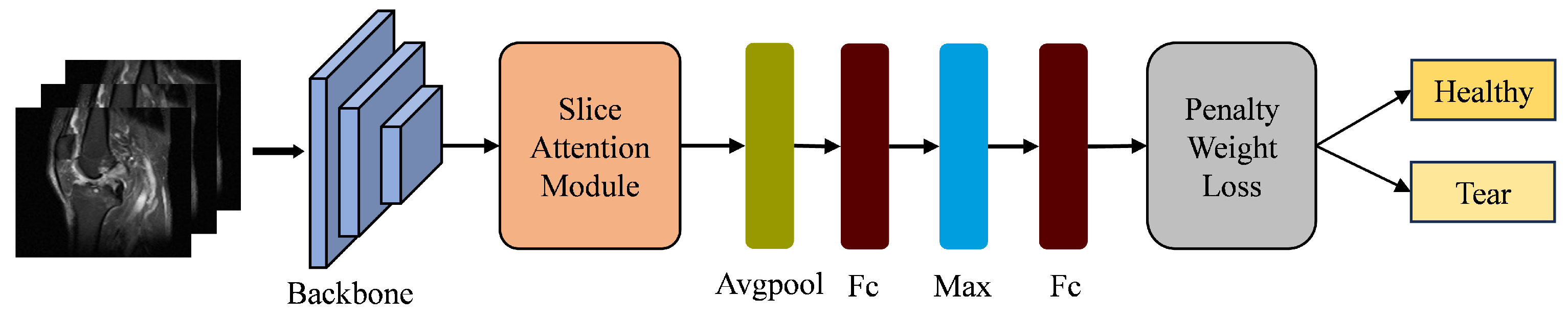
3. Deep Learning Model with Slice Attention Module and Penalty Weight Loss Function
3.1. Deep Learning Framework
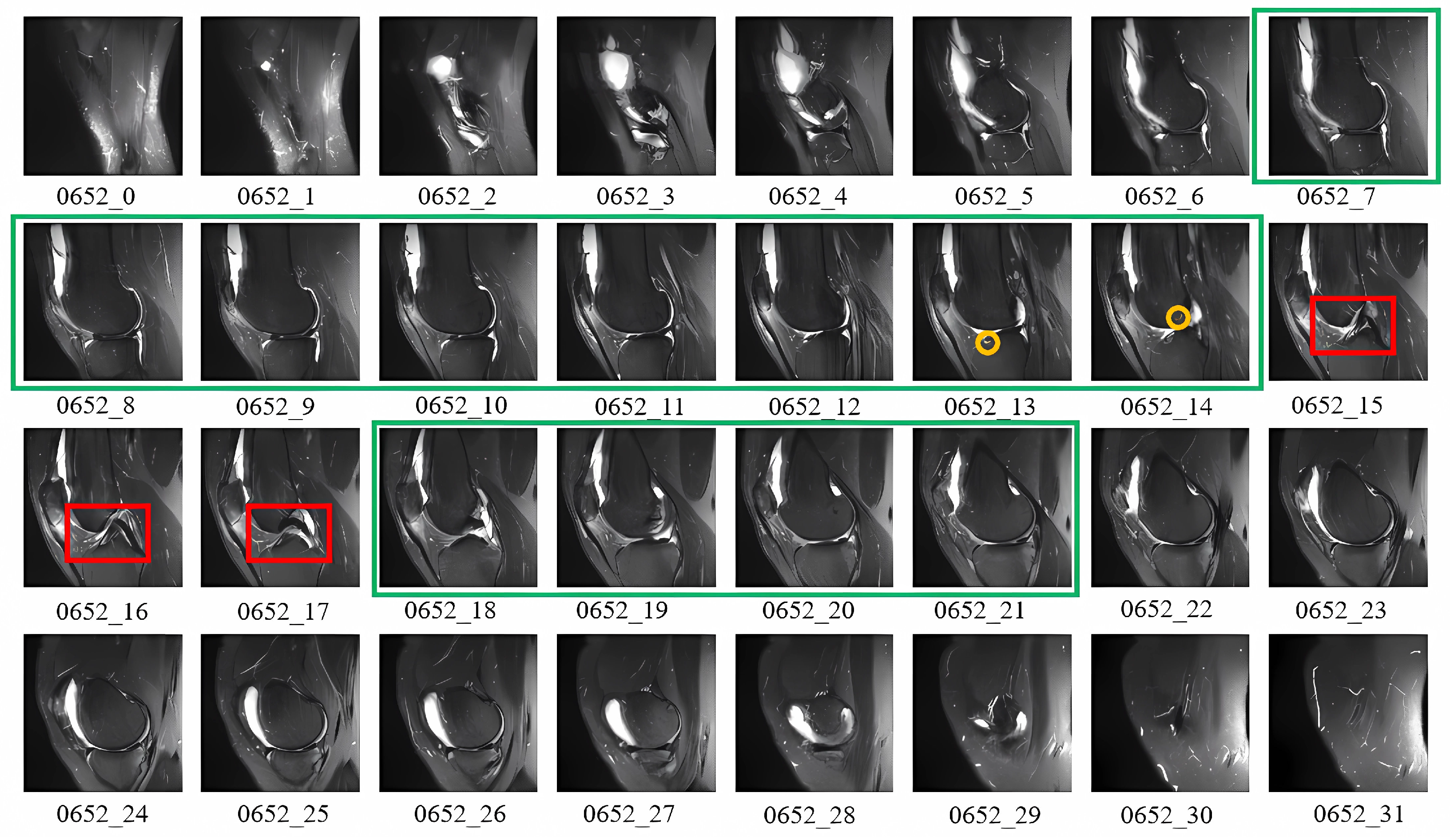
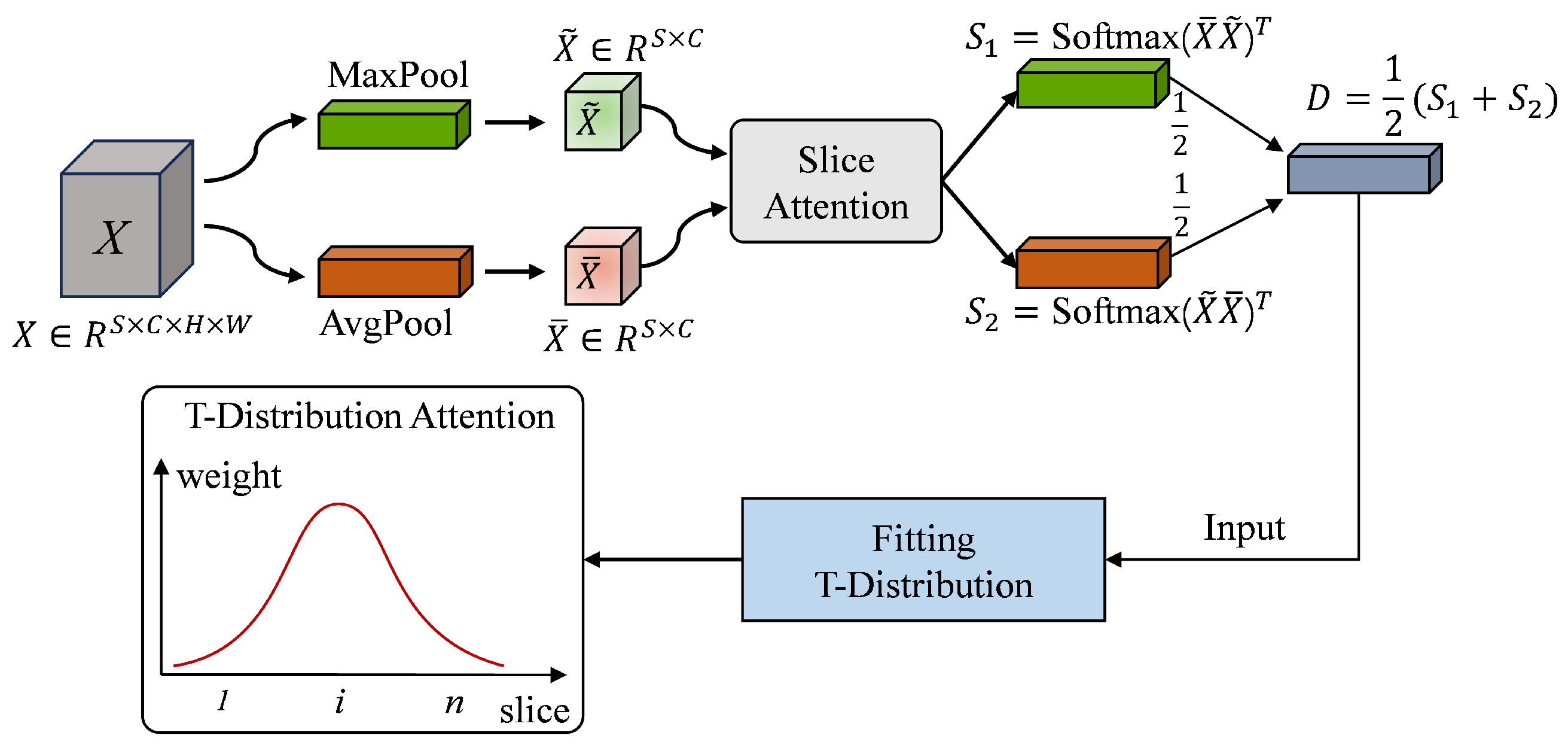
3.2. T-Distribution Slice Attention Module
| Algorithm 1 T-distribution Slice Attention |
|
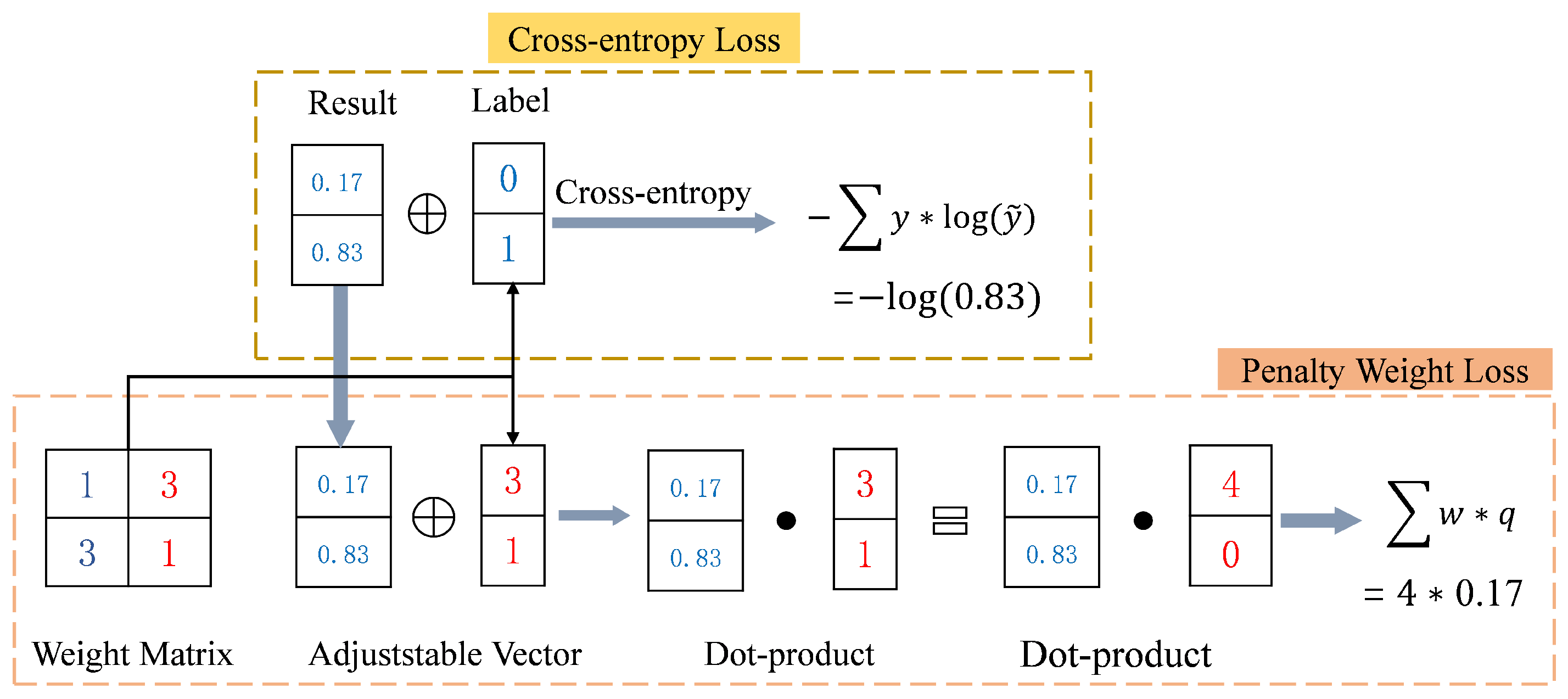
3.3. Penalty Weight Loss
4. Experiments and Results
4.1. MRNet Dataset and Preprocessing
4.2. Experimental Design and Evaluation Metrics
4.2.1. Experimental Design
4.2.2. Performance Evaluation Metrics
4.3. Experimental Result Analysis
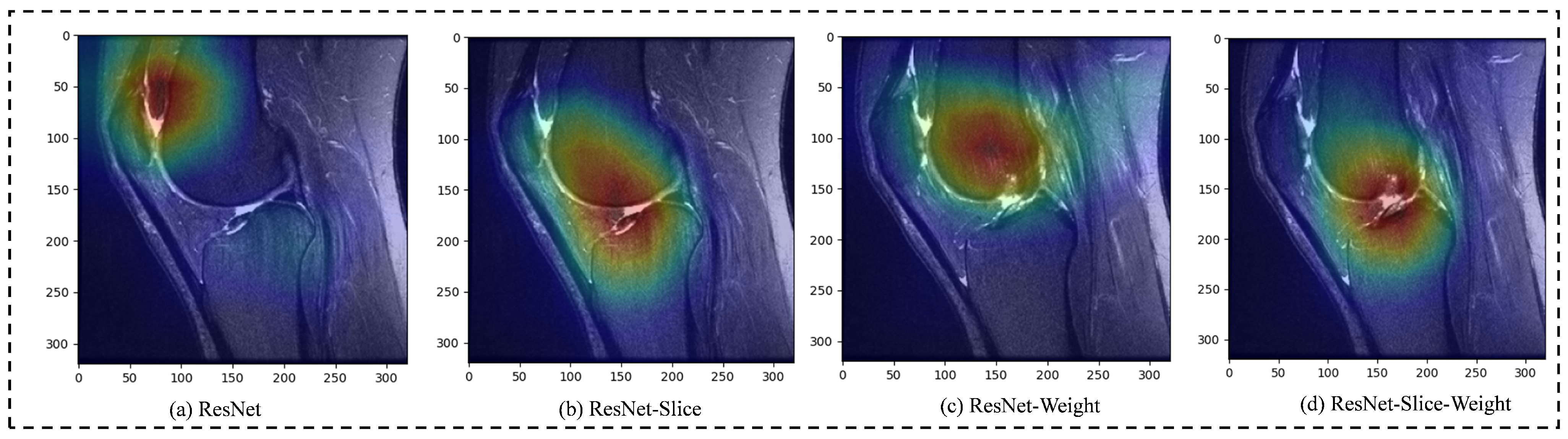
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, Y. Knee Joint Vibroarthrographic Signal Processing and Analysis; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Wu, Y.; Chen, P.; Luo, X.; Huang, H.; Liao, L.; Yao, Y.; Wu, M.; Rangayyan, R.M. Quantification of knee vibroarthrographic signal irregularity associated with patellofemoral joint cartilage pathology based on entropy and envelope amplitude measures. Comput. Meth. Prog. Bio. 2016, 130, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Duthon, V.; Barea, C.; Abrassart, S.; Fasel, J.; Fritschy, D.; Ménétrey, J. Anatomy of the anterior cruciate ligament. Knee Surg. Sport. Traumatol. Arthrosc. 2006, 14, 204–213. [Google Scholar] [CrossRef] [PubMed]
- Pache, S.; Aman, Z.; Kennedy, M.; Nakama, G.; Moatshe, G.; Ziegler, C.; LaPrade, R. Posterior cruciate ligament: Current concepts review. Arch. Bone Joint Surg. 2018, 6, 8–18. [Google Scholar] [CrossRef]
- Musahl, V.; Karlsson, J. Anterior cruciate ligament tear. N. Engl. J. Med. 2019, 380, 2341–2348. [Google Scholar] [CrossRef] [PubMed]
- Dekker, T.; Rush, J.; Schmitz, M. What’s new in pediatric and adolescent anterior cruciate ligament injuries? J. Pediatr. Orthoped. 2018, 38, 185–192. [Google Scholar] [CrossRef]
- Aichroth, P.; Patel, D.; Zorrilla, P. The natural history and treatment of rupture of the anterior cruciate ligament in children and adolescents: A prospective review. J. Bone Joint Surg. Br. 2002, 84, 38–41. [Google Scholar] [CrossRef]
- Heering, T.; Lander, N.; Barnett, L.; Ducan, M. What is needed to reduce the risk of anterior cruciate ligament injuries in children? Hearing from experts. Phys. Ther. Sport 2023, 61, 37–44. [Google Scholar] [CrossRef]
- Knapik, D.; Voos, J. Anterior cruciate ligament injuries in skeletally immature patients: A meta-analysis comparing repair versus reconstruction techniques. J. Pediatr. Orthoped. 2020, 40, 492–502. [Google Scholar] [CrossRef]
- Li, B.; Guo, Z.; Qu, J.; Zhan, Y.; Shen, Z.; Lei, X. The value of different involvement patterns of the knee “synovio-entheseal complex” in the differential diagnosis of spondyloarthritis, rheumatoid arthritis, and osteoarthritis: An MRI-based study. Eur. Radiol. 2023, 33, 3178–3187. [Google Scholar] [CrossRef]
- Lutz, P.M.; Höher, L.S.; Feucht, M.J.; Neumann, J.; Junker, D.; Wörtler, K.; Imhoff, A.B.; Achtnich, A. Ultrasound-based evaluation revealed reliable postoperative knee stability after combined acute ACL and MCL injuries. J. Exp. Orthop. 2021, 8, 76. [Google Scholar] [CrossRef]
- Iorio, R.; Vadalà, A.; Argento, G.; Di Sanzo, V.; Ferretti, A. Bone tunnel enlargement after ACL reconstruction using autologous hamstring tendons: A CT study. Int. Orthop. 2007, 31, 49–55. [Google Scholar] [CrossRef] [PubMed]
- Frobell, R.; Le Graverand, M.P.; Buck, R.; Roos, E.; Roos, H.; Tamez-Pena, J.; Totterman, S.; Lohmander, L. The acutely ACL injured knee assessed by MRI: Changes in joint fluid, bone marrow lesions, and cartilage during the first year. Osteoarthr. Cartil. 2009, 17, 161–167. [Google Scholar] [CrossRef] [PubMed]
- Crawford, R.; Walley, G.; Bridgman, S.; Maffulli, N. Magnetic resonance imaging versus arthroscopy in the diagnosis of knee pathology, concentrating on meniscal lesions and ACL tears: A systematic review. Brit. Med. Bull. 2007, 84, 5–23. [Google Scholar] [CrossRef]
- Liu, Y.; Song, C.; Ning, X.; Gao, Y.; Wang, D. nnSegNeXt: A 3D convolutional network for brain tissue segmentation based on quality evaluation. Bioengineering 2024, 11, 575. [Google Scholar] [CrossRef]
- Du, Y.; Wang, T.; Qu, L.; Li, H.; Guo, Q.; Wang, H.; Liu, X.; Wu, X.; Song, Z. Preoperative molecular subtype classification prediction of ovarian cancer based on multi-parametric magnetic resonance imaging multi-sequence feature fusion network. Bioengineering 2024, 11, 472. [Google Scholar] [CrossRef]
- Lee, J.; Lee, G.; Kwak, T.Y.; Kim, S.W.; Jin, M.S.; Kim, C.; Chang, H. MurSS: A multi-resolution selective segmentation model for breast cancer. Bioengineering 2024, 11, 463. [Google Scholar] [CrossRef]
- AlZoubi, A.; Eskandari, A.; Yu, H.; Du, H. Explainable DCNN decision framework for breast lesion classification from ultrasound images based on cancer characteristics. Bioengineering 2024, 11, 453. [Google Scholar] [CrossRef]
- Saeed, Z.; Bouhali, O.; Ji, J.X.; Hammoud, R.; Al-Hammadi, N.; Aouadi, S.; Torfeh, T. Cancerous and non-cancerous MRI classification using dual DCNN approach. Bioengineering 2024, 11, 410. [Google Scholar] [CrossRef]
- Zhang, M.; Huang, C.; Druzhinin, Z. A new optimization method for accurate anterior cruciate ligament tear diagnosis using convolutional neural network and modified golden search algorithm. Biomed. Signal Proces. 2024, 89, 105697. [Google Scholar] [CrossRef]
- Zhang, T.; Wei, D.; Zhu, M.; Gu, S.; Zheng, Y. Self-supervised learning for medical image data with anatomy-oriented imaging planes. Med. Image Anal. 2024, 94, 103151. [Google Scholar] [CrossRef]
- Bien, N.; Rajpurkar, P.; Ball, R.L.; Irvin, J.; Park, A.; Jones, E.; Bereket, M.; Patel, B.N.; Yeom, K.W.; Shpanskaya, K.; et al. Deep-learning-assisted diagnosis for knee magnetic resonance imaging: Development and retrospective validation of MRNet. PLoS Med. 2018, 15, e1002699. [Google Scholar] [CrossRef] [PubMed]
- Štajduhar, I.; Mamula, M.; Miletić, D.; Uenal, G. Semi-automated detection of anterior cruciate ligament injury from MRI. Comput. Meth. Prog. Bio. 2017, 140, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Awan, M.J.; Rahim, M.S.M.; Salim, N.; Mohammed, M.A.; Garcia-Zapirain, B.; Abdulkareem, K.H. Efficient detection of knee anterior cruciate ligament from magnetic resonance imaging using deep learning approach. Diagnostics 2021, 11, 105. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.H.; Kiryati, N.; Konen, E.; Eshed, I.; Mayer, A. Knee injury detection using MRI with efficiently-layered network (ELNet). In Proceedings of the Medical Imaging with Deep Learning, Montreal, QC, Canada, 6–8 July 2020; pp. 784–794. [Google Scholar]
- Dunnhofer, M.; Martinel, N.; Micheloni, C. Improving MRI-based knee disorder diagnosis with pyramidal feature details. In Proceedings of the Medical Imaging with Deep Learning, Lübeck, Germany, 7–9 July 2021; pp. 131–147. [Google Scholar]
- Belton, N.; Welaratne, I.; Dahlan, A.; Hearne, R.T.; Hagos, M.T.; Lawlor, A.; Curran, K.M. Optimising knee injury detection with spatial attention and validating localisation ability. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Oxford, UK, 12–14 July 2021; pp. 71–86. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention mechanisms in computer vision: A survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the 2018 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2018), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the 15th European Conference on Computer Vision (ECCV 2018), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar] [CrossRef]
- Fu, G.; Li, J.; Wang, R.; Ma, Y.; Chen, Y. Attention-based full slice brain CT image diagnosis with explanations. Neurocomputing 2021, 452, 263–274. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Zhang, Q.; Kim, J.; Zhang, S.; Gauthier, S.A.; Spincemaille, P.; Nguyen, T.D.; Sabuncu, M.; Wang, Y. RSANet: Recurrent slice-wise attention network for multiple sclerosis lesion segmentation. In Proceedings of the 22nd International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2019), Shenzhen, China, 13–17 October 2019; pp. 411–419. [Google Scholar] [CrossRef]
- Yu, C.; Wang, M.; Chen, S.; Qiu, C.; Zhang, Z.; Zhang, X. Improving anterior cruciate ligament tear detection and grading through efficient use of inter-slice information and simplified transformer module. Biomed. Signal Proces. 2023, 86, 105356. [Google Scholar] [CrossRef]
- Tao, Q.; Ge, Z.; Cai, J.; Yin, J.; See, S. Improving deep lesion detection using 3D contextual and spatial attention. In Proceedings of the 22nd International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2019), Shenzhen, China, 13–17 October 2019; pp. 185–193. [Google Scholar] [CrossRef]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view convolutional neural networks for 3D shape recognition. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV 2015), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar] [CrossRef]
- Robertson, P.L.; Schweitzer, M.E.; Bartolozzi, A.R.; Ugoni, A. Anterior cruciate ligament tears: Evaluation of multiple signs with MR imaging. Radiology 1994, 193, 829–834. [Google Scholar] [CrossRef]
- Tung, G.A.; Davis, L.M.; Wiggins, M.E.; Fadale, P.D. Tears of the anterior cruciate ligament: Primary and secondary signs at MR imaging. Radiology 1993, 188, 661–667. [Google Scholar] [CrossRef]
- Schlemper, J.; Oktay, O.; Schaap, M.; Heinrich, M.; Kainz, B.; Glocker, B.; Rueckert, D. Attention gated networks: Learning to leverage salient regions in medical images. Med. Image Anal. 2019, 53, 197–207. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial transformer networks. In Proceedings of the 28th International Conference on Neural Information Processing Systems (NeurIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 2017–2025. Available online: https://proceedings.neurips.cc/paper_files/paper/2015/file/33ceb07bf4eeb3da587e268d663aba1a-Paper.pdf (accessed on 24 July 2024).
- Guzzo, A.; Fortino, G.; Greco, G.; Maggiolini, M. Data and model aggregation for radiomics applications: Emerging trend and open challenges. Inform. Fusion 2023, 100, 101923. [Google Scholar] [CrossRef]
- Atmakuru, A.; Chakraborty, S.; Faust, O.; Salvi, M.; Barua, P.D.; Molinari, F.; Acharya, U.R.; Homaira, N. Deep learning in radiology for lung cancer diagnostics: A systematic review of classification, segmentation, and predictive modeling techniques. Expert Syst. Appl. 2024, 255, 124665. [Google Scholar] [CrossRef]
- Chen, P.; Gao, L.; Shi, X.; Allen, K.; Yang, L. Fully automatic knee osteoarthritis severity grading using deep neural networks with a novel ordinal loss. Comput. Med. Imag. Grap. 2019, 75, 84–92. [Google Scholar] [CrossRef]
- Nyúl, L.G.; Udupa, J.K. On standardizing the MR image intensity scale. Magn. Reson. Med. 1999, 42, 1072–1081. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Honolulu, HI, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), Las Vegas, NV, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2016), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient convolutional neural networks for mobile vision applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Tan, M.; Le, Q. EfficientNet: Rethinking model scaling for convolutional neural networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. Available online: https://proceedings.mlr.press/v97/tan19a.html (accessed on 24 July 2024).
- Motwani, A.; Shukla, P.K.; Pawar, M.; Kumar, M.; Ghosh, U.; Alnumay, W.; Nayak, S.R. Enhanced framework for COVID-19 prediction with computed tomography scan images using dense convolutional neural network and novel loss function. Comput. Electr. Eng. 2023, 105, 108479. [Google Scholar] [CrossRef]
- Papanastasiou, G.; Dikaios, N.; Huang, J.; Wang, C.; Yang, G. Is attention all you need in medical image analysis? A review. IEEE J. Biomed. Health 2023, 28, 1398–1411. [Google Scholar] [CrossRef]
- Iqbal, S.; Qureshi, A.N.; Aurangzeb, K.; Alhussein, M.; Haider, S.I.; Rida, I. AMIAC: Adaptive medical image analyzes and classification, a robust self-learning framework. Neural Comput. Appl. 2023; in press. [Google Scholar] [CrossRef]
- Azizi, S.; Culp, L.; Freyberg, J.; Mustafa, B.; Baur, S.; Kornblith, S.; Chen, T.; Tomasev, N.; Mitrović, J.; Strachan, P.; et al. Robust and data-efficient generalization of self-supervised machine learning for diagnostic imaging. Nat. Biomed. Eng. 2023, 7, 756–779. [Google Scholar] [CrossRef]
- Zeng, W.; Shan, L.; Yuan, C.; Du, S. Advancing cardiac diagnostics: Exceptional accuracy in abnormal ECG signal classification with cascading deep learning and explainability analysis. Appl. Soft Comput. 2024, 165, 112056. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, L.; Gu, X.; Zhang, M.; Qin, Y.; Yao, F.; Wang, Z.; Gu, Y.; Yang, G.Z. Trustworthy learning with (un) sure annotation for lung nodule diagnosis with CT. Med. Image Anal. 2023, 83, 102627. [Google Scholar] [CrossRef] [PubMed]
- Mosquera, C.; Ferrer, L.; Milone, D.H.; Luna, D.; Ferrante, E. Class imbalance on medical image classification: Towards better evaluation practices for discrimination and calibration performance. Eur. Radiol. 2024; in press. [Google Scholar] [CrossRef]
- Chamlal, H.; Kamel, H.; Ouaderhman, T. A hybrid multi-criteria meta-learner based classifier for imbalanced data. Knowl. Based Syst. 2024, 285, 111367. [Google Scholar] [CrossRef]
- Abbasian, M.; Khatibi, E.; Azimi, I.; Oniani, D.; Abad, S.H.Z.; Thieme, A.; Sriram, R.; Yang, Z.; Wang, Y.; Lin, B.; et al. Foundation metrics for evaluating effectiveness of healthcare conversations powered by generative AI. NPJ Digit. Med. 2024, 7, 82. [Google Scholar] [CrossRef] [PubMed]
- Akkem, Y.; Biswas, S.K.; Varanasi, A. A comprehensive review of synthetic data generation in smart farming by using variational autoencoder and generative adversarial network. Eng. Appl. Artif. Intel. 2024, 131, 107881. [Google Scholar] [CrossRef]
| Actual True Label | |||
|---|---|---|---|
| Positive Class | Negative Class | ||
| Predicted label | Positive class | TP | FP |
| Negative class | FN | TN | |
| Model | AUC | ACC | Precision | Recall | Specificity | |
|---|---|---|---|---|---|---|
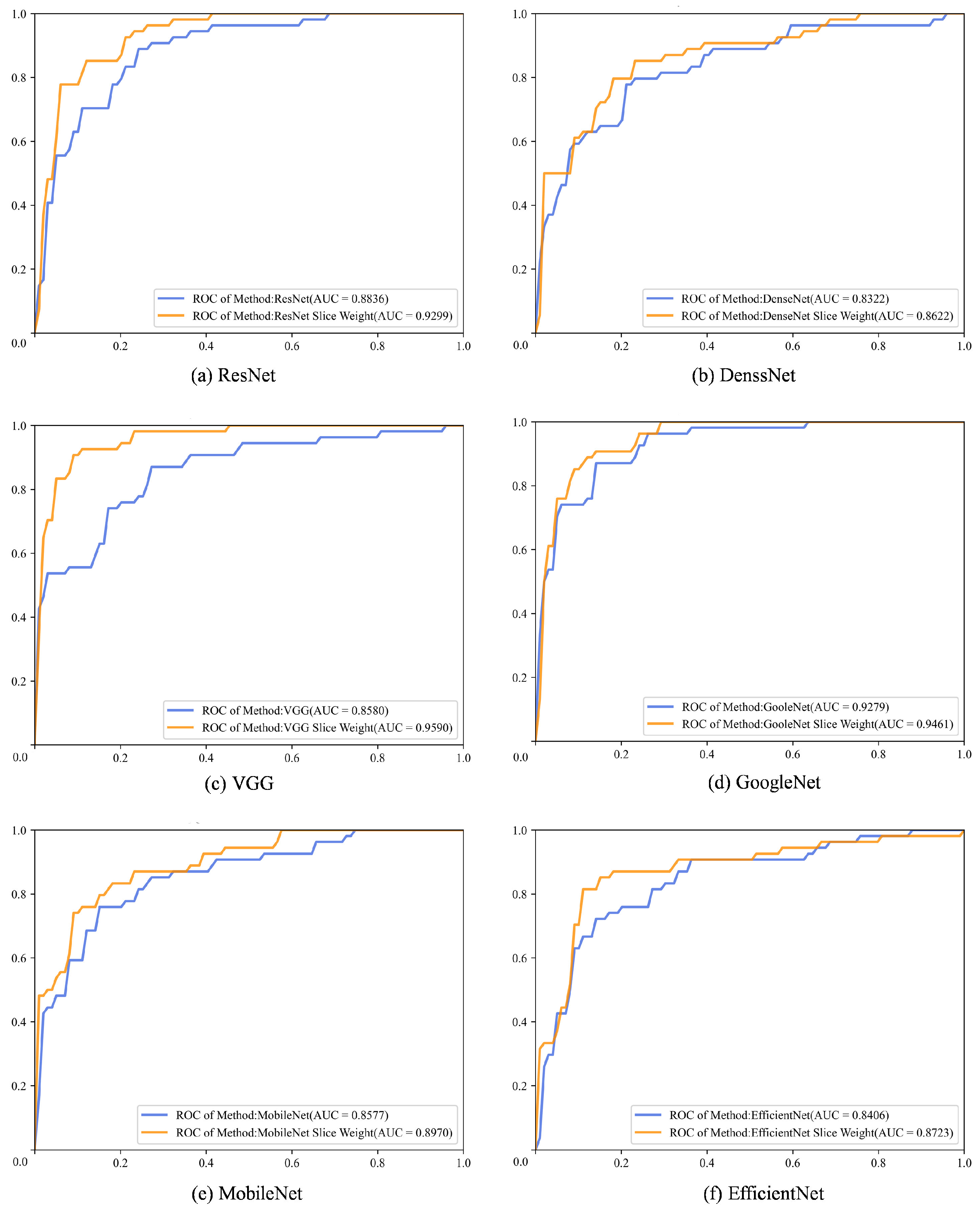
| ResNet-CE | 0.8836 | 0.7917 | 0.7899 | 0.7921 | 0.7879 | 0.7905 |
| ResNet-Weight | 0.9186 | 0.8333 | 0.8320 | 0.8350 | 0.8182 | 0.8326 |
| ResNet-Slice-CE | 0.9099 | 0.8250 | 0.8243 | 0.8274 | 0.8030 | 0.8244 |
| ResNet-Slice-Weight | 0.9299 | 0.8583 | 0.8646 | l0.8510 | 0.9242 | 0.8547 |
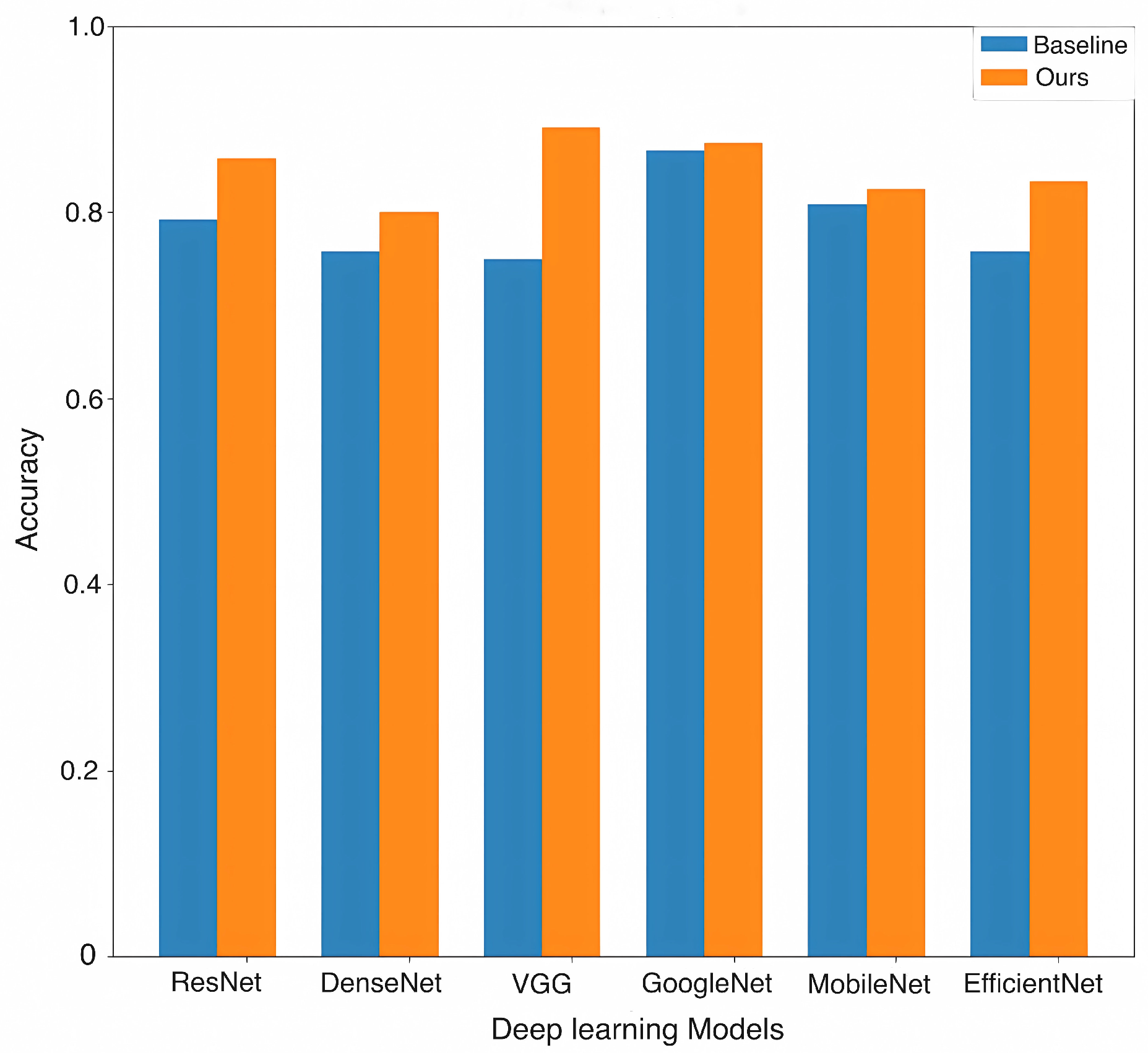
| Backbone | Methods | AUC | ACC | Precision | Recall | Specificity | |
|---|---|---|---|---|---|---|---|
| ResNet | Baseline | 0.8836 | 0.7917 | 0.7899 | 0.7921 | 0.7879 | 0.7905 |
| Ours | 0.9299 | 0.8583 | 0.8646 | 0.8510 | 0.9242 | 0.8547 | |
| DenseNet | Baseline | 0.8322 | 0.7583 | 0.7592 | 0.7619 | 0.7273 | 0.7579 |
| Ours | 0.8622 | 0.8000 | 0.7980 | 0.7980 | 0.8182 | 0.7980 | |
| VGG | Baseline | 0.8580 | 0.7500 | 0.7548 | 0.7391 | 0.8485 | 0.7413 |
| Ours | 0.9590 | 0.8917 | 0.8930 | 0.8880 | 0.9242 | 0.8899 | |
| GoogleNet | Baseline | 0.9279 | 0.8667 | 0.8650 | 0.8670 | 0.8636 | 0.8657 |
| Ours | 0.9461 | 0.8750 | 0.8760 | 0.8712 | 0.9091 | 0.8730 | |
| MobileNet | Baseline | 0.8577 | 0.8083 | 0.8078 | 0.8039 | 0.8485 | 0.8053 |
| Ours | 0.8970 | 0.8250 | 0.8233 | 0.8258 | 0.8182 | 0.8240 | |
| EfficientNet | Baseline | 0.8406 | 0.7583 | 0.7643 | 0.7652 | 0.6970 | 0.7583 |
| Ours | 0.8723 | 0.8333 | 0.8316 | 0.8316 | 0.8485 | 0.8316 |
| Backbone | Methods | Params | Params_Delta | Flops | Flops_Delta | Train_Time |
|---|---|---|---|---|---|---|
| ResNet | Baseline | 11,690.51 K | - | 113,240.46 K | - | 249.56 s |
| Ours | 11,690.54 K | 0.03 K | 113,240.47 K | 0.01 K | 262.09 s | |
| DenseNet | Baseline | 7979.86 K | - | 179,849.75 K | - | 267.25 s |
| Ours | 7979.89 K | 0.03 K | 179,849.76 K | 0.01 K | 280.33 s | |
| VGG | Baseline | 132,869.84 K | - | 470,390.17 K | - | 276.38 s |
| Ours | 132,869.87 K | 0.03 K | 470,390.18 K | 0.01 K | 286.06 s | |
| GoogleNet | Baseline | 23,835.57 K | - | 194,058.13 K | - | 260.15 s |
| Ours | 23,835.60 K | 0.03 K | 194,058.14 K | 0.01 K | 273.20 s | |
| MobileNet | Baseline | 3505.87 K | - | 20,297.49 K | - | 266.96 s |
| Ours | 3505.90 K | 0.03 K | 20,297.50 K | 0.01 K | 269.77 s | |
| EfficientNet | Baseline | 1324.02 K | - | 1716.29 K | - | 256.38 s |
| Ours | 1324.05 K | 0.03 K | 1716.30 K | 0.01 K | 268.08 s |
| Model | AUC | ACC | Precision | Recall | Specificity | |
|---|---|---|---|---|---|---|
| AlexNet [22] | 0.8836 | 0.8333 | 0.8354 | 0.8384 | 0.7879 | 0.8331 |
| ResNet-Space [27] | 0.8763 | 0.8000 | 0.8000 | 0.8030 | 0.7727 | 0.7995 |
| ELNET [25] | 0.8072 | 0.7167 | 0.7168 | 0.7071 | 0.8030 | 0.7086 |
| MRPyrNet-ELNET [26] | 0.9172 | 0.8333 | 0.8402 | 0.8249 | 0.9091 | 0.8286 |
| MRPyrNet-MRNet [26] | 0.9526 | 0.8417 | 0.8523 | 0.8510 | 0.7576 | 0.8417 |
| VGG-Slice-Weight | 0.9590 | 0.8917 | 0.8930 | 0.8880 | 0.9242 | 0.8899 |
| MRPyrNet-MRNet-Slice-Weight | 0.9686 | 0.8443 | 0.8884 | 0.8443 | 0.9848 | 0.8508 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Wu, Y. Anterior Cruciate Ligament Tear Detection Based on T-Distribution Slice Attention Framework with Penalty Weight Loss Optimisation. Bioengineering 2024, 11, 880. https://doi.org/10.3390/bioengineering11090880
Liu W, Wu Y. Anterior Cruciate Ligament Tear Detection Based on T-Distribution Slice Attention Framework with Penalty Weight Loss Optimisation. Bioengineering. 2024; 11(9):880. https://doi.org/10.3390/bioengineering11090880
Chicago/Turabian StyleLiu, Weiqiang, and Yunfeng Wu. 2024. "Anterior Cruciate Ligament Tear Detection Based on T-Distribution Slice Attention Framework with Penalty Weight Loss Optimisation" Bioengineering 11, no. 9: 880. https://doi.org/10.3390/bioengineering11090880
APA StyleLiu, W., & Wu, Y. (2024). Anterior Cruciate Ligament Tear Detection Based on T-Distribution Slice Attention Framework with Penalty Weight Loss Optimisation. Bioengineering, 11(9), 880. https://doi.org/10.3390/bioengineering11090880








