1. Introduction
Lately, transcranial magnetic stimulation (TMS) is undergoing significant interest due to its non-invasive approach and lower side effects than its counterparts [
1,
2,
3,
4,
5,
6]. TMS can be successfully used for diagnostic purposes (e.g., myelopathy, amyotrophic lateral sclerosis, and multiple sclerosis) or the treatment of several mental disorders. Recently, it received significant attention for its application in the treatment of Alzheimer’s disease in patients at the early stage of the pathology, as proposed by [
7], thanks to its ability to modulate the synaptic plasticity of specific brain areas devoted to memory and cognition. In all cases, a changing magnetic field is applied to induce an electric field at a specific area of the brain through Faraday’s law of induction.
During the design stage, the use of numerical tools for predicting this induced electric field is paramount. Low frequency (LF) numerical dosimetry for TMS studies is therefore more and more relevant [
8,
9,
10,
11]. Several ad hoc (or in-house) models have been developed [
12,
13,
14,
15,
16,
17,
18], but commercial software tools are more user-friendly and general-purpose. Among these, SimNIBS [
19] and Sim4Life (ZMT, Zurich MedTech, Zürich, Switzerland) are the most widely used. The former uses a pipeline that interpolates data from a Neuroimaging Informatics Technology Initiative (NifTI) format image to obtain a model with an unstructured tetrahedral mesh, whereas the latter employs voxel-based models in a structured or rectilinear grid. The computational techniques to evaluate the induced electric fields are based on the finite element method (FEM) for both software, but with different numerical solvers. The results of these two software packages have been compared in simplified geometries consisting of a homogeneous and non-homogeneous sphere or in a realistic anatomical model of the head and brain.
In the past, several inter-comparison studies have examined LF numerical issues [
20,
21,
22,
23]. These studies employed various anatomical models, but primarily focused on uniform exposures and voxelized models prone to staircasing errors, using methods like the scalar potential finite difference (SPFD) or the scalar potential finite element (SPFE). In a study by Poljak et al. [
15], different computational models and/or solvers (i.e., surface integral Equation (SIE)-based Method of Moments (SIE/MoM) [
14,
24], the FEM with cubical elements [
12], the BEM and the hybrid FEM/BEM [
25,
26], and the FEM with rectilinear elements using Sim4Life software [
15]) have been used for a non-uniform exposure (i.e., TMS application), but only for a homogeneous sphere or head. The only works where more realistic anatomical models for a TMS application were applied for both voxelized grids and tetrahedral mesh are found in [
16,
18,
27]. However, the comparison in the induced electric field (E-field) was made only for a simplified homogeneous sphere in [
16], or a multi-layered sphere with E-field looping tangentially on it [
18,
27], while for the realistic head, it was evaluated on a plane situated in the middle between the surfaces of the white and gray matter [
16] to avoid evaluating the field on the boundary of tissues having different conductivities. In [
27], the excitation source was also a simple circular coil far from realistic TMS applications, while in [
18], the head was made of four tissues only.
In this paper, the comparison between the two solvers adopting different grids (structured and unstructured) is, instead, performed in the overall domain consisting of both homogeneous and moreover non-homogeneous spheres intentionally created to enhance the induced E-field at these discontinuities that have been poorly investigated so far. A more realistic non-homogeneous anatomical model is also considered for TMS applications (with a realistic figure-of-8 coil) to validate both commercial software. These results could sign an important advancement in exposure assessment, which is based more and more on computational tools.
3. Results
Table 1 summarizes the maximum values of the E-field for all exposure scenarios considering an input current for the coil of 1 A. Looking at the
, the two software packages yield very close results, while the
exhibits a higher discrepancy. For both software packages,
overestimates the expected maximum induced field, so tetrahedral meshes are not capable of suppressing numerical errors caused by stair-casing in voxelized models when curved boundaries are approximated with voxels. However, nothing can be said about the actual maximum induced field, because, in such localized exposure with the figure-eight coil, no direct comparison with the analytic solution can be made. The contrast of conductivities between tissues and low-quality tetrahedral mesh cause numerical artifacts as well, but
calculated for both software return stable and comparable values.
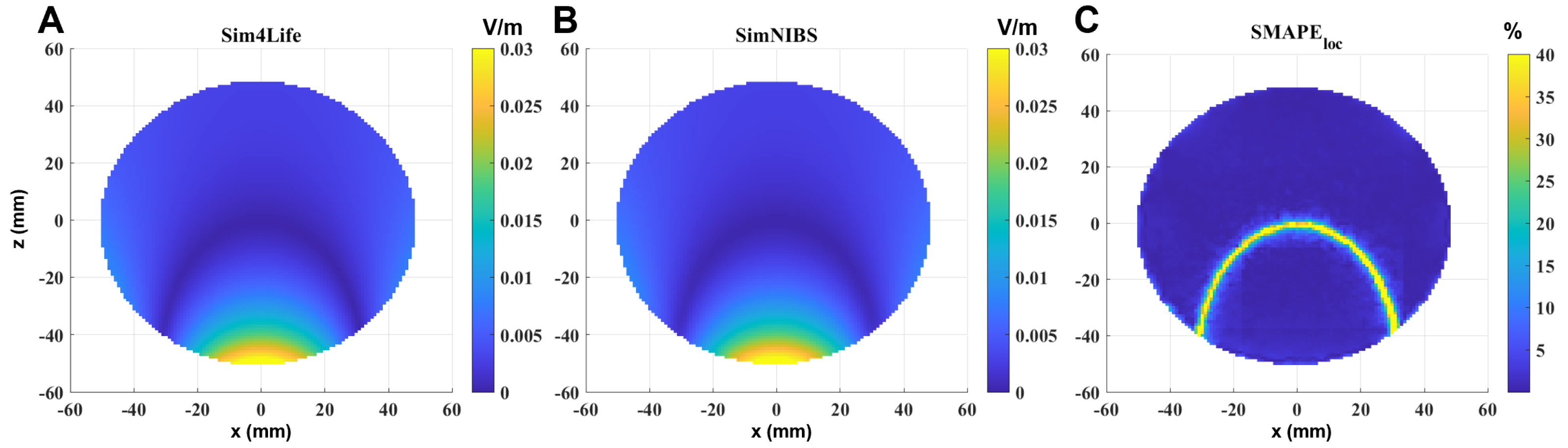
An example of E-field distribution induced in a single-shell sphere model calculated in Sim4Life (panel A) and in SimNIBS (panel B) for an input current of 1 A is reported in
Figure 2. The selected slice is perpendicular to the coil, and passes through the center of the sphere, i.e., also through the maximum of the localized induced E-field. By visual inspection, meshes and grids produce similar field distributions, meaning physically reasonable results. Panel C shows the
calculated in the sphere. To enhance visibility, the results have been saturated to 40%. As can be observed, the error becomes significant only in the volume in which the calculated E-field is very low, so it can be given to numerical errors.
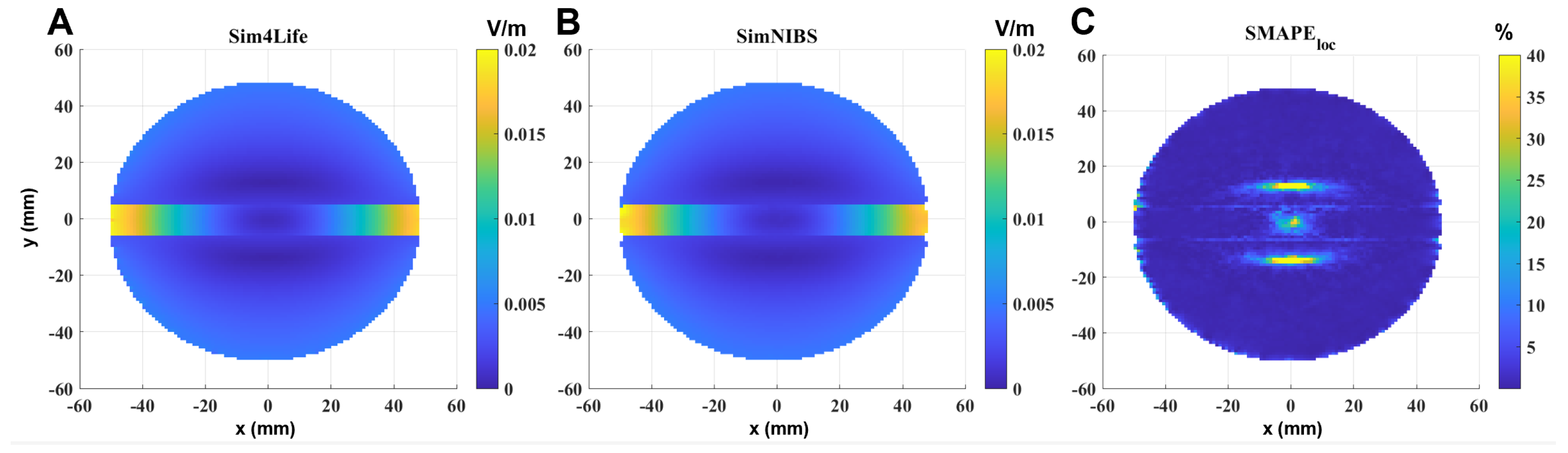
Similar considerations can be performed in the single-shell sphere with the orthogonal slab (
Figure 3). In this case, to better visualize what happens near the discontinuity between the two materials, the selected slice is parallel to the coil, perpendicular to the slab and passing through the center of the sphere. It is also possible to see that, in this case, the error is significant and exceeds 40% only where the calculated E-field is very low, i.e., in the inner part of the sphere (due to Faraday’s law); however, the error also slightly increases near the interface between the two materials (
Figure 3C).
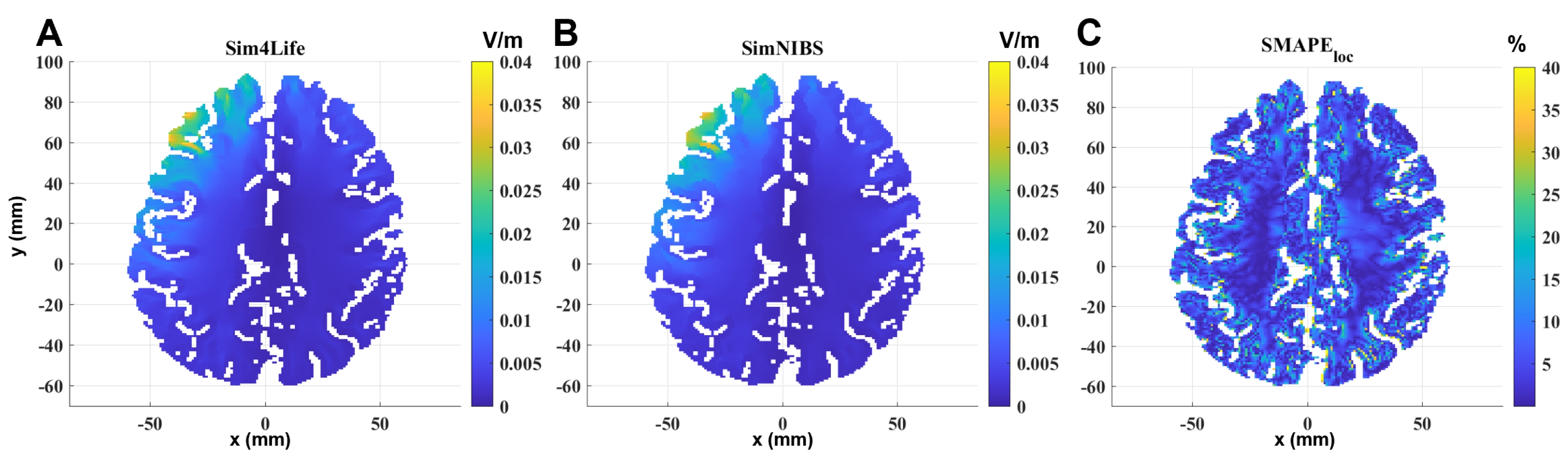
Figure 4 shows the same comparison on a transverse section passing through the maximum of the localized induced E-field of the MRI-derived head model. Results on materials not belonging to the brain are neglected, so the calculated E-field is shown only on the GM and WM. In this case, the geometrical and electrical discontinuities are more pronounced than in the other two models, and the difference between the two solvers becomes more evident at the interface between GM and WM and between GM and materials outside the brain.
Table 2 summarizes all of the global error metrics between the two software for the three models. As the model becomes more complex, the computational differences between the two software packages increase, albeit remaining within acceptable bounds (below 5% for the spherical models and below 12% for the realistic head model).
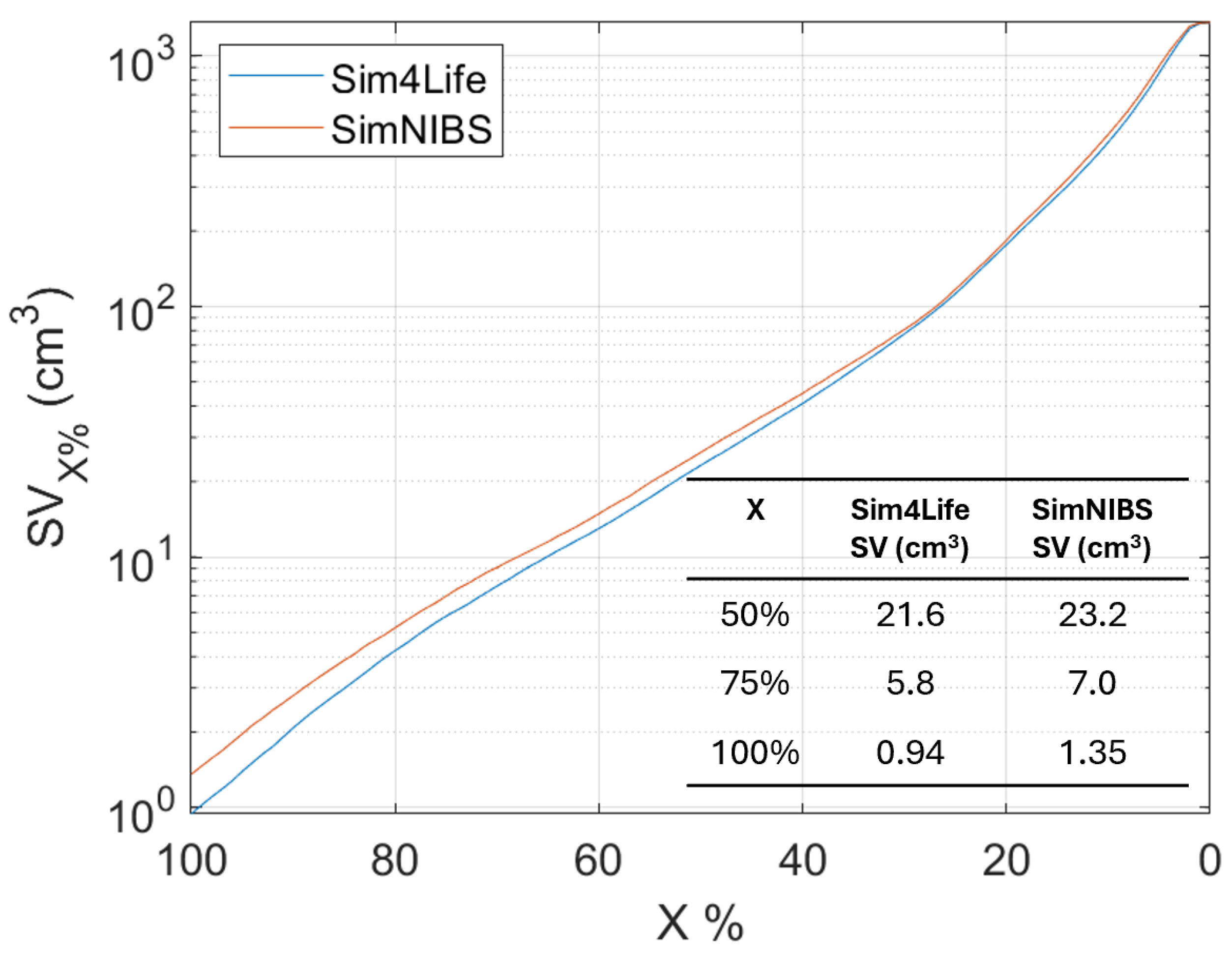
An analysis of the Stimulating Volume X (
), i.e., the volume exposed to E-field equal to or greater than
of
, varying
has been conducted for the head model (as shown in
Figure 5). This metric is interesting when a localized exposure is considered, because it is an estimation of the focality of the stimulation. In particular, many authors [
10] take the
to quantify the focality.
Figure 5 shows that the focality (
) slightly differs (of about 5%) between the two software.
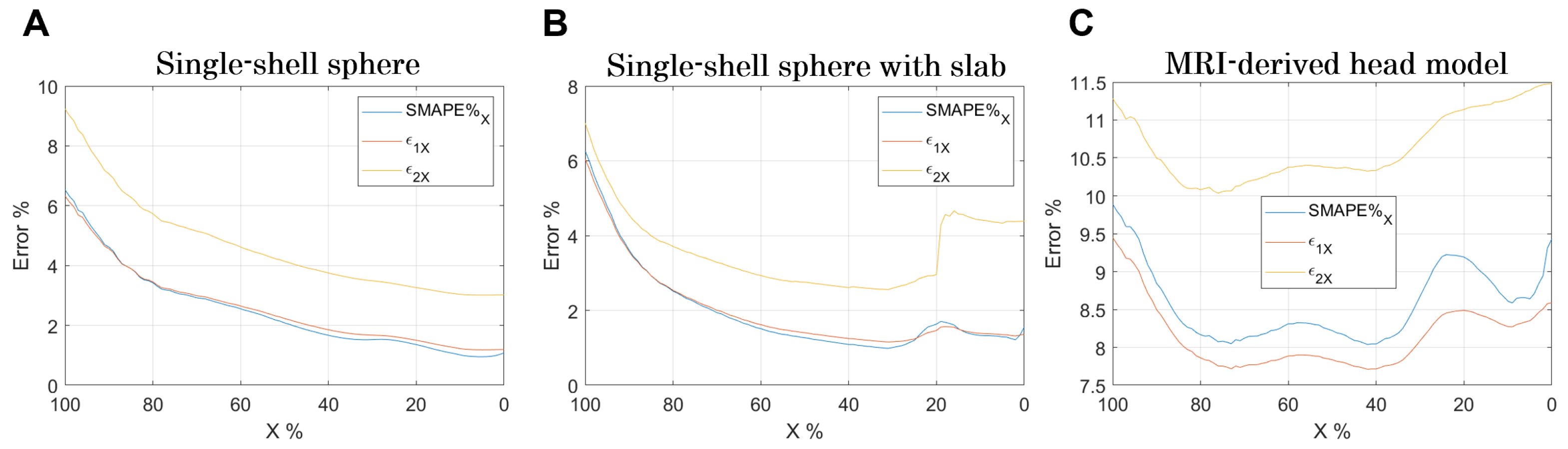
Finally, an analysis of the errors varying
is shown in
Figure 6. As
decreases, the comparison is conducted over an increasingly larger volume (
Figure 5). Indeed, when
, it means that the comparison is made in the volume in which the E-field is equal or higher than the
, whereas when
, the comparison is made in the entire volume.
Certainly, the stair-casing error, which, as already described, results in an overestimation of the E-field at certain points, and maximizes the error when the analysis focuses on that volume. However, by widening the analysis volume, the error reduces and increases again when considering volumes where the E-field is very low (
Figure 6B,C).
4. Discussion
The comparison of LF numerical dosimetry results between conformal and non-conformal discretization of the human bodies, specifically the head and brain, has been deeply investigated [
15,
16,
18,
27]. Usually, conformal meshes are employed in solvers adopting the FEM or BEM/MoM or hybrid combinations of them for solving the induced electric field. This generally yields more accurate results, at the expense however of computationally heavier simulations. On the other hand, non-conformal solvers (e.g., SPFD or SPFE) using rectilinear grids are easier and faster to implement but suffer from staircasing errors.
When doing this discretization comparison, particular attention must therefore be paid to aligning or “matching” the nodes of the meshes with those of the grids. More precisely, the barycenter of tetrahedra should coincide with that of the voxel, in order to have a fair comparison of the dielectric properties of the material and hence of the obtained results. This is what has been made in [
27,
40], where special focus has been given to the parameters used to generate the meshes.
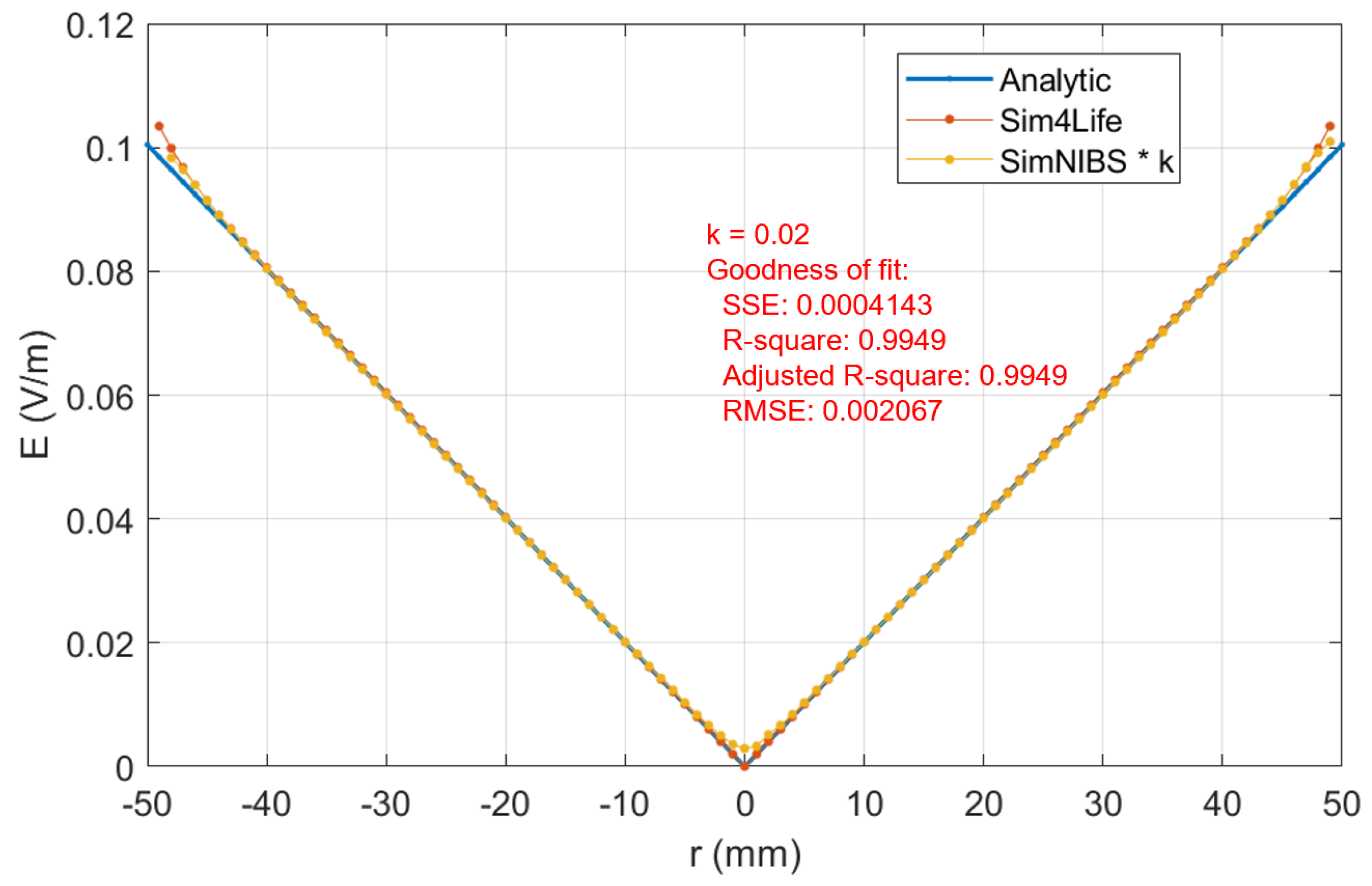
Such attention has been paid also in this study, where some parameters have been settled in SimNIBS to obtain a desired mesh. The rationale behind a fair comparison is to have a number of tetrahedral nodes similar to that of voxel numbers. This has been shown to be a good approach, as demonstrated in the supporting material with the analytic solution.
Besides paying attention to mesh generation, a lot of efforts have been made in the past to “remove” or quantify the staircasing error [
8,
35,
36,
37,
38,
39], finding, for instance, some smoothing techniques with fixed artifact removal (e.g., 99.9th or 99.99th [
35,
37,
38], rather than 99th percentiles (as suggested by ICNIRP-2010 [
41]) or flexible/variable removal artifact (depending on the grid resolution employed) [
36,
39]. However, among these suggested approaches, no one can be perfect in removing
of the numerical artifacts, as no analytic or experimental solution exists for realistic anatomical models. This is erroneously stated in [
16], even though we can draw the same conclusions that choosing a grid resolution of 1 mm (or below) is retained to be good enough for structured or rectilinear grids. Once again, this is confirmed by the results shown in our and their supporting materials when comparing the induced E-field in a homogeneous sphere with the analytic solution. Further, looking at the errors reported in
Figure 6, it emerges that their minimization is for X% between 40% and 60% for both software. This result indicates this volume % range as the optimal one for dosimetric assessment.
The comparison between structured and unstructured numerical solvers revealed that errors become more pronounced with increasing geometric complexity, this finding has several practical implications for TMS applications.
This comparison could be helpful when it is required to target small and specific brain regions. This is of interest for TMS applications in treating conditions such as Alzheimer’s disease [
7]. Their approach focuses on stimulating specific areas of the brain, which requires precise modeling to ensure effectiveness of the treatment. The increased error in complex geometries indicates the need for advanced solvers to accurately define exposure also in interconnected brain areas. This is important for TMS applications that aim to target networks of brain regions. Accurate modeling can help in understanding the effects of TMS on these interconnected areas, leading to more effective treatments. Understanding the limitations and potential errors of different numerical solvers can aid in optimizing TMS protocols. Clinicians and researchers can choose the most appropriate solver based on the complexity of the target geometry, improving the precision of TMS treatments and potentially enhancing clinical outcomes. In summary, the results underscore the importance of selecting the right numerical solver for accurate TMS application, particularly when dealing with complex brain geometries. This has direct implications for the treatment of neurological conditions like Alzheimer’s disease [
7], as well as for the broader use of TMS in targeting specific and interconnected brain areas.
Finally, regarding the comparison between the two commercial software packages, no preferences or endorsements are made. The computation time for the two software packages is comparable (below 10 s for the two spherical model, and about 2–3 min for the head model, cfr.
Figure 2,
Figure 3 and
Figure 4). The choice between the software packages should be based on practical considerations, such as the type of sources available. SimNIBS, for example, offers more specific commercial coils built into the software, while the other software may require the realization of specific geometries. Sim4Life, for instance, includes permittivity values for tissues, which are not included by default in the other software, and could be relevant in specific applications.
The flexibility in terms of GUI and computing interface varies, and the operator may prefer one over the other based on their skill set. Both software packages are user-friendly for standard cases and deliver computational results quickly.
Overall, these tools have the potential to open numerous doors in the treatment of various mental disorders using TMS applications. They allow for rigorous assessment of E-field values for different protocols in real-time patient scenarios.
5. Conclusions
In this study, a comparison of TMS dosimetry between structured and unstructured grids using different solvers was performed with the two most commonly used software packages for TMS dosimetry: Sim4Life and SimNIBS. The comparison was conducted on three different geometrical models of increasing complexity: a homogeneous sphere, a sphere with an internal discontinuity, and a head model derived from MRI data.
The results demonstrate that differences between the obtained results are larger as geometric complexity increases. However, these differences remain on overall contained (below 5% for spherical geometric models and below 12% for the head model) and locally significant only in areas of tissues where the electric field value is very low (and therefore much more susceptible to numerical errors) or, as expected, near the tissues discontinuities. These results could sign an important advancement in exposure assessment protocols, which are based more and more on computational tools.