Prostate Cancer Diagnosis via Visual Representation of Tabular Data and Deep Transfer Learning
Abstract
1. Introduction
- Radiographic and imaging-based diagnostic methods have shown high capabilities in detecting prostate cancer. However, these approaches often come at a high cost. Conversely, invasive procedures like biopsies raise concerns regarding potential harm to patients.
- Several of the aforementioned methods aim to reduce the need for invasive biopsies in prostate cancer diagnosis by utilizing machine learning techniques that rely on clinical biomarkers. These techniques utilize structured tabular data as input, which is easier and cheaper to obtain than medical images. Tabular data exhibit heterogeneity among their features, resulting in weaker correlations among them compared to homogeneous data, such as images or text. Tabular data often involve numerical and categorical features, where numerical features tend to have more dense representations, while categorical features tend to have more sparse representations. It thus becomes challenging to identify and exploit correlations among features without relying on spatial information.
- In classification problems involving tabular data, tree-based methods are frequently employed. These methods construct a hierarchical structure resembling a tree to make predictions about the target variable class using the available features. They are popular due to their ability to efficiently select relevant features and provide statistical information gains. Moreover, they offer advantages, such as quick training times, interpretability, and the ability to visualize the decision-making process, making them highly desirable for real-world applications.
- Deep neural networks (DNNs), particularly CNNs, excel in image classification tasks, offering automatic feature learning, spatial invariance, parameter sharing, and hierarchical representation. That is why they have been used in some existing approaches for PC diagnosis from radiographic [7,10,12] or histopathological images [8,9]. However, DNNs are not always effective for tabular data classification compared to tree-based methods. This justifies the few reported DNN-based methods for PC detection from non-radiographic data.
2. Dataset
3. Methods
3.1. Classical Machine Learning Methods
3.2. Tree-Based Machine Learning Methods
3.3. Deep Learning Methods for Tabular Data
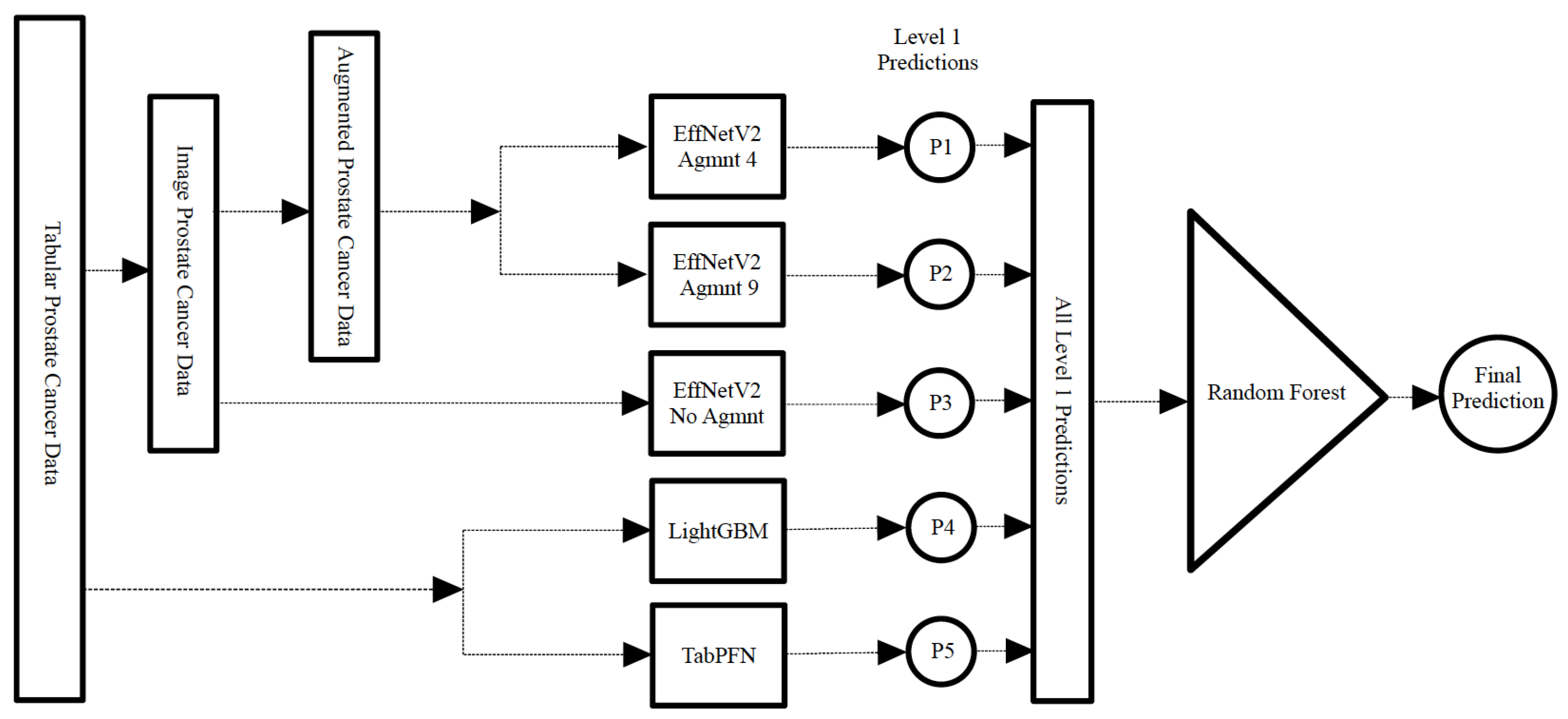
3.4. Ensemble Models
3.4.1. Voting Classifiers
3.4.2. Stacking Classifier
3.5. Tab2Visual: Graphical Representation of Tabular Data
- Data normalization: We begin by applying min-max normalization to the tabular dataset, ensuring that each feature’s values are scaled within the range [0, 1]. This normalization process standardizes the data and facilitates consistent comparisons between features.
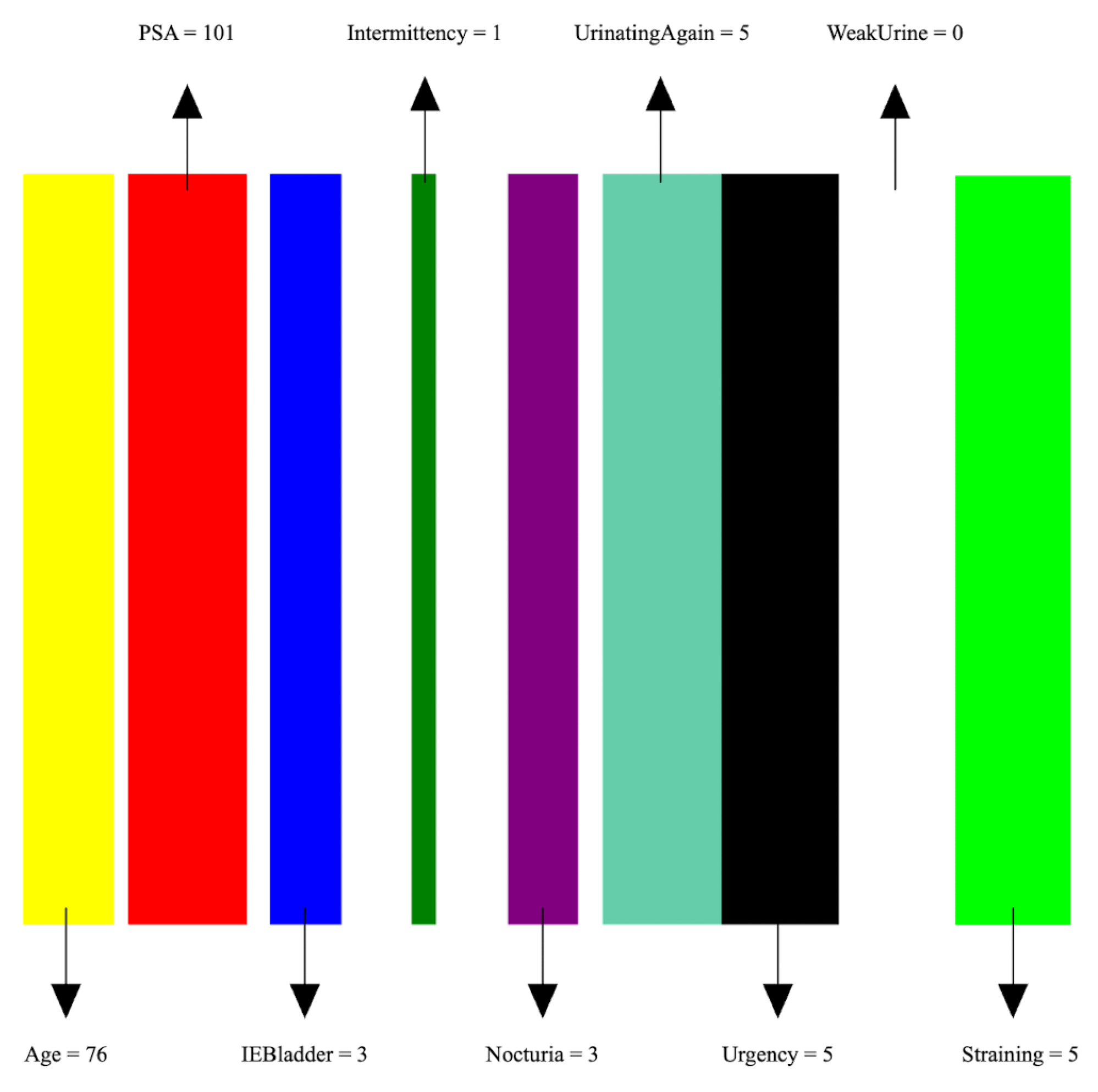
- Image preparation: We then create a visual representation by creating an image that consists of as many vertical bars as the number of features, m, in the dataset. Each bar has a maximum width of , where w is the image width, thus ensuring an equal division of the image’s spatial space among the features. For example, our prostate dataset has 9 features, thus the image representation for each sample consists of 9 bars, see Figure 5.
- Feature encoding: Each feature i is encoded as a vertical bar in the image, such that the bar width is taken as , where is the normalized feature value. A feature with the maximum normalized value of 1 will occupy the full bar width b. This encoding of features as width-modulated bars visually preserves the relative magnitudes of the features in the image. Additionally, each feature is assigned a distinct color for easier visual identification.An example is shown in Figure 5 which shows an image representation of a sample of the prostate cancer data.
- Image augmentation: In order to increase the data size, we apply various image augmentation techniques to each image. While image mirroring, rotation, and translation are more commonly used in the literature for this purpose, we propose to use a different set of operations that better fit the semantics of the image contents. We propose to employ elastic distortion, and the morphological operations of dilation, erosion, closing, and opening, with various degrees. These operations introduce subtle variations in the bar edges and cause varying degrees of widening or shrinking effects on the image bars. This in turn helps generate novel synthetic training samples for classification model training, improving the model’s generalization to unseen data.More specifically, our augmentation procedure first applies elastic distortion with a random deformation strength to the image. Then, morphological dilation and erosion are performed on the image with random probabilities in a random order with a structuring element of random size. This results in an image being subjected to dilation only, erosion only, dilation followed by erosion (morphological closing), or erosion followed by dilation (morphological opening) with random varying degrees. Figure 6 illustrates three samples of the PC dataset in image representations along with some of their augmentations.
- Transfer learning with CNNs: A CNN can then be trained on the augmented dataset. To leverage the power of deep learning in image classification, we adopt transfer learning with state-of-the-art CNN models. The augmented dataset is utilized to fine-tune these pre-trained models, allowing the network to learn meaningful patterns from the transformed tabular data images.
4. Evaluation Metrics
4.1. Precision
4.2. Recall
4.3. F1-Score
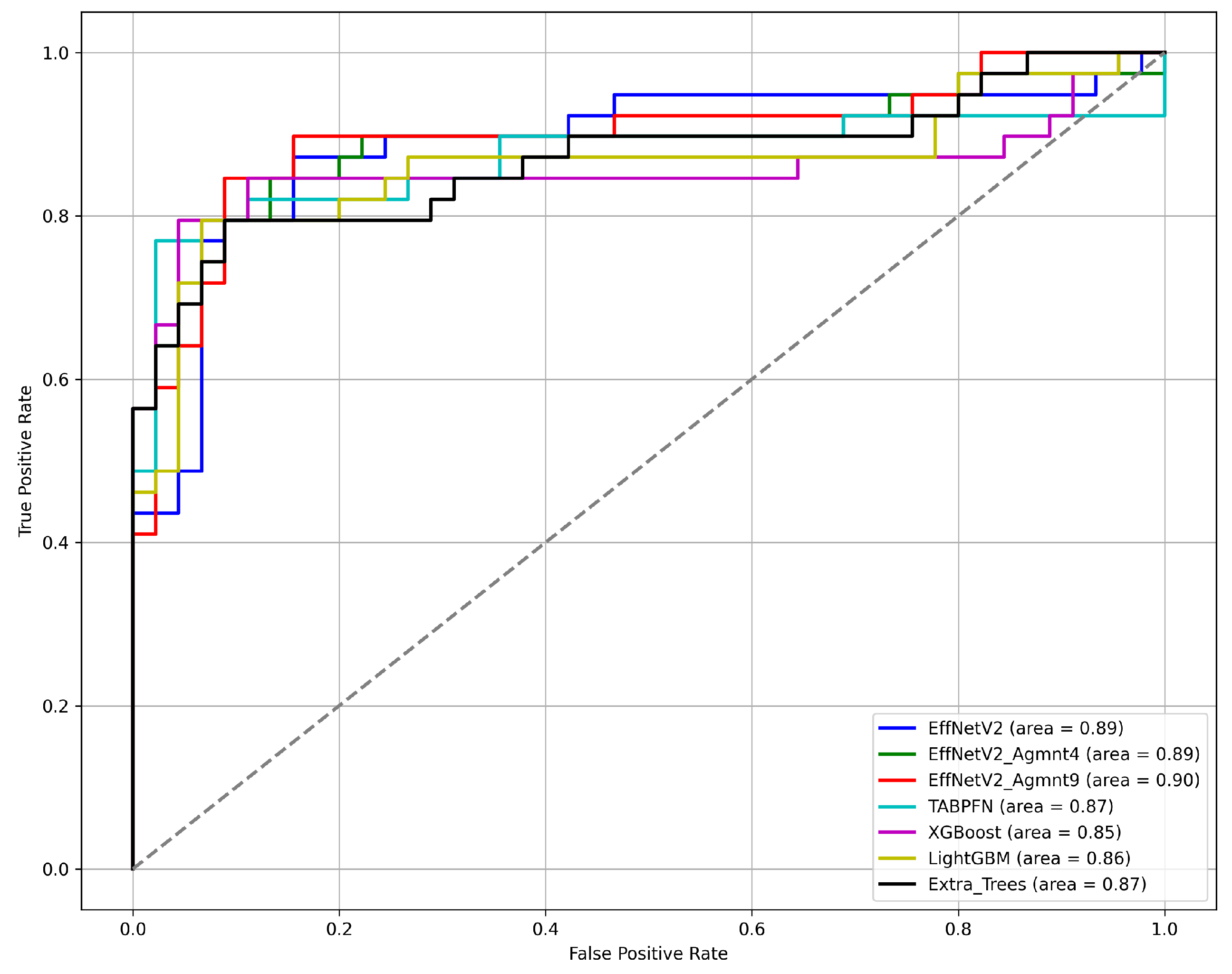
4.4. Area under the Curve (AUC)
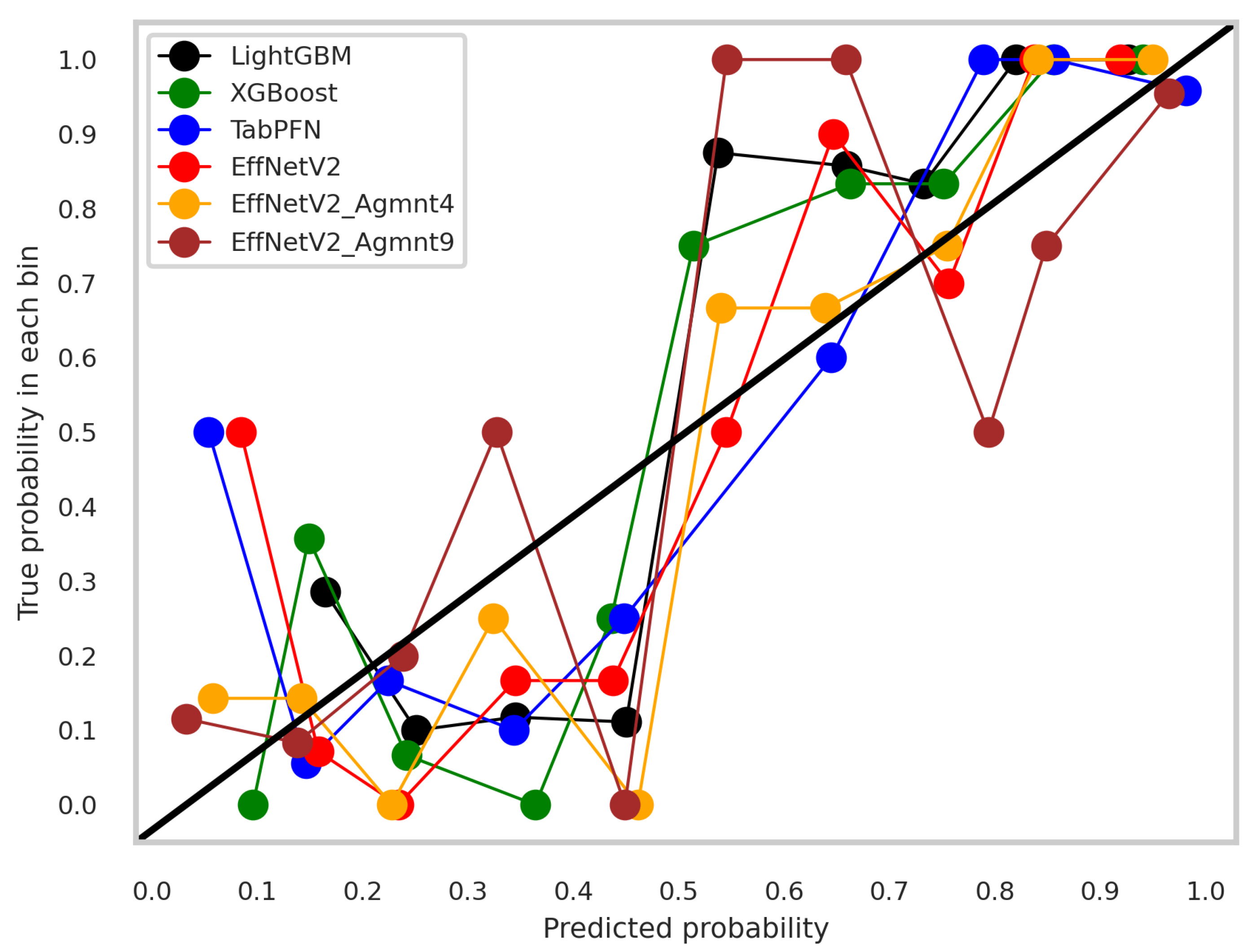
5. Experimental Results
5.1. Experiments on Tabular Representations
5.2. Experiments on Image Representations
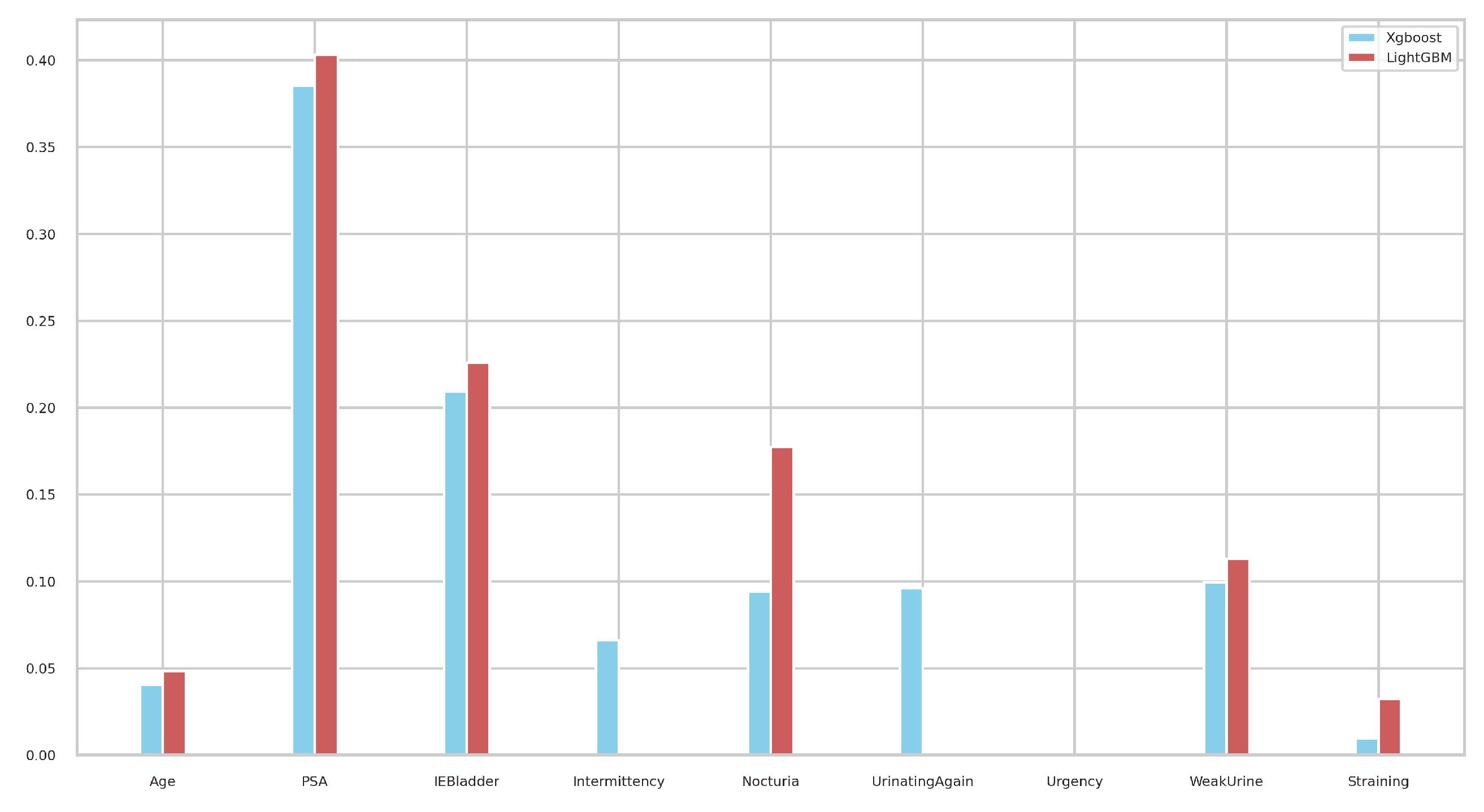
5.3. Discussion
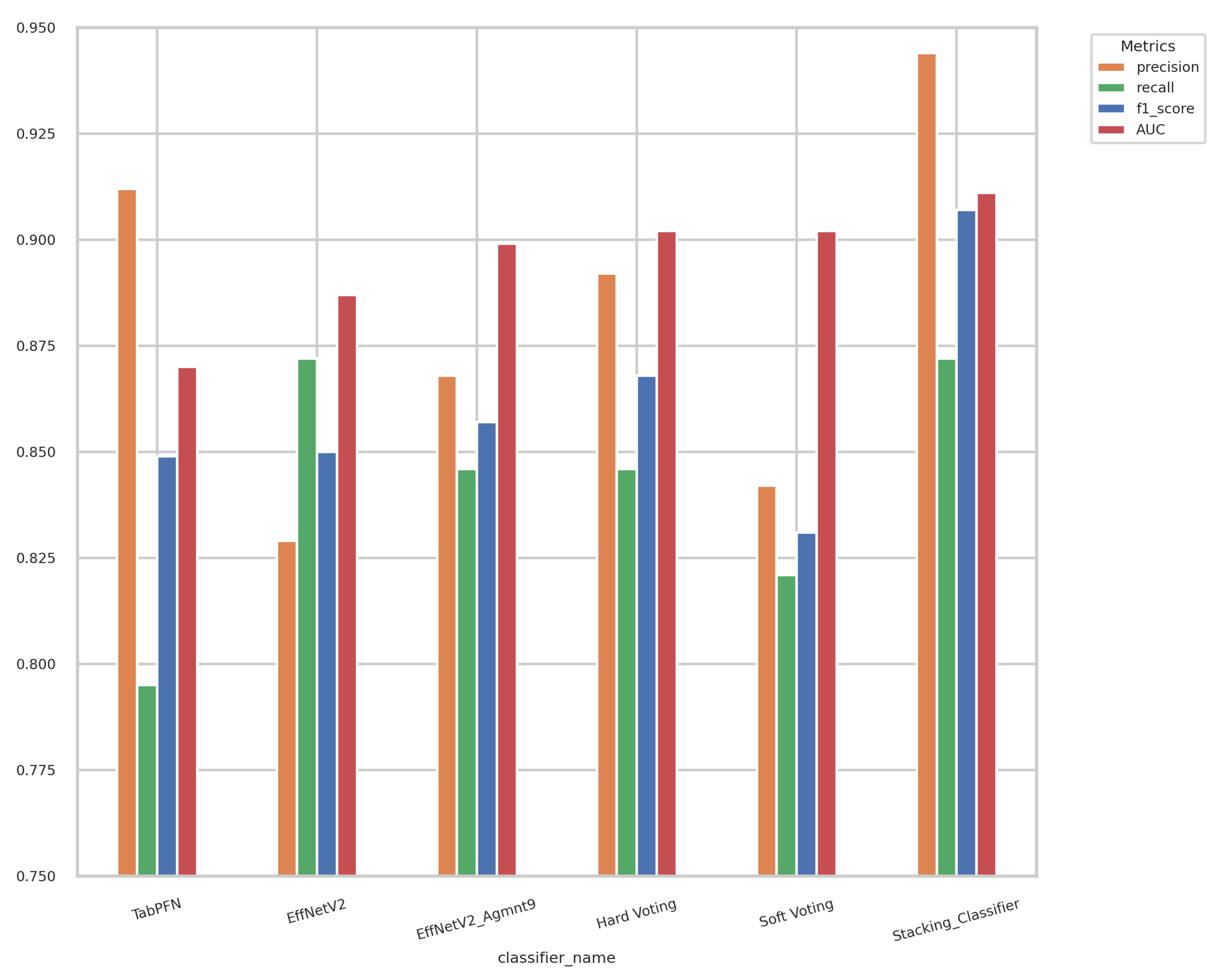
5.4. Ensemble Models
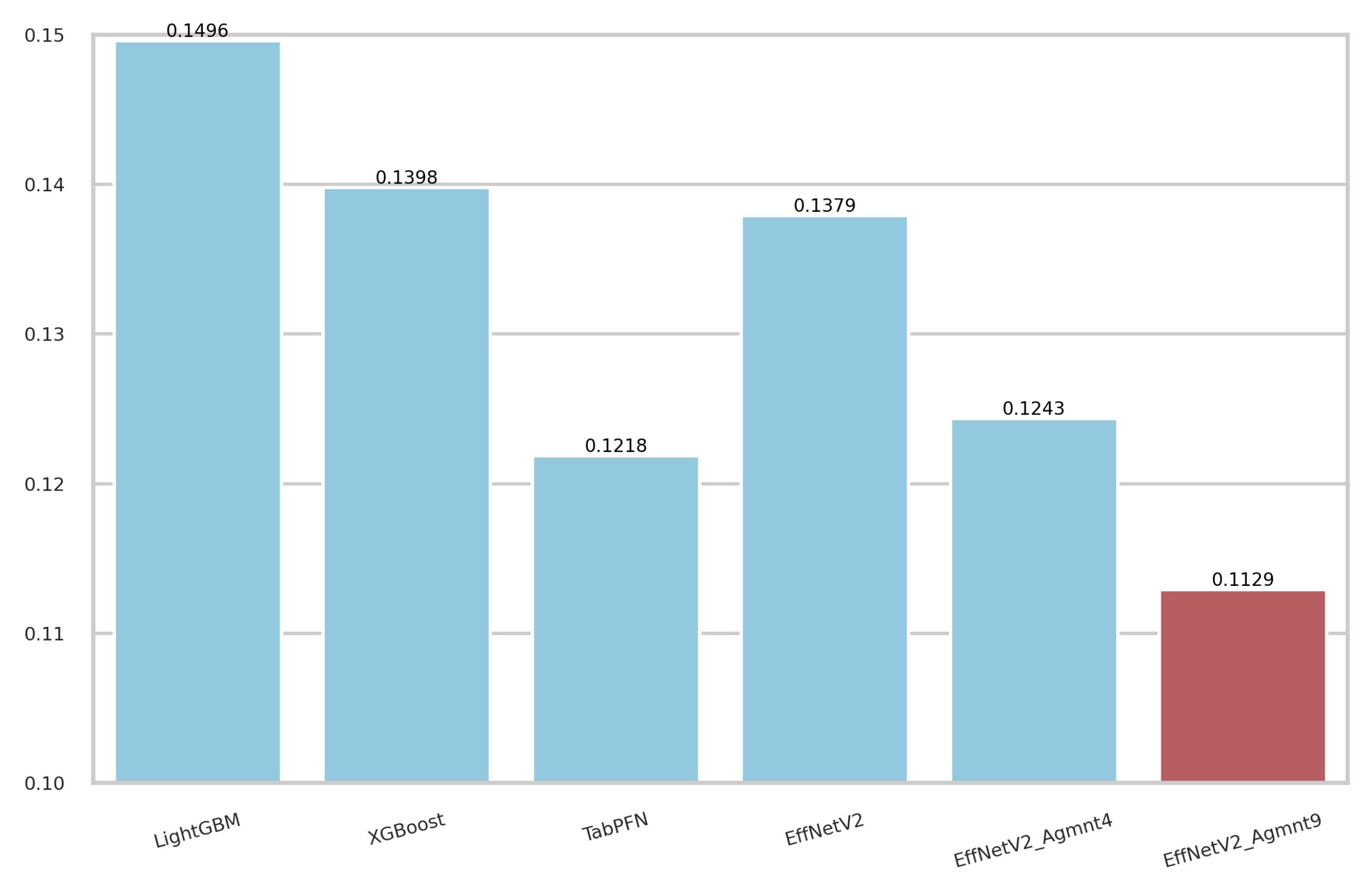
5.5. Overfitting Mitigation and Regularization
6. Conclusions
- Addressing a novel research problem of predicting prostate cancer from PSA levels and individualized questionnaires without relying on expensive or invasive diagnostic procedures.
- Collection of clinical data from 84 patients, including PSA levels and personalized information through questionnaires, to develop this predictive model.
- Comprehensive assessment and comparison of various machine learning techniques, including traditional, tree-based approaches, and advanced tabular deep neural network architectures (TabNet and TabPFN) for accurate and cost-effective prostate cancer prediction.
- Introduction of Tab2Visual modeling, a novel approach that converts tabular samples into image representations, enabling powerful and novel image augmentations to increase the dataset size and enhance the model’s ability to generalize to unseen data. It allows the use of CNNs with transfer learning, resulting in higher prediction accuracy.
- Development of a stacked classifier integrating the most effective methods identified in the study, demonstrating highly promising performance in prostate cancer prediction.
- Sharing our best predictive model with the research community through its deployment on the Internet as a web application using the Streamlit open-source framework.
7. Limitations and Future Work
- The use of deep learning models such as EfficientNet V2 involves significant computational overhead in terms of training time and hardware resources. To address this, we are optimizing our models for efficiency by exploring lightweight architectures and pruning techniques that maintain high performance while reducing computational demands.
- The Tab2Visual modeling converts tabular data into an image of width-modulated bars arranged in a single row. When dealing with datasets with many features, each feature is allocated a narrower bar in the image, which can make it challenging for the model to distinguish between features. To address this, we are exploring alternative layouts for the visual representation, such as arranging the bars in multiple rows or using other geometric shapes that can better accommodate a higher number of features without compromising clarity.
- Transforming tabular data into visual representations can sometimes lead to a loss of interpretability, especially for domain experts accustomed to traditional tabular formats. To improve interpretability, we are developing tools and interfaces that allow users to seamlessly switch between the tabular and visual representations and are working on enhancing the explainability of our models by integrating visualization techniques that highlight the most important features and their contributions to the model’s predictions.
- The dataset used in this study is relatively small, comprising only 84 samples, which may affect the generalizability of the model. We are actively seeking to expand our dataset by collaborating with additional medical institutions and incorporating data from different demographics and geographical locations, which will enable more robust training and validation of our model.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siegal, R.; Miller, K.D.; Jemal, A. Cancer statistics, 2020. Cancer J. Clin. 2020, 70, 30. [Google Scholar] [CrossRef]
- Rawla, P. Epidemiology of prostate cancer. World J. Oncol. 2019, 10, 63. [Google Scholar] [CrossRef]
- Matoso, A.; Epstein, J.I. Defining clinically significant prostate cancer on the basis of pathological findings. Histopathology 2019, 74, 135–145. [Google Scholar] [CrossRef]
- Catalona, W.J.; Richie, J.P.; Ahmann, F.R.; M’Liss, A.H.; Scardino, P.T.; Flanigan, R.C.; Dekernion, J.B.; Ratliff, T.L.; Kavoussi, L.R.; Dalkin, B.L.; et al. Comparison of digital rectal examination and serum prostate specific antigen in the early detection of prostate cancer: Results of a multicenter clinical trial of 6630 men. J. Urol. 1994, 151, 1283–1290. [Google Scholar] [CrossRef]
- Epstein, J.I.; Walsh, P.C.; Sanfilippo, F. Clinical and cost impact of second-opinion pathology: Review of prostate biopsies prior to radical prostatectomy. Am. J. Surg. Pathol. 1996, 20, 851–857. [Google Scholar] [CrossRef]
- Chan, T.Y.; Epstein, J.I. Patient and urologist driven second opinion of prostate needle biopsies. J. Urol. 2005, 174, 1390–1394. [Google Scholar] [CrossRef]
- Wang, T.H.; Lee, C.Y.; Lee, T.Y.; Huang, H.D.; Hsu, J.B.K.; Chang, T.H. Biomarker identification through multiomics data analysis of prostate cancer prognostication using a deep learning model and similarity network fusion. Cancers 2021, 13, 2528. [Google Scholar] [CrossRef]
- Song, Z.; Zou, S.; Zhou, W.; Huang, Y.; Shao, L.; Yuan, J.; Gou, X.; Jin, W.; Wang, Z.; Chen, X.; et al. Clinically applicable histopathological diagnosis system for gastric cancer detection using deep learning. Nat. Commun. 2020, 11, 4294. [Google Scholar] [CrossRef]
- Varghese, B.; Chen, F.; Hwang, D.; Palmer, S.L.; De Castro Abreu, A.L.; Ukimura, O.; Aron, M.; Aron, M.; Gill, I.; Duddalwar, V.; et al. Objective risk stratification of prostate cancer using machine learning and radiomics applied to multiparametric magnetic resonance images. In Proceedings of the 11th ACM International Conference on Bioinformatics, Computational Biology and Health Informatics, Virtual Event, 21–24 September 2020; pp. 1–10. [Google Scholar]
- Peng, T.; Xiao, J.; Li, L.; Pu, B.; Niu, X.; Zeng, X.; Wang, Z.; Gao, C.; Li, C.; Chen, L.; et al. Can machine learning-based analysis of multiparameter MRI and clinical parameters improve the performance of clinically significant prostate cancer diagnosis. Int. J. Comput. Assist. Radiol. Surg. 2021, 16, 2235–2249. [Google Scholar] [CrossRef] [PubMed]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Bhattacharya, I.; Seetharaman, A.; Shao, W.; Sood, R.; Kunder, C.A.; Fan, R.E.; Soerensen, S.J.C.; Wang, J.B.; Ghanouni, P.; Teslovich, N.C.; et al. Corrsignet: Learning correlated prostate cancer signatures from radiology and pathology images for improved computer aided diagnosis. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2020: 23rd International Conference, Lima, Peru, 4–8 October 2020; pp. 315–325. [Google Scholar]
- Wang, G.; Teoh, J.Y.C.; Choi, K.S. Diagnosis of prostate cancer in a Chinese population by using machine learning methods. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 1–4. [Google Scholar]
- Perera, M.; Mirchandani, R.; Papa, N.; Breemer, G.; Effeindzourou, A.; Smith, L.; Swindle, P.; Smith, E. PSA-based machine learning model improves prostate cancer risk stratification in a screening population. World J. Urol. 2021, 39, 1897–1902. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Yang, S.W.; Lee, S.; Hyon, Y.K.; Kim, J.; Jin, L.; Lee, J.Y.; Park, J.M.; Ha, T.; Shin, J.H.; et al. Machine learning approaches for the prediction of prostate cancer according to age and the prostate-specific antigen level. Korean J. Urol. Oncol. 2019, 17, 110–117. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd Acm sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3149–3157. [Google Scholar]
- ElKarami, B.; Alkhateeb, A.; Qattous, H.; Alshomali, L.; Shahrrava, B. Multi-omics data integration model based on UMAP embedding and convolutional neural network. Cancer Inform. 2022, 21, 11769351221124205. [Google Scholar] [CrossRef] [PubMed]
- Qattous, H.; Azzeh, M.; Ibrahim, R.; AbedalGhafer, I.; Al Sorkhy, M.; Alkhateeb, A. Pacmap-embedded convolutional neural network for multi-omics data integration. Heliyon 2024, 10, e23195. [Google Scholar] [CrossRef] [PubMed]
- Arik, S.Ö.; Pfister, T. Tabnet: Attentive interpretable tabular learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 6679–6687. [Google Scholar]
- Hollmann, N.; Müller, S.; Eggensperger, K.; Hutter, F. Tabpfn: A transformer that solves small tabular classification problems in a second. arXiv 2022, arXiv:2207.01848. [Google Scholar]
- Sharma, A.; Vans, E.; Shigemizu, D.; Boroevich, K.A.; Tsunoda, T. DeepInsight: A methodology to transform a non-image data to an image for convolution neural network architecture. Sci. Rep. 2019, 9, 11399. [Google Scholar] [CrossRef] [PubMed]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Bazgir, O.; Zhang, R.; Dhruba, S.R.; Rahman, R.; Ghosh, S.; Pal, R. Representation of features as images with neighborhood dependencies for compatibility with convolutional neural networks. Nat. Commun. 2020, 11, 4391. [Google Scholar] [CrossRef]
- Zhu, Y.; Brettin, T.; Xia, F.; Partin, A.; Shukla, M.; Yoo, H.; Evrard, Y.A.; Doroshow, J.H.; Stevens, R.L. Converting tabular data into images for deep learning with convolutional neural networks. Sci. Rep. 2021, 11, 11325. [Google Scholar] [CrossRef] [PubMed]
- Quinlan, J.R. C4. 5: Programs for Machine Learning; Morgan Kaufmann Publishers, Inc.: Burlington, MA, USA, 1993. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1, pp. 278–282. [Google Scholar]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 6105–6114. [Google Scholar]
- Tan, M.; Le, Q. Efficientnetv2: Smaller models and faster training. In Proceedings of the International Conference on Machine Learning, PMLR, Virtual, 18–24 July 2021; pp. 10096–10106. [Google Scholar]
- Kim, S.; Rim, B.; Choi, S.; Lee, A.; Min, S.; Hong, M. Deep learning in multi-class lung diseases’ classification on chest X-ray images. Diagnostics 2022, 12, 915. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Suo, H.; Li, D. Deepfake video detection based on EfficientNet-V2 network. Comput. Intell. Neurosci. 2022, 2022, 3441549. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, S.; Monir, M.K.H. CEIMVEN: An Approach of Cutting Edge Implementation of Modified Versions of EfficientNet (V1-V2) Architecture for Breast Cancer Detection and Classification from Ultrasound Images. arXiv 2023, arXiv:2308.13356. [Google Scholar]
- Shao, Z.; Er, M.J.; Wang, N. An Efficient Leave-One-Out Cross-Validation-Based Extreme Learning Machine (ELOO-ELM) with Minimal User Intervention. IEEE Trans. Cybern. 2016, 46, 1939–1951. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Wightman, R. PyTorch Image Models. 2019. Available online: https://github.com/huggingface/pytorch-image-models (accessed on 5 March 2024).
- Rufibach, K. Use of Brier score to assess binary predictions. J. Clin. Epidemiol. 2010, 63, 938–939. [Google Scholar] [CrossRef]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, NSW, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
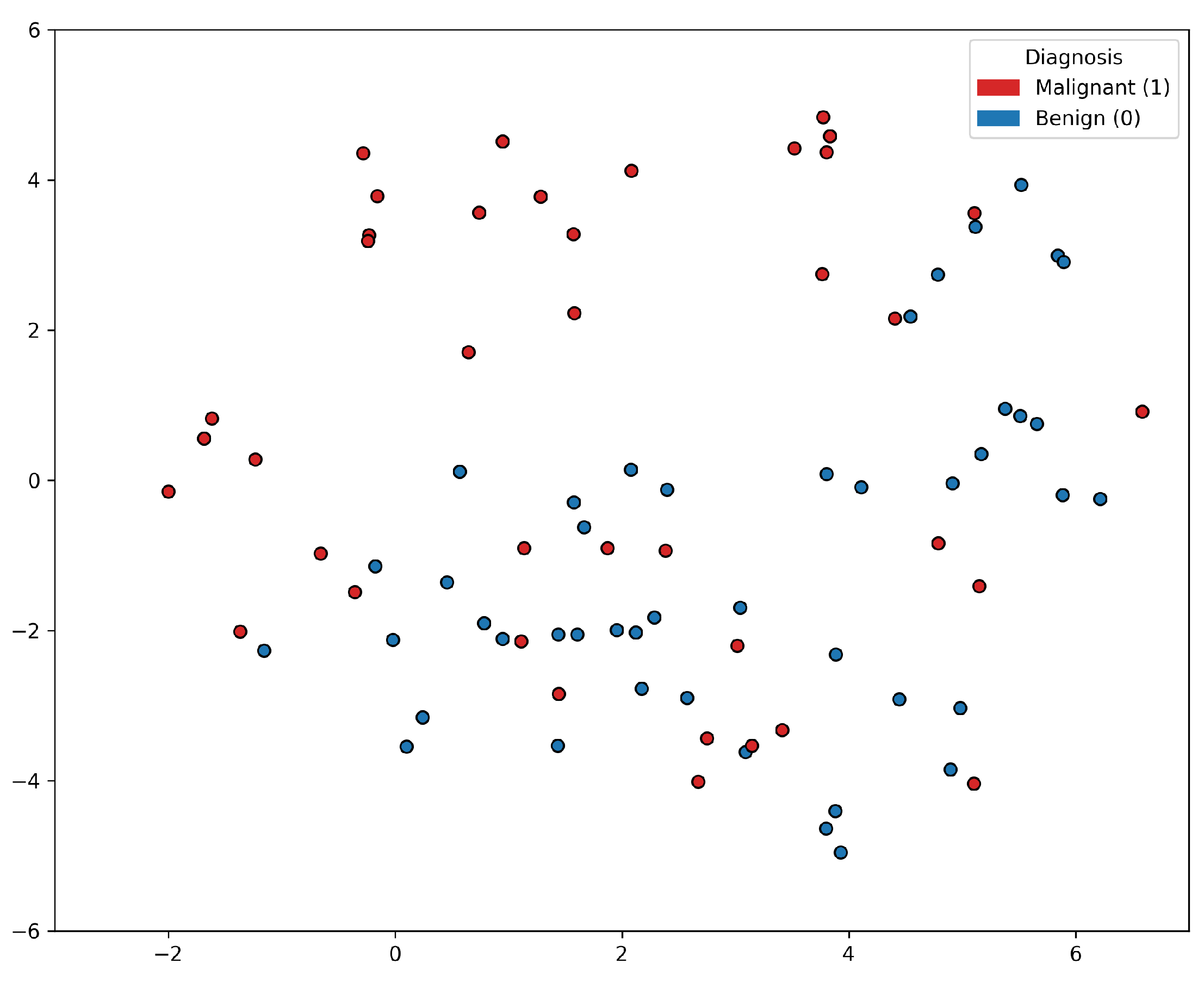

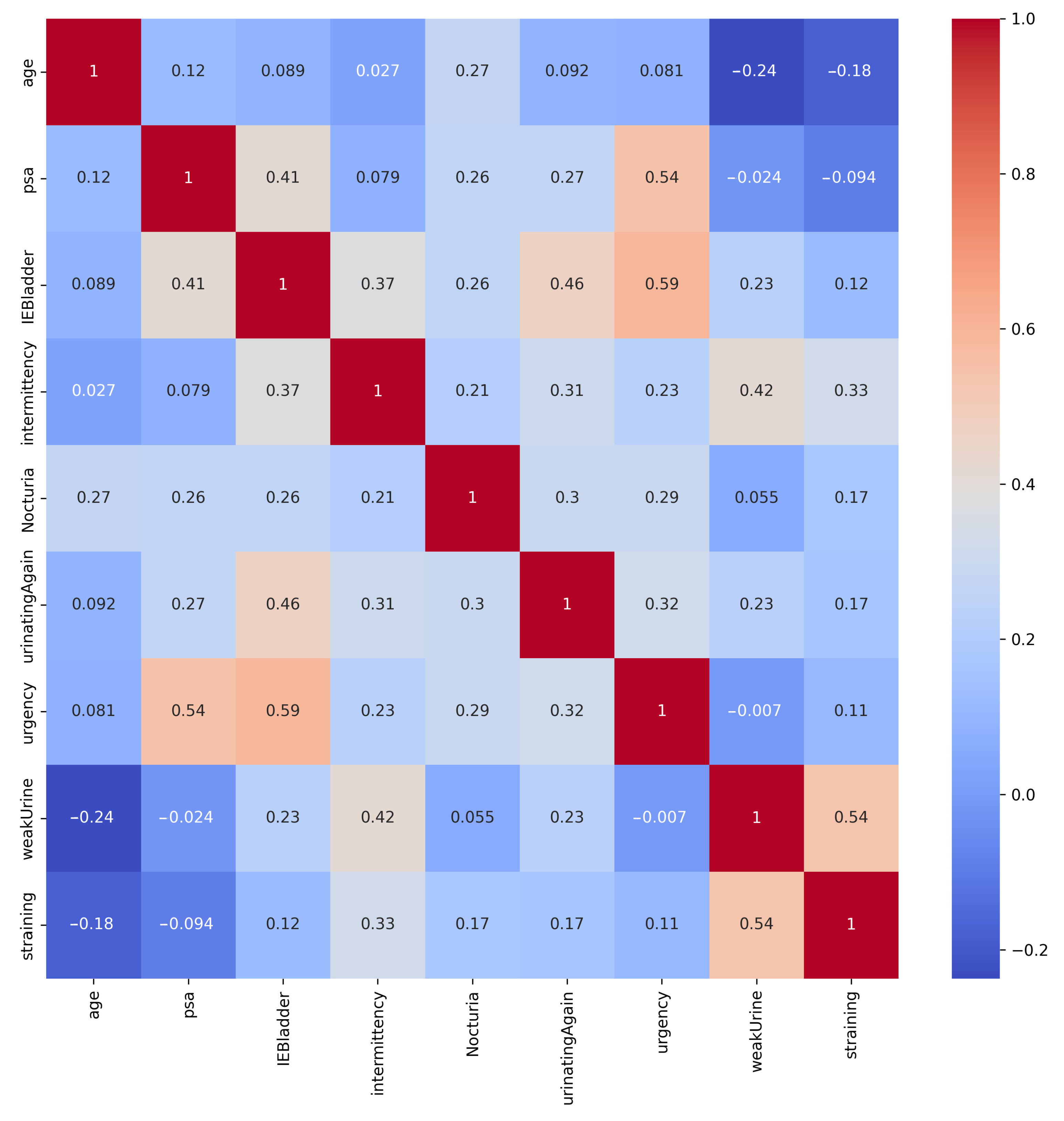



| Feature Name | Description | Feature Type |
|---|---|---|
| PSA | Prostate-specific antigen value | Continuous |
| AGE | Age | Continuous |
| IEBladder | Frequency of feeling that the bladder is not completely empty after urination | Categorical |
| UrinateAgain | Frequency of urinating again in less than 2 h | Categorical |
| Intermittency | Frequency of the urine stream cut-off during urination | Categorical |
| Urgency | Frequency of difficulty to delay urination | Categorical |
| Nocturia | Frequency of getting up at night to urinate | Categorical |
| Straining | Frequency of difficulty to start urination | Categorical |
| WeakUrine | Frequency of feeling the weakness of the urine stream | Categorical |
| Method | Hyperparameter | Search Space | Best Value |
|---|---|---|---|
| Logistic regression | penalty | [l1, l2] | l1 |
| C | 0.01 to 1 | 0.248 | |
| SVM | C | 0.001 to 100 | 3 |
| kernel | [‘linear’, ‘poly’, ‘rbf’] | ‘rbf’ | |
| gamma | 0.001 to 100 | 0.1 | |
| Random forest | n_estimators | 1 to 500 | 46 |
| max_depth | 1 to 40 | 8 | |
| min_samples_split | 2 to 14 | 1 | |
| min_samples_leaf | 1 to 14 | 1 | |
| max_features | [‘auto’, ‘sqrt’, ‘log2’] | ‘log2’ | |
| Extra Trees | n_estimators | 1 to 500 | 96 |
| max_depth | 1 to 40 | 10 | |
| min_samples_split | 2 to 14 | 51 | |
| min_samples_leaf | 1 to 14 | 1 | |
| max_features | [‘auto’, ‘sqrt’, ‘log2’] | ‘sqrt’ | |
| XGBoost | n_estimators | 1 to 500 | 18 |
| max_depth | 1 to 40 | 3 | |
| gamma | 0 to 5 | 4.2854 | |
| learning_rate | 0.01 to 1 | 0.307 | |
| reg_alpha | 0 to 2 | 1.779 | |
| reg_lambda | 0 to 2 | 0.439 | |
| subsample | 0.5 to 1 | 0.996 | |
| colsample_bytree | 0.5 to 1 | 0.733 | |
| LightGBM | n_estimators | 1 to 500 | 18 |
| max_depth | 1 to 20 | 6 | |
| num_leaves | 2 to 256 | 98 | |
| learning_rate | 0.01 to 1 | 0.358 | |
| reg_alpha | 0 to 2 | 1.699 | |
| reg_lambda | 0 to 2 | 0.872 | |
| subsample | 0.5 to 1 | 0.698 | |
| colsample_bytree | 0.5 to 1 | 0.762 | |
| CatBoost | iterations | 50 to 300 | 72 |
| learning_rate | 0.01 to 0.3 | 0.3720 | |
| depth | 2 to 12 | 2 | |
| l2_leaf_reg | 1 to 10 | 8.712 | |
| Shallow ANN | n_hidden_layers | [1, 3] | 2 |
| n_neurons_hidden_layer | 1 to 256 | 32–8 | |
| learning_rate | 0.0001 to 0.1 | 0.0501 | |
| batch_size | [16, 32, 64, 128] | 16 | |
| weight_decay | 0.00001 to 0.01 | 0.001 | |
| drop_prob | 0.1 to 0.7 | 0.5 | |
| TabNet | batch_size | [8, 16, 32, 64] | 16 |
| mask_type | [‘entmax’, ‘sparsemax’] | ‘sparsemax’ | |
| n_d | 8 to 64 (step 4) | 8 | |
| n_a | 8 to 64 (step 4) | 8 | |
| n_steps | 1 to 8 (step 1) | 5 | |
| gamma | 1.0 to 1.4 (step 0.2) | 1.2 | |
| n_shared | 1 to 3 | 2 | |
| lambda_sparse | 0.0001 to 1 | 0.000106 | |
| patienceScheduler | 3 to 10 | 6 | |
| learning_rate | 0.001 to 1 | 0.02 | |
| TabPFN | n_ensemble_configurations | [1, 32] | 3 |
| Classifier | Precision | Recall | F1-Score | AUC |
|---|---|---|---|---|
| LR | 0.931 | 0.692 | 0.825 | 0.836 |
| SVM | 0.903 | 0.718 | 0.800 | 0.816 |
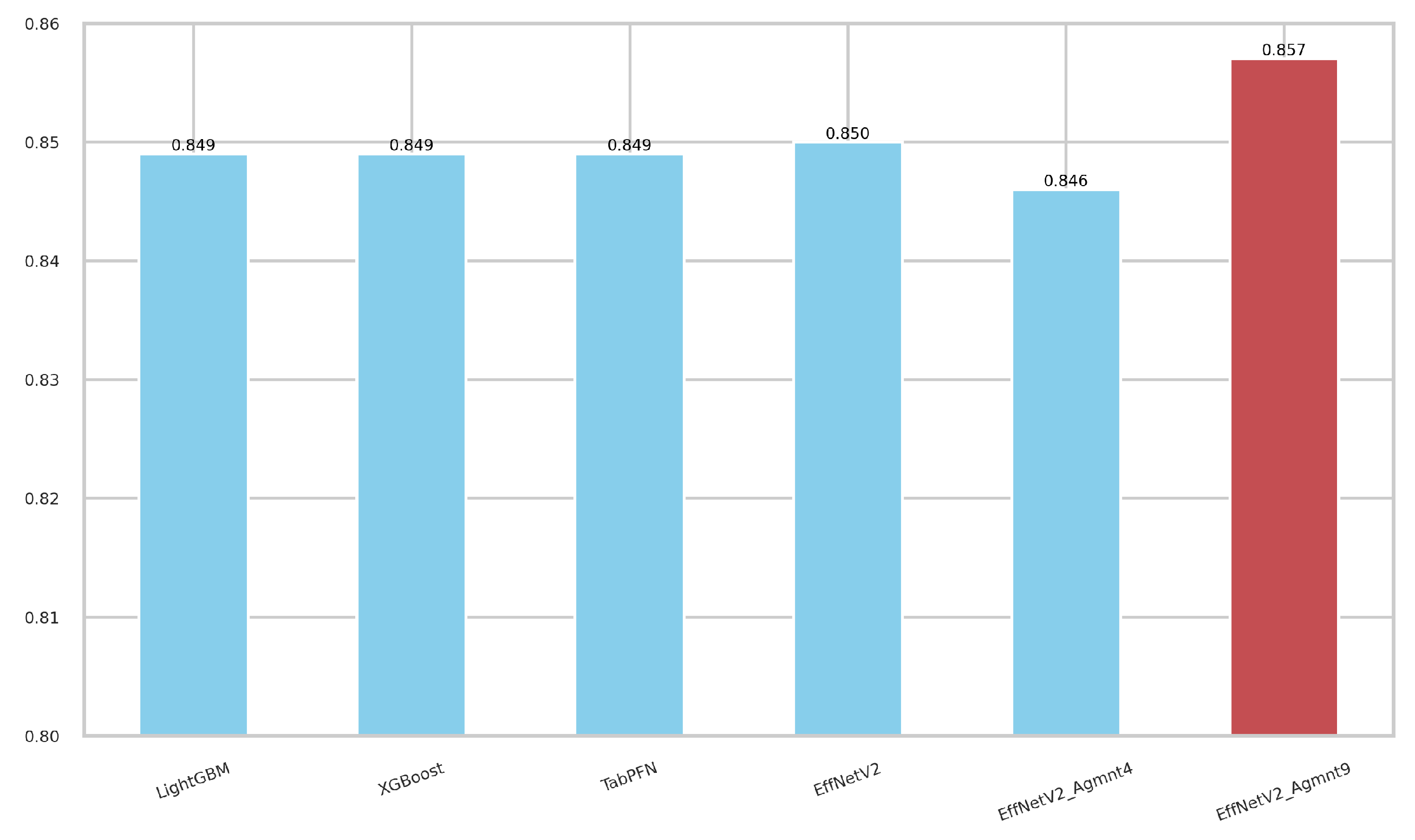
| LightGBM | 0.912 | 0.795 | 0.849 | 0.861 |
| XGBoost | 0.912 | 0.795 | 0.849 | 0.854 |
| Random forest | 0.815 | 0.795 | 0.805 | 0.862 |
| ExtraTrees | 0.886 | 0.795 | 0.838 | 0.869 |
| ANN | 0.816 | 0.795 | 0.805 | 0.856 |
| TabNet | 0.811 | 0.769 | 0.789 | 0.859 |
| TabPFN | 0.912 | 0.795 | 0.849 | 0.870 |
| Augmentation | Training Size | Precision | Recall | F1-Score | AUC |
|---|---|---|---|---|---|
| No Agmnt | 83 | 0.829 | 0.872 | 0.850 | 0.887 |
| Agmnt_1 | 166 | 0.864 | 0.820 | 0.842 | 0.870 |
| Agmnt_2 | 249 | 0.833 | 0.769 | 0.800 | 0.877 |
| Agmnt_3 | 332 | 0.800 | 0.821 | 0.810 | 0.872 |
| Agmnt_4 | 415 | 0.846 | 0.846 | 0.846 | 0.886 |
| Agmnt_5 | 498 | 0.861 | 0.794 | 0.827 | 0.875 |
| Agmnt_6 | 581 | 0.886 | 0.795 | 0.839 | 0.873 |
| Agmnt_7 | 664 | 0.886 | 0.795 | 0.839 | 0.901 |
| Agmnt_8 | 747 | 0.825 | 0.846 | 0.835 | 0.897 |
| Agmnt_9 | 830 | 0.868 | 0.846 | 0.857 | 0.899 |
| Method | Parameter | Search Space | Best Value | Method Evaluation |
|---|---|---|---|---|
| ResNet18 | n_hidden_layers | {0, 1, 2} | 0 | Precision: 0.806 Recall: 0.872 F1-Score: 0.850 AUC: 0.887 |
| n_neurons_layer | {32, 64, 128, 256} | No hidden layer | ||
| learning_rate | [0.000001, 1] | 0.001 | ||
| weight_decay | [0.0001, 0.5] | 0.01 | ||
| drop_out_probability | [0.1, 0.7] | 0.5 | ||
| EffNetV2_B0 | n_hidden_layers | {0, 1, 2} | 0 | Precision: 0.806 Recall: 0.872 F1-Score: 0.850 AUC: 0.887 |
| n_neurons_layer | {32, 64, 128, 256} | No hidden layer | ||
| learning_rate | [0.000001, 1] | 0.001 | ||
| weight_decay | [0.0001, 0.5] | 0.01 | ||
| drop_out_probability | [0.1, 0.7] | 0.5 |
| Classifier | Training Time (s) | Inference Time (ms) |
|---|---|---|
| LR | 2.3 | 1.2 |
| SVM | 4.4 | 0.2 |
| Random forest | 18 | 1.7 |
| ExtraTrees | 9 | 1 |
| LightGBM | 6.8 | 1.5 |
| XGBoost | 11.4 | 2 |
| ANN | 67 | 10 |
| TabNet | 544 | 7 |
| TabPFN | 21 | 101 |
| EffNetV2_B0 | 3780 | 21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Melegy, M.; Mamdouh, A.; Ali, S.; Badawy, M.; El-Ghar, M.A.; Alghamdi, N.S.; El-Baz, A. Prostate Cancer Diagnosis via Visual Representation of Tabular Data and Deep Transfer Learning. Bioengineering 2024, 11, 635. https://doi.org/10.3390/bioengineering11070635
El-Melegy M, Mamdouh A, Ali S, Badawy M, El-Ghar MA, Alghamdi NS, El-Baz A. Prostate Cancer Diagnosis via Visual Representation of Tabular Data and Deep Transfer Learning. Bioengineering. 2024; 11(7):635. https://doi.org/10.3390/bioengineering11070635
Chicago/Turabian StyleEl-Melegy, Moumen, Ahmed Mamdouh, Samia Ali, Mohamed Badawy, Mohamed Abou El-Ghar, Norah Saleh Alghamdi, and Ayman El-Baz. 2024. "Prostate Cancer Diagnosis via Visual Representation of Tabular Data and Deep Transfer Learning" Bioengineering 11, no. 7: 635. https://doi.org/10.3390/bioengineering11070635
APA StyleEl-Melegy, M., Mamdouh, A., Ali, S., Badawy, M., El-Ghar, M. A., Alghamdi, N. S., & El-Baz, A. (2024). Prostate Cancer Diagnosis via Visual Representation of Tabular Data and Deep Transfer Learning. Bioengineering, 11(7), 635. https://doi.org/10.3390/bioengineering11070635







