nnSegNeXt: A 3D Convolutional Network for Brain Tissue Segmentation Based on Quality Evaluation
Abstract
1. Introduction
- We present a novel framework for brain tissue segmentation, leveraging a quality evaluation approach. This framework consists of two essential processes: dataset preprocessing and network training.
- We incorporate a 3D Multiscale Convolutional Attention Module instead of conventional convolutional blocks, enabling simultaneous encoding of contextual information. These attention mechanisms significantly curtail computational overhead while eliciting spatial attention via multiscale convolutional features.
- We devise a Data Quality Loss metric that appraises label quality on training images, thereby attenuating the impact of label quality on segmentation precision during the training process.
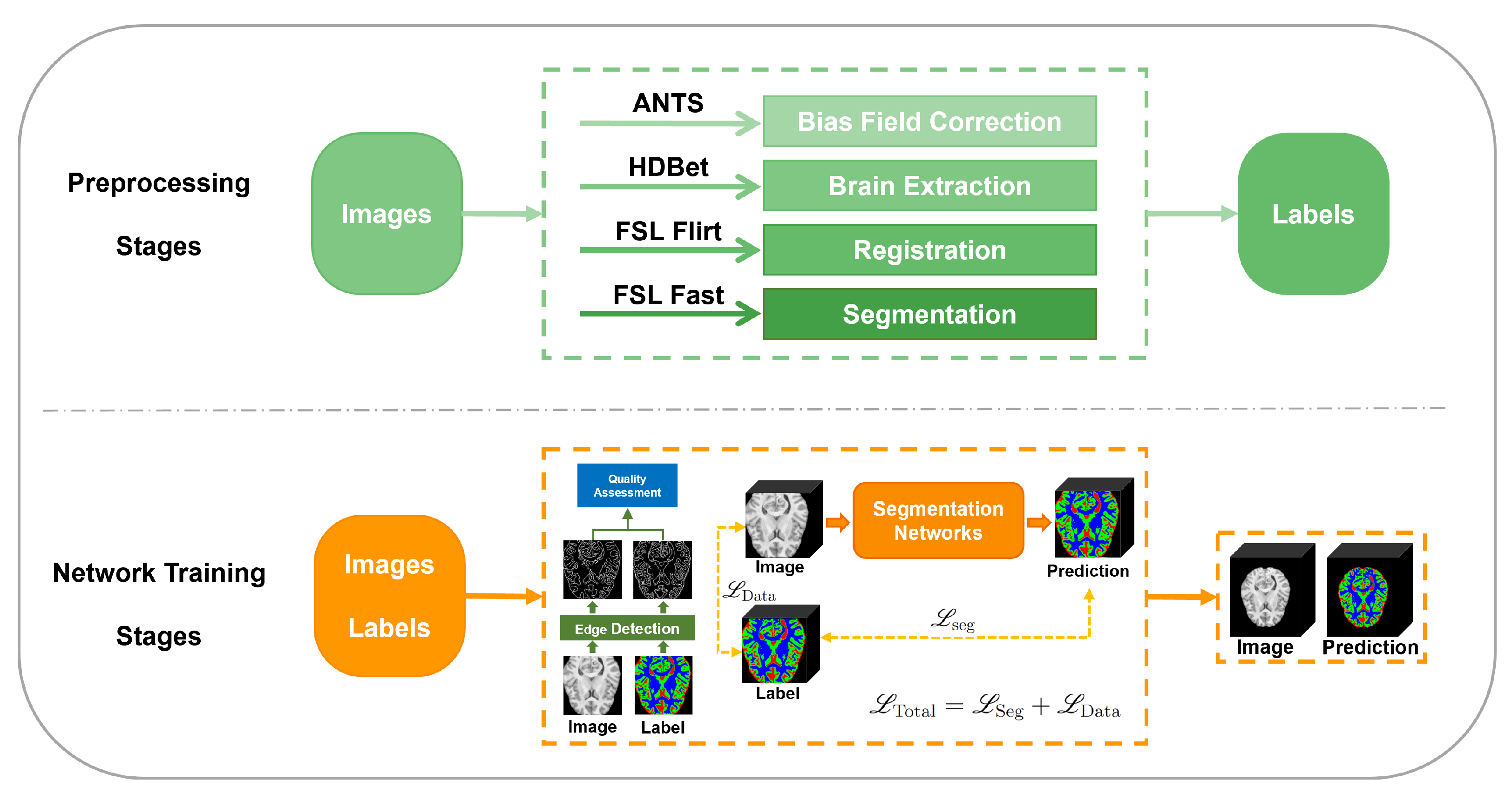
2. Method
2.1. The Proposed Segmentation Framework
2.1.1. The Preprocessing Stage
2.1.2. The Network Training Stage
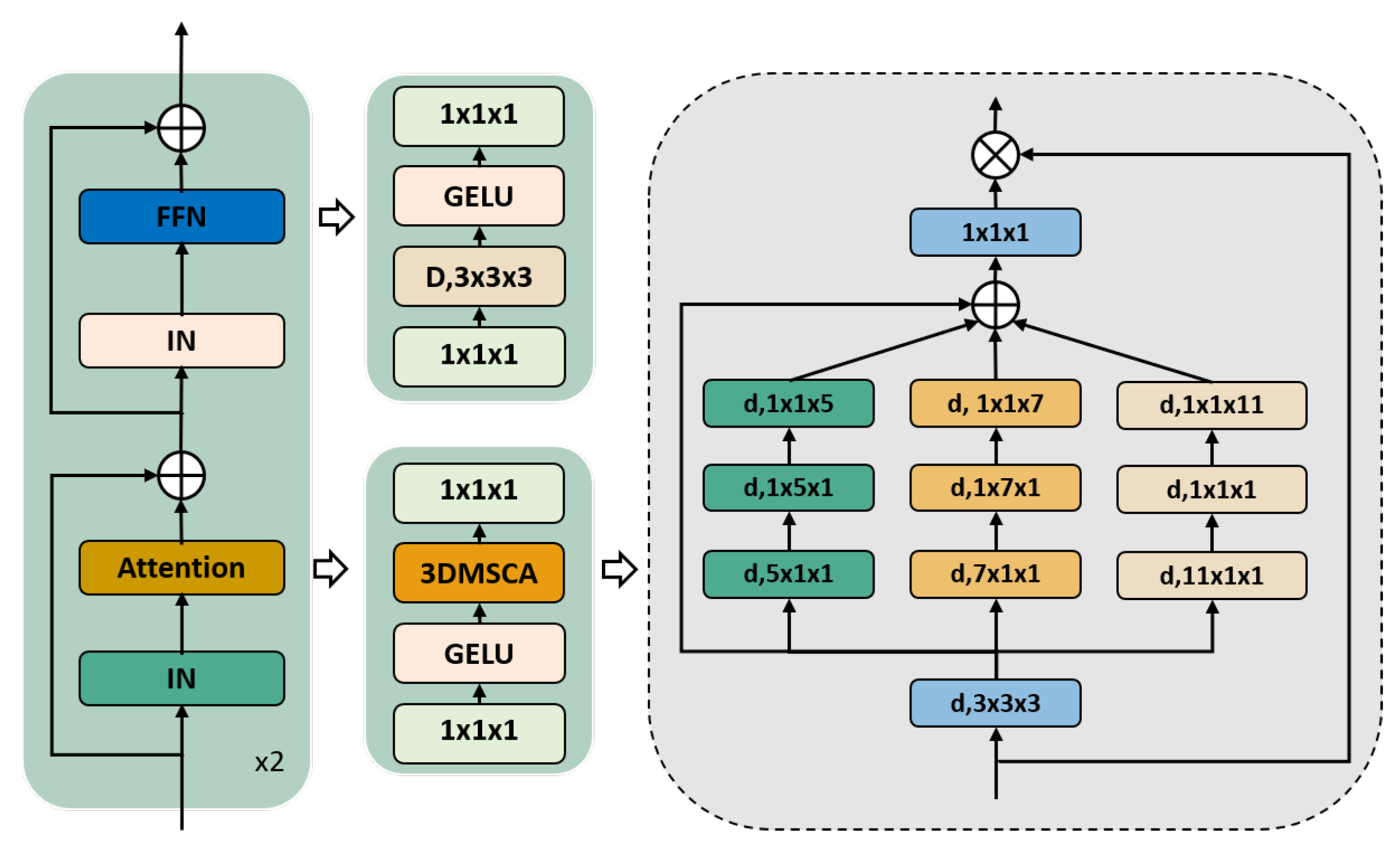
2.2. Network Architecture
2.3. 3D Multiscale Convolutional Attention Module
Loss Function
3. Experiments
3.1. Datasets
3.2. Evaluation Metrics
3.3. Implementation Details
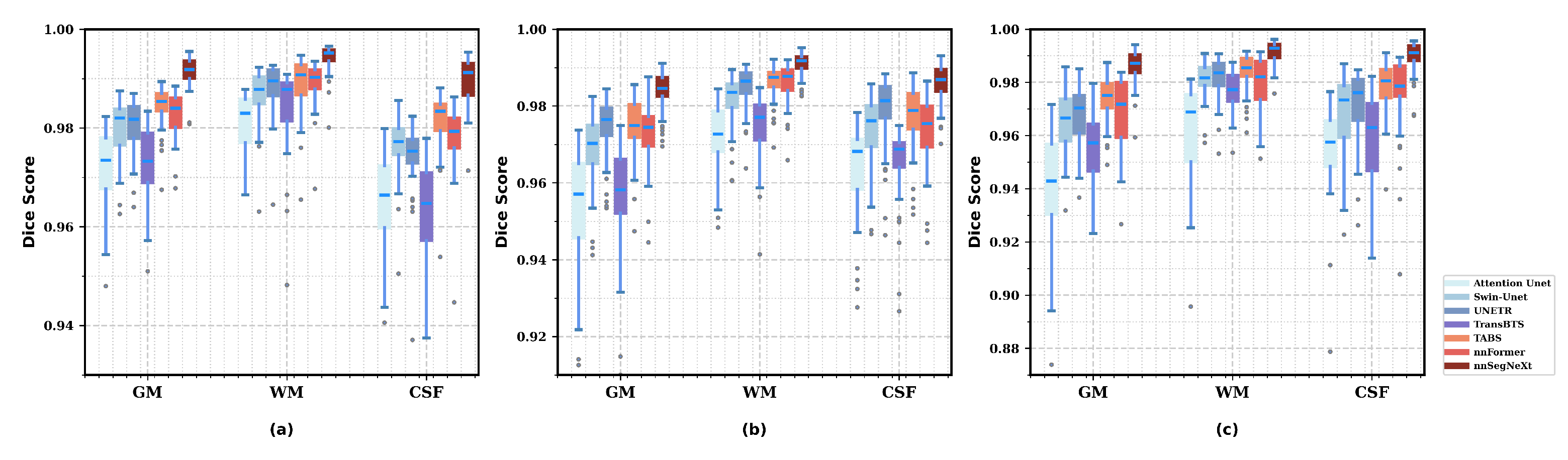
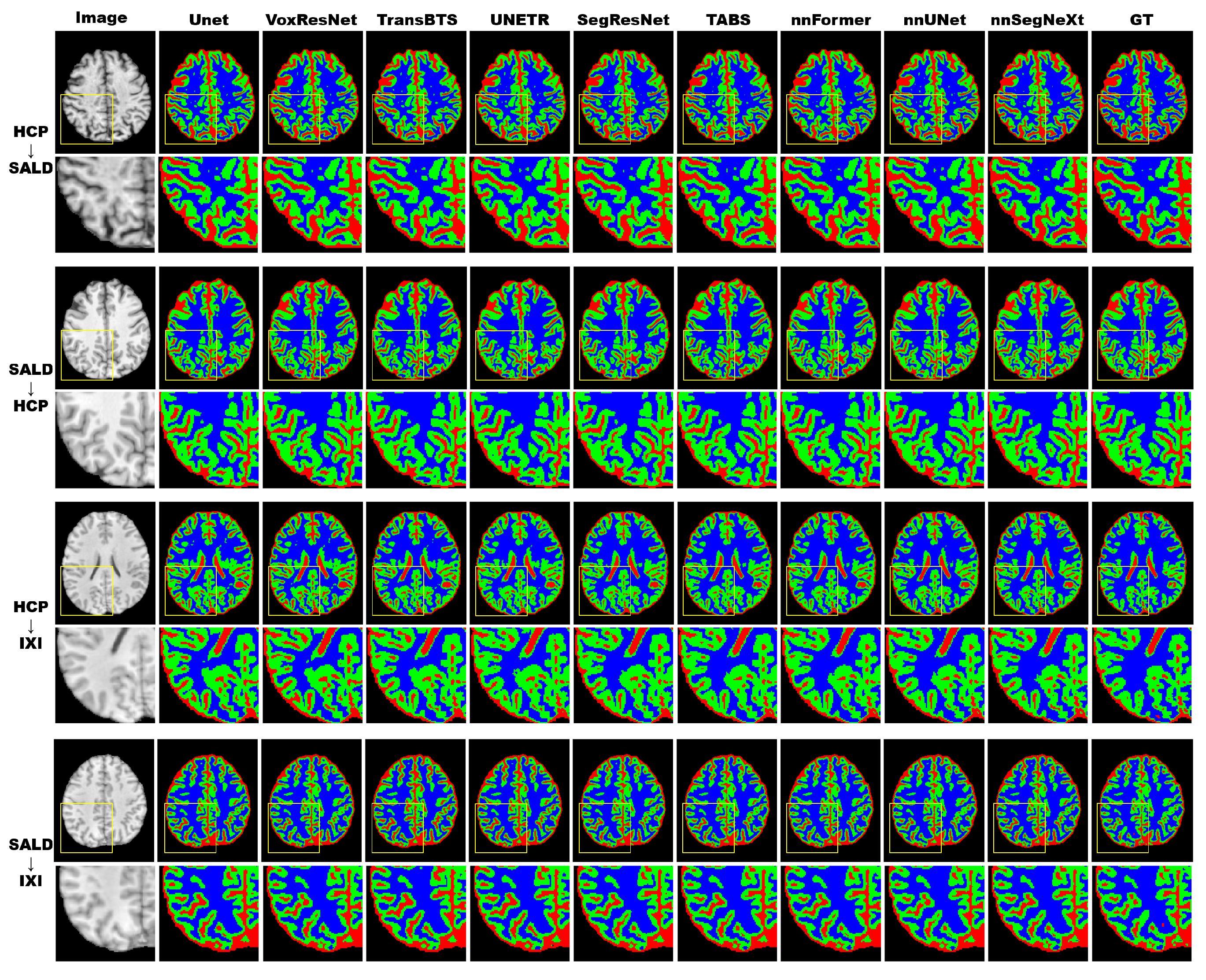
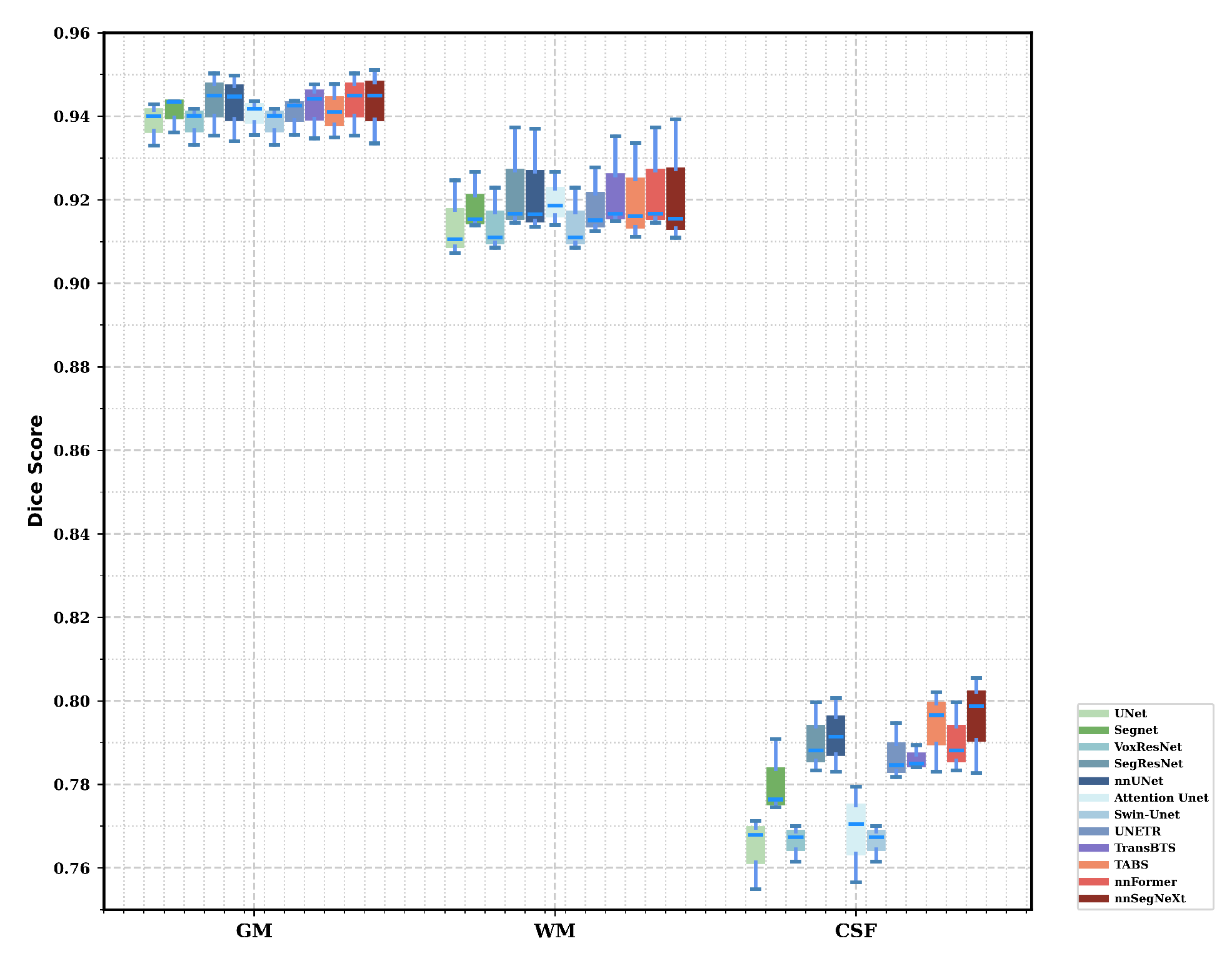
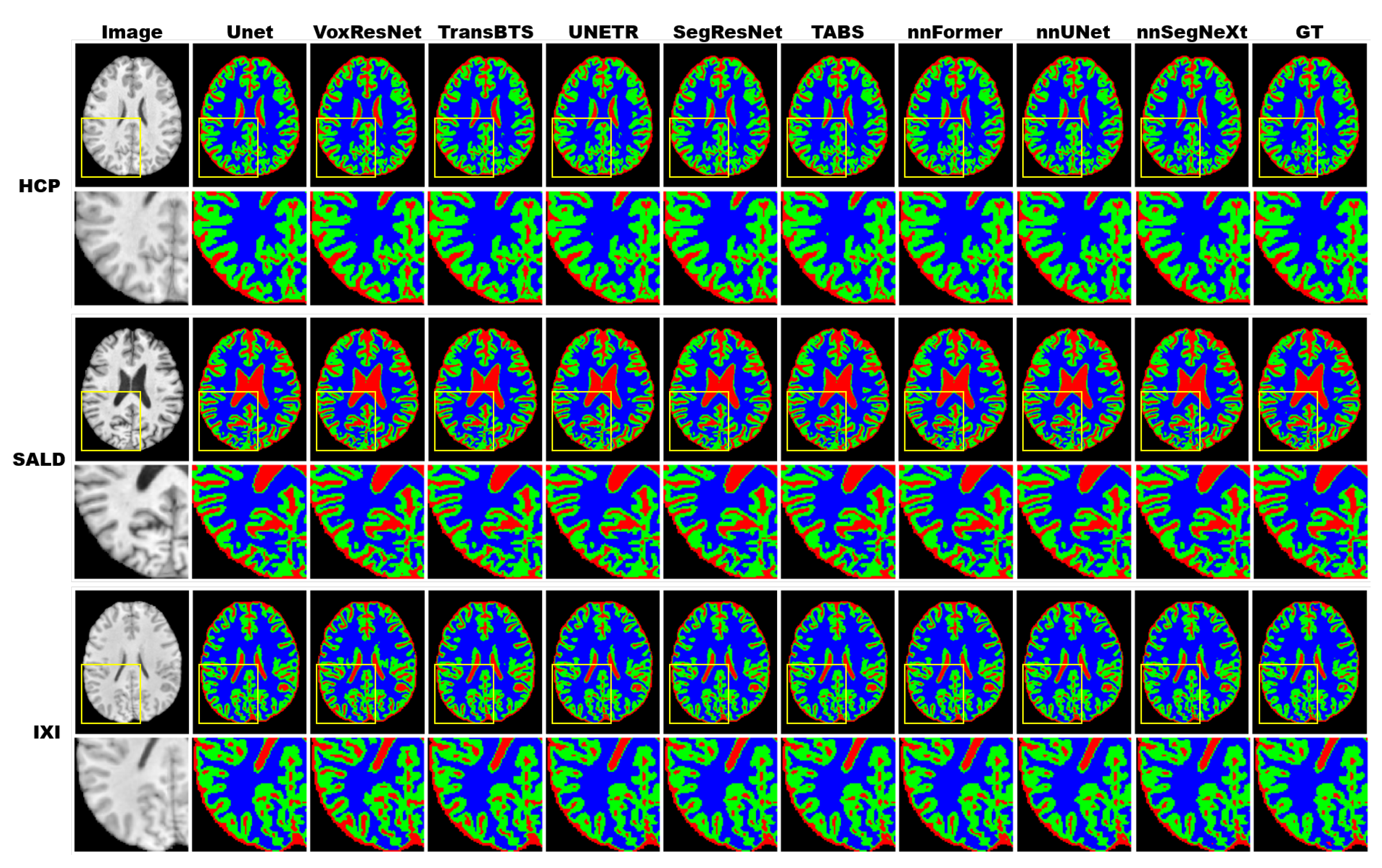
3.4. Results
3.4.1. Model Performance
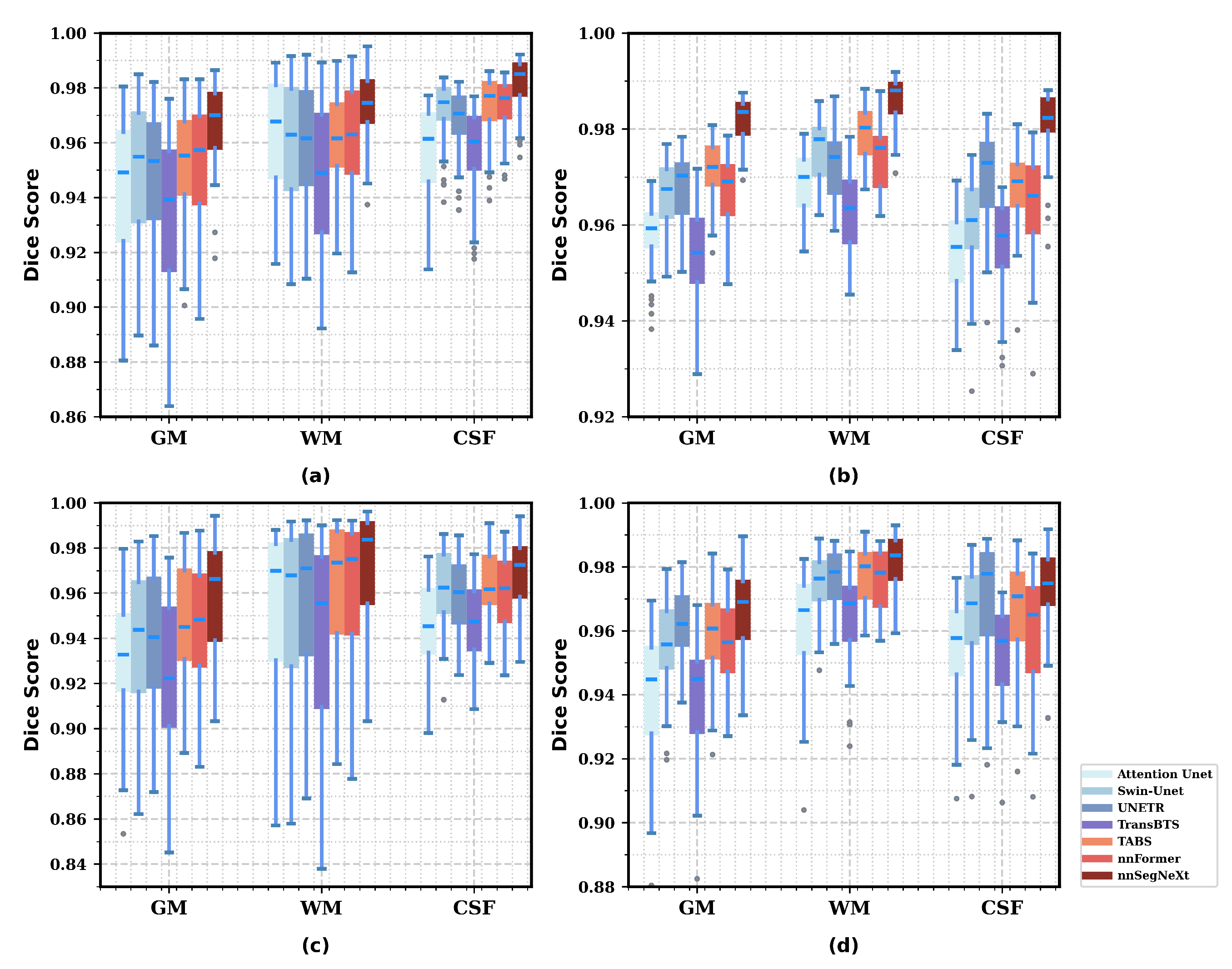
3.4.2. Model Generality
3.5. Validation on IBSR Dataset
3.5.1. Comparison with nnUNet
3.5.2. Ablation Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A


References
- Fischl, B.; Salat, D.H.; Busa, E.; Albert, M.; Dieterich, M.; Haselgrove, C.; van der Kouwe, A.; Killiany, R.; Kennedy, D.; Klaveness, S.; et al. Whole Brain Segmentation: Automated Labeling of Neuroanatomical Structures in the Human Brain. Neuron 2002, 33, 341–355. [Google Scholar] [CrossRef] [PubMed]
- Igual, L.; Soliva, J.C.; Gimeno, R.; Escalera, S.; Vilarroya, O.; Radeva, P. Automatic Internal Segmentation of Caudate Nucleus for Diagnosis of Attention-Deficit/Hyperactivity Disorder. In Proceedings of the Image Analysis and Recognition: 9th International Conference, ICIAR 2012, Aveiro, Portugal, 25–27 June 2012; pp. 222–229. [Google Scholar]
- Li, D.J.; Huang, B.L.; Peng, Y. Comparisons of Artificial Intelligence Algorithms in Automatic Segmentation for Fungal Keratitis Diagnosis by Anterior Segment Images. Front. Neurosci. 2023, 17, 1195188. [Google Scholar] [CrossRef] [PubMed]
- Kikinis, R.; Shenton, M.; Iosifescu, D.; McCarley, R.; Saiviroonporn, P.; Hokama, H.; Robatino, A.; Metcalf, D.; Wible, C.; Portas, C.; et al. A Digital Brain Atlas for Surgical Planning, Model-Driven Segmentation, and Teaching. IEEE Trans. Vis. Comput. Graph. 1996, 2, 232–241. [Google Scholar] [CrossRef]
- Pitiot, A.; Delingette, H.; Thompson, P.M.; Ayache, N. Expert Knowledge-Guided Segmentation System for Brain MRI. NeuroImage 2004, 23, S85–S96. [Google Scholar] [CrossRef] [PubMed]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Maitra, M.; Chatterjee, A. A Novel Technique for Multilevel Optimal Magnetic Resonance Brain Image Thresholding Using Bacterial Foraging. Measurement 2008, 41, 1124–1134. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active Contour Models. Int. J. Comput. Vision 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Cootes, T.F.; Taylor, C.J.; Cooper, D.H.; Graham, J. Active Shape Models-Their Training and Application. Comput. Vis. Image Underst. 1995, 61, 38–59. [Google Scholar] [CrossRef]
- Cootes, T.; Edwards, G.; Taylor, C. Active Appearance Models. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 681–685. [Google Scholar] [CrossRef]
- Chuang, K.S.; Tzeng, H.L.; Chen, S.; Wu, J.; Chen, T.J. Fuzzy C-Means Clustering with Spatial Information for Image Segmentation. Comput. Med. Imaging Graph. 2006, 30, 9–15. [Google Scholar] [CrossRef]
- Deoni, S.C.L.; Rutt, B.K.; Parrent, A.G.; Peters, T.M. Segmentation of Thalamic Nuclei Using a Modified K-Means Clustering Algorithm and High-Resolution Quantitative Magnetic Resonance Imaging at 1.5 T. NeuroImage 2007, 34, 117–126. [Google Scholar] [CrossRef] [PubMed]
- Kruggel, F.; Turner, J.; Muftuler, L.T. Impact of Scanner Hardware and Imaging Protocol on Image Quality and Compartment Volume Precision in the ADNI Cohort. NeuroImage 2010, 49, 2123–2133. [Google Scholar] [CrossRef] [PubMed]
- Long, J.; Shelhamer, E.; Darrell, T. Fully Convolutional Networks for Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- çicek, O.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016, Athens, Greece, 17–21 October 2016; Ourselin, S., Joskowicz, L., Sabuncu, M.R., Unal, G., Wells, W., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 424–432. [Google Scholar]
- Milletari, F.; Navab, N.; Ahmadi, S.A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. In Proceedings of the 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Myronenko, A. 3D MRI Brain Tumor Segmentation Using Autoencoder Regularization. In Lecture Notes in Computer Science, Proceedings of the Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Granada, Spain, 16 September 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 311–320. [Google Scholar]
- Isensee, F.; Schell, M.; Pflueger, I.; Brugnara, G.; Bonekamp, D.; Neuberger, U.; Wick, A.; Schlemmer, H.P.; Heiland, S.; Wick, W.; et al. Automated Brain Extraction of Multisequence MRI Using Artificial Neural Networks. Hum. Brain Mapp. 2019, 40, 4952–4964. [Google Scholar] [CrossRef] [PubMed]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A Self-Configuring Method for Deep Learning-Based Biomedical Image Segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention U-Net: Learning Where to Look for the Pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Chen, B.; Liu, Y.; Zhang, Z.; Lu, G.; Kong, A.W.K. TransAttUnet: Multi-Level Attention-Guided U-Net With Transformer for Medical Image Segmentation. IEEE Trans. Emerg. Top. Comput. Intell. 2023, 8, 55–68. [Google Scholar] [CrossRef]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: Unet-Like Pure Transformer for Medical Image Segmentation. In Computer Vision—ECCV 2022 Workshops; Springer Nature: Cham, Switzerland, 2023; Volume 13803, pp. 205–218. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer Using Shifted Windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Rao, V.M.; Wan, Z.; Arabshahi, S.; Ma, D.J.; Lee, P.Y.; Tian, Y.; Zhang, X.; Laine, A.F.; Guo, J. Improving Across-Dataset Brain Tissue Segmentation for MRI Imaging Using Transformer. Front. Neuroimaging 2022, 1, 1023481. [Google Scholar] [CrossRef] [PubMed]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. UNETR: Transformers for 3D Medical Image Segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 574–584. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2017; Volume 30. [Google Scholar]
- Zhou, H.Y.; Guo, J.; Zhang, Y.; Han, X.; Yu, L.; Wang, L.; Yu, Y. nnFormer: Volumetric Medical Image Segmentation via a 3D Transformer. IEEE Trans. Image Process. 2023, 32, 4036–4045. [Google Scholar] [CrossRef] [PubMed]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.J.; Woolrich, M.W.; Smith, S.M. FSL. NeuroImage 2012, 62, 782–790. [Google Scholar] [CrossRef]
- Roy, A.G.; Conjeti, S.; Navab, N.; Wachinger, C. Inherent Brain Segmentation Quality Control from Fully ConvNet Monte Carlo Sampling. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2018, Granada, Spain, 16–20 September 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 664–672. [Google Scholar]
- Hann, E.; Biasiolli, L.; Zhang, Q.; Popescu, I.A.; Werys, K.; Lukaschuk, E.; Carapella, V.; Paiva, J.M.; Aung, N.; Rayner, J.J.; et al. Quality Control-Driven Image Segmentation Towards Reliable Automatic Image Analysis in Large-Scale Cardiovascular Magnetic Resonance Aortic Cine Imaging. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 750–758. [Google Scholar]
- Li, X.; Wei, Y.; Wang, L.; Fu, S.; Wang, C. MSGSE-Net: Multi-Scale Guided Squeeze-and-Excitation Network for Subcortical Brain Structure Segmentation. Neurocomputing 2021, 461, 228–243. [Google Scholar] [CrossRef]
- Feng, X.; Tustison, N.J.; Patel, S.H.; Meyer, C.H. Brain Tumor Segmentation Using an Ensemble of 3D U-Nets and Overall Survival Prediction Using Radiomic Features. Front. Comput. Neurosci. 2020, 14, 25. [Google Scholar] [CrossRef] [PubMed]
- Sled, J.; Zijdenbos, A.; Evans, A. A Nonparametric Method for Automatic Correction of Intensity Nonuniformity in MRI Data. IEEE Trans. Med. Imaging 1998, 17, 87–97. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M.; Jenkinson, M.; Woolrich, M.W.; Beckmann, C.F.; Behrens, T.E.J.; Johansen-Berg, H.; Bannister, P.R.; De Luca, M.; Drobnjak, I.; Flitney, D.E.; et al. Advances in Functional and Structural MR Image Analysis and Implementation as FSL. NeuroImage 2004, 23, S208–S219. [Google Scholar] [CrossRef] [PubMed]
- Peng, C.; Zhang, X.; Yu, G.; Luo, G.; Sun, J. Large Kernel Matters—Improve Semantic Segmentation by Global Convolutional Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4353–4361. [Google Scholar]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- De Boer, P.T.; Kroese, D.P.; Mannor, S.; Rubinstein, R.Y. A tutorial on the cross-entropy method. Ann. Oper. Res. 2005, 134, 19–67. [Google Scholar] [CrossRef]
- Ding, L.; Goshtasby, A. On the Canny Edge Detector. Pattern Recognit. 2001, 34, 721–725. [Google Scholar] [CrossRef]
- Van Essen, D.C.; Smith, S.M.; Barch, D.M.; Behrens, T.E.J.; Yacoub, E.; Ugurbil, K. The WU-Minn Human Connectome Project: An Overview. NeuroImage 2013, 80, 62–79. [Google Scholar] [CrossRef] [PubMed]
- Wei, D.; Zhuang, K.; Ai, L.; Chen, Q.; Yang, W.; Liu, W.; Wang, K.; Sun, J.; Qiu, J. Structural and Functional Brain Scans from the Cross-Sectional Southwest University Adult Lifespan Dataset. Sci. Data 2018, 5, 180134. [Google Scholar] [CrossRef]
- Beauchemin, M.; Thomson, K.; Edwards, G. On the Hausdorff Distance Used for the Evaluation of Segmentation Results. Can. J. Remote Sens. 1998, 24, 3–8. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. In Advances in Neural Information Processing Systems; Curran Associates, Inc.: New York, NY, USA, 2019; Volume 32. [Google Scholar]
- Armstrong, R.A. When to use the B onferroni correction. Ophthalmic Physiol. Opt. 2014, 34, 502–508. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Chung, A.C.S. A Fine-Grain Error Map Prediction and Segmentation Quality Assessment Framework for Whole-Heart Segmentation. In Lecture Notes in Computer Science, Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI 2019, Shenzhen, China, 13–17 October 2019; pp. 550–558.
- Zhang, J.; Sheng, V.S.; Li, T.; Wu, X. Improving crowdsourced label quality using noise correction. IEEE Trans. Neural Netw. Learn. Syst. 2017, 29, 1675–1688. [Google Scholar] [CrossRef] [PubMed]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef]
- Cheng, B.; Girshick, R.; Dollár, P.; Berg, A.C.; Kirillov, A. Boundary IoU: Improving object-centric image segmentation evaluation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 15334–15342. [Google Scholar]
- Zhu, Z.; He, X.; Qi, G.; Li, Y.; Cong, B.; Liu, Y. Brain tumor segmentation based on the fusion of deep semantics and edge information in multimodal MRI. Inf. Fusion 2023, 91, 376–387. [Google Scholar] [CrossRef]


| Scan Parameters | HCP | SALD | IXI | IBSR |
|---|---|---|---|---|
| Scanner | Siemens Skyra | Siemens TrioTim | Philips Intera | - |
| Field Strength | 3T | 3T | 1.5T | 3T |
| Sequence | MPRAGE | MPRAGE | MPRAGE | MPRAGE |
| Voxel Size (mm) | ||||
| TR/TE (ms) | 2400/2.14 | 1900/2.52 | 9.81/4.60 | - |
| FA (degrees) | 8 | 90 | 8 | - |
| Number of Scans (Train/Test) | 160/40 | 200/51 | 179/45 | 15/3 |
| Age Range (years) | 22-35 | 19-80 | 7-71 | - |
| Datasets | Models | GM | WM | CSF | Average | ||||
|---|---|---|---|---|---|---|---|---|---|
| Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | ||
| HCP | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| SALD | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| IXI | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| Datasets | Models | GM | WM | CSF | Average | ||||
|---|---|---|---|---|---|---|---|---|---|
| Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | ||
| HCP | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| SALD | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| IXI | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| Projects | Models | GM | WM | CSF | Average | ||||
|---|---|---|---|---|---|---|---|---|---|
| Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | ||
| HCP → SALD | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| SALD → HCP | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| HCP → IXI | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| SALD → IXI | UNet | ||||||||
| SegNet | |||||||||
| VoxResNet | |||||||||
| SegResNet | |||||||||
| nnUNet | |||||||||
| nnSegNeXt (ours) | |||||||||
| Projects | Models | GM | WM | CSF | Average | ||||
|---|---|---|---|---|---|---|---|---|---|
| Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | ||
| HCP → SALD | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| SALD → HCP | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| HCP → IXI | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| SALD → IXI | Attention UNet | ||||||||
| Swin-UNet | |||||||||
| UNETR | |||||||||
| TransBTS | |||||||||
| TABS | |||||||||
| nnFormer | |||||||||
| nnSegNeXt (ours) | |||||||||
| Models | GM | WM | CSF | Average | ||||
|---|---|---|---|---|---|---|---|---|
| Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | Dice↑ | HD95↓ | |
| UNet | ||||||||
| SegNet | ||||||||
| VoxResNet | ||||||||
| SegResNet | ||||||||
| nnUNet | ||||||||
| Attention UNet | ||||||||
| Swin-UNet | ||||||||
| UNETR | ||||||||
| TransBTS | ||||||||
| TABS | ||||||||
| nnFormer | ||||||||
| nnSegNeXt (ours) | ||||||||
| Datasets | Models | Average | Meandiff | p-Values | |
|---|---|---|---|---|---|
| Dice↑ | HD95↓ | ||||
| HCP | nnUNet | 0.0034 (Dice) | 0.0002 (Dice) | ||
| nnSegNeXt | −0.174 (HD95) | 0.0045 (HD95) | |||
| SALD | nnUNet | 0.0055 (Dice) | 0.0001 (Dice) | ||
| nnSegNeXt | −0.205 (HD95) | 0.0001 (HD95) | |||
| IXI | nnUNet | 0.0041 (Dice) | <0.005 (Dice) | ||
| nnSegNeXt | −0.155 (HD95) | <0.005 (HD95) | |||
| Architecture | HCP | SALD | IXI |
|---|---|---|---|
| nnSegNeXt w/o 3DMSCA and | 0.985 | 0.978 | 0.981 |
| nnSegNeXt w/o | 0.991 | 0.985 | 0.986 |
| nnSegNeXt w/o Conv and | 0.989 | 0.983 | 0.985 |
| nnSegNeXt w/o 3DMSCA | 0.989 | 0.982 | 0.983 |
| nnSegNeXt | 0.992 | 0.987 | 0.989 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Song, C.; Ning, X.; Gao, Y.; Wang, D. nnSegNeXt: A 3D Convolutional Network for Brain Tissue Segmentation Based on Quality Evaluation. Bioengineering 2024, 11, 575. https://doi.org/10.3390/bioengineering11060575
Liu Y, Song C, Ning X, Gao Y, Wang D. nnSegNeXt: A 3D Convolutional Network for Brain Tissue Segmentation Based on Quality Evaluation. Bioengineering. 2024; 11(6):575. https://doi.org/10.3390/bioengineering11060575
Chicago/Turabian StyleLiu, Yuchen, Chongchong Song, Xiaolin Ning, Yang Gao, and Defeng Wang. 2024. "nnSegNeXt: A 3D Convolutional Network for Brain Tissue Segmentation Based on Quality Evaluation" Bioengineering 11, no. 6: 575. https://doi.org/10.3390/bioengineering11060575
APA StyleLiu, Y., Song, C., Ning, X., Gao, Y., & Wang, D. (2024). nnSegNeXt: A 3D Convolutional Network for Brain Tissue Segmentation Based on Quality Evaluation. Bioengineering, 11(6), 575. https://doi.org/10.3390/bioengineering11060575






