Investigation of the Role of Osteoporotic Vertebra Degeneration on the Stability of the Lumbar Spine: In Silico Modelling under Compressive Loading
Abstract
1. Introduction
2. Materials and Methods
2.1. Geometric Model
2.2. Mechanical Properties
| Bone Type | Young’s Modulus [MPa] | Poisson’s Ratio |
|---|---|---|
| Vertebral cortical bone [36] | Exx = 2667 | νxy = 0.3 |
| Eyy = 2667 | νyz = 0.2 | |
| Ezz = 8000 | νxz = 0.2 | |
| Gxy = 1026 | ||
| Gyz = 1539 | ||
| Gxz = 1539 | ||
| Vertebral cancellous bone | Exx = 72.3/13 | νxy = 0.3 |
| (healthy/osteoporotic) | Eyy = 72.3/13 | νyz = 0.2 |
| Ezz = 723/130 | νxz = 0.2 | |
| Gxy = 27.8/5 | ||
| Gyz = 48.2/8.7 | ||
| Gxz = 48.2/8.7 | ||
| Vertebral bony endplate | E = 50 | ν = 0.4 |
| Posterior Bone | E = 3500 | ν = 0.25 |
2.3. FE Model
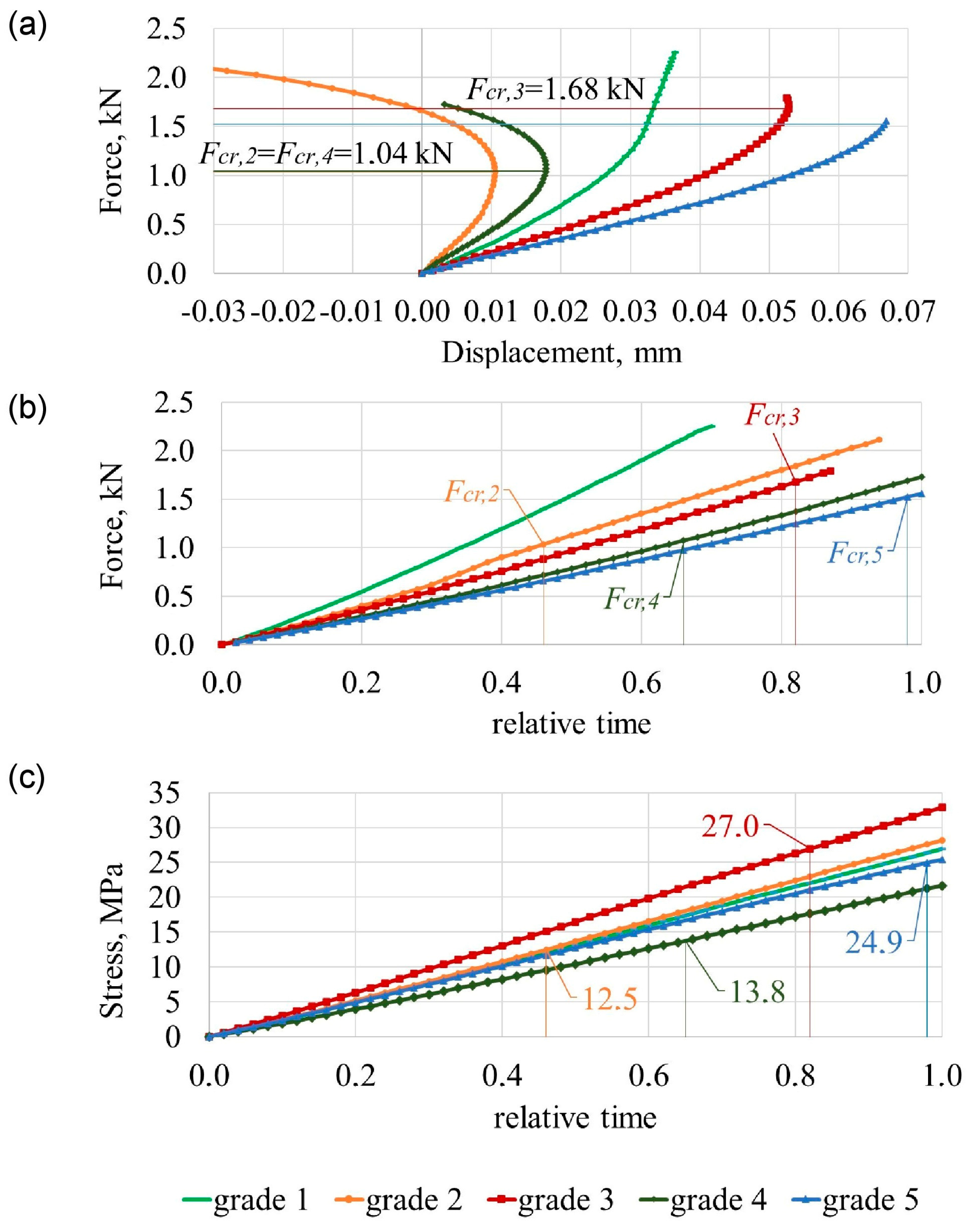
3. Results
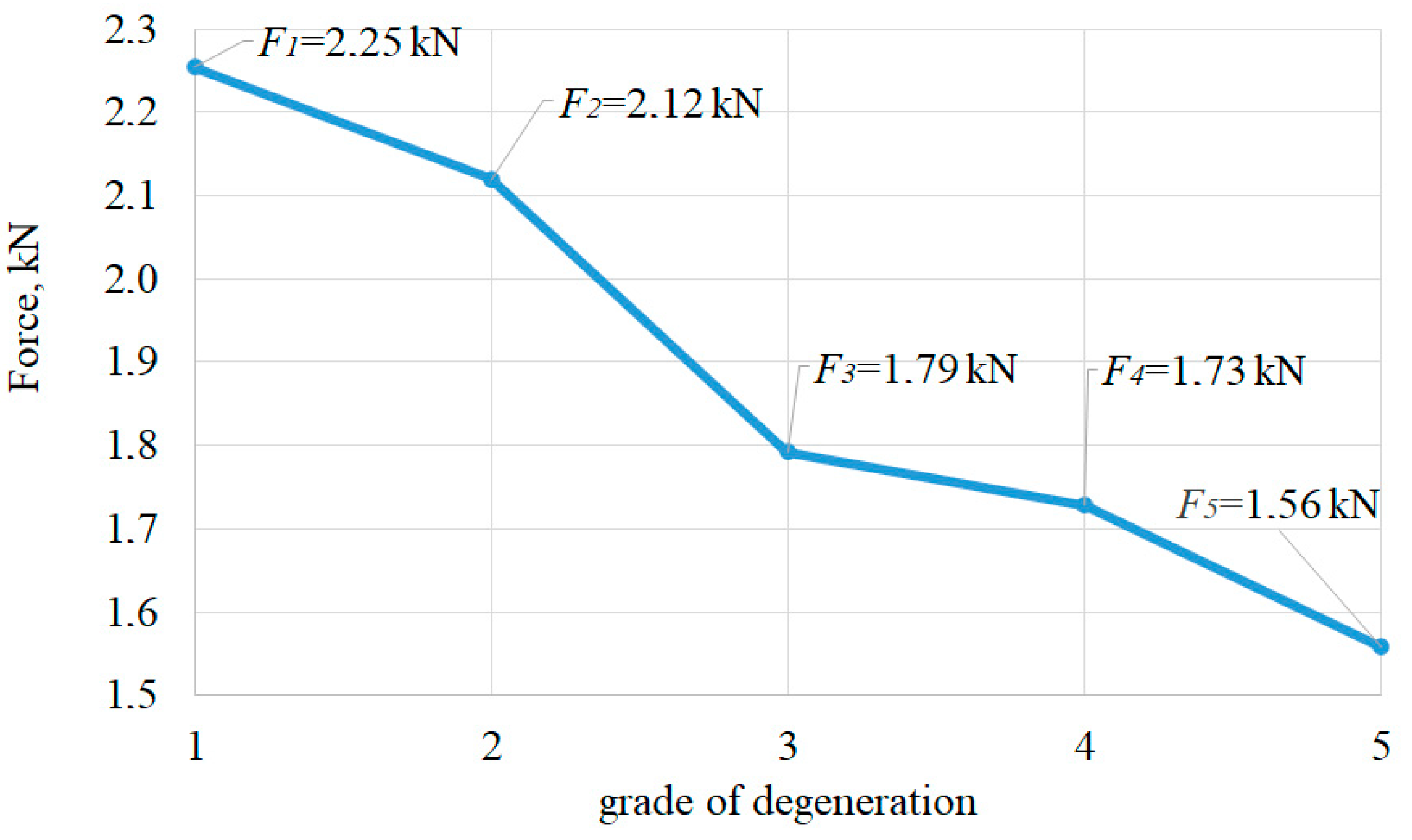
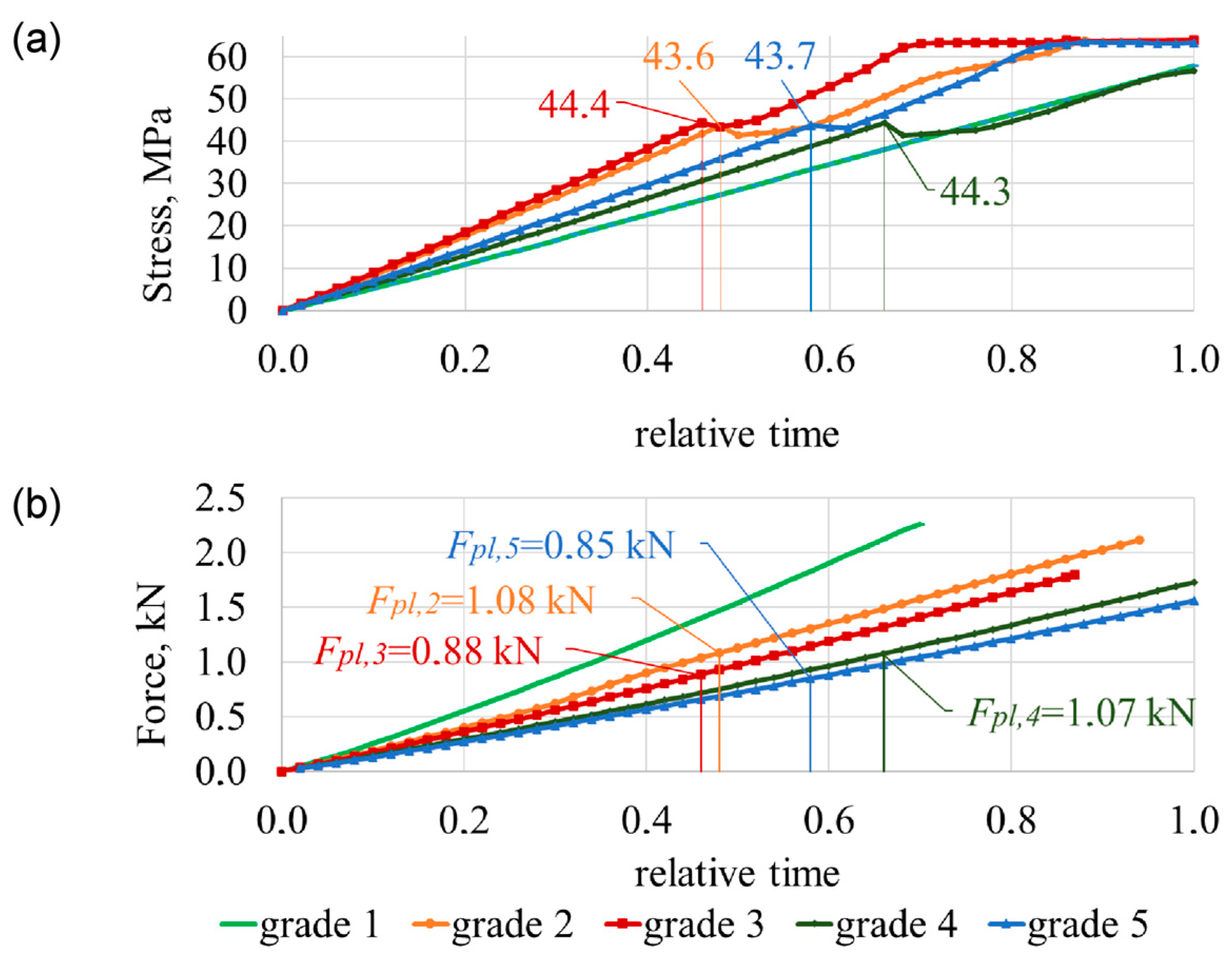
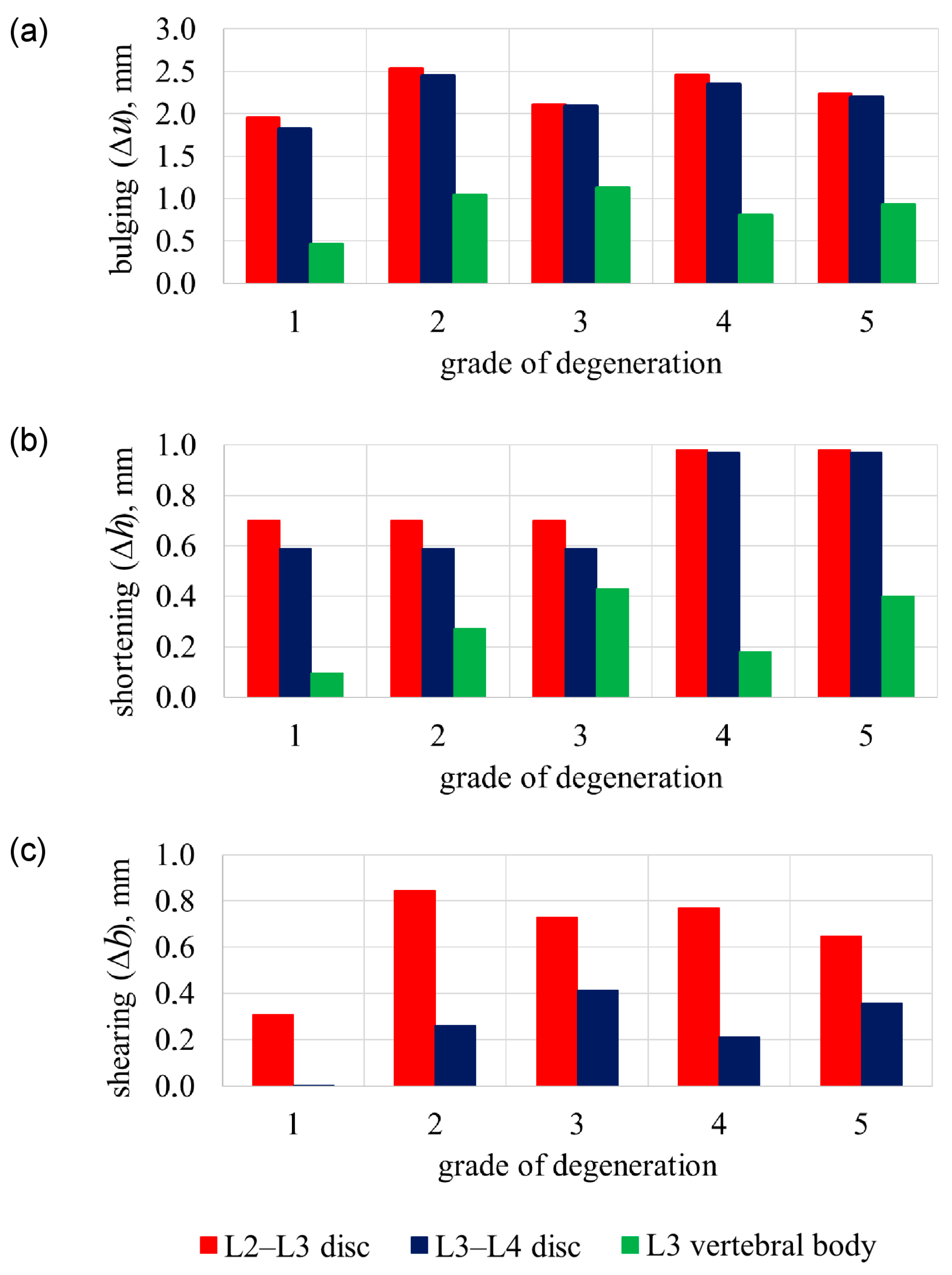
3.1. Failure Mechanisms of the Two Lumbar Segments
3.2. L3 Vertebra’s Failure Mechanisms
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, H.J.; Yang, J.H.; Chang, D.G.; Suk, S., II; Suh, S.W.; Song, K.S.; Park, J.B.; Cho, W. Adult Spinal Deformity: Current Concepts and Decision-Making Strategies for Management. Asian Spine J. 2020, 14, 886. [Google Scholar] [CrossRef]
- Zhang, Q.; Chon, T.; Zhang, Y.; Baker, J.S.; Gu, Y. Finite Element Analysis of the Lumbar Spine in Adolescent Idiopathic Scoliosis Subjected to Different Loads. Comput. Biol. Med. 2021, 136, 104745. [Google Scholar] [CrossRef] [PubMed]
- Argirò, R.; Diacinti, D.; Sacconi, B.; Iannarelli, A.; D’Adamo, E.A.; Sandolo, F.; Bezzi, M.; Catalano, C. MRI Assessment of Vertebral Fractures Identified by Conventional Radiography in Osteoporotic Patients: A Preliminary Study. In Proceedings of the European Congress of Radiology—ECR 2013, Vienna, Austria, 7–11 March 2013. [Google Scholar]
- Öhman-Mägi, C.; Holub, O.; Wu, D.; Hall, R.M.; Persson, C. Density and Mechanical Properties of Vertebral Trabecular Bone—A Review. JOR Spine 2021, 4, e1176. [Google Scholar] [CrossRef] [PubMed]
- Loughenbury, P.R.; Tsirikos, A.I.; Gummerson, N.W. Spinal Biomechanics-Biomechanical Considerations of Spinal Stability in the Context of Spinal Injury. Orthop. Trauma 2016, 30, 369–377. [Google Scholar] [CrossRef]
- Kanis, J.A.; Norton, N.; Harvey, N.C.; Jacobson, T.; Johansson, H.; Lorentzon, M.; McCloskey, E.V.; Willers, C.; Borgström, F. SCOPE 2021: A New Scorecard for Osteoporosis in Europe. Arch. Osteoporos. 2021, 16, 82. [Google Scholar] [CrossRef] [PubMed]
- Lems, W.F.; Paccou, J.; Zhang, J.; Fuggle, N.R.; Chandran, M.; Harvey, N.C.; Cooper, C.; Javaid, K.; Ferrari, S.; Akesson, K.E.; et al. Vertebral Fracture: Epidemiology, Impact and Use of DXA Vertebral Fracture Assessment in Fracture Liaison Services. Osteoporos. Int. 2021, 32, 399–411. [Google Scholar] [CrossRef]
- Cornaz, F.; Widmer, J.; Farshad-Amacker, N.A.; Spirig, J.M.; Snedeker, J.G.; Farshad, M. Intervertebral Disc Degeneration Relates to Biomechanical Changes of Spinal Ligaments. Spine J. 2021, 21, 1399–1407. [Google Scholar] [CrossRef] [PubMed]
- Dicko, A.H.; Tong-Yette, N.; Gilles, B.; Faure, F.; Palombi, O. Construction and Validation of a Hybrid Lumbar Spine Model for the Fast Evaluation of Intradiscal Pressure and Mobility. Int. J. Med. Health Sci. 2015, 9, 134–145. [Google Scholar]
- Wáng, Y.X.J.; Lentle, B.C. Radiographic Osteoporotic Vertebral Fractures in Elderly Men: A Brief Review Focusing on Differences between the Sexes. Quant. Imaging Med. Surg. 2020, 10, 1863. [Google Scholar] [CrossRef]
- Widmer, J.; Cornaz, F.; Scheibler, G.; Spirig, J.M.; Snedeker, J.G.; Farshad, M. Biomechanical Contribution of Spinal Structures to Stability of the Lumbar Spine—Novel Biomechanical Insights. Spine J. 2020, 20, 1705–1716. [Google Scholar] [CrossRef]
- Wan, S.; Xue, B.; Xiong, Y. Three-Dimensional Biomechanical Finite Element Analysis of Lumbar Disc Herniation in Middle Aged and Elderly. J. Healthc. Eng. 2022, 2022, 7107702. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.-X.; Li, Y.-H.; Wen, J.; Li, Z.; Yu, B.-S.; Huang, Y.-C. Annular Defects Impair the Mechanical Stability of the Intervertebral Disc. Glob. Spine J. 2021, 13, 724–729. [Google Scholar] [CrossRef] [PubMed]
- Naoum, S.; Vasiliadis, A.V.; Koutserimpas, C.; Mylonakis, N.; Kotsapas, M.; Katakalos, K. Finite Element Method for the Evaluation of the Human Spine: A Literature Overview. J. Funct. Biomater. 2021, 12, 43. [Google Scholar] [CrossRef] [PubMed]
- López, E.; Ibarz, E.; Herrera, A.; Puértolas, S.; Gabarre, S.; Más, Y.; Mateo, J.; Gil-Albarova, J.; Gracia, L. A Predictive Mechanical Model for Evaluating Vertebral Fracture Probability in Lumbar Spine under Different Osteoporotic Drug Therapies. Comput. Methods Programs Biomed. 2016, 131, 37–50. [Google Scholar] [CrossRef] [PubMed]
- Tsouknidas, A.; Sarigiannidis, S.O.; Anagnostidis, K.; Michailidis, N.; Ahuja, S. Assessment of Stress Patterns on a Spinal Motion Segment in Healthy versus Osteoporotic Bony Models with or without Disc Degeneration: A Finite Element Analysis. Spine J. 2015, 15, 17S–22S. [Google Scholar] [CrossRef] [PubMed]
- Huang, K.; Zhang, J. Three-Dimensional Lumbar Spine Generation Using Variational Autoencoder. Med. Eng. Phys. 2023, 120, 104046. [Google Scholar] [CrossRef] [PubMed]
- Wáng, J.-Q.; Káplár, Z.; Deng, M.; Griffith, J.F.; Leung, J.C.S.; Kwok, A.W.L.; Kwok, T.; Leung, P.C.; Wáng, Y.X.J. Thoracolumbar Intervertebral Disc Area Morphometry in Elderly Chinese Men and Women. Spine 2018, 43, E607–E614. [Google Scholar] [CrossRef]
- Luo, H.; Liu, G.; Fu, J.; Yu, C. Vibration Response Analysis of the Lumbar Spine Based on High-Speed Train Crew. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Honolulu, HI, USA, 31 July–4 August 2017; pp. 220–224. [Google Scholar]
- 3D Slicer Image Computing Platform|3D Slicer. Available online: https://www.slicer.org/ (accessed on 8 January 2023).
- MeshLab. Available online: https://www.meshlab.net/ (accessed on 8 January 2023).
- Solidworks. 3D CAD Design Software & PDM Systems. Available online: https://www.solidworks.com/ (accessed on 8 January 2023).
- Wierszycki, M.; Szajek, K.; Łodygowski, T.; Nowak, M. A Two-Scale Approach for Trabecular Bone Microstructure Modeling Based on Computational Homogenization Procedure. Comput. Mech. 2014, 54, 287–298. [Google Scholar] [CrossRef]
- Li, S.; Demirci, E.; Silberschmidt, V.V. Variability and Anisotropy of Mechanical Behavior of Cortical Bone in Tension and Compression. J. Mech. Behav. Biomed. Mater. 2013, 21, 109–120. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, K.; Tian, H.-J.; Wu, A.-M.; Cheng, X.-F.; Zhou, T.-J.; Zhao, J. Correlation between Lumbar Intervertebral Disc Height and Lumbar Spine Sagittal Alignment among Asymptomatic Asian Young Adults. J. Orthop. Surg. Res. 2018, 13, 34. [Google Scholar] [CrossRef]
- Teichtahl, A.J.; Finnin, M.A.; Wang, Y.; Wluka, A.E.; Urquhart, D.M.; O’Sullivan, R.; Jones, G.; Cicuttini, F.M. The Natural History of Modic Changes in a Community-Based Cohort. Jt. Bone Spine 2017, 84, 197–202. [Google Scholar] [CrossRef]
- Xu, M.; Yang, J.; Lieberman, I.H.; Haddas, R. Lumbar Spine Finite Element Model for Healthy Subjects: Development and Validation. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Maknickas, A.; Alekna, V.; Ardatov, O.; Chabarova, O.; Zabulionis, D.; Tamulaitiene, M.; Kačianauskas, R. FEM-Based Compression Fracture Risk Assessment in Osteoporotic Lumbar Vertebra L1. Appl. Sci. 2019, 9, 3013. [Google Scholar] [CrossRef]
- Amjadi Kashani, M.R.; Nikkhoo, M.; Khalaf, K.; Firoozbakhsh, K.; Arjmand, N.; Razmjoo, A.; Parnianpour, M. An in Silico Parametric Model of Vertebrae Trabecular Bone Based on Density and Microstructural Parameters to Assess Risk of Fracture in Osteoporosis. Proc. Inst. Mech. Eng. H 2014, 228, 1281–1295. [Google Scholar] [CrossRef] [PubMed]
- Alkalay, R.N.; Groff, M.W.; Stadelmann, M.A.; Buck, F.M.; Hoppe, S.; Theumann, N.; Mektar, U.; Davis, R.B.; Hackney, D.B. Improved Estimates of Strength and Stiffness in Pathologic Vertebrae with Bone Metastases Using CT-Derived Bone Density Compared with Radiographic Bone Lesion Quality Classification. J. Neurosurg. Spine 2021, 36, 113–124. [Google Scholar] [CrossRef] [PubMed]
- Osterhoff, G.; Morgan, E.F.; Shefelbine, S.J.; Karim, L.; McNamara, L.M. Bone Mechanical Properties and Changes with Osteoporosis. Injury 2016, 47, S11–S20. [Google Scholar] [CrossRef]
- Hamilton, E.J.; Ghasem-Zadeh, A.; Gianatti, E.; Lim-Joon, D.; Bolton, D.; Zebaze, R.; Seeman, E.; Zajac, J.D.; Grossmann, M. Structural Decay of Bone Microarchitecture in Men with Prostate Cancer Treated with Androgen Deprivation Therapy. J. Clin. Endocrinol. Metab. 2010, 95, E456–E463. [Google Scholar] [CrossRef] [PubMed]
- Zahaf, S.; Habib, H.; Mansouri, B.; Belarbi, A.; Azari, Z. The Effect of the Eccentric Loading on the Components of the Spine Global Journal of Researches in Engineering: A Mechanical and Mechanics Engineering The Effect of the Eccentric Loading on the Components of the Spine. Glob. J. Res. Eng. A Mech. Mech. Eng. 2016, 16, 2249–4596. [Google Scholar]
- Jones, A.C.; Wilcox, R.K. Finite Element Analysis of the Spine: Towards a Framework of Verification, Validation and Sensitivity Analysis. Med. Eng. Phys. 2008, 30, 1287–1304. [Google Scholar] [CrossRef]
- Monteiro, N.M.B.; da Silva, M.P.T.; Folgado, J.O.M.G.; Melancia, J.P.L. Structural Analysis of the Intervertebral Discs Adjacent to an Interbody Fusion Using Multibody Dynamics and Finite Element Cosimulation. Multibody Syst. Dyn. 2011, 25, 245–270. [Google Scholar] [CrossRef]
- Tapp, A.; Polanco, M.; Kumi, I.; Bawab, S.; Ringleb, S.; Kakar, R.; Remy, C.S.; Bennett, J.; Audette, M. Generating Scoliotic Computed Tomography Volumes from Finite Element Spine Models. In Computational Biomechanics for Medicine: Towards Translation and Better Patient Outcomes; Springer: Cham, Switzerland, 2022; pp. 91–103. [Google Scholar] [CrossRef]
- Alkalay, R.N.; Harrigan, T.P. Mechanical Assessment of the Effects of Metastatic Lytic Defect on the Structural Response of Human Thoracolumbar Spine. J. Orthop. Res. 2016, 34, 1808–1819. [Google Scholar] [CrossRef] [PubMed]
- López, E.; Ibarz, E.; Herrera, A.; Mateo, J.; Lobo-Escolar, A.; Puértolas, S.; Gracia, L. Probability of Osteoporotic Vertebral Fractures Assessment Based on DXA Measurements and Finite Element Simulation. Adv. Biosci. Biotechnol. 2014, 5, 527–545. [Google Scholar] [CrossRef]
- Zhu, R.; Niu, W.-X.; Zeng, Z.-L.; Tong, J.-H.; Zhen, Z.-W.; Zhou, S.; Yu, Y.; Cheng, L.-M. The Effects of Muscle Weakness on Degenerative Spondylolisthesis: A Finite Element Study. Clin. Biomech. 2017, 41, 34–38. [Google Scholar] [CrossRef] [PubMed]
- Niemeyer, F.; Wilke, H.-J.; Schmidt, H. Geometry Strongly Influences the Response of Numerical Models of the Lumbar Spine—A Probabilistic Finite Element Analysis. J. Biomech. 2012, 45, 1414–1423. [Google Scholar] [CrossRef]
- Casaroli, G.; Galbusera, F.; Jonas, R.; Schlager, B.; Wilke, H.-J.; Villa, T. A Novel Finite Element Model of the Ovine Lumbar Intervertebral Disc with Anisotropic Hyperelastic Material Properties. PLoS ONE 2017, 12, e0177088. [Google Scholar] [CrossRef] [PubMed]
- Ellingson, A.M.; Shaw, M.N.; Giambini, H.; An, K.-N. Comparative Role of Disc Degeneration and Ligament Failure on Functional Mechanics of the Lumbar Spine. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 1009–1018. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, M.A.; Moraes, R.; Castanha, E.B.; Prevedello, A.S.; Vieira Filho, J.; Bussolaro, F.A.; García Cava, D. Osteoporosis Screening: Applied Methods and Technological Trends. Med. Eng. Phys. 2022, 108, 103887. [Google Scholar] [CrossRef] [PubMed]
- Schröder, G.; Reichel, M.; Spiegel, S.; Schulze, M.; Götz, A.; Bugaichuk, S.; Andresen, J.R.; Kullen, C.M.; Andresen, R.; Schober, H.C. Breaking Strength and Bone Microarchitecture in Osteoporosis: A Biomechanical Approximation Based on Load Tests in 104 Human Vertebrae from the Cervical, Thoracic, and Lumbar Spines of 13 Body Donors. J. Orthop. Surg. Res. 2022, 17, 228. [Google Scholar] [CrossRef]
- Hauser, R.A.; Matias, D.; Woznica, D.; Rawlings, B.; Woldin, B.A. Lumbar Instability as an Etiology of Low Back Pain and Its Treatment by Prolotherapy: A Review. J. Back Musculoskelet. Rehabil. 2022, 35, 701. [Google Scholar] [CrossRef]
- Leone, A.; Cassar-Pullicino, V.N.; Guglielmi, G.; Bonomo, L. Degenerative Lumbar Intervertebral Instability: What Is It and How Does Imaging Contribute? Skelet. Radiol. 2009, 38, 529–533. [Google Scholar] [CrossRef]
- Kim, J.; Yang, S.J.; Kim, H.; Kim, Y.; Park, J.B.; Dubose, C.; Lim, T.H. Effect of Shear Force on Intervertebral Disc (IVD) Degeneration: An in Vivo Rat Study. Ann. Biomed. Eng. 2012, 40, 1996–2004. [Google Scholar] [CrossRef]
- Karas, S.; Temes, B. Addition of the Anterior Shear Test in Diagnosing Lumbar Segmental Instability: A Case Report. Orthop. Pract. 2018, 30, 26–31. [Google Scholar]
- Raymond, L.; Evans, J. An in Vivo Study of the Intervertebral Movements Produced by Posteroanterior Mobilization. Clin. Biomech. 1997, 12, 400–408. [Google Scholar] [CrossRef] [PubMed]
- Kurutz, M.; Donáth, J.; Gálos, M.; Varga, P.; Fornet, B. Age- and Sex-Related Regional Compressive Strength Characteristics of Human Lumbar Vertebrae in Osteoporosis. J. Multidiscip. Healthc. 2008, 1, 105–121. [Google Scholar] [CrossRef] [PubMed]
- Tranquilli Leali, P.; Doria, C.; Zachos, A.; Ruggiu, A.; Milia, F.; Barca, F. Bone Fragility: Current Reviews and Clinical Features. Clin. Cases Miner. Bone Metab. 2009, 6, 109. [Google Scholar] [PubMed]
- Adams, M.A.; Bogduk, N.; Burton, K.; Dolan, P. The Biomechanics of Back Pain, 2nd ed.; Churchill Livingstone: London, UK, 2006; ISBN 9780443100680. [Google Scholar]
- Benoist, M. Natural History of the Aging Spine. Eur. Spine J. 2003, 12 (Suppl. S2), S86–S89. [Google Scholar] [CrossRef]
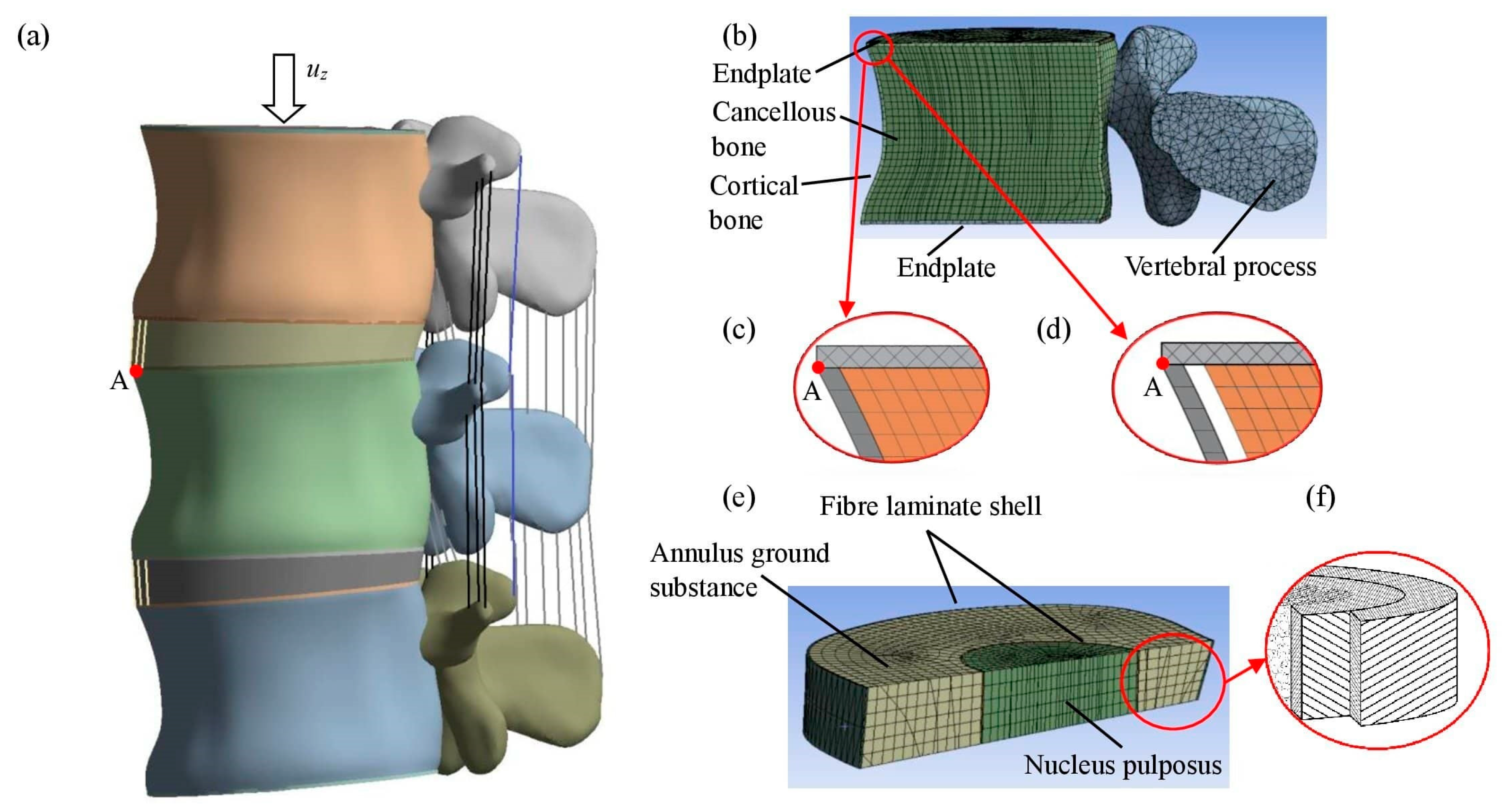


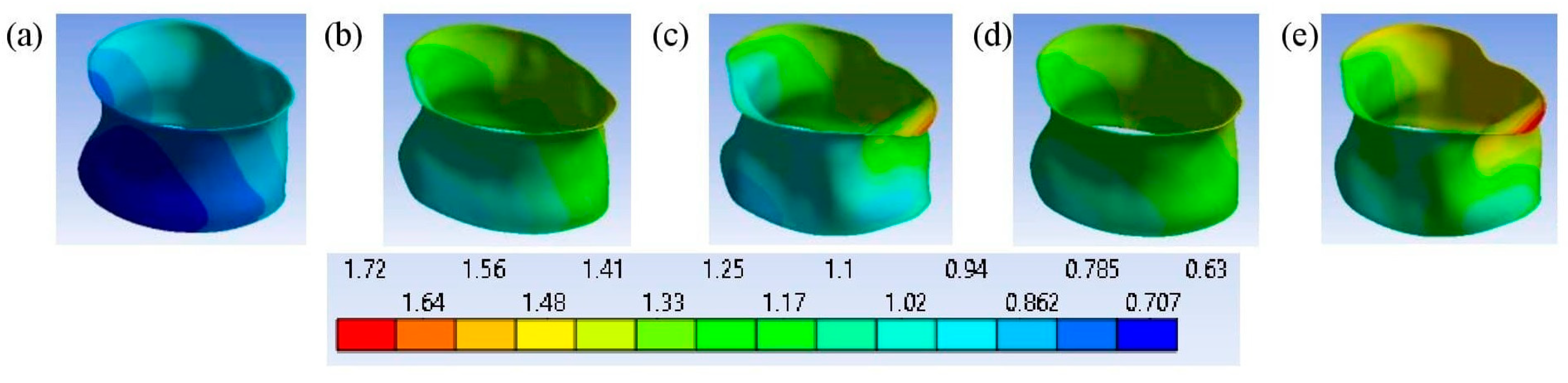
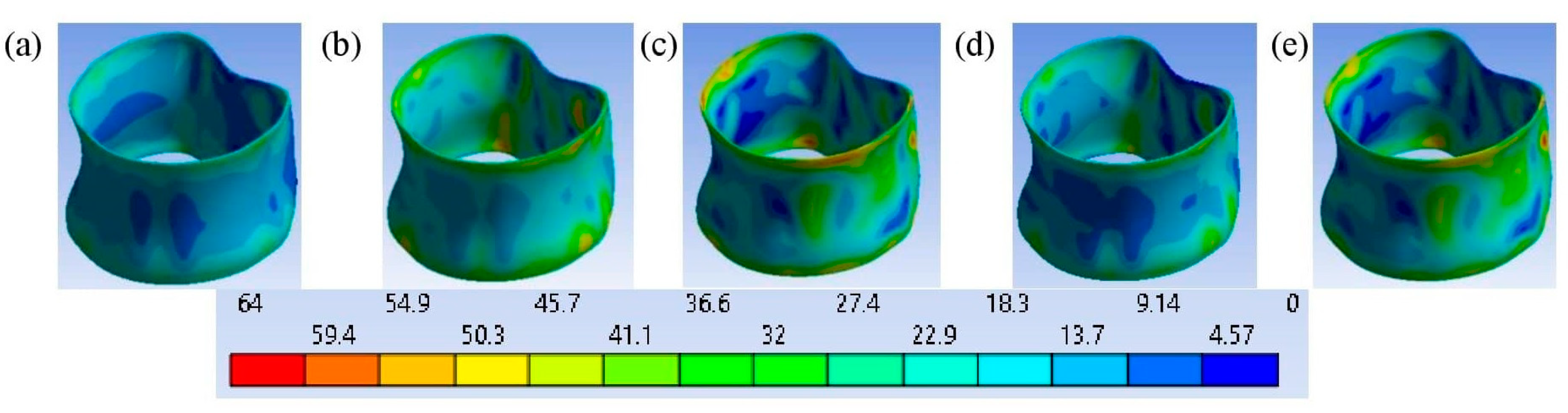
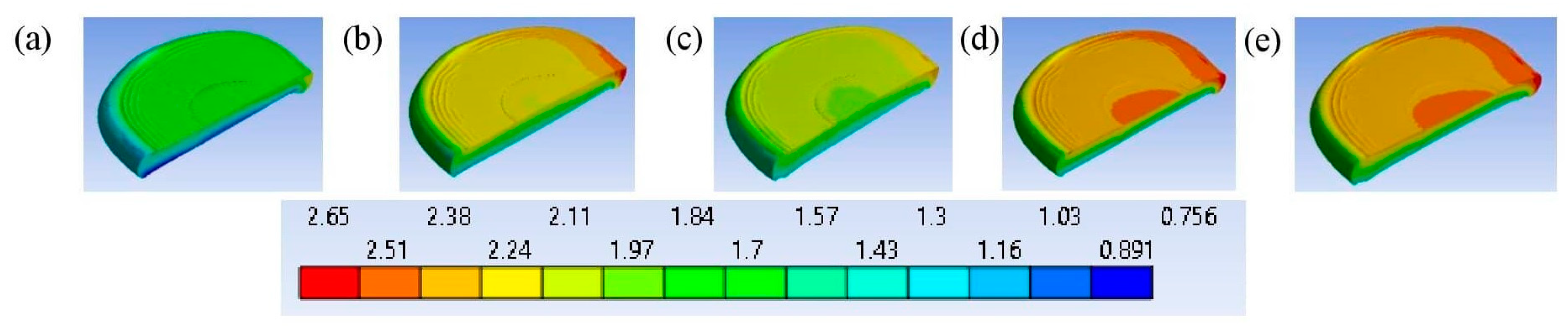
| Grades of Age-Related Degeneration * | Grade 1 | Grade 2 | Grade 3 | Grade 4 | Grade 5 |
|---|---|---|---|---|---|
| Cancellous bone (density [kg/m3]) | 300 | 100 | 100 | 100 | 100 |
| Cortical bone | bonded | bonded | unbonded | bonded | unbonded |
| Nucleus (Elastic Modulus [MPa]/Poisson’s Ratio, ν) | 1/0.4999 | 1/0.4999 | 1/0.4999 | 1.66/0.4 | 1.66/0.4 |
| Annulus ground substance (Coefficients of Neo-Hookean material/Poisson’s Ratio, ν) | C10 = 0.25; D1 = 0.86/0.40 | C10 = 0.25; D1 = 0.86/0.40 | C10 = 0.25; D1 = 0.86/0.40 | C10 = 1.13; D1 = 0.19/0.40 | C10 = 1.13; D1 = 0.19/0.40 |
| Annular Fibres (external/internal) | 500/300 | 500/300 | 500/300 | 500/300 | 500/300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chabarova, O.; Selivonec, J.; Menendez Hurtado, A. Investigation of the Role of Osteoporotic Vertebra Degeneration on the Stability of the Lumbar Spine: In Silico Modelling under Compressive Loading. Bioengineering 2024, 11, 507. https://doi.org/10.3390/bioengineering11050507
Chabarova O, Selivonec J, Menendez Hurtado A. Investigation of the Role of Osteoporotic Vertebra Degeneration on the Stability of the Lumbar Spine: In Silico Modelling under Compressive Loading. Bioengineering. 2024; 11(5):507. https://doi.org/10.3390/bioengineering11050507
Chicago/Turabian StyleChabarova, Olga, Jelena Selivonec, and Alicia Menendez Hurtado. 2024. "Investigation of the Role of Osteoporotic Vertebra Degeneration on the Stability of the Lumbar Spine: In Silico Modelling under Compressive Loading" Bioengineering 11, no. 5: 507. https://doi.org/10.3390/bioengineering11050507
APA StyleChabarova, O., Selivonec, J., & Menendez Hurtado, A. (2024). Investigation of the Role of Osteoporotic Vertebra Degeneration on the Stability of the Lumbar Spine: In Silico Modelling under Compressive Loading. Bioengineering, 11(5), 507. https://doi.org/10.3390/bioengineering11050507








