MMG-Based Knee Dynamic Extension Force Estimation Using Cross-Talk and IGWO-LSTM
Abstract
1. Introduction
2. Materials and Methods
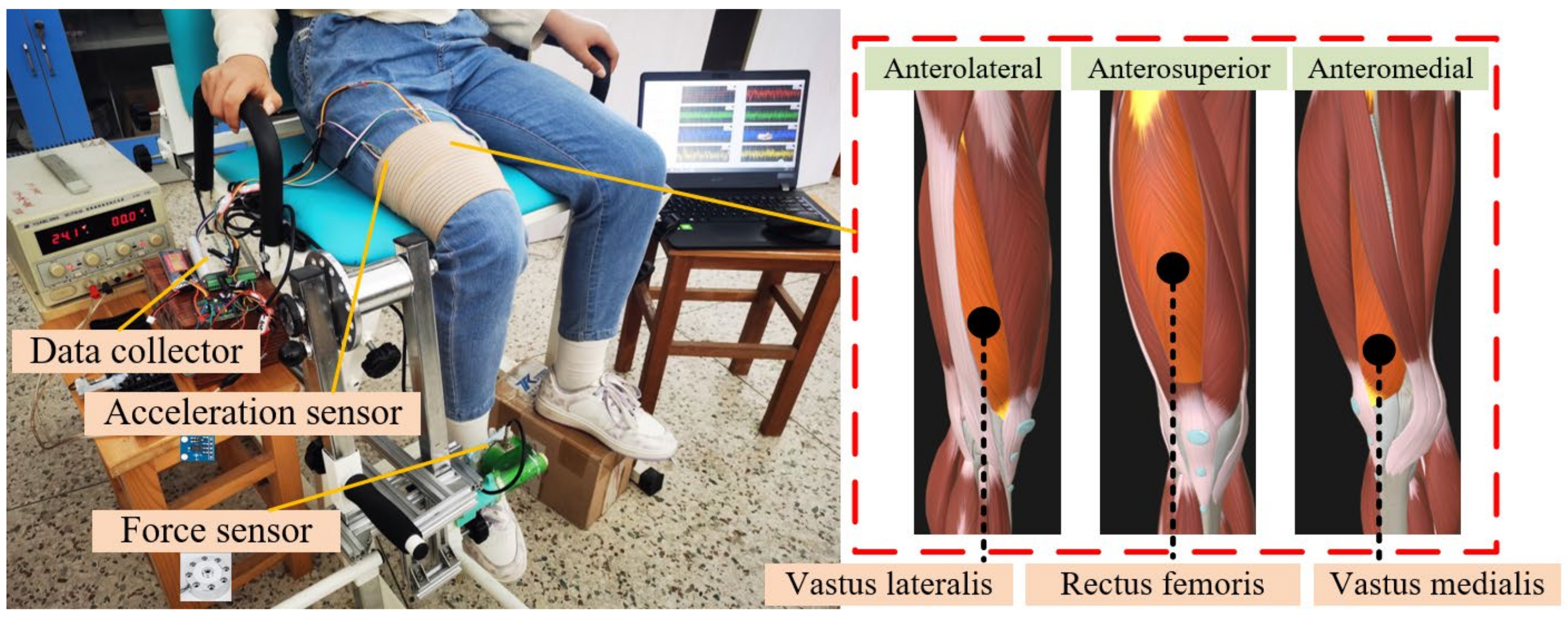
2.1. Experimental Devices and Procedures
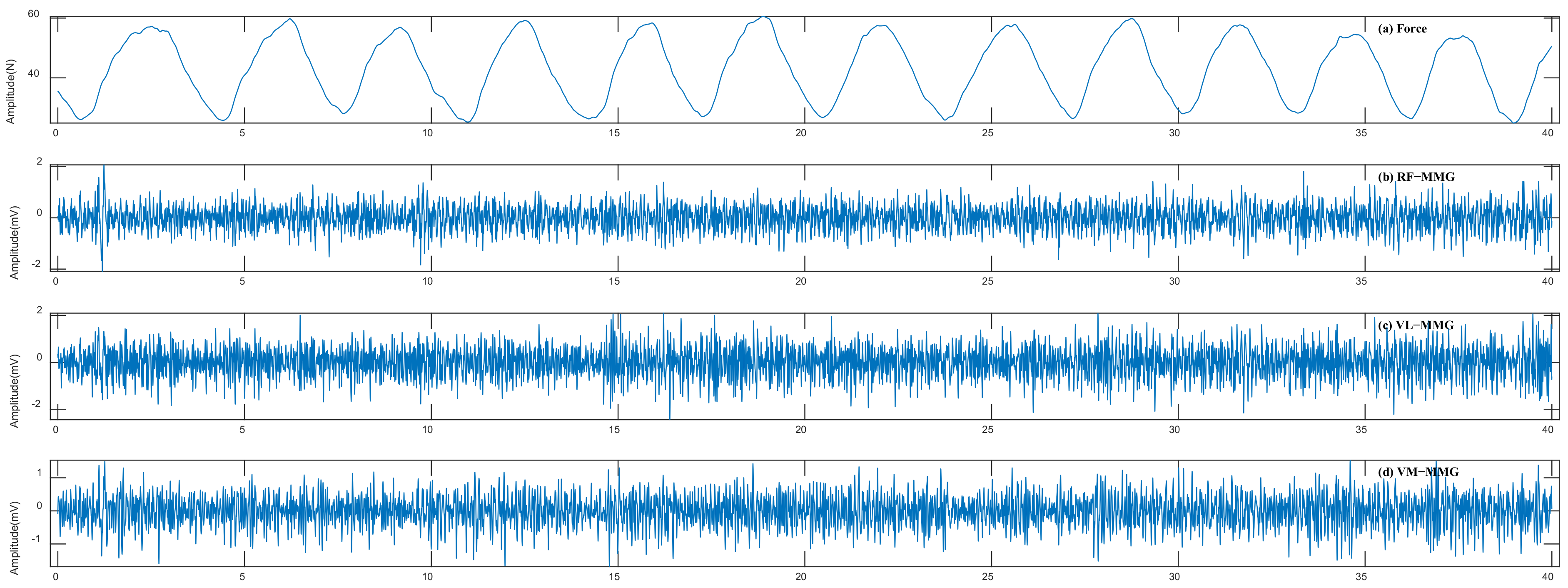
2.2. Signal Processing
2.3. Data Cross-Talk Analysis
2.4. Estimation Model
2.4.1. BPNN Model
2.4.2. IGWO-SVR Model
2.4.3. LSTM Model
2.4.4. IGWO-LSTM Model
2.4.5. Model Evaluation Indicators
3. Results
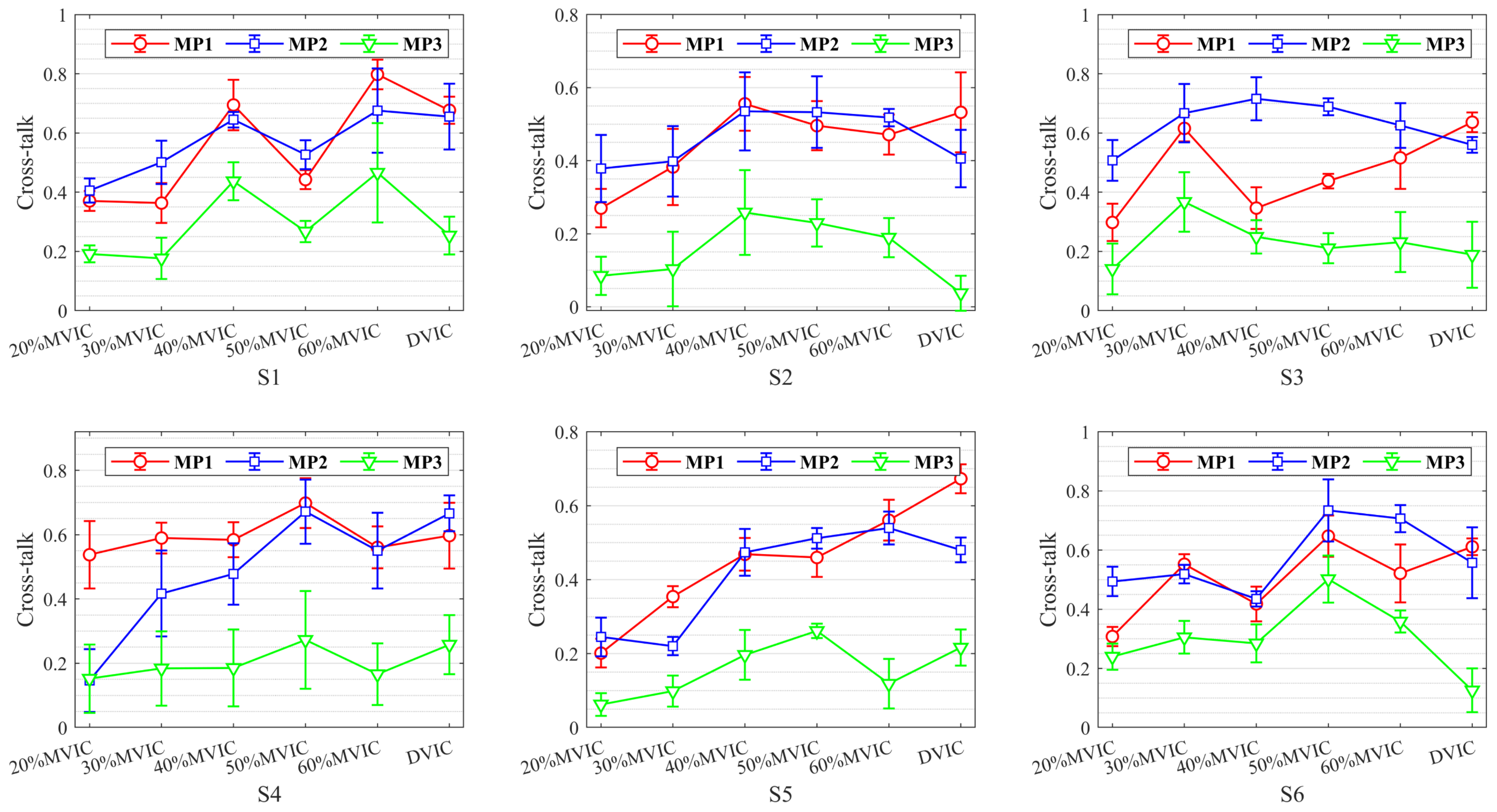
3.1. Cross-Talk Analysis of Different Muscle Pairs
3.2. Knee Dynamic Extension Force Estimation with Different Muscle Feature Combinations
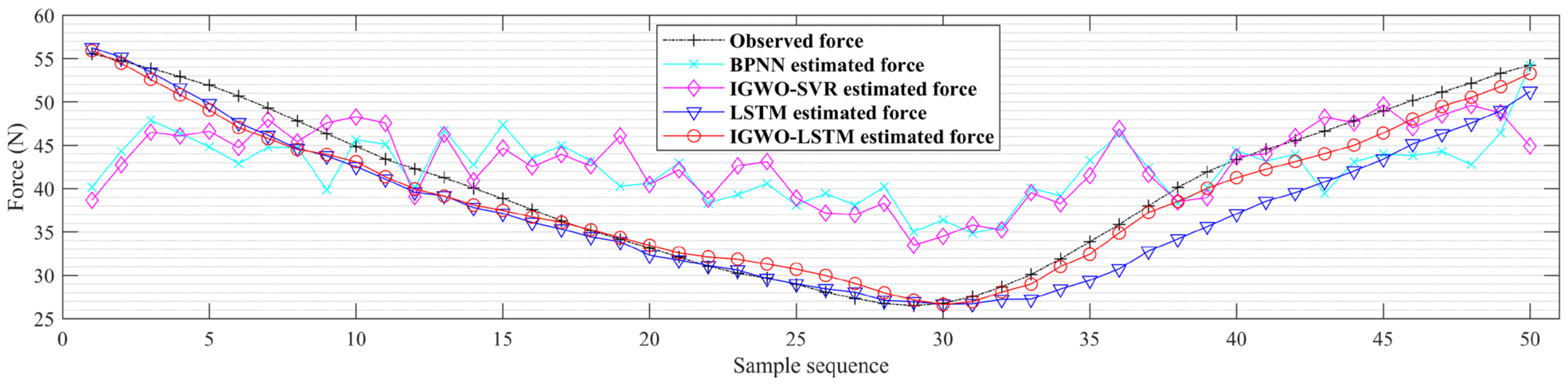
3.3. Applying the IGWO-LSTM Model to Estimate Knee Dynamic Extension Force
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, H.; Huang, Q.; Wang, D.; Gao, L. A CNN-SVM combined model for pattern recognition of knee motion using mechanomyography signals. J. Electromyogr. Kinesiol. 2018, 42, 136–142. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Yang, C.; Xie, Q. Human-machine interfaces based on EMG and Kinect applied to teleoperation of a mobile humanoid robot. In Proceedings of the IEEE 10th World Congress on Intelligent Control & Automation (WCICA), Beijing, China, 24 November 2012; pp. 3903–3908. [Google Scholar]
- Sun, N.; Cao, M.; Chen, Y.; Wang, J.; Wang, Q. Continuous estimation of human knee joint angles by fusing kinematic and myoelectric signals. IEEE Trans. Neural. Syst. Rehabil. Eng. 2022, 30, 2446–2455. [Google Scholar] [CrossRef] [PubMed]
- Xie, C.; Wang, D.; Wu, H.; Gao, L. A long short-term memory neural network model for knee joint acceleration estimation using mechanomyography signals. Int. J. Adv. Robot. Syst. 2020, 17, 1–10. [Google Scholar] [CrossRef]
- Ibitoye, M.O.; Hamzaid, N.A.; Abdul Wahab, A.K.; Hasnan, N.; Olatunji, S.O.; Davis, G.M. Estimation of Electrically-Evoked Knee Torque from Mechanomyography Using Support Vector Regression. Sensors 2016, 16, 1115. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Fernandez, J.W.; Akbarshahi, M.; Walter, J.P.; Fregly, B.J.; Pandy, M.G. Evaluation of predicted knee-joint muscle forces during gait using an instrumented knee implant. J. Orthop. Res. 2009, 27, 1326–1331. [Google Scholar] [CrossRef]
- Lei, K.F.; Cheng, S.C.; Lee, M.Y.; Lin, W.Y. Measurement and estimation of muscle contraction strength using mechanomyography based on artificial neural network algorithm. Biomed. Eng. Appl. Basis. Commun. 2013, 25, 1350020. [Google Scholar] [CrossRef]
- Sidek, S.N.; Mohideen, A.J.H. Mapping of EMG signal to hand grip force at varying wrist angles. In Proceedings of the IEEE-EMBS Conference on Biomedical Engineering and Sciences (CBES), Langkawi, Malaysia, 15 April 2013; pp. 648–653. [Google Scholar]
- Wang, D.; Guo, W.; Wu, H.; Gao, L. An estimation method of quadriceps femoris contraction strength using mechanomyography signal. Chin. J. Sen. Actu. 2018, 31, 1700–1706. [Google Scholar]
- Mohamad Ismail, M.R.; Lam, C.K.; Sundaraj, K.; Rahiman, M.H.F. Fatigue effect on cross-talk in mechanomyography signals of extensor and flexor forearm muscles during maximal voluntary isometric contractions. J. Musculoskelet. Neuronal. Interact. 2021, 21, 481–494. [Google Scholar] [PubMed]
- Doheny, E.P.; Lowery, M.M.; Fitzpatrick, D.P.; O’Malley, M.J. Effect of elbow joint angle on force-EMG relationships in human elbow flexor and extensor muscles. J. Electromyogr. Kinesiol. 2008, 18, 760–770. [Google Scholar] [CrossRef] [PubMed]
- Wilson, S.; Vaidyanathan, R. Upper-limb prosthetic control using wearable multichannel mechanomyography. In Proceedings of the International Conference on Rehabilitation Robotics (ICORR), London, UK, 14 August 2017; pp. 1293–1298. [Google Scholar]
- Talib, I.; Sundaraj, K.; Lam, C.K.; Sundaraj, S. A systematic review of muscle activity assessment of the biceps brachii muscle using mechanomyography. J. Musculoskelet. Neuronal Interact. 2018, 18, 446–462. [Google Scholar] [PubMed]
- Zhang, L.; Soselia, D.; Wang, R.; Gutierrez-Farewik, E.M. Estimation of Joint Torque by EMG-Driven Neuromusculoskeletal Models and LSTM Networks. IEEE Trans. Neural Syst. Rehabil. Eng. 2023, 31, 3722–3731. [Google Scholar] [CrossRef] [PubMed]
- Ma, R.; Zhang, L.; Li, G.; Jiang, D.; Xu, S.; Chen, D. Grasping force prediction based on sEMG signals. Alex. Eng. J. 2020, 59, 1135–1147. [Google Scholar] [CrossRef]
- Talib, I.; Sundaraj, K.; Lam, C.K. Crosstalk in mechanomyographic signals from elbow flexor muscles during submaximal to maximal isometric flexion, pronation, and supination torque tasks. J. Biomech. Eng. 2021, 143, 011001. [Google Scholar] [CrossRef] [PubMed]
- Harrison, A.P. A more precise, repeatable and diagnostic alternative to surface electromyography—An appraisal of the clinical utility of acoustic myography. Clin. Physiol. Funct. Imaging 2018, 38, 312–325. [Google Scholar] [CrossRef] [PubMed]
- Youn, W.; Kim, J. Estimation of elbow flexion force during isometric muscle contraction from mechanomyography and electromyography. Med. Biol. Eng. Comput. 2010, 48, 1149–1157. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Wang, D.; Huang, Q.; Gao, L. Real-time continuous recognition of knee motion using multi-channel mechanomyography signals detected on clothes. J. Electromyogr. Kinesiol. 2018, 38, 94–102. [Google Scholar] [CrossRef] [PubMed]
- Xi, X.; Yang, C.; Miran, S.M.; Zhao, Y.B.; Lin, S.; Luo, Z. sEMG-MMG state-space model for the continuous estimation of multijoint angle. Complexity 2020, 2020, 4503271. [Google Scholar] [CrossRef]
- Xie, C.; Wang, D.; Wu, H.; Gao, L. Angular velocity estimation of knee joint based on MMG signals. In Proceedings of the International Conference on Intelligent Robotics and Applications (ICIRA), Shenyang, China, 8–11 August 2019; pp. 15–25. [Google Scholar]
- Talib, I.; Sundaraj, K.; Lam, C.K.; Hussain, J.; Ali, M.A. A review on crosstalk in myographic signals. Eur. J. Appl. Physiol. 2019, 119, 9–28. [Google Scholar] [CrossRef] [PubMed]
- Talib, I.; Sundaraj, K.; Lam, C.K. Analysis of the crosstalk in mechanomyographic signals along the longitudinal, lateral and transverse axes of elbow flexor muscles during sustained isometric forearm flexion, supination and pronation exercises. J. Musculoskelet. Neuronal Interact. 2020, 20, 194–205. [Google Scholar] [PubMed]
- Talib, I.; Sundaraj, K.; Lam, C.K. Association of anthropometric parameters with amplitude and crosstalk of mechanomyographic signals during forearm flexion, pronation and supination torque tasks. Sci. Rep. 2019, 9, 16166. [Google Scholar] [CrossRef] [PubMed]
- Beck, T.W.; Dillon, M.A.; DeFreitas, J.M.; Stock, M.S. Cross-correlation analysis of mechanomyographic signals detected in two axes. Physiol. Meas. 2009, 30, 1465–1471. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.A.; Sundaraj, K.; Ahmad, R.B.; Sundaraj, S.; Ahamed, N.U.; Ali, M.A. Longitudinal, lateral and transverse axes of forearm muscles infuence the crosstalk in the mechanomyographic signals during isometric wrist postures. PLoS ONE 2014, 9, e104280. [Google Scholar] [CrossRef]
- Beck, T.W.; DeFreitas, J.M.; Stock, M.S. An examination of cross-talk among surface mechanomyographic signals from the superfcial quadriceps femoris muscles during isometric muscle actions. Hum. Mov. Sci. 2010, 29, 165–171. [Google Scholar] [CrossRef]
- Youn, W.; Kim, J. Feasibility of using an artificial neural network model to estimate the elbow flexion force from mechanomyography. J. Neurosci. Methods 2011, 194, 386–393. [Google Scholar] [CrossRef]
- Wang, D.; Xie, C.; Wu, H.; Hu, D.; Zhang, Q.; Gao, L. Estimation of knee extension force using mechanomyography signals detected through clothing. In Proceedings of the 12th International Conference on Intelligent Robotics and Applications (ICIRA), Shenyang, China, 8–11 August 2019; pp. 3–14. [Google Scholar]
- Li, Z.; Gao, L.; Lu, W.; Wang, D.; Xie, C.; Cao, H. Estimation of knee joint extension force using mechanomyography based on IGWO-SVR algorithm. Electronics 2021, 10, 2972. [Google Scholar] [CrossRef]
- Li, Z.; Gao, L.; Lu, W.; Wang, D.; Cao, H.; Zhang, G. Estimation of knee extension force using mechanomyography signals based on GRA and ICS-SVR. Sensors 2022, 22, 4651. [Google Scholar] [CrossRef] [PubMed]
- Hondo, N.; Tsuji, T. Torque estimation of knee flexion and extension movements from a mechanomyogram of the femoral muscle. IEEE Trans. Neural Syst. Rehabil. Eng. 2022, 30, 1120–1126. [Google Scholar] [CrossRef]
- He, J.; Guo, Z.; Shao, Z.; Zhao, J.; Dan, G. An LSTM-based prediction method for lower limb intention perception by integrative analysis of kinect visual signal. J. Healthc. Eng. 2020, 2020, 8024789. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Yu, S.; Ma, K.; Huang, S.; Li, G.; Cai, S. A continuous estimation model of upper limb joint angles by using surface electromyography and deep learning method. IEEE Access 2019, 7, 174940–174950. [Google Scholar] [CrossRef]
- Dao, T.T. From deep learning to transfer learning for the prediction of skeletal muscle forces. Med. Biol. Eng. Comput. 2019, 57, 1049–1058. [Google Scholar] [CrossRef] [PubMed]
- Aufa, B.Z.; Suyanto, S.; Arifianto, A. Hyperparameter setting of LSTM-based language model using grey wolf optimizer. In Proceedings of the 2020 International Conference on Data Science and Its Applications (ICoDSA), Bandung, Indonesia, 5–6 August 2020; pp. 1–5. [Google Scholar]
- Rashid, T.A.; Fattah, P.; Awla, D.K. Using accuracy measure for improving the training of LSTM with metaheuristic algorithms. Proc. Comput. Sci. 2018, 140, 324–333. [Google Scholar] [CrossRef]
- Xie, Q.; Guo, Z.; Liu, D.; Chen, Z.; Wang, X. Optimization of heliostat field distribution based on improved gray wolf optimization algorithm. Renew. Energy 2021, 176, 447–458. [Google Scholar] [CrossRef]
- Akataki, K.; Mita, K.; Watakabe, M.; Ito, K. Age-related change in motor unit activation strategy in force production: A mechanomyographic investigation. Muscle Nerve 2002, 25, 505–512. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Gao, L.; Lu, W.; Wang, D.; Cao, H.; Zhang, G. A novel noise suppression and artifact removal method of mechanomyography based on RLS, IGWO-VMD, and CEEMDAN. J. Sensors 2022, 2022, 4239211. [Google Scholar] [CrossRef]
- Islam, M.A.; Sundaraj, K.; Ahmad, R.B.; Sundaraj, S.; Ahamed, N.U.; Ali, M.A. Cross-talk in mechanomyographic signals from the forearm muscles during sub-maximal to maximal isometric grip force. PLoS ONE 2014, 9, e96628. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Wang, X.; Yang, J. Modified particle swarm optimization with attention-based LSTM for wind power prediction. Energies 2022, 15, 4334. [Google Scholar] [CrossRef]
- Hui, L.; Wang, R.; Wang, C. Prediction of partial ring current index using LSTM neural network. Chin. J. Space Sci. 2022, 42, 873–883. [Google Scholar]
- Mohamad Ismail, M.R.; Lam, C.K.; Sundaraj, K.; Rahiman, M.H.F. Cross-talk level of mechanomyography signal on compartmental forearm muscle. In Proceedings of the 10th International Conference on Robotics, Vision, Signal Processing and Power Applications (ROVISP), Singapore, 2 April 2019; Springer: Berlin/Heidelberg, Germany; pp. 575–581. [Google Scholar]
- Beck, T.W.; DeFreitas, J.M.; Stock, M.S. Cross-talk among monopolar surface electromyographic signals from the superficial quadriceps femoris muscles. Electromyogr. Clin. Neurophysiol. 2010, 50, 245–250. [Google Scholar] [PubMed]
- Islam, A.; Sundaraj, K.; Ahmad, R.B.; Sundaraj, S.; Ahamed, N.U.; Ali, M.A. Analysis of crosstalk in the mechanomyographic signals generated by forearm muscles during different wrist postures. Muscle Nerve 2015, 51, 899–906. [Google Scholar] [CrossRef] [PubMed]
- Fara, S.; Gavriel, C.; Vikram, C.S.; Faisal, A.A. Prediction of arm end point force using multi-channel MMG. In Proceedings of the 11th International Conference on Wearable and Implantable Body Sensor Networks (BSN), Zurich, Switzerland, 16–19 June 2014; pp. 27–32. [Google Scholar]


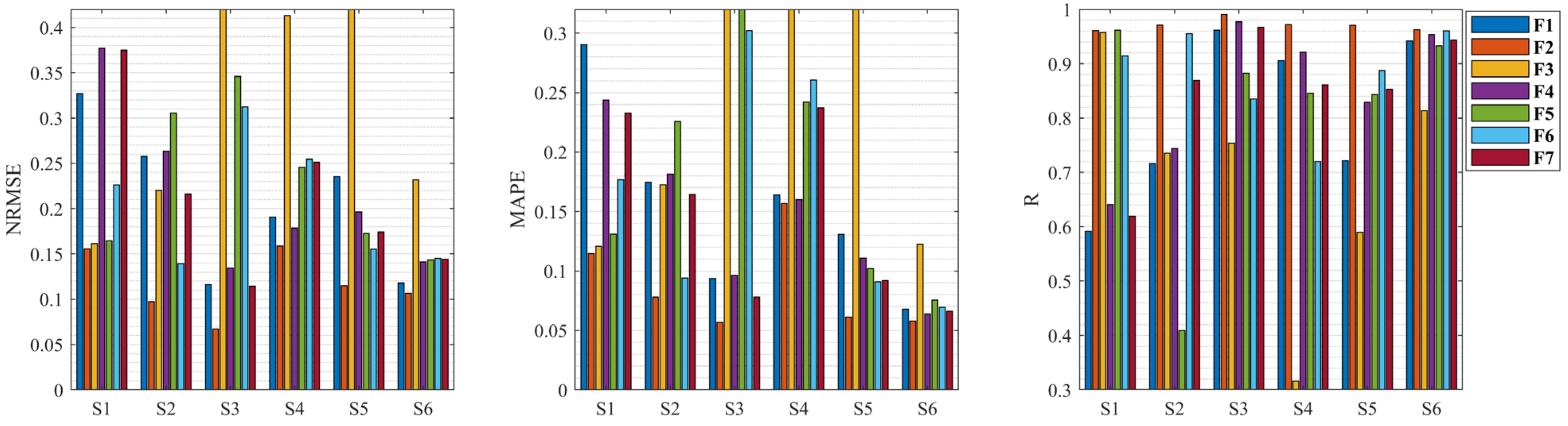
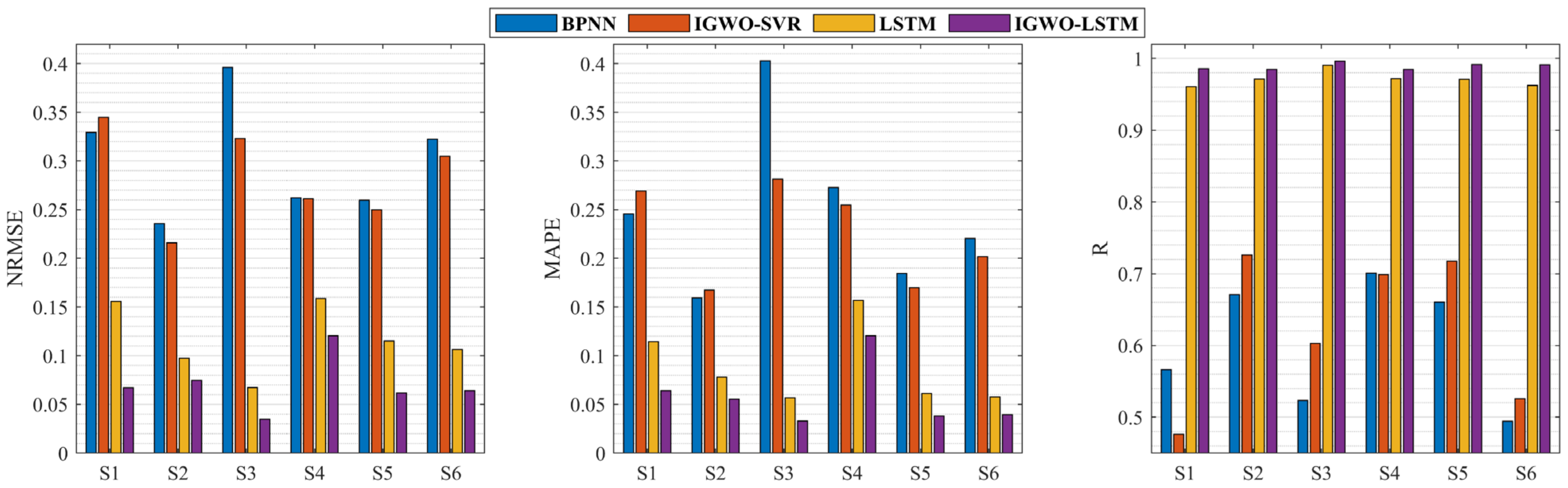
| Feature Combination | NRMSE | MAPE | R |
|---|---|---|---|
| F1 | 0.2076 ± 0.0827 | 0.1534 ± 0.0783 | 0.8066 ± 0.1507 |
| F2 | 0.1167 ± 0.0352 | 0.0875 ± 0.0404 | 0.9714 ± 0.0106 |
| F3 | 0.3794 ± 0.2080 | 0.3158 ± 0.2134 | 0.6943 ± 0.2202 |
| F4 | 0.2151 ± 0.0918 | 0.1427 ± 0.0654 | 0.8443 ± 0.1320 |
| F5 | 0.2295 ± 0.0830 | 0.1884 ± 0.1052 | 0.8126 ± 0.2031 |
| F6 | 0.2055 ± 0.0705 | 0.1656 ± 0.0978 | 0.8788 ± 0.0905 |
| F7 | 0.2126 ± 0.0934 | 0.1450 ± 0.0776 | 0.8522 ± 0.1233 |
| BP | IGWO-SVR | LSTM | IGWO-LSTM | |
|---|---|---|---|---|
| NRMSE | 0.3008 ± 0.0596 | 0.2833 ± 0.0490 | 0.1168 ± 0.0352 | 0.0704 ± 0.0280 |
| MAPE | 0.2476 ± 0.0863 | 0.2241 ± 0.0508 | 0.0875 ± 0.0404 | 0.0583 ± 0.0326 |
| R | 0.6028 ± 0.0860 | 0.6244 ± 0.1065 | 0.9714 ± 0.0106 | 0.9891 ± 0.0048 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Gao, L.; Zhang, G.; Lu, W.; Wang, D.; Zhang, J.; Cao, H. MMG-Based Knee Dynamic Extension Force Estimation Using Cross-Talk and IGWO-LSTM. Bioengineering 2024, 11, 470. https://doi.org/10.3390/bioengineering11050470
Li Z, Gao L, Zhang G, Lu W, Wang D, Zhang J, Cao H. MMG-Based Knee Dynamic Extension Force Estimation Using Cross-Talk and IGWO-LSTM. Bioengineering. 2024; 11(5):470. https://doi.org/10.3390/bioengineering11050470
Chicago/Turabian StyleLi, Zebin, Lifu Gao, Gang Zhang, Wei Lu, Daqing Wang, Jinzhong Zhang, and Huibin Cao. 2024. "MMG-Based Knee Dynamic Extension Force Estimation Using Cross-Talk and IGWO-LSTM" Bioengineering 11, no. 5: 470. https://doi.org/10.3390/bioengineering11050470
APA StyleLi, Z., Gao, L., Zhang, G., Lu, W., Wang, D., Zhang, J., & Cao, H. (2024). MMG-Based Knee Dynamic Extension Force Estimation Using Cross-Talk and IGWO-LSTM. Bioengineering, 11(5), 470. https://doi.org/10.3390/bioengineering11050470







