Morphology and Composition of Lumbar Intervertebral Discs: Comparative Analyses of Manual Measurement and Computer-Assisted Algorithms
Abstract
1. Introduction
2. Materials and Methods
2.1. Populations
2.1.1. Archived Medical Records (AMRs)
2.1.2. Asymptomatic Subjects (ASYs)
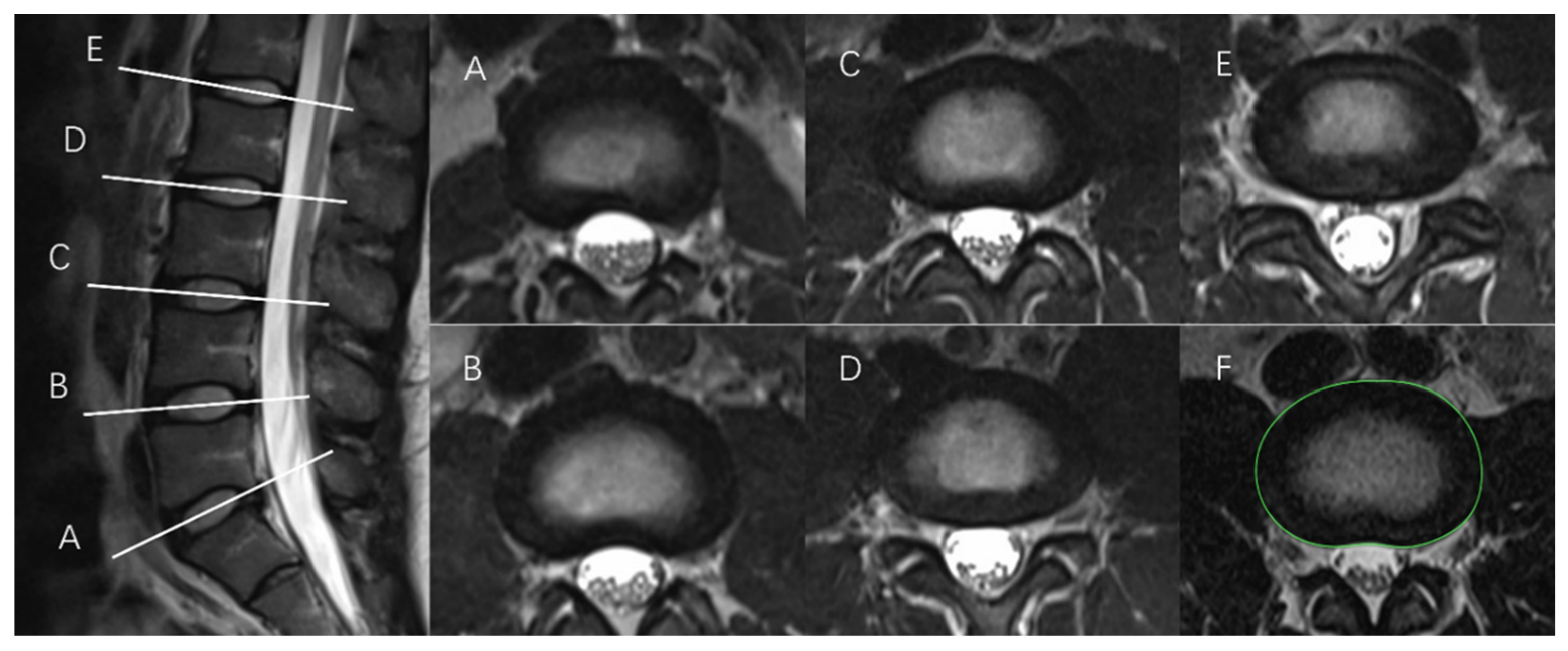
2.2. Measurement of IVD Structures
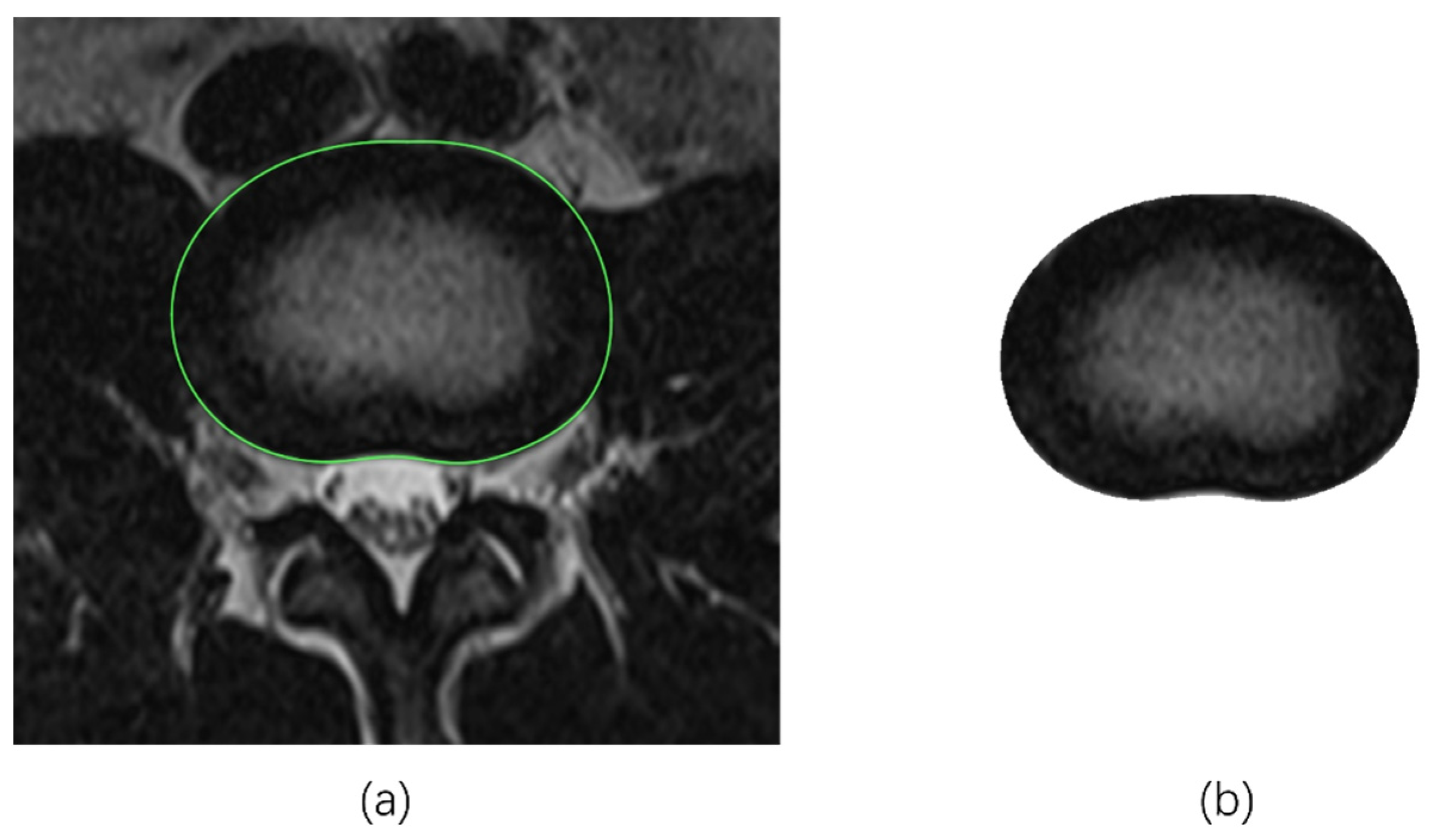
2.2.1. Tracing the IVD Contours
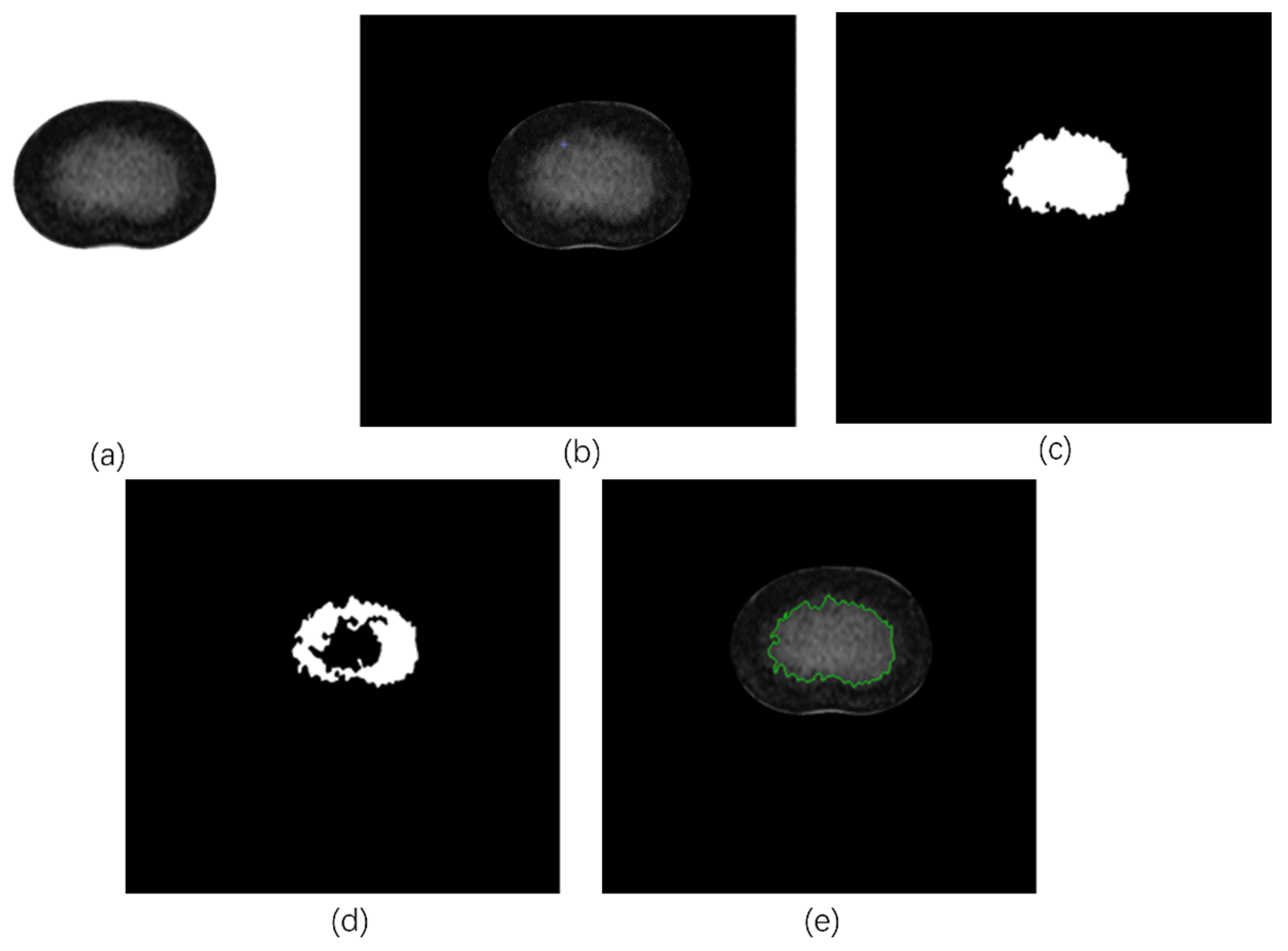
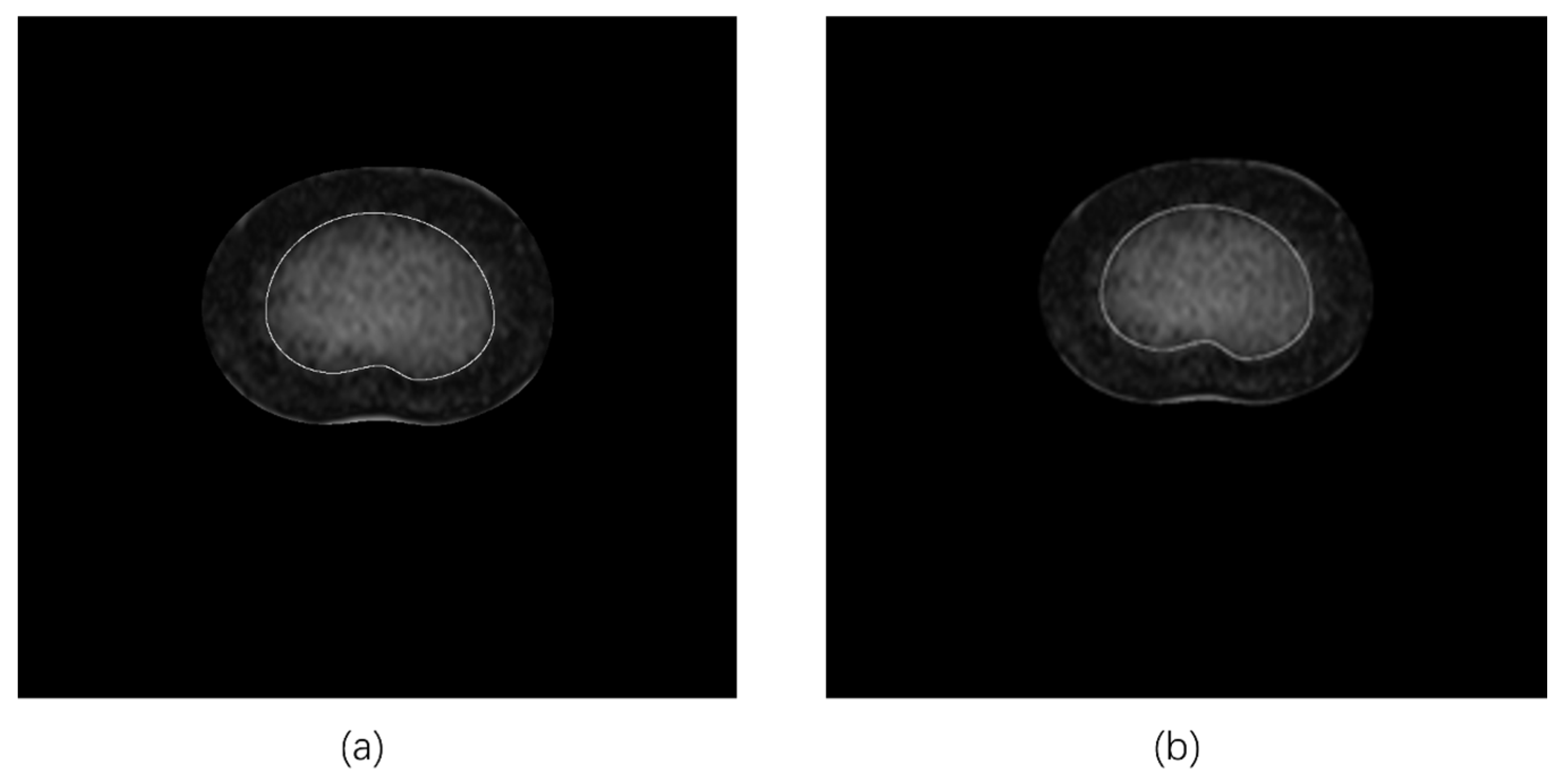
2.2.2. Tracing the NP Contours
- Fuzzy C-means algorithm (FCM)
- (a)
- Initialize the affiliation matrix with random numbers between 0 and 1 so that it satisfies the constraint in Equation (3):
- (b)
- Obtain the cluster centers ) using Equation (2).
- (c)
- Calculate the Euclidean distance between the cluster center and the data point.
- (d)
- The algorithm stops if the value function obtained by Equation (1) is less than a determined threshold value or if the change of the value function relative to the last iteration is less than the threshold value. The algorithm skips to step f.
- (e)
- Use Equation (4) to compute the new matrix; then, return to step b and keep iterating.
- (f)
- Output clustering center and the affiliation matrix [1].
- Region growing algorithm (RG)
- (a)
- Select the initial pixels based on the nature of the image. In the case of this nucleus pulposus segmentation, because the boundary of the NP is blurred and the gray value near the boundary is significantly lower than that at the center of the NP, the point close to the boundary of the NP is selected as the seed pixel. This choice has shown better results in practice. The center of the NP is not the seed pixel because sometimes the NP contour cannot be obtained from the center of the NP.
- (b)
- Set as the center and add its four neighboring pixels into the stack to be scanned (known as ), whose coordinates are, and . The growth criterion is interpreted as pixel t from to make the difference between the gray value of this point and the mean gray value of the segmented area the smallest.
- If does not exceed the image boundary and satisfies the growth criterion, divide and into the same region and add the 4 neighboring pixels of to . Then, calculate the new mean gray value of the region:where denotes the new mean, denotes the old mean value, indicates the number of pixel points in the segmented area, and indicates the gray value of the current newly selected point.
- (c)
- Take a pixel from and treat it as the initial pixel and return to step 2 for iteration.
- (d)
- When is empty, return to step 1.
- (e)
- Repeat steps 1 through 4, when the gray value distances of all the neighboring pixels to be analyzed and already segmented in Seeds are all greater than the pre-set threshold (i.e., maxdis), the region growing ends.
- (f)
- Perform expansion corrosion and opening–closing operations on the obtained region, draw the outline of the obtained mask, and complete the extraction of the NP region.
- Manual tracing (MT)
2.3. Determination of NP-to-CSA Ratios
2.4. Data Analysis
3. Results
3.1. Repeatability of Measurement
3.2. Comparison of Results Derived from Different Methods
3.3. Influencing Factors of the NP-to-CSA Ratio
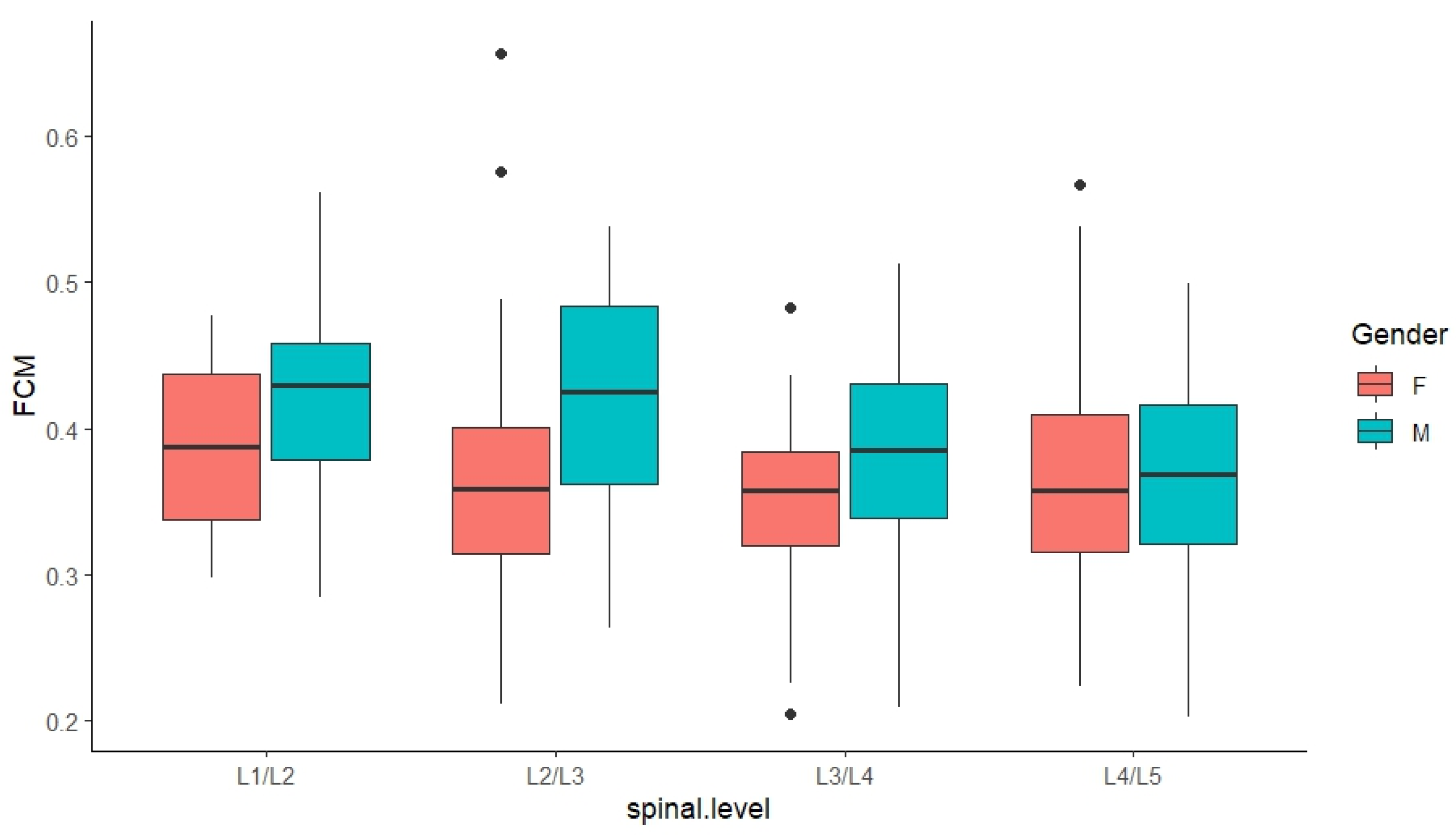
3.3.1. FCM-Derived Results
3.3.2. RG-Derived Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Noailly, J.; Wilke, H.J.; Planell, J.A.; Lacroix, D. How does the geometry affect the internal biomechanics of a lumbar spine bi-segment finite element model? Consequences on the validation process. J. Biomech. 2007, 40, 2414–2425. [Google Scholar] [CrossRef] [PubMed]
- Robin, S.; Skalli, W.; Lavaste, F. Influence of geometrical factors on the behavior of lumbar spine segments: A finite element analysis. Eur. Spine J. 1994, 3, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.M.; Hutton, W.C.; Gharpuray, V.M. Can variations in intervertebral disc height affect the mechanical function of the disc? Spine 1996, 21, 2208–2216; discussion 2217. [Google Scholar] [CrossRef]
- Natarajan, R.N.; Andersson, G.B. The influence of lumbar disc height and cross-sectional area on the mechanical response of the disc to physiologic loading. Spine 1999, 24, 1873–1881. [Google Scholar] [CrossRef]
- Niemeyer, F.; Wilke, H.J.; Schmidt, H. Geometry strongly influences the response of numerical models of the lumbar spine--a probabilistic finite element analysis. J. Biomech. 2012, 45, 1414–1423. [Google Scholar] [CrossRef]
- Tang, R. Morphometric Analysis of the Human Lower Lumbar Intervertebral Discs and Vertebral Endplates: Experimental Approach and Regression Models. Ph.D. Dissertation, Auburn University, Auburn, AL, USA, 2013. [Google Scholar]
- Tang, R.; Gungor, C.; Sesek, R.F.; Foreman, K.B.; Gallagher, S.; Davis, G.A. Morphometry of the lower lumbar intervertebral discs and endplates: Comparative analyses of new MRI data with previous findings. Eur. Spine J. 2016, 25, 4116–4131. [Google Scholar] [CrossRef]
- White, A.A., III; Panjabi, M.M. Clinical Biomechanics of the Spine; J. B. Lippincott: Philadelphia, PA, USA, 1990; Volume 446. [Google Scholar]
- Farfan, H.F. Mechanical Disorders of the Low Back; Lea and Febiger: Philadelphia, PA, USA, 1973. [Google Scholar]
- Kunkel, M.E.; Herkommer, A.; Reinehr, M.; Bockers, T.M.; Wilke, H.J. Morphometric analysis of the relationships between intervertebral disc and vertebral body heights: An anatomical and radiographic study of the human thoracic spine. J. Anat. 2011, 219, 375–387. [Google Scholar] [CrossRef] [PubMed]
- Tang, R.; Gungor, C.; Sesek, R.F.; Gallagher, S.; Davis, G.A.; Foreman, K.B. Prediction models for the cross-sectional areas of lower lumbar intervertebral discs and vertebral endplates. Int. J. Ind. Ergon. 2019, 72, 12–34. [Google Scholar] [CrossRef]
- Wu, G.; Liu, Y.; Wen, W.; Zhang, Y.; Tang, R.; Gungor, C.; Sesek, R.F. Morphological Analysis of the Human Lumbar Spine Using Sagittal Magnetic Resonance Imaging. Proc. Int. Symp. Hum. Human. Factors Ergon. Health Care 2021, 10, 59–62. [Google Scholar] [CrossRef]
- Gundry, C.R.; Fritts, H.M. Magnetic resonance imaging of the musculoskeletal system. Part 8. The spine, section 2. Clin. Orthop. Relat. Res. 1997, 338, 260–271. [Google Scholar] [CrossRef] [PubMed]
- Moon, S.M.; Yoder, J.H.; Wright, A.C.; Smith, L.J.; Vresilovic, E.J.; Elliott, D.M. Evaluation of intervertebral disc cartilaginous endplate structure using magnetic resonance imaging. Eur. Spine J. 2013, 22, 1820–1828. [Google Scholar] [CrossRef] [PubMed]
- Chowdhary, C.L.; Mittal, M.; Kumaresan, P.; Pattanaik, P.A.; Marszalek, Z. An Efficient Segmentation and Classification System in Medical Images Using Intuitionist Possibilistic Fuzzy C-Mean Clustering and Fuzzy SVM Algorithm. Sensors 2020, 20, 3903. [Google Scholar] [CrossRef] [PubMed]
- Goceri, E.; Shah, Z.K.; Gurcan, M.N. Vessel segmentation from abdominal magnetic resonance images: Adaptive and reconstructive approach. Int. J. Numer. Method. Biomed. Eng. 2017, 33, e2811. [Google Scholar] [CrossRef] [PubMed]
- Mapayi, T.; Tapamo, J.-R.; Viriri, S. Retinal Vessel Segmentation: A Comparative Study of Fuzzy C-means and Sum Entropy Information on Phase Congruency. Int. J. Adv. Robot. Syst. 2015, 12, 133. [Google Scholar] [CrossRef]
- Mehnert, A.; Jackway, P. An improved seeded region growing algorithm. Pattern Recognit. Lett. 1997, 18, 1065–1071. [Google Scholar] [CrossRef]
- Biratu, E.S.; Schwenker, F.; Debelee, T.G.; Kebede, S.R.; Negera, W.G.; Molla, H.T. Enhanced Region Growing for Brain Tumor MR Image Segmentation. J. Imaging 2021, 7, 22. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Qian, J.; Lu, S.; Tao, Y.; Lin, J.; Lin, H. LRVRG: A local region-based variational region growing algorithm for fast mandible segmentation from CBCT images. Oral. Radiol. 2021, 37, 631–640. [Google Scholar] [CrossRef]
- Gungor, C.; Tang, R.; Sesek, R.F.; Foreman, K.B.; Gallagher, S.; Davis, G.A. Morphological investigation of low back erector spinae muscle: Historical data populations. Int. J. Ind. Ergon. 2015, 49, 108–115. [Google Scholar] [CrossRef]
- Gungor, C.; Tang, R.; Sesek, R.F.; Foreman, K.B.; Gallagher, S.; Davis, G.A. Prediction models for the erector spinae muscle cross-sectional area. J. Biomech. Eng. 2015, 137, 071012. [Google Scholar] [CrossRef] [PubMed]
- Gungor, C.; Tang, R.; Sesek, R.F.; Davis, G.A.; Gallagher, S. Regression Models for the Erector Spinae Muscle Mass (ESMM) Cross-Sectional Area: Asymptomatic Populations. J. Biomech. Eng. 2019, 141, 081009. [Google Scholar] [CrossRef]
- Pfirrmann, C.W.; Metzdorf, A.; Zanetti, M.; Hodler, J.; Boos, N. Magnetic resonance classification of lumbar intervertebral disc degeneration. Spine 2001, 26, 1873–1878. [Google Scholar] [CrossRef] [PubMed]
- Rosset, A.; Spadola, L.; Ratib, O. OsiriX: An open-source software for navigating in multidimensional DICOM images. J. Digit. Imaging 2004, 17, 205–216. [Google Scholar] [CrossRef] [PubMed]
- Izakian, H.; Abraham, A. Fuzzy C-means and fuzzy swarm for fuzzy clustering problem. Expert. Syst. Appl. 2011, 38, 1835–1838. [Google Scholar] [CrossRef]
- Preetha, M.M.S.J.; Suresh, L.P.; Bosco, M.J. Image segmentation using seeded region growing. In Proceedings of the 2012 International Conference on Computing, Electronics and Electrical Technologies (ICCEET), Nagercoil, India, 21–22 March 2012; pp. 576–583. [Google Scholar]
- Mayerhoefer, M.E.; Stelzeneder, D.; Bachbauer, W.; Welsch, G.H.; Mamisch, T.C.; Szczypinski, P.; Weber, M.; Peters, N.H.; Fruehwald-Pallamar, J.; Puchner, S.; et al. Quantitative analysis of lumbar intervertebral disc abnormalities at 3.0 Tesla: Value of T(2) texture features and geometric parameters. NMR Biomed. 2012, 25, 866–872. [Google Scholar] [CrossRef] [PubMed]
- Weiler, C.; Schietzsch, M.; Kirchner, T.; Nerlich, A.G.; Boos, N.; Wuertz, K. Age-related changes in human cervical, thoracal and lumbar intervertebral disc exhibit a strong intra-individual correlation. Eur. Spine J. 2012, 21 (Suppl. S6), S810–S818. [Google Scholar] [CrossRef] [PubMed]
- Zander, T.; Rohlmann, A.; Bergmann, G. Influence of different artificial disc kinematics on spine biomechanics. Clin. Biomech. 2009, 24, 135–142. [Google Scholar] [CrossRef]
- Yang, B.; Lu, Y.; Um, C.; O’Connell, G.D. Relative Nucleus Pulposus Area and Position Alter Disk Joint Mechanics. J. Biomech. Eng. 2019, 141, 051004. [Google Scholar] [CrossRef] [PubMed]
- Noailly, J.; Lacroix, D.; Planell, J.A. Finite element study of a novel intervertebral disc substitute. Spine 2005, 30, 2257–2264. [Google Scholar] [CrossRef]
- Natarajan, R.N.; Lavender, S.A.; An, H.A.; Andersson, G.B. Biomechanical response of a lumbar intervertebral disc to manual lifting activities: A poroelastic finite element model study. Spine 2008, 33, 1958–1965. [Google Scholar] [CrossRef]
- Chen, X.L.; Li, X.Y.; Wang, Y.; Lu, S.B. Relation of lumbar intervertebral disc height and severity of disc degeneration based on Pfirrmann scores. Heliyon 2023, 9, e20764. [Google Scholar] [CrossRef] [PubMed]
- Tang, R.; Gungor, C.; Sesek, R.F.; Gallagher, S.; Davis, G.A.; Foreman, K.B. Predicting the Cross-sectional Areas of Low Back Intervertebral Discs: Archived Medical Record Versus MRI Scans from Asymptomatic Subjects. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting, Online, 5–9 October 2020; pp. 1451–1455. [Google Scholar]
- Mardani, K.; Maghooli, K. Enhancing retinal blood vessel segmentation in medical images using combined segmentation modes extracted by DBSCAN and morphological reconstruction. Biomed. Signal Process. Control 2021, 69, 102837. [Google Scholar] [CrossRef]
- van der Houwen, E.B.; Baron, P.; Veldhuizen, A.G.; Burgerhof, J.G.; van Ooijen, P.M.; Verkerke, G.J. Geometry of the intervertebral volume and vertebral endplates of the human spine. Ann. Biomed. Eng. 2010, 38, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Karabekir, H.S.; Gocmen-Mas, N.; Edizer, M.; Ertekin, T.; Yazici, C.; Atamturk, D. Lumbar vertebra morphometry and stereological assesment of intervertebral space volumetry: A methodological study. Ann. Anat. 2011, 193, 231–236. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Jiang, D.; Ou, Y.; Zhong, J.; Lv, F. Geometry of thoracolumbar vertebral endplates of the human spine. Eur. Spine J. 2011, 20, 1814–1820. [Google Scholar] [CrossRef] [PubMed]
- Mosekilde, L.; Mosekilde, L. Sex differences in age-related changes in vertebral body size, density and biomechanical competence in normal individuals. Bone 1990, 11, 67–73. [Google Scholar] [CrossRef] [PubMed]
- Aharinejad, S.; Bertagnoli, R.; Wicke, K.; Firbas, W.; Schneider, B. Morphometric analysis of vertebrae and intervertebral discs as a basis of disc replacement. Am. J. Anat. 1990, 189, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Amonoo-Kuofi, H.S. Morphometric changes in the heights and anteroposterior diameters of the lumbar intervertebral discs with age. J. Anat. 1991, 175, 159–168. [Google Scholar]
- Kang, K.S.; Song, K.S.; Lee, J.S.; Yang, J.J.; Song, I.S. Comparison of radiographic and computed tomographic measurement of pedicle and vertebral body dimensions in Koreans: The ratio of pedicle transverse diameter to vertebral body transverse diameter. Eur. Spine J. 2011, 20, 414–421. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mahato, N.K. Disc spaces, vertebral dimensions, and angle values at the lumbar region: A radioanatomical perspective in spines with L5-S1 transitions: Clinical article. J. Neurosurg. Spine 2011, 15, 371–379. [Google Scholar] [CrossRef] [PubMed]
- Turk, Z.; Celan, D. Importance of intervertebral disc size in low back pain. Croat. Med. J. 2004, 45, 734–739. [Google Scholar]
- Colombini, D.; Occhipinti, E.; Grieco, A.; Faccini, M. Estimation of lumbar disc areas by means of anthropometric parameters. Spine 1989, 14, 51–55. [Google Scholar] [CrossRef] [PubMed]




| N | Mean | SD | Sig. | |||
|---|---|---|---|---|---|---|
| L1/L2 | Age (years) | Female | 21 | 29.7 | 5.2 | 0.730 |
| Male * | 37 | 29.2 | 5.3 | |||
| Ht (m) | Female | 21 | 1.7 | 0.1 | <0.001 | |
| Male * | 37 | 1.8 | 0.1 | |||
| Wt (kg) | Female | 21 | 74.0 | 14.9 | 0.019 | |
| Male * | 37 | 86.1 | 19.9 | |||
| BMI (kg/m2) | Female | 21 | 25.9 | 5.6 | 0.438 | |
| Male * | 37 | 27.1 | 5.3 | |||
| L2/L3 | Age (years) | Female | 55 | 28.7 | 5.4 | 0.801 |
| Male * | 50 | 28.5 | 4.7 | |||
| Ht (m) | Female | 55 | 1.7 | 0.1 | <0.001 | |
| Male * | 50 | 1.8 | 0.1 | |||
| Wt (kg) | Female | 55 | 69.5 | 18.4 | <0.001 | |
| Male * | 50 | 82.7 | 19.0 | |||
| BMI (kg/m2) | Female | 55 | 25.2 | 5.8 | 0.490 | |
| Male * | 50 | 25.9 | 4.9 | |||
| L3/L4 | Age (years) | Female | 52 | 28.9 | 5.4 | 0.925 |
| Male * | 50 | 29.0 | 4.9 | |||
| Ht (m) | Female | 52 | 1.7 | 0.1 | <0.001 | |
| Male * | 50 | 1.8 | 0.1 | |||
| Wt (kg) | Female | 52 | 68.5 | 17.3 | <0.001 | |
| Male * | 50 | 84.6 | 18.7 | |||
| BMI (kg/m2) | Female | 52 | 24.9 | 5.7 | 0.160 | |
| Male * | 50 | 26.4 | 5.0 | |||
| L4/L5 | Age (years) | Female | 39 | 28.6 | 5.4 | 0.492 |
| Male | 34 | 29.4 | 4.4 | |||
| Ht (m) | Female | 39 | 1.7 | 0.1 | <0.001 | |
| Male | 34 | 1.8 | 0.1 | |||
| Wt (kg) | Female | 39 | 72.5 | 18.3 | 0.016 | |
| Male | 34 | 83.4 | 19.4 | |||
| BMI (kg/m2) | Female | 39 | 26.0 | 5.9 | 0.682 | |
| Male | 34 | 26.6 | 5.4 | |||
| L5/S1 | Age (years) | Female | 36 | 28.5 | 5.3 | 0.654 |
| Male | 23 | 29.1 | 5.1 | |||
| Ht (m) | Female | 36 | 1.7 | 0.1 | <0.001 | |
| Male | 23 | 1.8 | 0.1 | |||
| Wt (kg) | Female | 36 | 71.7 | 19.2 | 0.014 | |
| Male | 23 | 82.8 | 10.7 | |||
| BMI (kg/m2) | Female | 36 | 25.5 | 6.2 | 0.561 | |
| Male | 23 | 26.3 | 3.0 |
| Manual | FCM | RG | |
|---|---|---|---|
| RatioNP-to-CSA (%) | 46 ± 6 | 39 ± 6 | 38 ± 7 |
| N | FCM | RG | Mean Absolute Difference | p Value | |
|---|---|---|---|---|---|
| Gender | |||||
| Female | 203 | 36 ± 7 | 36 ± 7 | 0.5 | 0.078 |
| Male | 197 | 40 ± 7 | 39 ± 7 | 0.7 | 0.025 |
| Spinal level | |||||
| L1/L2 | 59 | 41 ± 6 | 40 ± 6 | 1.0 | 0.037 |
| L2/L3 | 106 | 39 ± 8 | 38 ± 8 | 1.0 | 0.031 |
| L3/L4 | 103 | 37 ± 6 | 36 ± 6 | 0.5 | 0.184 |
| L4/L5 | 73 | 36 ± 7 | 36 ± 7 | 0.5 | 0.335 |
| L5/S1 | 59 | 38 ± 7 | 37 ± 7 | 1.0 | 0.076 |
| Total | 400 | 38 ± 7 | 37 ± 7 | 0.6 | 0.004 |
| Spinal Level | Gender | N | FCM | L1/L2 | L2/L3 | L3/L4 | L4/L5 | L5/S1 |
|---|---|---|---|---|---|---|---|---|
| L1/L2 | F | 21 | 39 ± 5 * | |||||
| M | 38 | 42 ± 7 * | 0.01 | |||||
| L2/L3 | F | 55 | 36 ± 8 § | |||||
| M | 51 | 42 ± 7 § | 0.072 | 0.005 | 0.091 | |||
| L3/L4 | F | 52 | 35 ± 5 | |||||
| M | 51 | 38 ± 6 | ||||||
| L4/L5 | F | 39 | 35 ± 6 | |||||
| M | 34 | 37 ± 7 | ||||||
| L5/S1 | F | 36 | 38 ± 8 | |||||
| M | 23 | 38 ± 6 |
| Spinal Level | Gender | N | RG | L1/L2 | L2/L3 | L3/L4 | L4/L5 | L5/S1 |
|---|---|---|---|---|---|---|---|---|
| L1/L2 | F | 21 | 40 ± 6 * | 0.046 | 0.021 | 0.025 | ||
| M | 38 | 40 ± 6 * | ||||||
| L2/L3 | F | 55 | 35 ± 7 § | |||||
| M | 51 | 41 ± 7 § | 0.036 | |||||
| L3/L4 | F | 52 | 35 ± 5 | |||||
| M | 51 | 38 ± 5 | ||||||
| L4/L5 | F | 39 | 34 ± 6 | |||||
| M | 34 | 38 ± 7 | ||||||
| L5/S1 | F | 36 | 37 ± 7 | |||||
| M | 23 | 36 ± 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Ma, Y.; Li, K.; Gungor, C.; Sesek, R.; Tang, R. Morphology and Composition of Lumbar Intervertebral Discs: Comparative Analyses of Manual Measurement and Computer-Assisted Algorithms. Bioengineering 2024, 11, 466. https://doi.org/10.3390/bioengineering11050466
Cheng Y, Ma Y, Li K, Gungor C, Sesek R, Tang R. Morphology and Composition of Lumbar Intervertebral Discs: Comparative Analyses of Manual Measurement and Computer-Assisted Algorithms. Bioengineering. 2024; 11(5):466. https://doi.org/10.3390/bioengineering11050466
Chicago/Turabian StyleCheng, Yiting, Yuyan Ma, Kang Li, Celal Gungor, Richard Sesek, and Ruoliang Tang. 2024. "Morphology and Composition of Lumbar Intervertebral Discs: Comparative Analyses of Manual Measurement and Computer-Assisted Algorithms" Bioengineering 11, no. 5: 466. https://doi.org/10.3390/bioengineering11050466
APA StyleCheng, Y., Ma, Y., Li, K., Gungor, C., Sesek, R., & Tang, R. (2024). Morphology and Composition of Lumbar Intervertebral Discs: Comparative Analyses of Manual Measurement and Computer-Assisted Algorithms. Bioengineering, 11(5), 466. https://doi.org/10.3390/bioengineering11050466








