The Lower Limb Muscle Co-Activation Map during Human Locomotion: From Slow Walking to Running
Abstract
1. Introduction
2. Materials and Methods
2.1. Subjects
2.2. Experimental Procedure
2.3. Data Acquisition
2.4. Data Analysis
2.4.1. Cycle Definition and Temporal Normalization
2.4.2. Global, Flexor, Extensor and Rostro–Caudal Co-Activation of Lower Limb Muscles
2.4.3. Co-Activation Parameters
- (i)
- the synthetic co-activation index (CIglob; CIext; CIflex; CIL3; CIL4; CIL5; CIS1; CIS2) which is calculated as the mean value of the TMCf and represents the average of the co-activation level [% co-activation];
- (ii)
- the maximum value of the TMCf (Maxglob; Maxext; Maxflex; MaxL3; MaxL4; MaxL5; MaxS1; MaxS2) [% co-activation];
- (iii)
- the full width at half maximum (FWHMglob; FWHMext; FWHMflex; FWHML3; FWHML4; FWHML5; FWHMS1; FWHMS2) of the co-activation, which reflects the sum of the time durations within the gait cycle during which the TMCf curve is higher than its half maximum value [% gait cycle];
- (iv)
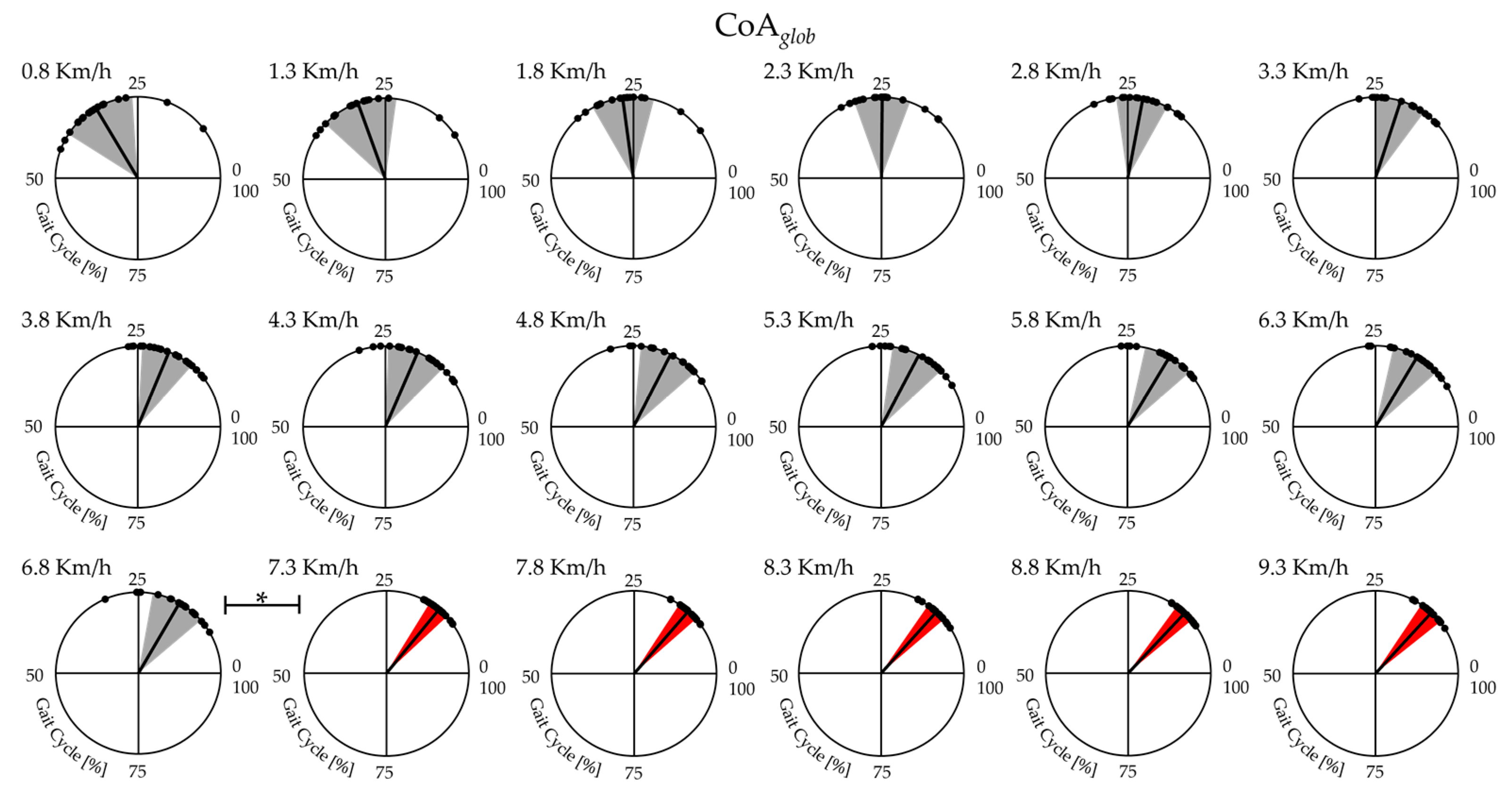
- the center of activity (CoAglob; CoAext; CoAflex; CoAL3; CoAL4; CoAL5; CoAS1; CoAS2) which is calculated with circular statistics and plotted in polar coordinates to show where the most co-activation is concentrated within the walk and run cycles, and, in this study, also to show the instant of co-activation onset on the rostro–caudal maps [% gait cycle] [38,65]:where is the angle in polar coordinates that varies from 0 to 360°.
- (v)
- is the coefficient of multiple correlation (CMC), which measures the overall waveform similarity of a group of curves (the closer to 1 the CMC is, the more similar the curves are) [66,67,68]. The CMC was calculated according to the following formula:where (number of points within the curve), is the number of curves, is the value at the point in the curve, is the average of the two curves at point , and is the grand mean of all .
2.4.4. Cross-Correlation
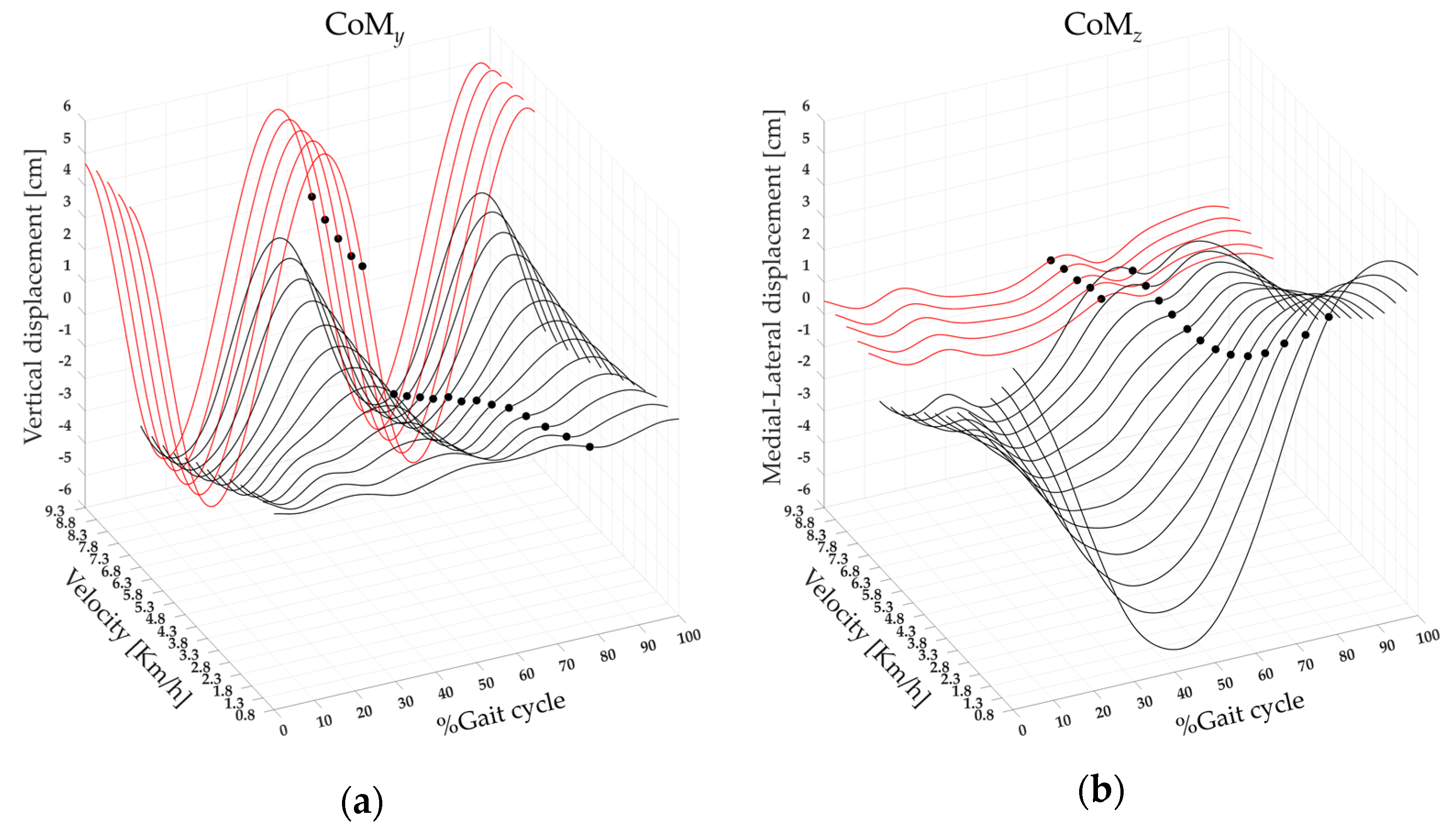
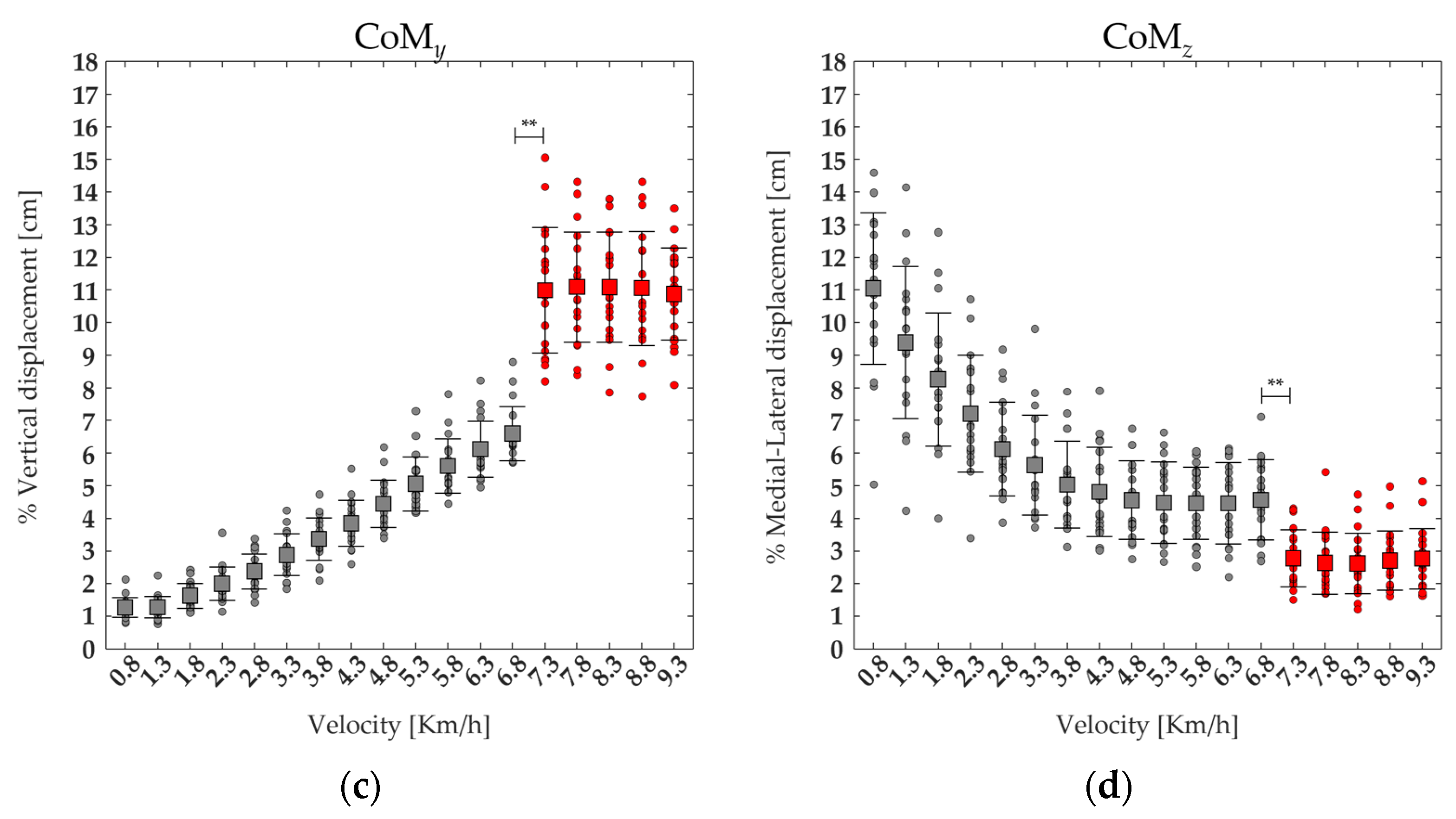
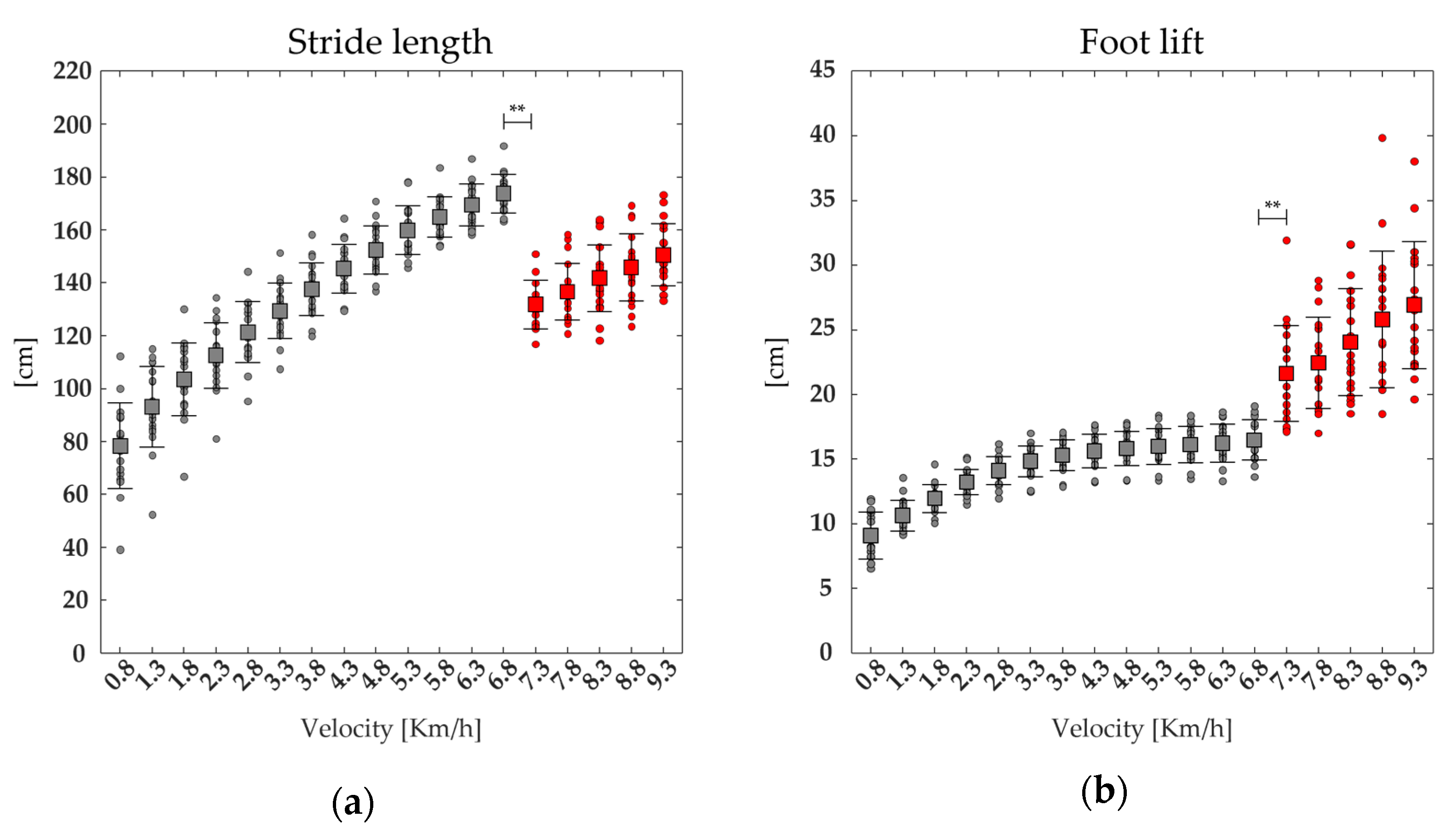
2.4.5. Center of Mass Displacement and Spatiotemporal Parameters
2.4.6. Statistical Analysis
3. Results
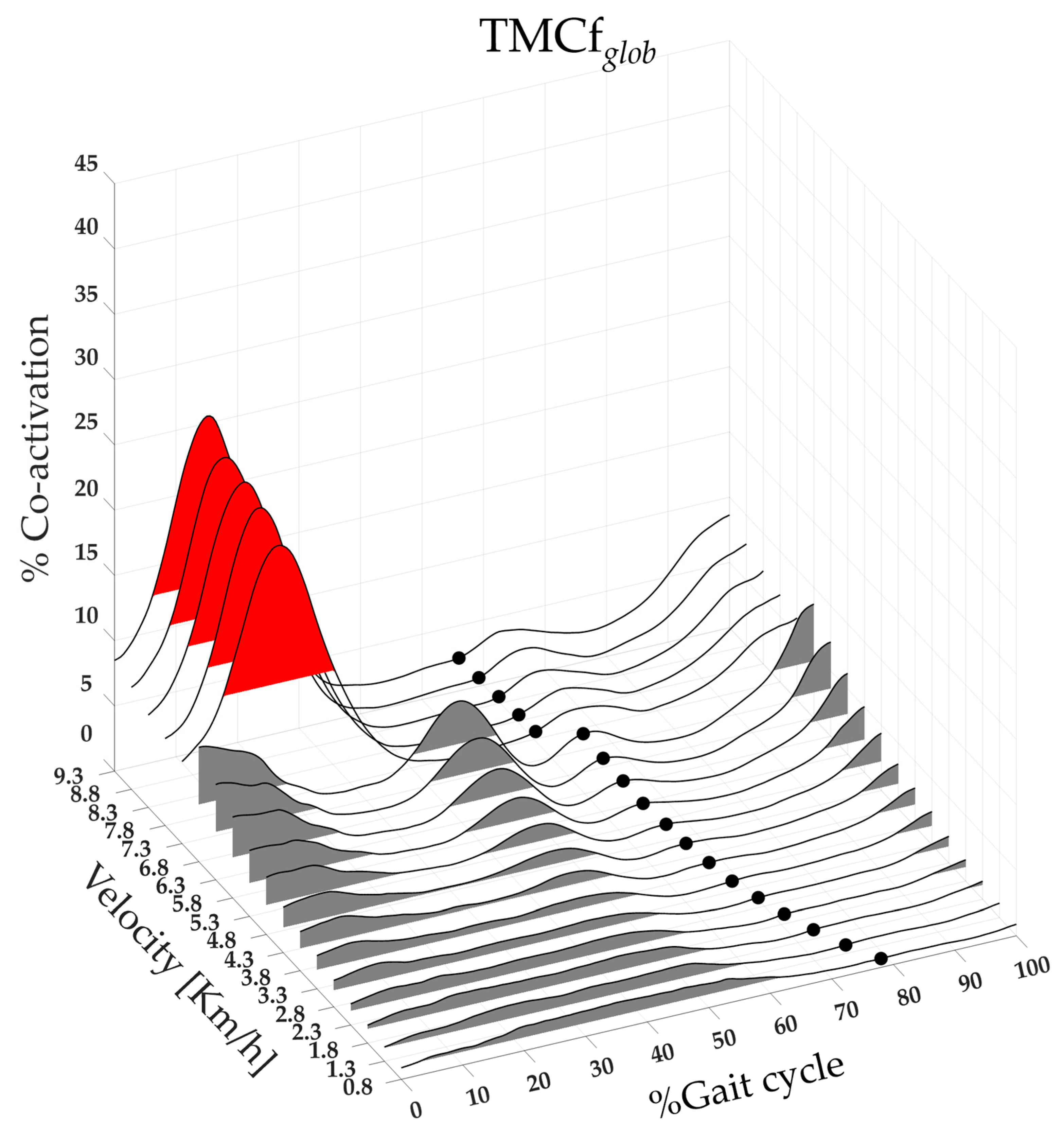
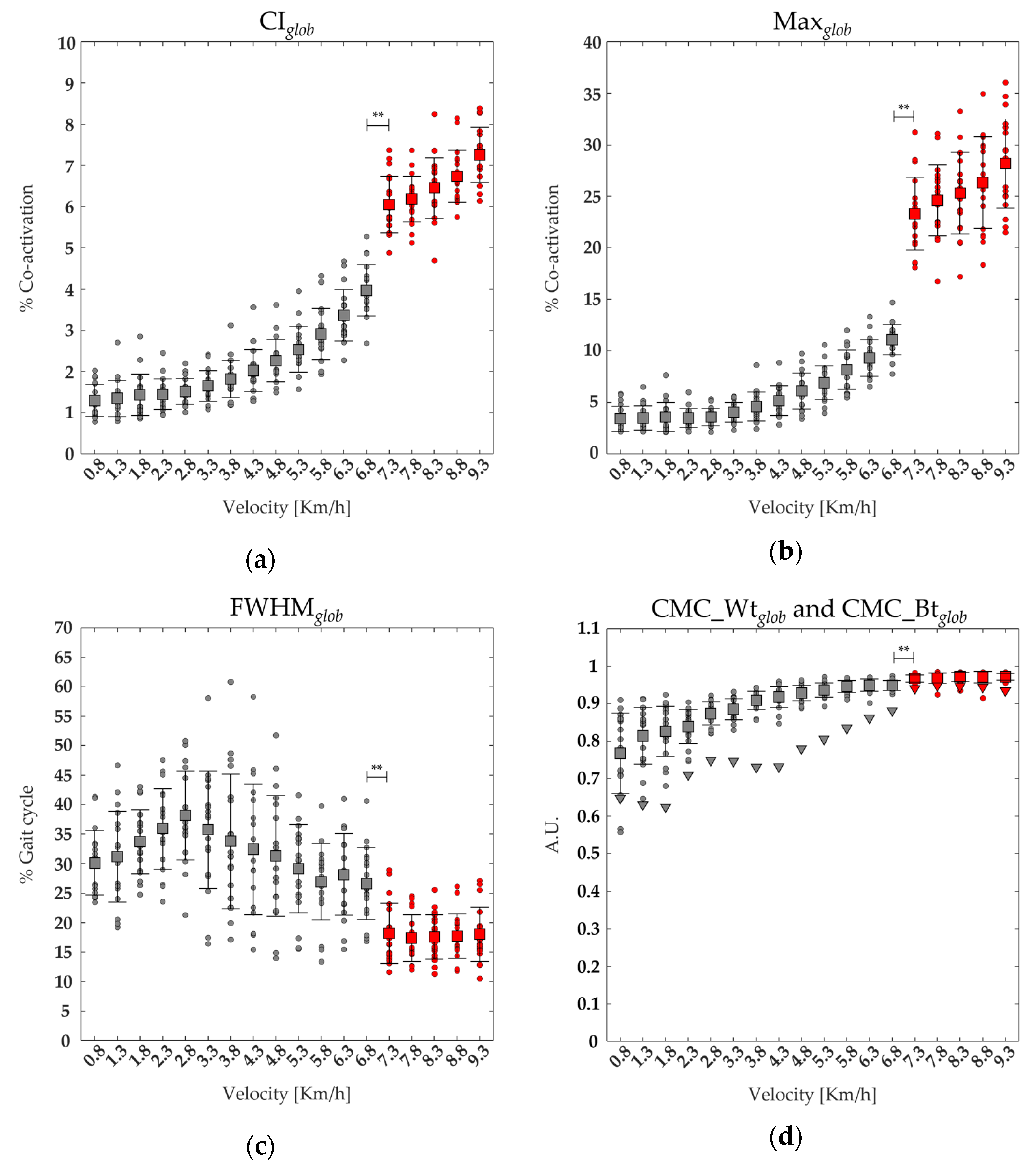
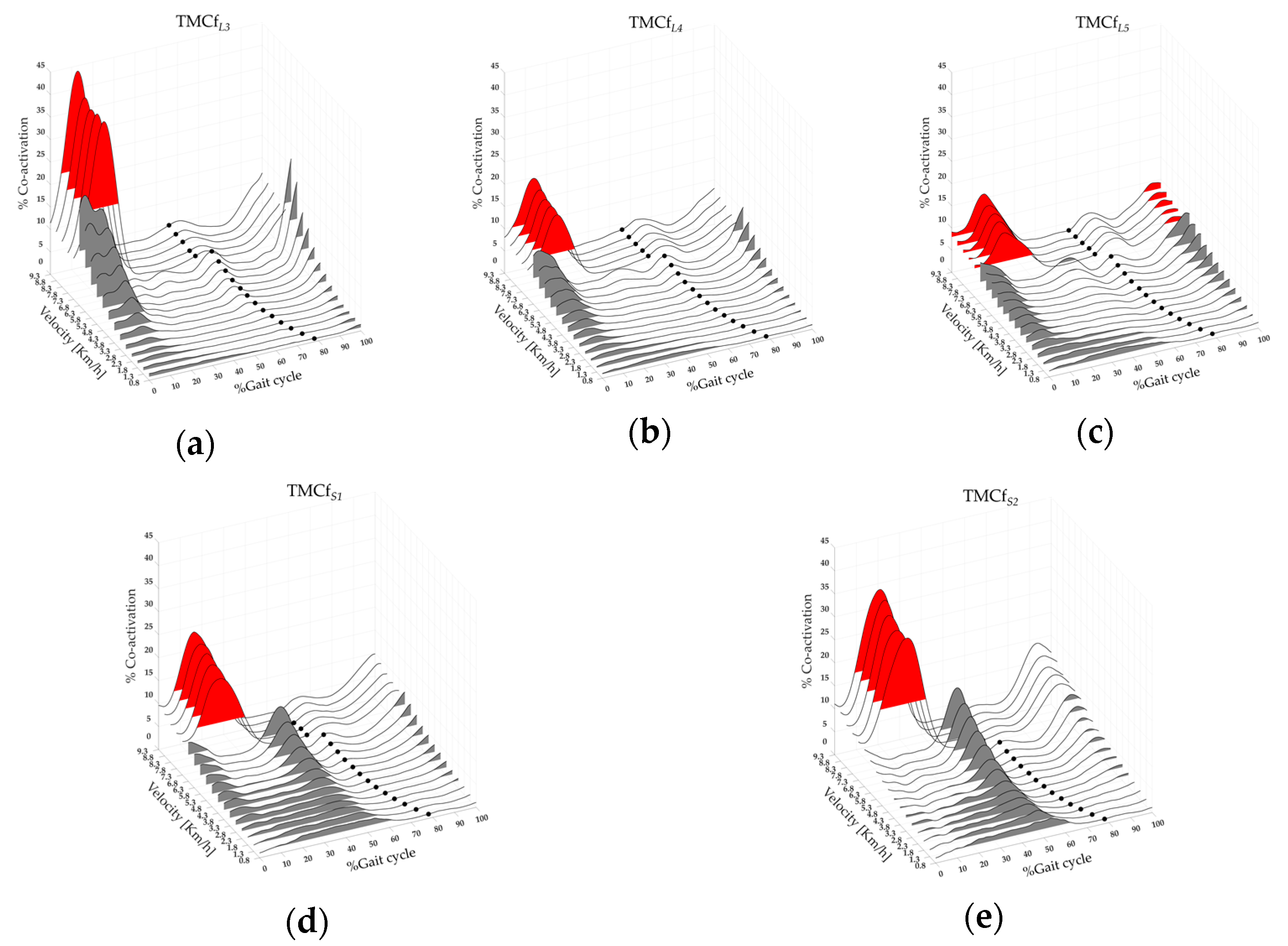
3.1. Global, Flexor, Extensor, and Rostro–Caudal Co-Activation Maps and Parameters
3.2. Cross-Correlation
3.3. Center of Mass Displacement and Spatiotemporal Parameters
3.4. Correlations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hasan, Z. Biological Cybernetics Optimized Movement Trajectories and Joint Stiffness in Unperturbed, Inertially Loaded Movements; Springer: Berlin/Heidelberg, Germany, 1986; Volume 53. [Google Scholar]
- Latash, M.L. Muscle Coactivation: Definitions, Mechanisms, and Functions. J. Neurophysiol. 2018, 120, 88–104. [Google Scholar] [CrossRef]
- Le, P.; Best, T.M.; Khan, S.N.; Mendel, E.; Marras, W.S. A Review of Methods to Assess Coactivation in the Spine. J. Electromyogr. Kinesiol. 2017, 32, 51–60. [Google Scholar] [CrossRef]
- Rosa, M.C.N.; Marques, A.; Demain, S.; Metcalf, C.D.; Rodrigues, J. Methodologies to Assess Muscle Co-Contraction during Gait in People with Neurological Impairment—A Systematic Literature Review. J. Electromyogr. Kinesiol. 2014, 24, 179–191. [Google Scholar] [CrossRef]
- Cappellini, G.; Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Motor Patterns in Human Walking and Running. J. Neurophysiol. 2006, 95, 3426–3437. [Google Scholar] [CrossRef] [PubMed]
- Heise, G.D.; Morgan, D.W.; Hough, H.; Craib, M. Relationships between Running Economy and Temporal EMG Characteristics of Bi-Articular Leg Muscles. Int. J. Sports Med. 1996, 17, 128–133. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Five Basic Muscle Activation Patterns Account for Muscle Activity during Human Locomotion. J. Physiol. 2004, 556, 267–282. [Google Scholar] [CrossRef] [PubMed]
- Kellis, E.; Zafeiridis, A.; Amiridis, L.G. Muscle Coactivation Before and After the Impact Phase of Running Following Isokinetic Fatigue. J. Athl. Train. 2011, 46, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Moore, I.S.; Jones, A.M.; Dixon, S.J. Relationship between Metabolic Cost and Muscular Coactivation across Running Speeds. J. Sci. Med. Sport 2014, 17, 671–676. [Google Scholar] [CrossRef] [PubMed]
- Shik, M.L.; Severin, F.V.; Orlovsky, G.N. Control of Walking and Running by Means of Electrical Stimulation of the Mesencephalon. Electroencephalogr. Clin. Neurophysiol. 1969, 26, 549. [Google Scholar] [PubMed]
- Blickhan, R. The Spring-Mass Model for Running and Hopping. J. Biomech. 1989, 22, 1217–1227. [Google Scholar] [CrossRef]
- McMahon, T.A.; Cheng, G.C. The Mechanics of Running: How Does Stiffness Couple with Speed? J. Biomech. 1990, 23, 65–78. [Google Scholar] [CrossRef]
- Sharbafi, M.A.; Seyfarth, A. FMCH: A New Model for Human-like Postural Control in Walking. IEEE Int. Conf. Intell. Robot. Syst. 2015, 2015, 5742–5747. [Google Scholar] [CrossRef]
- Alexander, R.M. Energy-Saving Mechanisms in Walking and Running. J. Exp. Biol. 1991, 160, 55–69. [Google Scholar] [CrossRef]
- Cavagna, G.A.; Thys, H.; Zamboni, A. The Sources of External Work in Level Walking and Running. J. Physiol. 1976, 262, 639–657. [Google Scholar] [CrossRef] [PubMed]
- Farley, C.T.; Glasheen, J.; McMahon, T.A. Running Springs: Speed and Animal Size. J. Exp. Biol. 1993, 185, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Zhou, H.; Quan, W.; Jiang, X.; Liang, M.; Li, S.; Ugbolue, U.C.; Baker, J.S.; Gusztav, F.; Ma, X.; et al. A New Method Proposed for Realizing Human Gait Pattern Recognition: Inspirations for the Application of Sports and Clinical Gait Analysis. Gait Posture 2024, 107, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Xu, D.; Quan, W.; Zhou, H.; Sun, D.; Baker, J.S.; Gu, Y. Explaining the Differences of Gait Patterns between High and Low-Mileage Runners with Machine Learning. Sci. Rep. 2022, 12, 2981. [Google Scholar] [CrossRef]
- Hreljac, A.; Imamura, R.T.; Escamilla, R.F.; Edwards, W.B. When Does A Gait Transition Occur During Human Locomotion? J. Sports Sci. Med. 2007, 6, 36. [Google Scholar] [PubMed]
- Rotstein, A.; Berginsky, T.; Meckel, Y. Preferred Transition Speed between Walking and Running: Effects of Training Status. Med. Sci. Sports Exerc. 2005, 37, 1864–1870. [Google Scholar] [CrossRef] [PubMed]
- Segers, V.; Aerts, P.; Lenoir, M.; De Clercq, D. Spatiotemporal Characteristics of the Walk-to-Run and Run-to-Walk Transition When Gradually Changing Speed. Gait Posture 2006, 24, 247–254. [Google Scholar] [CrossRef]
- Segers, V.; Aerts, P.; Lenoir, M.; De Clerq, D. Dynamics of the Body Centre of Mass during Actual Acceleration across Transition Speed. J. Exp. Biol. 2007, 210, 578–585. [Google Scholar] [CrossRef]
- Ker, R.F. The Design of Soft Collagenous Load-Bearing Tissues. J. Exp. Biol. 1999, 202, 3315–3324. [Google Scholar] [CrossRef]
- Hof, A.; Gazendam, M. Averaged EMG Profiles in Running Compared to Walking. Gait Posture 2006, 24, S77–S78. [Google Scholar] [CrossRef]
- Howard, R.; Conway, R.; Biomechanics, A.H.-S. Muscle Activity in Sprinting: A Review. Sports Biomech. 2018, 17, 1–17. [Google Scholar] [CrossRef]
- Zavorsky, G.S.; Montgomery, D.L.; Pearsall, D.J. Effect of Intense Interval Workouts on Running Economy Using Three Recovery Durations. Eur. J. Appl. Physiol. Occup. Physiol. 1998, 77, 224–230. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Peterson, D.S.; Martin, P.E. Effects of Age and Walking Speed on Coactivation and Cost of Walking in Healthy Adults. Gait Posture 2010, 31, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Prilutsky, B.I.; Gregor, R.J. Swing- and Support-Related Muscle Actions Differentially Trigger Human Walk–Run and Run–Walk Transitions. J. Exp. Biol. 2001, 204, 2277–2287. [Google Scholar] [CrossRef] [PubMed]
- Winter, D.A.; Yack, H.J. EMG Profiles during Normal Human Walking: Stride-to-Stride and Inter-Subject Variability. Electroencephalogr. Clin. Neurophysiol. 1987, 67, 402–411. [Google Scholar] [CrossRef] [PubMed]
- Lieberman, D.E.; Raichlen, D.A.; Pontzer, H.; Bramble, D.M.; Cutright-Smith, E. The Human Gluteus Maximus and Its Role in Running. J. Exp. Biol. 2006, 209, 2143–2155. [Google Scholar] [CrossRef] [PubMed]
- Heise, G.; Shinohara, M.; Binks, L. Biarticular Leg Muscles and Links to Running Economy. Int. J. Sports Med. 2008, 29, 688–691. [Google Scholar] [CrossRef]
- Mari, S.; Serrao, M.; Casali, C.; Conte, C.; Martino, G.; Ranavolo, A.; Coppola, G.; Draicchio, F.; Padua, L.; Sandrini, G.; et al. Lower Limb Antagonist Muscle Co-Activation and Its Relationship with Gait Parameters in Cerebellar Ataxia. Cerebellum 2014, 13, 226–236. [Google Scholar] [CrossRef] [PubMed]
- Fiori, L.; Ranavolo, A.; Varrecchia, T.; Tatarelli, A.; Conte, C.; Draicchio, F.; Castiglia, S.F.; Coppola, G.; Casali, C.; Pierelli, F.; et al. Impairment of Global Lower Limb Muscle Coactivation During Walking in Cerebellar Ataxias. Cerebellum 2020, 19, 583–596. [Google Scholar] [CrossRef]
- Penn, R.D.; Gottlieb, G.L.; Agarwal, G.C. Cerebellar Stimulation in Man: Quantitative Changes in Spasticity. J. Neurosurg. 1978, 48, 779–786. [Google Scholar] [CrossRef]
- Arias, P.; Espinosa, N.; Robles-García, V.; Cao, R.; Cudeiro, J. Antagonist Muscle Co-Activation during Straight Walking and Its Relation to Kinematics: Insight from Young, Elderly and Parkinson’s Disease. Brain Res. 2012, 1455, 124–131. [Google Scholar] [CrossRef] [PubMed]
- Houk, J.C. Agents of the Mind. Biol. Cybern. 2005, 92, 427–437. [Google Scholar] [CrossRef]
- Ranavolo, A.; Mari, S.; Conte, C.; Serrao, M.; Silvetti, A.; Iavicoli, S.; Draicchio, F. A New Muscle Co-Activation Index for Biomechanical Load Evaluation in Work Activities. Ergonomics 2015, 58, 966–979. [Google Scholar] [CrossRef] [PubMed]
- Varrecchia, T.; Rinaldi, M.; Serrao, M.; Draicchio, F.; Conte, C.; Conforto, S.; Schmid, M.; Ranavolo, A. Global Lower Limb Muscle Coactivation during Walking at Different Speeds: Relationship between Spatio-Temporal, Kinematic, Kinetic, and Energetic Parameters. J. Electromyogr. Kinesiol. 2018, 43, 148–157. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Cappellini, G.; Dominici, N.; Poppele, R.E.; Lacquaniti, F. Modular Control of Limb Movements during Human Locomotion. J. Neurosci. 2007, 27, 11149–11161. [Google Scholar] [CrossRef]
- Mo, S.; Chow, D.H.K. Differences in Lower-Limb Coordination and Coordination Variability between Novice and Experienced Runners during a Prolonged Treadmill Run at Anaerobic Threshold Speed. J. Sports Sci. 2019, 37, 1021–1028. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Poppele, R.E.; Lacquaniti, F. Spinal Cord Maps of Spatiotemporal Alpha-Motoneuron Activation in Humans Walking at Different Speeds. J. Neurophysiol. 2006, 95, 602–618. [Google Scholar] [CrossRef]
- La Scaleia, V.; Ivanenko, Y.P.; Zelik, K.E.; Lacquaniti, F. Spinal Motor Outputs during Step-to-Step Transitions of Diverse Human Gaits. Front. Hum. Neurosci. 2014, 8, 73500. [Google Scholar] [CrossRef] [PubMed]
- Martino, G.; Ivanenko, Y.; Serrao, M.; Ranavolo, A.; Draicchio, F.; Rinaldi, M.; Casali, C.; Lacquaniti, F. Differential Changes in the Spinal Segmental Locomotor Output in Hereditary Spastic Paraplegia. Clin. Neurophysiol. 2018, 129, 516–525. [Google Scholar] [CrossRef] [PubMed]
- Faul, F.; Erdfelder, E.; Lang, A.G.; Buchner, A. G*Power 3: A Flexible Statistical Power Analysis Program for the Social, Behavioral, and Biomedical Sciences. Behav. Res. Methods 2007, 39, 175–191. [Google Scholar] [CrossRef] [PubMed]
- Merletti, R.; Cerone, G.L. Tutorial. Surface EMG Detection, Conditioning and Pre-Processing: Best Practices. J. Electromyogr. Kinesiol. 2020, 54, 102440. [Google Scholar] [CrossRef]
- Merletti, R.; Muceli, S. Tutorial. Surface EMG Detection in Space and Time: Best Practices. J. Electromyogr. Kinesiol. 2019, 49, 102363. [Google Scholar] [CrossRef]
- Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of Recommendations for SEMG Sensors and Sensor Placement Procedures. J. Electromyogr. Kinesiol. 2000, 10, 361–374. [Google Scholar] [CrossRef]
- Barbero, M.; Merletti, R.; Rainoldi, A. Atlas of Muscle Innervation Zones: Understanding Surface Electromyography and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Benedetti, M.G.; Beghi, E.; De Tanti, A.; Cappozzo, A.; Basaglia, N.; Cutti, A.G.; Cereatti, A.; Stagni, R.; Verdini, F.; Manca, M.; et al. SIAMOC Position Paper on Gait Analysis in Clinical Practice: General Requirements, Methods and Appropriateness. Results of an Italian Consensus Conference. Gait Posture 2017, 58, 252–260. [Google Scholar] [CrossRef]
- Davis, R.B.; Õunpuu, S.; Tyburski, D.; Gage, J.R. A Gait Analysis Data Collection and Reduction Technique. Hum. Mov. Sci. 1991, 10, 575–587. [Google Scholar] [CrossRef]
- Butler, H.L.; Newell, R.; Hubley-Kozey, C.L.; Kozey, J.W. The Interpretation of Abdominal Wall Muscle Recruitment Strategies Change When the Electrocardiogram (ECG) Is Removed from the Electromyogram (EMG). J. Electromyogr. Kinesiol. 2009, 19, e102–e113. [Google Scholar] [CrossRef]
- Drake, J.D.M.; Callaghan, J.P. Elimination of Electrocardiogram Contamination from Electromyogram Signals: An Evaluation of Currently Used Removal Techniques. J. Electromyogr. Kinesiol. 2006, 16, 175–187. [Google Scholar] [CrossRef]
- Winter, D. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Baker, J.S.; Gu, Y. Adaptive Neuro-Fuzzy Inference System Model Driven by the Non-Negative Matrix Factorization-Extracted Muscle Synergy Patterns to Estimate Lower Limb Joint Movements. Comput. Methods Programs Biomed. 2023, 242, 107848. [Google Scholar] [CrossRef]
- Xu, D.; Zhou, H.; Quan, W.; Gusztav, F.; Wang, M.; Baker, J.S.; Gu, Y. Accurately and Effectively Predict the ACL Force: Utilizing Biomechanical Landing Pattern before and after-Fatigue. Comput. Methods Programs Biomed. 2023, 241, 107761. [Google Scholar] [CrossRef]
- Burden, A. How Should We Normalize Electromyograms Obtained from Healthy Participants? What We Have Learned from over 25 Years of Research. J. Electromyogr. Kinesiol. 2010, 20, 1023–1035. [Google Scholar] [CrossRef]
- Rinaldi, M.; D’Anna, C.; Schmid, M.; Conforto, S. Assessing the Influence of SNR and Pre-Processing Filter Bandwidth on the Extraction of Different Muscle Co-Activation Indexes from Surface EMG Data. J. Electromyogr. Kinesiol. 2018, 43, 184–192. [Google Scholar] [CrossRef]
- Serrao, M.; Rinaldi, M.; Ranavolo, A.; Lacquaniti, F.; Martino, G.; Leonardi, L.; Conte, C.; Varrecchia, T.; Draicchio, F.; Coppola, G.; et al. Gait Patterns in Patients with Hereditary Spastic Paraparesis. PLoS ONE 2016, 11, e0164623. [Google Scholar] [CrossRef]
- Tatarelli, A.; Serrao, M.; Varrecchia, T.; Fiori, L.; Draicchio, F.; Silvetti, A.; Conforto, S.; Marchis De, C.; Ranavolo, A. Global Muscle Coactivation of the Sound Limb in Gait of People with Transfemoral and Transtibial Amputation. Sensors 2020, 20, 2543. [Google Scholar] [CrossRef]
- Kendall, F.; McCreary, E.; Provance, P.; Rodgers, M. Muscles: Testing and Function with Posture and Pain; Lippincott Williams & Wilkins: Baltimore, MD, USA, 2005. [Google Scholar]
- Nilsson, J.; Thorstensson, A.; Halbertsma, J. Changes in Leg Movements and Muscle Activity with Speed of Locomotion and Mode of Progression in Humans. Acta Physiol. Scand. 1985, 123, 457–475. [Google Scholar] [CrossRef]
- Prilutsky, B.I. Coordination of Two- and One-Joint Muscles: Functional Consequences and Implications for Motor Control. Motor Control 2000, 4, 1–44. [Google Scholar] [CrossRef] [PubMed]
- Dewolf, A.H.; Sylos-Labini, F.; Cappellini, G.; Zhvansky, D.; Willems, P.A.; Ivanenko, Y.; Lacquaniti, F. Neuromuscular Age-Related Adjustment of Gait When Moving Upwards and Downwards. Front. Hum. Neurosci. 2021, 15, 621. [Google Scholar] [CrossRef]
- Ivanenko, Y.P.; Dominici, N.; Lacquaniti, F. Development of Independent Walking in Toddlers. Exerc. Sport Sci. Rev. 2007, 35, 67–73. [Google Scholar] [CrossRef]
- Martino, G.; Ivanenko, Y.P.; Serrao, M.; Ranavolo, A.; d’Avella, A.; Draicchio, F.; Conte, C.; Casali, C.; Lacquaniti, F. Locomotor Patterns in Cerebellar Ataxia. J. Neurophysiol. 2014, 112, 2810–2821. [Google Scholar] [CrossRef]
- Kadaba, M.P.; Ramakrishnan, H.K.; Wootten, M.E.; Gainey, J.; Gorton, G.; Cochran, G.V.B. Repeatability of Kinematic, Kinetic, and Electromyographic Data in Normal Adult Gait. J. Orthop. Res. 1989, 7, 849–860. [Google Scholar] [CrossRef]
- Ranavolo, A.; Don, R.; Draicchio, F.; Bartolo, M.; Serrao, M.; Padua, L.; Cipolla, G.; Pierelli, F.; Iavicoli, S.; Sandrini, G. Modelling the Spine as a Deformable Body: Feasibility of Reconstruction Using an Optoelectronic System. Appl. Ergon. 2013, 44, 192–199. [Google Scholar] [CrossRef]
- Varrecchia, T.; Serrao, M.; Rinaldi, M.; Ranavolo, A.; Conforto, S.; De Marchis, C.; Simonetti, A.; Poni, I.; Castellano, S.; Silvetti, A.; et al. Common and Specific Gait Patterns in People with Varying Anatomical Levels of Lower Limb Amputation and Different Prosthetic Components. Hum. Mov. Sci. 2019, 66, 9–21. [Google Scholar] [CrossRef]
- Wren, T.A.L.; Patrick Do, K.; Rethlefsen, S.A.; Healy, B. Cross-Correlation as a Method for Comparing Dynamic Electromyography Signals during Gait. J. Biomech. 2006, 39, 2714–2718. [Google Scholar] [CrossRef]
- Ranavolo, A.; Conte, C.; Iavicoli, S.; Serrao, M.; Silvetti, A.; Sandrini, G.; Pierelli, F.; Draicchio, F. Walking Strategies of Visually Impaired People on Trapezoidal- and Sinusoidal-Section Tactile Groundsurface Indicators. Ergonomics 2011, 54, 246–256. [Google Scholar] [CrossRef]
- Rinaldi, M.; Ranavolo, A.; Conforto, S.; Martino, G.; Draicchio, F.; Conte, C.; Varrecchia, T.; Bini, F.; Casali, C.; Pierelli, F.; et al. Increased Lower Limb Muscle Coactivation Reduces Gait Performance and Increases Metabolic Cost in Patients with Hereditary Spastic Paraparesis. Clin. Biomech. 2017, 48, 63–72. [Google Scholar] [CrossRef]
- Whittle, M.W. Three-Dimensional Motion of the Center of Gravity of the Body during Walking. Hum. Mov. Sci. 1997, 16, 347–355. [Google Scholar] [CrossRef]
- Serrao, M.; Ranavolo, A.; Casali, C. Neurophysiology of Gait. Handb. Clin. Neurol. 2018, 154, 299–303. [Google Scholar] [CrossRef]
- Don, R.; Serrao, M.; Vinci, P.; Ranavolo, A.; Cacchio, A.; Ioppolo, F.; Paoloni, M.; Procaccianti, R.; Frascarelli, F.; De Santis, F.; et al. Foot Drop and Plantar Flexion Failure Determine Different Gait Strategies in Char-cot-Marie-Tooth Patients. Clin. Biomech. 2007, 22, 905–916. [Google Scholar] [CrossRef]
- Watson, G.S.; Williams, E.J. On the Construction of Significance Tests on the Circle and the Sphere. Biometrika 1956, 43, 344. [Google Scholar] [CrossRef]
- Harrison, D.; Kanji, G.K. The Development of Analysis of Variance for Circular Data. J. Appl. Stat. 2006, 15, 197–223. [Google Scholar] [CrossRef]
- Schober, P.; Schwarte, L.A. Correlation Coefficients: Appropriate Use and Interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef]
- Fukuchi, C.A.; Fukuchi, R.K.; Duarte, M. Effects of Walking Speed on Gait Biomechanics in Healthy Participants: A Systematic Review and Meta-Analysis. Syst. Rev. 2019, 8, 153. [Google Scholar] [CrossRef]
- Tesio, L.; Rota, V. The Motion of Body Center of Mass During Walking: A Review Oriented to Clinical Applications. Front. Neurol. 2019, 10, 999. [Google Scholar] [CrossRef]
- Chen, S.; Wang, D.; Zhang, Q.; Shi, Y.; Ding, H.; Li, F. Relationship Between Isokinetic Lower-Limb Joint Strength, Isometric Time Force Characteristics, and Leg-Spring Stiffness in Recreational Runners. Front. Physiol. 2022, 12, 2421. [Google Scholar] [CrossRef]
- Struzik, A.; Karamanidis, K.; Lorimer, A.; Keogh, J.W.L.; Gajewski, J. Application of Leg, Vertical, and Joint Stiffness in Running Performance: A Literature Overview. Appl. Bionics. Biomech. 2021, 2021, 9914278. [Google Scholar] [CrossRef] [PubMed]
- Dzeladini, F.; van den Kieboom, J.; Ijspeert, A. The Contribution of a Central Pattern Generator in a Reflex-Based Neuromuscular Model. Front. Hum. Neurosci. 2014, 8, 371. [Google Scholar] [CrossRef]
- Feldman, A.G.; Levin, M.F.; Garofolini, A.; Piscitelli, D.; Zhang, L. Central Pattern Generator and Human Locomotion in the Context of Referent Control of Motor Actions. Clin. Neurophysiol. 2021, 132, 2870–2889. [Google Scholar] [CrossRef] [PubMed]
- Minassian, K.; Hofstoetter, U.S.; Dzeladini, F.; Guertin, P.A.; Ijspeert, A. The Human Central Pattern Generator for Locomotion: Does It Exist and Contribute to Walking? Neuroscientist 2017, 23, 649–663. [Google Scholar] [CrossRef]
- Møller, M.; Sinkjaer, T.; Duysens, J. Contributions to the Understanding of Gait Control; University of Copenhagen: Copenhagen, Denmark, 2014. [Google Scholar]
- Dewolf, A.H.; Ivanenko, Y.P.; Zelik, K.E.; Lacquaniti, F.; Willems, P.A. Differential Activation of Lumbar and Sacral Motor Pools during Walking at Different Speeds and Slopes. J. Neurophysiol. 2019, 122, 872–887. [Google Scholar] [CrossRef]
- Martino, G.; Ivanenko, Y.P.; d’Avella, A.; Serrao, M.; Ranavolo, A.; Draicchio, F.; Cappellini, G.; Casali, C.; Lacquaniti, F. Neuromuscular Adjustments of Gait Associated with Unstable Conditions. J. Neurophysiol. 2015, 114, 2867–2882. [Google Scholar] [CrossRef] [PubMed]
- Tam, N.; Tucker, R.; Santos-Concejero, J.; Prins, D.; Lamberts, R.P. Running Economy: Neuromuscular and Joint-Stiffness Contributions in Trained Runners. Int. J. Sports Physiol. Perform. 2019, 14, 16–22. [Google Scholar] [CrossRef]
- Zhang, Q.; Nassis, G.P.; Chen, S.; Shi, Y.; Li, F. Not Lower-Limb Joint Strength and Stiffness but Vertical Stiffness and Isometric Force-Time Characteristics Correlate With Running Economy in Recreational Male Runners. Front. Physiol. 2022, 13, 1321. [Google Scholar] [CrossRef]


| Maps | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Global | Extensor | Flexor | L3 | L4 | L5 | S1 | S2 | ||
| Muscles | GM | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | |||
| RF | ⬤ | ⬤ | ⬤ | ⬤ | |||||
| VL | ⬤ | ⬤ | ⬤ | ||||||
| VM | ⬤ | ⬤ | ⬤ | ⬤ | |||||
| TFL | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | |||
| ST | ⬤ | ⬤ | • | ⬤ | ⬤ | ⬤ | |||
| BF | ⬤ | ⬤ | ● | ● | ⬤ | ||||
| TA | ⬤ | ⬤ | ⬤ | ⬤ | ⬤ | ||||
| GasM | ⬤ | ⬤ | ⬤ | ⬤ | |||||
| GasL | ⬤ | ⬤ | ⬤ | ⬤ | |||||
| SOL | ⬤ | ● | ⬤ | ⬤ | |||||
| P | ⬤ | ● | ⬤ | ⬤ | |||||
| Parameters | Main Effect Velocity | Post-Hoc Velocity Transition | |||
|---|---|---|---|---|---|
| F(df) | p | Value at 6.8 km/h (Mean ± Std) | Value at 7.3 km/h (Mean ± Std) | p Value | |
| CIglob | F(1,17) = 641.04 | <0.001 | 3.97 ± 0.62 | 6.05 ± 0.69 | <0.001 |
| CIext | F(1,17) = 388.04 | <0.001 | 3.82 ± 0.83 | 6.53 ± 0.99 | <0.001 |
| CIflex | F(1,17) = 240.06 | <0.001 | 9.03 ± 1.72 | 10.3 ± 2.4 | / |
| CIL3 | F(1,17) = 137.28 | <0.001 | 6.21 ± 2.06 | 8.09 ± 2.28 | / |
| CIL4 | F(1,17) = 409.77 | <0.001 | 3.85 ± 0.71 | 5.22 ± 0.72 | <0.001 |
| CIL5 | F(1,17) = 351.04 | <0.001 | 4.22 ± 0.72 | 5.87 ± 0.78 | <0.001 |
| CIS1 | F(1,17) = 461.13 | <0.001 | 5.14 ± 0.70 | 6.88 ± 0.91 | <0.001 |
| CIS2 | F(1,17) = 464.98 | <0.001 | 5.83 ± 1.26 | 9.24 ± 1.5 | <0.001 |
| Maxglob | F(1,17) = 321.71 | <0.001 | 11.08 ± 1.48 | 23.30 ± 3.54 | <0.001 |
| Maxext | F(1,17) = 152.36 | <0.001 | 12.32 ± 2.77 | 24.42 ± 5.48 | <0.001 |
| Maxflex | F(1,17) = 104.01 | <0.001 | 30.16 ± 8.91 | 26.51 ± 7.28 | / |
| MaxL3 | F(1,17) = 76.83 | <0.001 | 31.5 ± 14.27 | 40.2 ± 14.41 | / |
| MaxL4 | F(1,17) = 156.75 | <0.001 | 11.93 ± 3.75 | 14.47 ± 4.13 | / |
| MaxL5 | F(1,17) = 93.91 | <0.001 | 11.7 ± 2.33 | 15.18 ± 3.5 | / |
| MaxS1 | F(1,17) = 192.85 | <0.001 | 16 ± 3.07 | 24.64 ± 4.39 | <0.001 |
| MaxS2 | F(1,17) = 189.34 | <0.001 | 18.91 ± 4.04 | 34.19 ± 6.3 | <0.001 |
| FWHMglob | F(1,17) = 29.31 | <0.001 | 26.62 ± 6.08 | 18.17 ± 5.14 | 0.01 |
| FWHMext | F(1,17) = 9.31 | <0.001 | 21.15 ± 6.3 | 20.07 ± 6.7 | / |
| FWHMflex | F(1,17) = 11.13 | <0.001 | 20.74 ± 6.66 | 31.14 ± 8.65 | / |
| FWHML3 | F(1,17) = 11.37 | <0.001 | 14.45 ± 3.81 | 15.69 ± 3.39 | / |
| FWHML4 | F(1,17) = 20.28 | <0.001 | 16.86 ± 4.58 | 18.32 ± 4.6 | / |
| FWHML5 | F(1,17) = 8.22 | <0.001 | 25.45 ± 7 | 29.33 ± 7.67 | / |
| FWHMS1 | F(1,17) = 13.48 | <0.001 | 20.68 ± 6.17 | 20.53 ± 5.81 | / |
| FWHMS2 | F(1,17) = 4.06 | <0.001 | 20.34 ± 7.9 | 20.08 ± 5.65 | / |
| CoAglob | F(1,17) = 24.96 | <0.001 | 16.74 ± 5.38 | 14.05 ± 2.12 | <0.01 |
| CoAext | F(1,17) = 22.95 | <0.001 | 9.1 ± 4.09 | 12.76 ± 2.88 | <0.001 |
| CoAflex | F(1,17) = 8.74 | <0.001 | 97.18 ± 11.8 | 15.63 ± 13.91 | <0.001 |
| CoAL3 | F(4,17) = 58.01 | <0.001 | 7.31 ± 2.58 | 13.2 ± 2.28 | <0.001 |
| CoAL4 | 5.96 ± 2.93 | 11.63 ± 2.31 | <0.001 | ||
| CoAL5 | 5.72 ± 5.31 | 8.89 ± 3.82 | <0.01 | ||
| CoAS1 | 30.35 ± 4.3 | 15.2 ± 2.17 | <0.001 | ||
| CoAS2 | 28.01 ± 5.1 | 15.88 ± 2.98 | <0.001 | ||
| CMC_Wtglob (CMC_Btglob) | F(1,17) = 54.38 | <0.001 | 0.95 ± 0.01 (0.86) | 0.97 ± 0.01 (0.88) | 0.02 |
| CMC_Wtext (CMC_Btext) | F(1,17) = 44.98 | <0.001 | 0.95 ± 0.02 (0.86) | 0.96 ± 0.01 (0.89) | / |
| CMC_Wtflex (CMC_Btflex) | F(1,17) = 55.77 | <0.001 | 0.93 ± 0.04 (0.79) | 0.92 ± 0.03 (0.75) | / |
| CMC_WtL3 (CMC_BtL3) | F(1,17) = 24.31 | <0.001 | 0.97 ± 0.02 (0.81) | 0.96 ± 0.02 (0.90) | / |
| CMC_WtL4 (CMC_BtL4) | F(1,17) = 42.25 | <0.001 | 0.96 ± 0.01 (0.87) | 0.96 ± 0.01 (0.92) | / |
| CMC_WtL5 (CMC_Btglob) | F(1,17) = 38.82 | <0.001 | 0.93 ± 0.02 (0.84) | 0.92 ± 0.03 (0.83) | / |
| CMC_WtS1 (CMC_BtS1) | F(1,17) = 49.56 | <0.001 | 0.94 ± 0.01 (0.86) | 0.96 ± 0.01 (0.91) | 0.04 |
| CMC_WtS2 (CMC_BtS2) | F(1,17) = 48.76 | <0.001 | 0.94 ± 0.02 (0.85) | 0.95 ± 0.02 (0.89) | 0.02 |
| CoMy | F(1,17) = 426.2 | <0.001 | 6.60 ± 0.83 | 10.99 ± 1.92 | <0.001 |
| CoMz | F(1,17) = 120.29 | <0.001 | 4.57 ± 1.23 | 2.78 ± 0.88 | <0.001 |
| TOe | F(1,17) = 940.64 | <0.001 | 62.57 ± 0.70 | 57.91 ± 1.06 | <0.001 |
| stride length | F(1,17) = 253.03 | <0.001 | 173.78 ± 7.25 | 131 ± 9.24 | <0.001 |
| stride frequency | F(1,17) = 714.22 | <0.001 | 1.13 ± 0.05 | 1.31 ± 0.07 | <0.001 |
| foot lift | F(1,17) = 108.03 | <0.001 | 16.47 ± 1.57 | 21.63 ± 3.69 | <0.01 |
| Main Effect Level | Velocity | Post-Hoc Level | ||||||
|---|---|---|---|---|---|---|---|---|
| F(df) | p | CoAL3 | CoAL4 | CoAL5 | CoAS1 | CoAS2 | ||
| F(4,17) = 511.50 | <0.001 | 6.8 km/h | CoAL3 | / | ||||
| CoAL4 | <0.01 | / | ||||||
| CoAL5 | 0.01 | 0.04 | / | |||||
| CoAS1 | <0.001 | <0.001 | <0.001 | / | ||||
| CoAS2 | <0.001 | <0.001 | <0.001 | <0.01 | / | |||
| 7.3 km/h | CoAL3 | / | ||||||
| CoAL4 | <0.01 | / | ||||||
| CoAL5 | <0.001 | <0.001 | / | |||||
| CoAS1 | <0.01 | <0.001 | <0.001 | / | ||||
| CoAS2 | <0.001 | <0.001 | <0.001 | <0.001 | / | |||
| Shape Similarity (Mean ± Std) | t-Test p | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| RG-E | 0.97 ± 0.02 | <0.001 | |||||||
| RG-F | 0.70 ± 0.12 | ||||||||
| Main effect shape similarity | Post-hoc shape similarity | ||||||||
| F(df) | p | RG-L3 | RG-L4 | RG-L5 | RG-S1 | RG-S2 | |||
| RG-L3 | 0.88 ± 0.08 | F(1,4) = 11.23 | <0.001 | RG-L3 | / | ||||
| RG-L4 | 0.93 ± 0.03 | RG-L4 | 0.02 | / | |||||
| RG-L5 | 0.89 ± 0.04 | RG-L5 | / | / | / | ||||
| RG-S1 | 0.96 ± 0.02 | RG-S1 | <0.001 | / | <0.01 | / | |||
| RG-S2 | 0.87 ± 0.06 | RG-S2 | / | <0.01 | / | <0.001 | / | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiori, L.; Castiglia, S.F.; Chini, G.; Draicchio, F.; Sacco, F.; Serrao, M.; Tatarelli, A.; Varrecchia, T.; Ranavolo, A. The Lower Limb Muscle Co-Activation Map during Human Locomotion: From Slow Walking to Running. Bioengineering 2024, 11, 288. https://doi.org/10.3390/bioengineering11030288
Fiori L, Castiglia SF, Chini G, Draicchio F, Sacco F, Serrao M, Tatarelli A, Varrecchia T, Ranavolo A. The Lower Limb Muscle Co-Activation Map during Human Locomotion: From Slow Walking to Running. Bioengineering. 2024; 11(3):288. https://doi.org/10.3390/bioengineering11030288
Chicago/Turabian StyleFiori, Lorenzo, Stefano Filippo Castiglia, Giorgia Chini, Francesco Draicchio, Floriana Sacco, Mariano Serrao, Antonella Tatarelli, Tiwana Varrecchia, and Alberto Ranavolo. 2024. "The Lower Limb Muscle Co-Activation Map during Human Locomotion: From Slow Walking to Running" Bioengineering 11, no. 3: 288. https://doi.org/10.3390/bioengineering11030288
APA StyleFiori, L., Castiglia, S. F., Chini, G., Draicchio, F., Sacco, F., Serrao, M., Tatarelli, A., Varrecchia, T., & Ranavolo, A. (2024). The Lower Limb Muscle Co-Activation Map during Human Locomotion: From Slow Walking to Running. Bioengineering, 11(3), 288. https://doi.org/10.3390/bioengineering11030288







