Brain Tumor Detection and Categorization with Segmentation of Improved Unsupervised Clustering Approach and Machine Learning Classifier
Abstract
1. Introduction
Research Contributions
- ➢
- The study contributes by utilizing the Fig share and Kaggle datasets for brain tumor detection. These datasets provide a diverse and comprehensive set of brain images, ensuring the applicability and robustness of the proposed methods across various scenarios.
- ➢
- A novel contribution lies in the proposal of an improved fuzzy C-Means clustering algorithm. This technique specifically addresses the challenge of detecting minute tumors, showcasing an advancement in the ability to identify smaller lesions that might be overlooked by traditional methods.
- ➢
- The research conducts an extensive investigation by evaluating the proposed improved fuzzy C-Means clustering against five state-of-the-art segmentation models. This comparative analysis contributes valuable insights into the strengths and weaknesses of different segmentation approaches, providing a basis for selecting optimal methods in brain tumor detection.
- ➢
- The study introduces a rigorous evaluation framework by incorporating key metrics such as accuracy, precision, recall, and F1-score. These metrics offer a comprehensive assessment of the proposed approach’s performance, allowing for a nuanced understanding of its effectiveness in comparison to existing models.
- ➢
- A significant research contribution is the demonstration of fast and accurate tumor detection achieved by the proposed approach. This highlights the practical viability of the method in real-time scenarios, contributing to the efficiency of brain tumor detection over existing state-of-the-art approaches.
2. Literature Review
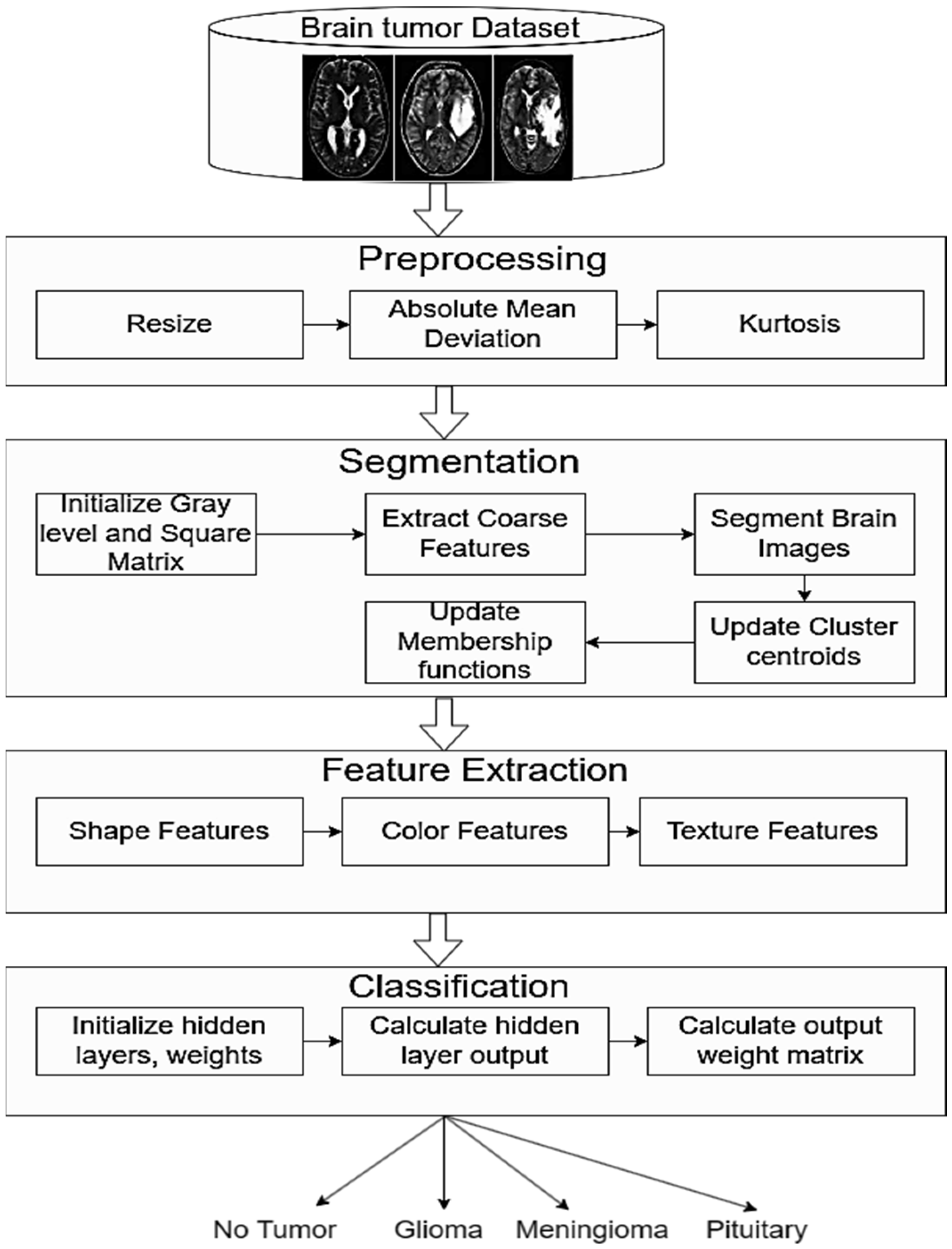
3. Materials and Methods
- (a)
- Glioma:
- (b)
- Meningioma:
- (c)
- Pituitary:
3.1. Image Preprocessing
3.2. Segmentation
| Algorithm 1: Improved FCM |
| Input: Gray level image Output: Segmented image |
|
3.3. Feature Extraction
3.4. Feature Selection
3.5. Classification
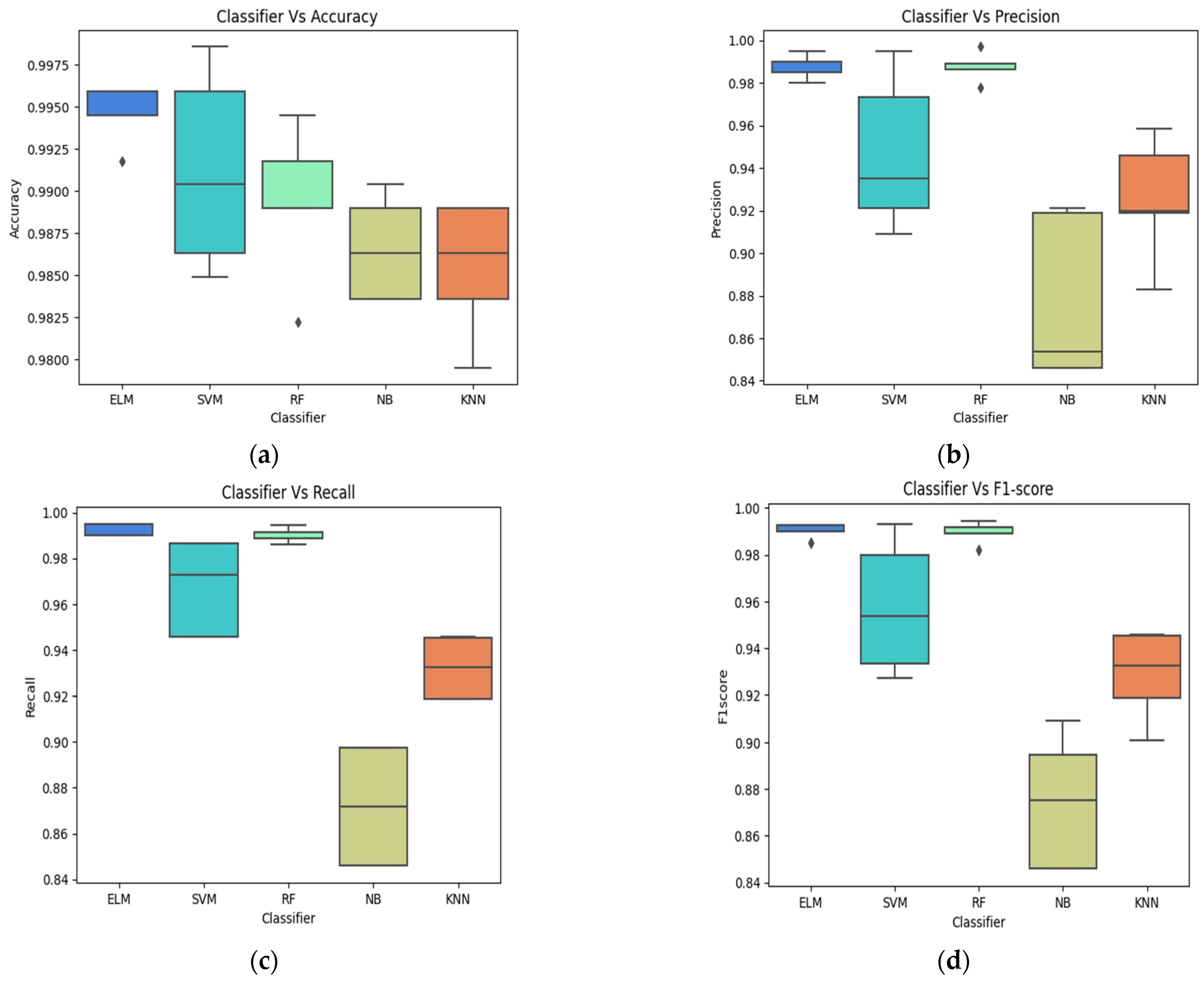
3.6. Performance Evaluation
- ➢
- Accuracy in brain tumor classification represents the overall correctness of the model in predicting different types of brain tumors.
- ➢
- Precision in brain tumor classification measures the accuracy of the model in correctly identifying a specific type of tumor among the predicted positive cases.
- ➢
- Recall in brain tumor classification assesses the ability of the model to correctly identify all instances of a particular brain tumor type among the actual positive cases.
- ➢
- F1 score in brain tumor classification provides a balance between the precision and recall, giving an overall measure of the model’s effectiveness.
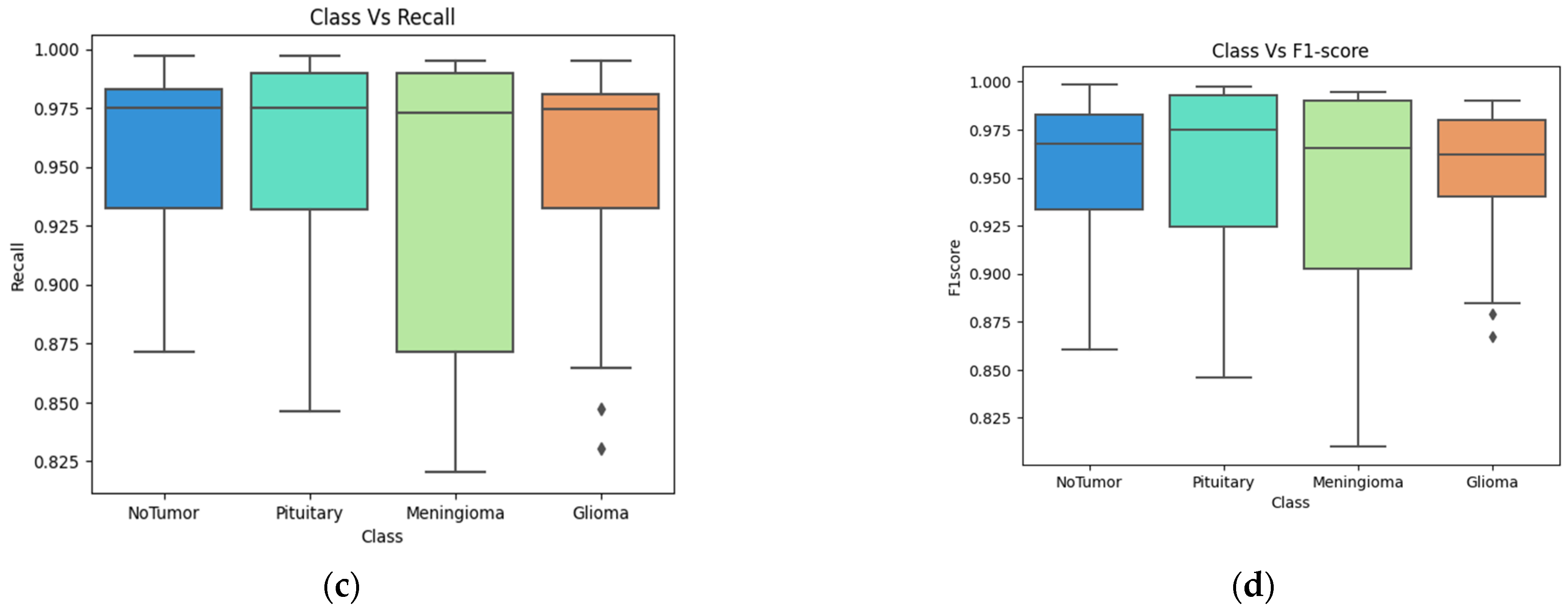
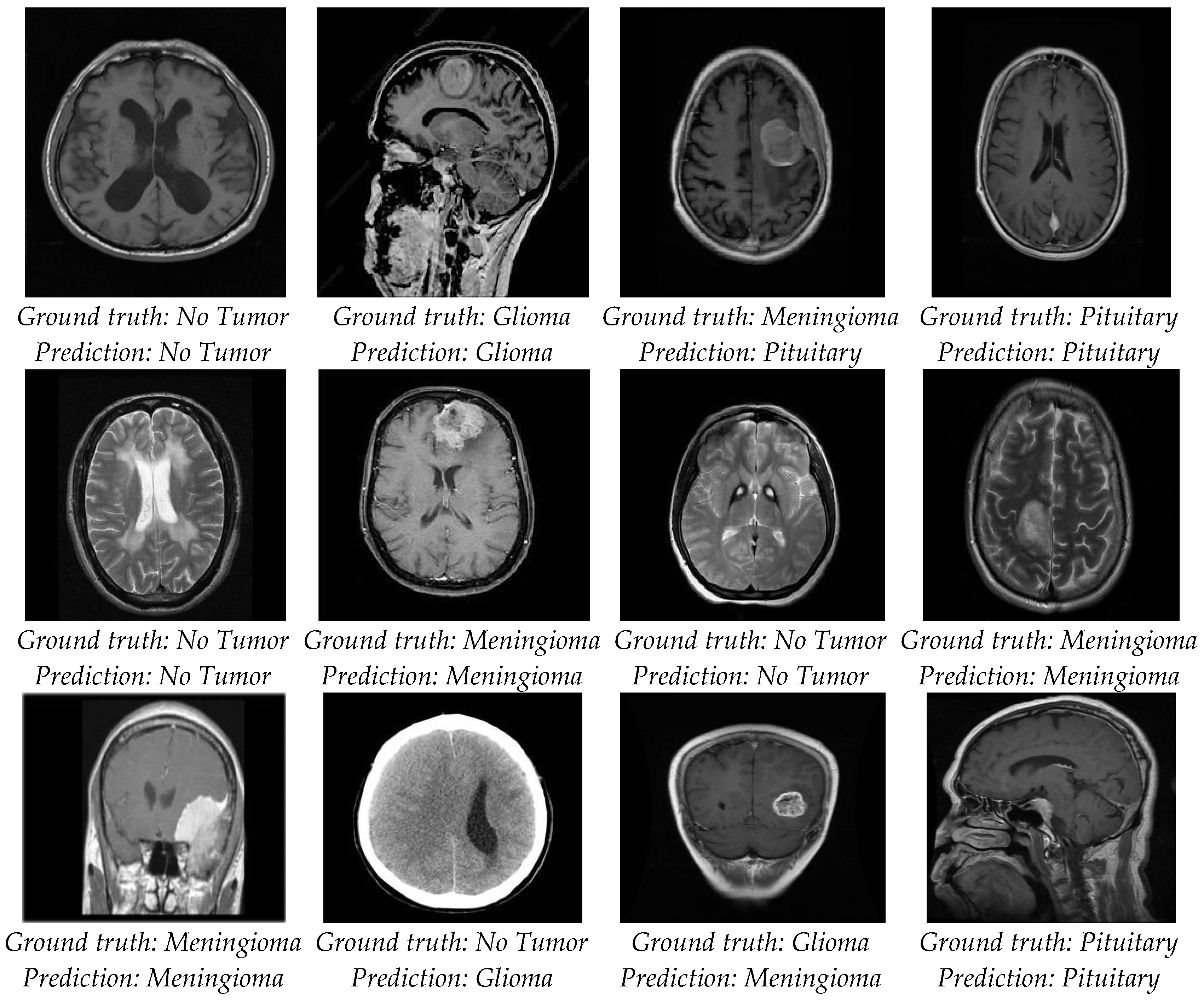
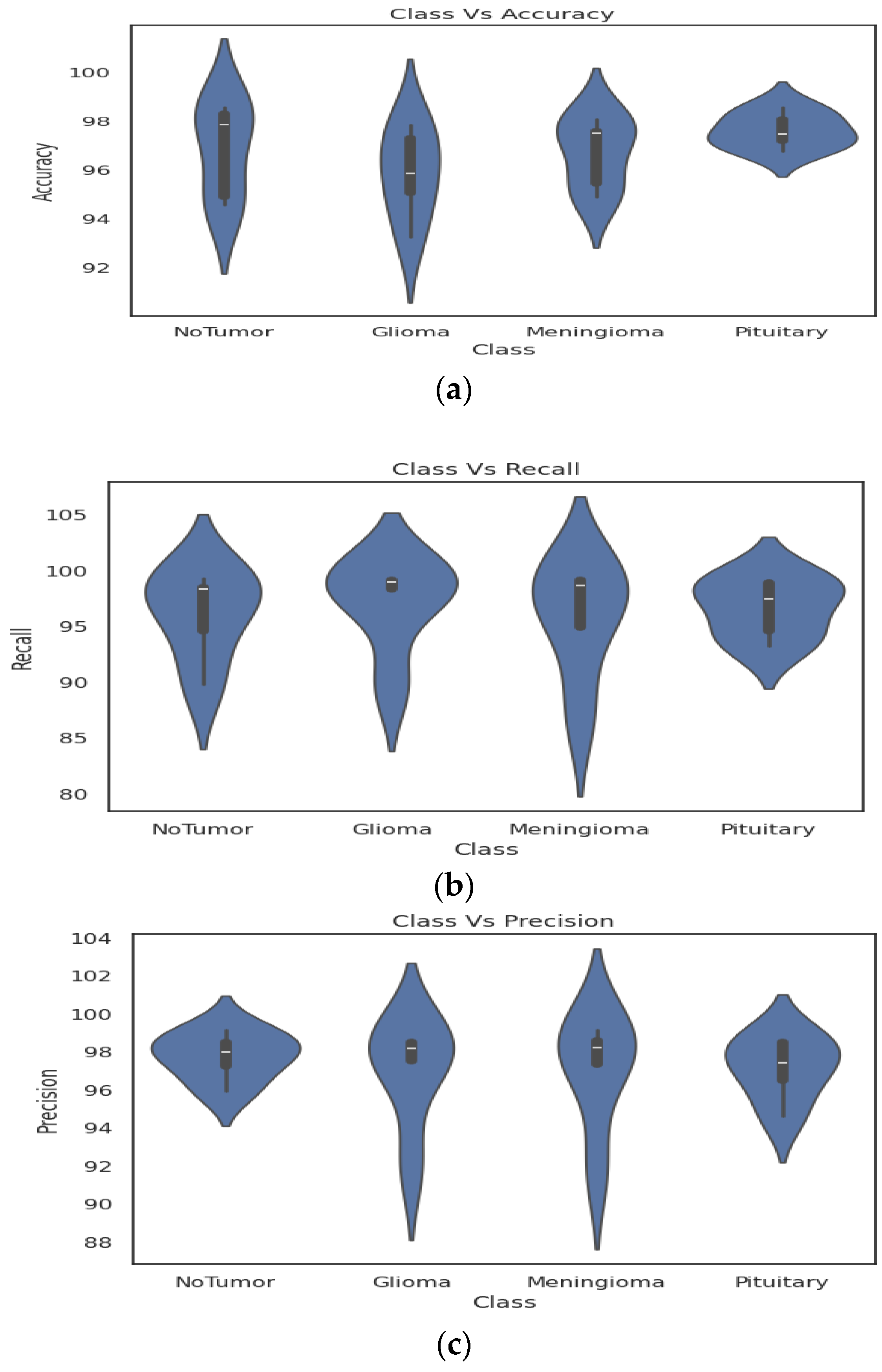
4. Results
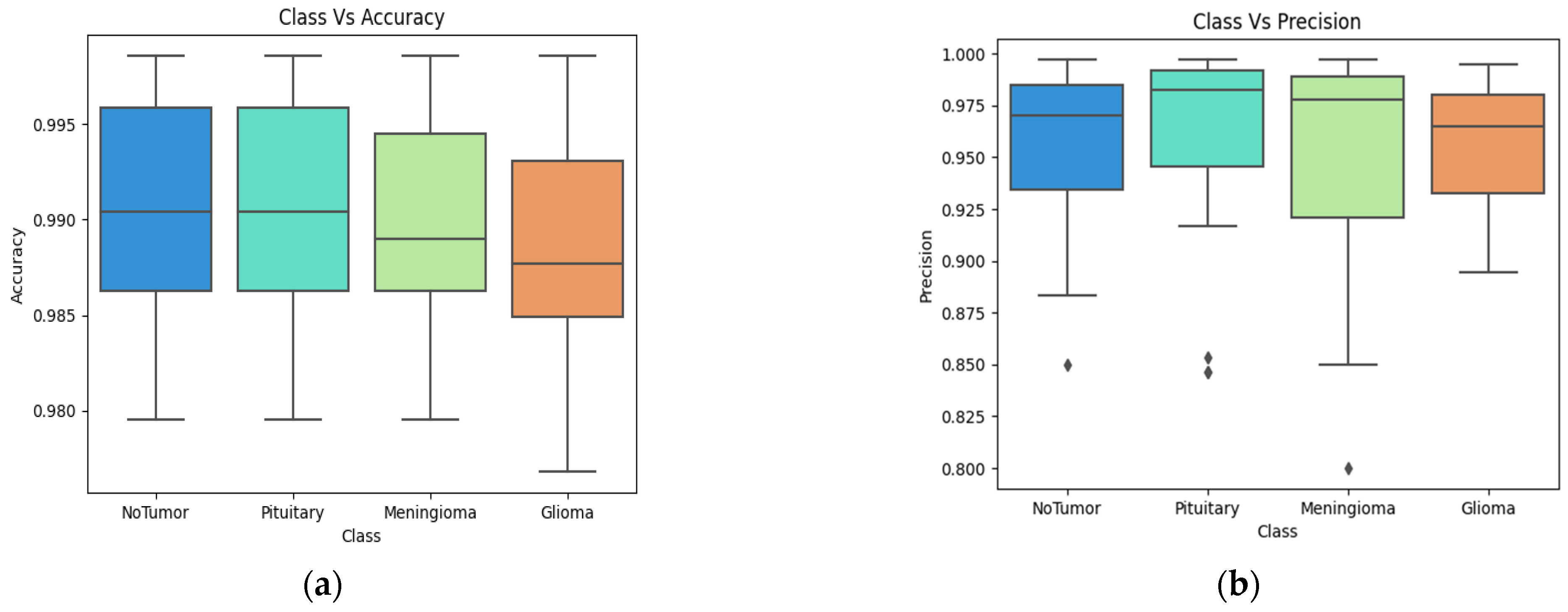
4.1. Segmentation Evaluation
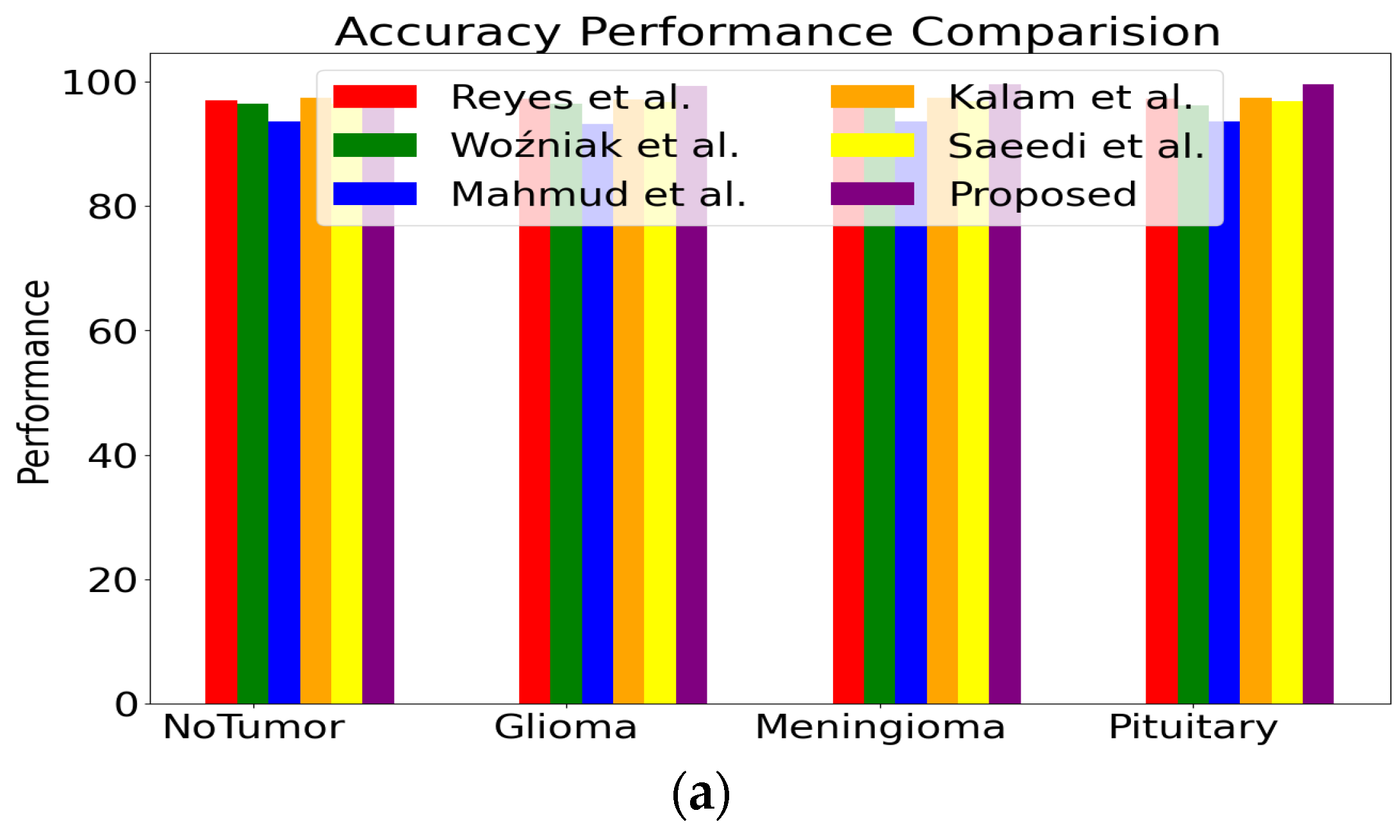
4.2. Classification Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Reynoso-Noverón, N.; Mohar-Betancourt, A.; Ortiz-Rafael, J. Epidemiology of brain tumors. In Principles of Neuro-Oncology: Brain Skull Base; Springer: Cham, Switzerland, 2021; pp. 15–25. [Google Scholar] [CrossRef]
- Brunese, L.; Mercaldo, F.; Reginelli, A.; Santone, A. An ensemble learning approach for brain cancer detection exploiting radi-omic features. Comput. Methods Programs Biomed. 2020, 185, 105134. [Google Scholar] [CrossRef] [PubMed]
- Casanova, M.P.; Mariné, A.F.; Pumarola i Batlle, M.; Feliu-Pascual, A.L. Meningioma and glioma as the first collision brain tumour re-ported in small animals. J. Comp. Pathol. 2023, 204, 55–58. [Google Scholar] [CrossRef] [PubMed]
- Altinoz, M.A.; Ozpinar, A. Oxamate targeting aggressive cancers with special emphasis to brain tumors. Biomed. Pharmacother. 2022, 147, 112686. [Google Scholar] [CrossRef]
- Song, C.; Ren, Y.; Liu, Y.; Cao, R.; Duan, G. Oxygen comfort evaluation method based on symptom index for short-term internal migrants to Tibet. Sci. Total Environ. 2023, 902, 166418. [Google Scholar] [CrossRef] [PubMed]
- Amin, J.; Sharif, M.; Raza, M.; Saba, T.; Anjum, M.A. Brain tumor detection using statistical and machine learning method. Com-Puter. Methods Programs Biomed. 2019, 177, 69–79. [Google Scholar] [CrossRef] [PubMed]
- National Brain Tumor Society. Available online: https://braintumor.org/ (accessed on 22 May 2023).
- Rovira, À.; Auger, C. Beyond McDonald: Updated perspectives on MRI diagnosis of multiple sclerosis. Expert Rev. Neurother. 2021, 21, 895–911. [Google Scholar] [CrossRef]
- Pilli, R.; Goel, T.; Murugan, R.; Tanveer, M. Association of white matter volume with brain age classification using deep learn-ing network and region wise analysis. Eng. Appl. Artif. Intell. 2023, 125, 106596. [Google Scholar] [CrossRef]
- Bahadure, N.B.; Ray, A.K.; Thethi, H.P. Image analysis for MRI based brain tumor detection and feature extraction using biolog-ically inspired BWT and SVM. Int. J. Biomed. Imaging 2017, 2017, 9749108. [Google Scholar] [CrossRef]
- Mittal, H.; Pandey, A.C.; Saraswat, M.; Kumar, S.; Pal, R.; Modwel, G. A comprehensive survey of image segmentation: Clustering methods, performance parameters, and benchmark datasets. Multimed. Tools Appl. 2021, 81, 35001–35026. [Google Scholar] [CrossRef] [PubMed]
- Tseng, C.J.; Tang, C. An optimized XGBoost technique for accurate brain tumor detection using feature selection and image segmentation. Healthc. Anal. 2023, 4, 100217. [Google Scholar] [CrossRef]
- American Brain Tumor Association. Available online: https://www.abta.org/ (accessed on 20 May 2023).
- Islam, M.K.; Ali, M.S.; Miah, M.S.; Rahman, M.M.; Alam, M.S.; Hossain, M.A. Brain tumor detection in MR image using superpixels, principal component analysis and template based K-means clustering algorithm. Mach. Learn. Appl. 2021, 5, 100044. [Google Scholar] [CrossRef]
- Swati, Z.N.; Zhao, Q.; Kabir, M.; Ali, F.; Ali, Z.; Ahmed, S.; Lu, J. Brain tumor classification for MR images using transfer learning and fine-tuning. Comput. Med. Imaging Graph. 2019, 75, 34–46. [Google Scholar] [CrossRef]
- Zeng, W.; Liu, Y.; Cui, H.; Ma, R.; Xu, Z. Interval possibilistic C-means algorithm and its application in image segmentation. Inf. Sci. 2022, 612, 465–480. [Google Scholar] [CrossRef]
- Zhu, J.; Ma, X.; Martínez, L.; Zhan, J. A probabilistic linguistic three-way decision method with regret theory via fuzzy c-means clustering algorithm. IEEE Trans. Fuzzy Syst. 2023, 31, 2821–2835. [Google Scholar] [CrossRef]
- Kollem, S.; Reddy, K.R.; Rao, D.S. An optimized SVM based possibilistic fuzzy c-means clustering algorithm for tumor seg-mentation. Multimed. Tools Appl. 2021, 80, 409–437. [Google Scholar] [CrossRef]
- Cebeci, Z.; Cebeci, C.; Tahtali, Y.; Bayyurt, L. Two novel outlier detection approaches based on unsupervised possibilistic and fuzzy clustering. PeerJ Comput. Sci. 2022, 8, e1060. [Google Scholar] [CrossRef] [PubMed]
- Garg, H.; Rani, D. Novel distance measures for intuitionistic fuzzy sets based on various triangle centers of isosceles triangu-lar fuzzy numbers and their applications. Expert Syst. Appl. 2022, 191, 116228. [Google Scholar] [CrossRef]
- Shaik, N.S.; Cherukuri, T.K. Multi-level attention network: Application to brain tumor classification. Signal Image Video Process. 2022, 16, 817–824. [Google Scholar] [CrossRef]
- Guan, Y.; Aamir, M.; Rahman, Z.; Ali, A.; Abro, W.A.; Dayo, Z.A.; Bhutta, M.S.; Hu, Z. A framework for efficient brain tumor classification using MRI images. Math. Biosci. Eng. 2021, 18, 5790–5815. [Google Scholar] [CrossRef]
- Badža, M.M.; Barjaktarović, M.Č. Classification of brain tumors from MRI images using a convolutional neural network. Appl. Sci. 2020, 10, 1999. [Google Scholar] [CrossRef]
- Deepak, S.; Ameer, P.M. Brain tumor classification using deep CNN features via transfer learning. Comput. Biol. Med. 2019, 111, 103345. [Google Scholar] [CrossRef]
- Díaz-Pernas, F.J.; Martínez-Zarzuela, M.; Antón-Rodríguez, M.; González-Ortega, D. A deep learning approach for brain tumor classification and segmentation using a multiscale convolutional neural network. Healthcare 2021, 9, 153. [Google Scholar] [CrossRef]
- Alhassan, A.M.; Zainon, W.M. Brain tumor classification in magnetic resonance image using hard swish-based RELU activation function-convolutional neural network. Neural Comput. Appl. 2021, 33, 9075–9087. [Google Scholar] [CrossRef]
- Ghassemi, N.; Shoeibi, A.; Rouhani, M. Deep neural network with generative adversarial networks pre-training for brain tumor classification based on MR images. Biomed. Signal Process. Control 2020, 57, 101678. [Google Scholar] [CrossRef]
- Noreen, N.; Palaniappan, S.; Qayyum, A.; Ahmad, I.; Alassafi, M.O. Brain Tumor Classification Based on Fine-Tuned Models and the Ensemble Method. Comput. Mater. Contin. 2021, 67, 3967–3982. [Google Scholar] [CrossRef]
- Gumaei, A.; Hassan, M.M.; Hassan, M.R.; Alelaiwi, A.; Fortino, G. A hybrid feature extraction method with regularized extreme learning machine for brain tumor classification. IEEE Access 2019, 7, 36266–36273. [Google Scholar] [CrossRef]
- Haq, E.U.; Jianjun, H.; Li, K.; Haq, H.U.; Zhang, T. An MRI-based deep learning approach for efficient classification of brain tumors. J. Ambient. Intell. Humaniz. Comput. 2021, 14, 6697–6718. [Google Scholar] [CrossRef]
- Ghosal, P.; Nandanwar, L.; Kanchan, S.; Bhadra, A.; Chakraborty, J.; Nandi, D. Brain tumor classification using ResNet-101 based squeeze and excitation deep neural network. In Proceedings of the 2019 Second International Conference on Advanced Computational and Communication Paradigms (ICACCP), Gangtok, India, 25–28 February 2019; IEEE: Piscataway, NJ, USA; pp. 1–6. [Google Scholar]
- Nawaz, M.; Nazir, T.; Masood, M.; Mehmood, A.; Mahum, R.; Khan, M.A.; Kadry, S.; Thinnukool, O. Analysis of brain MRI images using improved cornernet approach. Diagnostics 2021, 11, 1856. [Google Scholar] [CrossRef] [PubMed]
- Verma, A.; Singh, V.P. HSADML: Hyper-sphere angular deep metric based learning for brain tumor classification. In Proceedings of the Satellite Workshops of ICVGIP 2021, Jodhpur, India, 16 June 2021; Springer Nature: Singapore; pp. 105–120. [Google Scholar]
- Cinar, N.; Kaya, M.; Kaya, B. A novel convolutional neural network-based approach for brain tumor classification using magnetic resonance images. Int. J. Imaging Syst. Technol. 2023, 33, 895–908. [Google Scholar] [CrossRef]
- Deepak, S.; Ameer, P.M. Automated categorization of brain tumor from mri using cnn features and svm. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 8357–8369. [Google Scholar] [CrossRef]
- Deepak, S.; Ameer, P.M. Brain tumor categorization from imbalanced MRI dataset using weighted loss and deep feature fusion. Neurocomputing 2023, 520, 94–102. [Google Scholar] [CrossRef]
- Kumar, K.K.; Dinesh, P.M.; Rayavel, P.; Vijayaraja, L.; Dhanasekar, R.; Kesavan, R.; Raju, K.; Khan, A.A.; Wechtaisong, C.; Haq, M.A.; et al. Brain Tumor Identification Using Data Augmentation and Transfer Learning Approach. Comput. Syst. Sci. Eng. 2023, 46, 1845–1861. [Google Scholar] [CrossRef]
- Figshare Dataset. Available online: https://figshare.com/articles/dataset/brain_tumor_dataset/1512427 (accessed on 5 June 2023).
- Kaggle Dataset. Available online: https://kaggle.com/datasets/masoudnickparvar/brain-tumor-mri-dataset (accessed on 5 June 2023).
- Hashemi, S.E.; Gholian-Jouybari, F.; Hajiaghaei-Keshteli, M. A fuzzy C-means algorithm for optimizing data clustering. Expert Syst. Appl. 2023, 227, 120377. [Google Scholar] [CrossRef]
- Saeedi, S.; Rezayi, S.; Keshavarz, H.; RNiakan Kalhori, S. MRI-based brain tumor detection using convolutional deep learning methods and chosen machine learning techniques. BMC Med. Inform. Decis. Mak. 2023, 23, 16. [Google Scholar] [CrossRef] [PubMed]
- Kalam, R.; Thomas, C.; Rahiman, M.A. Brain tumor detection in MRI images using adaptive-ANFIS classifier with segmentation of tumor and edema. Soft Comput. 2023, 27, 2279–2297. [Google Scholar] [CrossRef]
- Lu, S.; Liu, S.; Hou, P.; Yang, B.; Liu, M.; Yin, L.; Zheng, W. Soft Tissue Feature Tracking Based on DeepMatching Network. CMES-Comput. Model. Eng. Sci. 2023, 136, 363–379. [Google Scholar]
- Lu, S.; Yang, J.; Yang, B.; Yin, Z.; Liu, M.; Yin, L.; Zheng, W. Analysis and Design of Surgical Instrument Localization Algorithm. CMES-Comput. Model. Eng. Sci. 2023, 137, 669–685. [Google Scholar] [CrossRef]
- Wang, W.; Qi, F.; Wipf, D.; Cai, C.; Yu, T.; Li, Y.; Yu, Z.; Wu, W. Sparse Bayesian Learning for End-to-End EEG Decoding. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 15632–15649. [Google Scholar] [CrossRef]
- He, B.; Lu, Q.; Lang, J.; Yu, H.; Peng, C.; Bing, P.; Li, S.; Zhou, Q.; Liang, Y.; Tian, G. A new method for CTC images recognition based on machine learning. Front. Bioeng. Biotechnol. 2020, 8, 897. [Google Scholar] [CrossRef]
- Lin, Q.; Xiongbo, G.; Zhang, W.; Cai, L.; Yang, R.; Chen, H.; Cai, K. A Novel Approach of Surface Texture Mapping for Cone-beam Computed Tomography in Image-guided Surgical Navigation. IEEE J. Biomed. Health Inform. 2023, 1–18. [Google Scholar] [CrossRef]
- Ahmad, M.; Qadri, S.F.; Qadri, S.; Saeed, I.A.; Zareen, S.S.; Iqbal, Z.; Alabrah, A.; Alaghbari, H.M.; Rahman, M.; Md, S. A lightweight convolutional neural network model for liver segmentation in medical diagnosis. Comput. Intell. Neurosci. 2022, 2022, 7954333. [Google Scholar] [CrossRef]
- Qadri, S.F.; Ahmad, M.; Ai, D.; Yang, J.; Wang, Y. Deep belief network based vertebra segmentation for CT images. In Proceedings of the Image and Graphics Technologies and Applications: 13th Conference on Image and Graphics Technologies and Applications, IGTA 2018, Beijing, China, 8–10 April 2018; Volume 757, pp. 536–545. [Google Scholar]
- Rajinikanth, V.; Fernandes, S.L.; Bhushan, B.; Harisha; Sunder, N.R. Segmentation and analysis of brain tumor using Tsallis en-tropy and regularised level set. In Proceedings of the 2nd International Conference on Micro-Electronics, Electromagnetics and Telecommunications: ICMEET 2016; Springer: Singapore, 2018; pp. 313–321. [Google Scholar]
- Bal, A.; Banerjee, M.; Sharma, P.; Maitra, M. Brain tumor segmentation on MR image using K-Means and fuzzy-possibilistic clustering. In Proceedings of the 2018 2nd International Conference on Electronics, Materials Engineering & Nano-Technology (IEMENTech), Kolkata, India, 4–5 May 2018; IEEE: Piscataway, NJ, USA; pp. 1–8. [Google Scholar]
- Chowdhary, C.L.; Mittal, M.P.K.; Pattanaik, P.A.; Marszalek, Z. An efficient segmentation and classification system in medical images using intuitionist possibilistic fuzzy C-mean clustering and fuzzy SVM algorithm. Sensors 2020, 20, 3903. [Google Scholar] [CrossRef] [PubMed]
- Sharif, M.; Amin, J.; Raza, M.; Yasmin, M.; Satapathy, S.C. An integrated design of particle swarm optimization (PSO) with fusion of features for detection of brain tumor. Pattern Recognit. Lett. 2020, 129, 150–157. [Google Scholar] [CrossRef]
- Rundo, L.; Militello, C.; Russo, G.; Vitabile, S.; Gilardi, M.C.; Mauri, G. GTV cut for neuro-radiosurgery treatment planning: An MRI brain cancer seeded image segmentation method based on a cellular automata model. Nat. Comput. 2018, 17, 521–536. [Google Scholar] [CrossRef]
- Alanazi, M.F.; Ali, M.U.; Hussain, S.J.; Zafar, A.; Mohatram, M.; Irfan, M.; AlRuwaili, R.; Alruwaili, M.; Ali, N.H.; Albarrak, A.M. Brain tumor/mass classification framework using magnetic-resonance-imaging-based isolated and developed transfer deep-learning model. Sensors 2022, 22, 372. [Google Scholar] [CrossRef] [PubMed]
- Zahoor, M.M.; Qureshi, S.A.; Bibi, S.; Khan, S.H.; Khan, A.; Ghafoor, U.; Bhutta, M.R. A new deep hybrid boosted and ensemble learning-based brain tumor analysis using MRI. Sensors 2022, 22, 2726. [Google Scholar] [CrossRef] [PubMed]
- Ait Amou, M.; Xia, K.; Kamhi, S.; Mouhafid, M. A Novel MRI Diagnosis Method for Brain Tumor Classification Based on CNN and Bayesian Optimization. Healthcare 2022, 10, 494. [Google Scholar] [CrossRef] [PubMed]
- Kibriya, H.; Amin, R.; Alshehri, A.H.; Masood, M.; Alshamrani, S.S.; Alshehri, A. A novel and effective brain tumor classification model using deep feature fusion and famous machine learning classifiers. Comput. Intell. Neurosci. 2022, 2022, 7897669. [Google Scholar] [CrossRef] [PubMed]
- Poonguzhali, R.; Ahmad, S.; Sivasankar, P.T.; Babu, S.A.; Joshi, P.; Joshi, G.P.; Kim, S.W. Automated brain tumor diagnosis using deep residual u-net segmentation model. Comput. Mater. Contin. 2023, 74, 2179–2194. [Google Scholar]
- Rahman, T.; Islam, M.S. MRI brain tumor detection and classification using parallel deep convolutional neural networks. Meas. Sens. 2023, 26, 100694. [Google Scholar] [CrossRef]
- Malla, P.P.; Sahu, S.; Alutaibi, A.I. Classification of Tumor in Brain MR Images Using Deep Convolutional Neural Network and Global Average Pooling. Processes 2023, 11, 679. [Google Scholar] [CrossRef]
- Mahmud, M.I.; Mamun, M.; Abdelgawad, A. A deep analysis of brain tumor detection from mr images using deep learning networks. Algorithms 2023, 16, 176. [Google Scholar] [CrossRef]
- Woźniak, M.; Siłka, J.; Wieczorek, M. Deep neural network correlation learning mechanism for CT brain tumor detection. Neural Comput. Appl. 2023, 35, 14611–14626. [Google Scholar] [CrossRef]
- Reyes, D.; Sánchez, J. Performance of convolutional neural networks for the classification of brain tumors using magnetic resonance imaging. Heliyon 2024, 10, e25468. [Google Scholar] [CrossRef]
- Stadlbauer, A.; Marhold, F.; Oberndorfer, S.; Heinz, G.; Buchfelder, M.; Kinfe, T.M.; Meyer-Bäse, A. Radiophysiomics: Brain tumors classification by machine learning and physiological MRI data. Cancers 2022, 14, 2363. [Google Scholar] [CrossRef]
- Prastawa, M.; Bullitt, E.; Ho, S.; Gerig, G. A brain tumor segmentation framework based on outlier detection. Med. Image Anal. 2004, 8, 275–283. [Google Scholar] [CrossRef]
- Sobhaninia, Z.; Rezaei, S.; Noroozi, A.; Ahmadi, M.; Zarrabi, H.; Karimi, N.; Emami, A.; Samavi, S. Brain tumor segmentation using deep learning by type specific sorting of images. arXiv 2018, arXiv:1809.07786. [Google Scholar]
- Mzoughi, H.; Njeh, I.; Wali, A.; Slima, M.B.; BenHamida, A.; Mhiri, C.; Mahfoudhe, K.B. Deep multi-scale 3D convolutional neural network (CNN) for MRI gliomas brain tumor classification. J. Digit. Imaging 2020, 33, 903–915. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.L.; Kakarla, J.; Isunuri, B.V.; Singh, M. Multi-class brain tumor classification using residual network and global average pooling. Multimed. Tools Appl. 2021, 80, 13429–13438. [Google Scholar] [CrossRef]
- Obeidavi, M.R.; Maghooli, K. Tumor Detection in Brain MRI using Residual Convolutional Neural Networks. In Proceedings of the 2022 International Conference on Machine Vision and Image Processing (MVIP), Ahvaz, Iran, 23–24 February 2022; IEEE: Piscataway, NJ, USA; pp. 1–5. [Google Scholar]
- Khalil, H.A.; Darwish, S.; Ibrahim, Y.M.; Hassan, O.F. 3D-MRI brain tumor detection model using modified version of level set segmentation based on dragonfly algorithm. Symmetry 2020, 12, 1256. [Google Scholar] [CrossRef]
- Sajid, S.; Hussain, S.; Sarwar, A. Brain tumor detection and segmentation in MR images using deep learning. Arab. J. Sci. Eng. 2019, 44, 9249–9261. [Google Scholar] [CrossRef]
- Kumar, D.; Verma, H.; Mehra, A.; Agrawal, R.K. A modified intuitionistic fuzzy c-means clustering approach to segment human brain MRI image. Multimed. Tools Appl. 2019, 78, 12663–12687. [Google Scholar] [CrossRef]
- Wei, D.; Wang, Z.; Si, L.; Tan, C.; Lu, X. An image segmentation method based on a modified local-information weighted intui-tionistic Fuzzy C-means clustering and Gold-panning Algorithm. Eng. Appl. Artif. Intell. 2021, 101, 104209. [Google Scholar] [CrossRef]
- Vilar, C.; Krug, S.; O’Nils, M. Realworld 3d object recognition using a 3d extension of the hog descriptor and a depth camera. Sensors 2021, 21, 910. [Google Scholar] [CrossRef] [PubMed]
- Tandel, G.S.; Tiwari, A.; Kakde, O.G. Performance enhancement of MRI-based brain tumor classification using suitable segmen-tation method and deep learning-based ensemble algorithm. Biomed. Signal Process. Control 2022, 78, 104018. [Google Scholar] [CrossRef]
- Ding, S.; Xu, X.; Nie, R. Extreme learning machine and its applications. Neural Comput. Appl. 2014, 25, 549–556. [Google Scholar] [CrossRef]



| Class | Fig Share | Kaggle |
|---|---|---|
| meningioma | 708 | 306 |
| Pituitary | 930 | 300 |
| Glioma | 1426 | 300 |
| No tumour | - | 405 |
| Feature | Definition | Equation |
|---|---|---|
| Standard deviation (SD) | Determines the spread of data | |
| Skewness | Finds the symmetry of the possibility distribution | |
| Energy | Determines the spread of pixel values | |
| Entropy | Find the data needed to code the data | − |
| Kurtosis | Determines the probability distribution | |
| Contrast | Determines local fluctuations | |
| Correlation | Determines the joint probability | |
| Energy | Determine the sum of the squared pixel values | |
| Homogeneity | Determines local uniformity | |
| Busyness | Determines changes in the neighbouring pixels | |
| Strength | Determines the primitives of the brain image |
| Classifier | Accuracy | Precision | Recall | Class |
|---|---|---|---|---|
| Proposed | 98.56 | 99.14 | 99.25 | No Tumor |
| 98.24 | 98.66 | 99.19 | Glioma | |
| 98.50 | 99.14 | 99.10 | Meningioma | |
| 98.56 | 97.43 | 97.43 | Pituitary | |
| Alanazi et al. [55] (2022) | 97.86 | 98.49 | 98.33 | No Tumor |
| 97.31 | 98.17 | 99.14 | Glioma | |
| 97.59 | 97.33 | 98.64 | Meningioma | |
| 97.45 | 98.51 | 99.15 | Pituitary | |
| Zahoor et al. [56] (2022) | 98.31 | 97.22 | 89.74 | No Tumor |
| 97.86 | 98.49 | 98.30 | Glioma | |
| 97.09 | 98.62 | 99.16 | Meningioma | |
| 98.09 | 94.59 | 94.59 | Pituitary | |
| Ait Amou et al. et al. [57] (2022) | 94.57 | 98.00 | 98.50 | No Tumor |
| 95.85 | 92.10 | 89.74 | Glioma | |
| 95.45 | 98.24 | 94.91 | Meningioma | |
| 96.76 | 98.61 | 98.89 | Pituitary | |
| Kirbayi et al. [58] (2022) | 94.89 | 95.90 | 94.59 | No Tumor |
| 95.04 | 97.51 | 98.98 | Glioma | |
| 94.89 | 91.89 | 87.17 | Meningioma | |
| 97.17 | 96.49 | 93.22 | Pituitary | |
| Poonguzhali et al. [59] (2023) | 93.53 | 97.45 | 91.42 | Pituitary |
| 92.45 | 95.35 | 90.35 | No Tumor | |
| 95.35 | 88.45 | 96.56 | Glioma | |
| 95.45 | 90.35 | 97.45 | Meningioma | |
| Rahman et al. [60] (2023) | 97.34 | 98.02 | 95.67 | Pituitary |
| 97.57 | 98.11 | 95.78 | No Tumor | |
| 97.56 | 97.13 | 96.84 | Glioma | |
| 97.37 | 97.24 | 97.47 | Meningioma | |
| Malla et al. [61] (2023) | 98.35 | 97.36 | 97.25 | Pituitary |
| 98.64 | 97.46 | 97.19 | No Tumor | |
| 98.50 | 98.14 | 99.01 | Glioma | |
| 98.36 | 97.43 | 97.43 | Meningioma |
| Classifier | Accuracy | Precision | Recall | Class |
|---|---|---|---|---|
| Proposed | 99.37 | 99.84 | 99.57 | No Tumor |
| 99.24 | 99.74 | 99.85 | Glioma | |
| 99.50 | 99.85 | 99.84 | Meningioma | |
| 99.56 | 99.57 | 97.85 | Pituitary | |
| Saeedi S et al. [41] | 96.46 | 97.57 | 98.54 | No Tumor |
| 96.75 | 97.14 | 98.36 | Glioma | |
| 96.84 | 97.47 | 98.27 | Meningioma | |
| 96.85 | 97.78 | 98.73 | Pituitary | |
| Kalam R et al. [42] | 97.35 | 98.46 | 98.68 | No Tumor |
| 97.15 | 98.73 | 98.74 | Glioma | |
| 97.36 | 98.27 | 98.37 | Meningioma | |
| 97.37 | 98.21 | 98.62 | Pituitary | |
| Mahmud MI et al. [62] | 93.53 | 94.36 | 95.63 | No Tumor |
| 93.14 | 94.62 | 95.63 | Glioma | |
| 93.62 | 94.52 | 94.63 | Meningioma | |
| 93.52 | 94.26 | 95.62 | Pituitary | |
| Woźniak M et al. [63] | 96.46 | 95.45 | 95.46 | No Tumor |
| 96.46 | 95.63 | 95.74 | Glioma | |
| 96.73 | 95.36 | 95.47 | Meningioma | |
| 96.13 | 95.63 | 95.37 | Pituitary | |
| Reyes D et al. [64] | 97.03 | 98.17 | 98.67 | No Tumor |
| 97.19 | 98.31 | 98.91 | Glioma | |
| 97.25 | 98.25 | 98.89 | Meningioma | |
| 97.26 | 98.37 | 98.59 | Pituitary |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhimavarapu, U.; Chintalapudi, N.; Battineni, G. Brain Tumor Detection and Categorization with Segmentation of Improved Unsupervised Clustering Approach and Machine Learning Classifier. Bioengineering 2024, 11, 266. https://doi.org/10.3390/bioengineering11030266
Bhimavarapu U, Chintalapudi N, Battineni G. Brain Tumor Detection and Categorization with Segmentation of Improved Unsupervised Clustering Approach and Machine Learning Classifier. Bioengineering. 2024; 11(3):266. https://doi.org/10.3390/bioengineering11030266
Chicago/Turabian StyleBhimavarapu, Usharani, Nalini Chintalapudi, and Gopi Battineni. 2024. "Brain Tumor Detection and Categorization with Segmentation of Improved Unsupervised Clustering Approach and Machine Learning Classifier" Bioengineering 11, no. 3: 266. https://doi.org/10.3390/bioengineering11030266
APA StyleBhimavarapu, U., Chintalapudi, N., & Battineni, G. (2024). Brain Tumor Detection and Categorization with Segmentation of Improved Unsupervised Clustering Approach and Machine Learning Classifier. Bioengineering, 11(3), 266. https://doi.org/10.3390/bioengineering11030266








