Reliable Off-Resonance Correction in High-Field Cardiac MRI Using Autonomous Cardiac B0 Segmentation with Dual-Modality Deep Neural Networks
Abstract
1. Introduction
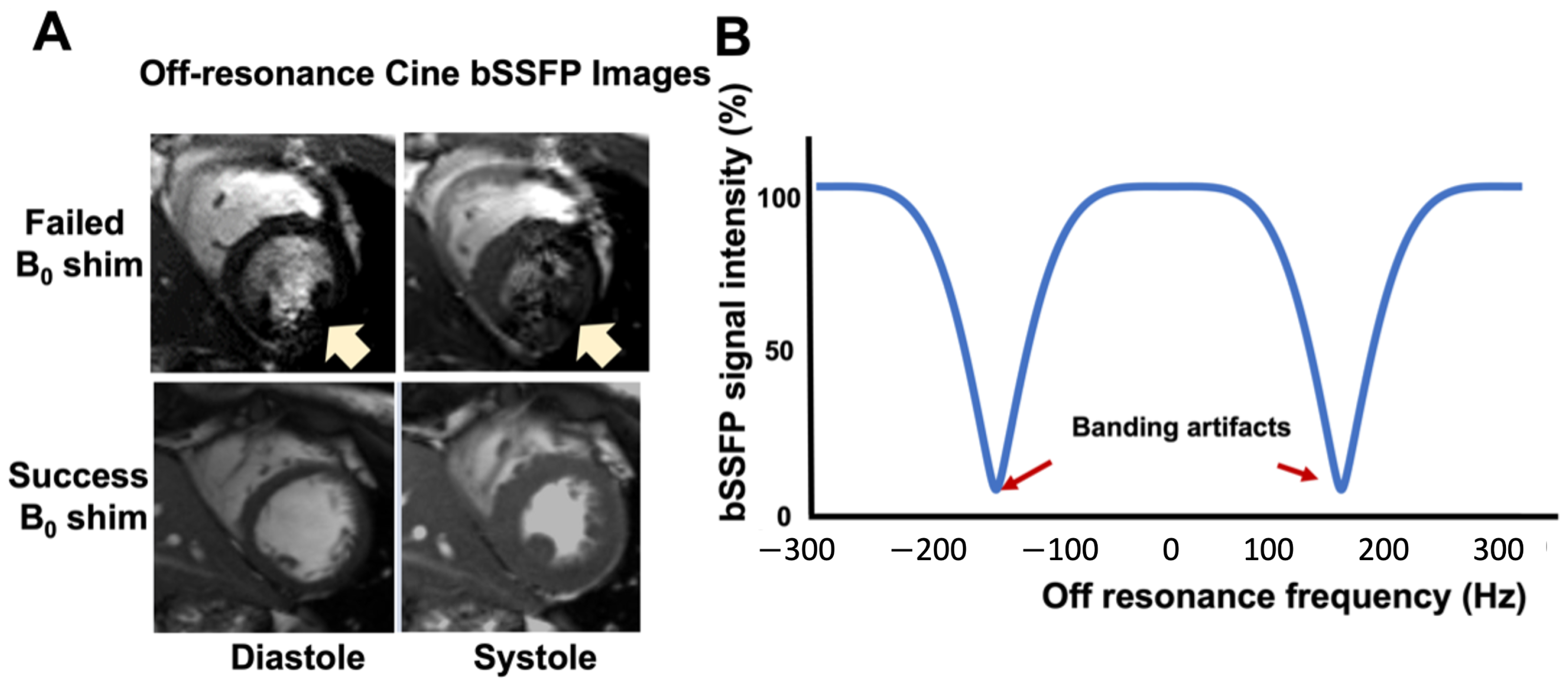
1.1. Inhomogeneity Effect on 3.0T CMR
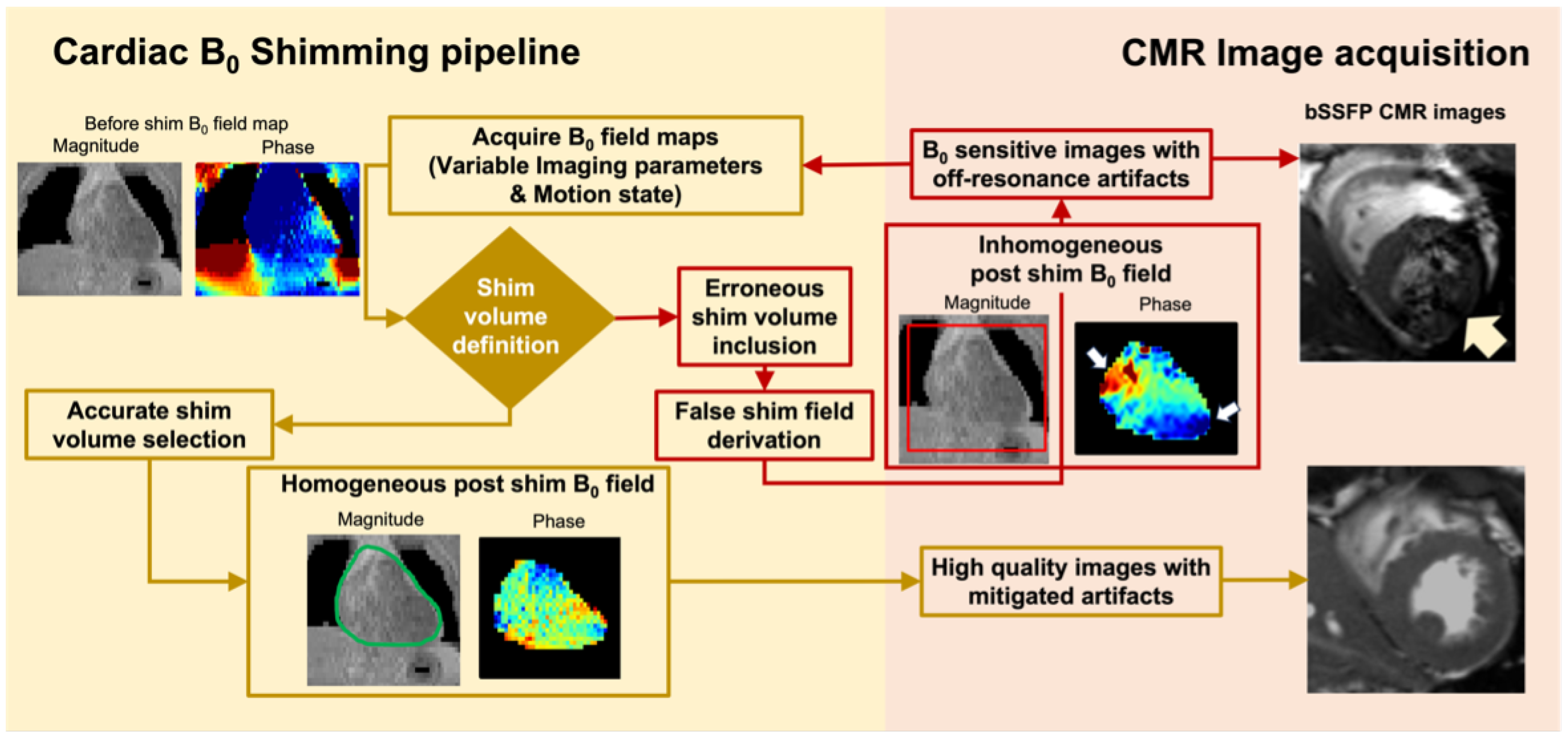
1.2. Cardiac Shimming to Improve Image Quality of High-Field CMR
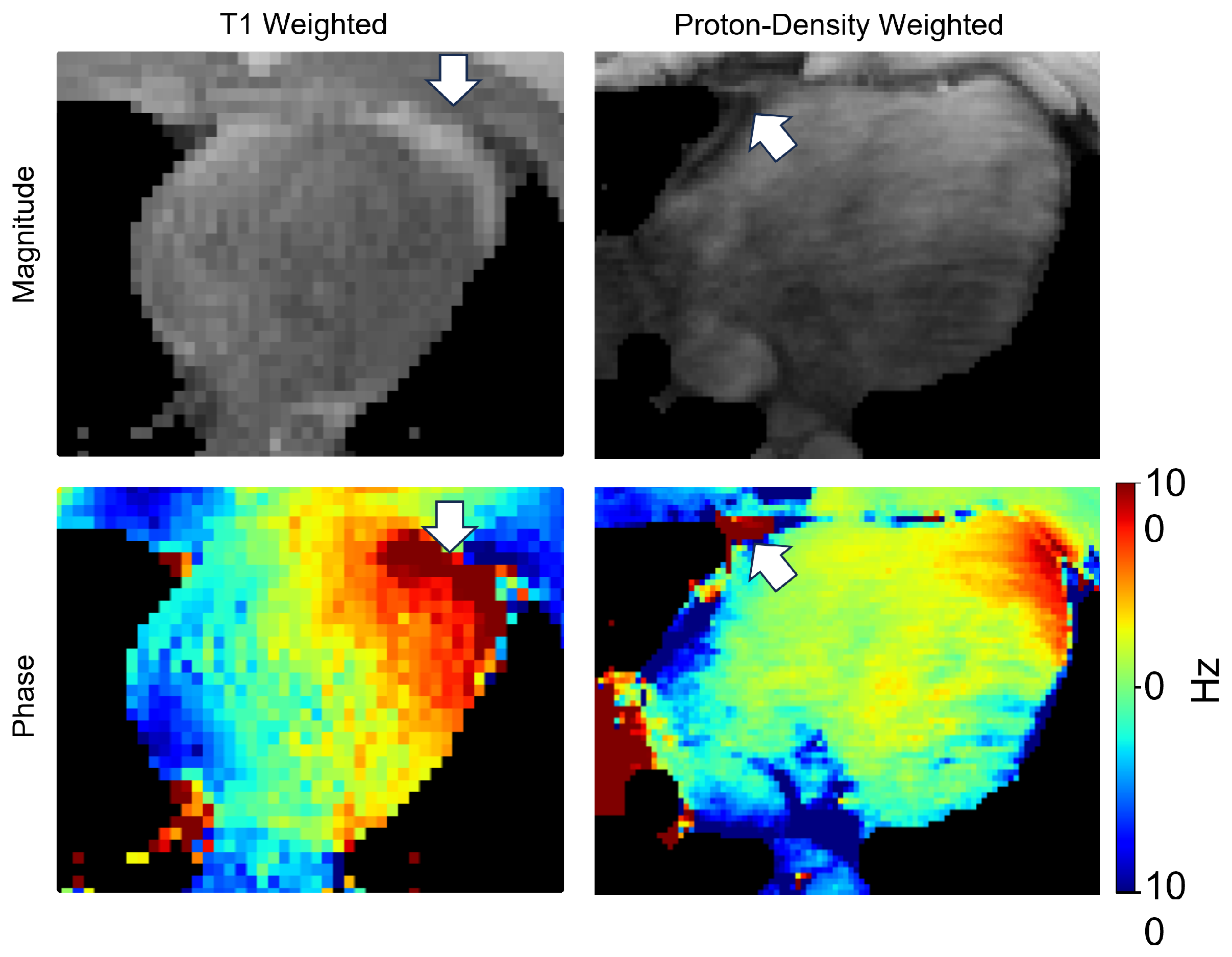
1.3. State-of-the-Art CMR Segmentation Models Are Not Optimized for Field Maps
- We developed a dual-channel CNN model to improve cardiac segmentation for shimming in high-field CMR by combining magnitude and phase images.
- We thoroughly evaluated the performance of the proposed model under different imaging parameters and compared it with state-of-the-art medical image segmentation techniques. Besides, we demonstrated the generalizability of dual-channel module on different existing models to improve the performance.
- We further demonstrated the application of this dual-channel segmentation model in providing the foundation of high-quality shimming in the heart.
2. Methodology
2.1. Image Preprocessing
- (1)
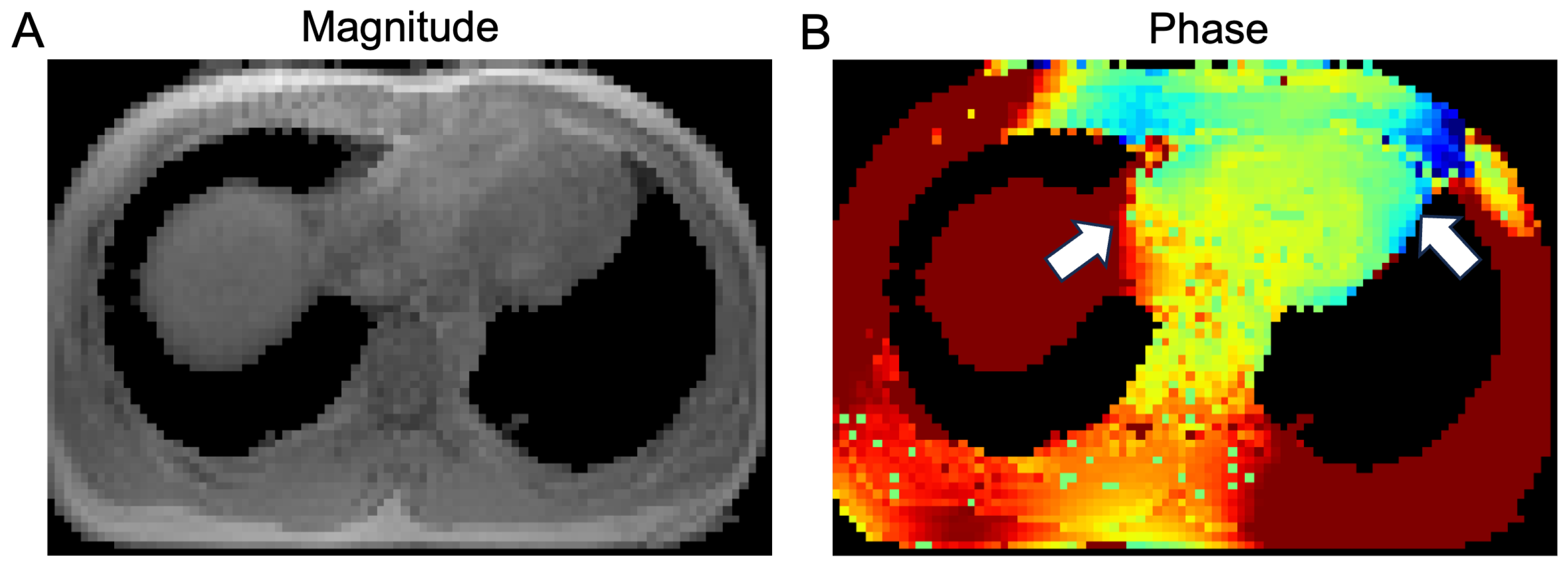
- Background removal: The raw data contained some redundant air introduced during the image acquisition and reconstruction. As a first step, Otsu’s method [44] was derived from the magnitude maps with number of threshold values equal to 2. The rough mask was generated based on the threshold level and followed by a post-processed operation using morphological closing. The structuring element was a disk-shape one defined by the resolution of the image.and applied to both the magnitude and phase map. It helped effectively segregate the region of interest from extraneous air.
- (2)
- Resolution and FOV Alignment: The voxel spacing within our acquired data was heterogeneous. The large spacing might cause the loss of detailed information, while the small spacing requires a larger computational budget. To reconcile this, we established a target voxel spacing based on the median spacing observed across all subjects for each axis. Given the anisotropic nature of our dataset, we resampled all images to the uniform target voxel spacing using third-order spline interpolation. Subsequently, images were either cropped or padded to match the dimension at the center region, if necessary.
- (3)
- Noise Standardization: All images were normalized based on mean and standard deviation values per case. The normalization step ensured all data conformed to a consistent scale and distribution.
- (4)
- Dataset split: The T1-w data set, including 54 subjects, was randomly partitioned into a training set (comprising 40 volumes) and a test set (comprising 14 volumes). Additionally, 10 PD-w volumes from subjects not included in the training set were reserved for an independent test set to validate the model’s generalizability across varied imaging protocols.
2.2. Model Architecture
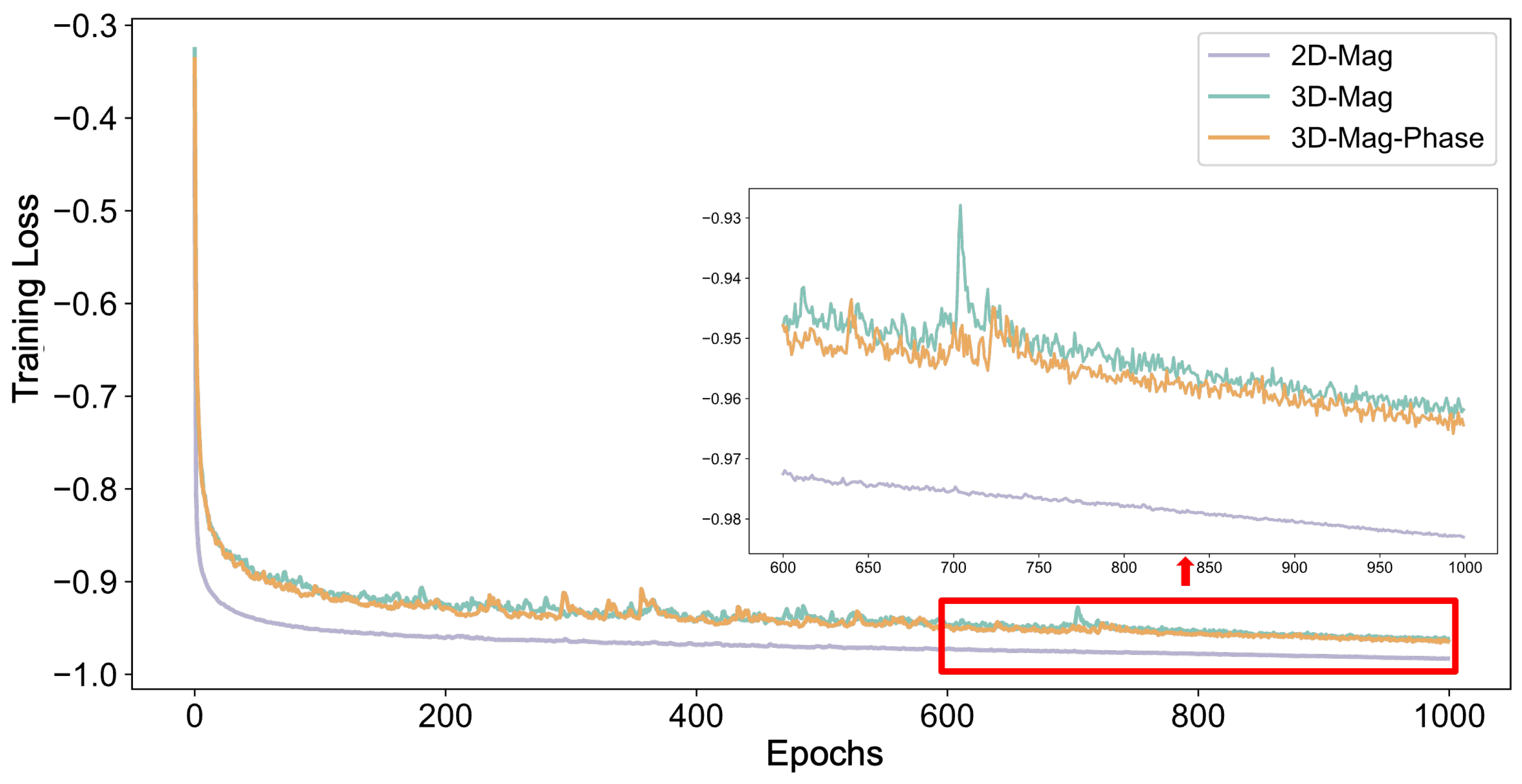
2.3. Training Strategy
2.4. Data Augmentation
2.5. Evaluation Metrics
2.6. Statistical Analysis
3. Results
3.1. Datasets
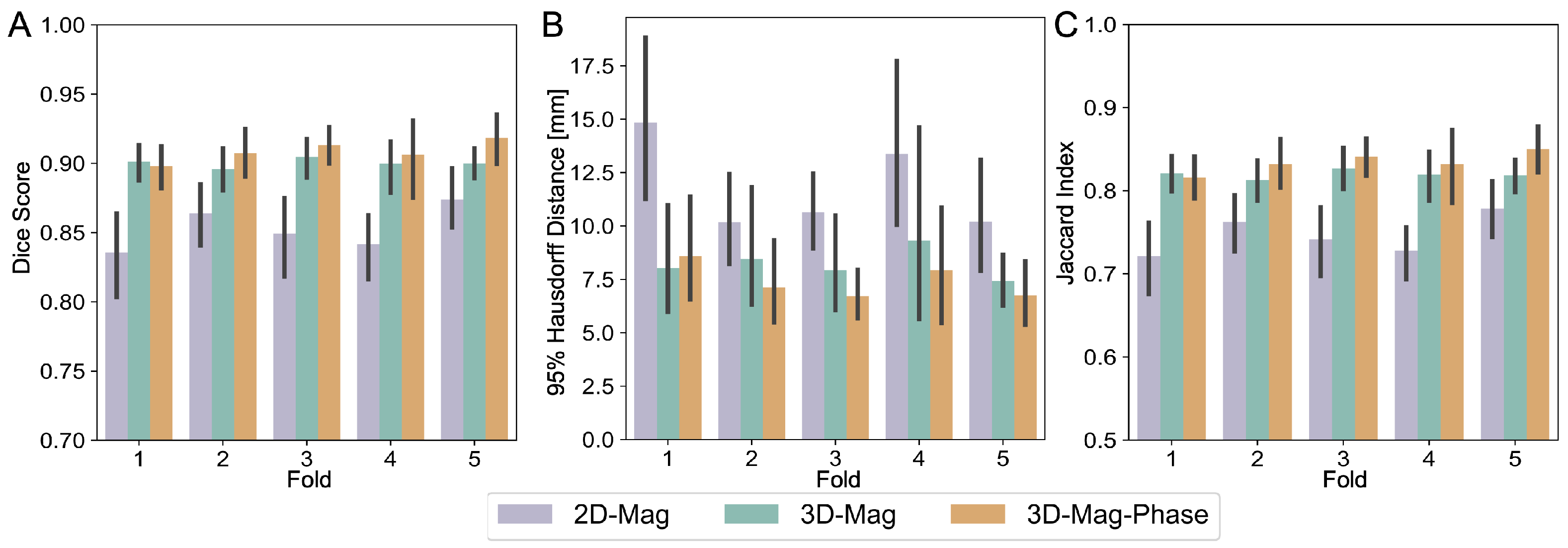
3.2. Model Performance
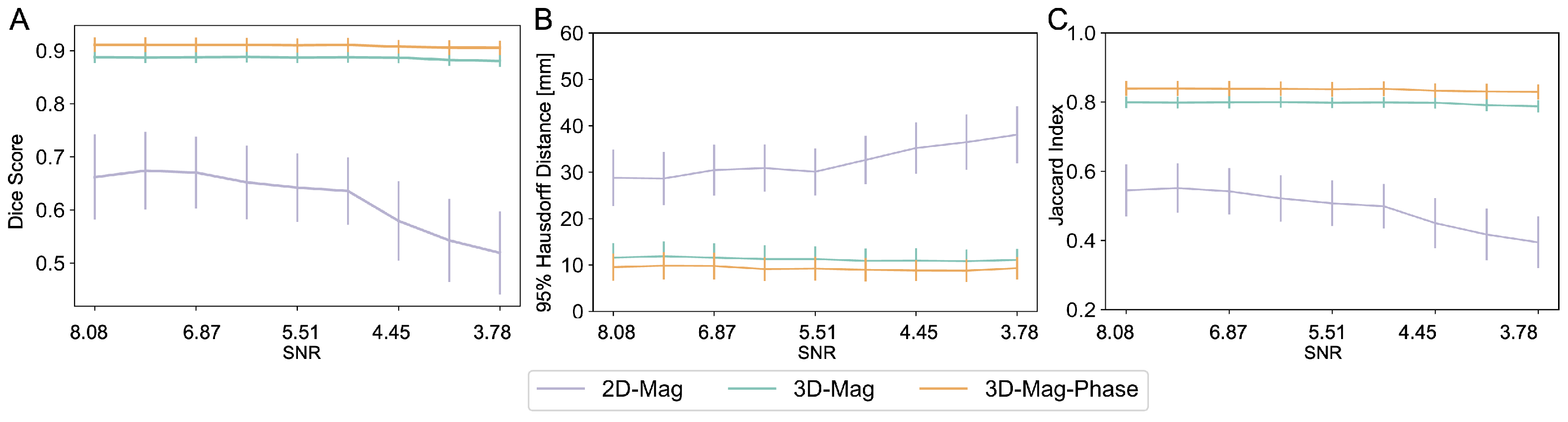
3.3. Generalizability Analysis
3.3.1. SNR Variations
3.3.2. Imaging Protocol Variations
3.3.3. Comparisions between Model Architectures
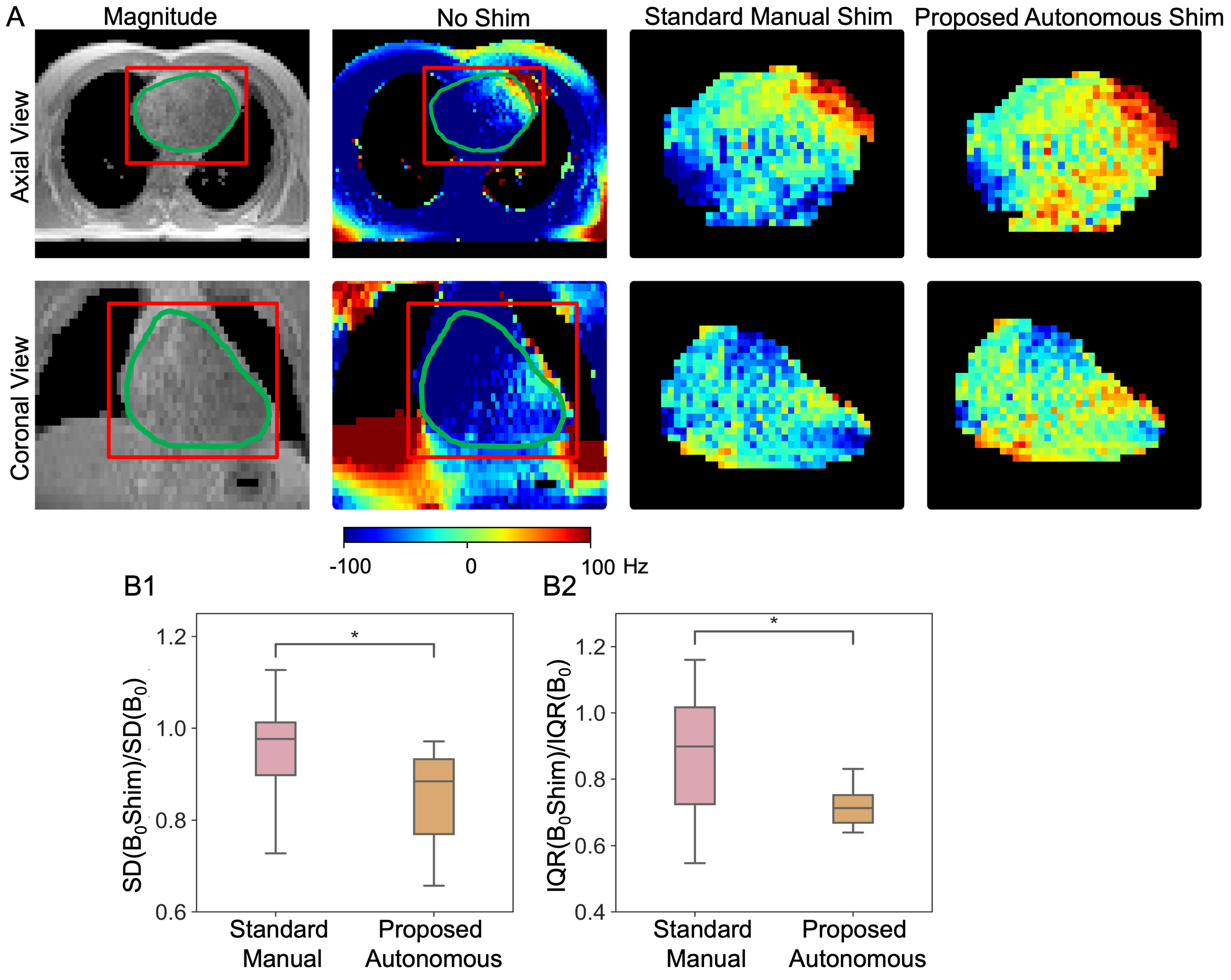
3.3.4. Cardiac Shimming Experiments and Performance Comparison
3.3.5. Ablation Study
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MRI | Magnetic Resonance Imaging |
| CMR | Cardiac Magnetic Resonance Imaging |
| LGE | Late gadolinium enhancement |
| CEST | Chemical Exchange Saturation Transfer |
| SNR | Signal-to-Noise Ratio |
| SSFP | Steady-state Free Precession |
| EPI | Echo-Planar Imaging |
| CNN | Convolutional Neural Network |
| FOV | Field of View |
| ReLU | Rectified Linear Unit |
| HD | Hausdorff Distance |
| PDw | Proton density-weighted |
References
- Rajiah, P.S.; François, C.J.; Leiner, T. Cardiac MRI: State of the Art. Radiology 2023, 307, e223008. [Google Scholar] [CrossRef]
- Kali, A.; Tang, R.L.Q.; Kumar, A.; Min, J.K.; Dharmakumar, R. Detection of Acute Reperfusion Myocardial Hemorrhage with Cardiac MR Imaging: T2 versus T2*. Radiology 2013, 269, 387–395. [Google Scholar] [CrossRef]
- Jenista, E.R.; Wendell, D.C.; Azevedo, C.F.; Klem, I.; Judd, R.M.; Kim, R.J.; Kim, H.W. Revisiting how we perform late gadolinium enhancement CMR: Insights gleaned over 25 years of clinical practice. J. Cardiovasc. Magn. Reson. 2023, 25, 18. [Google Scholar] [CrossRef]
- Yang, H.J.; Dey, D.; Sykes, J.; Butler, J.; Biernaski, H.; Kovacs, M.; Bi, X.; Sharif, B.; Cokic, I.; Tang, R.; et al. Heart Rate-Independent 3D Myocardial Blood Oxygen Level-Dependent MRI at 3.0 T with Simultaneous 13N-Ammonia PET Validation. Radiology 2020, 295, 82–93. [Google Scholar] [CrossRef]
- Kali, A.; Choi, E.Y.; Sharif, B.; Kim, Y.J.; Bi, X.; Spottiswoode, B.; Cokic, I.; Yang, H.J.; Tighiouart, M.; Conte, A.H.; et al. Native T1 Mapping by 3-T CMR Imaging for Characterization of Chronic Myocardial Infarctions. JACC Cardiovasc. Imaging 2015, 8, 1019–1030. [Google Scholar] [CrossRef]
- Carr, J.C.; Simonetti, O.; Bundy, J.; Li, D.; Pereles, S.; Finn, J.P. Cine MR angiography of the heart with segmented true fast imaging with steady-state precession. Radiology 2001, 219, 828–834. [Google Scholar] [CrossRef]
- Haaf, P.; Garg, P.; Messroghli, D.R.; Broadbent, D.A.; Greenwood, J.P.; Plein, S. Cardiac T1 Mapping and Extracellular Volume (ECV) in clinical practice: A comprehensive review. J. Cardiovasc. Magn. Reson. 2016, 18, 89. [Google Scholar] [CrossRef]
- Nojiri, A.; Hongo, K.; Kawai, M.; Komukai, K.; Sakuma, T.; Taniguchi, I.; Yoshimura, M. Scoring of late gadolinium enhancement in cardiac magnetic resonance imaging can predict cardiac events in patients with hypertrophic cardiomyopathy. J. Cardiol. 2011, 58, 253–260. [Google Scholar] [CrossRef]
- Eitel, I.; Friedrich, M.G. T2-weighted cardiovascular magnetic resonance in acute cardiac disease. J. Cardiovasc. Magn. Reson. 2011, 13, 13. [Google Scholar] [CrossRef]
- Triadyaksa, P.; Oudkerk, M.; Sijens, P.E. Cardiac T2* mapping: Techniques and clinical applications. J. Magn. Reson. Imaging 2020, 52, 1340–1351. [Google Scholar] [CrossRef]
- Oshinski, J.N.; Delfino, J.G.; Sharma, P.; Gharib, A.M.; Pettigrew, R.I. Cardiovascular magnetic resonance at 3.0 T: Current state of the art. J. Cardiovasc. Magn. Reson. 2010, 12, 1–13. [Google Scholar] [CrossRef]
- Bottomley, P.A.; Foster, T.H.; Argersinger, R.E.; Pfeifer, L.M. A review of normal tissue hydrogen NMR relaxation times and relaxation mechanisms from 1–100 MHz: Dependence on tissue type, NMR frequency, temperature, species, excision, and age. Med. Phys. 1984, 11, 425–448. [Google Scholar] [CrossRef]
- Edelstein, W.; Glover, G.; Hardy, C.; Redington, R. The intrinsic signal-to-noise ratio in NMR imaging. Magn. Reson. Med. 1986, 3, 604–618. [Google Scholar] [CrossRef]
- Sharma, P.; Socolow, J.; Patel, S.; Pettigrew, R.I.; Oshinski, J.N. Effect of Gd-DTPA-BMA on blood and myocardial T1 at 1.5 T and 3T in humans. J. Magn. Reson. Imaging Off. J. Int. Soc. Magn. Reson. Med. 2006, 23, 323–330. [Google Scholar] [CrossRef]
- Zhou, Z.; Nguyen, C.; Chen, Y.; Shaw, J.L.; Deng, Z.; Xie, Y.; Dawkins, J.; Marbán, E.; Li, D. Optimized CEST cardiovascular magnetic resonance for assessment of metabolic activity in the heart. J. Cardiovasc. Magn. Reson. 2017, 19, 1–7. [Google Scholar] [CrossRef]
- Wen, Y.; Nguyen, T.D.; Liu, Z.; Spincemaille, P.; Zhou, D.; Dimov, A.; Kee, Y.; Deh, K.; Kim, J.; Weinsaft, J.W.; et al. Cardiac quantitative susceptibility mapping (QSM) for heart chamber oxygenation. Magn. Reson. Med. 2018, 79, 1545–1552. [Google Scholar] [CrossRef]
- Noeske, R.; Seifert, F.; Rhein, K.H.; Rinneberg, H. Human cardiac imaging at 3 T using phased array coils. Magn. Reson. Med. Off. J. Int. Soc. Magn. Reson. Med. 2000, 44, 978–982. [Google Scholar]
- Reeder, S.B.; Faranesh, A.Z.; Boxerman, J.L.; McVeigh, E.R. In vivo measurement of T* 2 and field inhomogeneity maps in the human heart at 1.5 T. Magn. Reson. Med. 1998, 39, 988–998. [Google Scholar] [CrossRef]
- Hock, M.; Terekhov, M.; Stefanescu, M.R.; Lohr, D.; Herz, S.; Reiter, T.; Ankenbrand, M.; Kosmala, A.; Gassenmaier, T.; Juchem, C.; et al. B0 shimming of the human heart at 7T. Magn. Reson. Med. 2021, 85, 182–196. [Google Scholar] [CrossRef]
- Deux, J.F.; Maatouk, M.; Vignaud, A.; Luciani, A.; Lenczner, G.; Mayer, J.; Lim, P.; Dubois-Randé, J.L.; Kobeiter, H.; Rahmouni, A. Diffusion-weighted echo planar imaging in patients with recent myocardial infarction. Eur. Radiol. 2011, 21, 46–53. [Google Scholar] [CrossRef]
- Nezafat, M.; Henningsson, M.; Ripley, D.P.; Dedieu, N.; Greil, G.; Greenwood, J.P.; Börnert, P.; Plein, S.; Botnar, R.M. Coronary MR angiography at 3T: Fat suppression versus water-fat separation. Magn. Reson. Mater. Phys. Biol. Med. 2016, 29, 733–738. [Google Scholar] [CrossRef]
- Sengupta, S.; Welch, E.B.; Zhao, Y.; Foxall, D.; Starewicz, P.; Anderson, A.W.; Gore, J.C.; Avison, M.J. Dynamic B0 shimming at 7 T. Magn. Reson. Imaging 2011, 29, 483–496. [Google Scholar] [CrossRef]
- Schwerter, M.; Hetherington, H.; Moon, C.H.; Pan, J.; Felder, J.; Tellmann, L.; Shah, N.J. Interslice current change constrained B0 shim optimization for accurate high-order dynamic shim updating with strongly reduced eddy currents. Magn. Reson. Med. 2019, 82, 263–275. [Google Scholar] [CrossRef]
- Han, H.; Song, A.W.; Truong, T. Integrated parallel reception, excitation, and shimming (iPRES). Magn. Reson. Med. 2013, 70, 241–247. [Google Scholar] [CrossRef]
- Hsin-Jung, Y.; John, S.; Linda, A.; Waishing, L.; Meng, L.; Yuheng, H.; Yoosefian, G.; Skyler, S.; Richard, H.; Yujie, S.; et al. Whole Heart High-Order B0 Shimming at 3T Using a UNIfied Coil (UNIC) for RF receive and shimming. In Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM), Sydney, Australia, 8–14 August 2020; Volume 2183. [Google Scholar]
- Lee, J.; Lustig, M.; Kim, D.; Pauly, J.M. Improved shim method based on the minimization of the maximum off-resonance frequency for balanced steady-state free precession (bSSFP). Magn. Reson. Med. 2009, 61, 1500–1506. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Guan, X.; Zhang, X.; Yoosefian , G.; Bi, X.; Han, F.; Lee, H.; Christodoulou, A.; Li, D.; et al. Correcting motion induced B0 shim failure at 3T CMR using a deep learning-enabled 3D motion-resolved B0 shimming. In Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM), Toronto, ON, Canada, 3–8 June 2023; Volume 4977. [Google Scholar]
- Huang, Y.; Guan, X.; Zhang, X.; Tang, L.; Yoosefian, G.; Bi, X.; Han, F.; Lee, H.; Han, H.; Christodoulou, A.; et al. The Effect of Respiratory and Cardiac Motion States on B0 Shimming at 3T. In Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM), Toronto, ON, Canada, 3–8 June 2023; Volume 1150. [Google Scholar]
- Osuna-Enciso, V.; Cuevas, E.; Sossa, H. A comparison of nature inspired algorithms for multi-threshold image segmentation. Expert Syst. Appl. 2013, 40, 1213–1219. [Google Scholar] [CrossRef]
- Pohle, R.; Toennies, K.D. Segmentation of medical images using adaptive region growing. In Proceedings of the Medical Imaging 2001: Image Processing, San Diego, CA, USA, 17–22 February 2001; Volume 4322, pp. 1337–1346. [Google Scholar]
- Freedman, D.; Zhang, T. Interactive graph cut based segmentation with shape priors. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–26 June 2005; Volume 1, pp. 755–762. [Google Scholar]
- Hatamizadeh, A.; Nath, V.; Tang, Y.; Yang, D.; Roth, H.R.; Xu, D. Swin UNETR: Swin Transformers for Semantic Segmentation of Brain Tumors in MRI Images. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Springer International Publishing: Cham, Switzerland, 2022; pp. 272–284. [Google Scholar] [CrossRef]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]
- Tang, Y.; Yang, D.; Li, W.; Roth, H.R.; Landman, B.; Xu, D.; Nath, V.; Hatamizadeh, A. Self-Supervised Pre-Training of Swin Transformers for 3D Medical Image Analysis. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: Proceedings of the 18th International Conference, Munich, Germany, 5–9 October 2015, Proceedings, Part III 18; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar] [CrossRef]
- Li, X.; Huang, Y.; Yoosefian, G.; Hui, H.; Yang, H.-J. Autonomous cardiac field map segmentation for B0 shimming pipeline using a dual-modality Deep-learning model. In Proceedings of the 26th Annual Scientific Sessions of the Society for Cardiovascular Magnetic Resonance (SCMR), San Diego, CA, USA, 25–28 January 2023. [Google Scholar]
- Wang, H.; Cao, P.; Wang, J.; Zaiane, O.R. UCTransNet: Rethinking the Skip Connections in U-Net from a Channel-Wise Perspective with Transformer. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 22 February–1 March 2022; Volume 36, pp. 2441–2449. [Google Scholar] [CrossRef]
- Çiçek; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016: Proceedings of the 19th International Conference, Athens, Greece, 17–21 October 2016, Proceedings, Part II 19; Springer International Publishing: Cham, Switzerland, 2016; pp. 424–432. [Google Scholar] [CrossRef]
- Yu, L.; Cheng, J.Z.; Dou, Q.; Yang, X.; Chen, H.; Qin, J.; Heng, P.A. Automatic 3D Cardiovascular MR Segmentation with Densely-Connected Volumetric ConvNets. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2017: Proceedings of the 20th International Conference, Quebec City, QC, Canada, 11–13 September 2017, Proceedings, Part II 20; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2017; pp. 287–295. [Google Scholar] [CrossRef]
- Li, P.; Wu, W.; Liu, L.; Michael Serry, F.; Wang, J.; Han, H. Automatic brain tumor segmentation from Multiparametric MRI based on cascaded 3D U-Net and 3D U-Net++. Biomed. Signal Process. Control 2022, 78, 103979. [Google Scholar] [CrossRef]
- Chen, T.; Wang, C.; Shan, H. BerDiff: Conditional Bernoulli Diffusion Model for Medical Image Segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI, Vancouver, BC, Canada, 8–12 October 2023; Greenspan, H., Madabhushi, A., Mousavi, P., Salcudean, S., Duncan, J., Syeda-Mahmood, T., Taylor, R., Eds.; Springer: Cham, Switzerland, 2023; pp. 491–501. [Google Scholar]
- Fan, C.; Su, Q.; Xiao, Z.; Su, H.; Hou, A.; Luan, B. ViT-FRD: A Vision Transformer Model for Cardiac MRI Image Segmentation Based on Feature Recombination Distillation. IEEE Access 2023, 11, 129763–129772. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man, Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Schulz-Menger, J.; Bluemke, D.A.; Bremerich, J.; Flamm, S.D.; Fogel, M.A.; Friedrich, M.G.; Kim, R.J.; von Knobelsdorff-Brenkenhoff, F.; Kramer, C.M.; Pennell, D.J.; et al. Standardized image interpretation and post-processing in cardiovascular magnetic resonance—2020 update. J. Cardiovasc. Magn. Reson. 2020, 22, 19. [Google Scholar] [CrossRef]
- Kandel, I.; Castelli, M. The effect of batch size on the generalizability of the convolutional neural networks on a histopathology dataset. ICT Express 2020, 6, 312–315. [Google Scholar] [CrossRef]
- Pérez-García, F.; Sparks, R.; Ourselin, S. TorchIO: A Python library for efficient loading, preprocessing, augmentation and patch-based sampling of medical images in deep learning. Comput. Methods Programs Biomed. 2021, 208, 106236. [Google Scholar] [CrossRef]
- Touvron, H.; Vedaldi, A.; Douze, M.; Jegou, H. Fixing the Train-Test Resolution Discrepancy. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Mohan, G.; Subashini, M.M. Chapter 4—Medical Imaging With Intelligent Systems: A Review. In Deep Learning and Parallel Computing Environment for Bioengineering Systems; Sangaiah, A.K., Ed.; Academic Press: Cambridge, MA, USA, 2019; pp. 53–73. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and Statistical Modeling with Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010; Volume 57, pp. 10–25080. [Google Scholar]
- Cardoso, M.J.; Li, W.; Brown, R.; Ma, N.; Kerfoot, E.; Wang, Y.; Murray, B.; Myronenko, A.; Zhao, C.; Yang, D.; et al. MONAI: An open-source framework for deep learning in healthcare. arXiv 2022, arXiv:2211.02701. [Google Scholar]
- Wang, H.; Guo, S.; Ye, J.; Deng, Z.; Cheng, J.; Li, T.; Chen, J.; Su, Y.; Huang, Z.; Shen, Y.; et al. SAM-Med3D. arXiv 2023, arXiv:2310.15161v2. [Google Scholar]
- Wang, Z.; Bai, Y.; Zhou, Y.; Xie, C. Can CNNs Be More Robust Than Transformers? In Proceedings of the Eleventh International Conference on Learning Representations, Kigali, Rwanda, 1–5 May 2023. [Google Scholar]
- Edalati, M.; Zheng, Y.; Watkins, M.P.; Chen, J.; Liu, L.; Zhang, S.; Song, Y.; Soleymani, S.; Lenihan, D.J.; Lanza, G.M. Implementation and prospective clinical validation of AI-based planning and shimming techniques in cardiac MRI. Med. Phys. 2022, 49, 129–143. [Google Scholar] [CrossRef]
- Chavez, S.; Qing-San, X.; An, L. Understanding phase maps in MRI: A new cutline phase unwrapping method. IEEE Trans. Med. Imaging 2002, 21, 966–977. [Google Scholar] [CrossRef]
- Zhou, H.; Cheng, C.; Peng, H.; Liang, D.; Liu, X.; Zheng, H.; Zou, C. The PHU-NET: A robust phase unwrapping method for MRI based on deep learning. Magn. Reson. Med. 2021, 86, 3321–3333. [Google Scholar] [CrossRef]
- Siddique, N.; Paheding, S.; Elkin, C.P.; Devabhaktuni, V. U-Net and Its Variants for Medical Image Segmentation: A Review of Theory and Applications. IEEE Access 2021, 9, 82031–82057. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Xiao, H.; Li, L.; Liu, Q.; Zhu, X.; Zhang, Q. Transformers in medical image segmentation: A review. Biomed. Signal Process. Control 2023, 84, 104791. [Google Scholar] [CrossRef]
- Lu, Y.; Fu, J.; Li, X.; Zhou, W.; Liu, S.; Zhang, X.; Wu, W.; Jia, C.; Liu, Y.; Chen, Z. Rtn: Reinforced transformer network for coronary ct angiography vessel-level image quality assessment. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Singapore, 18–22 September 2022; Springer: Berlin, Germany, 2022; pp. 644–653. [Google Scholar]
- Tabatabaei, S.; Rezaee, K.; Zhu, M. Attention transformer mechanism and fusion-based deep learning architecture for MRI brain tumor classification system. Biomed. Signal Process. Control 2023, 86, 105119. [Google Scholar] [CrossRef]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jegou, H. Training data-efficient image transformers & distillation through attention. In Proceedings of the International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 10347–10357. [Google Scholar]
- Liu, Z.; Mao, H.; Wu, C.Y.; Feichtenhofer, C.; Darrell, T.; Xie, S. A ConvNet for the 2020s. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 11966–11976. [Google Scholar] [CrossRef]
- Chen, Q.; Luo, C.; Tie, C.; Cheng, C.; Zou, C.; Zhang, X.; Liu, X.; Zheng, H.; Li, Y. A 5-channel local B0 shimming coil combined with a 3-channel RF receiver coil for rat brain imaging at 3 T. Magn. Reson. Med. 2023, 89, 477–486. [Google Scholar] [CrossRef]
- Gao, Y.; Mareyam, A.; Sun, Y.; Witzel, T.; Arango, N.; Kuang, I.; White, J.; Roe, A.W.; Wald, L.; Stockmann, J.; et al. A 16-channel AC/DC array coil for anesthetized monkey whole-brain imaging at 7T. NeuroImage 2020, 207, 116396. [Google Scholar] [CrossRef]
- Juchem, C.; Nixon, T.W.; Mcintyre, S.; Boer, V.O.; Rothman, D.L.; De Graaf, R.A. Dynamic multi-coil shimming of the human brain at 7T. J. Magn. Reson. 2011, 212, 280–288. [Google Scholar] [CrossRef]



| Aspects | Before Augmentation | After Augmentation |
|---|---|---|
| Orientation | RAS | RAS, LAS |
| Resolution | 3.57 × 3.57 × 5.2 | 3.57 × 3.57 × 5.2 , 4.46 × 4.46 × 5.2 |
| Scaling | ×1 | ×1, ×2, ×3 |
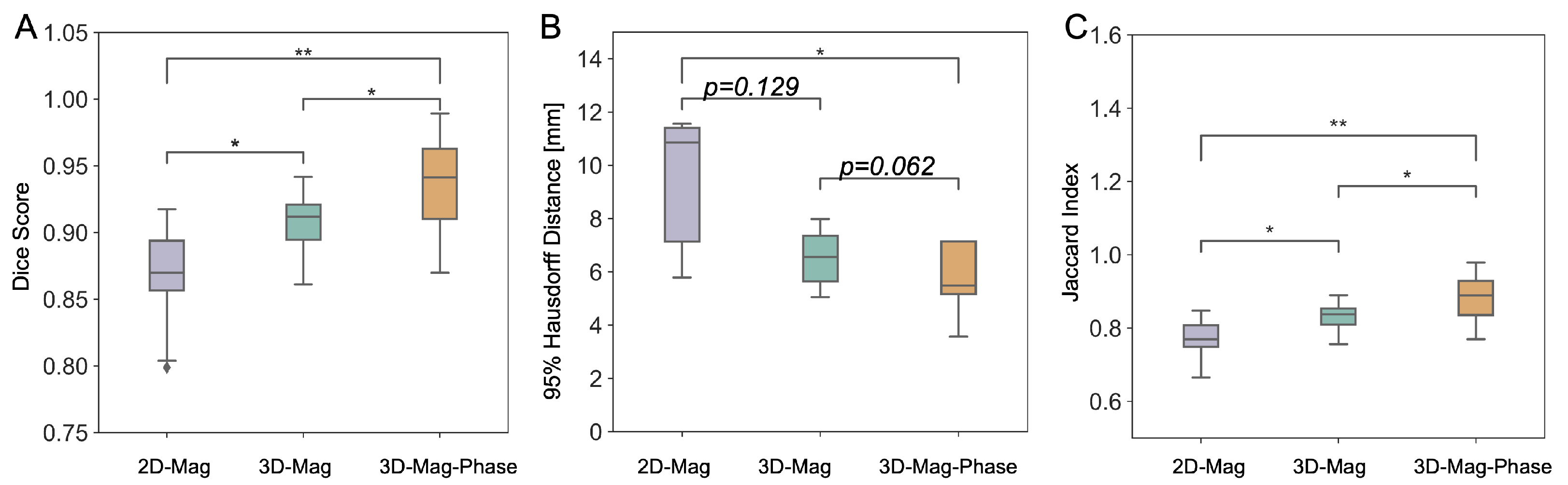
| Motion States | Model | Dice Score ↑ | 95%HD [mm] ↓ | Jaccard Index ↓ |
|---|---|---|---|---|
| End-Expiration | 2D-Mag | 0.85 ± 0.04 | 6.61 ±0.92 | 0.80 ± 0.06 |
| 3D-Mag | 0.89 ± 0.02 | 6.02 ±0.80 | 0.86 ± 0.03 | |
| 3D-Mag-Phase | 0.93± 0.02 | 5.78 ± 1.49 | 0.94 ± 0.03 | |
| End-Inspiration | 2D-Mag | 0.83 ± 0.11 | 7.82 ± 2.42 | 0.78 ± 0.13 |
| 3D-Mag | 0.89 ± 0.02 | 6.40 ± 1.08 | 0.86 ± 0.04 | |
| 3D-Mag-Phase | 0.93 ± 0.03 | 5.92 ± 1.84 | 0.93 ± 0.05 |
| Models | Magnitude Only | Magnitude-Phase |
|---|---|---|
| SAM-Med3D | 0.5814 (0.051) | - |
| U-Net | 0.7988 (0.064) | 0.8252 (0.049) |
| Swin UNETR | 0.8571 (0.045) | 0.8623 (0.044) |
| Ours (3D-mag-phase-net) * | 0.9065 (0.023) | 0.9379 (0.038) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Huang, Y.; Malagi, A.; Yang, C.-C.; Yoosefian, G.; Huang, L.-T.; Tang, E.; Gao, C.; Han, F.; Bi, X.; et al. Reliable Off-Resonance Correction in High-Field Cardiac MRI Using Autonomous Cardiac B0 Segmentation with Dual-Modality Deep Neural Networks. Bioengineering 2024, 11, 210. https://doi.org/10.3390/bioengineering11030210
Li X, Huang Y, Malagi A, Yang C-C, Yoosefian G, Huang L-T, Tang E, Gao C, Han F, Bi X, et al. Reliable Off-Resonance Correction in High-Field Cardiac MRI Using Autonomous Cardiac B0 Segmentation with Dual-Modality Deep Neural Networks. Bioengineering. 2024; 11(3):210. https://doi.org/10.3390/bioengineering11030210
Chicago/Turabian StyleLi, Xinqi, Yuheng Huang, Archana Malagi, Chia-Chi Yang, Ghazal Yoosefian, Li-Ting Huang, Eric Tang, Chang Gao, Fei Han, Xiaoming Bi, and et al. 2024. "Reliable Off-Resonance Correction in High-Field Cardiac MRI Using Autonomous Cardiac B0 Segmentation with Dual-Modality Deep Neural Networks" Bioengineering 11, no. 3: 210. https://doi.org/10.3390/bioengineering11030210
APA StyleLi, X., Huang, Y., Malagi, A., Yang, C.-C., Yoosefian, G., Huang, L.-T., Tang, E., Gao, C., Han, F., Bi, X., Ku, M.-C., Yang, H.-J., & Han, H. (2024). Reliable Off-Resonance Correction in High-Field Cardiac MRI Using Autonomous Cardiac B0 Segmentation with Dual-Modality Deep Neural Networks. Bioengineering, 11(3), 210. https://doi.org/10.3390/bioengineering11030210






