Abstract
Single-view cone-beam X-ray luminescence computed tomography (CB-XLCT) has recently gained attention as a highly promising imaging technique that allows for the efficient and rapid three-dimensional visualization of nanophosphor (NP) distributions in small animals. However, the reconstruction performance is hindered by the ill-posed nature of the inverse problem and the effects of depth variation as only a single view is acquired. To tackle this issue, we present a methodology that integrates an automated restarting strategy with depth compensation to achieve reconstruction. The present study employs a fast proximal gradient descent (FPGD) method, incorporating L0 norm regularization, to achieve efficient reconstruction with accelerated convergence. The proposed approach offers the benefit of retrieving neighboring multitarget distributions without the need for CT priors. Additionally, the automated restarting strategy ensures reliable reconstructions without the need for manual intervention. Numerical simulations and physical phantom experiments were conducted using a custom CB-XLCT system to demonstrate the accuracy of the proposed method in resolving adjacent NPs. The results showed that this method had the lowest relative error compared to other few-view techniques. This study signifies a significant progression in the development of practical single-view CB-XLCT for high-resolution 3−D biomedical imaging.
1. Introduction
X-ray luminescence computed tomography (XLCT) is a novel hybrid imaging technique that combines X-ray radiography and optical luminescence tomography in a synergistic manner [1,2,3]. In XLCT, the process involves the utilization of targeted X-ray irradiation to stimulate specific nanophosphors (NPs) that are introduced into the tissues of interest. The luminescent signals produced as a result are then detected and used to reconstruct three-dimensional (3−D) images. These images offer supplementary anatomical, functional, and molecular information. Compared to computed tomography (CT) and magnetic resonance imaging (MRI), XLCT provides enhanced functional and molecular imaging capabilities. This is achieved through the utilization of targeted NPs that enable the visualization of molecular processes, such as gene expression and enzyme activity. Furthermore, the utilization of X-rays as the excitation source in XLCT offers enhanced depth penetration and resolution for soft tissue imaging, surpassing the capabilities of pure optical techniques, such as fluorescence molecular tomography (FMT) [4,5] and bioluminescence tomography (BLT) [6,7]. XLCT’s distinctive capability to generate 3−D images with exceptional sensitivity, resolution, and penetration depth positions it as a promising and emerging tool for multifunctional imaging.
First introduced in 2010 by Pratx et al. [1], XLCT has experienced substantial advancements over the past decade, encompassing the development of NPs, imaging systems, and reconstruction techniques. Various types of NPs have been the subject of extensive research [8]. Notably, NPs such as LaAlO3:Eu3+ [9] and NaGdF4:Eu3+ [10] have demonstrated exceptional performance in terms of X-ray excitation efficiency, luminous efficiency, and chemical stability. Advanced XLCT systems, such as pencil/narrow-beam XLCT (PB-XLCT or NB-XLCT) [1,11,12,13,14] and cone-beam XLCT (CB-XLCT) [2,15,16,17], have been proposed. PB-XLCT offers superior image quality through selective excitation, albeit at the cost of longer scan durations. While certain techniques, such as the continuous scanning scheme [18,19], have been shown to enhance imaging efficiency, their imaging geometry necessitates linear steps that are not conducive to rapid imaging, such as in the case of drug biokinetics [20]. The scanning time of cone-beam XLCT is significantly reduced due to the simultaneous irradiation of the entire object. Nevertheless, the spatial resolution of the imaging is compromised due to the ill-posed nature of the reconstruction process. Additionally, the size and location of the X-ray beam cannot be utilized as prior information during the reconstruction of PB-XLCT.
To enhance the imaging performance of CB-XLCT, researchers have made significant contributions from various perspectives. Model-based iterative reconstruction algorithms, such as the Bayesian framework-based method proposed by Zhang et al. [16], have the capability to automatically estimate regularization parameters and effectively preserve target edges. To enhance the quality of images obtained from a reduced number of projections, which is advantageous for rapid biomedical imaging applications, the utilization of compressed sensing (CS) theory has been employed for reconstruction. Various methods, including the L1-TV method [21], robust elastic net-ℓ1ℓ2 method [22], and T-FISTA method [23], have been utilized to achieve this goal. With the utilization of sparsity or group sparsity as a prior, our research team has successfully shown that CB-XLCT has the capability to differentiate between two targets with an edge-to-edge distance (EED) of 0.1 cm by employing two imaging views [24]. Although the acquisition time is notably decreased by using two views, it is important to note that the imaging object undergoes inevitable rotation during the view span, which is deemed unacceptable in numerous clinical scenarios. Thus, the proposal of single-view CB-XLCT has been put forward [15,25,26]. Current single-view CB-XLCT reconstruction demonstrates satisfactory performance in scenarios where there is a single target or multiple targets with prior CT information [27]. Challenges persist in the reconstruction of single-view multitarget CB-XLCT.
Single-view CB-XLCT imaging presents a complex ill-posed inverse problem, particularly when targets are situated at different depths, resulting in nonlinear depth sensitivity [28]. This paper employs two distinct strategies in order to address the challenge of single-view reconstruction. Firstly, in order to address the issue of depth inconsistency in single-view CB-XLCT, the technique of depth compensation is implemented to enhance the quality of imaging. Secondly, in order to address the ill-posed nature of the inverse problem, an automated restarting strategy is implemented during the reconstruction process. Given the satisfactory performance of L0-norm-based CB-XLCT reconstruction in single-view imaging, this study employs a fast proximal gradient descent (FPGD) method [29] to facilitate L0-norm-regularized sparse reconstruction, thereby enhancing convergence speed. This method exhibits three significant advantages in comparison to prior research. Firstly, it has the capability to recover adjacent multitarget distributions without the need for CT priors, as demonstrated in Liu’s work [27]. This showcases its wide applicability beyond fluorescence and bioluminescence tomography. Secondly, the implementation of the automated restarting strategy ensures the generation of reliable reconstructions without the need for manual intervention, as opposed to our previously proposed re-pdNCG method [28]. Thirdly, imaging performance is only marginally influenced by the positioning of the target and detector within a specific range.
To assess the effectiveness of the proposed methodology, numerical simulations and physical phantom experiments were conducted using a custom-made CB-XLCT system. In the context of the numerical simulations, a three-dimensional (3−D) digital mouse was employed as the imaging object, with luminescent targets representing tumors embedded within it. In the conducted physical phantom experiments, a cylinder phantom was utilized, wherein two transparent tubes containing NPs (Y2O3:Eu3+) were immersed. Two algorithms previously proposed by our research group, namely T-FISTA [23] and DC-FL [24], were utilized for the purpose of comparing the sparse-view and limited-view CB-XLCT imaging techniques. Our findings demonstrated that the accurate resolution of luminescent targets is achievable from a single-view image.
The subsequent sections of this paper are structured in the following manner. The forward and inverse problems of single-view CB-XLCT are discussed in Section 2 (Section 2.1 and Section 2.2). The numerical simulations and physical phantom experiments that were conducted to validate the reconstruction performance of the proposed algorithm are presented in Section 2 (Section 2.3). The results are summarized in Section 3. Section 4 presents the discussions and conclusions.
2. Materials and Methods
2.1. Photon Propagation Model of CB-XLCT
In CB-XLCT imaging, X-rays travel through imaging objects and can be converted into light by NPs. The X-ray intensity at position r and the generated light source density can be described as follows:
where X(r0) is the X-ray intensity at the initial position r0, μt(τ) is the reconstructed X-ray attenuation coefficient, η is the light yield, and ρ(r) is the nanophosphor concentration at position r.
Due to the weakly absorbing and highly scattering properties of biological tissues in the visible and NIR spectral windows, light transportation in tissues can be modeled by a diffusion equation (DE) with Robin-type boundary conditions [6]:
where D(r) is the diffusion coefficient (which can be calculated by D(r) = (3(μa(r) + (r)))−1, where μa and are the absorption and reduced scattering coefficients of the tissue, respectively), Φ(r) is the photon fluence at position r, Ω is the domain of the imaging object, ∂Ω denotes the boundary of Ω, is a constant describing the optical reflective index mismatch, and ν is the outward unit normal.
Based on the finite-element method (FEM), Equation (3) can be further discretized into the following matrix equation:
with
where Fij, Kij, and Aij are the elements of matrices F, K, and A, respectively, and ψi and ψj are the corresponding elements of test function.
Equation (5) can be converted into a linear relationship between the nanophosphor concentration ρ and photon measurements on the object surface Φmeas.
where H is a weight matrix with H = K−1FηA.
2.2. Automated Restarting CB-XLCT Reconstruction with Depth Compensation
In CB-XLCT, NPs are sparsely distributed in most biological applications and the luminescent targets are usually small compared to the entire reconstruction regions, especially when nanophosphors accumulate in early tumors. Thus, the compressive sensing (CS) technique can be adopted and Equation (6) can be solved with an L0-norm regularization to obtain sparse results as follows:
where λ is the regularization parameter.
It is known that detection sensitivity in optical imaging decreases nonlinearly as depth increases [30]. This causes CB-XLCT measurements to become hypersensitive to targets near the detector, a common occurrence in the single-view imaging of multiple targets. The resulting ill-posed weight matrices lead to reconstruction biases favoring superficial targets. Therefore, additional information should be provided to correct this nonlinear depth sensitivity.
To obtain effective depth compensation, a data weight matrix Wd and model weight matrix Wm are introduced in Equation (7).
Wd provides a weighting of or a constraint onto the solution, in which some a priori information, such as internal structural knowledge from CT or MRI modality or an initial estimate of the unknown parameter distribution, can be incorporated. Wd can be constructed as follows:
where is a rough approximation of the true solution N and q controls the compromise between a close fit to the data and the stability of the solution. In this paper, the standard Tikhonov regularization reconstruction result was adopted as a priori information, considering the robustness of the imaging performance. The value of q was empirically set from 0.4 to 0.8, according to the reconstruction results.
Wm is used to level differences in detection sensitivities and can be given by
where βj is a normalization factor that is inversely proportional to the absolute largest difference between the elements within each column and Aj is the j-th column of the matrix A. Wm is composed of two parts: the first part βj is used to compensate for differences in the relative sizes of elements within a column of the matrix A and the second part Aj is used to compensate each element in a column with the average distance from the corresponding voxel to all of the source–detector pairs.
The L0-norm regularization problem is NP-hard in general and efficient methods, such as orthogonal least squares (OLS) [31] and orthogonal matching pursuit [32], have been proposed. Bao et al. [33] used a proximal gradient descent (PGD) method to find an approximate solution to the L0-norm regularization problem, which proved to have a sublinear convergence rate, with satisfactory empirical results. In this paper, we employed a fast proximal gradient descent (FPGD) method to solve Equation (8), which can be described as follows:
Initialization: The regularization parameter λ = 1e−3, the initialization = 1, t0 = 0;
Step k (k):
where PQ(u) indicates the novel support projection operator which returns a vector. The details of this process can be found in [29].
To alleviate the ill-posed nature of single-view CB-XLCT reconstruction, an automated restarting strategy was proposed with two-level iteration. In the inner iteration, the FPGD method was used to solve Equation (8) to obtain the , values and the negative values of were set to zero. Then, a new optimization matrix was constructed by removing the columns in H corresponding to the zero values of as the outer iteration. The ill-posed nature could be alleviated by every outer iteration within a reset permissible region. The error threshold to stop the inner iteration was set to 1.0 × 10−5 and the regularization parameter λ was set to 1e-1, according to [29]. The outer iteration was automatically stopped when the 95% values of were zero and the initial guess was set to 1. The regularization parameter λ was set to 1.0 × 10−3. These parameters were selected empirically by comparing the reconstruction results to the actual shapes and positions of the luminescent targets.
The implementation of the proposed restarting FPGD method with depth compensation (re-DC-FPGD) is summarized in Figure 1.
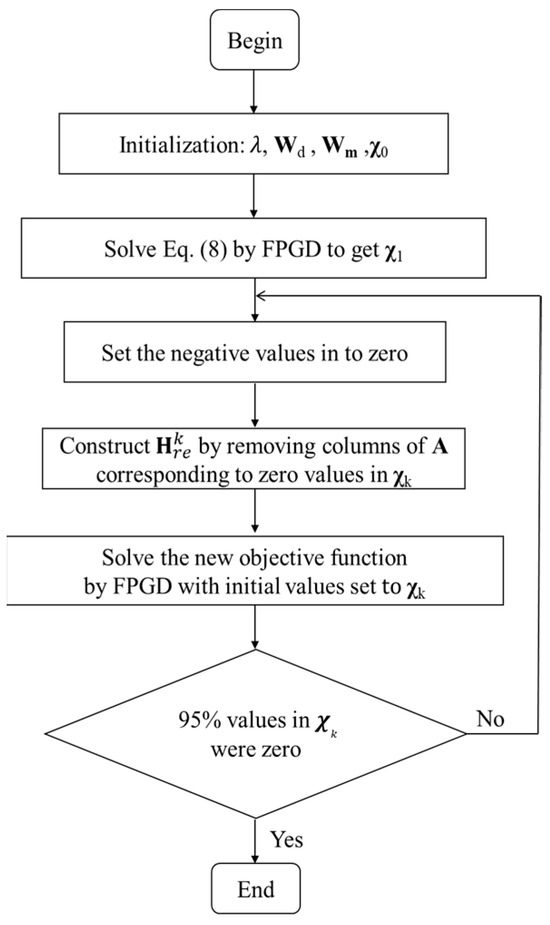
Figure 1.
Flowchart of the re-DC-FPGD method.
2.3. Experimental Setup
2.3.1. Numerical Simulations
Numerical simulations were initially conducted using a digital mouse as the imaging object in order to evaluate the effectiveness of the proposed method. The height of the mouse was 2.6 cm and it contained the primary organs, including the heart, lungs, liver, spleen, bone, and stomach. Additionally, two cylindrical tumors, measuring 3 mm in height and 4 mm in diameter, were inserted into the liver of the mouse (Figure 2a). The scattering and absorption coefficients were allocated to the organs based on the study conducted by [34].
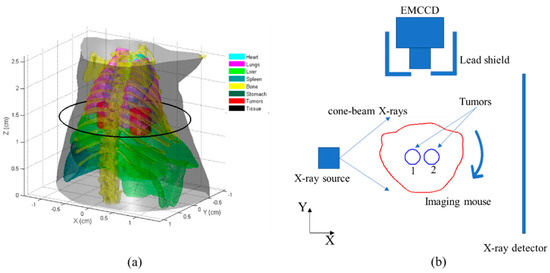
Figure 2.
Schematic of the numerical simulations: (a) 3−D digital mouse with main organs and tumors (the investigated region was 2.6 cm in height), where the black circles depict the central slices of the tumors (represented in red); (b) CB-XLCT imaging system with initial phantom position setup, where the red line depicts the tomographic outline of the mouse and the two blue circles depict the tumors with NPs.
The configuration of the CB-XLCT system is depicted in Figure 2b. An electron-multiplying charge-coupled device (EMCCD) camera, positioned at a 90° angle relative to the X-ray axis, was employed to capture the luminescent images. An X-ray detector was employed to gather the transmitted X-ray signals. The mouse was positioned on a rotation stage, with the z-axis designated as the rotational axis and the Z = 0 cm plane defined as the bottom plane. The two tumors were positioned to be perpendicular to the X-ray detector at the initial position. The mouse was subjected to cone-beam X-rays with a tube voltage of 40 kV and a tube current of 1 mA. White Gaussian noise was introduced to the boundary measurements with a signal-to-noise ratio (SNR) of 20 dB. To assess the imaging performance of the re-DC-FPDG method, three simulation cases were performed. In each case, the two tumors were positioned at the varying edge-to-edge distances (EEDs) of 0.3 cm, 0.2 cm, and 0.1 cm.
2.3.2. Physical Phantom Experiments
Physical phantom experiments were conducted using the CB-XLCT system, which was custom-made by our laboratory. Reference [35] provides comprehensive information regarding the system’s configuration.
The physical phantom utilized in the experiment comprised a transparent glass cylinder with a diameter of 3.0 cm and a height of 7.0 cm. The cylinder was filled with a mixture of 1% intralipid and water. The absorption coefficient and the reduced scattering coefficient of the medium were μa = 0.02 cm−1 and 10 cm−1, respectively. Two glass tubes, each with a diameter of 0.4 cm, were utilized to house Y2O3:Eu3+ nanoparticles with a concentration of 0.1 g/mL. These tubes were then implanted into the phantom. Two experimental cases were conducted to investigate the effects of the EED of two tubes. In case 1, the EED was set to 0.50 cm, while in case 2, it was set to 0.23 cm. These experiments were conducted in a manner similar to simulations.
For the purpose of single-view CB-XLCT imaging, the X-ray tube voltage was set to 40 kV and the current was set to 1 mA. The electron-multiplying (EM) gain, integration time, and binning settings of the electron-multiplying charge-coupled device (EMCCD) were configured to 260, 500 ms, and 1 × 1, respectively. For the purpose of CT imaging, a total of 360 images were acquired at 1° intervals. The CT reconstruction utilized the Feldkamp–Davis–Kress (FDK) algorithm [36].
Figure 3c,d displays the representative X-ray projections and tomographic images, respectively, of the phantom experiments for the initial position of the phantom. The area of interest under investigation was the region bounded by the green and red lines, measuring 2.6 cm in height. The tomographic images indicated by the blue lines in Figure 3a,b are represented as Figure 3c and Figure 3d, respectively. The tubes on the left and right sides are designated as tube 1 and tube 2, respectively.

Figure 3.
Setup of the phantom experiments: (a,b) representative X-ray projections of the phantom in case 1 and case 2. Regions between the blue and green lines are used for the study; (c,d) CT slices indicated by the red lines shown in (a,b).
2.3.3. Quantitative Evaluation
The reconstructed images were compared using several indices, including location error (LE) [15], dice similarity coefficient (DICE) [37], and spatial resolution index (SPI) [23].
LE is defined as the Euclidean distance between the reconstructed and true positions of a target.
where pr denotes the maximum value position of the reconstructed target and pt denotes the real center position.
DICE is used to evaluate the similarity between reconstructed and true luminescent areas to assess the quality of morphological reconstructions.
where ROIr and ROIt denote the reconstructed and true luminescent areas, respectively. The higher the DICE value, the higher the similarity between the target in the reconstructed image and the original position.
SPI denotes the spatial resolutions of two targets and is defined as
where ρl denotes the value of the profile along a given line that connects the two centers of the reconstructed cross-sections and , and are the maximal, valley, and minimal values between the two peak values, respectively. Large SPI values indicate the high spatial resolutions of reconstructed images.
In this paper, to quantitatively evaluate the performance of the proposed method, two CB-XLCT reconstruction methods previously proposed by our group were used for comparison, including the sparse-view-based T-FISTA method and the limited-view-based DC-FL method. The iteration numbers were chosen empirically according to the results and to ensure the convergence of the calculations. For XLCT reconstruction, each phantom was discretized into 2124 nodes and 9765 tetrahedral elements using COMSOL Multiphysics 3.3 (COMSOL, Inc., Burlington, MA, USA), which corresponded to normal discretization. It should be noted that with finer discretization, the computation time costs would increase substantially but the spatial resolution would not be improved since the optimization difficulty would increase accordingly. The proposed algorithm was implemented on an Intel 3.40-GHz processor and 32-GB RAM personal computer and the calculation time was about 14.2 s.
3. Results
3.1. Numerical Simulations
To demonstrate the performance of the proposed method for different imaging views, reconstructions in case 1 were conducted at imaging views of 0°, 30°, and 60°, with an EED of 0.3 cm. The reconstructed 2D slices are shown in Figure 4. All of the slices depicted in Figure 4 were taken at a height of Z = 1.3 cm. The two tumors could be effectively identified using the three single views with the proposed method. In the following simulations, all reconstructions were conducted using the luminescent image at a viewing angle of 30º, taking into account differences in tumor depth.
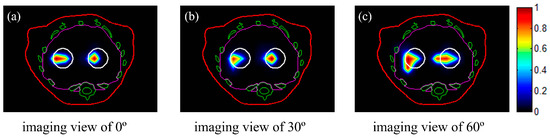
Figure 4.
Reconstructed images of the tumors with NPs at different imaging views. The slices are those indicated with black circles in Figure 2. The white circles represent the real positions of the tumors. The red, green, and magenta lines represent the boundaries of the animal’s body, bones, and liver, respectively: (a–c) imaging views of 0°, 30°, 60°, respectively. All images were normalized to the maximal value.
The reconstructed 2D slices of the three cases obtained by the T-FISTA, DC-FL, and proposed re-DC-FPGD algorithms are shown in Figure 5. The three columns in Figure 5 represent the reconstruction results obtained using the different methods, while the rows represent the different EEDs.
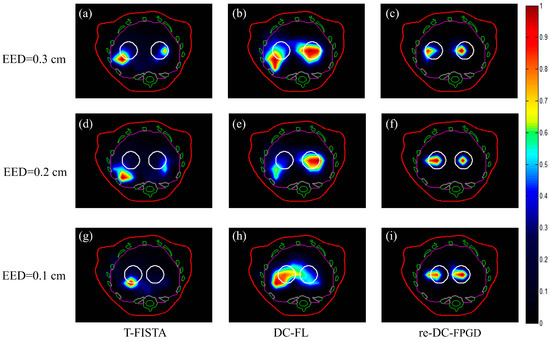
Figure 5.
Reconstructed images of the tumors in different cases using the three methods. The white circles represent the real positions of the tumors. The red, green, and magenta lines represent the boundaries of the animal’s body, bones, and liver, respectively (a–c) tomographic slices reconstructed by T-FISTA, DC-FL, and the proposed re-DC-FPGD algorithm with an EED of 0.3 cm. (d–f) tomographic slices reconstructed by different algorithms with an EED of 0.2 cm. (g–i) tomographic slices reconstructed by different algorithms with an EED of 0.1 cm.
The results indicated that the sparse-view-based T-FISTA method and the limited-view-based DC-FL method could not resolve the two tumors in all cases, as shown in the first and second columns of Figure 5. This was due to either a lack of depth compensation or the highly ill-posed nature of the reconstruction problem. With the revised strategy that incorporates depth compensation, it was possible to clearly recover the two targets, even when they were in close proximity (EED = 0.1 cm), as depicted in Figure 5i.
Figure 6 shows the 3−D results of the reconstructed CB-XLCT images using the proposed method. The blue objects represent the tumors. As expected, in all cases, the re-DC-FPGD method could clearly distinguish the two targets using a single-view luminescent image.
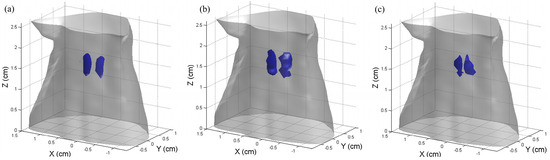
Figure 6.
The 3−D results of the reconstructed CB-XLCT images using the proposed method in the simulations of the three cases: (a–c) case 1 to case 3. Tumors are represented in blue.
The quantitative analysis results of case 3, obtained using the different methods, are presented in Table 1. Among the three methods compared, the proposed re-DC-FPGD method achieved the lowest LE, the highest DICE, and the highest SPI. This suggests that the re-DC-FPGD method outperformed the others in terms of localization accuracy, shape recovery, and the preservation of spatial resolution when reconstructing the target.

Table 1.
Quantitative evaluation of simulations (EED = 0.1 cm).
3.2. Numerical Simulations
Figure 7 presents the CB-XLCT reconstruction results for case 1 of the phantom experiments, which had an EED of 0.50 cm. The reconstructed images were based on the luminescent images taken at a 30° viewing angle. All images were normalized to the maximum intensity value. The first row of Figure 7 shows the reconstructed images (indicated by the red line in Figure 3a) using the T-FISTA, DC-FL, and proposed re-DC-FPGD methods. The second row displays the fused CB-XLCT/CT images, while the third row shows the 3−D rendering results. As expected, both the sparse-view-based T-FISTA and the limited-view-based DC-FL methods failed to separate the two targets. More noise is evident in Figure 7a compared to Figure 7b,c, indicating that the DC-FL and proposed methods performed better in terms of noise suppression. Owing to the depth compensation and the automatic restarting strategy, the proposed method clearly resolved the two tubes with a high contrast-to-noise ratio (CNR). The 3−D results (Figure 7h–j) further demonstrate the superiority of the proposed method over the other two.
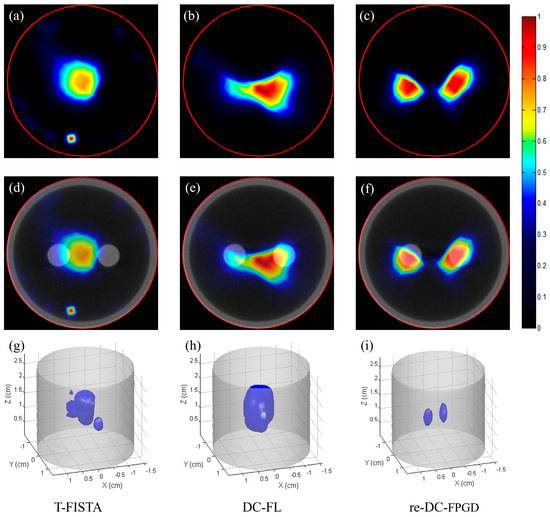
Figure 7.
Phantom experiment results for case 1: (a–c) CB-XLCT slices reconstructed by T-FISTA, DC-FL, and the proposed re-DC-FPGD algorithm, respectively. (d–f) CB-XLCT/CT fusion results of different methods. (g–i) 3−D rendering results of different methods. The red circles in the CB-XLCT images depict the boundaries of the phantom. The blue objects in the 3−D renderings represent the recovered targets.
Figure 8 presents the single-view CB-XLCT reconstruction results for the phantom experiments for case 2, which had an EED of 0.23 cm. Figure 8a–c show the CB-XLCT slices (indicated by the red line in Figure 3b) obtained using the T-FISTA, DC-FL, and proposed re-DC-FPGD algorithms, respectively. Figure 8d–f display the corresponding XLCT/CT fusion results. Figure 8h–j show the results of the 3−D rendering. Similar to case 1, both the T-FISTA and DC-FL methods failed to achieve high image quality. In contrast, the re-DC-FPGD approach achieved superior spatial resolution, as demonstrated by the tomographic images (Figure 8c,f) and 3−D results (Figure 8j). The location accuracy and shape recovery achieved by the re-DC-FPGD reconstruction demonstrated its ability to produce high-quality single-view CB-XLCT images, even at the low EED of 0.23 cm.
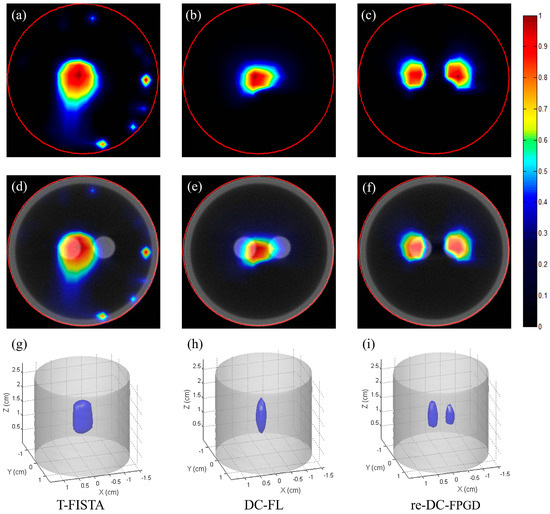
Figure 8.
Phantom experiment results for case 2: (a–c) CB-XLCT slices reconstructed by T-FISTA, DC-FL, and the proposed re-DC-FPGD algorithm, respectively. (d–f) CB-XLCT/CT fusion results of different methods. (g–i) 3−D rendering results of different methods. The red circles in the CB-XLCT images depict the boundaries of the phantom. The blue objects in the 3−D renderings represent the recovered targets.
Table 2 presents the results of the quantitative analysis of the reconstructions in the phantom experiments for case 2. In line with the numerical simulation findings, the proposed re-DC-FPGD method achieved the lowest LE, the highest DICE, and the highest SPI compared to the other two methods. This demonstrates that even for physical phantom experiments at the low EED of 0.23 cm, the re-DC-FPGD algorithm demonstrated superior performance in terms of target localization accuracy, shape recovery, and the preservation of structural details compared to T-FISTA and DC-FL. The quantitative metrics supported the observed improvements in visual quality in the re-DC-FPGD phantom reconstructions.

Table 2.
Quantitative evaluation of the phantom experiments.
4. Discussion
Single-view CB-XLCT imaging enables the fast and noninvasive 3−D visualization of NP distributions during biological processes, making it highly attractive for biomedical research. However, the reconstruction of CB-XLCT from a single view poses a severely ill-posed inverse problem since only one view of the data is acquired. To address this, the present work utilized automated restarting FPGD combined with depth compensation (re-DC-FPGD) to tackle single-view CB-XLCT reconstruction. Together, these strategies enabled high-quality single-view CB-XLCT reconstruction, as evidenced by simulations and phantom studies.
The simulation and phantom experiment results demonstrated that the proposed re-DC-FPGD method could accurately resolve two adjacent targets, even at the low EED of 0.1 cm (Figure 5i). In contrast, the targets could not be distinguished using the T-FISTA or DC-FL approaches. Quantitative evaluation showed that the re-DC-FPGD method achieved the best imaging performance with the lowest recovery error (Table 1 and Table 2) compared to other methods.
There are some limitations that need to be addressed in future work. Firstly, the parameters for the T-FISTA and DC-FL methods, as well as the construction parameters of Wd and Wm, were selected based on our previous study [24]. Automated parameter selection will be investigated. Secondly, for low photon counts, model-based frameworks, such as the Poisson distribution model [38], will be considered. Thirdly, as depth differences increase, such as at the 90° imaging view (the imaging setup of 0° view was shown in Figure 2b) in this study, the current depth compensation method fails to reveal targets that are far from the EMCCD. This issue will be addressed by incorporating additional priors. In addition, to achieve more accurate morphological reconstructions to obtain higher DICE values, more priors may be considered, such as group sparsity [39] or the luminescent intensity of adjacent voxels [40]. Overall, future work will focus on automated parameter selection, modeling low-flux statistics, and enhancing depth compensation to accommodate larger depth variations. Addressing these limitations will further enhance the proposed method’s utility for practical biomedical XLCT applications.
In conclusion, we propose a reconstruction method for single-view CB-XLCT. This method combines an automated restarting strategy with depth compensation. This approach enables high-quality imaging with high time resolutions as only a single view of data is required. Future work will focus on implementing the method for in vivo imaging, which could provide the rapid 3−D visualization of dynamic molecular processes.
Author Contributions
Conceptualization, P.G. and H.P.; methodology, P.G.; software, P.G.; validation, P.G., T.L. and Y.C.; formal analysis, P.G.; investigation, P.G.; resources, P.G.; data curation, W.L.; writing—original draft preparation, P.G., S.H. and R.L.; writing—review and editing, H.L. and J.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant numbers 12275355, 82372035, 12305350, and 11805274) and the National Key Research and Development Program of China (2023YFF0715400 and 2023YFF0715401).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pratx, G.; Carpenter, C.M.; Sun, C.; Xing, L. X-ray Luminescence Computed Tomography via Selective Excitation: A Feasibility Study. IEEE Trans. Med. Imaging 2010, 29, 1992–1999. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Zhu, S.; Yi, H.; Zhang, X.; Chen, D.; Liang, J.; Tian, J. Cone beam X-ray luminescence computed tomography: A feasibility study. Med. Phys. 2013, 40, 031111. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, M.; Pratx, G.; Bazalova, M.; Xing, L. X-ray Luminescence and X-ray Fluorescence Computed Tomography: New Molecular Imaging Modalities. IEEE Access 2014, 2, 1051–1061. [Google Scholar] [CrossRef]
- Liu, F.; Li, M.; Zhang, B.; Luo, J.; Bai, J. Weighted depth compensation algorithm for fluorescence molecular tomography reconstruction. Appl. Opt. 2012, 51, 8883–8892. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Gao, Y.; Yang, X.; Wang, K.; Tian, J. K-Nearest Neighbor Based Locally Connected Network for Fast Morphological Reconstruction in Fluorescence Molecular Tomography. IEEE Trans. Med. Imaging 2020, 39, 3019–3028. [Google Scholar] [CrossRef] [PubMed]
- Cong, W.; Wang, G.; Kumar, D.; Liu, Y.; Jiang, M.; Wang, L.V.; Hoffman, E.A.; McLennan, G.; McCray, P.B.; Zabner, J.; et al. Practical reconstruction method for bioluminescence tomography. Opt. Express 2005, 13, 6756–6771. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Cong, W.; Durairaj, K.; Qian, X.; Shen, H.; Sinn, P.; Hoffman, E.; McLennan, G.; Henry, M. In vivo mouse studies with bioluminescence tomography. Opt. Express 2006, 14, 7801–7809. [Google Scholar] [CrossRef]
- Lun, M.C.; Ranasinghe, M.; Arifuzzaman, M.; Fang, Y.; Guo, Y.; Anker, J.N.; Li, C. Contrast agents for X-ray luminescence computed tomography. Appl. Opt. 2021, 60, 6769–6775. [Google Scholar] [CrossRef]
- Fu, Z.; Liu, B. Solution combustion synthesis, photoluminescence and X-ray luminescence of Eu3+-doped LaAlO3 nanophosphors. Ceram. Int. 2016, 42, 2357–2363. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, Y.; Liu, M.; Gao, P.; Pu, H.; Fan, L.; Jiang, R.; Liu, Z.; Shi, F.; Lu, H. Sub-10 nm Water-Dispersible β-NaGdF4:X% Eu3+ Nanoparticles with Enhanced Biocompatibility for In Vivo X-ray Luminescence Computed Tomography. ACS Appl. Mater. Interfaces 2017, 9, 39985–39993. [Google Scholar] [CrossRef]
- Li, C.; Di, K.; Bec, J.; Cherry, S.R. X-ray luminescence optical tomography imaging: Experimental studies. Opt. Lett. 2013, 38, 2339–2341. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhu, D.; Lun, M.; Li, C. Multiple pinhole collimator based X-ray luminescence computed tomography. Biomed. Opt. Express 2016, 7, 2506–2523. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhu, D.; Lun, M.; Li, C. Collimated superfine X-ray beam based X-ray luminescence computed tomography. J. X-ray Sci. Technol. 2017, 25, 945–957. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lun, M.C.; Li, C.; Zhou, Z. Method for improving the spatial resolution of narrow X-ray beam-based X-ray luminescence computed tomography imaging. J. Biomed. Opt. 2019, 24, 086002. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liao, Q.; Wang, H. Fast X-ray Luminescence Computed Tomography Imaging. IEEE Trans. Biomed. Eng. 2014, 61, 1621–1627. [Google Scholar]
- Zhang, G.; Liu, F.; Liu, J.; Luo, J.; Xie, Y.; Bai, J.; Xing, L. Cone beam X-ray luminescence computed tomography based on Bayesian method. IEEE Trans. Med. Imaging 2016, 36, 225–235. [Google Scholar] [CrossRef]
- Chen, D.; Zhu, S.; Cao, X.; Zhao, F.; Liang, J. X-ray luminescence computed tomography imaging based on X-ray distribution model and adaptively split Bregman method. Biomed. Opt. Express 2015, 6, 2649–2663. [Google Scholar] [CrossRef]
- Fang, Y.; Lun, M.C.; Zhang, Y.; Anker, J.N.; Wang, G.; Li, C. Super-fast three-dimensional focused X-ray luminescence computed tomography with a gated photon counter. In Proceedings of the Medical Imaging 2022: Biomedical Applications in Molecular, Structural, and Functional Imaging, San Diego, CA, USA, 20–22 February 2022; SPIE: Bellingham, WA, USA, 2022; p. 120360K. [Google Scholar]
- Fang, Y.; Zhang, Y.; Lun, M.C.; Anker, J.N.; Wang, G.; Li, C. Development of fast and three-dimensional focused X-ray luminescence tomography system. In Proceedings of the Medical Imaging 2023: Biomedical Applications in Molecular, Structural, and Functional Imaging, San Diego, CA, USA, 19–22 February 2023; SPIE: Bellingham, WA, USA, 2023; p. 124680Z. [Google Scholar]
- Man, F.; Tang, J.; Swedrowska, M.; Forbes, B.; de Rosales, R.T.M. Imaging drug delivery to the lungs: Methods and applications in oncology. Adv. Drug Deliv. Rev. 2023, 192, 114641. [Google Scholar] [CrossRef]
- Liu, T.; Rong, J.; Gao, P.; Pu, H.; Zhang, W.; Zhang, X.; Liang, Z.; Lu, H. Regularized reconstruction based on joint L1 and total variation for sparse-view cone-beam X-ray luminescence computed tomography. Biomed. Opt. Express 2019, 10, 1–17. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, H.; Yu, J.; Yi, H.; Hou, Y.; He, X. A robust elastic net-ℓ1ℓ2 reconstruction method for X-ray luminescence computed tomography. Phys. Med. Biol. 2021, 66, 195005. [Google Scholar] [CrossRef]
- Gao, P.; Rong, J.; Pu, H.; Liu, T.; Zhang, W.; Zhang, X.; Lu, H. Sparse view cone beam X-ray luminescence tomography based on truncated singular value decomposition. Opt. Express 2018, 26, 23233–23250. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Rong, J.; Liu, T.; Zhang, W.; Lan, B.; Ouyang, X.; Lu, H. Limited view cone-beam X-ray luminescence tomography based on depth compensation and group sparsity prior. J. Biomed. Opt. 2020, 25, 016004. [Google Scholar] [CrossRef]
- Liu, X.; Wang, H.; Xu, M.; Nie, S.; Lu, H. A wavelet-based single-view reconstruction approach for cone beam X-ray luminescence tomography imaging. Biomed. Opt. Express 2014, 5, 3848–3858. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Liao, Q.; Wang, H. In vivo X-ray luminescence tomographic imaging with single-view data. Opt. Lett. 2013, 38, 4530–4533. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Tang, X.; Shu, Y.; Zhao, L.; Liu, Y.; Zhou, T. Single-view cone-beam X-ray luminescence optical tomography based on Group_YALL1 method. Phys. Med. Biol. 2019, 64, 105004. [Google Scholar] [CrossRef]
- Gao, P.; Cheng, K.; Schüler, E.; Jia, M.; Zhao, W.; Xing, L. Restarted primal–dual Newton conjugate gradient method for enhanced spatial resolution of reconstructed cone-beam X-ray luminescence computed tomography images. Phys. Med. Biol. 2020, 65, 135008. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, J. Fast Proximal Gradient Descent for a Class of Non-convex and Non-smooth Sparse Learning Problems. In Proceedings of the 35th Uncertainty in Artificial Intelligence Conference, PMLR, Proceedings of Machine Learning Research, Tel Aviv, Israel, 22–25 July 2019; Ryan, P.A., Vibhav, G., Eds.; Elsevier B.V.: Tel Aviv, Israel, 2020; pp. 1253–1262. [Google Scholar]
- Tian, F.; Liu, H. Depth-compensated diffuse optical tomography enhanced by general linear model analysis and an anatomical atlas of human head. Neuroimage 2014, 85, 166–180. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Gradient Pursuits. IEEE Trans. Signal Process. 2008, 56, 2370–2382. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Bao, C.; Ji, H.; Quan, Y.; Shen, Z. L0 Norm Based Dictionary Learning by Proximal Methods with Global Convergence. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; IEEE: New York, NY, USA; pp. 3858–3865. [Google Scholar]
- Alexandrakis, G.; Rannou, F.R.; Chatziioannou, A.F. Tomographic bioluminescence imaging by use of a combined optical-PET (OPET) system: A computer simulation feasibility study. Phys. Med. Biol. 2005, 50, 4225–4241. [Google Scholar] [CrossRef]
- Gao, P.; Pu, H.; Rong, J.; Zhang, W.; Liu, T.; Liu, W.; Zhang, Y.; Lu, H. Resolving adjacent nanophosphors of different concentrations by excitation-based cone-beam X-ray luminescence tomography. Biomed. Opt. Express 2017, 8, 3952–3965. [Google Scholar] [CrossRef]
- Feldkamp, L.A.; Davis, L.C.; Kress, J.W. Practical cone-beam algorithm. J. Opt. Soc. Am. A 1984, 1, 612–619. [Google Scholar] [CrossRef]
- An, Y.; Liu, J.; Zhang, G.; Ye, J.; Du, Y.; Mao, Y.; Chi, C.; Tian, J. A Novel Region Reconstruction Method for Fluorescence Molecular Tomography. IEEE Trans. Biomed. Eng. 2015, 62, 1818–1826. [Google Scholar] [CrossRef]
- Liu, T.; Ruan, J.; Rong, J.; Hao, W.; Li, W.; Li, R.; Zhan, Y.; Lu, H. Cone-beam X-ray luminescence computed tomography based on MLEM with adaptive FISTA initial image. Comput. Methods Programs Biomed. 2023, 229, 107265. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Liu, J.; An, Y.; Gao, Y.; Meng, H.; Wang, K.; Tian, J. Fluorescence Molecular Tomography Based on Group Sparsity Priori for Morphological Reconstruction of Glioma. IEEE Trans. Biomed. Eng. 2020, 67, 1429–1437. [Google Scholar] [CrossRef] [PubMed]
- Meng, H.; Wang, K.; Gao, Y.; Jin, Y.; Ma, X.; Tian, J. Adaptive Gaussian Weighted Laplace Prior Regularization Enables Accurate Morphological Reconstruction in Fluorescence Molecular Tomography. IEEE Trans. Med. Imaging 2019, 38, 2726–2734. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).