Analyzing How Skinfold Thickness Affects Log-Transformed EMG Amplitude–Power Output Metrics
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Design and Approach
2.2. Subjects
2.3. Incremental Single-Leg Knee-Extensor Ergometer
2.4. Placement of EMG Electrodes
2.5. EMG Signal Acquisition and Processing
2.6. Skinfold Measurements
2.7. Statistical Analysis
3. Results
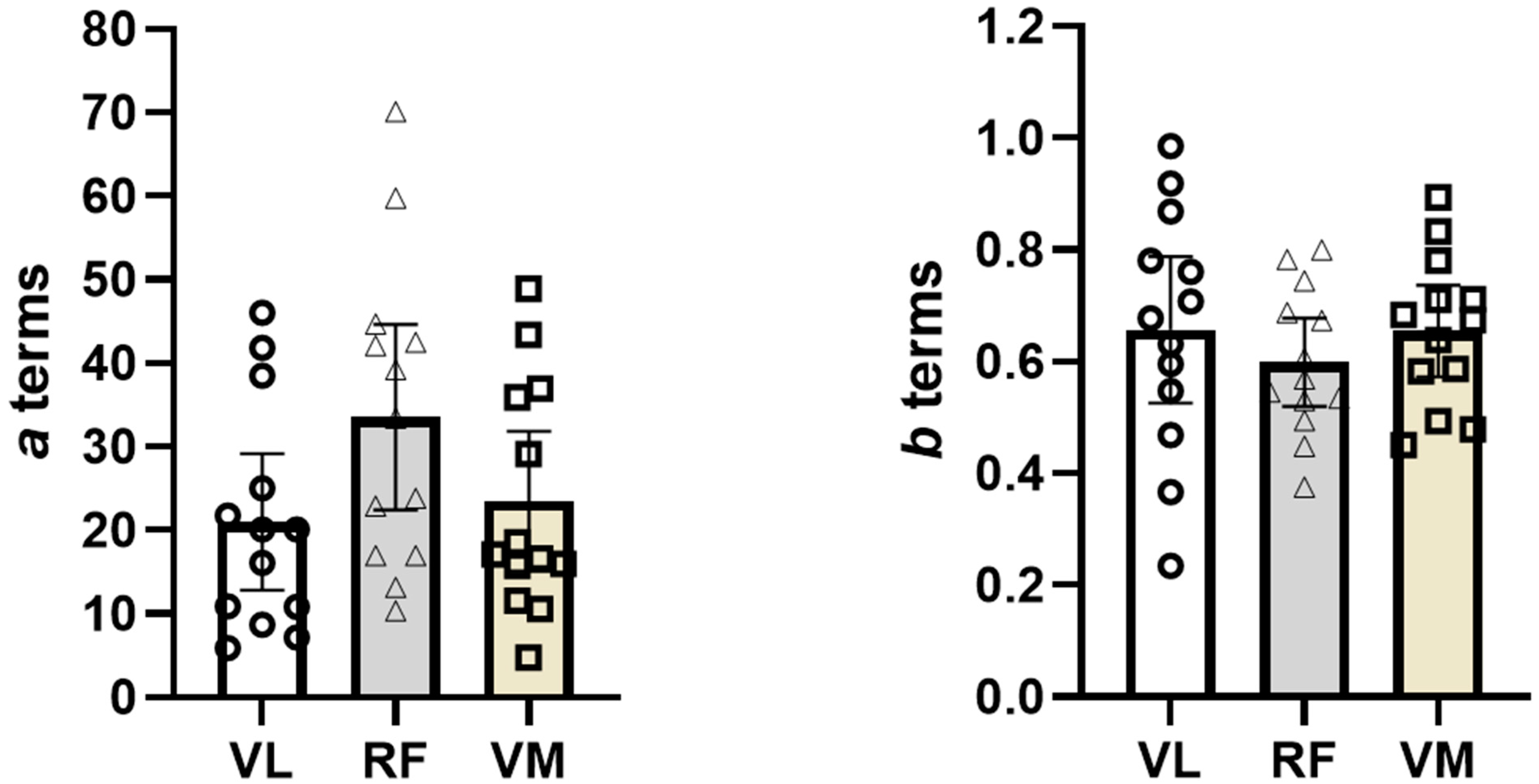
3.1. Comparison of a Terms Across Muscles with and Without Covariate
3.2. Comparison of b Terms Across Muscles with and Without Covariate
4. Discussion
4.1. y-Intercept (a Term)
4.2. Slope (b Term)
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Basmajian, J.V.; De Luca, C.J. Muscles Alive, Their Functions Revealed by Electromyography, 5th ed.; Williams & Wilkins: Baltimore, MD, USA, 1985; pp. 1–200. [Google Scholar]
- Feldpausch, J.E.; Blok, A.L.; Frederick, E.L.; Coburn, J.W.; Malek, M.H. The evolution of the physical work capacity at the fatigue threshold test: Past, Present, and Future. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2021, 35, 3529–3536. [Google Scholar] [CrossRef] [PubMed]
- Malek, M.H.; Coburn, J.W. The utility of electromyography and mechanomyography for assessing neuromuscular function: A noninvasive approach. Phys. Med. Rehabil. Clin. N. Am. 2012, 23, 23–32. [Google Scholar] [CrossRef] [PubMed]
- Blaesser, R.J.; Couls, L.M.; Lee, C.F.; Zuniga, J.M.; Malek, M.H. Comparing EMG amplitude patterns of responses during dynamic exercise: Polynomial vs log-transformed regression. Scand. J. Med. Sci. Sports 2015, 25, 159–165. [Google Scholar] [CrossRef] [PubMed]
- Herda, T.J.; Housh, T.J.; Fry, A.C.; Weir, J.P.; Schilling, B.K.; Ryan, E.D.; Cramer, J.T. A noninvasive, log-transform method for fiber type discrimination using mechanomyography. J. Electromyogr. Kinesiol. Off. J. Int. Soc. Electrophysiol. Kinesiol. 2010, 20, 787–794. [Google Scholar] [CrossRef]
- Herda, T.J.; Walter, A.A.; Costa, P.B.; Ryan, E.D.; Stout, J.R.; Cramer, J.T. Differences in the log-transformed electromyographic-force relationships of the plantar flexors between high- and moderate-activated subjects. J. Electromyogr. Kinesiol. Off. J. Int. Soc. Electrophysiol. Kinesiol. 2011, 21, 841–846. [Google Scholar] [CrossRef]
- Herda, T.J.; Weir, J.P.; Ryan, E.D.; Walter, A.A.; Costa, P.B.; Hoge, K.M.; Beck, T.W.; Stout, J.R.; Cramer, J.T. Reliability of absolute versus log-transformed regression models for examining the torque-related patterns of response for mechanomyographic amplitude. J. Neurosci. Methods 2009, 179, 240–246. [Google Scholar] [CrossRef] [PubMed]
- Eason, T.; Gavel, C.R.; Hawley, K.A.; Galen, S.S.; Malek, M.H. Reliability of the Log-Transformed EMG Amplitude-Power Output Relationship for Incremental Knee-Extensor Ergometry. Muscle Nerve 2015, 52, 428–434. [Google Scholar] [CrossRef] [PubMed]
- Boccomino, H.L.; Daoud, B.T.; Hudas, A.; North, W.A.; Malek, M.H. Log-Transformed Electromyography Amplitude Power Output Relationship: Nondominant vs. Dominant Limb. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2022, 36, 851–856. [Google Scholar] [CrossRef] [PubMed]
- Malek, M.H.; Coburn, J.W.; Marelich, W.D. Advanced Statistics for Kinesiology and Exercise Science: A Practical Guide to ANOVA and Regression Analyses; Routledge: Milton Park, NY, USA, 2018; pp. 57–99. [Google Scholar]
- Noble, E.B.; Pilarski, J.M.; Vora, H.K.; Zuniga, J.M.; Malek, M.H. Log-Transformed Electromyography Amplitude-Power Output Relationship: Single-Leg Knee-Extensor Versus Single-Leg Cycle Ergometry. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2019, 33, 1311–1319. [Google Scholar] [CrossRef] [PubMed]
- De la Barrera, E.J.; Milner, T.E. The effects of skinfold thickness on the selectivity of surface EMG. Electroencephalogr. Clin. Neurophysiol. 1994, 93, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Cooper, M.A.; Herda, T.J.; Vardiman, J.P.; Gallagher, P.M.; Fry, A.C. Relationships between skinfold thickness and electromyographic and mechanomyographic amplitude recorded during voluntary and non-voluntary muscle actions. J. Electromyogr. Kinesiol. Off. J. Int. Soc. Electrophysiol. Kinesiol. 2014, 24, 207–213. [Google Scholar] [CrossRef] [PubMed]
- Roeleveld, K.; Blok, J.H.; Stegeman, D.F.; van Oosterom, A. Volume conduction models for surface EMG; confrontation with measurements. J. Electromyogr. Kinesiol. Off. J. Int. Soc. Electrophysiol. Kinesiol. 1997, 7, 221–232. [Google Scholar] [CrossRef] [PubMed]
- Petrofsky, J.; Schwab, E. A re-evaluation of modelling of the current flow between electrodes: Consideration of blood flow and wounds. J. Med. Eng. Technol. 2007, 31, 62–74. [Google Scholar] [CrossRef]
- Ohmine, Y.; Morimoto, T.; Kinouchi, Y.; Iritani, T.; Takeuchi, M.; Haku, M.; Nishitani, H. Basic study of new diagnostic modality according to non-invasive measurement of the electrical conductivity of tissues. J. Med. Investig. 2004, 51, 218–225. [Google Scholar] [CrossRef] [PubMed]
- Petrofsky, J. The effect of the subcutaneous fat on the transfer of current through skin and into muscle. Med. Eng. Phys. 2008, 30, 1168–1176. [Google Scholar] [CrossRef]
- Baniqued, A.N.; Zuniga, J.M.; Strunc, T.C.; Keenan, K.M.; Boken, A.K.; Anderson, J.J. The Effect of Skinfold on the Assessment of the Mean Power Frequency at the Fatigue Threshold. Int. J. Exerc. Sci. 2016, 9, 376–383. [Google Scholar] [CrossRef] [PubMed]
- Zaheer, F.; Roy, S.H.; De Luca, C.J. Preferred sensor sites for surface EMG signal decomposition. Physiol. Meas. 2012, 33, 195–206. [Google Scholar] [CrossRef] [PubMed]
- Convertino, V.A.; Armstrong, L.E.; Coyle, E.F.; Mack, G.W.; Sawka, M.N.; Senay, L.C., Jr.; Sherman, W.M. American College of Sports Medicine position stand. Exercise and fluid replacement. Med. Sci. Sports Exerc. 1996, 28, i–vii. [Google Scholar] [CrossRef] [PubMed]
- Harlan, K.G.; Merucci, R.B.; Weaver, J.J.; Windle, T.C.; Malek, M.H. Preexhaustion exercise differentially influences neuromuscular fatigue based on habitual physical activity history. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2021, 35, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Ferris, J.R.; Tomlinson, M.A.; Ward, T.N.; Pepin, M.E.; Malek, M.H. Reduced Electromyographic Fatigue Threshold after Performing a Cognitive Fatiguing Task. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2021, 35, 267–274. [Google Scholar] [CrossRef]
- Elhaj, H.M.; Imam, O.; Page, B.W.; Vitale, J.M.; Malek, M.H. Perceived consumption of a high dose caffeine drink delays neuromuscular fatigue. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2022, 36, 1185–1190. [Google Scholar] [CrossRef]
- Centala, J.; Pogorel, C.; Pummill, S.W.; Malek, M.H. Listening to fast-temp music delays the onset of neuromuscular fatigue. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2020, 34, 617–622. [Google Scholar] [CrossRef] [PubMed]
- Bremer, N.; Peoples, G.; Hasler, B.; Litzenburg, R.; Johnson, A.; Malek, M.H. Repeated Incremental Workbouts Separated by 1 Hour Increase the Electromyographic Fatigue Threshold. J. Strength Cond. Res./Natl. Strength Cond. Assoc. 2021, 35, 1397–1402. [Google Scholar] [CrossRef] [PubMed]
- Malek, M.H.; Coburn, J.W.; Tedjasaputra, V. Comparison of electromyographic responses for the superficial quadriceps muscles: Cycle versus knee-extensor ergometry. Muscle Nerve 2009, 39, 810–818. [Google Scholar] [CrossRef] [PubMed]
- Hermens, H.J.; Freriks, B.; Disselhorst-Klug, C.; Rau, G. Development of recommendations for SEMG sensors and sensor placement procedures. J. Electromyogr. Kinesiol. Off. J. Int. Soc. Electrophysiol. Kinesiol. 2000, 10, 361–374. [Google Scholar] [CrossRef] [PubMed]
- Nordander, C.; Willner, J.; Hansson, G.A.; Larsson, B.; Unge, J.; Granquist, L.; Skerfving, S. Influence of the subcutaneous fat layer, as measured by ultrasound, skinfold calipers and BMI, on the EMG amplitude. Eur. J. Appl. Physiol. 2003, 89, 514–519. [Google Scholar] [CrossRef] [PubMed]
- Richardson, R.S.; Frank, L.R.; Haseler, L.J. Dynamic knee-extensor and cycle exercise: Functional MRI of muscular activity. Int. J. Sports Med. 1998, 19, 182–187. [Google Scholar] [CrossRef]
| Index | Mean ± SEM |
|---|---|
| Age (y) | 25.5 ± 0.7 |
| Height (m) | 1.84 ± 0.03 |
| Body mass (kg) | 87.0 ± 3.2 |
| Vastus lateralis skinfold thickness (mm) | 35.7 ± 2.1 |
| Rectus femoris skinfold thickness (mm) | 36.1 ± 2.2 |
| Vastus medialis skinfold thickness (mm) | 33.2 ± 2.2 |
| EMG Amplitude (Log Transformed) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Vastus Lateralis | Rectus Femoris | Vastus Medialis | |||||||
| Subject | R2 | a | b (95% CI) | R2 | a | b (95% CI) | R2 | a | b (95% CI) |
| 1 | 0.404 | 41.824 | 0.234 (−0.0498 to 0.518) | 0.825 | 22.920 | 0.494 (0.267 to 0.721) | 0.784 | 35.874 | 0.479 (0.228 to 0.731) |
| 2 | 0.814 | 46.063 | 0.469 (0.269 to 0.670) | 0.772 | 44.701 | 0.448 (0.230 to 0.666) | 0.826 | 43.380 | 0.450 (0.265 to 0.635) |
| 3 | 0.833 | 5.930 | 0.918 (0.645 to 1.19) | 0.809 | 33.448 | 0.605 (0.410 to 0.800) | 0.859 | 11.588 | 0.780 (0.571 to 0.990) |
| 4 | 0.824 | 10.913 | 0.631 (0.438 to 0.825) | 0.906 | 16.945 | 0.545 (0.429 to 0.661) | 0.895 | 4.759 | 0.832 (0.643 to 1.02) |
| 5 | 0.950 | 21.758 | 0.677 (0.522 to 0.832) | 0.977 | 42.521 | 0.673 (0.571 to 0.775) | 0.893 | 15.800 | 0.893 (0.491 to 1.01) |
| 6 | 0.738 | 8.671 | 0.868 (0.583 to 1.15) | 0.744 | 10.381 | 0.688 (0.465 to 0.910) | 0.712 | 16.610 | 0.638 (0.414 to 0.861) |
| 7 | 0.894 | 16.119 | 0.780 (0.512 to 1.05) | 0.950 | 23.807 | 0.799 (0.616 to 0.981) | 0.880 | 18.541 | 0.673 (0.425 to 0.922) |
| 8 | 0.777 | 20.086 | 0.595 (0.355 to 0.837) | 0.672 | 59.740 | 0.534 (0.253 to 0.815) | 0.643 | 15.959 | 0.582 (0.254 to 0.909) |
| 9 | 0.693 | 25.028 | 0.547 (0.354 to 0.740) | 0.651 | 39.252 | 0.569 (0.349 to 0.790) | 0.735 | 29.079 | 0.586 (0.399 to 0.772) |
| 10 | 0.712 | 20.086 | 0.707 (0.340 to 1.07) | 0.827 | 13.197 | 0.744 (0.467 to 1.02) | 0.710 | 36.966 | 0.710 (0.352 to 1.07) |
| 11 | 0.985 | 7.171 | 0.985 (0.769 to 0.927) | 0.685 | 70.105 | 0.375 (0.183 to 0.566) | 0.933 | 10.591 | 0.683 (0.545 to 0.822) |
| 12 | 0.842 | 10.805 | 0.760 (0.528 to 0.991) | 0.712 | 16.945 | 0.782 (0.431 to 1.13) | 0.826 | 17.116 | 0.711 (0.481 to 0.941) |
| 13 | 0.670 | 38.475 | 0.366 (0.070 to 0.662) | 0.895 | 42.098 | 0.530 (0.321 to 0.739) | 0.846 | 48.911 | 0.493 (0.251 to 0.735) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kraydich, M.J.; Gonzalez, J.; Ziebold, M.A.; Asmar, P.N.; Chehab, A.; Malek, M.H. Analyzing How Skinfold Thickness Affects Log-Transformed EMG Amplitude–Power Output Metrics. Bioengineering 2024, 11, 1294. https://doi.org/10.3390/bioengineering11121294
Kraydich MJ, Gonzalez J, Ziebold MA, Asmar PN, Chehab A, Malek MH. Analyzing How Skinfold Thickness Affects Log-Transformed EMG Amplitude–Power Output Metrics. Bioengineering. 2024; 11(12):1294. https://doi.org/10.3390/bioengineering11121294
Chicago/Turabian StyleKraydich, Matthew J., Jacob Gonzalez, Marcus A. Ziebold, Patrick N. Asmar, Amanda Chehab, and Moh H. Malek. 2024. "Analyzing How Skinfold Thickness Affects Log-Transformed EMG Amplitude–Power Output Metrics" Bioengineering 11, no. 12: 1294. https://doi.org/10.3390/bioengineering11121294
APA StyleKraydich, M. J., Gonzalez, J., Ziebold, M. A., Asmar, P. N., Chehab, A., & Malek, M. H. (2024). Analyzing How Skinfold Thickness Affects Log-Transformed EMG Amplitude–Power Output Metrics. Bioengineering, 11(12), 1294. https://doi.org/10.3390/bioengineering11121294






