Machine Learning-Driven GLCM Analysis of Structural MRI for Alzheimer’s Disease Diagnosis
Abstract
1. Introduction
- To introduce the utilization of 22 sMRI gray-level co-occurrence matrix features for the characterization of AD activity;
- To strengthen the differentiation between healthy control, MCI, and AD patients by systematically comparing the synergistic power of GLCM features extracted across different sMRI planes;
- To thoroughly evaluate the discriminatory performance of the GLCM features by employing an extensive set of machine learning models.
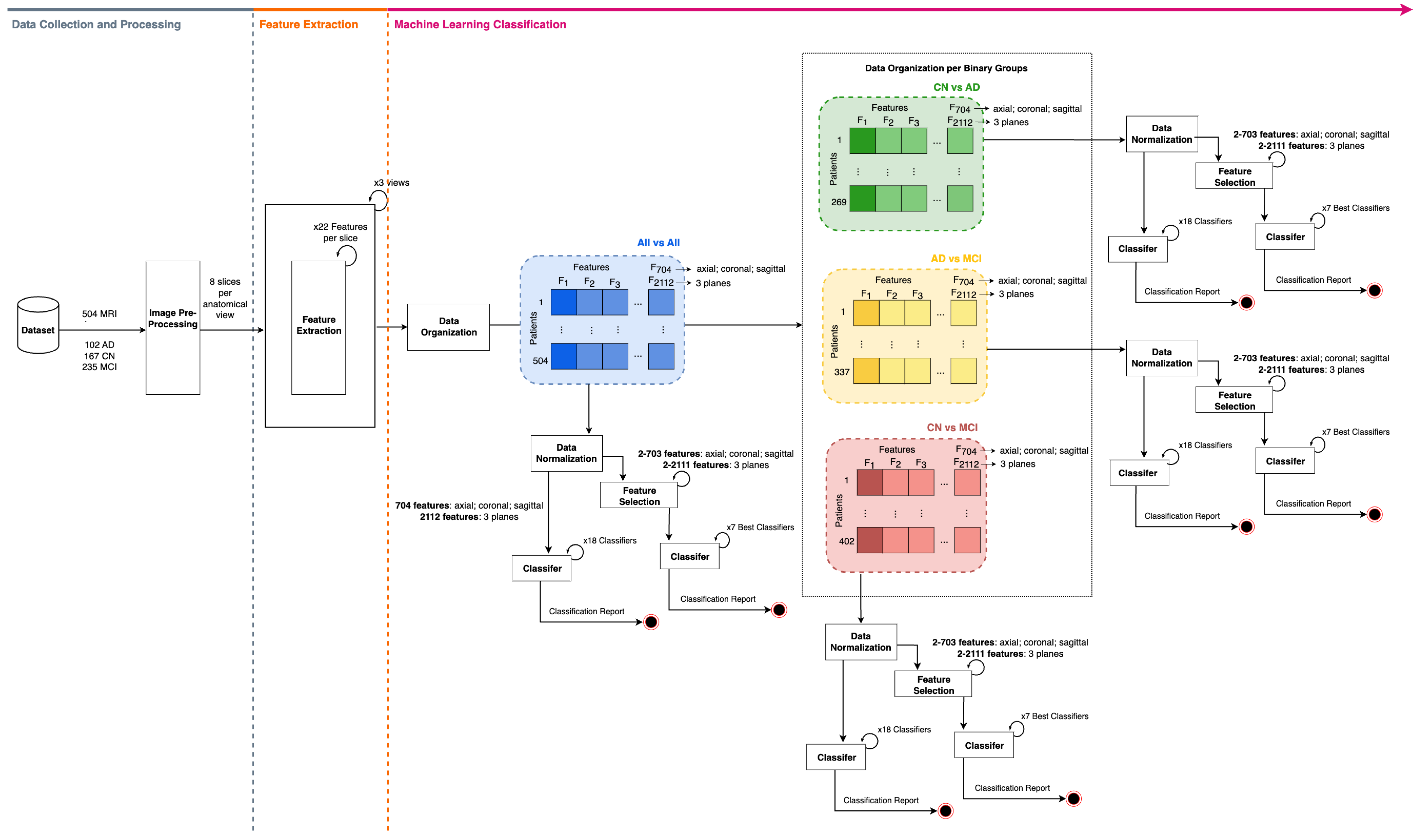
2. Materials and Methods
2.1. Dataset Description
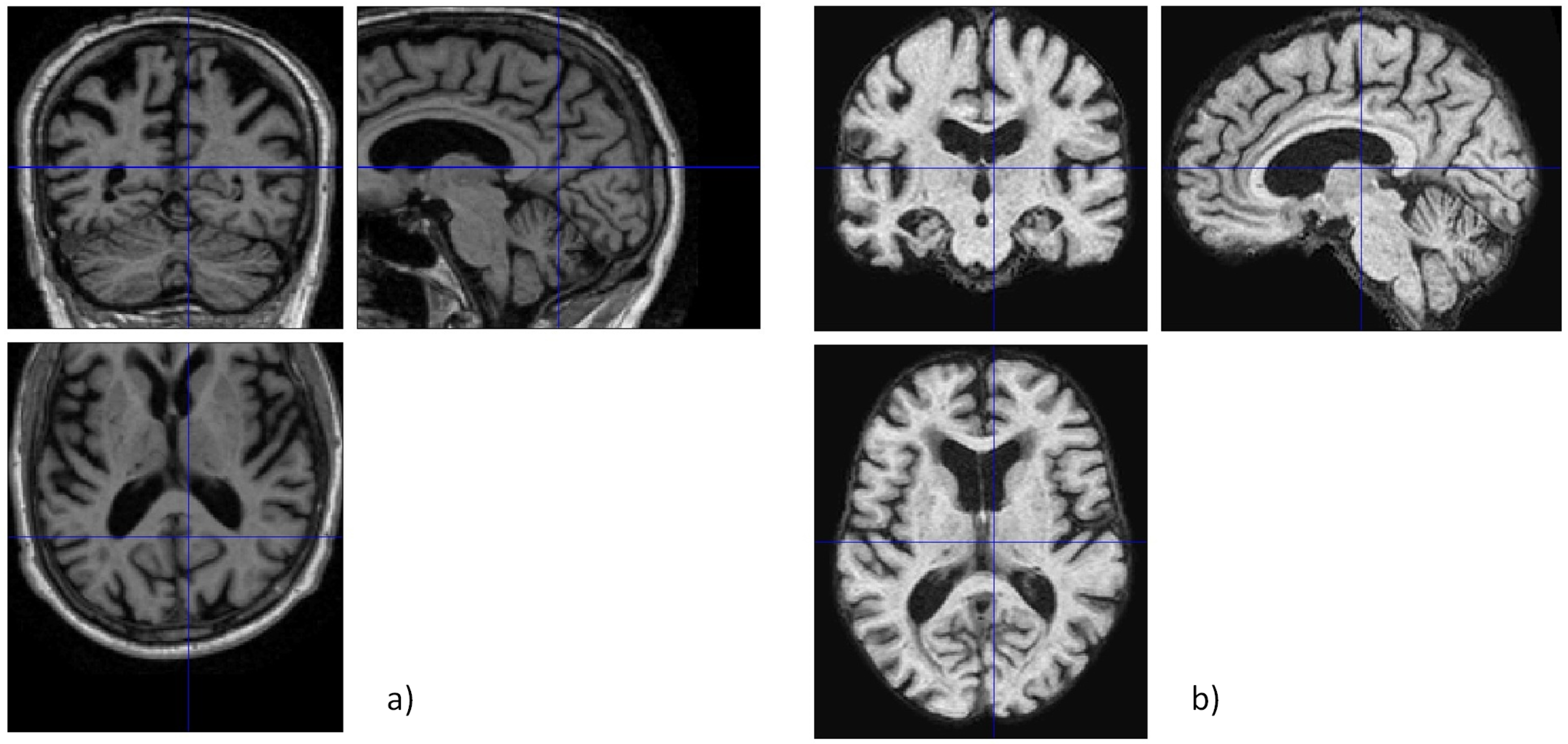
2.2. Image Pre-Processing
2.2.1. Data Cleaning
2.2.2. Skull Stripping
2.2.3. Slicing and Final Pre-Processing Steps
2.3. Feature Extraction
Texture Analysis via GLCM
2.4. Classification Framework
2.4.1. ML Discrimination Between Study Groups—No Feature Selection Approach
2.4.2. ML Discrimination Between Study Groups—Feature Selection Approach
2.4.3. Classification Metrics
3. Classification Results
3.1. Discrimination Results Without Feature Selection
- CN vs. AD: Referring to Table 5, the highest of 85.2% was achieved using information from the three planes, obtained through the cML algorithms LinSVC or OvsR. The lowest classification was 66.7%, obtained using the axial plane.
- AD vs. MCI: From Table 6, the highest classification of 98.5% was achieved from the three planes using the LogReg classifier. The axial plane exhibited the lowest classification , recording a value of 64.7%.
- CN vs. MCI: As seen in Table 7, the most notable classification outcome was 88.9%, achieved from the coronal plane using the ExTreeC cML algorithm. The axial plane yielded the least favorable outcome, demonstrating of 56.8%.
- all vs. all: Table 8 shows that the most significant classification of 82.2% was achieved through the cML algorithms LinSVC or OvsR. The minimum attained was 49.5%, again from the axial plane.
3.2. Discrimination Results with Feature Selection
- CN vs. AD: Referring to Table 9, the highest classification of 85.2% was achieved utilizing the sagittal plane, incorporating 491 selected features and employing the ExTreeC classifier. The lowest classification was 72.2% using the axial plane.
- AD vs. MCI: From Table 10, the highest classification of 98.5% was attained through the ML algorithms LinSVC or OvsR, using 3 planes and 1379 features. The lowest classification attained was 80.9% using the axial plane.
- CN vs. MCI: From Table 11, the peak value of 95.1% was obtained using 1129 features selected from the three planes and the ExTreeC classifier. The minimum reached was 67.9% from the axial plane.
- all vs. all: As indicated in Table 12, the classification presented the highest , 87.1%, for the three planes using 1366 features selected and the LinSVC classifier. The axial plane demonstrated the lowest classification , registering 55.4%.
4. Discussion
4.1. No Feature Selection Approach vs. Feature Selection Approach
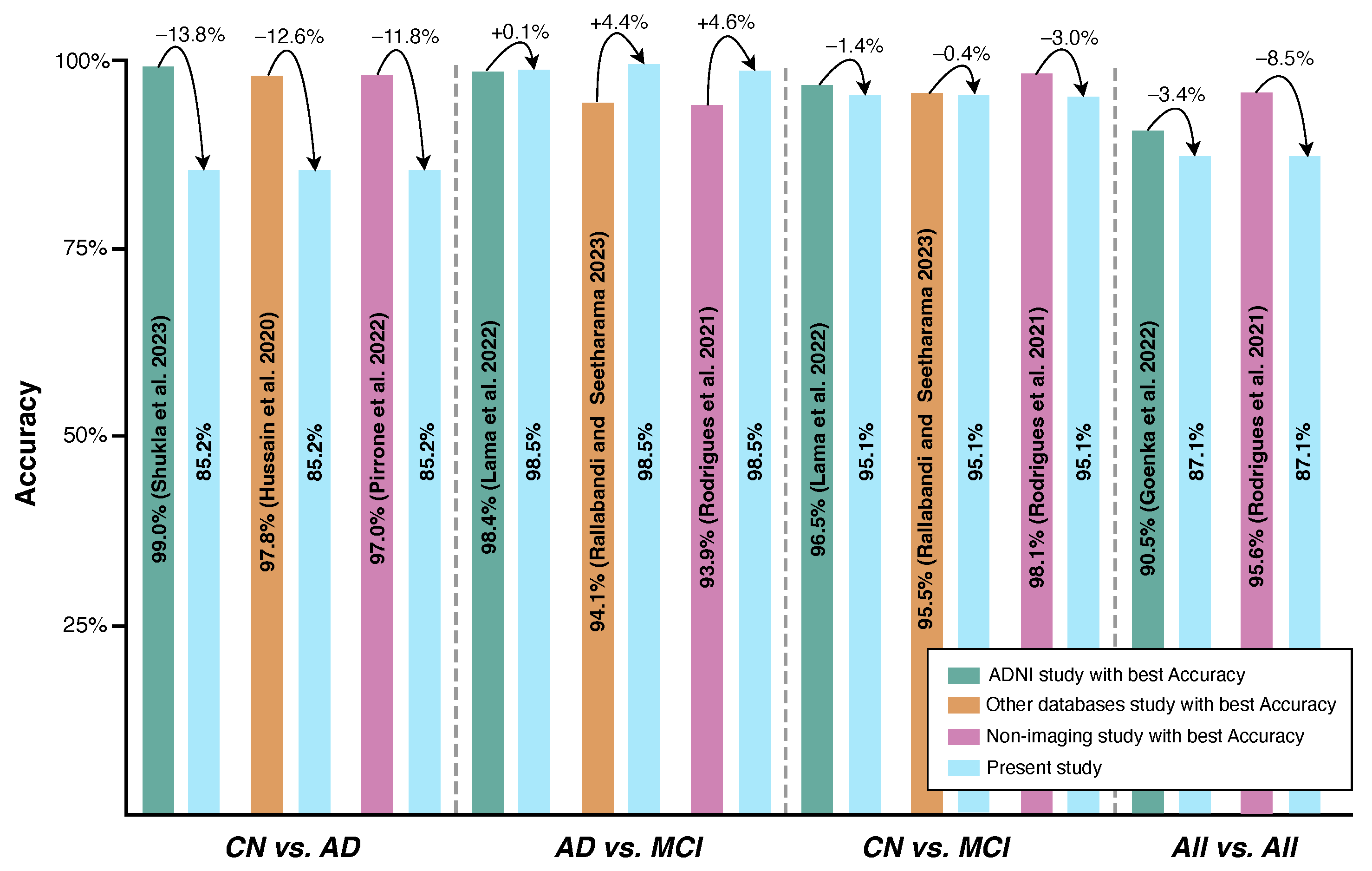
4.2. Study Results vs. State-of-the-Art Results
- Not all state-of-the-art studies attempted the three binary classifications conducted in the present work.
- In terms of the pair CN vs. MCI, the proposed model outperformed the majority of the consulted state-of-the-art sMRI-based studies [9,12,15,16,17,18,19,20] by 9.5%, 6.9%, 2.2%, 15.9%, 17.1%, 22.7%, 18.2%, and 5.9%, respectively. The one that yielded better performance than the current work did so by a maximum of 1.4% [14].
- The pair that showed the higher classification , AD vs. MCI, successfully outperformed not only all sMRI-based studies but also the ones related to fMRI and PET, enhancing the importance of the present work’s findings. Higher results have been obtained with differences ranging from 0.10% [14] to 25.8% [19] regarding . Although the classes were imbalanced in the present work, due to the high number of MCI patients when compared with AD patients, the attained was accompanied by a value of 99.0%, suggesting that the model generalizes well, avoiding overfitting. This is a significant finding, opening the door to more efficient early diagnosis in real-world settings since MCI is considered a precursor to AD.
- Compared with the study in [23], the present study shows a gain of 4.4% regarding the for the AD vs. MCI pair, but a loss of 0.4% for the CN vs. MCI pair.
- It outperformed the study in [26] by 12.1%, but was outperformed by the algorithms employed in the studies in [27,28] by 8.5% and 2.9% in terms of , respectively; nevertheless, it was unable to outperform the state-of-the-art for the pair CN vs. AD, being surpassed by 11.8% [26], 10.8% [27], and 9.8% [28];
- It underperformed with regard to the Rodrigues et al., 2021 study [27] for the multi-classification set ( vs. ), with differences of about 8.5%.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| th entry in a normalized gray-tone | |
| spatial dependence matrix. | |
| Number of distinct gray levels in the | |
| quantized image | |
| , | Mean gray level intensities of and , |
| respectively | |
| , | Standard deviations of and , respectively |
| Entropy of | |
| Entropy of | |
| Marginal row probabilities | |
| Marginal column probabilities | |
References
- Scheltens, P.; De Strooper, B.; Kivipelto, M.; Holstege, H.; Chételat, G.; Teunissen, C.E.; Cummings, J.; van der Flier, W.M. Alzheimer’s disease. Lancet 2021, 397, 1577–1590. [Google Scholar] [CrossRef] [PubMed]
- Alzheimer Portugal. A Doença de Alzheimer. Available online: https://alzheimerportugal.org/a-doenca-de-alzheimer/ (accessed on 21 January 2024).
- World Health Organization. World Failing to Address Dementia Challenge. Available online: https://www.who.int/news/item/02-09-2021-world-failing-to-address-dementia-challenge (accessed on 21 January 2024).
- Porsteinsson, A.; Isaacson, R.; Knox, S.; Sabbagh, M.; Rubino, I. Diagnosis of Early Alzheimer’s Disease: Clinical Practice in 2021. J. Prev. Alzheimer’s Dis. 2021, 8, 371–386. [Google Scholar] [CrossRef] [PubMed]
- Raza, N.; Naseer, A.; Tamoor, M.; Zafar, K. Alzheimer Disease Classification through Transfer Learning Approach. Diagnostics 2023, 13, 801. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.; Kivipelto, M.; von Strauss, E. Epidemiology of Alzheimer’s disease: Occurrence, determinants, and strategies toward intervention. Dialogues Clin. Neurosci. 2009, 11, 111–128. [Google Scholar] [CrossRef]
- Alzheimer’s Association. 2023 Alzheimer’s disease facts and figures. Alzheimer’s Dement. 2023, 19, 1598–1695. [Google Scholar] [CrossRef]
- Tahami Monfared, A.A.; Byrnes, M.; White, L.; Zhang, Q. Alzheimer’s Disease: Epidemiology and Clinical Progression. Neurol. Ther. 2022, 11, 553–569. [Google Scholar] [CrossRef]
- Zhang, Q.; Long, Y.; Cai, H.; Chen, Y.W. Lightweight neural network for Alzheimer’s disease classification using multi-slice sMRI. Magn. Reson. Imaging 2024, 107, 164–170. [Google Scholar] [CrossRef]
- Srividhya, L.; Sowmya, V.; Vinayakumar, R.; Gopalakrishnan, E.A.; Sowmya, K.P. Deep learning-based approach for multi-stage diagnosis of Alzheimer’s disease. Multimed. Tools Appl. 2023, 83, 16799–16822. [Google Scholar] [CrossRef]
- Shukla, A.; Tiwari, R.; Tiwari, S. Structural biomarker-based Alzheimer’s disease detection via ensemble learning techniques. Int. J. Imaging Syst. Technol. 2023, 34, e22967. [Google Scholar] [CrossRef]
- Silva, J.; Bispo, B.C.; Rodrigues, P.M. Structural MRI Texture Analysis for Detecting Alzheimer’s Disease. J. Med. Biol. Eng. 2023, 43, 227–238. [Google Scholar] [CrossRef]
- Wang, L.; Sheng, J.; Zhang, Q.; Zhou, R.; Li, Z.; Xin, Y.; Zhang, Q. Functional Brain Network Measures for Alzheimer’s Disease Classification. IEEE Access 2023, 11, 111832–111845. [Google Scholar] [CrossRef]
- Lama, R.K.; Kim, J.I.; Kwon, G.R. Classification of Alzheimer’s Disease Based on Core-Large Scale Brain Network Using Multilayer Extreme Learning Machine. Mathematics 2022, 10, 1967. [Google Scholar] [CrossRef]
- Pei, Z.; Wan, Z.; Zhang, Y.; Wang, M.; Leng, C.; Yang, Y.H. Multi-scale attention-based pseudo-3D convolution neural network for Alzheimer’s disease diagnosis using structural MRI. Pattern Recognit. 2022, 131, 108825. [Google Scholar] [CrossRef]
- Prajapati, R.; Kwon, G.R. A Binary Classifier Using Fully Connected Neural Network for Alzheimer’s Disease Classification. J. Multimed. Inf. Syst. 2022, 9, 21–32. [Google Scholar] [CrossRef]
- Goenka, N.; Tiwari, S. Multi-class classification of Alzheimer’s disease through distinct neuroimaging computational approaches using Florbetapir PET scans. Evol. Syst. 2022, 14, 801–824. [Google Scholar] [CrossRef]
- Kang, W.; Lin, L.; Zhang, B.; Shen, X.; Wu, S. Multi-model and multi-slice ensemble learning architecture based on 2D convolutional neural networks for Alzheimer’s disease diagnosis. Comput. Biol. Med. 2021, 136, 104678. [Google Scholar] [CrossRef]
- Prajapati, R.; Khatri, U.; Kwon, G.R. An Efficient Deep Neural Network Binary Classifier for Alzheimer’s Disease Classification. In Proceedings of the 2021 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Jeju Island, Republic of Korea, 13–16 April 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Lee, E.; Choi, J.S.; Kim, M.; Suk, H.I. Toward an interpretable Alzheimer’s disease diagnostic model with regional abnormality representation via deep learning. NeuroImage 2019, 202, 116113. [Google Scholar] [CrossRef]
- Wen, J.; Thibeau-Sutre, E.; Diaz-Melo, M.; Samper-González, J.; Routier, A.; Bottani, S.; Dormont, D.; Durrleman, S.; Burgos, N.; Colliot, O. Convolutional neural networks for classification of Alzheimer’s disease: Overview and reproducible evaluation. Med. Image Anal. 2020, 63, 101694. [Google Scholar] [CrossRef]
- Hussain, E.; Hasan, M.; Hassan, S.; Azmi, T.; Rahman, M.A.; Parvez, M.Z. Deep Learning Based Binary Classification for Alzheimer’s Disease Detection using Brain MRI Images. In Proceedings of the 2020 15th IEEE Conference on Industrial Electronics and Applications (ICIEA), Kristiansand, Norway, 9–13 November 2020; pp. 1115–1120. [Google Scholar] [CrossRef]
- Rallabandi, V.S.; Seetharaman, K. Deep learning-based classification of healthy aging controls, mild cognitive impairment and Alzheimer’s disease using fusion of MRI-PET imaging. Biomed. Signal Process. Control 2023, 80, 104312. [Google Scholar] [CrossRef]
- Lahmiri, S. Integrating convolutional neural networks, kNN, and Bayesian optimization for efficient diagnosis of Alzheimer’s disease in magnetic resonance images. Biomed. Signal Process. Control 2023, 80, 104375. [Google Scholar] [CrossRef]
- Qiu, S.; Joshi, P.S.; Miller, M.I.; Xue, C.; Zhou, X.; Karjadi, C.; Chang, G.H.; Joshi, A.S.; Dwyer, B.; Zhu, S.; et al. Development and validation of an interpretable deep learning framework for Alzheimer’s disease classification. Brain 2020, 143, 1920–1933. [Google Scholar] [CrossRef] [PubMed]
- Pirrone, D.; Weitschek, E.; Di Paolo, P.; De Salvo, S.; De Cola, M.C. EEG Signal Processing and Supervised Machine Learning to Early Diagnose Alzheimer’s Disease. Appl. Sci. 2022, 12, 5413. [Google Scholar] [CrossRef]
- Rodrigues, P.M.; Bispo, B.C.; Garrett, C.; Alves, D.; Teixeira, J.P.; Freitas, D. Lacsogram: A New EEG Tool to Diagnose Alzheimer’s Disease. IEEE J. Biomed. Health Inform. 2021, 25, 3384–3395. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, P.M.; Freitas, D.R.; Teixeira, J.P.; Alves, D.; Garrett, C. Electroencephalogram Signal Analysis in Alzheimer’s Disease Early Detection. Int. J. Reliab. Qual. E-Healthc. 2018, 7, 40–59. [Google Scholar] [CrossRef]
- AlMansoori, M.E.; Jemimah, S.; Abuhantash, F.; AlShehhi, A. Predicting early Alzheimer’s with blood biomarkers and clinical features. Sci. Rep. 2024, 14, 6039. [Google Scholar] [CrossRef]
- Silva, M.; Ribeiro, P.; Bispo, B.C.; Rodrigues, P.M. Detecção da Doença de Alzheimer através de Parâmetros Não-Lineares de Sinais de Fala. In Proceedings of the Anais do XLI Simpósio Brasileiro de Telecomunicações e Processamento de Sinais, Rio de Janeiro, Brazil, 8–11 October 2023; Sociedade Brasileira de Telecomunicações: Rio de Janeiro, Brazi, 2023. SBrT2023. [Google Scholar] [CrossRef]
- Johnson, K.A.; Fox, N.C.; Sperling, R.A.; Klunk, W.E. Brain Imaging in Alzheimer Disease. Cold Spring Harb. Perspect. Med. 2012, 2, a006213. [Google Scholar] [CrossRef]
- Hu, X.; Meier, M.; Pruessner, J. Challenges and opportunities of diagnostic markers of Alzheimer’s disease based on structural magnetic resonance imaging. Brain Behav. 2023, 13, e2925. [Google Scholar] [CrossRef]
- Alzheimer’s Disease Neuroimaging Initiative-ADNI. Data Sharing and Publication Policy. Available online: https://adni.loni.usc.edu/wp-content/uploads/how_to_apply/ADNI_DSP_Policy.pdf (accessed on 15 May 2023).
- Jack, C.R.; Barnes, J.; Bernstein, M.A.; Borowski, B.J.; Brewer, J.; Clegg, S.; Dale, A.M.; Carmichael, O.; Ching, C.; DeCarli, C.; et al. Magnetic resonance imaging in Alzheimer’s Disease Neuroimaging Initiative 2. Alzheimer’s Dement. 2015, 11, 740–756. [Google Scholar] [CrossRef]
- Kuhnke, P. Structural Pre-Processing Batch. Available online: https://github.com/PhilKuhnke/fMRI_analysis/blob/main/1Preprocessing/SPM12/batch_structural_preproc_job.m (accessed on 25 May 2023).
- Kuhnke, P.; Kiefer, M.; Hartwigsen, G. Task-Dependent Recruitment of Modality-Specific and Multimodal Regions during Conceptual Processing. Cereb. Cortex 2020, 30, 3938–3959. [Google Scholar] [CrossRef]
- Fatima, A.; Shahid, A.R.; Raza, B.; Madni, T.M.; Janjua, U.I. State-of-the-Art Traditional to the Machine- and Deep-Learning-Based Skull Stripping Techniques, Models, and Algorithms. J. Digit. Imaging 2020, 33, 1443–1464. [Google Scholar] [CrossRef]
- Arafa, D.; Moustafa, H.E.D.; Ali, H.; Ali-Eldin, A.; Saraya, S. A deep learning framework for early diagnosis of Alzheimer’s disease on MRI images. Multimed. Tools Appl. 2023, 83, 3767–3799. [Google Scholar] [CrossRef]
- MathWorks Help Center. Graycomatrix. Available online: https://www.mathworks.com/help/images/ref/graycomatrix.html (accessed on 7 October 2023).
- Uppuluri, A. GLCM Texture Features. Available online: https://www.mathworks.com/matlabcentral/fileexchange/22187-glcm-texture-features (accessed on 8 October 2023).
- Peck, R.; Olsen, C.; Devore, J. Introduction to Statistics and Data Analysis; Cengage Learning: Belmont, CA, USA, 2008; p. 880. [Google Scholar]
- Ribeiro, P.; Sá, J.; Paiva, D.; Rodrigues, P.M. Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis. Bioengineering 2024, 11, 58. [Google Scholar] [CrossRef] [PubMed]
- Sevani, N.; Hermawan, I.; Jatmiko, W. Feature Selection based on F-score for Enhancing CTG Data Classification. In Proceedings of the 2019 IEEE International Conference on Cybernetics and Computational Intelligence (CyberneticsCom), Banda Aceh, Indonesia, 22–24 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 18–22. [Google Scholar] [CrossRef]
- Hicks, S.A.; Strümke, I.; Thambawita, V.; Hammou, M.; Riegler, M.A.; Halvorsen, P.; Parasa, S. On evaluation metrics for medical applications of artificial intelligence. Sci. Rep. 2022, 12, 5979. [Google Scholar] [CrossRef] [PubMed]
- Mutasa, S.; Sun, S.; Ha, R. Understanding artificial intelligence based radiology studies: What is overfitting? Clin. Imaging 2020, 65, 96–99. [Google Scholar] [CrossRef]
- Dhal, P.; Azad, C. A comprehensive survey on feature selection in the various fields of machine learning. Appl. Intell. 2021, 52, 4543–4581. [Google Scholar] [CrossRef]
- Duara, R.; Barker, W. Heterogeneity in Alzheimer’s Disease Diagnosis and Progression Rates: Implications for Therapeutic Trials. Neurotherapeutics 2022, 19, 8–25. [Google Scholar] [CrossRef]
- Saleem, T.J.; Zahra, S.R.; Wu, F.; Alwakeel, A.; Alwakeel, M.; Jeribi, F.; Hijji, M. Deep Learning-Based Diagnosis of Alzheimer’s Disease. J. Pers. Med. 2022, 12, 815. [Google Scholar] [CrossRef]
- Ebrahimi-Ghahnavieh, A.; Luo, S.; Chiong, R. Transfer Learning for Alzheimer’s Disease Detection on MRI Images. In Proceedings of the 2019 IEEE International Conference on Industry 4.0, Artificial Intelligence, and Communications Technology(IAICT), Bali, Indonesia, 1–3 July 2019; IEEE: Piscataway, NJ, USA, 2019. [Google Scholar] [CrossRef]
| Study | Database | # of Subjects | Exam Modality | Features Extracted | Best Classifier | Feature Selection | Validation Approach | Accuracy |
|---|---|---|---|---|---|---|---|---|
| Within ADNI Database | ||||||||
| [9] | ADNI | 1200 | sMRI | Spatial Information | Lightweight Neural Network | Not Applied | Hold-out | CN vs. AD—95.0% CN vs. MCI—85.6% AD vs. MCI—87.5% |
| [10] | ADNI | 1296 | sMRI | Hierarchical Patterns, Textures, and Other Structural Features | 2D CNN (ResNet-50v2) | Not Applied | Cross-validation | CN vs. AD—91.2% All vs. All—90.3% |
| [11] | ADNI | 600 | sMRI | Statistical Features | Ensemble LR_SVM | K-Best | Cross-validation | CN vs. AD—99.0% CN vs. MCI—96.0% AD vs. MCI—85.0% |
| [12] | ADNI | 89 | sMRI | Statistical and Textural Features | BagT FGSVM QSVM SubKNN | F-score | Cross-validation | CN vs. AD—93.3% CN vs. MCI—88.2% AD vs. MCI—87.7% All vs. All—75.3% |
| [13] | ADNI | 96 | fMRI | Graph Theoretical Measures | Linear SVM | MRMR | Cross-validation | CN vs. AD—96.8% |
| [14] | ADNI | 95 | fMRI | Correlation Matrix Between Different ROIs | SL-RELM | Adaptive Structure Learning | Cross-validation | CN vs. AD—95.4% CN vs. MCI—96.5% AD vs. MCI—98.4% |
| [15] | ADNI | 2116 | sMRI | Multi-Scale and Hierarchical Transformed Features | CNN (PKG-Net) | Not Applied | Cross-validation | CN vs. AD—94.3% CN vs. MCI—92.9% AD vs. MCI—92.1% |
| [16] | ADNI | 178 | sMRI | Cortical Volumetric Features | Fully Connected Neural Network | PCA | Cross-validation | CN vs. AD—87.5% CN vs. MCI—79.2% AD vs. MCI—83.3% |
| [17] | ADNI | 381 | Amyloid PET | 3D Slice-Based Features | 3D CNN | Not Applied | Hold-out | CN vs. AD—92.9% CN vs. MCI—78.0% AD vs. MCI—87.2% All vs. All—90.5% |
| [18] | ADNI | 798 | sMRI | Spatial Features | Ensemble based on 2D CNN | Not Applied | Hold-out | CN vs. AD—90.4% CN vs. MCI—72.4% AD vs. MCI—77.2% |
| [19] | ADNI | 179 | sMRI | Cortical Surface Labels | DNN | Not Applied | Cross-validation | CN vs. AD—85.2% CN vs. MCI—76.9% AD vs. MCI—72.7% |
| [20] | ADNI | 801 | sMRI | Voxel-Level GM Volume Density | CNN Ensemble Model | Not Applied | Cross-validation | CN vs. AD—92.8% CN vs. MCI—89.2% AD vs. MCI—81.5% All vs. All—71% |
| Present Study | ADNI | 504 | sMRI | Statistical and Textural Features | ExTreeC LinSVC OvsR | F-Score | Hold-out | CN vs. AD—85.2% CN vs. MCI—95.1% AD vs. MCI—98.5% All vs. All—87.1% |
| Different Imaging Databases | ||||||||
| [21] | AIBL | 1455 | sMRI | Voxel-Based Features | SVM | Not Applied | Cross-validation | CN vs. AD—88.0% |
| [22] | OASIS | 416 | sMRI | Model Components | 12-layer CNN | Not Applied | Hold-out | CN vs. AD—97.8% |
| [23] | OASIS | 1098 | MRI-PET Fusion | MRI-PET Feature Maps | Inception–ResNet CNN Model | CNN-Based Ranking | Hold-out | CN vs. AD—95.9% CN vs. MCI—95.5% AD vs. MCI—94.1% |
| [24] | OASIS | 77 | MRI | CNN-Based Features | KNN | ROC-Based Ranking | Cross-validation | CN vs. AD—95.0% |
| [25] | FHS | 102 | sMRI | Disease Probability Maps | CNN | Not Applied | Hold-out | CN vs. AD—76.6% |
| [25] | NACC | 582 | sMRI | Disease Probability Maps | CNN | Not Applied | Hold-out | CN vs. AD—81.8% |
| Non-Imaging Modalities | ||||||||
| [26] | IRCCS | 105 | EEG | Frequency Domain Features | KNN | Information Gain Filter | Cross-validation | CN vs. AD—97.0% CN vs. MCI—95.0% AD vs. MCI—83.0% All vs. All—75.0% |
| [27] | University Hospital Center of São João | 38 | EEG | Cepstral and Lacstral Distances | ANN | KW test | Cross-validation | CN vs. ADM—96.0% CN vs. MCI—98.1% ADM-ADA vs. MCI—93.9% All vs. All—95.6% |
| [28] | University Hospital Center of São João | 38 | EEG | Relative Power, Spectral Ratios, Maxima, Minima, and Zero Crossing Distances | ANN | KW test | Cross-validation | CN vs. AD—95.0% CN vs. MCI—77.0% AD vs. MCI—83.0% All vs. All—90.0% |
| [29] | ADNI | 623 | Biomarkers | SNPs, Gene and Clinical Data | SVM | Mutual Information | Cross-validation | CN vs. MCI/AD—95.0% |
| [30] | DementiaBank | 269 | Speech Signals | Statistical and Non-Linear Parameters | LogReg | Not Applied | Cross-validation | CN vs. AD—85.2% |
| Group | # of Subjects | Age Average ± SD | Gender F | M | MMSE Average ± SD | |
|---|---|---|---|---|---|
| CN | 167 | 77.9 ± 5.33 | 82 | 85 | 29.1 ± 1.16 |
| MCI | 235 | 77.0 ± 7.04 | 77 | 158 | 25.0 ± 4.22 |
| AD | 102 | 77.0 ± 7.33 | 50 | 52 | 18.9 ± 6.12 |
| Feature | Formula | Description |
|---|---|---|
| Autocorrelation | Measures the magnitude of the fineness and coarseness of the texture | |
| Contrast | Measures the local variations between pixels | |
| Correlation 1 | Estimates the combined probability occurrence of the indicated pixel pairs | |
| Correlation 2 | Estimates the combined probability occurrence of the indicated pixel pairs | |
| Cluster Prominence | Measures the skewness and asymmetry of the GLCM | |
| Cluster Shade | Measures the skewness and uniformity of the GLCM | |
| Dissimilarity | Measures the local intensity variation, defined as the mean absolute difference between neighboring pairs | |
| Energy | Specifies the sum of squared elements in the GLCM | |
| Entropy | Assesses the randomness of an intensity image | |
| Homogeneity 1 | Measures the nearness of the distribution of elements in the GLCM to the GLCM diagonal | |
| Homogeneity 2 | Measures the nearness of the distribution of elements in the GLCM to the GLCM diagonal | |
| Maximum Probability | Occurrence of the most predominant pair of neighboring intensity values | |
| Variance | Measures the distribution of neighboring intensity level pairs about the mean intensity level in the GLCM | |
| Sum Average | Measures the relationship between the occurrences of pairs with lower intensity values and the occurrences of pairs with higher intensity values | |
| Sum Variance | Measures groupings of voxels with similar gray-level values | |
| Sum Entropy | Measures neighborhood intensity value differences | |
| Difference Variance | Measures the heterogeneity that places higher weights on differing intensity level pairs that deviate more from the mean | |
| Difference Entropy | Measures the randomness/variability in the neighborhood intensity value differences | |
| Information Measure of Correlation 1 | Assesses the correlation between the probability distributions of i and j | |
| Information Measure of Correlation 2 | Assesses the correlation between the probability distributions of i and j | |
| Inverse Difference Normalized | Measures the local homogeneity of an image | |
| Inverse Difference Moment Normalized | Measures the local homogeneity of an image |
| Classifier | Hyperparameters |
|---|---|
| GaussianProcessClassifier (GauPro) | |
| LinearSVC (LinSVC) | Default parameters |
| SGDClassifier (SGD) | max_iter: 100, tol: 0.001 |
| KNearestNeighborsClassifier (KNN) | Default parameters |
| LogisticRegression (LogReg) | solver: |
| LogisticRegressionCV (LogRegCV) | cv: 3 |
| BaggingClassifier (BaggC) | Default parameters |
| ExtraTreesClassifier (ExTreeC) | n_estimators: 300 |
| RandomForestClassifier (RF) | max_depth: 5, n_estimators: 300, max_features: 1 |
| GaussianNB (GauNB) | Default parameters |
| DecisionTreeClassifier (DeTreeC) | max_depth: 5 |
| MLPClassifier (MLP) | α: 1, max_iter: 1000 |
| AdaBoostClassifier (AdaBoost) | Default parameters |
| QuadraticDiscriminantAnalysis (QuaDis) | Default parameters |
| OnevsRestClassifier (OvsR) | random_state: 0 |
| LightGBMClassifier (LGBM) | Default parameters |
| GradientBoostingClassifier (GradBoost) | Default parameters |
| SGDClassifier (SGD) | max_iter: 100, tol: |
| CN vs. AD | Classifier | Accuracy | Recall | Precision | Specificity | F1-Score | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|
| 3 Planes | LinSVC/OvsR | 85.2% | 77.3% | 85.0% | 85.3% | 81.0% | 83.9% | 85.1% |
| Axial Plane | DeTreeC | 66.7% | 10.5% | 66.7% | 66.7% | 18.2% | 53.8% | 66.7% |
| Coronal Plane | LinSVC | 70.4% | 52.4% | 64.7% | 73.0% | 57.9% | 67.1% | 68.7% |
| Sagittal Plane | LogRegCV | 79.6% | 57.9% | 78.6% | 80.0% | 66.7% | 74.7% | 79.3% |
| AD vs. MCI | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|
| 3 Planes | LogReg | 98.5% | 94.1% | 100.0% | 98.1% | 97.0% | 97.1% | 99.0% |
| Axial Plane | BaggC | 64.7% | 40.0% | 40.0% | 75.0% | 40.0% | 57.5% | 54.8% |
| Coronal Plane | ExTC | 94.1% | 73.3% | 100.0% | 93.0% | 84.6% | 86.7% | 96.4% |
| Sagittal Plane | LinSVC/OvsR | 95.6% | 95.2% | 90.9% | 97.8% | 93.0% | 95.5% | 94.3% |
| CN vs. MCI | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|
| 3 Planes | LinSVC/OvsR | 80.2% | 74.4% | 82.9% | 78.3% | 78.4% | 80.0% | 80.5% |
| Axial Plane | BaggC | 56.8% | 40.0% | 50.0% | 60.4% | 44.4% | 54.8% | 54.9% |
| Coronal Plane | ExTreeC | 88.9% | 83.8% | 91.2% | 87.2% | 87.3% | 88.5% | 89.2% |
| Sagittal Plane | ExTreeC | 82.7% | 80.6% | 75.8% | 87.5% | 78.1% | 82.3% | 81.4% |
| All vs. All | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|
| 3 Planes | LinSVC/OvsR | 82.2% | 82.2% | 83.0% | 89.9% | 81.9% | 89.8% | 86.2% |
| Axial Plane | BaggC | 49.5% | 49.5% | 48.4% | 74.5% | 48.1% | 62.2% | 60.0% |
| Coronal Plane | ExTreeC | 65.3% | 65.3% | 62.5% | 84.2% | 63.6% | 86.6% | 71.8% |
| Sagittal Plane | ExTreeC | 68.3% | 68.3% | 68.1% | 85.6% | 66.3% | 86.4% | 76.2% |
| CN vs. AD | # of Features | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|---|
| 3 Planes | 943 | LogRegCV | 77.8% | 70.8% | 77.3% | 78.1% | 73.9% | 77.1% | 77.7% |
| Axial Plane | 204 | OvsR | 72.2% | 42.9% | 75.0% | 71.4% | 54.5% | 66.9% | 73.2% |
| Coronal Plane | 533 | LinSVC/OvsR | 79.6% | 65.2% | 83.3% | 77.8% | 73.2% | 77.8% | 80.5% |
| Sagittal Plane | 491 | ExTreeC | 85.2% | 71.4% | 88.2% | 83.8% | 78.9% | 82.7% | 86.0% |
| AD vs. MCI | # of Features | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|---|
| 3 Planes | 1379 | LinSVC/OvsR | 98.5% | 94.1% | 100.0% | 98.1% | 97.0% | 97.1% | 99.0% |
| Axial Plane | 8 | BaggC | 80.9% | 50.0% | 69.2% | 83.6% | 58.1% | 71.0% | 76.1% |
| Coronal Plane | 645 | ExTreeC | 91.2% | 80.0% | 95.2% | 89.4% | 87.0% | 88.8% | 92.3% |
| Sagittal Plane | 199 | ExTreeC | 95.6% | 95.8% | 92.0% | 97.7% | 93.9% | 95.6% | 94.8% |
| CN vs. MCI | # of Features | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|---|
| 3 Planes | 1129 | ExTreeC | 95.1% | 93.1% | 93.1% | 96.2% | 93.1% | 94.6% | 94.6% |
| Axial Plane | 5 | ExTreeC | 67.9% | 58.8% | 62.5% | 71.4% | 60.6% | 66.6% | 66.8% |
| Coronal Plane | 606 | ExTreeC | 86.4% | 75.0% | 93.1% | 82.7% | 83.1% | 85.3% | 87.7% |
| Sagittal Plane | 509 | ExTreeC | 88.9% | 75.9% | 91.7% | 87.7% | 83.0% | 86.0% | 89.7% |
| All vs. All | # of Features | Classifier | Accuracy | Recall | Precision | Specificity | F1 | AUC | Gmean |
|---|---|---|---|---|---|---|---|---|---|
| 3 Planes | 1366 | LinSVC | 87.1% | 87.1% | 87.7% | 92.7% | 87.3% | 94.7% | 90.0% |
| Axial Plane | 694 | BaggC | 55.4% | 55.4% | 57.0% | 75.2% | 55.2% | 73.8% | 64.7% |
| Coronal Plane | 495 | ExTreeC | 75.2% | 75.2% | 73.6% | 89.5% | 73.4% | 87.2% | 81.1% |
| Sagittal Plane | 608 | ExTreeC | 71.3% | 71.3% | 68.6% | 89.5% | 67.7% | 89.3% | 78.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, M.J.; Ribeiro, P.; Rodrigues, P.M. Machine Learning-Driven GLCM Analysis of Structural MRI for Alzheimer’s Disease Diagnosis. Bioengineering 2024, 11, 1153. https://doi.org/10.3390/bioengineering11111153
Oliveira MJ, Ribeiro P, Rodrigues PM. Machine Learning-Driven GLCM Analysis of Structural MRI for Alzheimer’s Disease Diagnosis. Bioengineering. 2024; 11(11):1153. https://doi.org/10.3390/bioengineering11111153
Chicago/Turabian StyleOliveira, Maria João, Pedro Ribeiro, and Pedro Miguel Rodrigues. 2024. "Machine Learning-Driven GLCM Analysis of Structural MRI for Alzheimer’s Disease Diagnosis" Bioengineering 11, no. 11: 1153. https://doi.org/10.3390/bioengineering11111153
APA StyleOliveira, M. J., Ribeiro, P., & Rodrigues, P. M. (2024). Machine Learning-Driven GLCM Analysis of Structural MRI for Alzheimer’s Disease Diagnosis. Bioengineering, 11(11), 1153. https://doi.org/10.3390/bioengineering11111153








