Improving EEG Forward Modeling Using High-Resolution Five-Layer BEM-FMM Head Models: Effect on Source Reconstruction Accuracy
Abstract
:1. Introduction
- (i)
- (ii)
- BEM-FMM models have been found to be comparable or superior to FEM in terms of speed and accuracy in certain applications; for example, it has been found [34] that zero-order BEM-FMM is comparable in accuracy to second-order FEM for TMS modeling in the concentric spheres model. It was also found in [34] that zero-order BEM-FMM was the highest-accuracy method that they could implement within their computational constraints using a realistic, high-resolution brain model. This leads them to use zero-order BEM-FMM as their ground truth solution.
- (iii)
- Prescribing arbitrary finite-length dipoles, or point dipoles—which are the most common mathematical model for the simultaneous firing of a large number of neurons [35]—is an easy task in BEM, as the method inherently allows for arbitrary incident fields anywhere in space. On the other hand, modeling dipoles in FEM is much more challenging: several approaches are available [36], but using them would involve an additional error estimation; see also the St. Venant approach used in [10,37].
- Section 2 describes the materials used throughout the paper and the methods used for the analysis of four dipole locations chosen consistently across subjects;
- Section 4 summarizes our results;
- Section 5 includes a brief discussion and interpretation.
2. Localization Error in Selected Locations Across Varying Subjects and Parameters
- (i)
- We placed a dipole at a location, , on the midsurface between the CSF-GM and GM-WM tissue interfaces of our subject with an orientation, , normal to the CSF-GM interface.
- (ii)
- We simulated a single time sample of noiseless EEG data using the charge-based formulation of the boundary element method with fast multipole method acceleration (BEM-FMM) and adaptive mesh refinement (AMR), over a high-resolution five-layer (seven-compartment) head volume conduction model.
- (iii)
- We used the simulated EEG data to perform source reconstruction with a low-resolution three-layer head model, which is similar to the ones widely used in EEG source reconstruction. By doing so, we found the best fit for location , and orientation was provided by the FieldTrip Toolbox’s [14] source localization procedures.
- (iv)
- We computed the distance between both locations and the angle between and to measure the error of the fit.
- (i)
- dip1 — Posterior wall of the central sulcus, somatosensory cortex, and tangential dipole; Figure 1;
- (ii)
- dip2 — region, primary motor cortex, and radial dipole; Figure 2;
- (iii)
- dip3 — Temporal lobe, along the Heschl’s gyri or transverse temporal gyri; Figure 3;
- (iv)
- dip4 — Medio-temporal region; Figure 4.
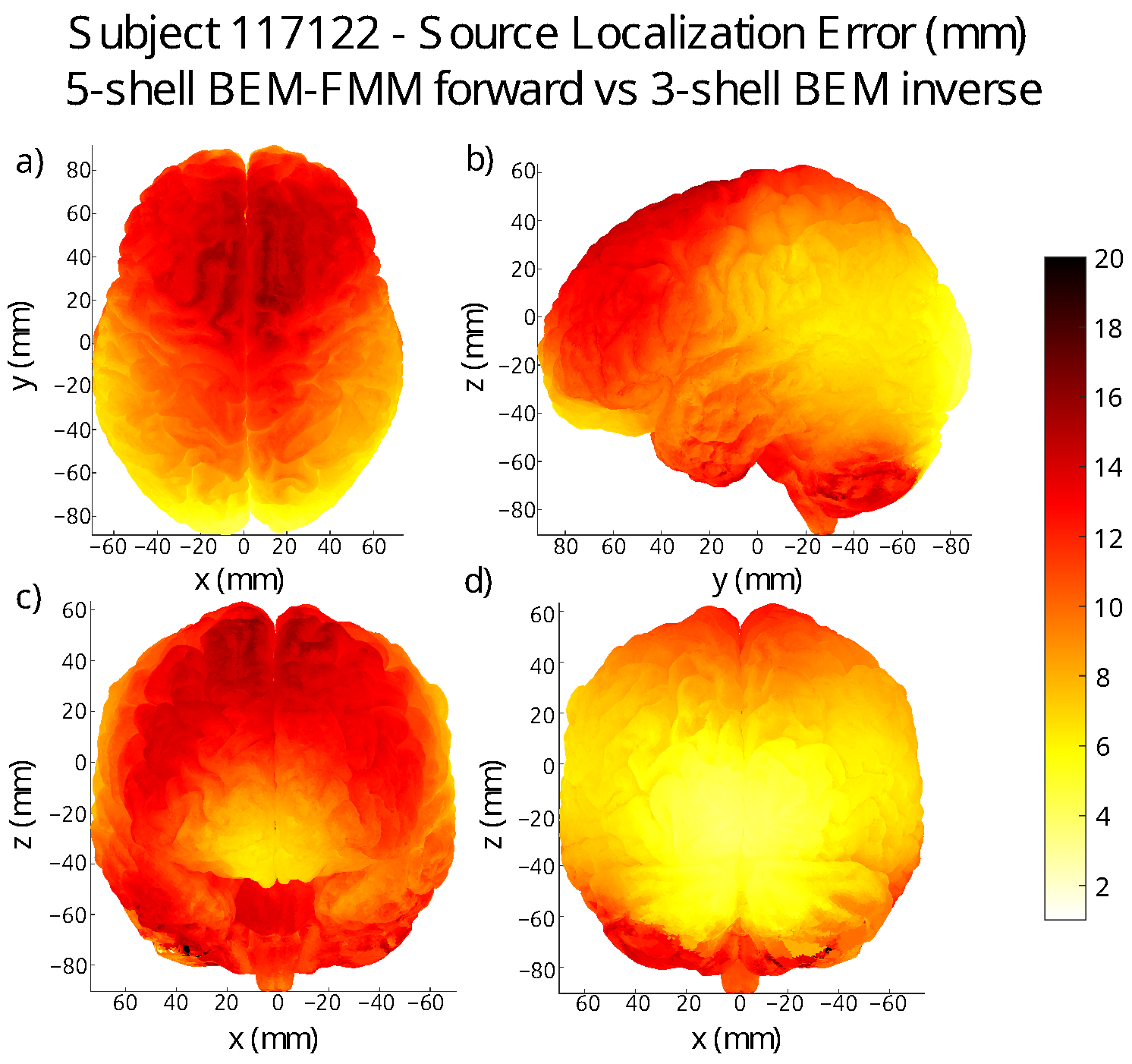
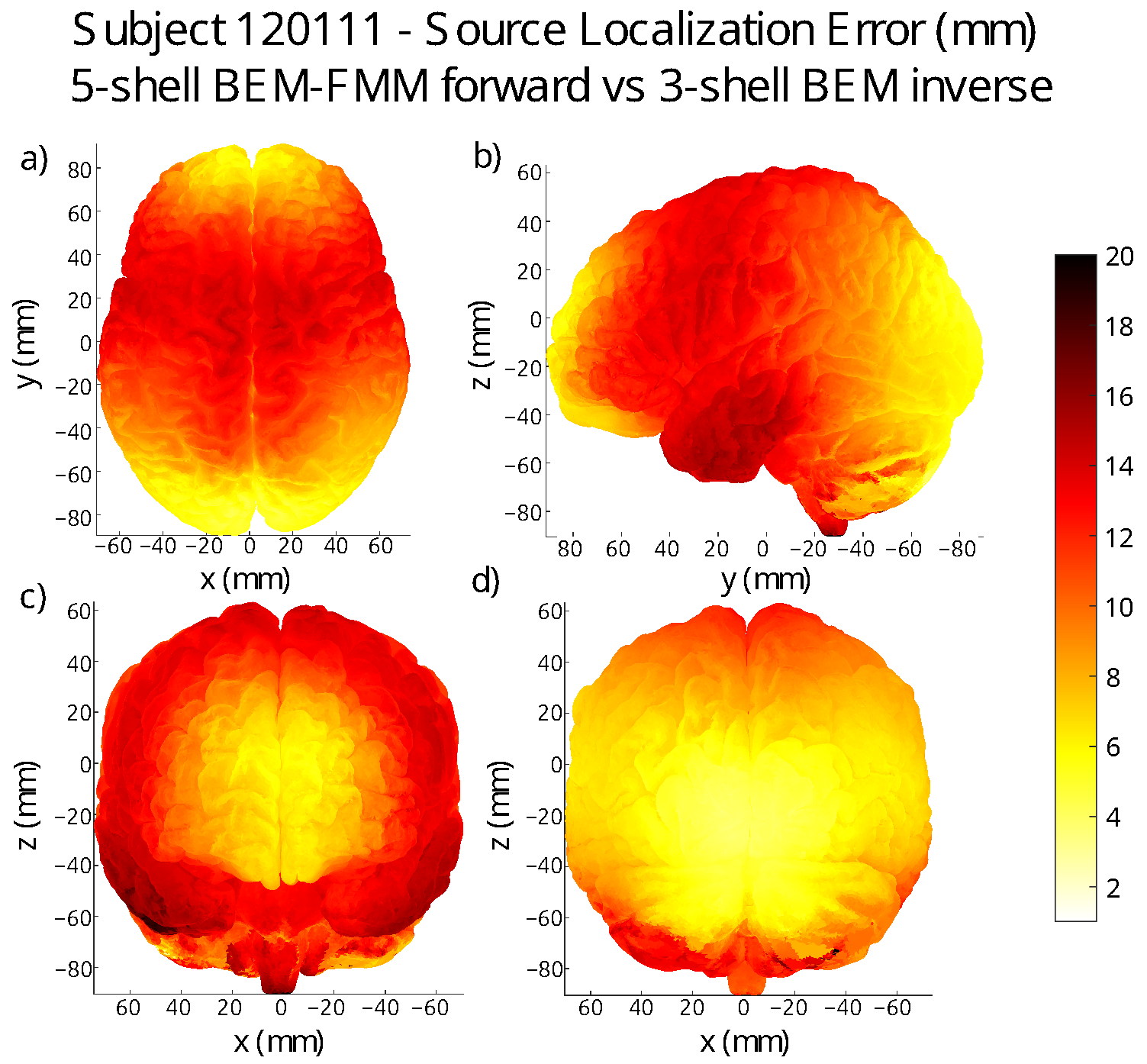
3. Localization Error Maps on the Grey Matter Surface of Each Subject
4. Results
5. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Knösche, T.R.; Haueisen, J. EEG/MEG Source Reconstruction; Springer: Cham, Switzerland, 2022. [Google Scholar]
- van Mierlo, P.; Vorderwülbecke, B.J.; Staljanssens, W.; Seeck, M.; Vulliémoz, S. Ictal eeg source localization in focal epilepsy: Review and future perspectives. Clin. Neurophysiol. 2020, 131, 2600–2616. [Google Scholar] [CrossRef] [PubMed]
- Guttmann-Flury, E.; Sheng, X.; Zhu, X. Channel selection from source localization: A review of four EEG-based brain–computer interfaces paradigms. Behav. Res. 2023, 55, 1980–2003. [Google Scholar] [CrossRef] [PubMed]
- Foti, D.; Weinberg, A.; Dien, J.; Hajcak, G. Event-related potential activity in the basal ganglia differentiates rewards from nonrewards: Temporospatial principal components analysis and source localization of the feedback negativity. Hum. Brain Mapp. 2011, 32, 2207–2216. [Google Scholar] [CrossRef] [PubMed]
- Hämäläinen, J.A.; Lohvansuu, K.; Ervast, L.; Leppänen, P.H.T. Event-related potentials to tones show differences between children with multiple risk factors for dyslexia and control children before the onset of formal reading instruction. Int. J. Psychophysiol. 2015, 95, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Pires, L.; Leitão, J.; Guerrini, C.; R Simões, M. Event-Related brain potentials in the study of inhibition: Cognitive control, source localization and Age-Related modulations. Neuropsychol. Rev. 2014, 24, 461–490. [Google Scholar] [CrossRef]
- Helmholtz, H. Ueber einige Gesetze der Vertheilung elektrischer Ströme in körperlichen Leitern, mit Anwendung auf die thierisch-elektrischen Versuche (Schluss.). Ann. Phys. Chem. 1853, 89, 211–233, 353–377. [Google Scholar] [CrossRef]
- Papageorgakis, C. Patient Specific Conductivity Models: Characterization of the Skull Bones. Ph.D. Thesis, Université Côte d’Azur, Nice, France, 2017. [Google Scholar]
- Vorwerk, J.; Cho, J.; Rampp, S.; Hamer, H.; Knösche, T.; Wolters, C. A guideline for head volume conductor modeling in EEG and MEG. Neuroimage 2014, 100, 590–607. [Google Scholar] [CrossRef]
- Vorwerk, J.; Aydin, Ü.; Wolters, C.H.; Butson, C.R. Influence of Head Tissue Conductivity Uncertainties on EEG Dipole Reconstruction. Front. Neurosci. 2019, 13, 531. [Google Scholar] [CrossRef]
- McCann, H.; Beltrachini, L. Impact of skull sutures, spongiform bone distribution, and aging skull conductivities on the eeg forward and inverse problems. J. Neural Eng. 2022, 19, 016014. [Google Scholar] [CrossRef]
- Kuratko, D.; Lacik, J.; Koudelka, V.; Vejmola, C.; Wójcik, D.K.; Raida, Z. Forward model of rat electroencephalogram: Comparative study of numerical simulations with measurements on rat head phantoms. IEEE Access 2022, 10, 92023–92035. [Google Scholar] [CrossRef]
- Tadel, F.; Baillet, S.; Mosher, J.C.; Pantazis, D.; Leahy, R.M. Brainstorm: A user-friendly application for MEG/EEG analysis. Comput. Intell. Neurosci. 2011, 2011, 879716. [Google Scholar] [CrossRef] [PubMed]
- Oostenveld, R.; Fries, P.; Maris, E.; Schoffelen, J.M. FieldTrip: Open Source Software for Advanced Analysis of MEG, EEG, and Invasive Electrophysiological Data. Comput. Intell. Neurosci. 2011, 2011, 156869. [Google Scholar] [CrossRef] [PubMed]
- Gramfort, A.; Luessi, M.; Larson, E.; Engemann, D.A.; Strohmeier, D.; Brodbeck, C.; Parkkonen, L.; Hämäläinen, M.S. MNE software for processing MEG and EEG data. NeuroImage 2014, 86, 446–460. [Google Scholar] [CrossRef] [PubMed]
- Delorme, A.; Makeig, S. EEGLAB: An open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J. Neurosci. Methods 2004, 134, 9–21. [Google Scholar] [CrossRef]
- Geselowitz, D.B. On Bioelectric Potentials in an Inhomogeneous Volume Conductor. Biophys. J. 1967, 7, 1–11. [Google Scholar] [CrossRef]
- Kybic, J.; Clerc, M.; Abboud, T.; Faugeras, O.; Keriven, R.; Papadopoulo, T. A common formalism for the integral formulations of the forward eeg problem. IEEE Trans. Med. Imaging 2005, 24, 12–28. [Google Scholar] [CrossRef] [PubMed]
- Ponasso, G.N. A survey on integral equations for bioelectric modeling. Phys. Med. Biol. 2024, 69, 17TR02. [Google Scholar] [CrossRef]
- Fischl, B.; Dale, A.M. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proc. Natl. Acad. Sci. USA 2000, 97, 11050–11055. [Google Scholar] [CrossRef]
- Wartman, W.A.; Weise, K.; Rachh, M.; Morales, L.; Deng, Z.; Nummenmaa, A.; Makaroff, S.N. An adaptive h-refinement method for the boundary element fast multipole method for quasi-static electromagnetic modeling. Phys. Med. Biol. 2024, 69, 055030. [Google Scholar] [CrossRef]
- Weise, K.; Wartman, W.A.; Knösche, T.R.; Nummenmaa, A.R.; Makarov, S.N. The effect of meninges on the electric fields in TES and TMS. Numerical modeling with adaptive mesh refinement. Brain Stimul. 2022, 15, 654–663. [Google Scholar] [CrossRef]
- Partheymüller, P.; Białecki, R.A.; Kuhn, G. Self-adapting algorithm for evaluation of weakly singular integrals arising in the boundary element method. Eng. Anal. Bound. Elem. 1994, 14, 285–292. [Google Scholar] [CrossRef]
- Fischl, B. FreeSurfer. NeuroImage 2012, 62, 774–781. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, J.D.; Madsen, K.H.; Puonti, O.; Siebner, H.R.; Bauer, C.; Madsen, C.G.; Saturnino, G.B.; Thielscher, A. Automatic skull segmentation from MR images for realistic volume conductor models of the head: Assessment of the state-of-the-art. NeuroImage 2018, 174, 587–598. [Google Scholar] [CrossRef]
- Makarov, S.N.; Noetscher, G.M.; Raij, T.; Nummenmaa, A. A Quasi-Static Boundary Element Approach With Fast Multipole Acceleration for High-Resolution Bioelectromagnetic Models. IEEE. Trans. Biomed. Eng. 2018, 65, 2675–2683. [Google Scholar] [CrossRef]
- Miinalainen, T.; Rezaei, A.; Us, D.; Nüßing, A.; Engwer, C.; Wolters, C.H.; Pursiainen, S. A realistic, accurate and fast source modeling approach for the eeg forward problem. NeuroImage 2019, 184, 56–67. [Google Scholar] [CrossRef]
- Bangera, N.B.; Schomer, D.L.; Dehghani, N.; Ulbert, I.; Cash, S.; Papavasiliou, S.; Eisenberg, S.R.; Dale, A.M.; Halgren, E. Experimental validation of the influence of white matter anisotropy on the intracranial EEG forward solution. J. Comput. Neurosci. 2010, 29, 371–387. [Google Scholar] [CrossRef]
- Güllmar, D.; Haueisen, J.; Reichenbach, J.R. Source analysis of EEG data is an important tool in scientific and clinical applications. This is the first study on EEG source analysis using the BEM. BEM can utilize true point-dipole sources, as opposed to past studies using FEM, which can only use approximate point-dipole sources. NeuroImage 2010, 51, 145–163. [Google Scholar]
- Acar, Z.A.; Makeig, S. Effects of forward model errors on eeg source localization. Brain Topogr. 2013, 26, 378–396. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, M.; Wagner, M.; Kastner, J. Development of volume conductor and source models to localize epileptic foci. J. Clin. Neurophysiol. 2007, 24, 101–119. [Google Scholar] [CrossRef]
- Whittingstall, K.; Stroink, G.; Gates, L.; Connolly, J.F.; Finley, A. Effects of dipole position, orientation and noise on the accuracy of eeg source localization. Biomed. Eng. Online 2003, 2, 14. [Google Scholar] [CrossRef]
- Lew, S.; Wolters, C.H.; Dierkes, T.; Röer, C.; MacLeod, R.S. Accuracy and run-time comparison for different potential approaches and iterative solvers in finite element method based eeg source analysis. Appl. Numer. Math. 2009, 59, 1970–1988. [Google Scholar] [CrossRef] [PubMed]
- Gomez, L.J.; Dannhauer, M.; Koponen, L.M.; Peterchev, A.V. Conditions for numerically accurate tms electric field simulation. Brain Stimul. 2020, 13, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Hämäläinen, M.; Hari, R.; Ilmoniemi, R.J.; Knuutila, J.; Lounasmaa, O.V. Magnetoencephalography—Theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev. Mod. Phys. 1993, 65, 413–497. [Google Scholar] [CrossRef]
- Schimpf, P.H.; Ramon, C.; Haueisen, J. Dipole models for the eeg and meg. IEEE Trans. Biomed. Eng. 2002, 49, 409–418. [Google Scholar] [CrossRef]
- Buchner, H.; Knoll, G.; Fuchs, M.; Rienäcker, A.; Beckmann, R.; Wagner, M.; Silny, J.; Pesch, J. Inverse localization of electric dipole current sources in finite element models of the human head. Electroencephalogr. Clin. Neurophysiol. 1997, 102, 267–278. [Google Scholar] [CrossRef]
- Olivi, E.; Papadopoulo, T.; Clerc, M. Handling white-matter anisotropy in bem for the eeg forward problem. In Proceedings of the 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011. [Google Scholar]
- Saturnino, G.B.; Puonti, O.; Nielsen, J.D.; Antonenko, D.; Madsen, K.H.; Thielscher, A. SimNIBS 2.1: A Comprehensive Pipeline for Individualized Electric Field Modelling for Transcranial Brain Stimulation. In Brain and Human Body Modeling: Computational Human Modeling at EMBC 2018; Springer: Cham, Switzerland, 2019; Chapter 1. [Google Scholar]
- Van Essen, D.C.; Ugurbil, K.; Auerbach, E.; Barch, D.; Behrens, T.E.J.; Bucholz, R.; Chang, A.; Chen, L.; Corbetta, M.; Curtiss, S.W.; et al. The human connectome project: A data acquisition perspective. NeuroImage 2012, 62, 2222–2231. [Google Scholar] [CrossRef]
- Htet, A.T.; Burnham, E.H.; Noetscher, G.M.; Pham, D.N.; Nummenmaa, A.; Makarov, S.N. Collection of CAD human head models for electromagnetic simulations and their applications. Biomed. Phys. Eng. Express 2019, 5, 067005. [Google Scholar] [CrossRef]
- Gabriel, C. Compilation of the Dielectric Properties of Body Tissues at Rf and Microwave Frequencies. 1996. N.AL/OE-TR-1996-0037, Occupational and Environmental Health Directorate, Radiofrequency Radiation Division, Brooks Air Force Base, Texas (USA). Available online: http://niremf.ifac.cnr.it/docs/DIELECTRIC/home.html (accessed on 1 September 2024).
- Hasgall, P.A.; Gennaro, F.D.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.C.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues, 2 2022. Version 4.1. Available online: https://itis.swiss/virtual-population/tissue-properties/database/low-frequency-conductivity/ (accessed on 1 September 2024).
- Vorwerk, J.; Wolters, C.H.; Baumgarten, D. Global sensitivity of EEG source analysis to tissue conductivity uncertainties. Front. Hum. Neurosci. 2024, 18, 1335212. [Google Scholar] [CrossRef]
- Akhtari, M.; Bryant, H.C.; Mamelak, A.N.; Flynn, E.R.; Heller, L.; Shih, J.J.; Mandelkem, M.; Matlachov, A.; Ranken, D.M.; Best, E.D.; et al. Conductivities of three-layer live human skull. Brain Topogr. 2002, 14, 151–167. [Google Scholar] [CrossRef]
- Baumann, S.B.; Wozny, D.R.; Kelly, S.K.; Meno, F.M. The electrical conductivity of human cerebrospinal fluid at body temperature. IEEE Trans. Biomed. Eng. 1997, 44, 220–223. [Google Scholar] [CrossRef]
- Dannhauer, M.; Lanfer, B.; Wolters, C.H.; Knösche, T.R. Modeling of the human skull in EEG source analysis. Hum. Brain Mapp. 2011, 32, 1383–1399. [Google Scholar] [CrossRef] [PubMed]
- Haueisen, J.; Ramon, C.; Eiselt, M.; Brauer, H.; Nowak, H. Influence of tissue resistivities on neuromagnetic fields and electric potentials studied with a finite element model of the head. IEEE Trans. Biomed. Eng. 1997, 44, 727–735. [Google Scholar] [CrossRef]
- Ramon, C.; Schimpf, P.; Haueisen, J.; Holmes, M.; Ishimaru, A. Role of soft bone, CSF and gray matter in EEG simulations. Brain Topogr. 2004, 16, 245–248. [Google Scholar] [CrossRef]
- Hirata, A.; Niitsu, M.; Phang, C.R.; Kodera, S.; Kida, T.; Rashed, E.A.; Fukunaga, M.; Sadato, N.; Wasaka, T. High-resolution eeg source localization in personalized segmentation-free head model with multi-dipole fitting. Phys. Med. Biol. 2024, 69, 055013. [Google Scholar] [CrossRef]
- Opitz, A.; Paulus, W.; Will, S.; Antunes, A.; Thielscher, A. Determinants of the electric field during transcranial direct current stimulation. NeuroImage 2015, 109, 140–150. [Google Scholar] [CrossRef]
- Wagner, T.A.; Zahn, M.; Grodzinsky, A.J.; Pascual-Leone, A. Three-dimensional head model simulation of transcranial magnetic stimulation. IEEE Transact. Biomed. Eng. 2004, 51, 1586–1598. [Google Scholar] [CrossRef]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: An Open-Source Mesh Processing Tool. In Eurographics Italian Chapter Conference, Salerno, Italy; Scarano, V., Chiara, R.D., Erra, U., Eds.; The Eurographics Association: Crete, Greece, 2008. [Google Scholar]
- Kazhdan, M.; Hoppe, H. Screened Poisson surface reconstruction. ACM Trans. Graph. (TOG) 2013, 32, 29. [Google Scholar] [CrossRef]
- Taubin, G. Curve and surface smoothing without shrinkage. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 852–857. [Google Scholar]
- Pittau, F.; Grouiller, F.; Spinelli, L.; Seeck, M.; Michel, C.M.; Vulliemoz, S. The Role of Functional Neuroimaging in Pre-Surgical Epilepsy Evaluation. Front. Neurol. 2014, 5, 31. [Google Scholar] [CrossRef] [PubMed]
- Ebersole, J.S.; Hawes-Ebersole, S. Clinical Application of Dipole Models in the Localization of Epileptiform Activity. J. Clin. Neurophysiol. 2007, 24, 120–129. [Google Scholar] [CrossRef]
- Fiedler, P.; Fonseca, C.; Supriyanto, E.; Zanow, F.; Haueisen, J. A high-density 256-channel cap for dry electroencephalography. Human Brain Mapp. 2022, 43, 1295–1308. [Google Scholar] [CrossRef]
- Graichen, U.; Eichardt, R.; Fiedler, P.; Strohmeier, D.; Zanow, F.; Haueisen, J. SPHARA—A Generalized Spatial Fourier Analysis for Multi-Sensor Systems with Non-Uniformly Arranged Sensors: Application to EEG. PLoS ONE 2015, 10, e0121741. [Google Scholar] [CrossRef] [PubMed]
- Barnard, A.C.; Duck, I.M.; Lynn, M.S. The application of electromagnetic theory to electrocardiology. i. derivation of the integral equations. Biophys. J. 1967, 7, 443–462. [Google Scholar] [CrossRef] [PubMed]
- Gelernter, H.L.; Swihart, J.C. A Mathematical-Physical Model of the Genesis of the Electrocardiogram. Biophys. J. 1964, 4, 285–301. [Google Scholar] [CrossRef]
- Greengard, L.; Rokhlin, J. A fast algorithm for particle simulations. J. Comp. Phys. 1987, 73, 325–348. [Google Scholar] [CrossRef]
- Nunez, P.L.; Srinivasan, R. Electric Fields of the Brain: The Neurophysics of EEG, 2nd ed.; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Makarov, S.N.; Wartman, W.A.; Noetscher, G.M.; Fujimoto, K.; Zaidi, T.; Burnham, E.T.; Daneshzand, M.; Nummenmaa, A. Degree of improving TMS focality through a geometrically stable solution of an inverse TMS problem. NeuroImage 2021, 241, 118437. [Google Scholar] [CrossRef] [PubMed]
- Makarov, S.N.; Hämäläinen, M.; Yoshio, O.; Noetscher, G.M.; Jyrki, A.; Nummenmaa, A. Boundary element fast multipole method for enhanced modeling of neurophysiological recordings. IEEE Trans. Biomed. Eng. 2021, 68, 308–318. [Google Scholar] [CrossRef]
- Makarov, S.N.; Noetscher, G.M.; Nazarian, A. Low-Frequency Electromagnetic Modeling for Electrical and Biological Systems Using MATLAB; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Rick, B.; Leslie, G. A Short Course on Fast Multipole Methods. 1997. Available online: https://math.nyu.edu/~greengar/shortcourse_fmm.pdf (accessed on 1 September 2024).
- Rokhlin, V. Rapid solution of integral equations of classical potential theory. J. Comput. Phys. 1985, 60, 187–207. [Google Scholar] [CrossRef]
- Askham, T.; Gimbutas, Z.; Greengard, L.; Lu, L.; Magland, J.; Malhotra, D.; O’Neil, M.; Rachh, M.; Rokhlin, V.; Vico, F. FMM3D: A Fast Multipole Method Library for Three-Dimensional Problems. Available online: https://github.com/flatironinstitute/FMM3D (accessed on 1 September 2024).
- Feischl, M.; Führer, T.; Heuer, N.; Karkulik, M.; Praetorius, D. Adaptive Boundary Element Methods. Arch. Computat. Methods Eng. 2015, 22, 309–389. [Google Scholar] [CrossRef]
- Wartman, W.A.; Ponasso, G.N.N.; Qi, Z.; Haueisen, J.; Maess, B.; Knösche, T.R.; Weise, K.; Noetscher, G.M.; Raij, T.; Makaroff, S.N. Fast and accurate eeg/meg bem-based forward problem solution for high-resolution head models. bioRxiv 2024. [Google Scholar] [CrossRef]
- Scherg, M. Fundamentals of dipole source potential analysis. Adv. Audiol. 1990, 6, 25. [Google Scholar]
- Phillips, C. Source Localisation in EEG: Combining Anatomical and Functional Constraints. Ph.D. Thesis, Université de Liège, Liège, Belgium, 2001. [Google Scholar]
- Sarvas, J. Basic mathematical and electromagnetic concepts of the biomagnetic inverse problem. Phys. Med. Biol. 1987, 32, 11–22. [Google Scholar] [CrossRef] [PubMed]
- Piastra, M.C.; Oostenveld, R.; Homölle, S.; Han, B.; Chen, Q.; Oostendorp, T. How to assess the accuracy of volume conduction models? A validation study with stereotactic eeg data. Front. Hum. Neurosci. 2024, 18, 1279183. [Google Scholar] [CrossRef] [PubMed]







| VWB7 | IT’IS7 | SimNIBS7 | |
| Skin | 0.430 | 0.147 | 0.465 |
| Skull | 0.010 | 0.0179 | 0.010 |
| CSF | 1.790 | 1.880 | 1.654 |
| GM | 0.330 | 0.419 | 0.275 |
| WM | 0.140 | 0.348 | 0.126 |
| Cerebellum | 0.216 | 0.577 | 0.126 |
| Ventricles | 1.790 | 1.880 | 1.654 |
| Eyes | 1.790 | 1.880 | 1.654 |
| VWB3 | IT’IS3 | SimNIBS3 | |
| SKIN | 0.430 | 0.147 | 0.465 |
| SKULL | 0.010 | 0.0179 | 0.010 |
| BRAIN | 0.330 | 0.375 | 0.330 |
| Dipole | mm | deg | RV | AMR |
| dip1 | 4.13 | 8.71 | 6.22 | |
| dip2 | 5.01 | 14.62 | 5.66 | |
| dip3 | 2.43 | 14.04 | 4.59 | |
| dip4 | 6.42 | 11.00 | 6.23 | |
| (a) Averages | ||||
| dip1 | 1.65 | 4.66 | 3.23 | |
| dip2 | 1.85 | 8.86 | 2.08 | |
| dip3 | 1.13 | 7.14 | 2.51 | |
| dip4 | 3.87 | 5.75 | 4.14 | |
| (b) Standard Deviations |
| Subject | Avg. Error (mm) | St. Dev. (mm) |
| 110411 | 10.28 | 3.63 |
| 117122 | 9.73 | 4.11 |
| 120111 | 10.11 | 4.48 |
| 122317 | 17.71 | 11.57 |
| 122620 | 5.99 | 2.27 |
| 124422 | 11.15 | 2.85 |
| 128632 | 8.05 | 3.47 |
| 130013 | 7.11 | 2.44 |
| 131722 | 9.71 | 3.75 |
| 138534 | 10.17 | 2.76 |
| 149337 | 7.41 | 2.51 |
| 149539 | 6.05 | 2.43 |
| 151627 | 5.57 | 2.29 |
| 160123 | 7.08 | 3.03 |
| 198451 | 7.41 | 3.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuñez Ponasso, G.; Wartman, W.A.; McSweeney, R.C.; Lai, P.; Haueisen, J.; Maess, B.; Knösche, T.R.; Weise, K.; Noetscher, G.M.; Raij, T.; et al. Improving EEG Forward Modeling Using High-Resolution Five-Layer BEM-FMM Head Models: Effect on Source Reconstruction Accuracy. Bioengineering 2024, 11, 1071. https://doi.org/10.3390/bioengineering11111071
Nuñez Ponasso G, Wartman WA, McSweeney RC, Lai P, Haueisen J, Maess B, Knösche TR, Weise K, Noetscher GM, Raij T, et al. Improving EEG Forward Modeling Using High-Resolution Five-Layer BEM-FMM Head Models: Effect on Source Reconstruction Accuracy. Bioengineering. 2024; 11(11):1071. https://doi.org/10.3390/bioengineering11111071
Chicago/Turabian StyleNuñez Ponasso, Guillermo, William A. Wartman, Ryan C. McSweeney, Peiyao Lai, Jens Haueisen, Burkhard Maess, Thomas R. Knösche, Konstantin Weise, Gregory M. Noetscher, Tommi Raij, and et al. 2024. "Improving EEG Forward Modeling Using High-Resolution Five-Layer BEM-FMM Head Models: Effect on Source Reconstruction Accuracy" Bioengineering 11, no. 11: 1071. https://doi.org/10.3390/bioengineering11111071
APA StyleNuñez Ponasso, G., Wartman, W. A., McSweeney, R. C., Lai, P., Haueisen, J., Maess, B., Knösche, T. R., Weise, K., Noetscher, G. M., Raij, T., & Makaroff, S. N. (2024). Improving EEG Forward Modeling Using High-Resolution Five-Layer BEM-FMM Head Models: Effect on Source Reconstruction Accuracy. Bioengineering, 11(11), 1071. https://doi.org/10.3390/bioengineering11111071








