Mathematical Models for Ultrasound Elastography: Recent Advances to Improve Accuracy and Clinical Utility
Abstract
1. Introduction
2. Fundamental Concepts
3. Classical Elasticity Theory
4. Viscoelasticity Theory
5. Poroelasticity Theory
6. Nonlocal Continuum Mechanics
7. Surface Acoustic Waves: Rayleigh and Scholte Waves
8. Recent Advancements
9. Future Directions
10. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wouters, O.J.; O’donoghue, D.J.; Ritchie, J.; Kanavos, P.G.; Narva, A.S. Early chronic kidney disease: Diagnosis, management and models of care. Nat. Rev. Nephrol. 2015, 11, 491–502. [Google Scholar] [CrossRef] [PubMed]
- Bhushan, A.; Gonsalves, A.; Menon, J.U. Current state of breast cancer diagnosis, treatment, and theranostics. Pharmaceutics 2021, 13, 723. [Google Scholar] [CrossRef]
- Lungu, N.; Popescu, D.-E.; Jura, A.M.C.; Zaharie, M.; Jura, M.-A.; Roșca, I.; Boia, M. Enhancing Early Detection of Sepsis in Neonates through Multimodal Biosignal Integration: A Study of Pulse Oximetry, Near-Infrared Spectroscopy (NIRS), and Skin Temperature Monitoring. Bioengineering 2024, 11, 681. [Google Scholar] [CrossRef]
- Marouf, A.A.; Mottalib, M.M.; Alhajj, R.; Rokne, J.; Jafarullah, O. An efficient approach to predict eye diseases from symptoms using machine learning and ranker-based feature selection methods. Bioengineering 2022, 10, 25. [Google Scholar] [CrossRef]
- Ginsburg, O.; Yip, C.H.; Brooks, A.; Cabanes, A.; Caleffi, M.; Dunstan Yataco, J.A.; Gyawali, B.; McCormack, V.; McLaughlin de Anderson, M.; Mehrotra, R. Breast cancer early detection: A phased approach to implementation. Cancer 2020, 126, 2379–2393. [Google Scholar] [CrossRef] [PubMed]
- Crosby, D.; Bhatia, S.; Brindle, K.M.; Coussens, L.M.; Dive, C.; Emberton, M.; Esener, S.; Fitzgerald, R.C.; Gambhir, S.S.; Kuhn, P. Early detection of cancer. Science 2022, 375, eaay9040. [Google Scholar] [CrossRef] [PubMed]
- Alizargar, A.; Chang, Y.-L.; Alkhaleefah, M.; Tan, T.-H. Precision Non-Alcoholic Fatty Liver Disease (NAFLD) Diagnosis: Leveraging Ensemble Machine Learning and Gender Insights for Cost-Effective Detection. Bioengineering 2024, 11, 600. [Google Scholar] [CrossRef]
- Tzror-Azankot, C.; Betzer, O.; Sadan, T.; Motiei, M.; Rahimipour, S.; Atkins, A.; Popovtzer, A.; Popovtzer, R. Glucose-functionalized liposomes for reducing false positives in cancer diagnosis. ACS Nano 2020, 15, 1301–1309. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, C.; Zhang, Y.; Li, J. An Automated Diagnosis Method for Lung Cancer Target Detection and Subtype Classification-Based CT Scans. Bioengineering 2024, 11, 767. [Google Scholar] [CrossRef]
- Gordon, L.G.; Leung, W.; Johns, R.; McNoe, B.; Lindsay, D.; Merollini, K.M.; Elliott, T.M.; Neale, R.E.; Olsen, C.M.; Pandeya, N. Estimated healthcare costs of melanoma and keratinocyte skin cancers in Australia and Aotearoa New Zealand in 2021. Int. J. Environ. Res. Public Health 2022, 19, 3178. [Google Scholar] [CrossRef]
- Bygrave, A.; Whittaker, K.; Paul, C.; Fradgley, E.A.; Varlow, M.; Aranda, S. Australian experiences of out-of-pocket costs and financial burden following a cancer diagnosis: A systematic review. Int. J. Environ. Res. Public Health 2021, 18, 2422. [Google Scholar] [CrossRef]
- Guimarães, C.F.; Gasperini, L.; Marques, A.P.; Reis, R.L. The stiffness of living tissues and its implications for tissue engineering. Nat. Rev. Mater. 2020, 5, 351–370. [Google Scholar] [CrossRef]
- Fitzgerald, R.C.; Antoniou, A.C.; Fruk, L.; Rosenfeld, N. The future of early cancer detection. Nat. Med. 2022, 28, 666–677. [Google Scholar] [CrossRef]
- Mousavi, S.R.; Wang, H.; Hesabgar, S.M.; Scholl, T.J.; Samani, A. A novel shape-similarity-based elastography technique for prostate cancer assessment. Med. Phys. 2015, 42, 5110–5119. [Google Scholar] [CrossRef] [PubMed]
- Samani, A.; Zubovits, J.; Plewes, D. Elastic moduli of normal and pathological human breast tissues: An inversion-technique-based investigation of 169 samples. Phys. Med. Biol. 2007, 52, 1565. [Google Scholar] [CrossRef]
- Petitclerc, L.; Sebastiani, G.; Gilbert, G.; Cloutier, G.; Tang, A. Liver fibrosis: Review of current imaging and MRI quantification techniques. J. Magn. Reson. Imaging 2017, 45, 1276–1295. [Google Scholar] [CrossRef] [PubMed]
- Shiina, T.; Maki, T.; Yamakawa, M.; Mitake, T.; Kudo, M.; Fujimoto, K. Mechanical model analysis for quantitative evaluation of liver fibrosis based on ultrasound tissue elasticity imaging. Jpn. J. Appl. Phys. 2012, 51, 07GF11. [Google Scholar] [CrossRef]
- Rhee, K.; Cho, Y. Artery wall viscoelasticity: Measurement, assessment, and clinical implications. Int. J. Precis. Eng. Manuf. 2021, 22, 1157–1168. [Google Scholar] [CrossRef]
- Islam, M.T.; Tang, S.; Liverani, C.; Saha, S.; Tasciotti, E.; Righetti, R. Non-invasive imaging of Young’s modulus and Poisson’s ratio in cancers in vivo. Sci. Rep. 2020, 10, 7266. [Google Scholar] [CrossRef] [PubMed]
- Sigrist, R.M.; Liau, J.; El Kaffas, A.; Chammas, M.C.; Willmann, J.K. Ultrasound elastography: Review of techniques and clinical applications. Theranostics 2017, 7, 1303. [Google Scholar] [CrossRef]
- Forte, A.J.; Huayllani, M.T.; Boczar, D.; Cinotto, G.; Ciudad, P.; Manrique, O.J.; Lu, X.; McLaughlin, S.A. The basics of ultrasound elastography for diagnosis, assessment, and staging breast cancer-related lymphedema: A systematic review of the literature. Gland Surg. 2020, 9, 589. [Google Scholar] [CrossRef]
- Ozturk, A.; Olson, M.C.; Samir, A.E.; Venkatesh, S.K. Liver fibrosis assessment: MR and US elastography. Abdom. Radiol. 2022, 47, 3037–3050. [Google Scholar] [CrossRef] [PubMed]
- Kanagaraju, V.; Ashlyin, P.; Elango, N.; Devanand, B. Role of transrectal ultrasound elastography in the diagnosis of prostate carcinoma. J. Med. Ultrasound 2020, 28, 173–178. [Google Scholar] [CrossRef]
- Pruijssen, J.T.; de Korte, C.L.; Voss, I.; Hansen, H.H. Vascular shear wave elastography in atherosclerotic arteries: A systematic review. Ultrasound Med. Biol. 2020, 46, 2145–2163. [Google Scholar] [CrossRef] [PubMed]
- Zúñiga, L.D.O.; López, C.A.G.; González, E.R. Ultrasound elastography in the assessment of the stiffness of spastic muscles: A systematic review. Ultrasound Med. Biol. 2021, 47, 1448–1464. [Google Scholar] [CrossRef]
- Oglat, A.A.; Abukhalil, T. Ultrasound Elastography: Methods, Clinical Applications, and Limitations: A Review Article. Appl. Sci. 2024, 14, 4308. [Google Scholar] [CrossRef]
- Sack, I. Magnetic resonance elastography from fundamental soft-tissue mechanics to diagnostic imaging. Nat. Rev. Phys. 2023, 5, 25–42. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Ma, J.; Meng, X.; Ma, Z.; Fan, F. Optical coherence elastography and its applications for the biomechanical characterization of tissues. J. Biophotonics 2023, 16, e202300292. [Google Scholar] [CrossRef]
- Zaitsev, V.Y.; Matveyev, A.L.; Matveev, L.A.; Sovetsky, A.A.; Hepburn, M.S.; Mowla, A.; Kennedy, B.F. Strain and elasticity imaging in compression optical coherence elastography: The two-decade perspective and recent advances. J. Biophotonics 2021, 14, e202000257. [Google Scholar] [CrossRef]
- Wu, C.-H.; Chiu, Y.-H.; Chang, K.-V.; Wu, W.-T.; Özçakar, L. Ultrasound elastography for the evaluation of plantar fasciitis: A systematic review and meta-analysis. Eur. J. Radiol. 2022, 155, 110495. [Google Scholar] [CrossRef]
- Caenen, A.; Bézy, S.; Pernot, M.; Nightingale, K.R.; Vos, H.J.; Voigt, J.-U.; Segers, P.; D’hooge, J. Ultrasound Shear Wave Elastography in Cardiology. Cardiovasc. Imaging 2024, 17, 314–329. [Google Scholar] [CrossRef]
- Stiver, M.L.; Mirjalili, S.A.; Agur, A.M. Measuring shear wave velocity in adult skeletal muscle with ultrasound 2-D shear wave elastography: A scoping review. Ultrasound Med. Biol. 2023, 49, 1353–1362. [Google Scholar] [CrossRef] [PubMed]
- Albakr, A.; Ben-Israel, D.; Yang, R.; Kruger, A.; Alhothali, W.; Al Towim, A.; Lama, S.; Ajlan, A.; Riva-Cambrin, J.; Prada, F. Ultrasound elastography in neurosurgery: Current applications and future perspectives. World Neurosurg. 2023, 170, 195–205.e191. [Google Scholar] [CrossRef]
- Lim, W.T.; Ooi, E.H.; Foo, J.J.; Ng, K.H.; Wong, J.H.; Leong, S.S. Shear wave elastography: A review on the confounding factors and their potential mitigation in detecting chronic kidney disease. Ultrasound Med. Biol. 2021, 47, 2033–2047. [Google Scholar] [CrossRef]
- Dewilde, K.; Vanthienen, M.; Van Schoubroeck, D.; Froyman, W.; Timmerman, D.; Van den Bosch, T. Elastography in ultrasound assessment of the uterus. J. Endometr. Uterine Disord. 2023, 1, 100014. [Google Scholar] [CrossRef]
- Molga-Magusiak, M.; Krawczyk, P.; Rzepakowska, A.; Niemczyk, K. Application of ultrasound shear wave elastography in tumors of head and neck region–a preliminary study and literature review. Pol. Otorhinolaryngol. Rev. 2024, 13, 22–28. [Google Scholar] [CrossRef]
- Mao, Y.-J.; Lim, H.-J.; Ni, M.; Yan, W.-H.; Wong, D.W.-C.; Cheung, J.C.-W. Breast tumour classification using ultrasound elastography with machine learning: A systematic scoping review. Cancers 2022, 14, 367. [Google Scholar] [CrossRef] [PubMed]
- Bian, J.; Zhang, J.; Hou, X. Diagnostic accuracy of ultrasound shear wave elastography combined with superb microvascular imaging for breast tumors: A protocol for systematic review and meta-analysis. Medicine 2021, 100, e26262. [Google Scholar] [CrossRef]
- Wang, B.; Guo, Q.; Wang, J.-Y.; Yu, Y.; Yi, A.-J.; Cui, X.-W.; Dietrich, C.F. Ultrasound elastography for the evaluation of lymph nodes. Front. Oncol. 2021, 11, 714660. [Google Scholar] [CrossRef]
- Liao, J.; Yang, H.; Yu, J.; Liang, X.; Chen, Z. Progress in the application of ultrasound elastography for brain diseases. J. Ultrasound Med. 2020, 39, 2093–2104. [Google Scholar] [CrossRef] [PubMed]
- Ślósarz, D.; Poniewierka, E.; Neubauer, K.; Kempiński, R. Ultrasound elastography in the assessment of the intestinal changes in inflammatory bowel disease—Systematic review. J. Clin. Med. 2021, 10, 4044. [Google Scholar] [CrossRef]
- Ophir, J.; Cespedes, I.; Ponnekanti, H.; Yazdi, Y.; Li, X. Elastography: A quantitative method for imaging the elasticity of biological tissues. Ultrason. Imaging 1991, 13, 111–134. [Google Scholar] [CrossRef]
- Muthupillai, R.; Lomas, D.; Rossman, P.; Greenleaf, J.F.; Manduca, A.; Ehman, R.L. Magnetic resonance elastography by direct visualization of propagating acoustic strain waves. Science 1995, 269, 1854–1857. [Google Scholar] [CrossRef]
- Sadd, M.H. Elasticity: Theory, Applications, and Numerics; Academic Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Varghese, T. Quasi-static ultrasound elastography. Ultrasound Clin. 2009, 4, 323. [Google Scholar] [CrossRef]
- Kinsler, L.E.; Frey, A.R.; Coppens, A.B.; Sanders, J.V. Fundamentals of Acoustics; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Nitta, N.; Yamakawa, M.; Hachiya, H.; Shiina, T. A review of physical and engineering factors potentially affecting shear wave elastography. J. Med. Ultrason. 2021, 48, 403–414. [Google Scholar] [CrossRef]
- O’Hara, S.; Edwards, C.; Zelesco, M. Two dimensional shear wave elastography—Basic principles and current applications. Sonography 2024, 11, 201–210. [Google Scholar] [CrossRef]
- Zaniker, E.J.; Zhang, M.; Hughes, L.; La Follette, L.; Atazhanova, T.; Trofimchuk, A.; Babayev, E.; Duncan, F.E. Shear wave elastography to assess stiffness of the human ovary and other reproductive tissues across the reproductive lifespan in health and disease. Biol. Reprod. 2024, 110, 1100–1114. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, X. Comparison of five viscoelastic models for estimating viscoelastic parameters using ultrasound shear wave elastography. J. Mech. Behav. Biomed. Mater. 2018, 85, 109–116. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Y.; Zheng, Y.; Lin, H.; Guo, Y.; Zhu, Y.; Zhang, X.; Wang, T.; Chen, S. Quantification of liver viscoelasticity with acoustic radiation force: A study of hepatic fibrosis in a rat model. Ultrasound Med. Biol. 2013, 39, 2091–2102. [Google Scholar] [CrossRef] [PubMed]
- Poul, S.S.; Ormachea, J.; Ge, G.R.; Parker, K.J. Comprehensive experimental assessments of rheological models’ performance in elastography of soft tissues. Acta Biomater. 2022, 146, 259–273. [Google Scholar] [CrossRef]
- Verruijt, A. Theory and problems of poroelasticity. Delft Univ. Technol. 2013, 71, 465. [Google Scholar]
- Leiderman, R.; Barbone, P.E.; Oberai, A.A.; Bamber, J.C. Coupling between elastic strain and interstitial fluid flow: Ramifications for poroelastic imaging. Phys. Med. Biol. 2006, 51, 6291. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.T.; Righetti, R. An analytical poroelastic model of a spherical tumor embedded in normal tissue under creep compression. J. Biomech. 2019, 89, 48–56. [Google Scholar] [CrossRef] [PubMed]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1957, 241, 376–396. [Google Scholar]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Nuhu, A.A.; Safaei, B. A comprehensive review on the vibration analyses of small-scaled plate-based structures by utilizing the nonclassical continuum elasticity theories. Thin-Walled Struct. 2022, 179, 109622. [Google Scholar] [CrossRef]
- Darban, H.; Fabbrocino, F.; Luciano, R. Size-dependent linear elastic fracture of nanobeams. Int. J. Eng. Sci. 2020, 157, 103381. [Google Scholar] [CrossRef]
- Gholipour, A.; Ghayesh, M.H. Nonlinear coupled mechanics of functionally graded nanobeams. Int. J. Eng. Sci. 2020, 150, 103221. [Google Scholar] [CrossRef]
- Goswami, S.; Ahmed, R.; Khan, S.; Doyley, M.M.; McAleavey, S.A. Shear induced non-linear elasticity imaging: Elastography for compound deformations. IEEE Trans. Med. Imaging 2020, 39, 3559–3570. [Google Scholar] [CrossRef] [PubMed]
- Favata, A.; Paroni, R.; Recrosi, F.; Tomassetti, G. Competition between epithelial tissue elasticity and surface tension in cancer morphogenesis. Int. J. Eng. Sci. 2022, 176, 103677. [Google Scholar] [CrossRef]
- Cieszko, M.; Kubik, J. Equations and fundamental characteristics of compressional waves propagating in fluid-saturated porous materials. Int. J. Eng. Sci. 2022, 171, 103619. [Google Scholar] [CrossRef]
- Tong, L.H.; Ding, H.B.; Yan, J.W.; Xu, C.; Lei, Z. Strain gradient nonlocal Biot poromechanics. Int. J. Eng. Sci. 2020, 156, 103372. [Google Scholar] [CrossRef]
- Caporale, A.; Darban, H.; Luciano, R. Nonlocal strain and stress gradient elasticity of Timoshenko nano-beams with loading discontinuities. Int. J. Eng. Sci. 2022, 173, 103620. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, L.; Hu, Y. A nonlocal surface theory for surface–bulk interactions and its application to mechanics of nanobeams. Int. J. Eng. Sci. 2022, 172, 103624. [Google Scholar] [CrossRef]
- Eringen, A.C.; Wegner, J. Nonlocal continuum field theories. Appl. Mech. Rev. 2003, 56, B20–B22. [Google Scholar] [CrossRef]
- Faghidian, S.A. Higher–order nonlocal gradient elasticity: A consistent variational theory. Int. J. Eng. Sci. 2020, 154, 103337. [Google Scholar] [CrossRef]
- Xu, X.; Shahsavari, D.; Karami, B. On the forced mechanics of doubly-curved nanoshell. Int. J. Eng. Sci. 2021, 168, 103538. [Google Scholar] [CrossRef]
- Farajpour, A.; Howard, C.Q.; Robertson, W.S. On size-dependent mechanics of nanoplates. Int. J. Eng. Sci. 2020, 156, 103368. [Google Scholar] [CrossRef]
- Rohani Rad, E.; Farajpour, M.R. Influence of taxol and CNTs on the stability analysis of protein microtubules. J. Comput. Appl. Mech. 2019, 50, 140–147. [Google Scholar]
- Farajpour, A.; Żur, K.K.; Kim, J.; Reddy, J.N. Nonlinear frequency behaviour of magneto-electromechanical mass nanosensors using vibrating MEE nanoplates with multiple nanoparticles. Compos. Struct. 2021, 260, 113458. [Google Scholar] [CrossRef]
- Kaplunov, J.; Prikazchikov, D.A.; Prikazchikova, L. On integral and differential formulations in nonlocal elasticity. Eur. J. Mech.-A/Solids 2023, 100, 104497. [Google Scholar] [CrossRef]
- Farajpour, A.; Ingman, W.V. Mechanics of Small-Scale Spherical Inclusions Using Nonlocal Poroelasticity Integrated with Light Gradient Boosting Machine. Micromachines 2024, 15, 210. [Google Scholar] [CrossRef] [PubMed]
- Masud, A.A.; Liu, J. Ultrasonic surface acoustic wave elastography: A review of basic theories, technical developments, and medical applications. Med. Phys. 2024, 51, 3220–3244. [Google Scholar] [CrossRef]
- Kundu, T. Ultrasonic Nondestructive Evaluation: Engineering and Biological Material Characterization; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Rose, J. Ultrasonic Guided Waves in Solid Media; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Zhang, X.; Greenleaf, J.F. Estimation of tissue’s elasticity with surface wave speed. J. Acoust. Soc. Am. 2007, 122, 2522–2525. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Identification of the Rayleigh surface waves for estimation of viscoelasticity using the surface wave elastography technique. J. Acoust. Soc. Am. 2016, 140, 3619–3622. [Google Scholar] [CrossRef] [PubMed]
- Kalra, S.; Bartholmai, B.; Zhang, X. Application of lung ultrasound surface wave elastography in the evaluation of diffuse lung diseases. J. Acoust. Soc. Am. 2023, 154, A221. [Google Scholar] [CrossRef]
- Zhou, B.; Chen, J.J.; Kazemi, A.; Sit, A.J.; Zhang, X. An ultrasound vibro-elastography technique for assessing papilledema. Ultrasound Med. Biol. 2019, 45, 2034–2039. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, B.; Osborn, T. Ultrasound surface wave elastography for assessing scleroderma. Ultrasound Med. Biol. 2020, 46, 1263–1269. [Google Scholar] [CrossRef]
- Banerjee, S.; Leckey, C.A. Computational Nondestructive Evaluation Handbook: Ultrasound Modeling Techniques; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Liu, J.; Leer, J.; Aglayomov, S.R.; Emelianov, S.Y. A Scholte wave approach for ultrasonic surface acoustic wave elastography. Med. Phys. 2023, 50, 4138–4150. [Google Scholar] [CrossRef]
- Langdon, J.H.; Elegbe, E.; Gonzalez, R.S.; Osapoetra, L.; Ford, T.; McAleavey, S.A. Measurement of liver stiffness using shear wave elastography in a rat model: Factors impacting stiffness measurement with multiple-and single-tracking-location techniques. Ultrasound Med. Biol. 2017, 43, 2629–2639. [Google Scholar] [CrossRef] [PubMed]
- Fuhs, T.; Wetzel, F.; Fritsch, A.W.; Li, X.; Stange, R.; Pawlizak, S.; Kießling, T.R.; Morawetz, E.; Grosser, S.; Sauer, F. Rigid tumours contain soft cancer cells. Nat. Phys. 2022, 18, 1510–1519. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Srinivasa, A.R.; Reddy, J. An overview of theories of continuum mechanics with nonlocal elastic response and a general framework for conservative and dissipative systems. Appl. Mech. Rev. 2017, 69, 030802. [Google Scholar] [CrossRef]
- Sadigh, G.; Carlos, R.C.; Neal, C.H.; Dwamena, B.A. Accuracy of quantitative ultrasound elastography for differentiation of malignant and benign breast abnormalities: A meta-analysis. Breast Cancer Res. Treat. 2012, 134, 923–931. [Google Scholar] [CrossRef] [PubMed]
- Farajpour, A.; Ingman, W.V. Flexural Eigenfrequency Analysis of Healthy and Pathological Tissues Using Machine Learning and Nonlocal Viscoelasticity. Computers 2024, 13, 179. [Google Scholar] [CrossRef]
- Cespedes, I.; Ophir, J.; Ponnekanti, H.; Maklad, N. Elastography: Elasticity imaging using ultrasound with application to muscle and breast in vivo. Ultrason. Imaging 1993, 15, 73–88. [Google Scholar] [CrossRef]
- De Korte, C.L.; Van Der Steen, A.F.; Céspedes, E.I.; Pasterkamp, G. Intravascular ultrasound elastography in human arteries: Initial experience in vitro. Ultrasound Med. Biol. 1998, 24, 401–408. [Google Scholar] [CrossRef] [PubMed]
- Insana, M.F.; Pellot-Barakat, C.; Sridhar, M.; Lindfors, K.K. Viscoelastic imaging of breast tumor microenvironment with ultrasound. J. Mammary Gland Biol. Neoplasia 2004, 9, 393–404. [Google Scholar] [CrossRef] [PubMed]
- Konofagou, E.E.; Harrigan, T.; Ophir, J.; Krouskop, T. Poroelastography: Estimating and imaging the poroelastic properties of tissues. In Proceedings of the 1999 IEEE Ultrasonics Symposium. Proceedings. International Symposium (Cat. No. 99CH37027), Tahoe, NV, USA, 17–20 October 1999; pp. 1627–1630. [Google Scholar]
- Walker, W.F.; Fernandez, F.J.; Negron, L.A. A method of imaging viscoelastic parameters with acoustic radiation force. Phys. Med. Biol. 2000, 45, 1437. [Google Scholar] [CrossRef] [PubMed]
- Berry, G.P.; Bamber, J.C.; Armstrong, C.G.; Miller, N.R.; Barbone, P.E. Towards an acoustic model-based poroelastic imaging method: I. Theoretical foundation. Ultrasound Med. Biol. 2006, 32, 547–567. [Google Scholar] [CrossRef]
- Berry, G.P.; Bamber, J.C.; Miller, N.R.; Barbone, P.E.; Bush, N.L.; Armstrong, C.G. Towards an acoustic model-based poroelastic imaging method: II. Experimental investigation. Ultrasound Med. Biol. 2006, 32, 1869–1885. [Google Scholar] [CrossRef]
- Hoyt, K.; Kneezel, T.; Castaneda, B.; Parker, K.J. Quantitative sonoelastography for the in vivo assessment of skeletal muscle viscoelasticity. Phys. Med. Biol. 2008, 53, 4063. [Google Scholar] [CrossRef][Green Version]
- Schmitt, C.; Henni, A.H.; Cloutier, G. Characterization of blood clot viscoelasticity by dynamic ultrasound elastography and modeling of the rheological behavior. J. Biomech. 2011, 44, 622–629. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Stegemann, J.P.; Deng, C.X. Microscale characterization of the viscoelastic properties of hydrogel biomaterials using dual-mode ultrasound elastography. Biomaterials 2016, 88, 12–24. [Google Scholar] [CrossRef]
- Bied, M.; Gennisson, J.-L. Acoustoelasticity in transversely isotropic soft tissues: Quantification of muscle nonlinear elasticity. J. Acoust. Soc. Am. 2021, 150, 4489–4500. [Google Scholar] [CrossRef] [PubMed]
- Aichele, J.; Catheline, S. Fluids alter elasticity measurements: Porous wave propagation accounts for shear wave dispersion in elastography. Front. Phys. 2021, 9, 697990. [Google Scholar] [CrossRef]
- Islam, M.T.; Tang, S.; Tasciotti, E.; Righetti, R. Non-invasive assessment of the spatial and temporal distributions of interstitial fluid pressure, fluid velocity and fluid flow in cancers in vivo. IEEE Access 2021, 9, 89222–89233. [Google Scholar] [CrossRef]
- Kishimoto, R.; Suga, M.; Usumura, M.; Iijima, H.; Yoshida, M.; Hachiya, H.; Shiina, T.; Yamakawa, M.; Konno, K.; Obata, T. Shear wave speed measurement bias in a viscoelastic phantom across six ultrasound elastography systems: A comparative study with transient elastography and magnetic resonance elastography. J. Med. Ultrason. 2022, 49, 143–152. [Google Scholar] [CrossRef]
- Khan, M.H.R.; Righetti, R. Ultrasound estimation of strain time constant and vascular permeability in tumors using a CEEMDAN and linear regression-based method. Comput. Biol. Med. 2022, 148, 105707. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Murgoitio-Esandi, J.; Qian, X.; Li, R.; Gong, C.; Nankali, A.; Hao, L.; Xu, B.Y.; Shung, K.K.; Oberai, A. High-frequency ultrasound elastography to assess the nonlinear elastic properties of the cornea and ciliary body. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2022, 69, 2621–2629. [Google Scholar] [CrossRef]
- Farajpour, A.; Ingman, W.V. In-Plane Wave Propagation Analysis of Human Breast Lesions Using a Higher-Order Nonlocal Model and Deep Learning. Mathematics 2023, 11, 4804. [Google Scholar] [CrossRef]
- Tang, S.; Weiner, B.; Taraballi, F.; Haase, C.; Stetco, E.; Mehta, S.M.; Shajudeen, P.; Hogan, M.; De Rosa, E.; Horner, P.J. Assessment of spinal cord injury using ultrasound elastography in a rabbit model in vivo. Sci. Rep. 2023, 13, 15323. [Google Scholar] [CrossRef]
- Khan, S.; Goswami, S.; Feng, F.; Doyley, M.M.; McAleavey, S.A. Quantifying Strain Dependence of Multi-Frequency Shearwave Elasticity Imaging. In Proceedings of the 2023 IEEE Western New York Image and Signal Processing Workshop (WNYISPW), Rochester, NY, USA , 3 November 2023; pp. 1–7. [Google Scholar]
- Pagé, G.; Bied, M.; Garteiser, P.; Van Beers, B.; Etaix, N.; Fraschini, C.; Bel-Brunon, A.; Gennisson, J.-L. Comparison of ultrasound elastography, magnetic resonance elastography and finite element model to quantify nonlinear shear modulus. Phys. Med. Biol. 2023, 68, 205003. [Google Scholar] [CrossRef] [PubMed]
- Kheirkhah, N.; Dempsey, S.; Sadeghi-Naini, A.; Samani, A. A novel tissue mechanics-based method for improved motion tracking in quasi-static ultrasound elastography. Med. Phys. 2023, 50, 2176–2194. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.H.R.; Islam, M.T.; Taraballi, F.; Righetti, R. Assessment of compression-induced solid stress, fluid pressure and mechanopathological parameters in cancers in vivo using poroelastography. Phys. Med. Biol. 2023, 68, 135014. [Google Scholar] [CrossRef]
- Majumder, S.; Islam, M.T.; Righetti, R. Non-invasive imaging of interstitial fluid transport parameters in solid tumors in vivo. Sci. Rep. 2023, 13, 7132. [Google Scholar] [CrossRef] [PubMed]
- Dwairy, M.; Reddy, J.; Righetti, R. Predicting stress and interstitial fluid pressure in tumors based on biphasic theory. Comput. Biol. Med. 2023, 167, 107651. [Google Scholar] [CrossRef]
- Kheirkhah, N.; Kornecki, A.; Czarnota, G.J.; Samani, A.; Sadeghi-Naini, A. Enhanced full-inversion-based ultrasound elastography for evaluating tumor response to neoadjuvant chemotherapy in patients with locally advanced breast cancer. Phys. Medica 2023, 112, 102619. [Google Scholar] [CrossRef]
- Tecse, A.; Romero, S.E.; Naemi, R.; Castaneda, B. Characterisation of the soft tissue viscous and elastic properties using ultrasound elastography and rheological models: Validation and applications in plantar soft tissue assessment. Phys. Med. Biol. 2023, 68, 105005. [Google Scholar] [CrossRef]
- Götschi, T.; Schärer, Y.; Gennisson, J.-L.; Snedeker, J.G. Investigation of the relationship between tensile viscoelasticity and unloaded ultrasound shear wave measurements in ex vivo tendon. J. Biomech. 2023, 146, 111411. [Google Scholar] [CrossRef]
- Duroy, A.-L.; Detti, V.; Coulon, A.; Basset, O.; Brusseau, E. Regularization-based 2D strain tensor imaging in quasi-static ultrasound elastography SAGE publications. Ultrason. Imaging 2023, 45, 187–205. [Google Scholar] [CrossRef] [PubMed]
- Elmeliegy, A.M.; Guddati, M.N. Correlation-based full-waveform shear wave elastography. Phys. Med. Biol. 2023, 68, 115001. [Google Scholar] [CrossRef]
- Osika, M.; Kijanka, P. Ultrasound shear wave propagation modeling in general tissue–like viscoelastic materials. Ultrasound Med. Biol. 2024, 50, 627–638. [Google Scholar] [CrossRef] [PubMed]
- Majumder, S.; Islam, M.T.; Taraballi, F.; Righetti, R. Non-invasive imaging of mechanical properties of cancers in vivo based on transformations of the Eshelby’s tensor using compression elastography. IEEE Trans. Med. Imaging 2024, 43, 3027–3043. [Google Scholar] [CrossRef]
- Cihan, A.; Holko, K.; Wei, L.; Vos, H.J.; Debbaut, C.; Caenen, A.; Segers, P. Effect of interstitial fluid pressure on shear wave elastography: An experimental and computational study. Phys. Med. Biol. 2024, 69, 075001. [Google Scholar] [CrossRef] [PubMed]
- Gautam, S.K.; Arora, M. Hyperelastic Strain Elastography to Measure Subcutaneous Adipose Tissue and Muscle Thickness: A Simulation Study. In Proceedings of the 2024 IEEE South Asian Ultrasonics Symposium (SAUS), Gujarat, India, 27–29 March 2024; pp. 1–4. [Google Scholar]
- Shiina, T. JSUM ultrasound elastography practice guidelines: Basics and terminology. J. Med. Ultrason. 2013, 40, 309–323. [Google Scholar] [CrossRef] [PubMed]
- Mariappan, Y.K.; Glaser, K.J.; Ehman, R.L. Magnetic resonance elastography: A review. Clin. Anat. 2010, 23, 497–511. [Google Scholar] [CrossRef] [PubMed]
- Regan, K.; LeBourdais, R.; Banerji, R.; Zhang, S.; Muhvich, J.; Zheng, S.; Nia, H.T. Multiscale elasticity mapping of biological samples in 3D at optical resolution. Acta Biomater. 2024, 176, 250–266. [Google Scholar] [CrossRef] [PubMed]
- Moritoki, Y.; Furukawa, T.; Sun, J.; Yokoyama, M.; Shimono, T.; Yamada, T.; Nishiwaki, S.; Kageyama, T.; Fukuda, J.; Mukai, M. 3D-printed micro-tweezers with a compliant mechanism designed using topology optimization. Micromachines 2021, 12, 579. [Google Scholar] [CrossRef] [PubMed]
- Jaiswal, D.; Cowley, N.; Bian, Z.; Zheng, G.; Claffey, K.P.; Hoshino, K. Stiffness analysis of 3D spheroids using microtweezers. PLoS ONE 2017, 12, e0188346. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, B.F.; Wijesinghe, P.; Sampson, D.D. The emergence of optical elastography in biomedicine. Nat. Photonics 2017, 11, 215–221. [Google Scholar] [CrossRef]
- Mok, S.; Al Habyan, S.; Ledoux, C.; Lee, W.; MacDonald, K.N.; McCaffrey, L.; Moraes, C. Mapping cellular-scale internal mechanics in 3D tissues with thermally responsive hydrogel probes. Nat. Commun. 2020, 11, 4757. [Google Scholar] [CrossRef] [PubMed]
- Krieg, M.; Fläschner, G.; Alsteens, D.; Gaub, B.M.; Roos, W.H.; Wuite, G.J.; Gaub, H.E.; Gerber, C.; Dufrêne, Y.F.; Müller, D.J. Atomic force microscopy-based mechanobiology. Nat. Rev. Phys. 2019, 1, 41–57. [Google Scholar] [CrossRef]
- Haase, K.; Pelling, A.E. Investigating cell mechanics with atomic force microscopy. J. R. Soc. Interface 2015, 12, 20140970. [Google Scholar] [CrossRef]
- Tseng, Y.; Kole, T.P.; Wirtz, D. Micromechanical mapping of live cells by multiple-particle-tracking microrheology. Biophys. J. 2002, 83, 3162–3176. [Google Scholar] [CrossRef] [PubMed]
- Robertson-Anderson, R.M. Optical tweezers microrheology: From the basics to advanced techniques and applications. ACS Macro Lett. 2018, 7, 968–975. [Google Scholar] [CrossRef] [PubMed]
- Park, A.Y.; Son, E.J.; Han, K.; Youk, J.H.; Kim, J.-A.; Park, C.S. Shear wave elastography of thyroid nodules for the prediction of malignancy in a large scale study. Eur. J. Radiol. 2015, 84, 407–412. [Google Scholar] [CrossRef] [PubMed]
- Barretta, R.; Iuorio, A.; Luciano, R.; Vaccaro, M.S. On wave propagation in nanobeams. Int. J. Eng. Sci. 2024, 196, 104014. [Google Scholar] [CrossRef]
- Malandrino, A.; Mak, M.; Kamm, R.D.; Moeendarbary, E. Complex mechanics of the heterogeneous extracellular matrix in cancer. Extrem. Mech. Lett. 2018, 21, 25–34. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Wang, L.; Xu, H.; Du, Q.; Li, L.; Wang, L.; Zhang, E.S.; Chen, G.; Wang, Y. Heterogeneous responses to mechanical force of prostate cancer cells inducing different metastasis patterns. Adv. Sci. 2020, 7, 1903583. [Google Scholar] [CrossRef] [PubMed]
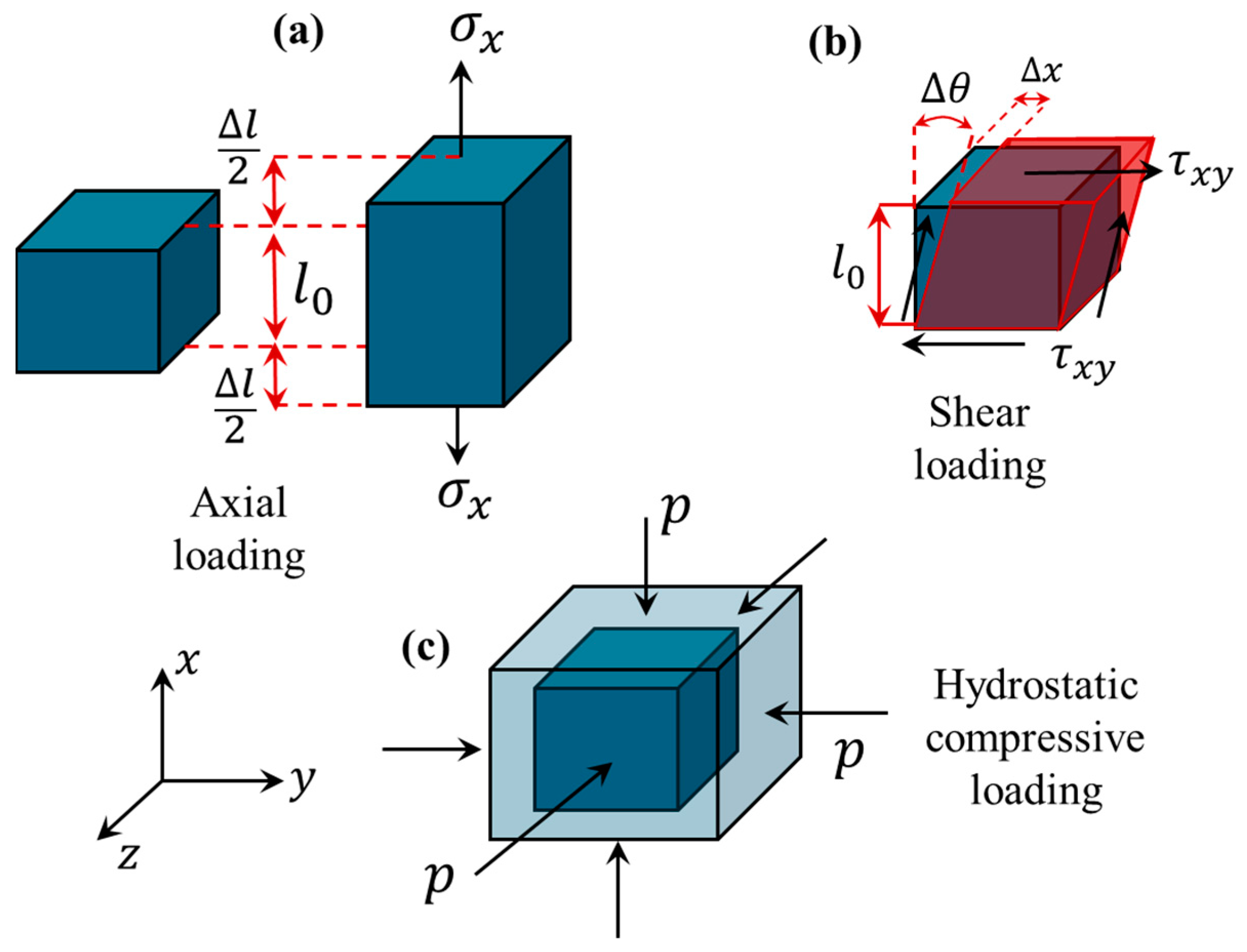

| Loading Condition | Stress | Strain | Mechanical Property | Hooke’s Law | Property Dependency | Strain Deformation |
|---|---|---|---|---|---|---|
| Axial | ||||||
| Shear | ||||||
| Hydrostatic |
| Wave Propagation | Wave Speed | Incompressible Medium | Particle Oscilation | Approximate Speed in Soft Tissue (m/s) | Imaging Techniques |
|---|---|---|---|---|---|
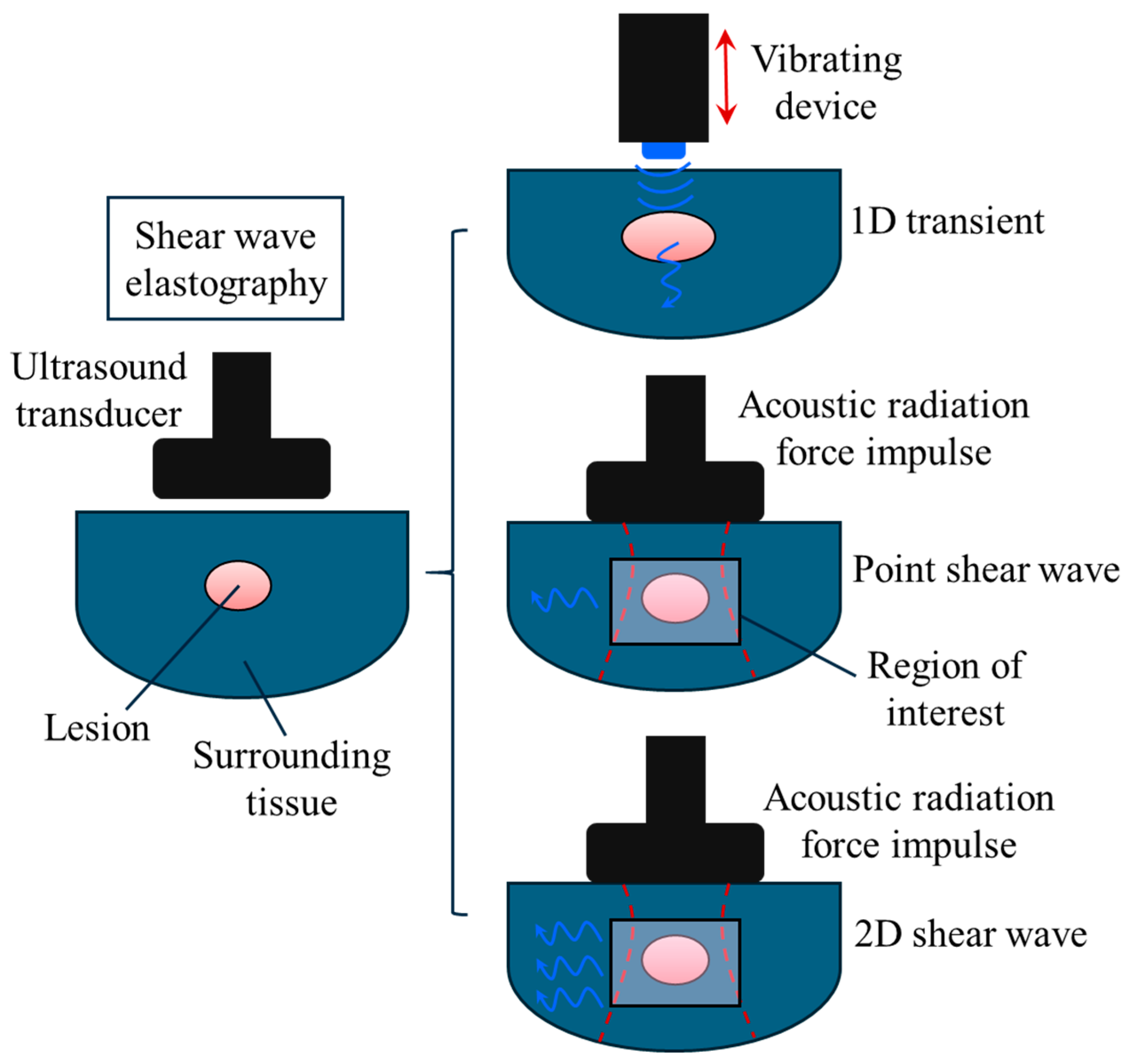
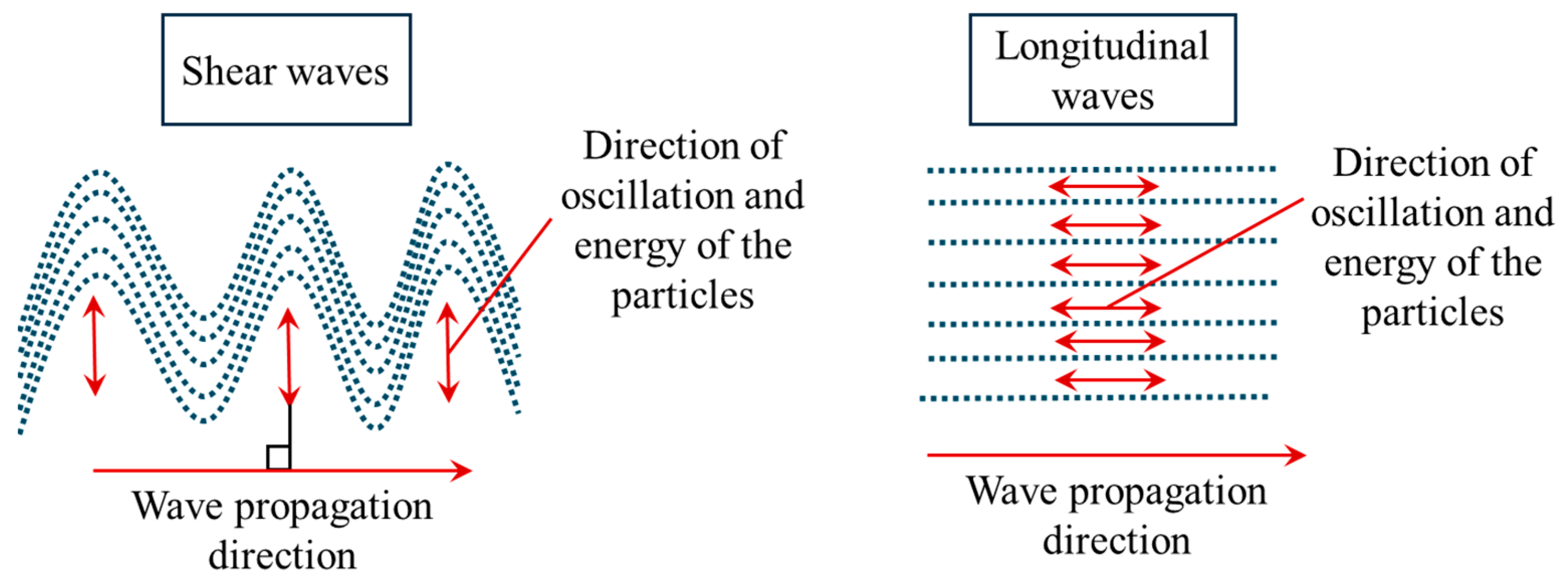
| Longitudinal waves | Parallel to the wave propagation direction | 1540 | 1-D transient and B-mode | ||
| Shear waves | Perpendicular to the wave propagation direction | 1 to 10 | Point and 2D shear wave ultrasound elastography |
| Model | Mechanical Properties | Independent Parameters | Microfiltration | Fluid Effects | Scale Effects | Computational Time |
|---|---|---|---|---|---|---|
| Classical elasticity | No | No | No | Very Low | ||
| Viscoelasticity | No | Yes | No | Low | ||
| Poroelasticity | Can be incorporated | Yes | No | Medium | ||
| Nonlocal elasticity | No | No | Yes | High | ||
| Nonlocal poroelasticity | Can be incorporated | Yes | Yes | Very high |
| Continuum Model | Evaluation Metric | Metric Value | Study Model | Computational Complexity Level | Potential Clinical Application |
|---|---|---|---|---|---|
| Classical local elasticity [90] | Specificity | 78–88% | Human breast tissue | Simple | Solid tumours |
| Viscoelasticity [51] | Residual error | 1.0529 | Tissue-mimicking phantom | Intermediate | Soft biological tissues |
| Poroelasticity [19] | Accuracy | 90% | Orthotopic mouse model | Intermediate | Solid tumours |
| Nonlocal viscoelasticity [91] | Test mean square error | 4.3 × 10−6 | In silico study | Complex | Ovarian diseases |
| Authors | Year | Model | Ultrasound Elastography | Tissue |
|---|---|---|---|---|
| Cespedes et al. [92] | 1993 | Classical elasticity | Ultrasound elastography by linear array transducers | Muscle and breast in vivo |
| Korte et al. [93] | 1998 | A geometry model | Strain imaging | Human arteries |
| Konofagou et al. [95] | 1999 | Poroelasticity | Poroelastography | Tissue mimicking phantoms |
| Walker et al. [96] | 2000 | Viscoelasticity | Acoustic radiation force ultrasound elastography | Tissue mimicking phantoms |
| Insana et al. [94] | 2004 | Viscoelasticity | Strain imaging | Tumour microenvironment |
| Berry et al. [97,98] | 2006 | Poroelasticity | Strain imaging | Tofu as a suitable poroelastic material |
| Hoyt et al. [99] | 2008 | Viscoelasticity | Shear wave | Skeletal muscle |
| Schmitt et al. [100] | 2011 | Viscoelasticity | plane shear wave | Blood clot |
| Chen et al. [52] | 2013 | Viscoelasticity | Shear wave | Liver |
| Mousavi et al. [14] | 2015 | Classical elasticity | Ultrasound or magnetic resonance imaging | Tissue-mimicking phantom for prostate cancer |
| Hong et al. [101] | 2016 | Viscoelasticity | Dual mode | protein hydrogels |
| Zhou and Zhang [51] | 2018 | Viscoelasticity | Shear wave | Phantom |
| Goswami et al. [62] | 2020 | Nonlinear elasticity | Quasi-static and shear wave | Gelatin phantoms |
| Bied and Gennisson [102] | 2021 | Nonlinear elasticity | Shear wave | Phantom and ex vivo bovine and porcine muscular tissues |
| Aichele and Catheline [103] | 2021 | Poroelasticity and viscoelasticity | Shear wave | Liver and phantom |
| Islam et al. [104] | 2021 | Poroelasticity | Poroelastography | Phantom and mice breast model |
| Kishimoto et al. [105] | 2022 | Viscoelasticity | Transient, point and 2D shear waves | Phantom |
| Khan and Righetti [106] | 2022 | Poroelasticity | Poroelastography | mice datasets with triple negative breast cancer |
| Zhang et al. [107] | 2022 | Hyperelasticity | High-frequency ultrasound elastography | Cornea and ciliary body |
| Farajpour and Ingman [108] | 2023 | Higher-order nonlocal elasticity | In-plane waves | Breast cancer |
| Tang et al. [109] | 2023 | Classical elasticity | Strain elastography | Spinal cord injury using an in-vivo rabbit model |
| Khan et al. [110] | 2023 | Hyperelasticity and viscoelasticity | Quasi-static and dynamic | Tissue mimic phantoms |
| Pagé et al. [111] | 2023 | Nonlinear elasticity | Shear wave | Gelatin-agar phantoms |
| Kheirkhah et al. [112] | 2023 | Hyperelasticity | Quasi-static | Tissue-mimicking phantom |
| Khan et al. [113] | 2023 | Poroelastic | Poroelastography | A mice model of triple-negative breast cancer |
| Majumder et al. [114] | 2023 | A bi-phasic poroelastic model | Poroelastography | Polyacrylamide samples and breast mouse model |
| Dwairy et al. [115] | 2023 | Biphasic theory | N/A | Solid tumour |
| Kheirkhah et al. [116] | 2023 | Inversion-based classical elasticity | Strain imaging | Locally breast cancer |
| Tecse et al. [117] | 2023 | Viscoelastic | Reverberant shear wave | Plantar soft tissue and gelatine phantom |
| Gotschi et al. [118] | 2023 | Viscoelastic | Shear wave | Tendon |
| Duroy et al. [119] | 2023 | Classical elasticity | Quasi-static ultrasound elastography | Phantoms and breast tissues |
| Elmeliegy and Guddati [120] | 2023 | Elasticity modelling | Shear wave | In silico simulation |
| Farajpour and Ingman [91] | 2024 | Nonlocal viscoelasticity | Scale-dependent elastography | Ovarian cancer, breast cancer, and ovarian fibrosis |
| Osika and Kijanka [121] | 2024 | Viscoelasticity | Shear wave | Phantom |
| Majumder et al. [122] | 2024 | Eshelby’s theory of continuum mechanics | Compression elastography | Phantoms and orthotopic mouse model of breast cancer |
| Cihan et al. [123] | 2024 | Poroelastic | Shear wave | Chicken breast |
| Gautam and Arora [124] | 2024 | Hyperelasticity | Strain elastography | Subcutaneous adipose tissue and Muscle thickness |
| Imaging Device | Scale Range | Scale Range (m) | Benefits | Drawbacks | Available Studies |
|---|---|---|---|---|---|
| Magnetic resonance elastography | Tissue-scale level | 10−4–10−3 | Non-invasive, entire organ assessment, quantitative | Bulky, relatively expensive, lack of cellular resolution, limited availability | [126] |
| Microscale tweezers | Microscale | 10−5 | Ability to apply in-plane forces with high precision | Restrictions in strain extraction and scalability | [128,129] |
| Thermo-responsive microgel probes | Microscale | 10−5–10−4 | Tracking mechanical features during microenvironment evolution over time | Restricted to local regions, scalability limitation, challenging validation | [131] |
| Microrheology | Nanoscale and microscale | 10−9–10−6 | Accurate viscoelasticity measurements | Scale restrictions (only microscales and local regions), incompatible with larger scales | [134,135] |
| Scanning force microscopy | Nanoscale and microscale | 10−9–10−6 | detailed and precise elasticity maps at nanoscale level | Destructive tissue preparation, only 2D surface imaging | [132,133] |
| μElastography | Microscale | 10−7–10−3 | 3D elasticity maps, multiplane details, Scalability | Depth limitations, reduced mechanical strain sensitivity | [127] |
| Ultrasound elastography | Tissue-scale level | 10−4 | Non-invasive, mobile, widespread availability, inexpensive, measurement flexibility | Reduced spatial resolution, not applicable at cellular level, signal attenuation due to fluid content | [49,125] |
| Optical coherence elastography | Microscale | 10−5–10−4 | Strong biocompatibility and enhanced mechanical sensitivity | Depth restriction, lack of capability to distinguish between elasticity and density | [130] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farajpour, A.; Ingman, W.V. Mathematical Models for Ultrasound Elastography: Recent Advances to Improve Accuracy and Clinical Utility. Bioengineering 2024, 11, 991. https://doi.org/10.3390/bioengineering11100991
Farajpour A, Ingman WV. Mathematical Models for Ultrasound Elastography: Recent Advances to Improve Accuracy and Clinical Utility. Bioengineering. 2024; 11(10):991. https://doi.org/10.3390/bioengineering11100991
Chicago/Turabian StyleFarajpour, Ali, and Wendy V. Ingman. 2024. "Mathematical Models for Ultrasound Elastography: Recent Advances to Improve Accuracy and Clinical Utility" Bioengineering 11, no. 10: 991. https://doi.org/10.3390/bioengineering11100991
APA StyleFarajpour, A., & Ingman, W. V. (2024). Mathematical Models for Ultrasound Elastography: Recent Advances to Improve Accuracy and Clinical Utility. Bioengineering, 11(10), 991. https://doi.org/10.3390/bioengineering11100991







