ECG Forecasting System Based on Long Short-Term Memory
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. ECG Data Description
3.2. Proposed Methods
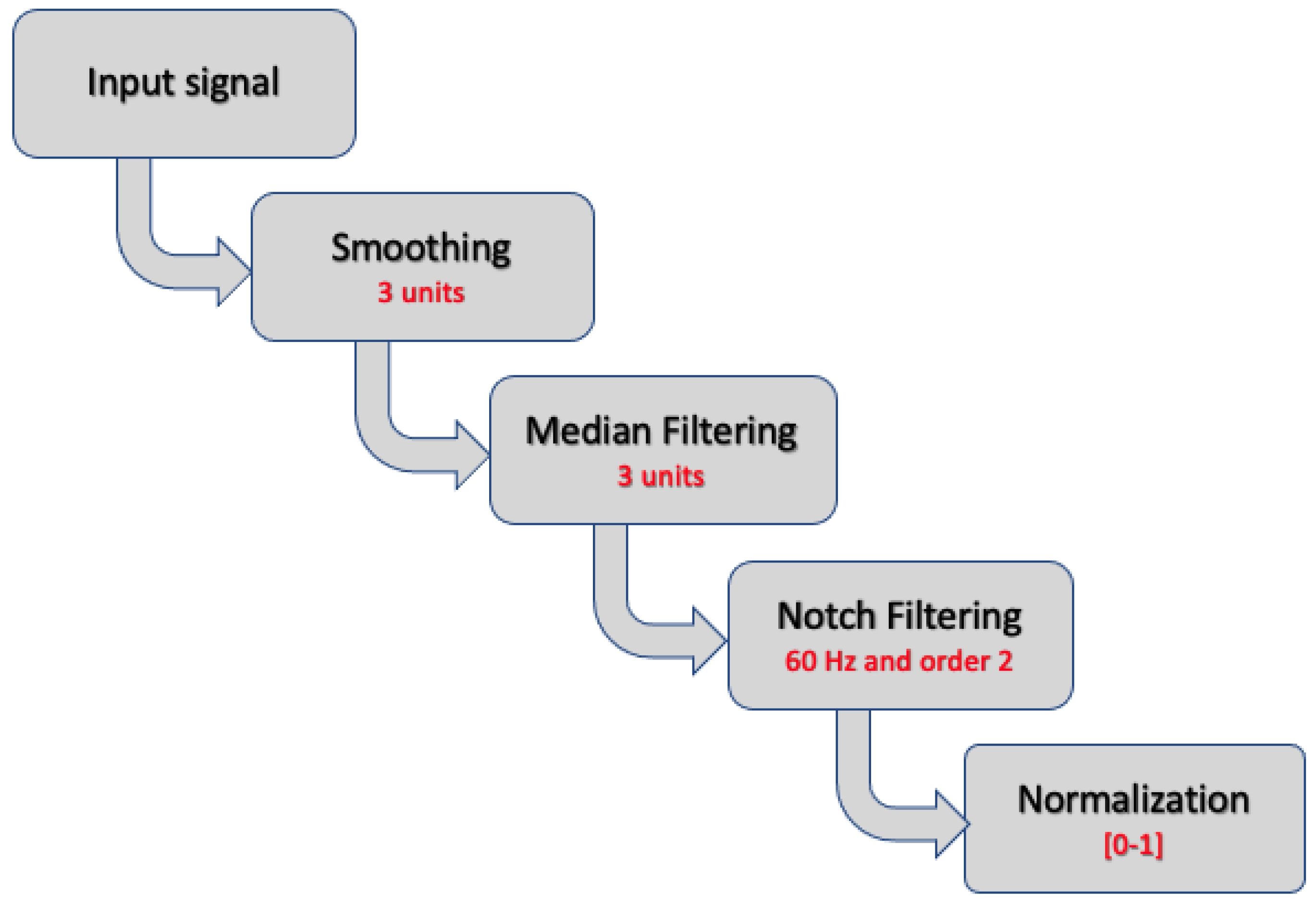
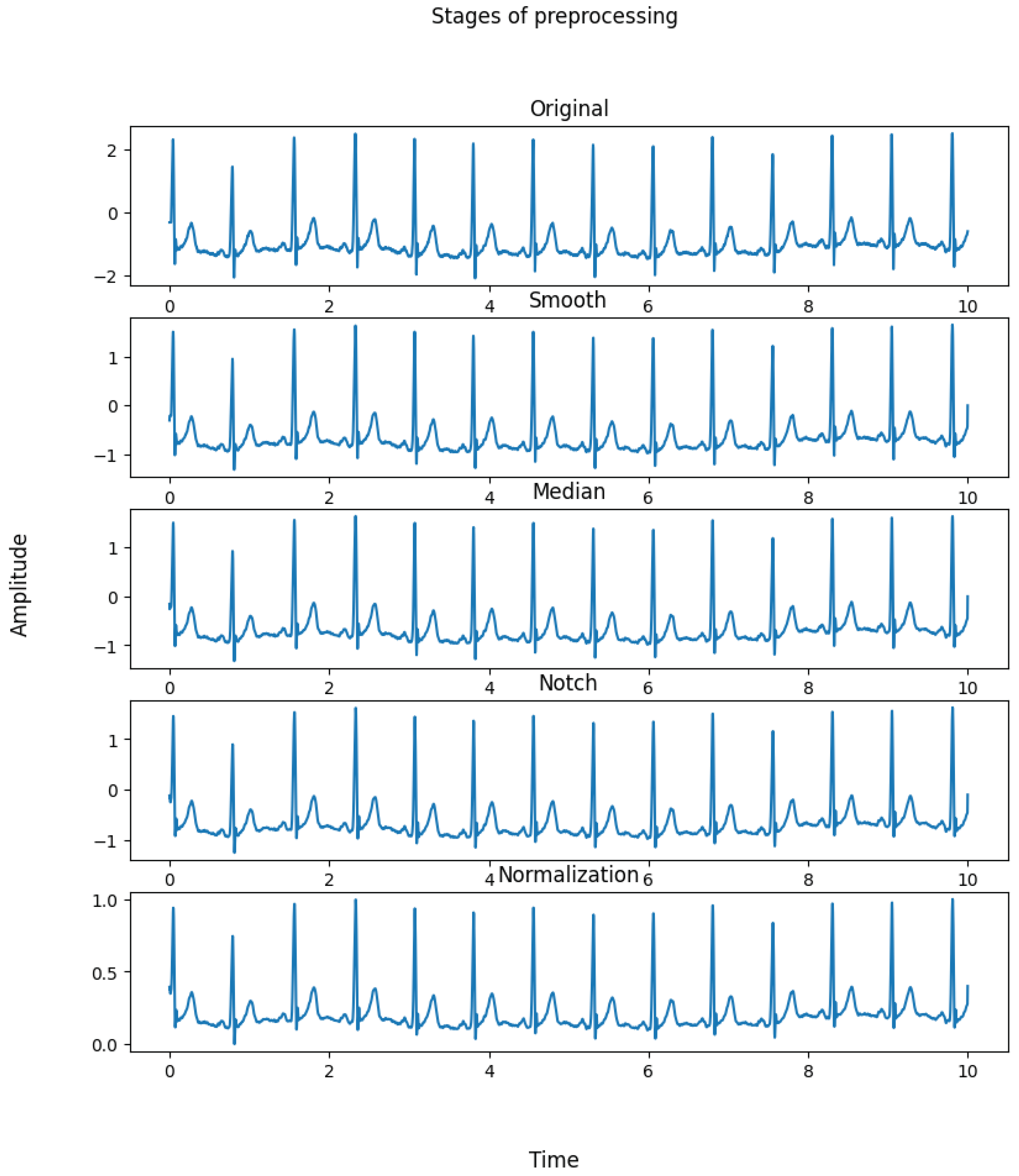
Pre-Processing
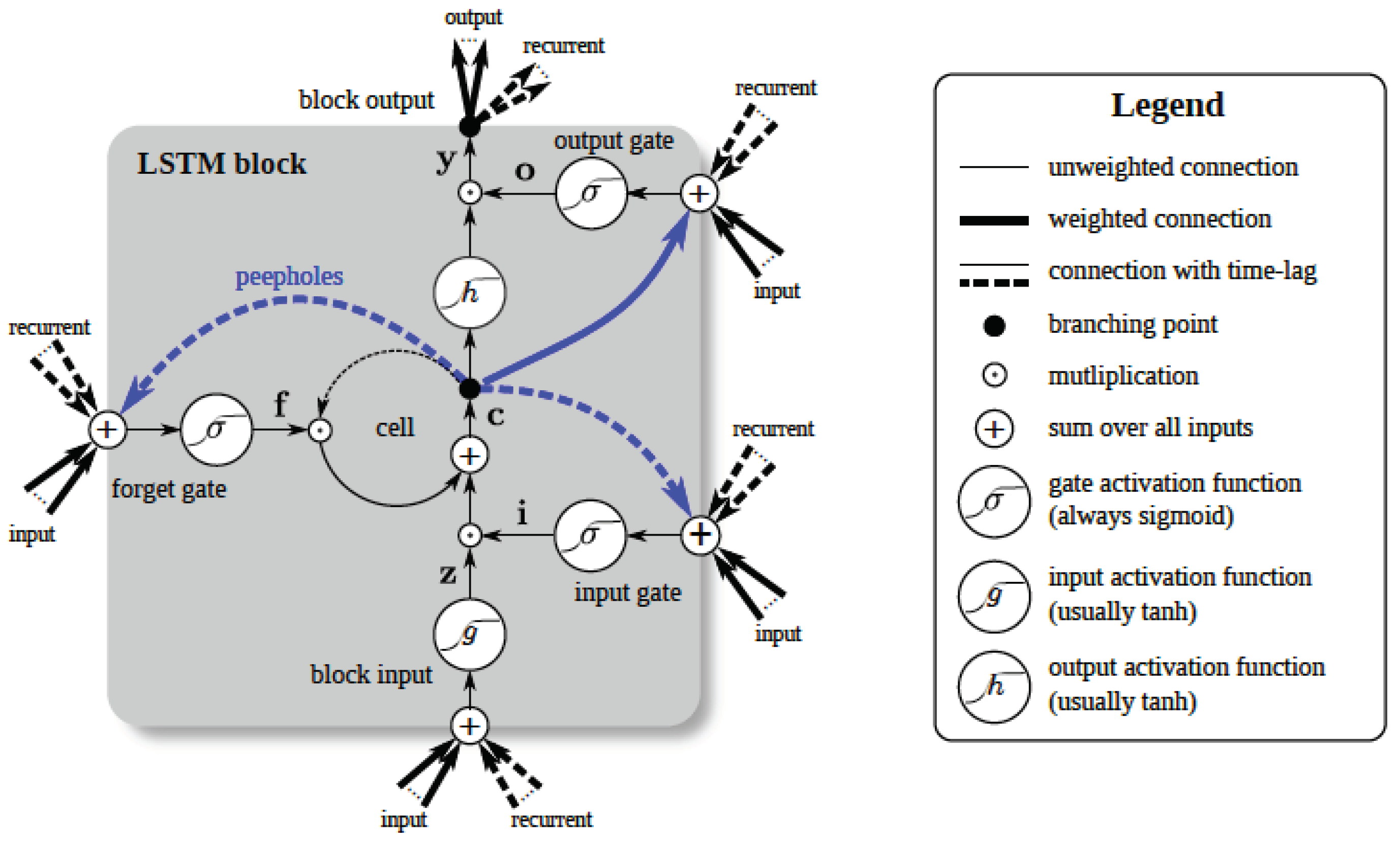
3.3. Long Short-Term Memory
- LSTM models are very adept at capturing extended relationships in sequential data, which makes them highly useful for representing the complex patterns found in ECG signals;
- LSTM models are the best choice for handling intricate, nonlinear, nonstationary, and dynamic patterns, which are frequently observed in ECG signals;
- LSTM models have the ability to effectively manage sequences of varying lengths, allowing them to be easily applied to ECG recordings of diverse durations without the need for any pre-processing modifications.
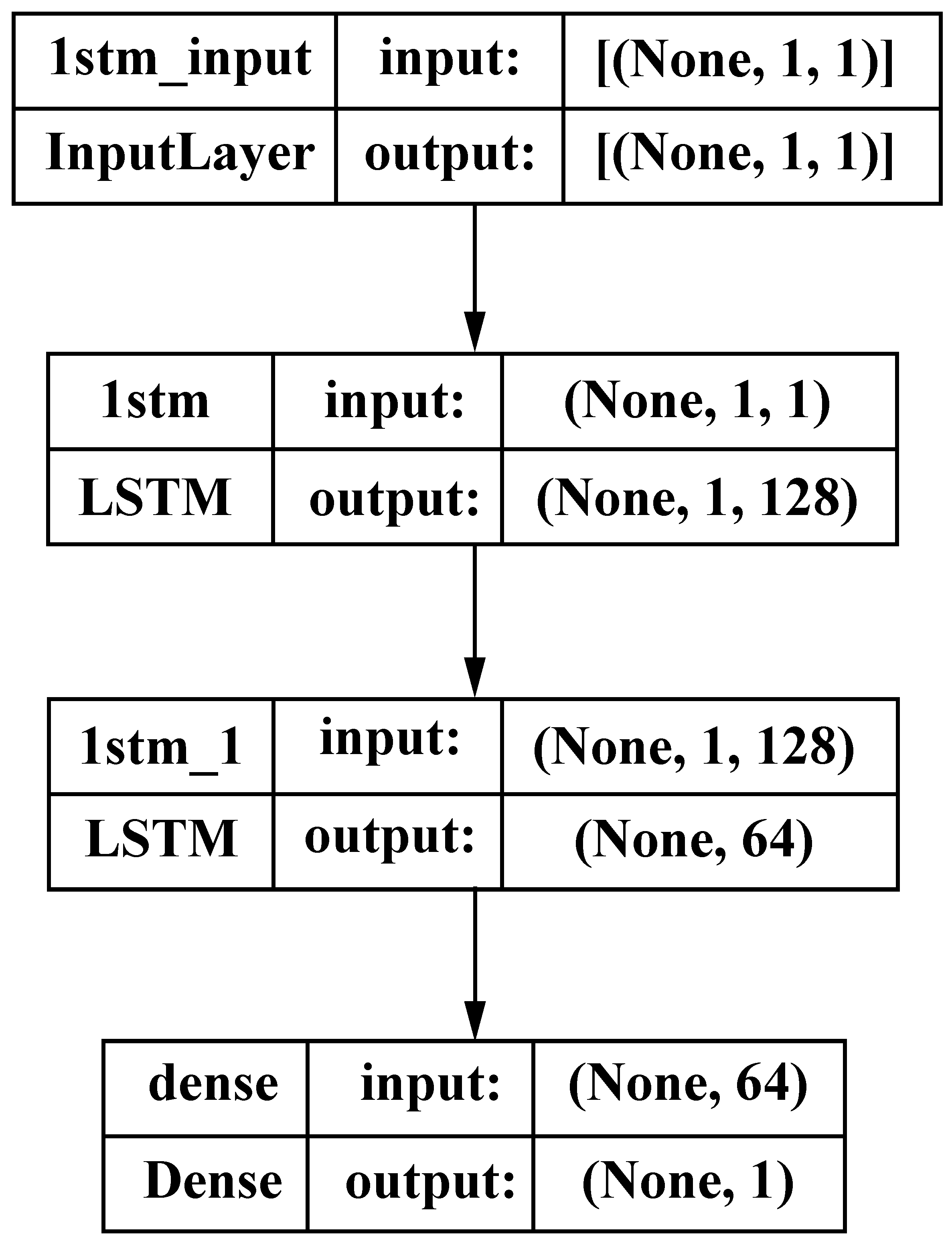
3.3.1. Forecasting Model
3.3.2. Measuring Time Series Forecasting Performance
4. Implementation
- Operating system: Windows 11 Pro;
- Processor: 12th Gen Intel® Core ™ i7-12,700 2.10 GHz;
- RAM: 64 GB (16*4 of DDR4);
- GPU: NVidia GeForce 1060—6 GB.
5. Results and Discussion
- The early detection of cardiac abnormalities as ECG signal forecasting can detect heart irregularities and potentially fatal illnesses; therefore, ECG data can be used to diagnose cardiac anomalies, such as arrhythmia, ischemia, heart obstructions, and more, and early diagnosis can lead to better patient outcomes;
- ECG signal forecasting aids in patient risk assessment and stratification as by studying ECG data and identifying problematic patterns or indications, healthcare providers can categorize patients and this information can help with resource allocation and treatment decisions;
- Doctors can better comprehend a patient’s cardiac condition by predicting ECG patterns as by using a patient’s historical ECG data, forecasting algorithms can predict future trends and identify changes in heart function, which enables tailored therapy and interventions;
- ECG signal forecasting is required for remote monitoring and telemedicine, so healthcare providers can remotely monitor patients with persistent heart conditions by continuously monitoring ECG data, which simplifies cardiac health management while also lowering healthcare costs and increasing patient convenience;
- ECG signal forecasting aids in determining the success of cardiac treatment, so healthcare providers can assess a patient’s cardiac health by comparing expected ECG patterns to actual data, which can improve treatment strategies and guide ongoing care;
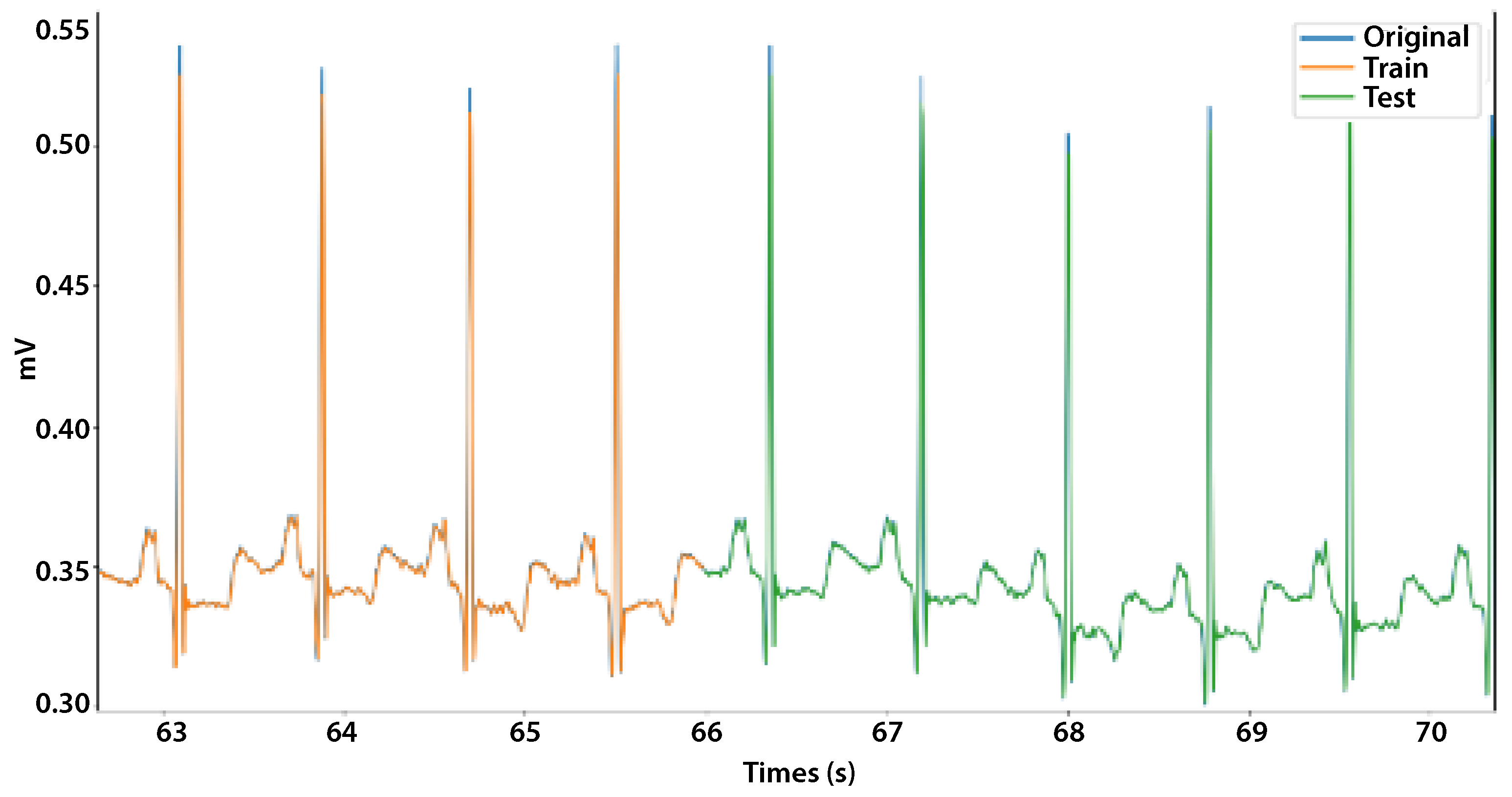
- ECG signal forecasting provides information on long-term cardiac health, so ECG data can help healthcare personnel to monitor cardiac issues, treatments, and treatment plans as the R-peaks have larger amplitudes than the other waves in the signals, which are where the most noticeable changes may be seen.
6. Conclusions
- The forecasting of ECG signals is, to a large extent, a rather unexplored field and this is one of the first papers to employ deep learning techniques (LSTM) to the forecasting of ECG time series;
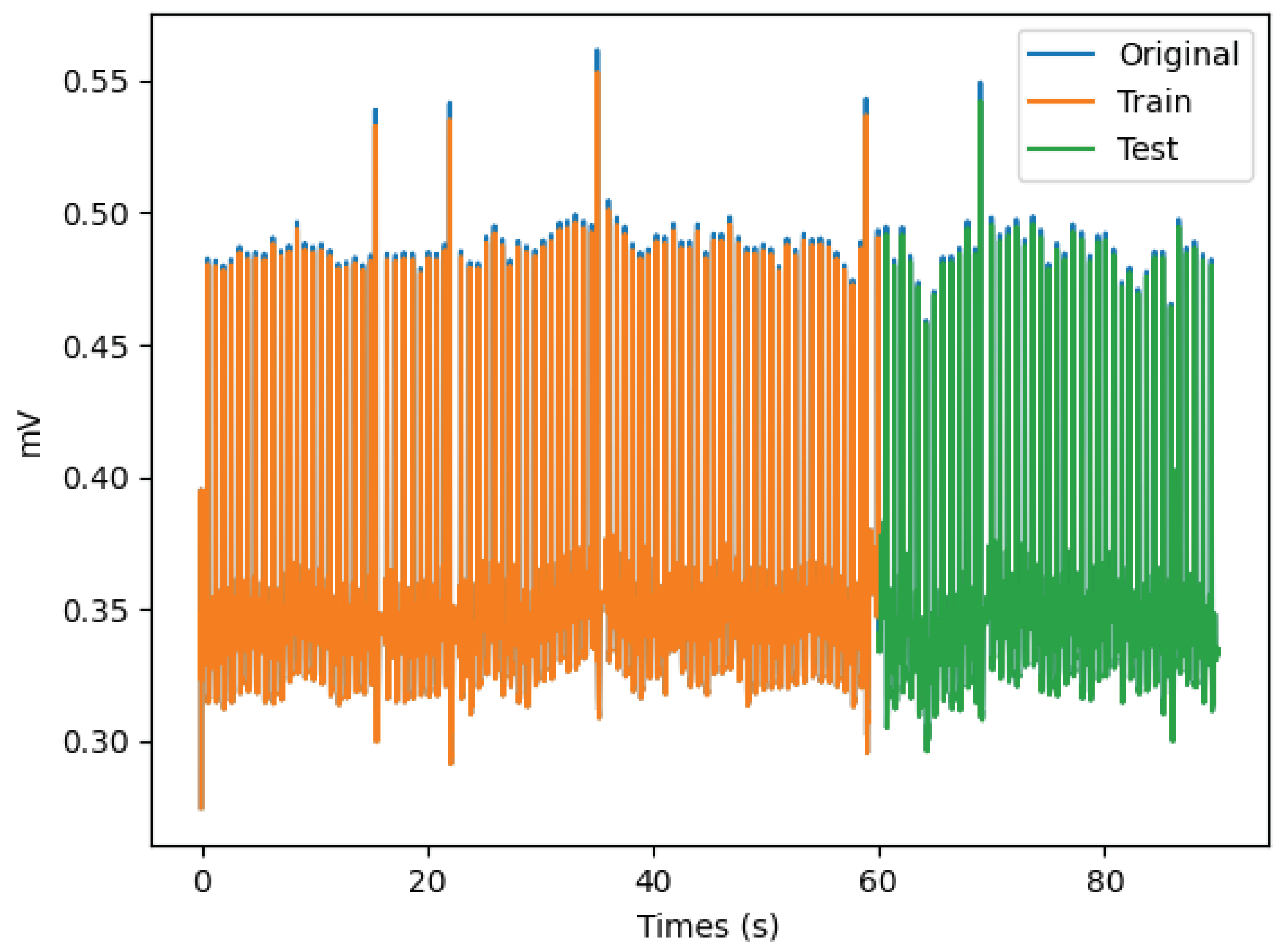
- The proposed LSTM model can predict the trends of changes in original data series (with the most visible differences being in the amplitudes of the R-peaks), which shows that the LSTM model can meet the requirement of forecasting accuracy;
- Considering the accuracy of the proposed model and taking into account the properties of the physiological signals, a similar approach could be applied to ECG signals and help to improve the efficiency of healthcare systems;
- Research within the field of ECG forecasting remains minimal, which allows for the development of other studies, such as the analysis of forecasting steps, the study of different forecasting strategies, or even the investigation of applications based on other methods.
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APB | Atrial premature beat |
| ARIMA | Autoregressive integrated moving average |
| BP | Back-propagation |
| BPNN | Back-propagation neural network |
| CVD | Cardiovascular disease |
| DL | Deep learning |
| DWT | Discrete wavelet transform |
| ECG | Electrocardiogram |
| EWT | Empirical wavelet transform |
| GAN | Generative adversarial network |
| GRU | Gated recurrent unit |
| HFCM | High-order fuzzy cognitive maps |
| IDE | Integrated development environment |
| LBBB | Left bundle branch block |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MI | Mutual information |
| ML | Machine learning |
| MSE | Mean square error |
| N | Normal beat |
| PVC | Premature ventricular complex |
| RBBB | Right bundle branch block |
| RMSE | Root mean square error |
| RNN | Recurrent neural network |
| SMA | Simple moving average |
| TCN | Temporal convolutional network |
| VMD | Variational mode decomposition |
| WHO | Word Heath Organization |
References
- Ebenezer, J.G.A.; Durga, S. Big data analytics in healthcare: A survey. J. Eng. Appl. Sci. 2015, 10, 3645–3650. [Google Scholar]
- World Health Organization. World Health Statistics 2021: Monitoring Health for the SDGs, Sustainable Development Goals; World Health Organization: Geneva, Switzerland, 2021; pp. 7–121. [Google Scholar]
- Kilic, A. Artificial Intelligence and Machine Learning in Cardiovascular Health Care. Ann. Thorac. Surg. 2020, 109, 1323–1329. [Google Scholar] [CrossRef] [PubMed]
- Marques, J.A.L.; Han, T.; Wu, W.; do Vale Madeiro, J.P.; Neto, A.V.L.; Gravina, R.; Fortino, G.; de Albuquerque, V.H.C. IoT-based smart health system for ambulatory maternal and fetal monitoring. IEEE Internet Things J. 2020, 8, 16814–16824. [Google Scholar] [CrossRef]
- do Vale Madeiro, J.P.; Marques, J.A.L.; Han, T.; Pedrosa, R.C. Evaluation of mathematical models for QRS feature extraction and QRS morphology classification in ECG signals. Measurement 2020, 156, 107580. [Google Scholar] [CrossRef]
- Torres, J.F.; Hadjout, D.; Sebaa, A.; Martínez-Álvarez, F.; Troncoso, A. Deep Learning for Time Series Forecasting: A Survey. Big Data 2021, 9, 3–21. [Google Scholar] [CrossRef] [PubMed]
- Belo, D.; Rodrigues, J.; Vaz, J.R.; Pezarat-Correia, P.; Gamboa, H. Biosignals learning and synthesis using deep neural networks. Biomed. Eng. Online 2017, 16, 115. [Google Scholar] [CrossRef]
- Madeiro, J.P.; Cortez, P.C.; Marques, J.A.; Seisdedos, C.R.; Sobrinho, C.R. An innovative approach of QRS segmentation based on first-derivative, Hilbert and Wavelet Transforms. Med. Eng. Phys. 2012, 34, 1236–1246. [Google Scholar] [CrossRef]
- Matias, I.; Garcia, N.; Pirbhulal, S.; Felizardo, V.; Pombo, N.; Zacarias, H.; Sousa, M.; Zdravevski, E. Prediction of Atrial Fibrillation using artificial intelligence on Electrocardiograms: A systematic review. Comput. Sci. Rev. 2020, 39, 100334. [Google Scholar] [CrossRef]
- Denysyuk, H.V.; Pinto, R.J.; Silva, P.M.; Duarte, R.P.; Marinho, F.A.; Pimenta, L.; Gouveia, A.J.; Gonçalves, N.J.; Coelho, P.J.; Zdravevski, E.; et al. Algorithms for automated diagnosis of cardiovascular diseases based on ECG data: A comprehensive systematic review. Heliyon 2023, 9, e13601. [Google Scholar] [CrossRef]
- Zivkovic, T. Forecasting and foreclosing futures: The temporal dissonance of advance care directives. Soc. Sci. Med. 2018, 215, 16–22. [Google Scholar] [CrossRef]
- Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J.; Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J. Artificial intelligence prediction for the covid-19 data based on lstm neural networks and h2o automl. Predict. Model. Decis. Support COVID-19 Crisis 2021, 1, 69–87. [Google Scholar] [CrossRef]
- Marques, J.A.L.; Gois, F.N.B.; Xavier-Neto, J.; Fong, S.J. Predictive Models for Decision Support in the COVID-19 Crisis; Springer Cham: Switzerland, 2021. [Google Scholar] [CrossRef]
- Bui, C.; Pham, N.; Vo, A.; Tran, A.; Nguyen, A.; Le, T. Time Series Forecasting for Healthcare Diagnosis and Prognostics with the Focus on Cardiovascular Diseases; Springer: Singapore, 2018; pp. 809–818. [Google Scholar]
- Sufi, F.; Khalil, I. Diagnosis of Cardiovascular Abnormalities from Compressed ECG: A Data Mining-Based Approach. IEEE Trans. Inf. Technol. Biomed. 2011, 15, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Sufi, F.; Khalil, I.; Mahmood, A.N. A clustering based system for instant detection of cardiac abnormalities from compressed ECG. Expert Syst. Appl. 2011, 38, 4705–4713. [Google Scholar] [CrossRef]
- Louzazni, M.; Mosalam, H.; Khouya, A. A non-linear auto-regressive exogenous method to forecast the photovoltaic power output. Sustain. Energy Technol. Assess. 2020, 38, 100670. [Google Scholar] [CrossRef]
- Mukasheva, A.; Saparkhojayev, N.; Akanov, Z.; Apon, A.; Kalra, S. Forecasting the Prevalence of Diabetes Mellitus Using Econometric Models. Diabetes Ther. 2019, 10, 2079–2093. [Google Scholar] [CrossRef]
- Fonseca, R.; Gomez, P. Automatic model selection in ensembles for time series forecasting. IEEE Lat. Am. Trans. 2016, 14, 3811–3819. [Google Scholar] [CrossRef]
- Majid, R. Advances in Statistical Forecasting Methods: An Overview. Econ. Aff. 2018, 63, 815–831. [Google Scholar] [CrossRef]
- Taieb, S.B.; Bontempi, G.; Atiya, A.F.; Sorjamaa, A. A review and comparison of strategies for multi-step ahead time series forecasting based on the NN5 forecasting competition. Expert Syst. Appl. 2012, 39, 7067–7083. [Google Scholar] [CrossRef]
- Ray, M.; Singh, K.N.; Ramasubramanian, V.; Paul, R.K.; Mukherjee, A.; Rathod, S. Integration of Wavelet Transform with ANN and WNN for Time Series Forecasting: An Application to Indian Monsoon Rainfall. Natl. Acad. Sci. Lett. 2020, 43, 509–513. [Google Scholar] [CrossRef]
- Bou-Hamad, I.; Jamali, I. Forecasting financial time-series using data mining models: A simulation study. Res. Int. Bus. Financ. 2020, 51, 101072. [Google Scholar] [CrossRef]
- Kaushik, S.; Choudhury, A.; Sheron, P.K.; Dasgupta, N.; Natarajan, S.; Pickett, L.A.; Dutt, V. AI in Healthcare: Time-Series Forecasting Using Statistical, Neural, and Ensemble Architectures. Front. Big Data 2020, 3, 4. [Google Scholar] [CrossRef]
- Cheng, C.; Sa-Ngasoongsong, A.; Beyca, O.; Le, T.; Yang, H.; Kong, Z.; Bukkapatnam, S.T. Time series forecasting for nonlinear and non-stationary processes: A review and comparative study. IIE Trans. (Inst. Ind. Eng.) 2015, 47, 1053–1071. [Google Scholar] [CrossRef]
- Tealab, A. Time series forecasting using artificial neural networks methodologies: A systematic review. Future Comput. Inform. J. 2018, 3, 334–340. [Google Scholar] [CrossRef]
- Garcia-Pedrero, A.; Gomez-Gil, P. Time series forecasting using recurrent neural networks and wavelet reconstructed signals. In Proceedings of the CONIELECOMP 2010—20th International Conference on Electronics Communications and Computers, Cholula, Puebla, Mexico, 22–24 February 2010; pp. 169–173. [Google Scholar] [CrossRef]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Totaro, S.; Hussain, A.; Scardapane, S. A non-parametric softmax for improving neural attention in time-series forecasting. Neurocomputing 2020, 381, 177–185. [Google Scholar] [CrossRef]
- Niu, T.; Wang, J.; Lu, H.; Yang, W.; Du, P. Developing a deep learning framework with two-stage feature selection for multivariate financial time series forecasting. Expert Syst. Appl. 2020, 148, 113237. [Google Scholar] [CrossRef]
- Greenaway-McGrevy, R. Multistep forecast selection for panel data. Econom. Rev. 2020, 39, 373–406. [Google Scholar] [CrossRef]
- Wang, H.; Lei, Z.; Zhang, X.; Zhou, B.; Peng, J. A review of deep learning for renewable energy forecasting. Energy Convers. Manag. 2019, 198, 111799. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Barak, S. A series of forecasting models for seismic evaluation of dams based on ground motion meta-features. Eng. Struct. 2020, 203, 109657. [Google Scholar] [CrossRef]
- Ahire, M.; Fernandes, P.O.; Teixeira, J.P. Forecasting and estimation of medical tourism demand in India. Smart Innov. Syst. Technol. 2020, 171, 211–222. [Google Scholar] [CrossRef]
- Bose, M.; Mali, K. Designing fuzzy time series forecasting models: A survey. Int. J. Approx. Reason. 2019, 111, 78–99. [Google Scholar] [CrossRef]
- Masum, S.; Chiverton, J.P.; Liu, Y.; Vuksanovic, B. Investigation of Machine Learning Techniques in Forecasting of Blood Pressure Time Series Data; Volume 11927 LNAI; Springer International Publishing: Berlin, Germany, 2019; pp. 269–282. [Google Scholar] [CrossRef]
- Awad, S.F.; Huangfu, P.; Ayoub, H.H.; Pearson, F.; Dargham, S.R.; Critchley, J.A.; Abu-Raddad, L.J. Forecasting the impact of diabetes mellitus on tuberculosis disease incidence and mortality in India. J. Glob. Health 2019, 9. [Google Scholar] [CrossRef]
- Čepulionis, P.; Lukoševičiūtė, K. Electrocardiogram Time Series Forecasting and Optimization Using Ant Colony Optimization Algorithm. Math. Model. Eng. (MME) 2016, 2, 69–77. Available online: https://api.semanticscholar.org/CorpusID:8713576 (accessed on 9 November 2023).
- Mohammadi, H.A.; Ghofrani, S.; Nikseresht, A. Using empirical wavelet transform and high-order fuzzy cognitive maps for time series forecasting. Appl. Soft Comput. 2023, 135, 109990. [Google Scholar] [CrossRef]
- Sun, Z.G.; Lei, Y.; Wang, J.; Liu, Q.; Tan, Q.Q. An ECG signal analysis and prediction method combined with VMD and neural network. In Proceedings of the 2017 7th IEEE International Conference on Electronics Information and Emergency Communication (ICEIEC), Macau, China, 21–23 July 2017; pp. 199–202. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Q.; Xue, Q.; Liu, Q.; Tan, Q. Data Prediction of ECG Based on Phase Space Reconstruction and Neural Network. In Proceedings of the 2018 8th International Conference on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, 15–17 June 2018; pp. 162–165. [Google Scholar] [CrossRef]
- Huang, F.; Qin, T.; Wang, L.; Wan, H.; Ren, J. An ECG Signal Prediction Method Based on ARIMA Model and DWT. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 20–22 December 2019; pp. 1298–1304. [Google Scholar] [CrossRef]
- Ratna Prakarsha, K.; Sharma, G. Time series signal forecasting using artificial neural networks: An application on ECG signal. Biomed. Signal Process. Control 2022, 76, 103705. [Google Scholar] [CrossRef]
- Sezer, O.B.; Gudelek, M.U.; Ozbayoglu, A.M. Financial time series forecasting with deep learning: A systematic literature review: 2005–2019. Appl. Soft Comput. J. 2020, 90, 106181. [Google Scholar] [CrossRef]
- Dudukcu, H.V.; Taskiran, M.; Cam Taskiran, Z.G.; Yildirim, T. Temporal Convolutional Networks with RNN approach for chaotic time series prediction. Appl. Soft Comput. 2023, 133, 109945. [Google Scholar] [CrossRef]
- Festag, S.; Spreckelsen, C. Medical multivariate time series imputation and forecasting based on a recurrent conditional Wasserstein GAN and attention. J. Biomed. Inform. 2023, 139, 104320. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Ebrahimi, Z.; Loni, M.; Daneshtalab, M.; Gharehbaghi, A. A review on deep learning methods for ECG arrhythmia classification. Expert Syst. Appl. X 2020, 7, 100033. [Google Scholar] [CrossRef]
- Sahoo, S.; Dash, M.; Behera, S.; Sabut, S. Machine Learning Approach to Detect Cardiac Arrhythmias in ECG Signals: A Survey. Irbm 2020, 41, 185–194. [Google Scholar] [CrossRef]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Greff, K.; Srivastava, R.K.; Koutník, J.; Steunebrink, B.R.; Schmidhuber, J. LSTM: A search space odyssey. IEEE Trans. Neural Netw. Learn. Syst. 2016, 28, 2222–2232. [Google Scholar] [CrossRef]
- Lindemann, B.; Maschler, B.; Sahlab, N.; Weyrich, M. A survey on anomaly detection for technical systems using LSTM networks. Comput. Ind. 2021, 131, 103498. [Google Scholar] [CrossRef]
- Jerez, T.; Kristjanpoller, W. Effects of the validation set on stock returns forecasting. Expert Syst. Appl. 2020, 150, 113271. [Google Scholar] [CrossRef]



| Study | Forecasting Technique | Database | Sequence Length | Forecasting Steps | Metric | |||
|---|---|---|---|---|---|---|---|---|
| MAE | MSE | RMSE | ||||||
| Sun et al. [40] | VMD and BPNN | MIT-BIH | N.S | 1 | 0.016 | x | 0.023 | x |
| Sun et al. [41] | MI and BPNN | MIT-BIH | N.S | 1 | 0.02 | x | 0.042 | x |
| Huang et al. [42] | ARIMA and DWT | MIT-BIH | N.S | 1 | 0.011 | x | 0.018 | x |
| Mohammadi et al. [39] | EWT and HFCM | N.F | N.S | 1 | x | x | 0.011 | x |
| Festag et al. [46] | rcGAN | Autonomic Aging Physio net | 1250 | 1 | x | 0.043 | x | x |
| 30 | x | 0.086 | x | x | ||||
| 250 | x | 0.090 | x | x | ||||
| Prakarsha et al. [43] | ANN | Simulated Data and Pyshio net ATM of Sleep Apnea | 64 | 1 | 0.045 | x | x | x |
| LMS | 0.21 | x | x | x | ||||
| Dudukcu et al. [45] | TCN-LSTM | MIT-BIH | 10 | 1 | 0.005 | x | 0.008 | 0.991 |
| TCN-GRU | 0.005 | x | 0.008 | 0.990 | ||||
| Type | Records |
|---|---|
| Normal beat | 100, 101, 103, 105, 108, 112, 113, 114, 115, 117, 121, 122, 123, 202, 205, 219, 230, 234, 109, 111, 207, 214. |
| LBBB beat | 109, 111, 207, 214. |
| RBBB beat | 118, 124, 212, 231. |
| PVC beat | 106, 116, 119, 200, 201, 203, 208, 213, 221, 228, 233. |
| APB beat | 209, 220, 222, 223, 232. |
| Parameter | Value |
|---|---|
| Batch size | 16 |
| LTSM unit | 192 |
| Optimizer | SGD |
| Max number of epochs | 500 |
| Training/test | 66/34 |
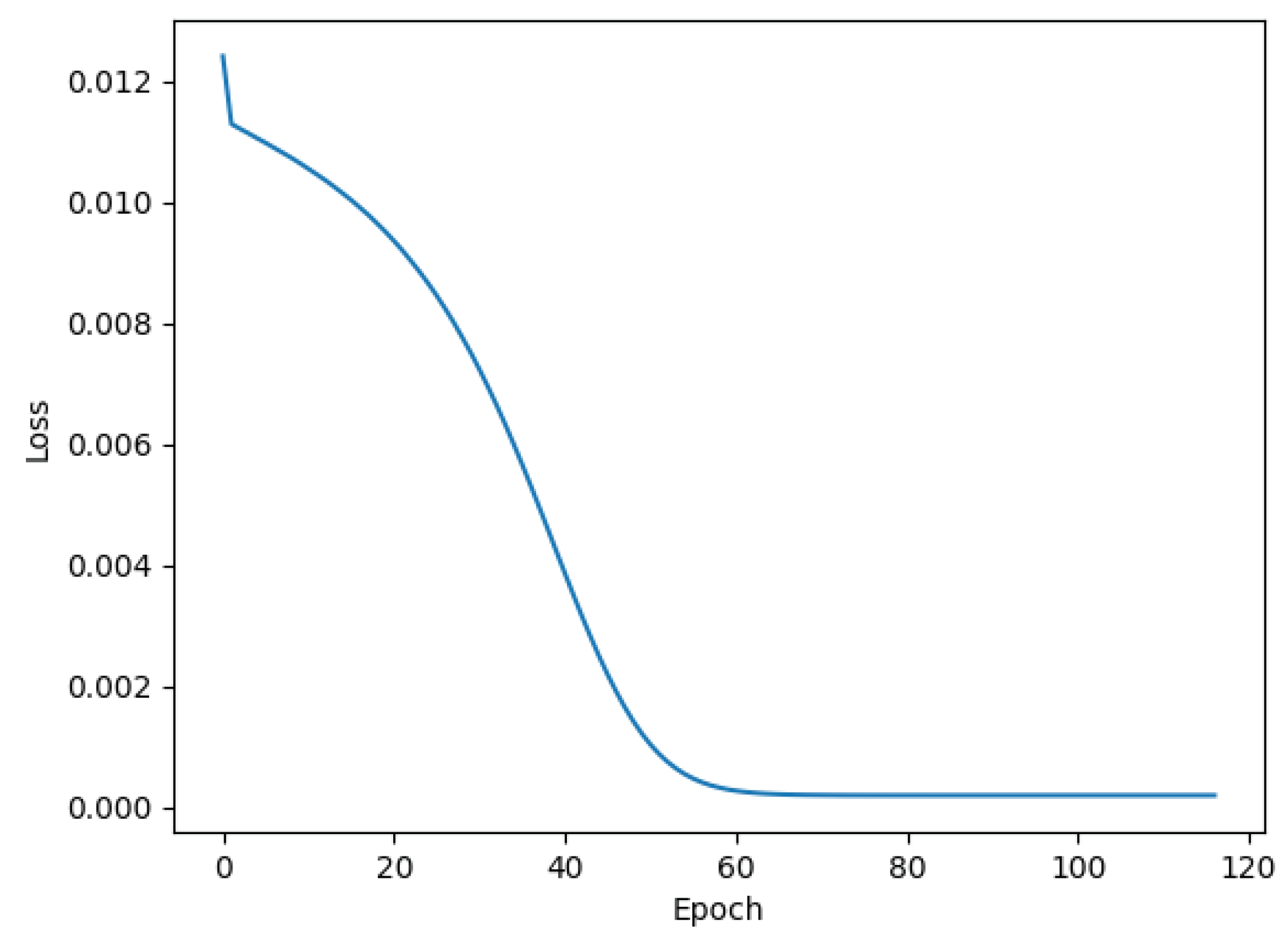
| Loss | Mean squared error |
| Activation | than |
| Metric | MAE |
| Early stopping | Patience = 20; mode = min; monitor = loss |
| Number of hidden LSTM layers | 2 |
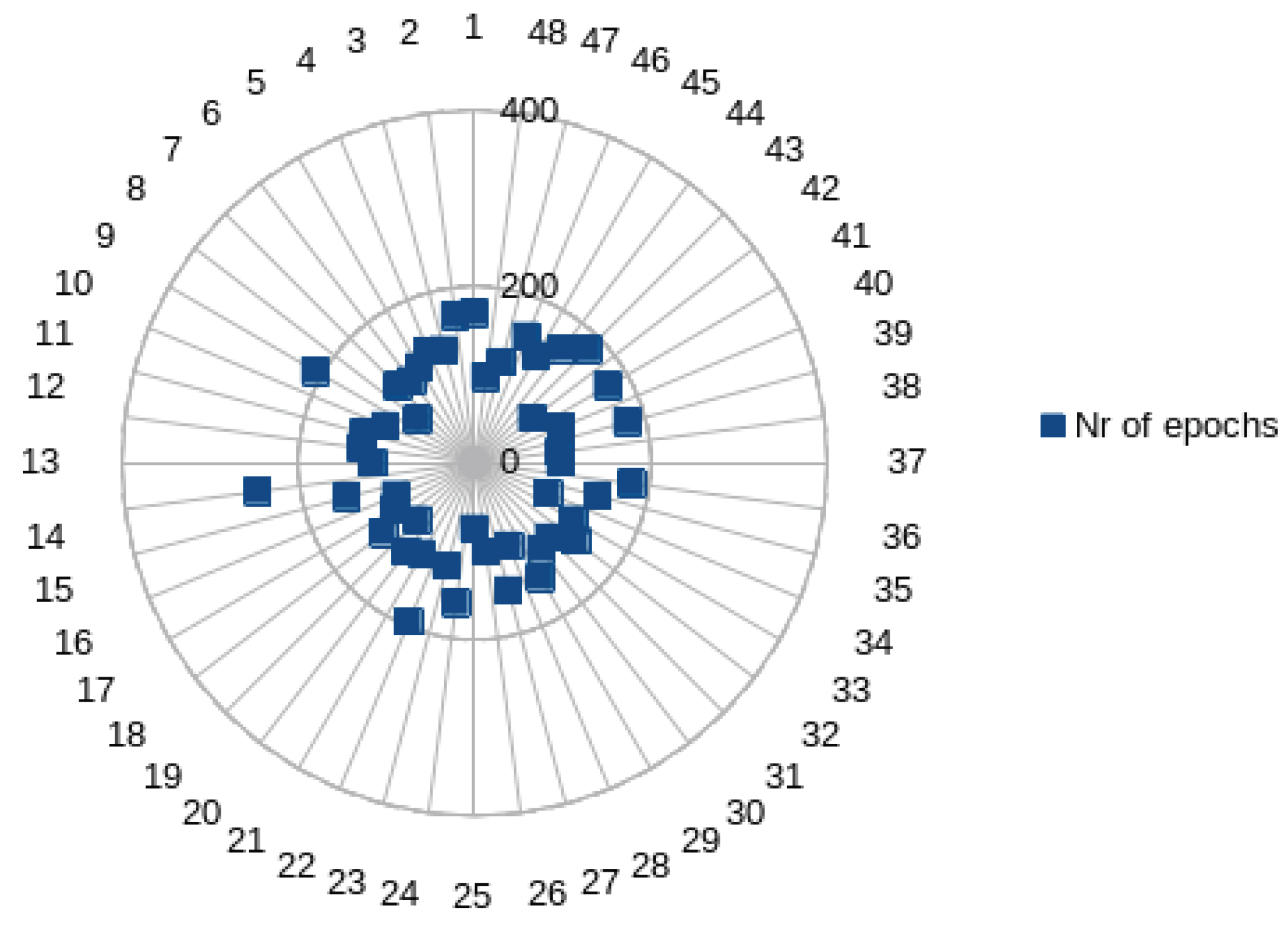
| Average number of epochs | 130 |
| Type | Metric | |
|---|---|---|
| MAE | RMSE | |
| Normal beat | 0.007 ± 0.0027 | 0.0506 ± 0.0093 |
| LBBB beat | 0.0042 ± 0.0016 | 0.0451 ± 0.0092 |
| RBBB beat | 0.0086 ±0.0030 | 0.05735 ± 0.0090 |
| PVC beat | 0.0071 ± 0.0024 | 0.0531 ± 0.0094 |
| APB beat | 0.0081 ± 0.0034 | 0.0656 ± 0.0097 |
| Study | Forecasting Technique | Number of ECG Signals | Sequence Length | MAE | RMSE |
|---|---|---|---|---|---|
| Sun et al. [40] | VMD and BPNN | 1 | Non | 0.0157 | 0.0233 |
| Sun et al. [41] | MI and BPNN | 1 | Non | 0.024 | 0.0423 |
| Huang et al. [42] | ARIMA and DWT | 4 | Non | 0.0111 | 0.0181 |
| Dudukcu et al. [45] | TCN-LSTM | 21 | 10 | 0.0051 | 0.0082 |
| TCN-GRU | 0.0052 | 0.0084 | |||
| Our study | LSTM | 47 | 720 | 0.0522 ± 0.01 | 0.0070 ± 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zacarias, H.; Marques, J.A.L.; Felizardo, V.; Pourvahab, M.; Garcia, N.M. ECG Forecasting System Based on Long Short-Term Memory. Bioengineering 2024, 11, 89. https://doi.org/10.3390/bioengineering11010089
Zacarias H, Marques JAL, Felizardo V, Pourvahab M, Garcia NM. ECG Forecasting System Based on Long Short-Term Memory. Bioengineering. 2024; 11(1):89. https://doi.org/10.3390/bioengineering11010089
Chicago/Turabian StyleZacarias, Henriques, João Alexandre Lôbo Marques, Virginie Felizardo, Mehran Pourvahab, and Nuno M. Garcia. 2024. "ECG Forecasting System Based on Long Short-Term Memory" Bioengineering 11, no. 1: 89. https://doi.org/10.3390/bioengineering11010089
APA StyleZacarias, H., Marques, J. A. L., Felizardo, V., Pourvahab, M., & Garcia, N. M. (2024). ECG Forecasting System Based on Long Short-Term Memory. Bioengineering, 11(1), 89. https://doi.org/10.3390/bioengineering11010089










