Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis
Abstract
1. Introduction
- Introduce the utilisation of 10 non-linear features (entropies—approximate, logarithmic, and Shannon, correlation dimension, detrended fluctuation analysis, energy, Higuchi fractal dimension, Hurst exponent, Katz fractal dimension, and Lyapunov exponent) extracted under discrete wavelet transform multi-band ECG signal analysis for characterising CVDs.
- Enhance the evaluation of distinguishing between various CVDs by accessing and comparing the individual and combined power of non-linear features.
- Evaluate the discriminatory performance of these features by inputting them into a comprehensive set of ML models.
2. Methodology
- Data collection/pre-processing and artifacts removal;
- Feature extraction;
- Data compressor;
- Machine Learning classification and statistical analysis.

2.1. Experimental Setup
2.2. Database Characterisation
2.3. Artifacts Removal
2.4. Signal Normalisation
Multi-Band Decomposition via Wavelet Transform and Features Extraction
2.5. Data Driven Framework Analysis
2.5.1. Individual Feature Power Analysis over Binary Groups
2.5.2. Combined Features Power Analysis for Groups Discrimination Using Sci-Learn ML Models
2.5.3. Classification Metrics
3. Results
4. Discussion
4.1. Data Driven Analysis—Individual Feature Power Analysis
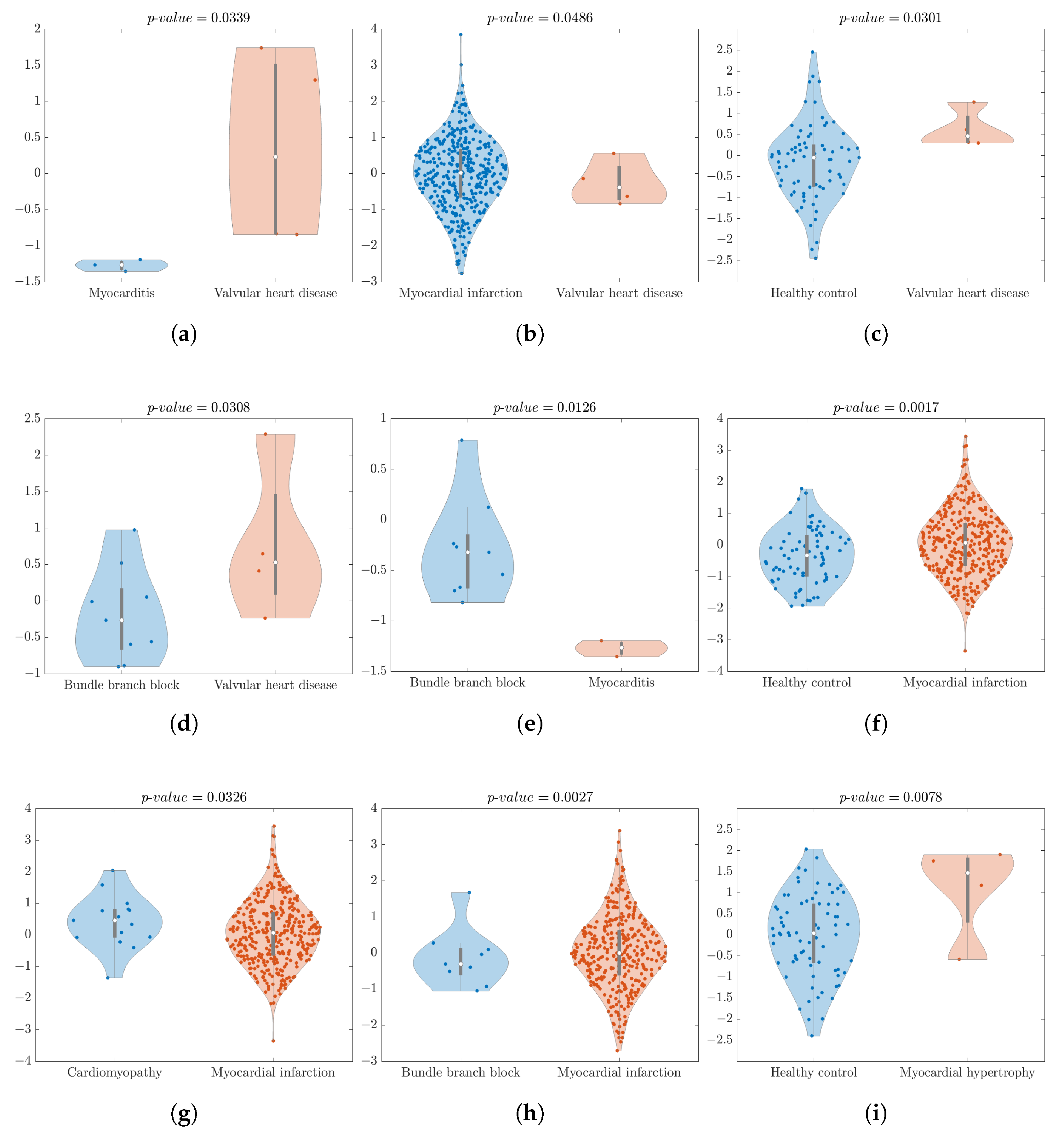
- vs. analysis yielded a significant p-value of 0.0339, and an and of 100%. The feature , with the compressor , and lead extracted from the 2nd sub-band provided excellent results. As shown in Figure 2a, the violin plot easily illustrates a distinct separation between these two classes.
- vs. statistical analysis produced a significant result (p-value = 0.0486). The XROC analysis achieved an of 98.91% and of 0% for this binary comparison. The achieved of 0% underscores one of the primary limitations of the dataset, namely its imbalance with the XROC, over-adjusting itself too much to the predominant class—, and it corroborates also the difficulty of splitting groups by the statistical test. In Figure 2b, we can see some outlier values but the highest density of the data is located close to the median.
- vs. statistical analysis revealed a non-significance p-value. The XROC metrics— and —demonstrated strong performance for discrimination between groups, with values of 87.50% and 75.00%, respectively.
- vs. group analysis displayed a significant difference, with a p-value of 0.0301. It achieved an of 94.94% and a of 0%. Figure 2c indicates some outliers in the class, but the highest data density is close to the median. Despite the good statistical analysis results, once more the XROC over-adjusts itself too much to the predominant class—, achieving a of 0% for discriminating the class . The imbalanced database and the ’s large number of outliers contribute to these results. The XROC employs an averaging method within its genesis, which assigns significant weight to outliers in the final results.
- vs. analysis resulted in a non-significant p-value, an of 80.00%, and a of 100%. Despite being statistically non-significant, the XROC results showed a good performance for discriminating.
- vs. analysis resulted in a non-significant p-value. The XROC metrics and were 78.94% and 50.00%, respectively.
- vs. statistical analysis yielded a p-value of 0.0308, and the XROC achieved an of 84.62% and of 75.00%. Figure 2d illustrates a higher density of ’s data being located close to the median.
- vs. statistical analysis yielded a p-value of non-significance. The achieved a value of 99.18% and the resulted in 0%.
- vs. statistical analysis exhibited no significant difference in the p-value. The and reached 85.71% and 100%, respectively.
- vs. analysis also showed no significant p-value. and demonstrated an interesting performance, achieving values of 96.15% and 0%, respectively. This underscores the difficulty of the XROC classifier in accurately discriminating between unbalanced data sample sizes.
- vs. analysis also revealed a non-significant p-value, with the and showcasing the values of 85.71% and 33.33%, respectively.
- vs. analysis resulted in a non-significant p-value, an of 94.44% and a of 66.67%. Despite being statistically non-significant, the XROC showed good behaviour for discriminating between classes.
- vs. statistical analysis indicated significant differences with a p-value of 0.0126. The and reached 100%. In Figure 2e, the violin plot displayed an outlier in the class, but the highest data density was slightly below the median. It is worth noting that there was a clear separation between the two classes.
- vs. analysis resulted in a non-significant p-value. Despite that, the XROC performed well with a discrimination of 98.91% and a of 100%.
- vs. statistical analysis yielded a p-value of 0.0017. The and the achieved values of 82.84% and 100%, respectively. In Figure 2f, the violin plot exhibited some outliers, but the highest data density was close to the median for both classes.
- vs. analysis was shown to be non-significant. The XROC metrics of and displayed significant performance percentages, with values of 97.05% and 100%, respectively.
- vs. statistical analysis revealed a p-value of 0.0326 alongside impressive classification metrics, boasting an of 96.29% and a perfect of 100%. In Figure 2g, the violin plot exhibited some outliers, but the highest data density was close to the median for both classes.
- vs. analysis showed statistical significance and the stood at 97.57%, with a flawless of 100%. Figure 2h gives us the opportunity to see some outliers in both classes but the majority of the data were located close to the median.
- vs. analysis achieved a significant p-value, reaching a statistical analysis value of 0.0078. The was 94.94% and the was 0%, which perfectly illustrates the imbalance of the dataset. Figure 2i shows the class, with the highest density of data close to the median.
- vs. analysis exhibited non-significant p-values, with rates of 80.00% and 50.00%, respectively.
- vs. demonstrated an of 84.21% and a of 50.00%, while the vs. group yielded an of 92.31% and a of 75.00%, with both analyses showing a non-statistical significance. While statistical significance may be elusive, the consistently high and values underscore the potential efficacy of the model in discriminating between different conditions within the studied groups.
- vs. analysis showed non-significant difference. The and displayed great performance, with values of 87.21% and 100%, respectively.
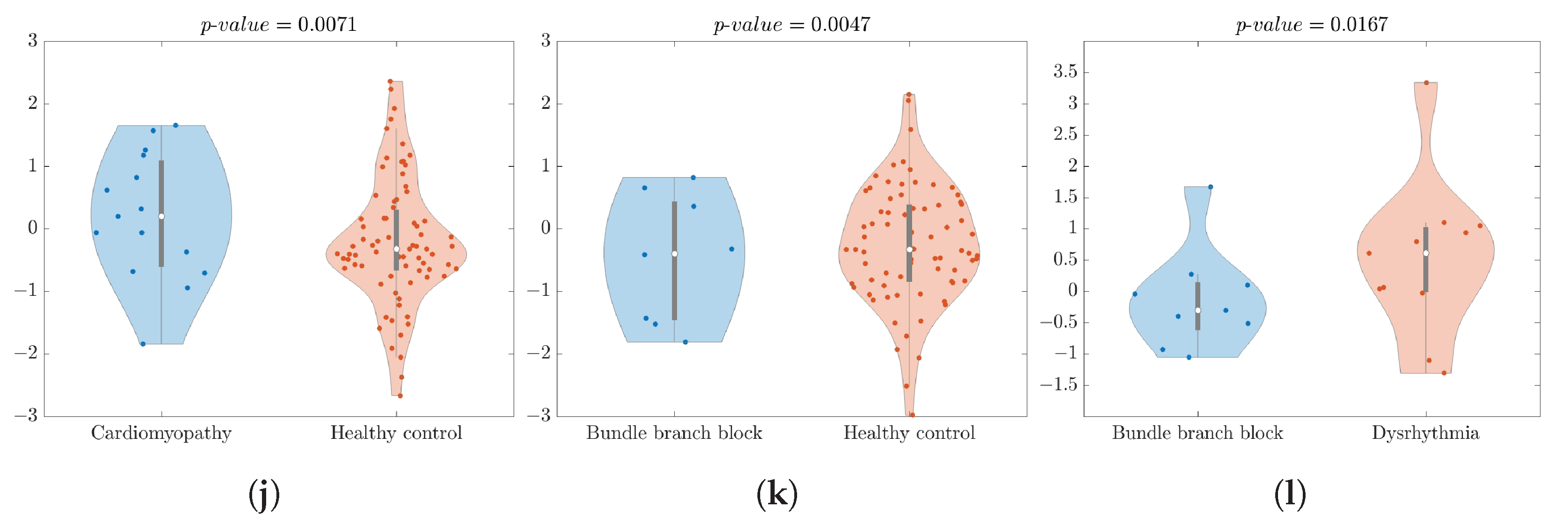
- vs. showed a significant difference, with a p-value of 0.0071. The and exhibited strong performance, with values of 83.33% and 94.67%, respectively. In Figure 2j, the violin plot displayed some outliers in the class, but the highest data density was close to the median.
- vs. analysis provided a significant p-value of 0.0047 accompanied by an of 89.29% and an impressive of 100%. Figure 2k shows the violin plot with some outliers in the class, but there was a higher density of data close to the median.
- vs. comparison analysis yielded a non-significant p-value, with an of 73.08% and a of 54.54%.
- vs. comparison analysis showed a p-value of 0.0167, achieving an of 80.00% and a of 81.81%. Figure 2l shows a violin plot with a couple of outliers in both classes, but the highest density of data was close to the median.
- vs. analysis provided a non-significant p-value, with an of 75.00% and a of 73.33%.
4.2. Data Driven Analysis—Combined Feature Power Analysis
4.3. Study Results vs. State-of-the-Art Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- American Heart Association. What is Cardiovascular Disease? 2017. Available online: https://www.heart.org/en/health-topics/consumer-healthcare/what-is-cardiovascular-disease (accessed on 5 October 2023).
- World Health Organization. Cardiovascular Diseases CVDs. 2021. Available online: https://www.who.int/news-room/fact-sheets/detail/cardiovascular-diseases-(cvds) (accessed on 5 October 2023).
- Visseren, F.L.J.; Mach, F.; Smulders, Y.M.; Carballo, D.; Koskinas, K.C.; Bäck, M.; Benetos, A.; Biffi, A.; Boavida, J.M.; Capodanno, D.; et al. 2021 ESC Guidelines on cardiovascular disease prevention in clinical practice. Eur. Heart J. 2021, 42, 3227–3337. [Google Scholar] [CrossRef] [PubMed]
- Arbelo, E.; Protonotarios, A.; Gimeno, J.; Arbustini, E.; Barriales-Villa, R.; Basso, C.; Bezzina, C.; Biagini, E.; Blom, N.; Boer, R.; et al. 2023 ESC Guidelines for the management of cardiomyopathies. Eur. Heart J. 2023, 44, 3503–3626. [Google Scholar] [CrossRef] [PubMed]
- Delgado, V.; Marsan, N.A.; de Waha, S.; Bonaros, N.; Brida, M.; Burri, H.; Caselli, S.; Doenst, T.; Ederhy, S.; Erba, P.A.; et al. 2023 ESC Guidelines for the management of endocarditis. Eur. Heart J. 2023, 44, 3948–4042. [Google Scholar] [CrossRef] [PubMed]
- Brito, D.; Cardim, N.; Rocha-Lopes, L.; Freitas, A.; Lacerda, A.P.D.; Menezes, M.; Belo, A.; Martins, E.; Peres, M.; Goncalves, L.; et al. P3514Diagnosis and treatment of acute myocarditis in Portugal. Data from the national multicenter registry on myocarditis. Eur. Heart J. 2017, 38, ehx504.P3514. [Google Scholar] [CrossRef]
- Adler, Y.; Charron, P.; Imazio, M.; Badano, L.; Barón-Esquivias, G.; Bogaert, J.; Brucato, A.; Gueret, P.; Klingel, K.; Lionis, C.; et al. 2015 ESC Guidelines for the diagnosis and management of pericardial diseases. Eur. Heart J. 2015, 36, 2921–2964. [Google Scholar] [CrossRef]
- Hamm, C.; Bassand, J.P.; Agewall, S.; Bax, J.; Boersma, E.; Bueno, H.; Caso, P.; Dudek, D.; Gielen, S.; Huber, K.; et al. ESC Guidelines for the management of acute coronary syndromes in patients presenting without persistent ST-segment elevation: The Task Force for the management of acute coronary syndromes (ACS) in patients presenting without persistent ST-segment elevation of the European Society of Cardiology (ESC). Eur. Heart J. 2011, 32, 2999–3054. [Google Scholar] [CrossRef]
- Byrne, R.; Rossello, X.; Coughlan, J.; Barbato, E.; Berry, C.; Chieffo, A.; Claeys, M.; Dan, G.A.; Dweck, M.; Galbraith, M.; et al. 2023 ESC Guidelines for the management of acute coronary syndromes: Developed by the task force on the management of acute coronary syndromes of the European Society of Cardiology (ESC). Eur. Heart J. 2023, 44, 3720–3826. [Google Scholar] [CrossRef]
- McDonagh, T.A.; Metra, M.; Adamo, M.; Gardner, R.S.; Baumbach, A.; Böhm, M.; Burri, H.; Butler, J.; Čelutkienė, J.; Chioncel, O.; et al. 2021 ESC Guidelines for the diagnosis and treatment of acute and chronic heart failure. Eur. Heart J. 2021, 42, 3599–3726. [Google Scholar] [CrossRef]
- Zeppenfeld, K.; Tfelt-Hansen, J.; de Riva, M.; Winkel, B.G.; Behr, E.R.; Blom, N.A.; Charron, P.; Corrado, D.; Dagres, N.; de Chillou, C.; et al. 2022 ESC Guidelines for the management of patients with ventricular arrhythmias and the prevention of sudden cardiac death. Eur. Heart J. 2022, 43, 3997–4126. [Google Scholar] [CrossRef]
- Kim, M.; Yoon, M.; Yang, P.; Kim, T.; Uhm, J.; Kim, J.; Pak, H.; Lee, M.; Joung, B. P6422Sex-based disparities in incidence, treatment, and outcomes of sudden cardiac arrest. Eur. Heart J. 2017, 38, ehx493.P6422. [Google Scholar] [CrossRef]
- Authors/Task Force Members.; Vahanian, A.; Alfieri, O.; Andreotti, F.; Antunes, M.J.; Barón-Esquivias, G.; Baumgartner, H.; Borger, M.A.; Carrel, T.P.; Bonis, M.D.; et al. Guidelines on the management of valvular heart disease (version 2012). Eur. Heart J. 2012, 33, 2451–2496. [Google Scholar] [CrossRef]
- Baumgartner, H.; Backer, J.D.; Babu-Narayan, S.V.; Budts, W.; Chessa, M.; Diller, G.P.; Lung, B.; Kluin, J.; Lang, I.M.; Meijboom, F.; et al. 2020 ESC Guidelines for the management of adult congenital heart disease. Eur. Heart J. 2020, 42, 563–645. [Google Scholar] [CrossRef] [PubMed]
- Kligfield, P.; Gettes, L.S.; Bailey, J.J.; Childers, R.; Deal, B.J.; Hancock, E.W.; van Herpen, G.; Kors, J.A.; Macfarlane, P.; Mirvis, D.M.; et al. Recommendations for the Standardization and Interpretation of the Electrocardiogram. Circulation 2007, 115, 1306–1324. [Google Scholar] [CrossRef] [PubMed]
- Garner, K.; Pomeroy, W.; Arnold, J. Exercise Stress Testing:Indications and Common Questions. Am. Acad. Fam. Physicians 2017, 96, 293–299. [Google Scholar]
- Maron, B. American College of Cardiology/European Society of Cardiology Clinical Expert Consensus Document on Hypertrophic Cardiomyopathy a Rteport of the American College of Cardiology Foundation Task Force on Clinical Expert Consensus Documents and the European Society of Cardiology Committee for Practice Guidelines. Eur. Heart J. 2003, 24, 1965–1991. [Google Scholar] [CrossRef]
- Perrot, B.; Clozel, J.P.; de la Chaise, A.T.; Cherrier, F.; Faivre, G. Electrophysiological effects of intravenous prostacyclin in man. Eur. Heart J. 1984, 5, 883–889. [Google Scholar] [CrossRef]
- Maseri, A. Safety of provocative tests of coronary artery spasm and prediction of long-term outcome: Need for an innovative clinical research strategy. Eur. Heart J. 2012, 34, 252–254. [Google Scholar] [CrossRef]
- Grondin, S.; Davies, B.; Cadrin-Tourigny, J.; Steinberg, C.; Cheung, C.C.; Jorda, P.; Healey, J.S.; Green, M.S.; Sanatani, S.; Alqarawi, W.; et al. Importance of genetic testing in unexplained cardiac arrest. Eur. Heart J. 2022, 43, 3071–3081. [Google Scholar] [CrossRef]
- Azmi, J.; Arif, M.; Nafis, M.T.; Alam, M.A.; Tanweer, S.; Wang, G. A systematic review on machine learning approaches for cardiovascular disease prediction using medical big data. Med. Eng. Phys. 2022, 105, 103825. [Google Scholar] [CrossRef]
- Rodrigues, P.M.; Madeiro, J.P.; Marques, J.A.L. Enhancing Health and Public Health through Machine Learning: Decision Support for Smarter Choices. Bioengineering 2023, 10, 792. [Google Scholar] [CrossRef]
- Krittanawong, C.; Virk, H.U.H.; Bangalore, S.; Wang, Z.; Johnson, K.W.; Pinotti, R.; Zhang, H.; Kaplin, S.; Narasimhan, B.; Kitai, T.; et al. Machine learning prediction in cardiovascular diseases: A meta-analysis. Sci. Rep. 2020, 10, 16057. [Google Scholar] [CrossRef] [PubMed]
- Qu, Z.; Hu, G.; Garfinkel, A.; Weiss, J. Nonlinear and stochastic dynamics in the heart. Phys. Rep. 2014, 543, 61–162. [Google Scholar] [CrossRef]
- Haraldsson, H.; Edenbrandt, L.; Ohlsson, M. Detecting acute myocardial infarction in the 12-lead ECG using Hermite expansions and neural networks. Artif. Intell. Med. 2004, 32, 127–136. [Google Scholar] [CrossRef] [PubMed]
- Begum, R.; Ramesh, M. Detection of cardiomyopathy using support vector machine and artificial neural network. Int. J. Comput. Appl. 2016, 133, 29–34. [Google Scholar] [CrossRef]
- Chowdhuryy, H.; Sultana, M.; Ghosh, R.; Ahamed, J.; Mahmood, M. AI Assisted Portable ECG for Fast and Patient Specific Diagnosis. In Proceedings of the 2018 International Conference on Computer, Communication, Chemical, Material and Electronic Engineering (IC4ME2), Rajshahi, Bangladesh, 8–9 February 2018. [Google Scholar] [CrossRef]
- Kachuee, M.; Fazeli, S.; Sarrafzadeh, M. ECG Heartbeat Classification: A Deep Transferable Representation. In Proceedings of the 2018 IEEE International Conference on Healthcare Informatics (ICHI), New York, NY, USA, 4–7 June 2018. [Google Scholar] [CrossRef]
- Baloglu, U.; Talo, M.; Yildirim, O.; Tan, R.; Acharya, U. Classification of myocardial infarction with multi-lead ECG signals and deep CNN. Pattern Recognit. Lett. 2019, 122, 23–30. [Google Scholar] [CrossRef]
- Ali, L.; Niamat, A.; Khan, J.A.; Golilarz, N.A.; Xingzhong, X.; Noor, A.; Nour, R.; Bukhari, S.A.C. An Optimized Stacked Support Vector Machines Based Expert System for the Effective Prediction of Heart Failure. IEEE Access 2019, 7, 54007–54014. [Google Scholar] [CrossRef]
- Ali, L.; Rahman, A.; Khan, A.; Zhou, M.; Javeed, A.; Khan, J.A. An Automated Diagnostic System for Heart Disease Prediction Based on χ2 Statistical Model and Optimally Configured Deep Neural Network. IEEE Access 2019, 7, 34938–34945. [Google Scholar] [CrossRef]
- Baghel, N.; Dutta, M.K.; Burget, R. Automatic diagnosis of multiple cardiac diseases from PCG signals using convolutional neural network. Comput. Methods Programs Biomed. 2020, 197, 105750. [Google Scholar] [CrossRef]
- Ahamed, A.; Hasan, K.; Monowar, K.; Mashnoor, N.; Hossain, A. ECG Heartbeat Classification Using Ensemble of Efficient Machine Learning Approaches on Imbalanced Datasets. In Proceedings of the 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT), Dhaka, Bangladesh, 28–29 November 2020. [Google Scholar] [CrossRef]
- Makimoto, H.; Höckmann, M.; Lin, T.; Glöckner, D.; Gerguri, S.; Clasen, L.; Schmidt, J.; Assadi-Schmidt, A.; Bejinariu, A.; Müller, P.; et al. Performance of a convolutional neural network derived from an ECG database in recognizing myocardial infarction. Sci. Rep. 2020, 10, 8445. [Google Scholar] [CrossRef]
- Khan, A.; Hussain, M.; Malik, M. Cardiac Disorder Classification by Electrocardiogram Sensing Using Deep Neural Network. Complexity 2021, 2021, 5512243. [Google Scholar] [CrossRef]
- Premanand, S.; Narayanan, S. A Tree Based Machine Learning Approach for PTB Diagnostic Dataset. J. Phys. Conf. Ser. 2021, 2115, 012042. [Google Scholar] [CrossRef]
- Kavitha, M.; Gnaneswar, G.; Dinesh, R.; Sai, Y.; Suraj, R. Heart Disease Prediction using Hybrid machine Learning Model. In Proceedings of the 2021 6th International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 20–22 January 2021. [Google Scholar] [CrossRef]
- Elhoseny, M.; Mohammed, M.; Mostafa, S.; Abdulkareem, K.; Maashi, M.; Garcia-Zapirain, B.; Mutlag, A.; Maashi, M. A New Multi-Agent Feature Wrapper Machine Learning Approach for Heart Disease Diagnosis. Comput. Mater. Contin. 2021, 67, 51–71. [Google Scholar] [CrossRef]
- Ahmad, G.; Fatima, H.; Ullah, S.; Saidi, A.; Imdadullah. Efficient Medical Diagnosis of Human Heart Diseases Using Machine Learning Techniques with and without GridSearchCV. IEEE Access 2022, 10, 80151–80173. [Google Scholar] [CrossRef]
- Ahmad, S.; Asghar, M.; Alotaibi, F.; Alotaibi, Y. Diagnosis of cardiovascular disease using deep learning technique. Soft Comput. 2022, 27, 8971–8990. [Google Scholar] [CrossRef]
- Mhamdi, L.; Dammak, O.; Cottin, F.; Dhaou, I. Artificial Intelligence for Cardiac Diseases Diagnosis and Prediction Using ECG Images on Embedded Systems. Biomedicines 2022, 10, 2013. [Google Scholar] [CrossRef] [PubMed]
- Karthik, S.; Santhosh, M.; Kavitha, M.S.; Christopher Paul, A. Automated Deep Learning Based Cardiovascular Disease Diagnosis Using ECG Signals. Comput. Syst. Sci. Eng. 2022, 42, 183–199. [Google Scholar] [CrossRef]
- Bousseljot, R.D.; Kreiseler, D.; Schnabel, A. Nutzung der EKG-Signaldatenbank CARDIODAT der PTB über das Internet. Biomed. Tech. Biomed. Eng. 1995, 40, 317–318. [Google Scholar] [CrossRef]
- Rodrigues, P.; Bispo, B.; Garrett, C.; Alves, D.; Teixeira, J.; Freitas, D. Lacsogram: A New EEG Tool to Diagnose Alzheimer’s Disease. IEEE J. Biomed. Health Inform. 2021, 25, 3384–3395. [Google Scholar] [CrossRef]
- Guido, R. Wavelets behind the scenes: Practical aspects, insights, and perspectives. Phys. Rep. 2022, 985, 1–23. [Google Scholar] [CrossRef]
- Malvar, H. Signal Processing with Lapped Transforms; Artech House: Norwood, MA, USA, 1992. [Google Scholar]
- Vetterli, M.; Kovačević, J. Wavelets and Subband Coding; Prentice Hall: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Chen, C.C.; Tsui, F.R. Comparing different wavelet transforms on removing electrocardiogram baseline wanders and special trends. BMC Med. Inform. Decis. Mak. 2020, 20, 343. [Google Scholar] [CrossRef]
- Ribeiro, P.; Marques, J.A.L.; Pordeus, D.; Zacarias, L.; Leite, C.F.; Sobreira-Neto, M.A.; Peixoto, A.A.; de Oliveira, A.; do Vale Madeiro, J.P.; Rodrigues, P.M. Machine learning-based cardiac activity non-linear analysis for discriminating COVID-19 patients with different degrees of severity. Biomed. Signal Process. Control. 2024, 87, 105558. [Google Scholar] [CrossRef]
- Rioul, O.; Vetterli, M. Wavelets and signal processing. IEEE Signal Process. Mag. 1991, 8, 14–38. [Google Scholar] [CrossRef]
- Peck, R.; Olsen, C.; Devore, J. Introduction to Statistics and Data Analysis; Cengage Learning: Boston, MA, USA, 2008; p. 880. [Google Scholar]
- Caesarendra, W.; Kosasih, B.; Tieu, K.; Moodie, C. An application of nonlinear feature extraction—A case study for low speed slewing bearing condition monitoring and prognosis. In Proceedings of the 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, NSW, Australia, 9–12 July 2013; pp. 1713–1718. [Google Scholar] [CrossRef]
- Hardstone, R.; Poil, S.S.; Schiavone, G.; Jansen, R.; Nikulin, V.; Mansvelder, H.; Linkenkaer-Hansen, K. Detrended Fluctuation Analysis: A Scale-Free View on Neuronal Oscillations. Front. Physiol. 2012, 3, 450. [Google Scholar] [CrossRef] [PubMed]
- Sundararajan, D. Discrete Wavelet Transform a Signal Processing Approach, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Silva, M.; Ribeiro, P.; Bispo, B.C.; Rodrigues, P.M. Detecção da Doença de Alzheimer através de Parâmetros Não-Lineares de Sinais de Fala. In Proceedings of the Anais do XLI Simpósio Brasileiro de Telecomunicações e Processamento de Sinais. Sociedade Brasileira de Telecomunicações, São José dos Campos, SP, Brazil, 8–11 October 2023. [Google Scholar] [CrossRef]
- Garcia, A.; Garcia, C.; Villasenor-Pineda, L.; Montoya, O. Biosignal Processing and Classification Using Computational Learning and Intelligence Principles, Algorithms, and Applications; Academic Press: London, UK, 2022; pp. 59–91. [Google Scholar]
- Silva, G.; Batista, P.; Rodrigues, P.M. COVID-19 activity screening by a smart-data-driven multi-band voice analysis. J. Voice 2022, in press. [Google Scholar] [CrossRef] [PubMed]
- Nakas, C.; Yiannoutsos, C. Ordered multiple-class ROC analysis with continuous measurements. Stat. Med. 2004, 23, 3437–3449. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Sammut, C.; Webb, G.I. (Eds.) Accuracy. In Encyclopedia of Machine Learning and Data Mining; Springer: New York, NY, USA, 2017; p. 8. [Google Scholar] [CrossRef]
- Doğan, O. Data Linkage Methods for Big Data Management in Industry 4.0. In Optimizing Big Data Management and Industrial Systems with Intelligent Techniques; IGI Global: Hershey, PA, USA, 2019; pp. 108–127. [Google Scholar] [CrossRef]
- Ting, K.M. Precision and Recall. In Encyclopedia of Machine Learning and Data Mining; Springer: New York, NY, USA, 2017; pp. 990–991. [Google Scholar] [CrossRef]
- Goutte, C.; Gaussier, E. A Probabilistic Interpretation of Precision, Recall and F-Score, with Implication for Evaluation. In Advances in Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2005; pp. 345–359. [Google Scholar] [CrossRef]
- Vieira, S.M.; Kaymak, U.; Sousa, J.M.C. Cohen’s kappa coefficient as a performance measure for feature selection. In Proceedings of the International Conference on Fuzzy Systems, Barcelona, Spain, 18–23 July 2010. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- Larner, A. Assessing cognitive screeners with the critical success index. Prog. Neurol. Psychiatry 2021, 25, 33–37. [Google Scholar] [CrossRef]
- Nahm, F. Receiver operating characteristic curve: Overview and practical use for clinicians. Korean J. Anesthesiol. 2022, 75, 25–36. [Google Scholar] [CrossRef]
- Spirito, P.; Bellone, P.; Harris, K.M.; Bernabò, P.; Bruzzi, P.; Maron, B.J. Magnitude of Left Ventricular Hypertrophy and Risk of Sudden Death in Hypertrophic Cardiomyopathy. N. Engl. J. Med. 2000, 342, 1778–1785. [Google Scholar] [CrossRef]
- Sossalla, S.; Vollmann, D. Arrhythmia-Induced Cardiomyopathy. Dtsch. Ärzteblatt Int. 2018, 115, 335. [Google Scholar] [CrossRef] [PubMed]
- Sun, B.; Wang, L.; Guo, W.; Chen, S.; Ma, Y.; Wang, D. New treatment methods for myocardial infarction. Front. Cardiovasc. Med. 2023, 10, 1251669. [Google Scholar] [CrossRef] [PubMed]


| Ref | Year | Database | Comparison Group (Number of Participants) | Feature Extracted | Classifier | Limitations | Validation | |
|---|---|---|---|---|---|---|---|---|
| [25] | 2004 | University Hospital in Lund database | Normal (1119) vs. Myocardial infarction (1119) | Hermite decomposition | ANN | Exclusive assessment of myocardial infarction. Lack of diversity of CVDs. | Cross-validation | 94% |
| [26] | 2016 | PTB diagnostic ECG database | Normal (49) vs. Cardiomyopathy (14) | ECG PR, QT, RR and QRS intervals | Feed-forward back-propagation Neural Network | Small and unbalanced dataset. Exclusive assessment of cardiomyopathy. Lack of diversity of CVDs. | Cross-validation | 95.2% |
| [27] | 2018 | PTB diagnostic ECG database | Normal (25) vs. Myocardial infarction (36) | Feature extracted from DNN | DNN (InceptionV3) | Small database for hold-on. Lack of diversity of CVDs. | Hold-on | 99.64% |
| [28] | 2018 | PTB diagnostic ECG datasets | Normal (52) vs. Myocardial infarction (148) | Features extracted from CNN | CNN | Small and unbalanced database for hold-on. It is impossible to know what features were extracted due to the nature of deep learning algorithms. Lack of diversity of CVDs. | Hold-on | 95.9% |
| [29] | 2019 | PTB diagnostic ECG database | Healthy (52) vs. Myocardial infarction (148) | Feature extracted from CNN | CNN | Small and unbalanced dataset.There was no discrimination of diseases outside of the MI class. Lack of diversity of CVDs. | Cross-validation | 99.78% |
| [30] | 2019 | Cleveland heart disease database | Healthy (150) vs. Heart Disease (147) | Patient clinical information | SVM | Small dataset. There was no discrimination of diseases outside of the Heart Disease class. Lack of diversity of CVDs. | Hold-on | 92.22% |
| [31] | 2019 | Cleveland heart disease database | Healthy (150) vs. Heart Disease (147) | Patient clinical information | DNN | Small dataset. There was no discrimination of diseases outside of the Heart Disease class. Lack of diversity of CVDs. | Hold-on | 93.33% |
| [32] | 2020 | Heart sound dataset | Normal (400) vs. Mitral valve prolapse (400) vs. Mitral stenosis (400) vs. Mitral regurgitation (400) vs. Aortic stenosis (400) | Feature extracted from CNN | CNN | Low variety of classes. There is a high risk of over-fitting because of the augmentation technique used. | Cross-validation | 98.6% |
| [33] | 2020 | PTB diagnostic ECG datasets | Normal (313) vs. Abnormal (318) | Features extracted from ANN | Ensemble | Use class weights when training with artificial neural networks to solve the class unbalance problem. | Hold-on | 94.14% |
| [34] | 2020 | PTB diagnostic ECG database | No Myocardial infarction (141) vs. Myocardial infarction (148) | Feature extracted from CNN | CNN | Small dataset. Just MI different types of discrimination. Small database. | Cross-validation | 81% |
| [35] | 2021 | Ch. Pervaiz Elahi Institute of Cardiology Multan Dataset | Normal (3408) vs. Abnormal (2796) vs. Myocardial infarction (2880) vs. Previous history of Myocardial infarction (2064) | Feature extracted from SSD MobileNetV2 (CNN) | SSD MobileNetV2 (CNN) | Just MI different types of discrimination. It is impossible to know what features were extracted due to the nature of deep learning algorithms. | Hold-on | 98.33% |
| [36] | 2021 | PTB diagnostic ECG database | Healthy (52) vs. Abnormal (216) | Domain features and disease-specific features | XGBoost | Small and unbalanced dataset. There is no disease discrimination, just normal vs. abnormal. Lack of diversity of CVDs. | Cross-validation | 98.23% |
| [37] | 2021 | Cleveland dataset | Normal (170) vs. Abnormal (140) | Patient clinical information | Decision tree and Random forest combined | Small database for hold-on. There is no disease discrimination, just normal vs. abnormal. Lack of diversity of CVDs. | Hold-on | 88.00% |
| [38] | 2021 | Cleveland HD dataset | Healthy (135) vs. Heart disease (135) | Feature extracted from MAFW | CNN model with the MAFW | Small dataset. A limited number of classifiers were used. High computational cost and time complexity. Runtime is not considered as an evaluation criterion. Lack of diversity of CVDs. | Cross-validation | 90.1% |
| [39] | 2022 | Cleveland, Hungary, Switzerland, and Long Beach V datasets | Healthy (500) vs. Heart disease (550) | Patient clinical information | Extreme gradient boosting | No disease discrimination, just normal vs. abnormal. Lack of diversity of CVDs. | Cross-validation | 100% |
| [40] | 2022 | UC Irvine Machine Learning Repository CVD datasets | Healthy (500) vs. Heart disease (550) | Patient clinical information | CNN and BiLSTM hybrid | No disease discrimination, just normal vs. abnormal. Lack of diversity of CVDs. | Hold-on | 94.51% |
| [41] | 2022 | ECG dataset of Cardiac and COVID-19 Patients and ECG dataset of Cardiac Patients | Normal (284) vs. Abnormal (233) vs. MI (239) vs. Previous history of MI (102) | Feature extracted from MobileNet V2 (CNN) | MobileNet V2 (CNN) | Small database for hold-on, lack of a truly independent test group. Did not consider optimisation techniques. | Hold-on | 95.18% |
| [42] | 2022 | PTB-XL dataset | Normal (1608) vs. Abnormal (1357) | Feature extracted from DNN | XGBoost | Lack of diversity of CVDs. Unbalanced dataset. | Hold-on | 78.65% |
| Present Work | 2023 | PTB diagnostic ECG database | vs. M, vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; M vs. ; M vs. ; M vs. ; M vs. ; M vs. ; M vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; vs. ; vs. and vs. | Approximate Entropy, Logarithmic Entropy, Shannon Entropy, Correlation Dimension, Detrended Fluctuation Analysis, Energy, Higuchi Fractal Dimension, Hurst Exponent, Katz Fractal Dimension and Lyapunov Exponent | 19 ML Classifiers | Small data sample for some classes and unbalanced dataset. | Cross-validation | 73–100% |
| Diagnostic Class | Number of ECGs |
|---|---|
| Bundle branch block () | 17 |
| Cardiomyopathy () | 20 |
| Healthy controls () | 80 |
| Myocarditis (M) | 4 |
| Myocardial hypertrophy () | 4 |
| Myocardial infarction () | 367 |
| Valvular heart disease () | 6 |
| Dysrhythmia () | 16 |
| Diagnostic Class | Number of ECGs |
|---|---|
| Bundle branch block | 9 |
| Cardiomyopathy | 15 |
| Healthy controls | 75 |
| Myocarditis | 3 |
| Myocardial hypertrophy | 4 |
| Myocardial infarction | 362 |
| Valvular heart disease | 4 |
| Dysrhythmia | 11 |
| Feature | Equation | Definition |
|---|---|---|
| Approximate Entropy () | evaluates the likelihood that similar patterns within the data will remain similar when additional data points are included. The lower the value is, the more regular or predictable the data are, whereas a higher value suggests greater complexity or irregularity. | |
| Correlation Dimension () | is used to measure self-similarity, and higher values of means a high degree of complexity and less similarity. | |
| Detrended Fluctuation Analysis () | is a technique for measuring the power scaling observed through R/S analysis. | |
| Energy () | is the capacity of a system to perform work [54]. | |
| Higuchi Fractal Dimension (H) | H estimates the fractal dimension of a time series signal [55]. | |
| Hurst Exponent () | quantifies how chaotic or unpredictable a time series is. | |
| Katz Fractal Dimension (K) | K estimates the fractal dimensions through a waveform analysis of a time series [56]. | |
| Logarithmic Entropy () | quantifies the average amount of information (in bits) needed to represent each event in the probability distribution. Higher logarithm entropy values indicate greater unpredictability or randomness in the distribution, while lower values suggest more certainty or order [54]. | |
| Lyapunov Exponent () | evaluates the system’s predictability and sensitivity to change. | |
| Shannon Entropy () | is measured in bits when the base-2 logarithm (log2) is used. This means that the result provides a quantification of the average number of bits required to represent each outcome in a given probability distribution. Higher entropy values indicate greater uncertainty, unpredictability, or randomness in the distribution, while lower values suggest more order or certainty [54]. |
| Classifier | Hyperparameters |
|---|---|
| AdaBoostClassifier (AdaBoost) | Default parameters |
| BaggingClassifier (BaggC) | Default parameters |
| DecisionTreeClassifier (DeTreeC) | max_depth: 5 |
| ExtraTreesClassifier (ExTreeC) | n_estimators: 300 |
| GaussianNB (GauNB) | Default parameters |
| GaussianProcessClassifier (GauPro) | 1.0 × RBF(1.0) |
| GradientBoostingClassifier (GradBoost) | Default parameters |
| KNearestNeighborsClassifier (KNN) | Default parameters |
| LinearDiscriminantAnalysis (LinDis) | Default parameters |
| LinearSVC (LinSVC) | Default parameters |
| LogisticRegression (LogReg) | solver: “lbfgs” |
| LogisticRegressionCV (LogRegCV) | cv: 3 |
| MLPClassifier (MLP) | : 1, max_iter: 1000 |
| OneVsRestClassifier (OvsR) | random_state: 0 |
| RandomForestClassifier (RF) | max_depth: 5, n_estimators: 300, max_features: 1 |
| SGDClassifier (SGD) | max_iter: 100, tol: 0.001 |
| SGDClassifierMod (SGDCMod) | Default parameters |
| Support-vector Machines (SVC) | : “auto” |
| Comparison Group | Feature | Compressor | mth Sub-Band | Lead | p-Value | ||
|---|---|---|---|---|---|---|---|
| vs. | 2 | 0.0339 | 100% | 100% | |||
| vs. | 2 | I | 0.0486 | 0% | 98.91% | ||
| vs. | 2 | N.S. | 75.00% | 87.50% | |||
| vs. | 2 | 0.0301 | 0% | 94.94% | |||
| vs. | 2 | N.S. | 100% | 80.00% | |||
| vs. | 2 | N.S. | 50.00% | 78.94% | |||
| vs. | 2 | 0.0308 | 75.00% | 84.62% | |||
| vs. | 2 | N.S. | 0% | 99.18% | |||
| vs. | 2 | N.S. | 100% | 85.71% | |||
| vs. | 2 | N.S. | 0% | 96.15% | |||
| vs. | 2 | N.S. | 33.33% | 85.71% | |||
| vs. | 2 | N.S. | 66.67% | 94.44% | |||
| vs. | 2 | 0.0126 | 100% | 100% | |||
| vs. | 2 | N.S. | 100% | 98.91% | |||
| vs. | 2 | 0.0017 | 100% | 82.84% | |||
| vs. | 2 | N.S. | 100% | 97.05% | |||
| vs. | 2 | 0.0326 | 100% | 96.02% | |||
| vs. | 2 | 0.0027 | 100% | 97.57% | |||
| vs. | 2 | 0.0078 | 0% | 94.94% | |||
| vs. | 2 | N.S. | 50.00% | 80.00% | |||
| vs. | 2 | N.S. | 50.00% | 84.21% | |||
| vs. | 2 | N.S. | 75.00% | 92.31% | |||
| vs. | 2 | N.S. | 100% | 87.21% | |||
| vs. | 2 | 0.0071 | 94.67% | 83.33% | |||
| vs. | 2 | 0.0047 | 100% | 89.29% | |||
| vs. | 2 | N.S. | 54.54% | 73.08% | |||
| vs. | 2 | 0.0167 | 81.81% | 80.00% | |||
| vs. | 2 | N.S. | 73.33% | 75.00% |
| Comparison Group | H | K | Total | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| vs. | 48 | 42 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 474 |
| vs. | 24 | 21 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 237 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 48 | 42 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 474 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 24 | 21 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 237 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 24 | 21 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 237 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 120 | 105 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 1185 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 48 | 42 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 474 |
| vs. | 48 | 41 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 473 |
| vs. | 24 | 21 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 237 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 48 | 42 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 48 | 474 |
| vs. | 120 | 104 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 120 | 1184 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| vs. | 24 | 21 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 237 |
| vs. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Total | 600 | 523 | 600 | 600 | 600 | 600 | 600 | 600 | 600 | 600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ribeiro, P.; Sá, J.; Paiva, D.; Rodrigues, P.M. Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis. Bioengineering 2024, 11, 58. https://doi.org/10.3390/bioengineering11010058
Ribeiro P, Sá J, Paiva D, Rodrigues PM. Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis. Bioengineering. 2024; 11(1):58. https://doi.org/10.3390/bioengineering11010058
Chicago/Turabian StyleRibeiro, Pedro, Joana Sá, Daniela Paiva, and Pedro Miguel Rodrigues. 2024. "Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis" Bioengineering 11, no. 1: 58. https://doi.org/10.3390/bioengineering11010058
APA StyleRibeiro, P., Sá, J., Paiva, D., & Rodrigues, P. M. (2024). Cardiovascular Diseases Diagnosis Using an ECG Multi-Band Non-Linear Machine Learning Framework Analysis. Bioengineering, 11(1), 58. https://doi.org/10.3390/bioengineering11010058








