The Potential of Deep Learning to Advance Clinical Applications of Computational Biomechanics
Abstract
:1. Introduction
2. Computational Biomechanics
3. Patient-Specific Computational Analysis
4. Machine-Learning and Deep-Learning Techniques
- Step 1.
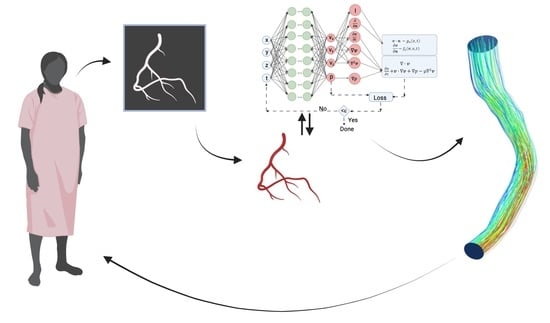
- Construct a neural network that predicts a solution for a key variable (e.g., velocity, stress) from the inputs using the parameters of the neural network.
- Step 2.
- Specify the two training sets for the equation and boundary/initial conditions. These data define the problem under study.
- Step 3.
- Specify a loss function between the neural-network output and both the PDE and the boundary-condition residuals.
- Step 4.
- Train the neural network to find the best parameters for the network that minimize the loss function. The stochastic gradient method provides a rapid algorithm to obtain the neural network’s parameters [48].
5. Machine-Learning and Deep-Learning Applications to Computational Biomechanics
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eichinger, J.F.; Haeusel, L.J.; Paukner, D.; Aydin, R.C.; Humphrey, J.D.; Cyron, C.J. Mechanical homeostasis in tissue equivalents: A review. Biomech. Model. Mechanobiol. 2021, 20, 833–850. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, J.D. Chapter 23—Enablers and drivers of vascular remodeling. In The Vasculome; Galis, Z.S., Ed.; Academic Press: Cambridge, MA, USA, 2022; pp. 277–285. [Google Scholar]
- Gilbert, S.J.; Bonnet, C.S.; Blain, E.J. Mechanical Cues: Bidirectional Reciprocity in the Extracellular Matrix Drives Mechano-Signalling in Articular Cartilage. Int. J. Mol. Sci. 2021, 22, 13595. [Google Scholar] [CrossRef] [PubMed]
- Keating, C.E.; Cullen, D.K. Mechanosensation in traumatic brain injury. Neurobiol. Dis. 2021, 148, 105210. [Google Scholar] [CrossRef] [PubMed]
- Stefanati, M.; Villa, C.; Torrente, Y.; Rodriguez Matas, J.F. A mathematical model of healthy and dystrophic skeletal muscle biomechanics. J. Mech. Phys. Solids 2020, 134, 103747. [Google Scholar] [CrossRef]
- Riaz, M.; Park, J.; Sewanan, L.R.; Ren, Y.; Schwan, J.; Das, S.K.; Pomianowski, P.T.; Huang, Y.; Ellis, M.W.; Luo, J.; et al. Muscle LIM Protein Force-Sensing Mediates Sarcomeric Biomechanical Signaling in Human Familial Hypertrophic Cardiomyopathy. Circulation 2022, 145, 1238–1253. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.A.; Fonte, T.A.; Min, J.K. Computational Fluid Dynamics Applied to Cardiac Computed Tomography for Noninvasive Quantification of Fractional Flow Reserve. J. Am. Coll. Cardiol. 2013, 61, 2233–2241. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Humphrey, J.D.; Delange, S.L. An Introduction to Biomechanics: Solids and FLuids, Analysis and Design; Springer: New York, NY, USA, 2004. [Google Scholar]
- Truskey, G.A.; Yuan, F.; Katz, D.F. Transport Phenomena in Biological Systems, 2nd ed.; Pearson: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Chien, S. Shear Dependence of Effective Cell Volume as a Determinant of Blood Viscosity. Science 1970, 168, 977–979. [Google Scholar] [CrossRef]
- Johnston, B.M.; Johnston, P.R.; Corney, S.; Kilpatrick, D. Non-Newtonian blood flow in human right coronary arteries: Transient simulations. J. Biomech. 2006, 39, 1116–1128. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Gasser, T.C.; Ogden, R.W. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. Phys. Sci. Solids 2000, 61, 1–48. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Niestrawska, J.A.; Ogden, R.W.; Reinisch, A.J.; Schriefl, A.J. Modelling non-symmetric collagen fibre dispersion in arterial walls. J. R. Soc. Interface 2015, 12, 20150188. [Google Scholar] [CrossRef]
- Hughes, T.J.R.; Cottrell, J.A.; Bazilevs, Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 2005, 194, 4135–4195. [Google Scholar] [CrossRef]
- Randles, A.; Draeger, E.W.; Bailey, P.E. Massively parallel simulations of hemodynamics in the primary large arteries of the human vasculature. J. Comput. Sci. 2015, 9, 70–75. [Google Scholar] [CrossRef] [PubMed]
- Soulat, G.; McCarthy, P.; Markl, M. 4D Flow with MRI. Annu. Rev. Biomed. Eng. 2020, 22, 103–126. [Google Scholar] [CrossRef]
- Fonseca, C.G.; Backhaus, M.; Bluemke, D.A.; Britten, R.D.; Chung, J.D.; Cowan, B.R.; Dinov, I.D.; Finn, J.P.; Hunter, P.J.; Kadish, A.H.; et al. The Cardiac Atlas Project—An imaging database for computational modeling and statistical atlases of the heart. Bioinformatics 2011, 27, 2288–2295. [Google Scholar] [CrossRef]
- Börner, K.; Teichmann, S.A.; Quardokus, E.M.; Gee, J.C.; Browne, K.; Osumi-Sutherland, D.; Herr, B.W.; Bueckle, A.; Paul, H.; Haniffa, M.; et al. Anatomical structures, cell types and biomarkers of the Human Reference Atlas. Nat. Cell Biol. 2021, 23, 1117–1128. [Google Scholar] [CrossRef]
- Liu, Y.; Keikhosravi, A.; Mehta, G.S.; Drifka, C.R.; Eliceiri, K.W. Methods for Quantifying Fibrillar Collagen Alignment. In Fibrosis: Methods and Protocols; Rittié, L., Ed.; Springer New York: New York, NY, USA, 2017; pp. 429–451. [Google Scholar]
- Izzo, R.; Steinman, D.; Manini, S.; ANtiga, L. The Vascular Modeling Toolkit: A Python Library for the Analysis of Tubular Structures in Medical Images. J. Open Source Softw. 2018, 25, 745. [Google Scholar] [CrossRef]
- Fedorov, A.; Beichel, R.; Kalpathy-Cramer, J.; Finet, J.; Fillion-Robin, J.-C.; Pujol, S.; Bauer, C.; Jennings, D.; Fennessy, F.; Sonka, M.; et al. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn. Reson. Imaging 2012, 30, 1323–1341. [Google Scholar] [CrossRef]
- Lösel, P.D.; van de Kamp, T.; Jayme, A.; Ershov, A.; Faragó, T.; Pichler, O.; Tan Jerome, N.; Aadepu, N.; Bremer, S.; Chilingaryan, S.A.; et al. Introducing Biomedisa as an open-source online platform for biomedical image segmentation. Nat. Commun. 2020, 11, 5577. [Google Scholar] [CrossRef]
- Ibanez, D.A.; Seol, E.S.; Smith, C.W.; Shephard, M.S. PUMI: Parallel Unstructured Mesh Infrastructure. ACM Trans. Math. Softw. 2016, 42, 17. [Google Scholar] [CrossRef]
- Buffa, A.; Gantner, G.; Giannelli, C.; Praetorius, D.; Vázquez, R. Mathematical Foundations of Adaptive Isogeometric Analysis. Arch. Comput. Methods Eng. 2022, 29, 4479–4555. [Google Scholar] [CrossRef] [PubMed]
- Vignon-Clementel, I.E.; Figueroa, C.A.; Jansen, K.E.; Taylor, C.A. Outflow boundary conditions for 3D simulations of non-periodic blood flow and pressure fields in deformable arteries. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 625–640. [Google Scholar] [CrossRef] [PubMed]
- Mineroff, J.; McCulloch, A.D.; Krummen, D.; Ganapathysubramanian, B.; Krishnamurthy, A. Optimization Framework for Patient-Specific Cardiac Modeling. Cardiovasc. Eng. Technol. 2019, 10, 553–567. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.J.; Vignon-Clementel, I.E.; Figueroa, C.A.; LaDisa, J.F.; Jansen, K.E.; Feinstein, J.A.; Taylor, C.A. On Coupling a Lumped Parameter Heart Model and a Three-Dimensional Finite Element Aorta Model. Ann. Biomed. Eng. 2009, 37, 2153–2169. [Google Scholar] [CrossRef]
- Schwarz, E.L.; Pegolotti, L.; Pfaller, M.R.; Marsden, A.L. Beyond CFD: Emerging methodologies for predictive simulation in cardiovascular health and disease. Biophys. Rev. 2023, 4, 011301. [Google Scholar] [CrossRef]
- Garber, L.; Khodaei, S.; Keshavarz-Motamed, Z. The Critical Role of Lumped Parameter Models in Patient-Specific Cardiovascular Simulations. Arch. Comput. Methods Eng. 2022, 29, 2977–3000. [Google Scholar] [CrossRef]
- Hirschhorn, M.; Tchantchaleishvili, V.; Stevens, R.; Rossano, J.; Throckmorton, A. Fluid–structure interaction modeling in cardiovascular medicine—A systematic review 2017–2019. Med. Eng. Phys. 2020, 78, 1–13. [Google Scholar] [CrossRef]
- Heyland, M.; Checa, S.; Kendoff, D.; Duda, G.N. Anatomic grooved stem mitigates strain shielding compared to established total hip arthroplasty stem designs in finite-element models. Sci. Rep. 2019, 9, 482. [Google Scholar] [CrossRef]
- Lisiak-Myszke, M.; Marciniak, D.; Bieliński, M.; Sobczak, H.; Garbacewicz, Ł.; Drogoszewska, B. Application of Finite Element Analysis in Oral and Maxillofacial Surgery—A Literature Review. Materials 2020, 13, 3063. [Google Scholar] [CrossRef]
- Poelert, S.; Valstar, E.; Weinans, H.; Zadpoor, A.A. Patient-specific finite element modeling of bones. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2012, 227, 464–478. [Google Scholar] [CrossRef] [PubMed]
- Choi, A.; Rim, Y.; Mun, J.S.; Kim, H. A novel finite element-based patient-specific mitral valve repair: Virtual ring annuloplasty. Bio-Med. Mater. Eng. 2014, 24, 341–347. [Google Scholar] [CrossRef] [PubMed]
- Schoch, N.; Kißler, F.; Stoll, M.; Engelhardt, S.; de Simone, R.; Wolf, I.; Bendl, R.; Heuveline, V. Comprehensive patient-specific information preprocessing for cardiac surgery simulations. Int. J. Comput. Assist. Radiol. Surg. 2016, 11, 1051–1059. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, S.S.; Gutierrez, C.A.; Thirugnanasambandam, M.; De Oliveira, V.; Muluk, S.C.; Eskandari, M.K.; Finol, E.A. The Association Between Geometry and Wall Stress in Emergently Repaired Abdominal Aortic Aneurysms. Ann. Biomed. Eng. 2017, 45, 1908–1916. [Google Scholar] [CrossRef]
- Tang, E.; Wei, Z.; Fogel, M.A.; Veneziani, A.; Yoganathan, A.P. Fluid-Structure Interaction Simulation of an Intra-Atrial Fontan Connection. Biology 2020, 9, 412. [Google Scholar] [CrossRef]
- Tanade, C.; Chen, S.J.; Leopold, J.A.; Randles, A. Analysis identifying minimal governing parameters for clinically accurate in silico fractional flow reserve. Front. Med. Technol. 2022, 4, 1034801. [Google Scholar] [CrossRef]
- Zhu, J.; Forman, J. A Review of Finite Element Models of Ligaments in the Foot and Considerations for Practical Application. J. Biomech. Eng. 2022, 144, 080801. [Google Scholar] [CrossRef]
- Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty Shades of Brain: A Review on the Mechanical Testing and Modeling of Brain Tissue. Arch. Comput. Methods Eng. 2020, 27, 1187–1230. [Google Scholar] [CrossRef]
- Phellan, R.; Hachem, B.; Clin, J.; Mac-Thiong, J.-M.; Duong, L. Real-time biomechanics using the finite element method and machine learning: Review and perspective. Med. Phys. 2021, 48, 7–18. [Google Scholar] [CrossRef]
- Mouloodi, S.; Rahmanpanah, H.; Burvill, C.; Martin, C.; Gohari, S.; Davies, H.M.S. How Artificial Intelligence and Machine Learning Is Assisting Us to Extract Meaning from Data on Bone Mechanics? In Biomedical Visualisation: Volume 11; Rea, P.M., Ed.; Springer International Publishing: Cham, Switzerland, 2022; pp. 195–221. [Google Scholar]
- Moen, E.; Bannon, D.; Kudo, T.; Graf, W.; Covert, M.; Van Valen, D. Deep learning for cellular image analysis. Nat. Methods 2019, 16, 1233–1246. [Google Scholar] [CrossRef]
- Dabiri, Y.; Van der Velden, A.; Sack, K.L.; Choy, J.S.; Kassab, G.S.; Guccione, J.M. Prediction of Left Ventricular Mechanics Using Machine Learning. Front. Phys. 2019, 7, 117. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Ketkar, N. Stochastic Gradient Descent. In Deep Learning with Python: A Hands-on Introduction; Ketkar, N., Ed.; Apress: Berkeley, CA, USA, 2017; pp. 113–132. [Google Scholar]
- Updegrove, A.; Wilson, N.M.; Merkow, J.; Lan, H.; Marsden, A.L.; Shadden, S.C. SimVascular: An Open Source Pipeline for Cardiovascular Simulation. Ann. Biomed. Eng. 2017, 45, 525–541. [Google Scholar] [CrossRef]
- Ma, Z.; Tavares, J.R.S.a.N.J.R.M. A Review On The Current Segmentation Algorithms For Medical Images. In Proceedings of the Proceedings of the First International Conference on Computer Imaging Theory and Applications, Lisboa, Portugal, 5–8 February 2009; pp. 135–140. [Google Scholar]
- Minaee, S.; Boykov, Y.; Porikli, F.; Plaza, A.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 3523–3542. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Song, L.; Liu, S.; Zhang, Y. A Review of Deep-Learning-Based Medical Image Segmentation Methods. Sustainability 2021, 13, 1224. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Muncih Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]
- Maher, G.; Wilson, N.; Marsden, A. Accelerating cardiovascular model building with convolutional neural networks. Med. Biol. Eng. Comput. 2019, 57, 2319–2335. [Google Scholar] [CrossRef] [PubMed]
- Iyer, K.; Najarian, C.P.; Fattah, A.A.; Arthurs, C.J.; Soroushmehr, S.M.R.; Subban, V.; Sankardas, M.A.; Nadakuditi, R.R.; Nallamothu, B.K.; Figueroa, C.A. AngioNet: A convolutional neural network for vessel segmentation in X-ray angiography. Sci. Rep. 2021, 11, 18066. [Google Scholar] [CrossRef]
- Chen, L.-C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017. [Google Scholar] [CrossRef]
- Fathi, M.F.; Bakhshinejad, A.; Baghaie, A.; Saloner, D.; Sacho, R.H.; Rayz, V.L.; D’Souza, R.M. Denoising and spatial resolution enhancement of 4D flow MRI using proper orthogonal decomposition and lasso regularization. Comput. Med. Imaging Graph. 2018, 70, 165–172. [Google Scholar] [CrossRef]
- Ferdian, E.; Suinesiaputra, A.; Dubowitz, D.J.; Zhao, D.; Wang, A.; Cowan, B.; Young, A.A. 4DFlowNet: Super-Resolution 4D Flow MRI Using Deep Learning and Computational Fluid Dynamics. Front. Phys. 2020, 8, 138. [Google Scholar] [CrossRef]
- Elsayed, A.; Mauger, C.A.; Ferdian, E.; Gilbert, K.; Scadeng, M.; Occleshaw, C.J.; Lowe, B.S.; McCulloch, A.D.; Omens, J.H.; Govil, S.; et al. Right Ventricular Flow Vorticity Relationships With Biventricular Shape in Adult Tetralogy of Fallot. Front. Cardiovasc. Med. 2022, 8, 806107. [Google Scholar] [CrossRef] [PubMed]
- Rutkowski, D.R.; Roldán-Alzate, A.; Johnson, K.M. Enhancement of cerebrovascular 4D flow MRI velocity fields using machine learning and computational fluid dynamics simulation data. Sci. Rep. 2021, 11, 10240. [Google Scholar] [CrossRef] [PubMed]
- Shit, S.; Zimmermann, J.; Ezhov, I.; Paetzold, J.C.; Sanches, A.F.; Pirkl, C.; Menze, B.H. SRflow: Deep learning based super-resolution of 4D-flow MRI data. Front. Artif. Intell. 2022, 5, 928181. [Google Scholar] [CrossRef]
- Arbabi, V.; Pouran, B.; Campoli, G.; Weinans, H.; Zadpoor, A.A. Determination of the mechanical and physical properties of cartilage by coupling poroelastic-based finite element models of indentation with artificial neural networks. J. Biomech. 2016, 49, 631–637. [Google Scholar] [CrossRef]
- Feiger, B.; Gounley, J.; Adler, D.; Leopold, J.A.; Draeger, E.W.; Chaudhury, R.; Ryan, J.; Pathangey, G.; Winarta, K.; Frakes, D.; et al. Accelerating massively parallel hemodynamic models of coarctation of the aorta using neural networks. Sci. Rep. 2020, 10, 9508. [Google Scholar] [CrossRef]
- Liang, L.; Liu, M.; Sun, W. A deep learning approach to estimate chemically-treated collagenous tissue nonlinear anisotropic stress-strain responses from microscopy images. Acta Biomater. 2017, 63, 227–235. [Google Scholar] [CrossRef]
- You, H.; Zhang, Q.; Ross, C.J.; Lee, C.-H.; Hsu, M.-C.; Yu, Y. A Physics-Guided Neural Operator Learning Approach to Model Biological Tissues From Digital Image Correlation Measurements. J. Biomech. Eng. 2022, 144, 121012. [Google Scholar] [CrossRef]
- Chabiniok, R.; Wang, V.Y.; Hadjicharalambous, M.; Asner, L.; Lee, J.; Sermesant, M.; Kuhl, E.; Young, A.A.; Moireau, P.; Nash, M.P.; et al. Multiphysics and multiscale modelling, data–model fusion and integration of organ physiology in the clinic: Ventricular cardiac mechanics. Interface Focus 2016, 6, 20150083. [Google Scholar] [CrossRef]
- Bar-Sinai, Y.; Hoyer, S.; Hickey, J.; Brenner, M.P. Learning data-driven discretizations for partial differential equations. Proc. Natl. Acad. Sci. 2019, 116, 15344–15349. [Google Scholar] [CrossRef]
- Zhang, W.; Rossini, G.; Kamensky, D.; Bui-Thanh, T.; Sacks, M.S. Isogeometric finite element-based simulation of the aortic heart valve: Integration of neural network structural material model and structural tensor fiber architecture representations. Int. J. Numer. Methods Biomed. Eng. 2021, 37, e3438. [Google Scholar] [CrossRef]
- Kissas, G.; Yang, Y.; Hwuang, E.; Witschey, W.R.; Detre, J.A.; Perdikaris, P. Machine learning in cardiovascular flows modeling: Predicting arterial blood pressure from non-invasive 4D flow MRI data using physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2020, 358, 112623. [Google Scholar] [CrossRef]
- Arzani, A.; Wang, J.-X.; D’Souza, R.M. Uncovering near-wall blood flow from sparse data with physics-informed neural networks. Phys. Fluids 2021, 33, 071905. [Google Scholar] [CrossRef]
- Gao, H.; Sun, L.; Wang, J.-X. Super-resolution and denoising of fluid flow using physics-informed convolutional neural networks without high-resolution labels. Phys. Fluids 2021, 33, 073603. [Google Scholar] [CrossRef]
- Holzapfel, G.A.; Linka, K.; Sherifova, S.; Cyron, C.J. Predictive constitutive modelling of arteries by deep learning. J. R. Soc. Interface 2021, 18, 20210411. [Google Scholar] [CrossRef] [PubMed]
- Linka, K.; Cavinato, C.; Humphrey, J.D.; Cyron, C.J. Predicting and understanding arterial elasticity from key microstructural features by bidirectional deep learning. Acta Biomater. 2022, 147, 63–72. [Google Scholar] [CrossRef] [PubMed]
- Motiwale, S.; Zhang, W.; Sacks, M.S. High-Speed High-Fidelity Cardiac Simulations Using a Neural Network Finite Element Approach. In Proceedings of the Functional Imaging and Modeling of the Heart, Lyon, France, 19–22 June 2023; pp. 537–544. [Google Scholar]
- Yin, M.; Zheng, X.; Humphrey, J.D.; Karniadakis, G.E. Non-invasive inference of thrombus material properties with physics-informed neural networks. Comput. Methods Appl. Mech. Eng. 2021, 375, 113603. [Google Scholar] [CrossRef] [PubMed]



| Topic | Reference | Key Results |
|---|---|---|
| Orthopedic Biomechanics | ||
| Design of stem for total hip arthroplasty | [33] | Identified novel design that produced strains comparable to those present before surgery. |
| Oral and maxillofacial surgery | [34] | Survey of various finite-element models in trauma and reconstructive surgery and implant design. |
| Modeling of bone | [35] | Overview of processes to model deformations, and implant interactions |
| Cardiovascular Biomechanics | ||
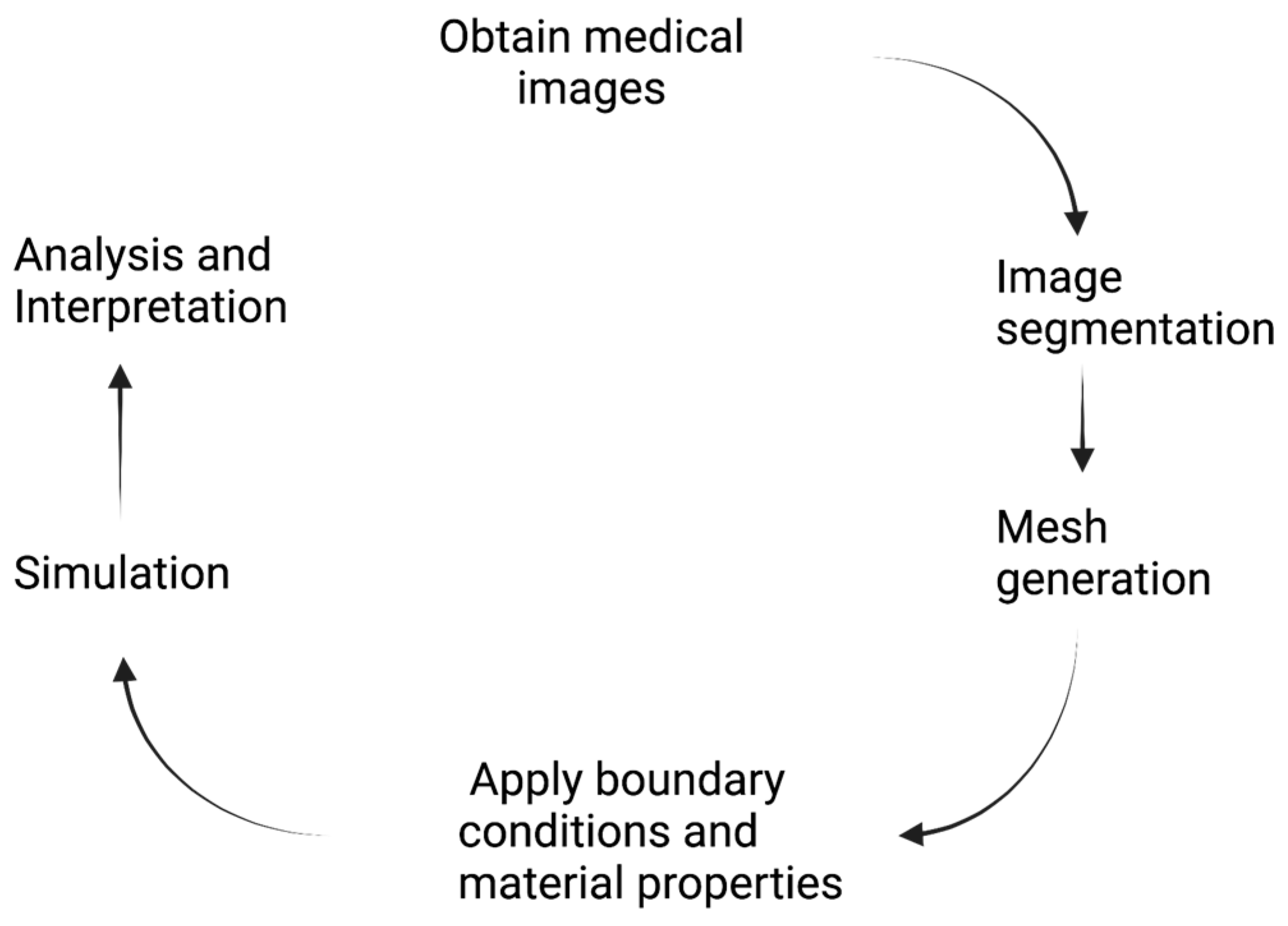
| Mitral valve repair | [36,37] | Model developed from 3D transesophageal echocardiography; workflow for steps in Figure 1. |
| Abdominal aortic aneurysms | [38] | Wall shear stress is a critical factor affecting rupture and can be predicted with four geometric parameters, which can be measured. |
| Single functional ventricles | [39] | Fluid-structure-interaction model indicates that a common surgical procedure can be modeled assuming rigid vessels. |
| Coronary-artery fractional -flow reserve | [40] | Identification of minimal number of patient variables to estimate fractional flow reserve |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truskey, G.A. The Potential of Deep Learning to Advance Clinical Applications of Computational Biomechanics. Bioengineering 2023, 10, 1066. https://doi.org/10.3390/bioengineering10091066
Truskey GA. The Potential of Deep Learning to Advance Clinical Applications of Computational Biomechanics. Bioengineering. 2023; 10(9):1066. https://doi.org/10.3390/bioengineering10091066
Chicago/Turabian StyleTruskey, George A. 2023. "The Potential of Deep Learning to Advance Clinical Applications of Computational Biomechanics" Bioengineering 10, no. 9: 1066. https://doi.org/10.3390/bioengineering10091066
APA StyleTruskey, G. A. (2023). The Potential of Deep Learning to Advance Clinical Applications of Computational Biomechanics. Bioengineering, 10(9), 1066. https://doi.org/10.3390/bioengineering10091066