Biomechanics of the JCT and SC Inner Wall Endothelial Cells with Their Basement Membrane Using 3D Serial Block-Face Scanning Electron Microscopy
Abstract
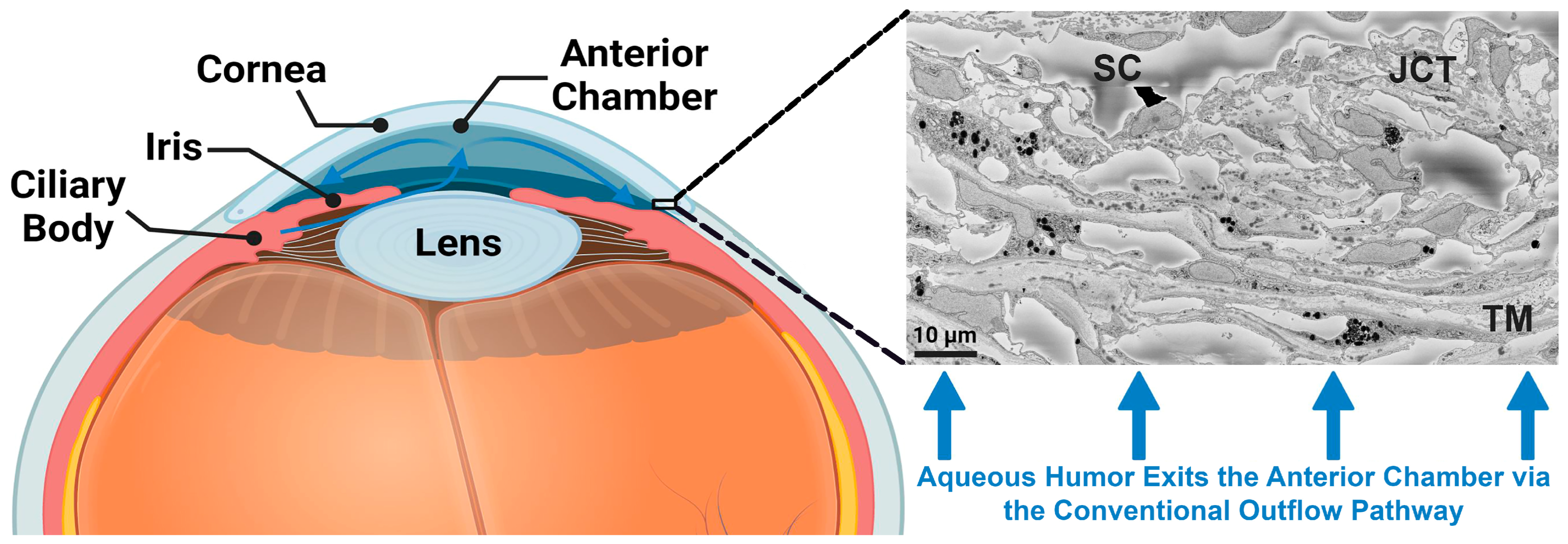
1. Introduction
2. Materials and Methods
2.1. Human Donor Eyes, Ocular Perfusion and Fixation, Global Imaging, and Serial Block-Face Scanning Electron Microscopy
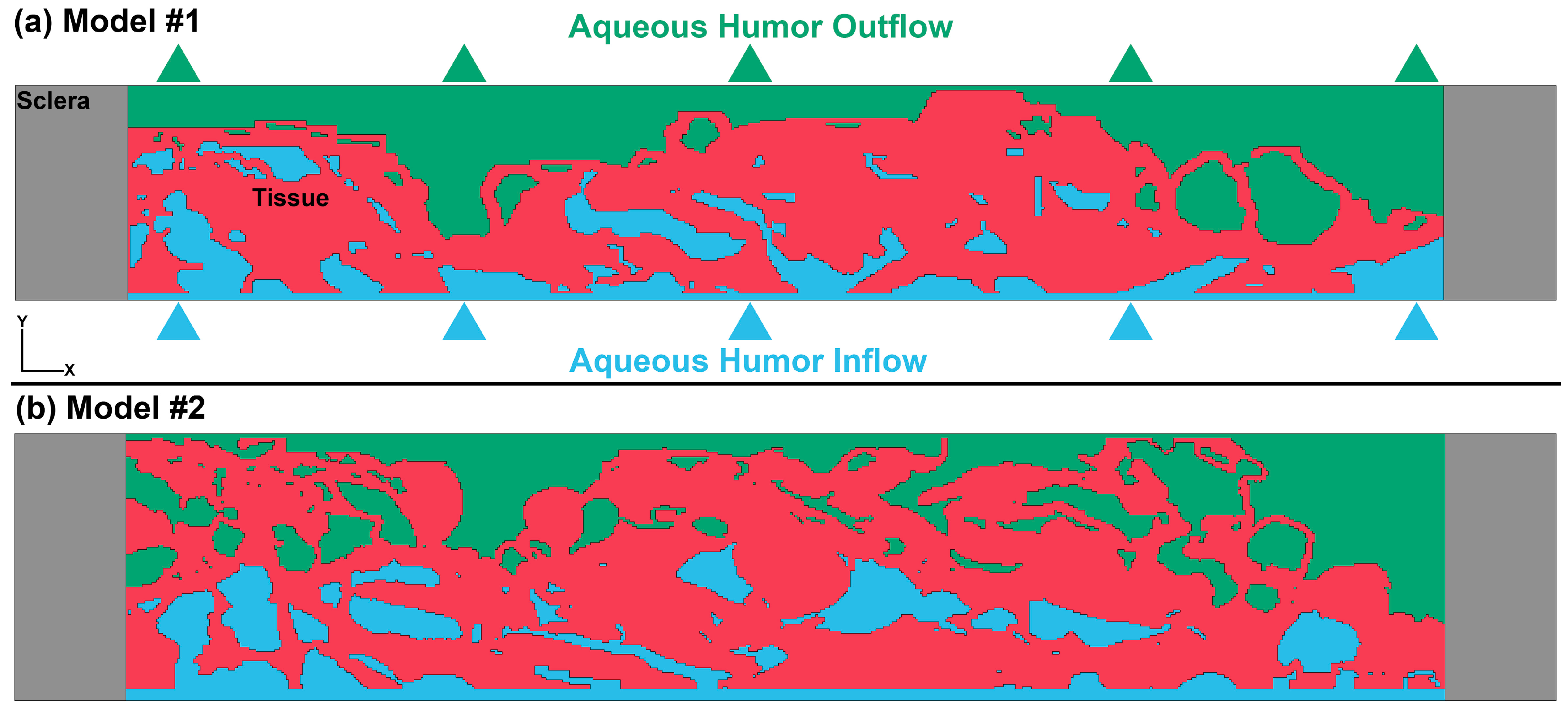
2.2. Segmentation, 3D Finite Element Model, Material Model, and Fluid–Structure Interaction
3. Results
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Dvorak-Theobald, G.; Kirk, H.Q. Aqueous pathways in some cases of glaucoma. Trans. Am. Ophthalmol. Soc. 1955, 53, 301. [Google Scholar]
- Quigley, H.A. Glaucoma. Lancet 2011, 377, 1367–1377. [Google Scholar] [CrossRef] [PubMed]
- Stamer, W.D.; Acott, T.S. Current understanding of conventional outflow dysfunction in glaucoma. Curr. Opin. Ophthalmol. 2012, 23, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Chang, J.Y.; Folz, S.J.; Laryea, S.N.; Overby, D.R. Multi-scale analysis of segmental outflow patterns in human trabecular meshwork with changing intraocular pressure. J. Ocul. Pharm. 2014, 30, 213–223. [Google Scholar] [CrossRef] [PubMed]
- Vranka, J.A.; Bradley, J.M.; Yang, Y.F.; Keller, K.E.; Acott, T.S. Mapping molecular differences and extracellular matrix gene expression in segmental outflow pathways of the human ocular trabecular meshwork. PLoS ONE 2015, 10, e0122483. [Google Scholar] [CrossRef]
- Weinreb, R.N.; Leung, C.K.; Crowston, J.G.; Medeiros, F.A.; Friedman, D.S.; Wiggs, J.L.; Martin, K.R. Primary open-angle glaucoma. Nat. Rev. Dis. Prim. 2016, 2, 16067. [Google Scholar] [CrossRef]
- Johnson, M. What controls aqueous humour outflow resistance? Exp. Eye Res. 2006, 82, 545–557. [Google Scholar] [CrossRef]
- Freddo, T.F.; Johnson, M. Aqueous humor outflow resistance. Curr. Top. Membr. 2008, 62, 161–192. [Google Scholar] [CrossRef]
- Acott, T.S.; Vranka, J.A.; Keller, K.E.; Raghunathan, V.; Kelley, M.J. Normal and glaucomatous outflow regulation. Prog. Retin. Eye Res. 2021, 82, 100897. [Google Scholar] [CrossRef]
- Johnson, M.C.; Kamm, R.D. The role of Schlemm’s canal in aqueous outflow from the human eye. Investig. Ophthalmol. Vis. Sci. 1983, 24, 320–325. [Google Scholar]
- Stamer, W.D.; Braakman, S.T.; Zhou, E.H.; Ethier, C.R.; Fredberg, J.J.; Overby, D.R.; Johnson, M. Biomechanics of Schlemm’s canal endothelium and intraocular pressure reduction. Prog. Retin. Eye Res. 2015, 44, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Rahmati, S.M.; Razaghi, R.; Crawford Downs, J.; Acott, T.S.; Wang, R.K.; Johnstone, M. Biomechanics of human trabecular meshwork in healthy and glaucoma eyes via dynamic Schlemm’s canal pressurization. Comput. Methods Programs Biomed. 2022, 221, 106921. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Razaghi, R.; Rahmati, S.M.; Downs, J.C.; Acott, T.S.; Wang, R.K.; Johnstone, M. Modeling the biomechanics of the conventional aqueous outflow pathway microstructure in the human eye. Comput. Methods Programs Biomed. 2022, 221, 106922. [Google Scholar] [CrossRef]
- Johnstone, M.A.; Grant, W.G. Pressure-dependent changes in structures of the aqueous outflow system of human and monkey eyes. Am. J. Ophthalmol. 1973, 75, 365–383. [Google Scholar] [CrossRef]
- Bradley, J.M.; Kelley, M.J.; Zhu, X.; Anderssohn, A.M.; Alexander, J.P.; Acott, T.S. Effects of mechanical stretching on trabecular matrix metalloproteinases. Investig. Ophthalmol. Vis. Sci. 2001, 42, 1505–1513. [Google Scholar]
- Johnson, M.; Chan, D.; Read, A.T.; Christensen, C.; Sit, A.; Ethier, C.R. The pore density in the inner wall endothelium of Schlemm’s canal of glaucomatous eyes. Investig. Ophthalmol. Vis. Sci. 2002, 43, 2950–2955. [Google Scholar]
- Overby, D.R.; Stamer, W.D.; Johnson, M. The changing paradigm of outflow resistance generation: Towards synergistic models of the JCT and inner wall endothelium. Exp. Eye Res. 2009, 88, 656–670. [Google Scholar] [CrossRef]
- Goel, M.; Picciani, R.G.; Lee, R.K.; Bhattacharya, S.K. Aqueous humor dynamics: A review. Open. Ophthalmol. J. 2010, 4, 52–59. [Google Scholar] [CrossRef]
- Acott, T.S.; Kelley, M.J.; Keller, K.E.; Vranka, J.A.; Abu-Hassan, D.W.; Li, X.; Aga, M.; Bradley, J.M. Intraocular pressure homeostasis: Maintaining balance in a high-pressure environment. J. Ocul. Pharm. 2014, 30, 94–101. [Google Scholar] [CrossRef]
- Abu-Hassan, D.W.; Li, X.; Ryan, E.I.; Acott, T.S.; Kelley, M.J. Induced pluripotent stem cells restore function in a human cell loss model of open-angle glaucoma. Stem Cells 2015, 33, 751–761. [Google Scholar] [CrossRef]
- Johnstone, M.; Xin, C.; Tan, J.; Martin, E.; Wen, J.; Wang, R.K. Aqueous outflow regulation–21st century concepts. Prog. Retin. Eye Res. 2020, 83, 100917. [Google Scholar] [CrossRef]
- Bill, A.; Svedbergh, B. Scanning electron microscopic studies of the trabecular meshwork and the canal of Schlemm—An attempt to localize the main resistance to outflow of aqueous humor in man. Acta Ophthalmol. 1972, 50, 295–320. [Google Scholar] [CrossRef]
- Johnson, M.; Shapiro, A.; Ethier, C.R.; Kamm, R.D. Modulation of outflow resistance by the pores of the inner wall endothelium. Investig. Ophthalmol. Vis. Sci. 1992, 33, 1670–1675. [Google Scholar]
- Johnson, M.; Overby, D.; Ruberti, J.; Freddo, T.F.; Gong, H. Hydrodynamics of aqueous humor outflow. In Proceedings of the First Joint BMES/EMBS Conference. 1999 IEEE Engineering in Medicine and Biology 21st Annual Conference and the 1999 Annual Fall Meeting of the Biomedical Engineering Society (Cat. N), Atlanta, GA, USA, 13–16 October 1999; Volume 1312, p. 1316. [Google Scholar]
- Karimi, A.; Crouch, D.J.; Razaghi, R.; Downs, J.C.; Acott, T.S.; Kelley, M.J.; Behnsen, J.G.; Bosworth, L.A.; Sheridan, C.M. Morphological and Biomechanical Analyses of the Human Healthy and Glaucomatous Aqueous Outflow Pathway: Imaging-to-Modeling. Comput. Methods Programs Biomed. 2023, 236, 107485. [Google Scholar] [CrossRef]
- Lütjen-Drecoll, E.; Futa, R.; Rohen, J. Ultrahistochemical studies on tangential sections of the trabecular meshwork in normal and glaucomatous eyes. Investig. Ophthalmol. Vis. Sci. 1981, 21, 563–573. [Google Scholar]
- Allingham, R.; de Kater, A.; Shahsafaei, A.; Epstein, D. Relationship between outflow facility and giant vacuoles of Schlemm’s canal in normal and glaucomatous human eyes. Investig. Ophthalmol. Vis. Sci. 1990, 31, 338. [Google Scholar]
- Ethier, C.R.; Coloma, F.M.; Sit, A.J.; Johnson, M. Two pore types in the inner-wall endothelium of Schlemm’s canal. Investig. Ophthalmol. Vis. Sci. 1998, 39, 2041–2048. [Google Scholar]
- Lai, J.; Su, Y.; Swain, D.L.; Huang, D.; Getchevski, D.; Gong, H. The role of Schlemm’s canal endothelium cellular connectivity in giant vacuole formation: A 3D electron microscopy study. Investig. Ophthalmol. Vis. Sci. 2019, 60, 1630–1643. [Google Scholar] [CrossRef] [PubMed]
- Swain, D.L.; Le, T.D.; Yasmin, S.; Fernandes, B.; Lamaj, G.; Dasgupta, I.; Gao, Y.; Gong, H. Morphological factors associated with giant vacuoles with I-pores in Schlemm’s canal endothelial cells of human eyes: A serial block-face scanning electron microscopy study. Exp. Eye Res. 2021, 205, 108488. [Google Scholar] [CrossRef]
- Zhu, J.-Y.; Ye, W.; Gong, H.-Y. Development of a novel two color tracer perfusion technique for the hydrodynamic study of aqueous outflow in bovine eyes. Chin. Med. J. 2010, 123, 599–605. [Google Scholar]
- Vranka, J.A.; Staverosky, J.A.; Reddy, A.P.; Wilmarth, P.A.; David, L.L.; Acott, T.S.; Russell, P.; Raghunathan, V.K. Biomechanical rigidity and quantitative proteomics analysis of segmental regions of the trabecular meshwork at physiologic and elevated pressures. Investig. Ophthalmol. Vis. Sci. 2018, 59, 246–259. [Google Scholar] [CrossRef] [PubMed]
- Cha, E.D.K.; Xu, J.; Gong, L.; Gong, H. Variations in active outflow along the trabecular outflow pathway. Exp. Eye Res. 2016, 146, 354–360. [Google Scholar] [CrossRef] [PubMed]
- Deerinck, T.J.; Bushong, E.A.; Thor, A.; Ellisman, M.H. NCMIR methods for 3D EM: A new protocol for preparation of biological specimens for serial block face scanning electron microscopy. Microscopy 2010, 1, 6–8. [Google Scholar]
- Karimi, A.; Razaghi, R.; Padilla, S.; Rahmati, S.M.; Downs, J.C.; Acott, T.S.; Kelley, M.J.; Wang, R.K.; Johnstone, M. Viscoelastic Biomechanical Properties of the Conventional Aqueous Outflow Pathway Tissues in Healthy and Glaucoma Human Eyes. J. Clin. Med. 2022, 11, 6049. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Razaghi, R.; Rahmati, S.M.; Downs, J.C.; Acott, T.S.; Kelley, M.J.; Wang, R.K.; Johnstone, M. The Effect of Intraocular Pressure Load Boundary on the Biomechanics of the Human Conventional Aqueous Outflow Pathway. Bioengineering 2022, 9, 672. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Khan, S.; Razaghi, R.; Rahmati, S.M.; Gathara, M.; Tudisco, E.; Aga, M.; Kelley, M.J.; Jian, Y.; Acott, T.S. Developing an experimental-computational workflow to study the biomechanics of the human conventional aqueous outflow pathway. Acta Biomater. 2023, 164, 346–362. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, S.M.; Razaghi, R.; Karimi, A. Biomechanics of the keratoconic cornea: Theory, segmentation, pressure distribution, and coupled FE-optimization algorithm. J. Mech. Behav. Biomed. Mater. 2021, 113, 104155. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Rahmati, S.M.; Grytz, R.G.; Girkin, C.A.; Downs, J.C. Modeling the biomechanics of the lamina cribrosa microstructure in the human eye. Acta Biomater. 2021, 134, 357–378. [Google Scholar] [CrossRef]
- Karimi, A.; Halabian, M.; Razaghi, R.; Downs, J.C.; Kelley, M.J.; Acott, T.S. Modeling the Endothelial Glycocalyx Layer in the Human Conventional Aqueous Outflow Pathway. Cells 2022, 11, 3925. [Google Scholar] [CrossRef]
- Karimi, A.; Razaghi, R.; Rahmati, S.M.; Girkin, C.A.; Downs, J.C. Relative Contributions of Intraocular and Cerebrospinal Fluid Pressures to the Biomechanics of the Lamina Cribrosa and Laminar Neural Tissues. Investig. Ophthalmol. Vis. Sci. 2022, 63, 14. [Google Scholar] [CrossRef]
- Eilaghi, A.; Flanagan, J.G.; Tertinegg, I.; Simmons, C.A.; Wayne Brodland, G.; Ross Ethier, C. Biaxial mechanical testing of human sclera. J. Biomech. 2010, 43, 1696–1701. [Google Scholar] [CrossRef] [PubMed]
- Souli, M. ALE incompressible fluid in LS-DYNA. In Proceedings of the 11th International LS-DYNA Conference, Detroit, MI, USA, 6–8 June 2010; pp. 29–36. [Google Scholar]
- Aquelet, N.; Souli, M. ALE Incompressible Fluid in LS-DYNA®. In FSI/ALE; Université de Lille: Lille, France, 2012; Volume 21. [Google Scholar]
- Peery, J.S.; Carroll, D.E. Multi-Material ALE methods in unstructured grids. Comput. Methods Appl. Mech. Eng. 2000, 187, 591–619. [Google Scholar] [CrossRef]
- Aquelet, N. ALE adaptive mesh refinement in LS-Dyna. In Proceedings of the 12th International LS-DYNA Users Conference, Detroit, MC, USA, 3–5 June 2012. [Google Scholar]
- Razaghi, R.; Biglari, H.; Karimi, A. Risk of rupture of the cerebral aneurysm in relation to traumatic brain injury using a patient-specific fluid-structure interaction model. Comput. Methods Programs Biomed. 2019, 176, 9–16. [Google Scholar] [CrossRef] [PubMed]
- Vass, C.; Hirn, C.; Unger, E.; Mayr, W.; Georgopoulos, M.; Rainer, G.; Richter-Maksch, S. Human aqueous humor viscosity in cataract, primary open angle glaucoma and pseudoexfoliation syndrome. Investig. Ophthalmol. Vis. Sci. 2004, 45, U564. [Google Scholar]
- Heuzé, O. General form of the Mie–Grüneisen equation of state. Comptes. Rendus. Mec. 2012, 340, 679–687. [Google Scholar] [CrossRef]
- Hallquist, J.O. LS-DYNA keyword user’s manual. Livermore Softw. Technol. Corp. 2007, 970, 299–800. [Google Scholar]
- Quigley, H.A. Open-angle glaucoma. N. Engl. J. Med. 1993, 328, 1097–1106. [Google Scholar] [CrossRef]
- Quigley, H.A. Number of people with glaucoma worldwide. Br. J. Ophthalmol. 1996, 80, 389–393. [Google Scholar] [CrossRef]
- Ethier, C.R.; Johnson, M.; Ruberti, J. Ocular biomechanics and biotransport. Annu. Rev. Biomed. Eng. 2004, 6, 249–273. [Google Scholar] [CrossRef]
- Needham, D.; Nunn, R.S. Elastic deformation and failure of lipid bilayer membranes containing cholesterol. Biophys. J. 1990, 58, 997–1009. [Google Scholar] [CrossRef]
- Grierson, I.; Lee, W.R. Light microscopic quantitation of the endothelial vacuoles in Schlemm’s canal. Am. J. Ophthalmol. 1977, 84, 234–246. [Google Scholar] [CrossRef] [PubMed]
- Hann, C.R.; Fautsch, M.P. Preferential fluid flow in the human trabecular meshwork near collector channels. Investig. Ophthalmol. Vis. Sci. 2009, 50, 1692–1697. [Google Scholar] [CrossRef] [PubMed]
- Braakman, S.T.; Read, A.T.; Chan, D.W.; Ethier, C.R.; Overby, D.R. Colocalization of outflow segmentation and pores along the inner wall of Schlemm’s canal. Exp. Eye Res. 2015, 130, 87–96. [Google Scholar] [CrossRef] [PubMed]
- Johnson, M.; Chan, D.; Reed, A.; Christensen, C.; Sit, A.; Ethier, C. Glaucomatous eyes have a reduced pore density in the inner wall endothelium of Schlemm’s canal. Investig. Ophthalmol. Vis. Sci. 2002, 43, 3961. [Google Scholar]
- Braakman, S.T.; Moore, J.E., Jr.; Ethier, C.R.; Overby, D.R. Transport across Schlemm’s canal endothelium and the blood-aqueous barrier. Exp. Eye Res. 2016, 146, 17–21. [Google Scholar] [CrossRef]
- Ethier, C.R.; Read, A.T.; Chan, D. Biomechanics of Schlemm’s canal endothelial cells: Influence on F-actin architecture. Biophys. J. 2004, 87, 2828–2837. [Google Scholar] [CrossRef]
- Stamer, W.D.; Lei, Y.; Boussommier-Calleja, A.; Overby, D.R.; Ethier, C.R. eNOS, a pressure-dependent regulator of intraocular pressure. Investig. Ophthalmol. Vis. Sci. 2011, 52, 9438–9444. [Google Scholar] [CrossRef]
- Grierson, I.; Lee, W.R. Changes in the monkey outflow apparatus at graded levels of intraocular pressure: A qualitative analysis by light microscopy and scanning electron microscopy. Exp. Eye Res. 1974, 19, 21–33. [Google Scholar] [CrossRef]
- Grierson, I.; Lee, W.R. Pressure-induced changes in the ultrastructure of the endothelium lining Schlemm’s canal. Am. J. Ophthalmol. 1975, 80, 863–884. [Google Scholar] [CrossRef]
- Pedrigi, R.M.; Simon, D.; Reed, A.; Stamer, W.D.; Overby, D.R. A model of giant vacuole dynamics in human Schlemm’s canal endothelial cells. Exp. Eye Res. 2011, 92, 57–66. [Google Scholar] [CrossRef]
- Karimi, A.; Grytz, R.; Rahmati, S.M.; Girkin, C.A.; Downs, J.C. Analysis of the effects of finite element type within a 3D biomechanical model of a human optic nerve head and posterior pole. Comput. Methods Programs Biomed. 2021, 198, 105794. [Google Scholar] [CrossRef] [PubMed]
- Carreon, T.; van der Merwe, E.; Fellman, R.L.; Johnstone, M.; Bhattacharya, S.K. Aqueous outflow—A continuum from trabecular meshwork to episcleral veins. Prog. Retin. Eye Res. 2017, 57, 108–133. [Google Scholar] [CrossRef] [PubMed]
- Grant, W.M. Facility of flow through the trabecular meshwork. AMA Arch. Ophthalmol. 1955, 54, 245–248. [Google Scholar] [CrossRef]
- Grant, W.M. Further studies on facility of flow through the trabecular meshwork. AMA Arch. Ophthalmol. 1958, 60, 523–533. [Google Scholar] [CrossRef]
- Yang, C.Y.; Huynh, T.; Johnson, M.; Gong, H. Endothelial glycocalyx layer in the aqueous outflow pathway of bovine and human eyes. Exp. Eye Res. 2014, 128, 27–33. [Google Scholar] [CrossRef]
- Johnstone, M.A. The aqueous outflow system as a mechanical pump: Evidence from examination of tissue and aqueous movement in human and non-human primates. J. Glaucoma 2004, 13, 421–438. [Google Scholar] [CrossRef] [PubMed]
- McDonnell, F.; Dismuke, W.M.; Overby, D.R.; Stamer, W.D. Pharmacological regulation of outflow resistance distal to Schlemm’s canal. Am. J. Physiol. Cell Physiol. 2018, 315, C44–C51. [Google Scholar] [CrossRef]
- Sosnowik, S.; Swain, D.L.; Liu, N.; Fan, S.; Toris, C.B.; Gong, H. Endothelial Glycocalyx Morphology in Different Flow Regions of the Aqueous Outflow Pathway of Normal and Laser-Induced Glaucoma Monkey Eyes. Cells 2022, 11, 2452. [Google Scholar] [CrossRef]
- Pries, A.R.; Secomb, T.W.; Gaehtgens, P. The endothelial surface layer. Pflug. Arch. 2000, 440, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Weinbaum, S.; Tarbell, J.M.; Damiano, E.R. The structure and function of the endothelial glycocalyx layer. Annu. Rev. Biomed. Eng. 2007, 9, 121–167. [Google Scholar] [CrossRef]
- Collins, S.R.; Blank, R.S.; Deatherage, L.S.; Dull, R.O. Special article: The endothelial glycocalyx: Emerging concepts in pulmonary edema and acute lung injury. Anesth. Analg. 2013, 117, 664–674. [Google Scholar] [CrossRef]
- Dewey, C., Jr. Effects of fluid flow on living vascular cells. J. Biomech. Eng. 1984, 106, 31–35. [Google Scholar] [CrossRef]
- Yao, Y.; Rabodzey, A.; Dewey, C.F., Jr. Glycocalyx modulates the motility and proliferative response of vascular endothelium to fluid shear stress. Am. J. Physiol. Heart Circ. Physiol. 2007, 293, H1023–H1030. [Google Scholar] [CrossRef] [PubMed]
- Vincent, P.E.; Weinberg, P.D. Flow-dependent concentration polarization and the endothelial glycocalyx layer: Multi-scale aspects of arterial mass transport and their implications for atherosclerosis. Biomech. Model. Mechanobiol. 2014, 13, 313–326. [Google Scholar] [CrossRef] [PubMed]
- Keller, K.E.; Bradley, J.M.; Vranka, J.A.; Acott, T.S. Segmental versican expression in the trabecular meshwork and involvement in outflow facility. Investig. Ophthalmol. Vis. Sci. 2011, 52, 5049–5057. [Google Scholar] [CrossRef]
- Wight, T.N. Versican: A versatile extracellular matrix proteoglycan in cell biology. Curr. Opin. Cell Biol. 2002, 14, 617–623. [Google Scholar] [CrossRef] [PubMed]
- Allingham, R.R.; Dekater, A.W.; Ethier, C.R.; Anderson, P.J.; Hertzmark, E.; Epstein, D.L. The Relationship between Pore Density and Outflow Facility in Human Eyes. Investig. Ophthalmol. Vis. Sci. 1992, 33, 1661–1669. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimi, A.; Razaghi, R.; Kelley, M.J.; Acott, T.S.; Gong, H. Biomechanics of the JCT and SC Inner Wall Endothelial Cells with Their Basement Membrane Using 3D Serial Block-Face Scanning Electron Microscopy. Bioengineering 2023, 10, 1038. https://doi.org/10.3390/bioengineering10091038
Karimi A, Razaghi R, Kelley MJ, Acott TS, Gong H. Biomechanics of the JCT and SC Inner Wall Endothelial Cells with Their Basement Membrane Using 3D Serial Block-Face Scanning Electron Microscopy. Bioengineering. 2023; 10(9):1038. https://doi.org/10.3390/bioengineering10091038
Chicago/Turabian StyleKarimi, Alireza, Reza Razaghi, Mary J. Kelley, Ted S. Acott, and Haiyan Gong. 2023. "Biomechanics of the JCT and SC Inner Wall Endothelial Cells with Their Basement Membrane Using 3D Serial Block-Face Scanning Electron Microscopy" Bioengineering 10, no. 9: 1038. https://doi.org/10.3390/bioengineering10091038
APA StyleKarimi, A., Razaghi, R., Kelley, M. J., Acott, T. S., & Gong, H. (2023). Biomechanics of the JCT and SC Inner Wall Endothelial Cells with Their Basement Membrane Using 3D Serial Block-Face Scanning Electron Microscopy. Bioengineering, 10(9), 1038. https://doi.org/10.3390/bioengineering10091038








