Learning Causal Biological Networks with Parallel Ant Colony Optimization Algorithm
Abstract
1. Introduction
- To the best of our knowledge, this is the first study to employ a parallel ant colony optimization algorithm to learn CBNs from biological signal data. The incorporation of parallelization allows for more accurate and efficient learning of CBNs, which will provide a significant reference for the causal discovery and bioinformatics fields.
- PACO incorporates the parallel ant colony optimization and information fusion strategy. This approach not only enhances the algorithm’s efficiency and reduces time complexity, but also facilitates the extraction of shared information from multiple data sets, thereby improving the accuracy of learn CBNs and more fully utilizes global information, effectively reducing the probability of falling into a local optima.
- Numerous experiments conducted on simulation data sets, fMRI signal data sets and Single-cell data set have demonstrated that the proposed method is capable of learning CBNs from different biological signal data, thereby improving inference performance, which has significant implications for a deeper understanding of the underlying causal relationships in biological systems.
2. Related Work
2.1. Causal Biological Networks
2.1.1. Causal Brain Networks
2.1.2. Causal Protein Signaling Networks
2.2. Ant Colony Optimization Algorithm
3. The Parallel Ant Colony Optimization Algorithm
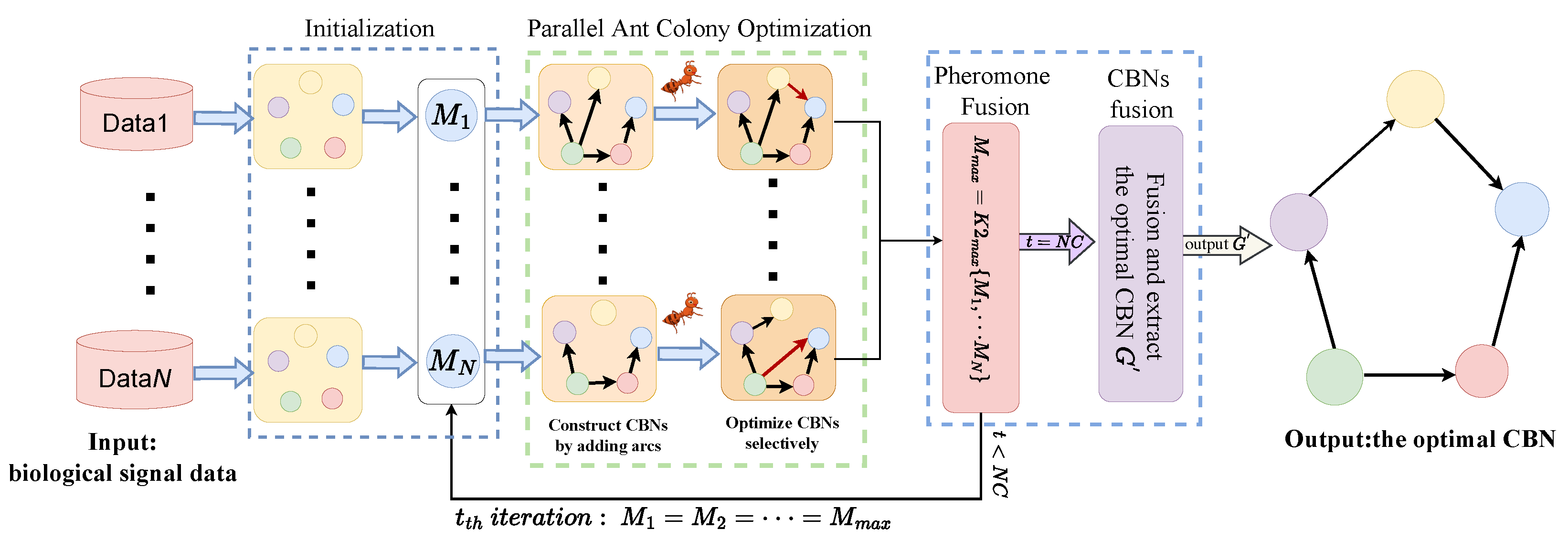
3.1. Main Idea
3.2. Initialization
3.3. Parallel Ant Colony Optimization
3.4. Pheromone Fusion and CBNs Fusion
3.5. Algorithm Description and Analysis
| Algorithm 1: PACO |
 |
4. Experimental Result of Learning CBNs
4.1. Data Description
4.1.1. Simulation Data Sets
4.1.2. fMRI Signal Data Sets
4.1.3. Single-Cell Data Sets
4.2. Evaluation Metrics
4.3. Contrast Algorithm Introduction and Experimental Setup
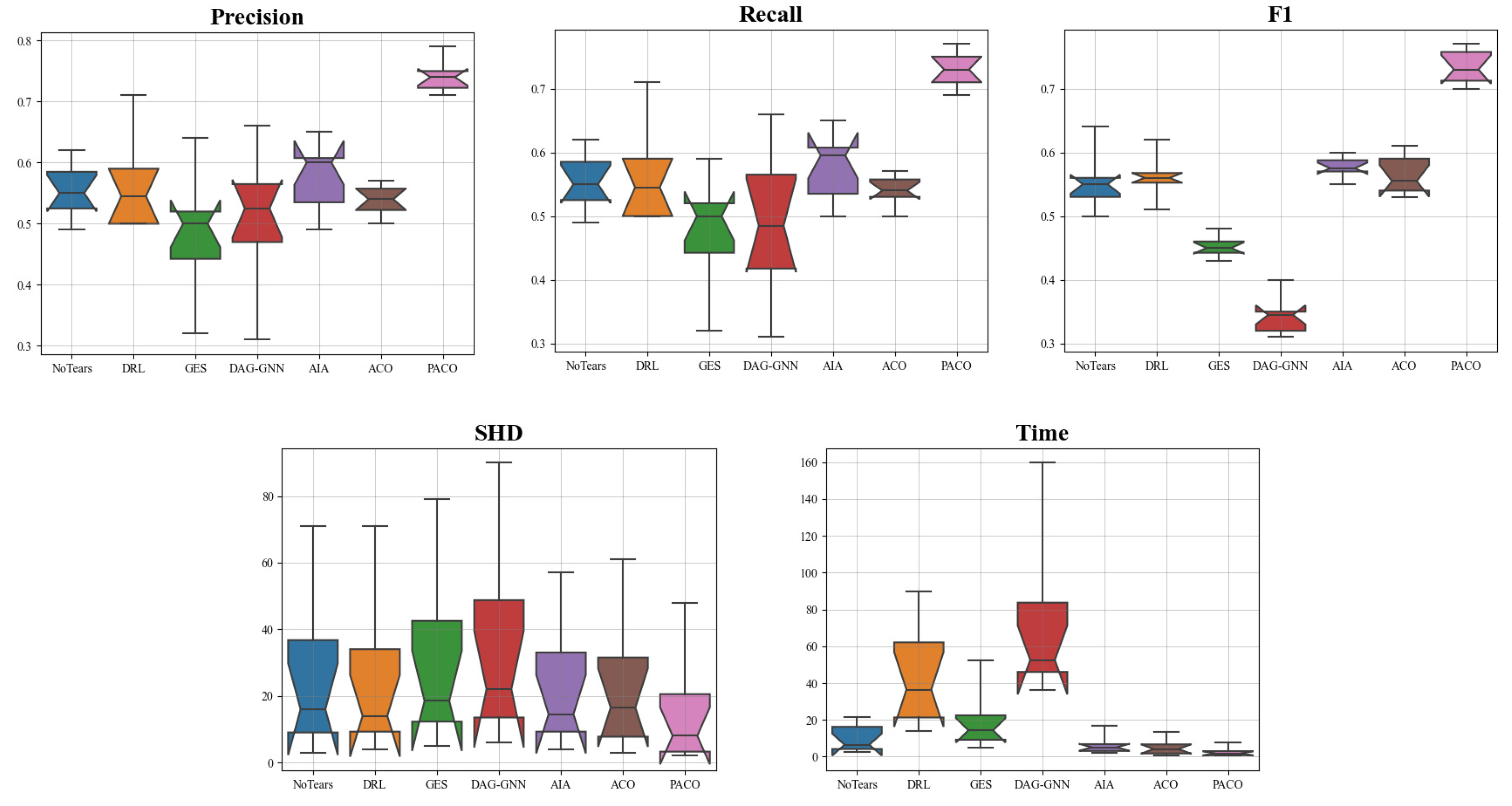
4.4. The Results of Learning CBNs from Simulation Data Sets
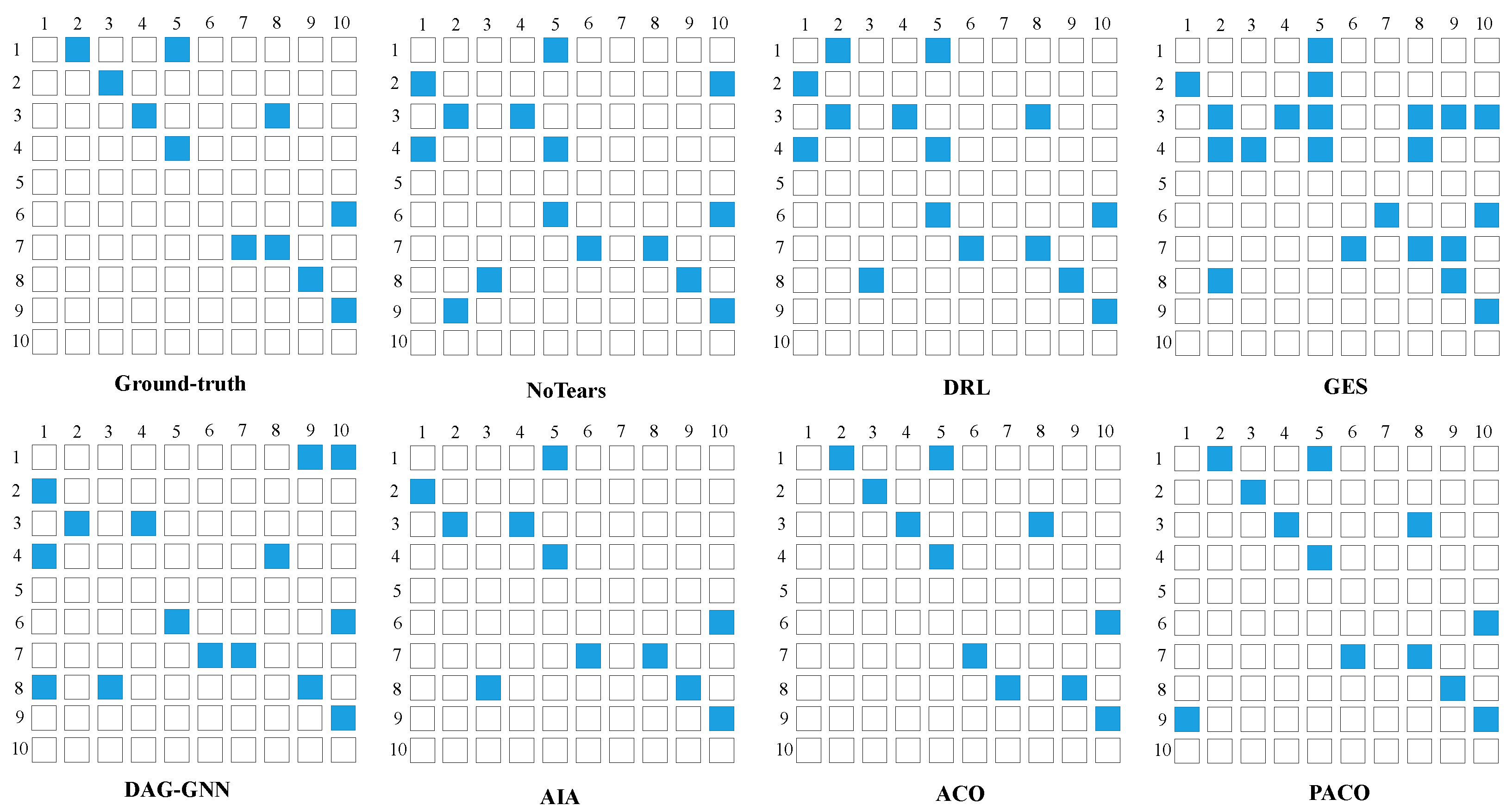
4.5. The Results of Learning Causal Brain Networks from fMRI Signal Data Sets
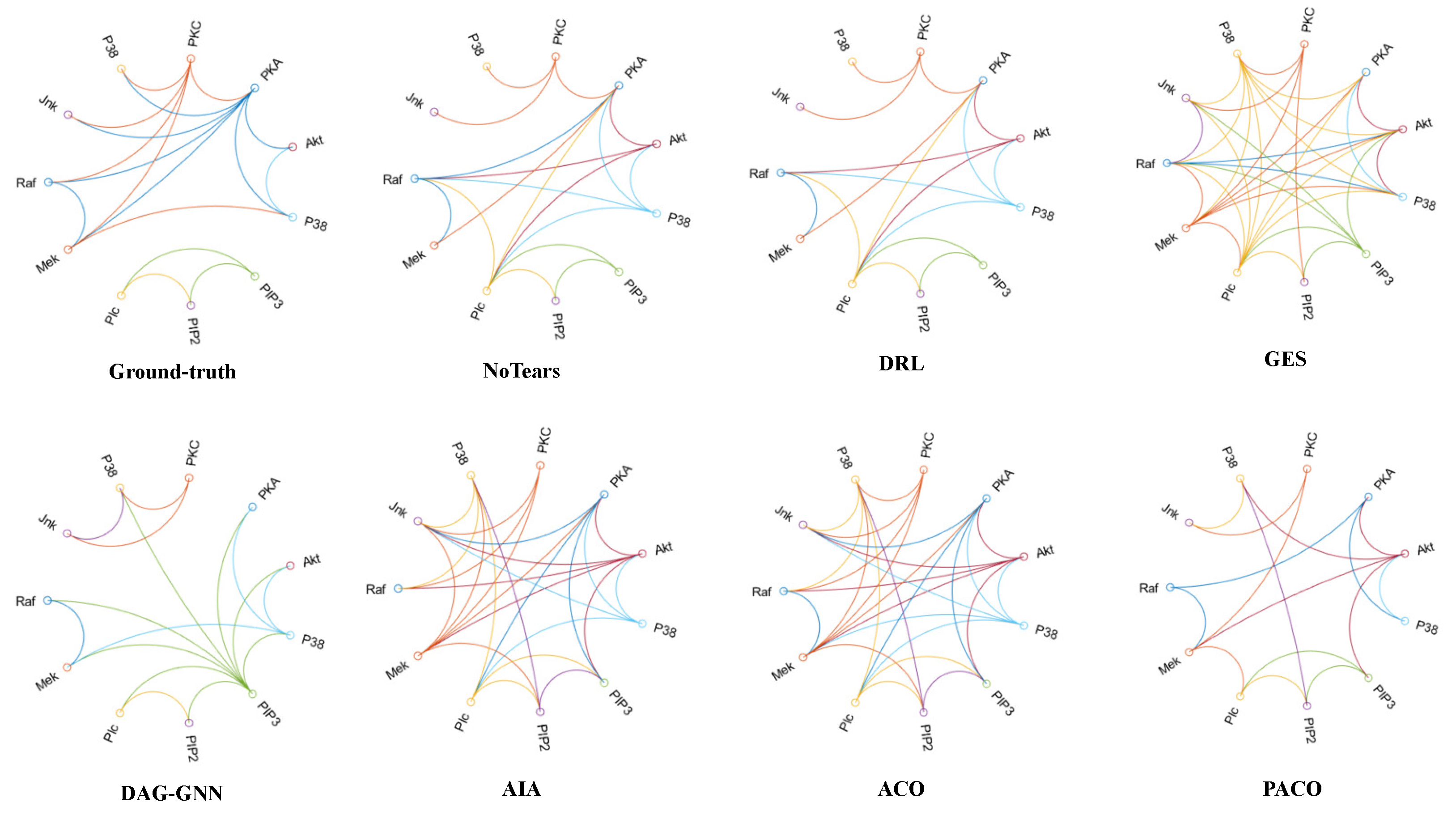
4.6. The Results of Learning Causal Protein Signaling Networks from Simulation Data Sets
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Babur, Ö.; Luna, A.; Korkut, A.; Durupinar, F.; Siper, M.C.; Dogrusoz, U.; Jacome, A.S.V.; Peckner, R.; Christianson, K.E.; Jaffe, J.D.; et al. Causal interactions from proteomic profiles: Molecular data meet pathway knowledge. Patterns 2021, 2, 100257. [Google Scholar] [CrossRef]
- Paul, I.; Bolzan, D.; Youssef, A.; Gagnon, K.A.; Hook, H.; Karemore, G.; Oliphant, M.U.; Lin, W.; Liu, Q.; Phanse, S.; et al. Parallelized multidimensional analytic framework applied to mammary epithelial cells uncovers regulatory principles in EMT. Nat. Commun. 2023, 14, 688. [Google Scholar] [CrossRef]
- Ji, J.; Zou, A.; Liu, J.; Yang, C.; Zhang, X.; Song, Y. A survey on brain effective connectivity network learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 1879–1899. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Ji, J.; Jia, X.; Zhang, A. Learning Brain Effective Connectivity Network Structure Using Ant Colony Optimization Combining with Voxel Activation Information. IEEE J. Biomed. Health Inform. 2020, 24, 2028–2040. [Google Scholar] [CrossRef]
- ElNakieb, Y.; Ali, M.T.; Elnakib, A.; Shalaby, A.; Mahmoud, A.; Soliman, A.; Barnes, G.N.; El-Baz, A. Understanding the Role of Connectivity Dynamics of Resting-State Functional MRI in the Diagnosis of Autism Spectrum Disorder: A Comprehensive Study. Bioengineering 2023, 10, 56. [Google Scholar] [CrossRef]
- Sachs, K.; Perez, O.; Pe’er, D.; Lauffenburger, D.A.; Nolan, G.P. Causal protein-signaling networks derived from multiparameter single-cell data. Science 2005, 308, 523–529. [Google Scholar] [CrossRef] [PubMed]
- Shalek, A.K.; Satija, R.; Adiconis, X.; Gertner, R.S.; Gaublomme, J.T.; Raychowdhury, R.; Schwartz, S.; Yosef, N.; Malboeuf, C.; Lu, D.; et al. Single-cell transcriptomics reveals bimodality in expression and splicing in immune cells. Nature 2013, 498, 236–240. [Google Scholar] [CrossRef]
- Fan, Y.; Ma, X. Gene regulatory network inference using 3d convolutional neural network. In Proceedings of the the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 99–106. [Google Scholar]
- Shu, H.; Zhou, J.; Lian, Q.; Li, H.; Zhao, D.; Zeng, J.; Ma, J. Modeling gene regulatory networks using neural network architectures. Nat. Comput. Sci. 2021, 1, 491–501. [Google Scholar] [CrossRef]
- Lages, J.; Shepelyansky, D.L.; Zinovyev, A. Inferring hidden causal relations between pathway members using reduced Google matrix of directed biological networks. PLoS ONE 2018, 13, e0190812. [Google Scholar] [CrossRef]
- Badsha, M.B.; Fu, A.Q. Learning causal biological networks with the principle of Mendelian randomization. Front. Genet. 2019, 10, 454043. [Google Scholar] [CrossRef]
- Hoyer, P.; Janzing, D.; Mooij, J.M.; Peters, J.; Schölkopf, B. Nonlinear causal discovery with additive noise models. Adv. Neural Inf. Process. Syst. 2008, 21, 689–696. [Google Scholar]
- Ji, J.; Wei, H.; Liu, C. An artificial bee colony algorithm for learning Bayesian networks. Soft Comput. 2013, 17, 983–994. [Google Scholar] [CrossRef]
- Shimizu, S.; Hoyer, P.O.; Hyvärinen, A.; Kerminen, A.; Jordan, M. A linear non-Gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 2006, 7, 2003–2030. [Google Scholar]
- Wei, X.; Zhang, Y.; Wang, C. Bayesian Network Structure Learning Method Based on Causal Direction Graph for Protein Signaling Networks. Entropy 2022, 24, 1351. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ng, I.; Gong, D.; Liu, Y.; Abbasnejad, E.; Gong, M.; Zhang, K.; Shi, J.Q. Truncated Matrix Power Iteration for Differentiable DAG Learning. Adv. Neural Inf. Process. Syst. 2022, 35, 18390–18402. [Google Scholar]
- Gao, M.; Tai, W.M.; Aragam, B. Optimal estimation of Gaussian DAG models. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Virtual, 28–30 March 2022; pp. 8738–8757. [Google Scholar]
- Yu, Y.; Chen, J.; Gao, T.; Yu, M. DAG-GNN: DAG structure learning with graph neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 7154–7163. [Google Scholar]
- Lu, Y.; Liu, J.; Ji, J.; Lv, H.; Huai, M. Brain Effective Connectivity Learning with Deep Reinforcement Learning. In Proceedings of the 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Las Vegas, NV, USA, 6–8 December 2022; pp. 1664–1667. [Google Scholar]
- Liu, J.; Ji, J.; Xun, G.; Yao, L.; Huai, M.; Zhang, A. EC-GAN: Inferring brain effective connectivity via generative adversarial networks. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 4852–4859. [Google Scholar]
- Ji, J.; Liu, J.; Han, L.; Wang, F. Estimating Effective Connectivity by Recurrent Generative Adversarial Networks. IEEE Trans. Med. Imaging 2021, 40, 3326–3336. [Google Scholar] [CrossRef]
- Friston, K.J.; Kahan, J.; Biswal, B.; Razi, A. A DCM for resting state fMRI. Neuroimage 2014, 94, 396–407. [Google Scholar] [CrossRef]
- Zheng, X.; Aragam, B.; Ravikumar, P.K.; Xing, E.P. Dags with no tears: Continuous optimization for structure learning. Adv. Neural Inf. Process. Syst. 2018, 31, 9492–9503. [Google Scholar]
- Liu, J.; Ji, J.; Zhang, A.; Liang, P. An ant colony optimization algorithm for learning brain effective connectivity network from fMRI data. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shenzhen, China, 15–18 December 2016; pp. 360–367. [Google Scholar]
- Ji, J.; Liu, J.; Liang, P.; Zhang, A. Learning effective connectivity network structure from fMRI data based on artificial immune algorithm. PLoS ONE 2016, 11, e0152600. [Google Scholar] [CrossRef]
- Zhu, S.; Ng, I.; Chen, Z. Causal discovery with reinforcement learning. arXiv 2019, arXiv:1906.04477. [Google Scholar]
- Baek, M.; DiMaio, F.; Anishchenko, I.; Dauparas, J.; Ovchinnikov, S.; Lee, G.R.; Wang, J.; Cong, Q.; Kinch, L.N.; Schaeffer, R.D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. [Google Scholar] [CrossRef]
- Li, G.; Liu, Y.; Zheng, Y.; Li, D.; Liang, X.; Chen, Y.; Cui, Y.; Yap, P.T.; Qiu, S.; Zhang, H.; et al. Large-scale dynamic causal modeling of major depressive disorder based on resting-state functional magnetic resonance imaging. Hum. Brain Mapp. 2020, 41, 865–881. [Google Scholar] [CrossRef] [PubMed]
- Squires, C.; Yun, A.; Nichani, E.; Agrawal, R.; Uhler, C. Causal structure discovery between clusters of nodes induced by latent factors. In Proceedings of the Conference on Causal Learning and Reasoning, PMLR, Eureka, CA, USA, 11–13 April 2022; pp. 669–687. [Google Scholar]
- Zhang, Z.; Zhang, Z.; Ji, J.; Liu, J. Amortization Transformer for Brain Effective Connectivity Estimation from fMRI Data. Brain Sci. 2023, 13, 995. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Shen, X.; Pan, W. Nonlinear causal discovery with confounders. J. Am. Stat. Assoc. 2023, 1–10. [Google Scholar] [CrossRef]
- Abazid, M.; Houmani, N.; Dorizzi, B.; Boudy, J.; Mariani, J.; Kinugawa, K. Weighted brain network analysis on different stages of clinical cognitive decline. Bioengineering 2022, 9, 62. [Google Scholar] [CrossRef]
- Chiarion, G.; Sparacino, L.; Antonacci, Y.; Faes, L.; Mesin, L. Connectivity Analysis in EEG Data: A Tutorial Review of the State of the Art and Emerging Trends. Bioengineering 2023, 10, 372. [Google Scholar] [CrossRef]
- Razi, A.; Seghier, M.L.; Zhou, Y.; McColgan, P.; Zeidman, P.; Park, H.J.; Sporns, O.; Rees, G.; Friston, K.J. Large-scale DCMs for resting-state fMRI. Netw. Neurosci. 2017, 1, 222–241. [Google Scholar] [CrossRef]
- Li, K.; Tian, Y.; Chen, H.; Ma, X.; Li, S.; Li, C.; Wu, S.; Liu, F.; Du, Y.; Su, W. Temporal Dynamic Alterations of Regional Homogeneity in Parkinson’s Disease: A Resting-State fMRI Study. Biomolecules 2023, 13, 888. [Google Scholar] [CrossRef]
- Whitaker, R.H.; Cook, J.G. Stress relief techniques: p38 MAPK determines the balance of cell cycle and apoptosis pathways. Biomolecules 2021, 11, 1444. [Google Scholar] [CrossRef]
- Dorigo, M.; Birattari, M.; Stutzle, T. Ant colony optimization. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Liang, S.; Jiao, T.; Du, W.; Qu, S. An improved ant colony optimization algorithm based on context for tourism route planning. PLoS ONE 2021, 16, e0257317. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M.; Miller, K.L.; Salimi-Khorshidi, G.; Webster, M.; Beckmann, C.F.; Nichols, T.E.; Ramsey, J.D.; Woolrich, M.W. Network modelling methods for FMRI. Neuroimage 2011, 54, 875–891. [Google Scholar] [CrossRef] [PubMed]
- Chickering, D.M. Optimal structure identification with greedy search. J. Mach. Learn. Res. 2002, 3, 507–554. [Google Scholar]
- Zhang, K.; Zhu, S.; Kalander, M.; Ng, I.; Ye, J.; Chen, Z.; Pan, L. gcastle: A python toolbox for causal discovery. arXiv 2021, arXiv:2111.15155. [Google Scholar]
| Category | Methods | Years | Category | Methods | Years |
|---|---|---|---|---|---|
| Causal Brain Network | spectral Dynamic Causal Modeling (spDCM) | 2014 [22] | Causal Protein Signaling Network | Continuous Optimization (NoTears) | 2018 [23] |
| Ant Colony Optimization (ACO) | 2016 [24] | Graph Neural Network (DAG-GNN) | 2019 [18] | ||
| Artificial Immune Algorithm (AIA) | 2016 [25] | Reinforcement Learning (RL) | 2019 [26] | ||
| Generative Adversarial Network (GAN) | 2020 [20] | Three Track Neural Network (TTNN) | 2021 [27] | ||
| Large-scale Dynamic Causal Mode (PEB) | 2020 [28] | Latent Factor Causal Models (LFCMs) | 2022 [29] | ||
| Recurrent Generative Adversarial Network (RGAN) | 2021 [21] | Truncated Matrix Power Iteration (TMPI) | 2022 [16] | ||
| Deep Reinforcement Learning (DRL) | 2022 [19] | BN with Pruning Strategies (CO-CDG) | 2022 [15] | ||
| Amortization Transformer (AT-EC) | 2023 [30] | Deconfounded Functional Structure Estimation (DeFuSE) | 2023 [31] |
| Algorithms | Parameters |
|---|---|
| NoTears [23] | = 0.3 |
| DRL [19] | |
| GES [40] | |
| DAG-GNN [18] | = 10, |
| AIA [25] | |
| ACO [24] | |
| PACO | |
| Data (v,N) | Metrics | Algorithms | ||||||
|---|---|---|---|---|---|---|---|---|
| NoTears | DRL | GES | DAG-GNN | AIA | ACO | PACO | ||
| Sim1(5,20) | Precision | 0.62 | 0.61 | 0.55 | 0.38 | 0.60 | 0.57 | 0.79 |
| Recall | 0.66 | 0.51 | 0.35 | 0.27 | 0.60 | 0.62 | 0.75 | |
| 0.64 | 0.56 | 0.45 | 0.32 | 0.60 | 0.59 | 0.77 | ||
| 3 | 4 | 5 | 6 | 4 | 3 | 2 | ||
| (s) | 2.76 | 14.12 | 5.19 | 36.12 | 1.98 | 0.79 | 0.51 | |
| Sim2 (5,50) | Precision | 0.59 | 0.62 | 0.51 | 0.35 | 0.60 | 0.56 | 0.75 |
| Recall | 0.61 | 0.52 | 0.35 | 0.35 | 0.50 | 0.62 | 0.77 | |
| 0.60 | 0.57 | 0.43 | 0.35 | 0.55 | 0.59 | 0.76 | ||
| 3 | 4 | 6 | 7 | 5 | 3 | 2 | ||
| (s) | 4.51 | 19.25 | 10.32 | 45.34 | 2.73 | 1.42 | 0.78 | |
| Sim3 (10,20) | Precision | 0.59 | 0.62 | 0.53 | 0.40 | 0.60 | 0.56 | 0.77 |
| Recall | 0.53 | 0.51 | 0.43 | 0.30 | 0.54 | 0.56 | 0.75 | |
| 0.56 | 0.56 | 0.48 | 0.35 | 0.57 | 0.56 | 0.76 | ||
| 9 | 9 | 12 | 13 | 10 | 7 | 4 | ||
| (s) | 4.12 | 17.22 | 8.91 | 39.73 | 2.36 | 1.34 | 0.68 | |
| Sim4 (10,50) | Precision | 0.57 | 0.55 | 0.49 | 0.38 | 0.60 | 0.52 | 0.75 |
| Recall | 0.55 | 0.51 | 0.45 | 0.40 | 0.52 | 0.54 | 0.75 | |
| 0.56 | 0.53 | 0.47 | 0.39 | 0.56 | 0.53 | 0.75 | ||
| 9 | 10 | 13 | 15 | 9 | 10 | 3 | ||
| (s) | 7.89 | 25.64 | 13.67 | 48.26 | 4.41 | 2.86 | 0.91 | |
| Sim5 (30,20) | Precision | 0.55 | 0.62 | 0.54 | 0.37 | 0.58 | 0.53 | 0.73 |
| Recall | 0.50 | 0.52 | 0.34 | 0.27 | 0.59 | 0.53 | 0.71 | |
| 0.53 | 0.57 | 0.44 | 0.32 | 0.59 | 0.53 | 0.72 | ||
| 17 | 15 | 19 | 23 | 14 | 17 | 9 | ||
| (s) | 7.54 | 24.33 | 14.98 | 54.66 | 4.61 | 3.64 | 1.56 | |
| Sim6 (30,50) | Precision | 0.56 | 0.63 | 0.55 | 0.39 | 0.61 | 0.54 | 0.75 |
| Recall | 0.56 | 0.61 | 0.35 | 0.31 | 0.54 | 0.56 | 0.73 | |
| 0.56 | 0.62 | 0.45 | 0.35 | 0.58 | 0.55 | 0.74 | ||
| 15 | 13 | 18 | 21 | 15 | 16 | 7 | ||
| (s) | 9.14 | 30.55 | 7.16 | 50.37 | 5.69 | 4.79 | 1.95 | |
| Sim7 (50,20) | Precision | 0.55 | 0.61 | 0.48 | 0.36 | 0.62 | 0.60 | 0.73 |
| Recall | 0.53 | 0.51 | 0.44 | 0.27 | 0.52 | 0.62 | 0.71 | |
| 0.54 | 0.56 | 0.46 | 0.31 | 0.57 | 0.61 | 0.72 | ||
| 36 | 34 | 43 | 48 | 33 | 30 | 19 | ||
| (s) | 13.36 | 45.62 | 18.96 | 75.33 | 5.97 | 5.65 | 2.73 | |
| Sim8 (50,50) | Precision | 0.54 | 0.59 | 0.51 | 0.38 | 0.63 | 0.57 | 0.72 |
| Recall | 0.52 | 0.53 | 0.32 | 0.27 | 0.54 | 0.61 | 0.70 | |
| 0.53 | 0.56 | 0.43 | 0.32 | 0.58 | 0.59 | 0.71 | ||
| 37 | 34 | 41 | 49 | 33 | 32 | 21 | ||
| (s) | 16.64 | 57.89 | 23.67 | 86.51 | 7.15 | 7.11 | 3.15 | |
| Sim9 (100,20) | Precision | 0.52 | 0.56 | 0.55 | 0.38 | 0.61 | 0.55 | 0.71 |
| Recall | 0.52 | 0.54 | 0.35 | 0.42 | 0.52 | 0.53 | 0.71 | |
| 0.52 | 0.55 | 0.45 | 0.40 | 0.57 | 0.54 | 0.71 | ||
| 68 | 60 | 79 | 86 | 57 | 61 | 48 | ||
| (s) | 32.76 | 98.75 | 41.63 | 139.87 | 10.36 | 10.88 | 5.87 | |
| Sim10 (100,50) | Precision | 0.49 | 0.51 | 0.45 | 0.35 | 0.58 | 0.54 | 0.71 |
| Recall | 0.51 | 0.51 | 0.47 | 0.33 | 0.60 | 0.54 | 0.69 | |
| 0.50 | 0.51 | 0.46 | 0.34 | 0.59 | 0.54 | 0.70 | ||
| 71 | 71 | 77 | 90 | 55 | 60 | 46 | ||
| (s) | 42.36 | 135.5 | 52.36 | 159.62 | 16.98 | 13.67 | 7.66 | |
| Algorithms | Precision | Recall | SHD | Time (s) | |
|---|---|---|---|---|---|
| NoTears | 0.47 | 0.64 | 0.54 | 9 | 9.20 |
| DRL | 0.57 | 0.73 | 0.64 | 6 | 16.10 |
| GES | 0.38 | 0.73 | 0.50 | 13 | 2.91 |
| DAG-GNN | 0.33 | 0.45 | 0.38 | 13 | 22.60 |
| AIA | 0.64 | 0.64 | 0.64 | 5 | 1.35 |
| ACO | 0.82 | 0.82 | 0.82 | 3 | 0.98 |
| PACO | 0.83 | 0.91 | 0.87 | 2 | 0.49 |
| Algorithms | Precision | Recall | SHD | Time (s) | |
|---|---|---|---|---|---|
| NoTears | 0.44 | 0.47 | 0.45 | 15 | 35.30 |
| DRL | 0.47 | 0.47 | 0.47 | 15 | 63.20 |
| GES | 0.20 | 0.41 | 0.27 | 30 | 11.60 |
| DAG-GNN | 0.44 | 0.41 | 0.42 | 17 | 122.70 |
| AIA | 0.19 | 0.35 | 0.24 | 31 | 3.80 |
| ACO | 0.25 | 0.47 | 0.33 | 26 | 3.10 |
| PACO | 0.53 | 0.53 | 0.53 | 15 | 1.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhai, J.; Ji, J.; Liu, J. Learning Causal Biological Networks with Parallel Ant Colony Optimization Algorithm. Bioengineering 2023, 10, 909. https://doi.org/10.3390/bioengineering10080909
Zhai J, Ji J, Liu J. Learning Causal Biological Networks with Parallel Ant Colony Optimization Algorithm. Bioengineering. 2023; 10(8):909. https://doi.org/10.3390/bioengineering10080909
Chicago/Turabian StyleZhai, Jihao, Junzhong Ji, and Jinduo Liu. 2023. "Learning Causal Biological Networks with Parallel Ant Colony Optimization Algorithm" Bioengineering 10, no. 8: 909. https://doi.org/10.3390/bioengineering10080909
APA StyleZhai, J., Ji, J., & Liu, J. (2023). Learning Causal Biological Networks with Parallel Ant Colony Optimization Algorithm. Bioengineering, 10(8), 909. https://doi.org/10.3390/bioengineering10080909





