Selection of Bifurcated Grafts’ Dimensions during Aorto-Iliac Vascular Reconstruction Based on Their Hemodynamic Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Setup
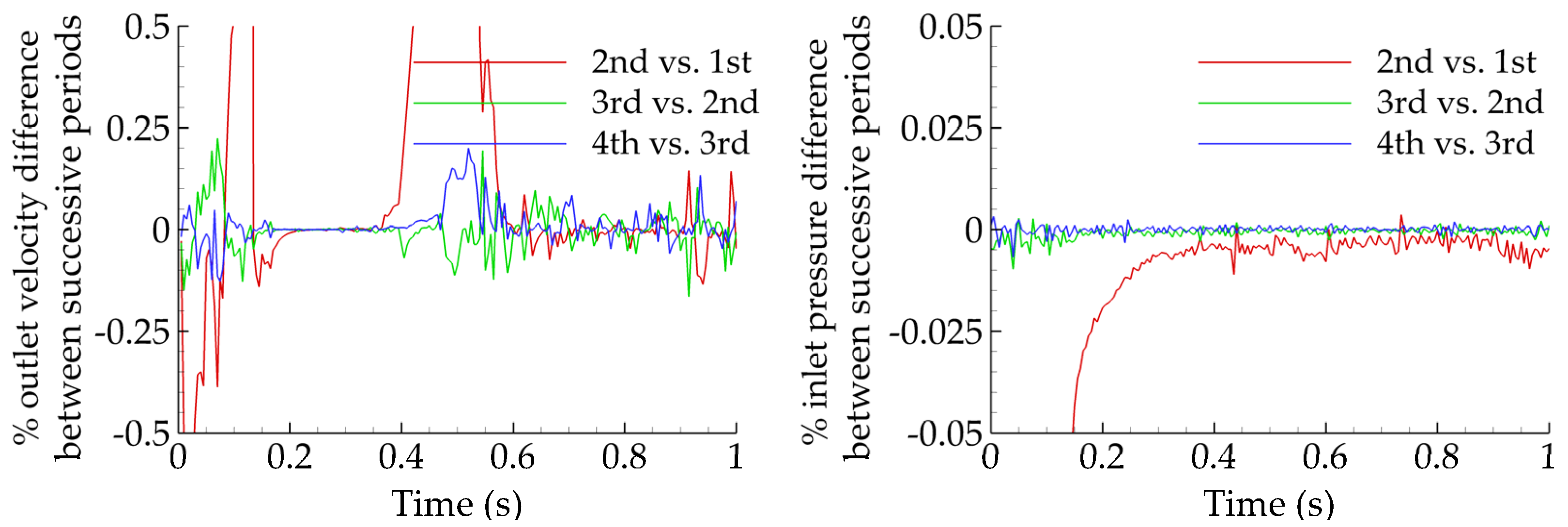
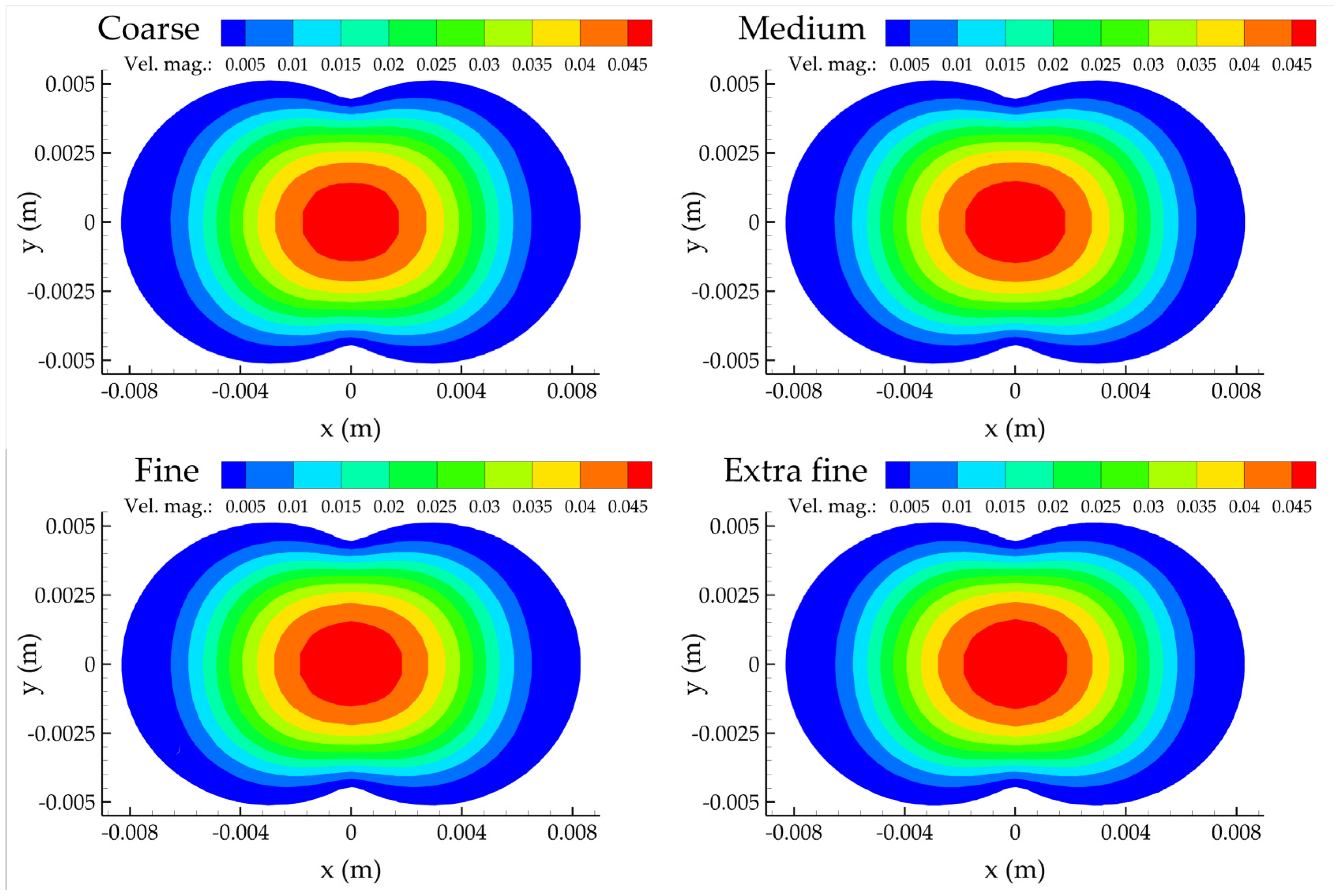
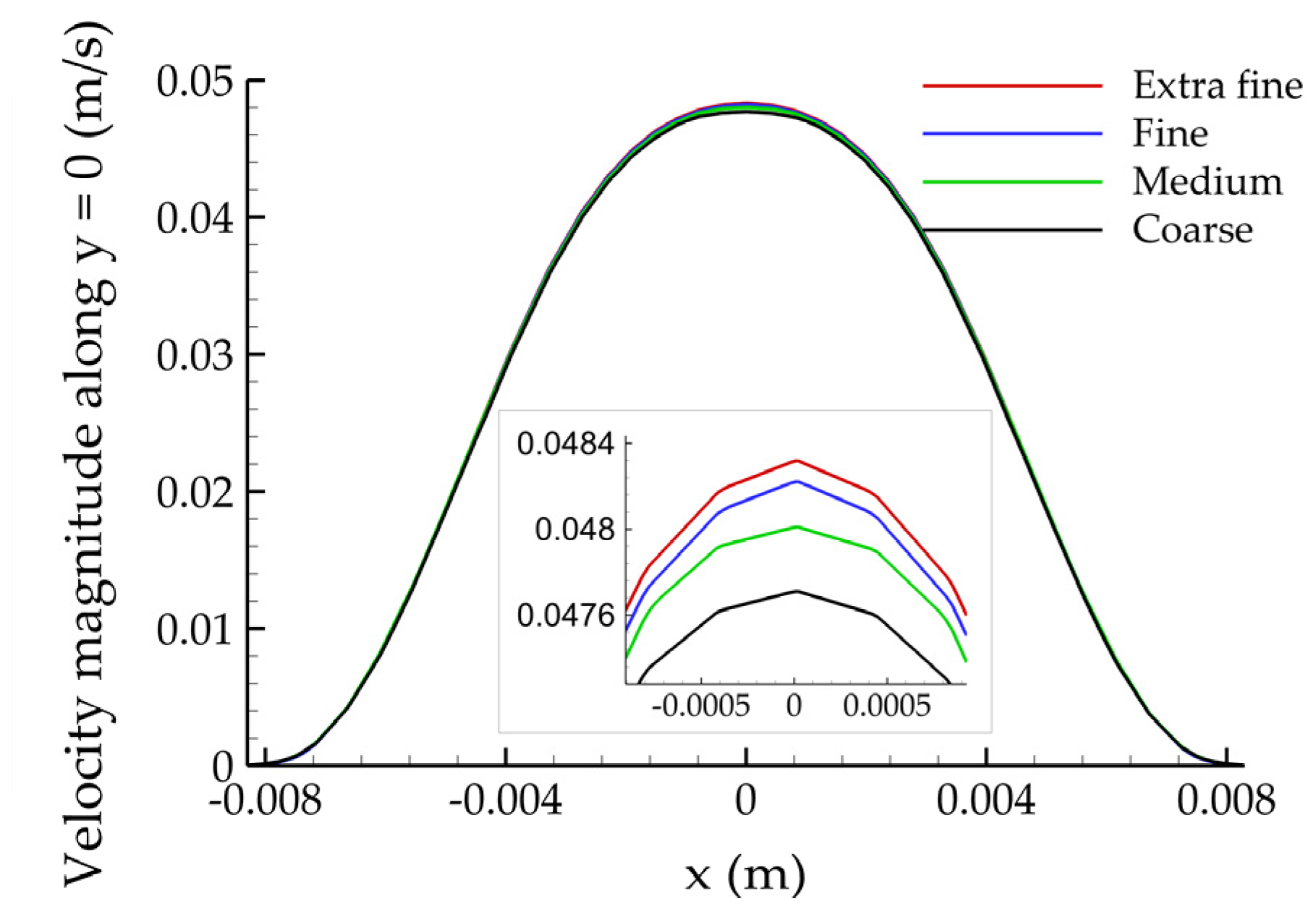
2.2. Mesh Generation and Convergence
2.3. Statistical Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| U | fluid velocity |
| P | fluid pressure |
| fluid density | |
| stress tensor | |
| shear rate | |
| μ | dynamic viscosity |
| T | period of cardiac cycle |
| CY | Carreau-Yasuda |
| ω | angular frequency |
| Bessel function | |
| Re | Reynolds number |
| α | Womersley number |
| WSS | Wall Shear Stress |
| TAWSS | Time Average Wall Shear Stress |
| OSI | Oscillatory Shear Index |
| RRT | Relative Residence Time |
| BL | Boundary Layer |
| L | distance between renal and femoral arteries |
| l | distance between femoral arteries and midline |
| AIC | Akaike Information Criterion |
| LAD | Least Absolute Deviations |
| MAD | Median Absolute Deviation |
| GoF | Goodness of Fit |
| GoFφ | Goodness of Fit based only on φ |
| GoFD | Goodness of Fit based only on D |
References
- Wanhainen, A.; Verzini, F.; Van Herzeele, I.; Allaire, E.; Bown, M.; Cohnert, T.; Dick, F.; van Herwaarden, J.; Karkos, C.; Koelemay, M.; et al. Editor’s Choice-European Society for Vascular Surgery (ESVS) 2019 Clinical Practice Guidelines on the Management of Abdominal Aorto-iliac Artery Aneurysms. Eur. J. Vasc. Endovasc. Surg. 2019, 57, 8–93. [Google Scholar] [CrossRef] [PubMed]
- Conte, M.S.; Bradbury, A.W.; Kolh, P.; White, J.V.; Dick, F.; Fitridge, R.; Mills, J.L.; Ricco, J.-B.; Suresh, K.R.; Murad, M.H.; et al. Global Vascular Guidelines on the Management of Chronic Limb-Threatening Ischemia. Eur. J. Vasc. Endovasc. Surg. 2019, 58, S1–S109.e33. [Google Scholar] [CrossRef] [PubMed]
- Norgren, L.; Hiatt, W.R.; Dormandy, J.A.; Nehler, M.R.; Harris, K.A.; Fowkes, F.G.R. on behalf of the TASC II Working Group. Inter-Society Consensus for the Management of Peripheral Arterial Disease (TASC II). J. Vasc. Surg. 2007, 45, S5–S67. [Google Scholar] [CrossRef]
- Georgakarakos, E.; Xenakis, A.; Georgiadis, G.S.; Argyriou, C.; Manopoulos, C.; Tsangaris, S.; Lazarides, M.K. Computational estimation of the influence of the main body-to-iliac limb length ratio on the displacement forces acting on an aortic endograft. Theoretical application to Bolton Treovance® Abdominal Stent-Graft. Int. Angiol. 2014, 33, 480–484. [Google Scholar]
- Georgakarakos, E.; Xenakis, A.; Georgiadis, G.S. Estimating the hemodynamic influence of variable main body-to-iliac limb length ratios in aortic endografts. Int. Angiol. 2018, 37, 41–45. [Google Scholar] [CrossRef]
- Kontopodis, N.; Tzirakis, K.; Stylianou, F.; Vavourakis, V.; Patou, G.M.; Ioannou, C.V. Should the proximal part of a bifurcated aortic graft be kept as short as possible? A computational study elucidates onaortic graft hemodynamics for various main body lengths. Ann. Vasc. Surg. 2022, 84, 344–353. [Google Scholar] [CrossRef] [PubMed]
- Georgakarakos, E.; Argyriou, C.; Schoretsanitis, N.; Ioannou, C.V.; Kontopodis, N.; Morgan, R.; Tsetis, D. Geometrical factors influencing the hemodynamic behavior of the AAA stent grafts: Essentials for the clinician. Cardiovasc. Interv. Radiol. 2014, 37, 1420–1429. [Google Scholar] [CrossRef] [PubMed]
- West, C.A., Jr.; Johnson, L.W.; Doucet, L.; Caldito, G.; Heldman, M.; Szarvas, T.; Speirs, R.D.; Carson, S. A contemporary experience of open aortic reconstruction in patients with chronic atherosclerotic occlusion of the abdominal aorta. J. Vasc. Surg. 2010, 52, 1164–1172. [Google Scholar] [CrossRef]
- Arzani, A. Accounting for residence-time in blood rheology models: Do we really need non-Newtonian blood flow modelling in large arteries? J. R. Soc. Interface 2018, 15, 20180486. [Google Scholar] [CrossRef]
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef]
- Weddell, J.C.; Kwack, J.; Imoukhuede, P.I.; Masud, A. Hemodynamic Analysis in an Idealized Artery Tree: Differences in Wall Shear Stress between Newtonian and Non-Newtonian Blood Models. PLoS ONE 2015, 10, e0124575. [Google Scholar] [CrossRef]
- Fisher, C.; Rossmann, J.S. Effect of non-newtonian behavior on hemodynamics of cerebral aneurysms. J. Biomech. Eng. 2009, 131, 091004. [Google Scholar] [CrossRef]
- Tzirakis, K.; Kamarianakis, Y.; Metaxa, E.; Kontopodis, N.; Ioannou, C.V.; Papaharilaou, Y. A robust approach for exploring hemodynamics and thrombus growth associations in abdominal aortic aneurysms. Med. Biol. Eng. Comput. 2017, 55, 1493–1506. [Google Scholar] [CrossRef]
- Valant, A.Z.; Ziberna, L.; Papaharilaou, Y.; Anayiotos, A.; Georgiou, G.C. The influence of temperature on rheological properties of blood mixtures with different volume expanders-implications in numerical arterial hemodynamics simulations. Rheol. Acta. 2011, 50, 389–402. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Tzirakis, K.; Kamarianakis, Y.; Kontopodis, N.; Ioannou, C.V. Classification of Blood Rheological Models through an Idealized Symmetrical Bifurcation. Symmetry 2023, 15, 630. [Google Scholar] [CrossRef]
- Pedley, T.J. The Fluid Mechanics of Large Blood Vessels; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Olufsen, M.S.; Peskin, C.S.; Kim, W.Y.; Pedersen, E.M.; Nadim, A.; Larsen, J. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann. Biomed. Eng. 2000, 28, 1281–1299. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef]
- He, X.; Ku, D.N. Pulsatile flow in the human left coronary artery bifurcation: Average conditions. J. Biomech. Eng. 1996, 118, 74–82. [Google Scholar] [CrossRef]
- Himburg, H.A.; Grzybowski, D.M.; Hazel, A.L.; LaMack, J.A.; Li, X.M.; Friedman, M.H. Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. Am. J. Physiol. Heart. Circ. Physiol. 2004, 286, H1916–H1922. [Google Scholar] [CrossRef]
- Malek, A.M.; Alper, S.L.; Izumo, S. Hemodynamic shear stress and its role in atherosclerosis. JAMA 1999, 282, 2035–2042. [Google Scholar] [CrossRef]
- Morbiducci, U.; Gallo, D.; Ponzini, R.; Massai, D.; Antiga, L.; Montevecchi, F.M.; Redaelli, A. Quantitative analysis of bulk flow in imagebased hemodynamic models of the carotid bifurcation: The influence of outflow conditions as test case. Ann. Biomed. Eng. 2010, 38, 3688–3705. [Google Scholar] [CrossRef] [PubMed]
- Suess, T.; Anderson, J.; Danielson, L.; Pohlson, K.; Remund, T.; Blears, E.; Gent, S.; Kelly, P. Examination of near-wall hemodynamic parameters in the renal bridging stent of various stent graft configurations for repairing visceral branched aortic aneurysms. J. Vasc. Surg. 2011, 64, 788–796. [Google Scholar] [CrossRef] [PubMed]
- Tran, K.; Feliciano, K.B.; Yang, W.; Schwarz, E.L.; Marsden, A.L.; Dalman, R.L.; Lee, J.T. Patient-specific changes in aortic hemodynamics is associated with thrombotic risk after fenestrated endovascular aneurysm repair with large diameter endografts. JVS Vasc. Sci. 2022, 3, 219–231. [Google Scholar] [CrossRef] [PubMed]
- De Santis, G.; Mortier, P.; De Beule, M.; Segers, P.; Verdonck, P.; Verhegghe, B. Patient-specific computational fluid dynamics: Structured mesh generation from coronary angiography. Med. Biol. Eng. Comput. 2010, 48, 371–380. [Google Scholar] [CrossRef] [PubMed]
- Burnham, K.P.; Anderson, J.R. Model Election and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Barton, K. MuMIN: Multi-Model Inference, R-Rackage Version 0.12.0. 2009. Available online: https://www.semanticscholar.org/paper/MuMIn-%3A-multi-model-inference%2C-R-package-version-Barton/af1086127738956d63fce81690819de979b6dfcf (accessed on 31 May 2023).
- Koenker, R. Quantile Regression (Econometric Society Monographs); Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Sheather, S.J. A Modern Approach to Regression with R; Springer Texts in Statistics; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Tzirakis, K.; Kamarianakis, Y.; Kontopodis, N.; Ioannou, C.V. The Effect of Blood Rheology and Inlet Boundary Conditions on Realistic Abdominal Aortic Aneurysms under Pulsatile Flow Conditions. Bioengineering 2023, 10, 272. [Google Scholar] [CrossRef] [PubMed]
- Bosch, J.A.T.; Waasdorp, E.J.; de Vries, J.P.; Moll, F.L.; Teijink, J.A.; van Herwaarden, J.A. The durability of endovascular repair of para-anastomotic aneurysms after previous open aortic reconstruction. J. Vasc. Surg. 2011, 54, 1571–1578. [Google Scholar] [CrossRef]
- Wu, Z.; Xu, L.; Raithel, D.; Qu, L. Endovascular repair of proximal para-anastomotic aneurysms after previous open abdominal aortic aneurysm reconstruction. Vascular 2016, 24, 227–232. [Google Scholar] [CrossRef]
- Krievins, D.; Krämer, A.; Savlovskis, J.; Oszkinis, G.; Debus, E.S.; Oberhuber, A.; Zarins, C.K. Initial Clinical Experience Using the Low-Profile Altura Endograft System with Double D-Shaped Proximal Stents for Endovascular Aneurysm Repair. J. Endovasc. Ther. 2018, 25, 379–386. [Google Scholar] [CrossRef]
- Kontopodis, N.; Galanakis, N.; Tzartzalou, I.; Tavlas, E.; Georgakarakos, E.; Dimopoulos, I.; Tsetis, D.; Ioannou, C.V. An update on the improvement of patient eligibility with the use of new generation endografts for the treatment of abdominal aortic aneurysms. Expert Rev. Med. Devices 2020, 17, 1231–1238. [Google Scholar] [CrossRef]
- Georgakarakos, E.; Papatheodorou, N.; Argyriou, C.; Tasopoulou, K.M.; Doukas, D.; Georgiadis, G.S. An update on the ovation abdominal stent graft for the treatment of abdominal aortic aneurysms: Current evidence and future perspectives. Expert Rev. Med. Devices 2020, 17, 1249–1256. [Google Scholar] [CrossRef]
- İşcan, H.Z.; Karahan, M.; Akkaya, B.B.; Başar, V.; Aşkın, G.; Kubat, E.; Aytekin, B.; Ünal, E.U. Long-term results of endovascular intervention with unibody bifurcation endograft for elective abdominal aortic aneurysm management. Rev. Cardiovasc. Med. 2021, 22, 453–459. [Google Scholar] [CrossRef]
- Van Prehn, J.; Schlösser, F.J.; Muhs, B.E.; Verhagen, H.J.; Moll, F.L.; van Herwaarden, J.A. Oversizing of aortic stent grafts for abdominal aneurysm repair: A systematic review of the benefits and risks. Eur. J. Vasc. Endovasc. Surg. 2009, 38, 42–53. [Google Scholar] [CrossRef]
- Liu, M.Y.; Jiao, Y.; Liu, J.; Zhang, S.; Li, W. Hemodynamic Parameters Predict In-stent Thrombosis After Multibranched Endovascular Repair of Complex Abdominal Aortic Aneurysms: A Retrospective Study of Branched Stent-Graft Thrombosis. Front. Cardiovasc. Med. 2021, 8, 654412. [Google Scholar] [CrossRef]
- Gholampour, S.; Mehrjoo, S. Effect of bifurcation in the hemodynamic changes and rupture risk of small intracranial aneurysm. Neurosurg. Rev. 2021, 44, 1703–1712. [Google Scholar] [CrossRef]
- Hajirayat, K.; Gholampour, S.; Sharifi, I.; Bizari, D. Biomechanical Simulation to Compare the Blood Hemodynamics and Cerebral Aneurysm Rupture Risk in Patients with Different Aneurysm Necks. J. Appl. Mech. Tech. Phys. 2017, 58, 968–974. [Google Scholar] [CrossRef]
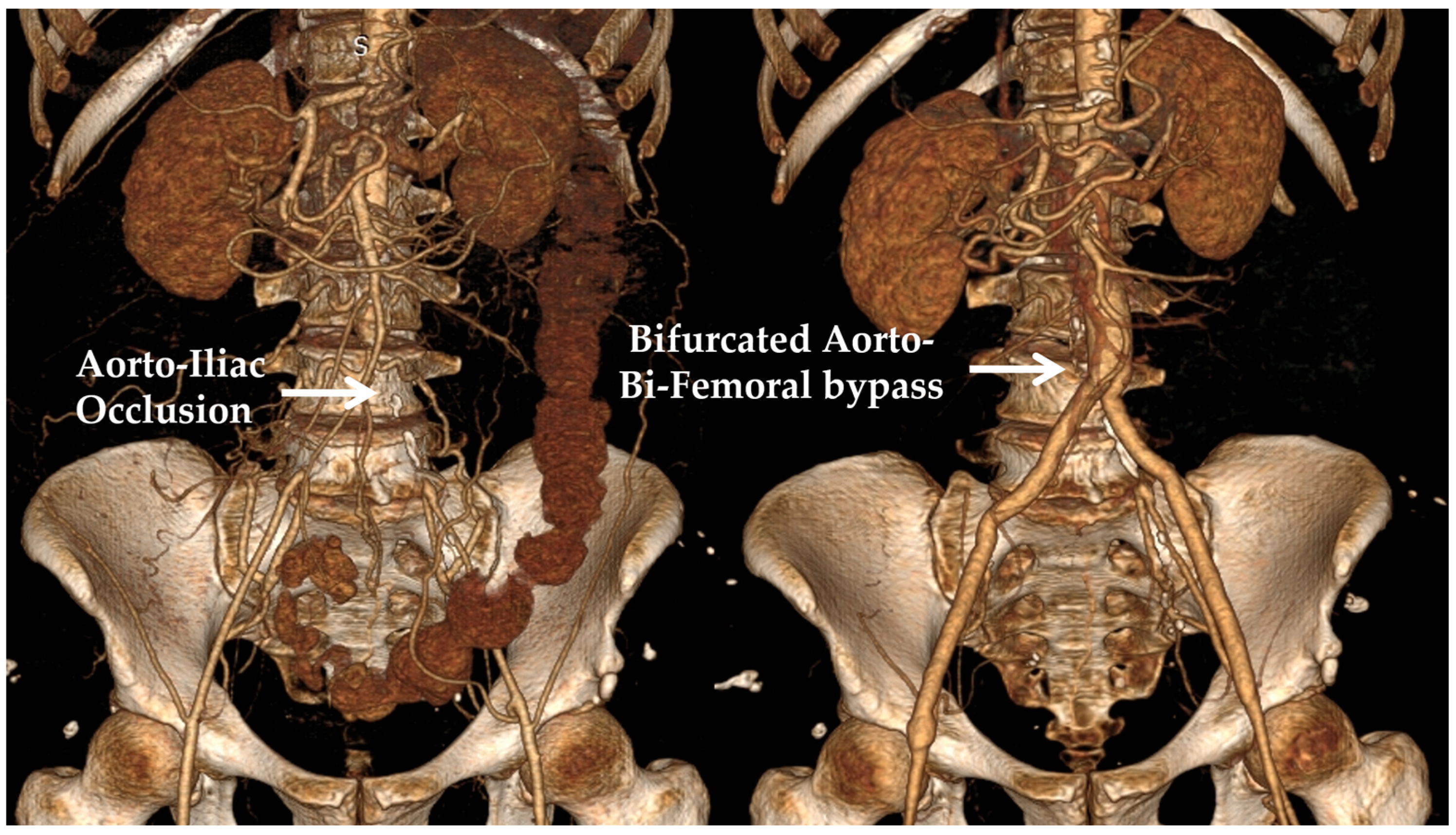




| Inlet Diameter, D (mm) | Mean Re, Remean | Max Re, Remax | Womersley Number, α |
|---|---|---|---|
| 12 | 237 | 1055 | 8.29 |
| 14 | 277 | 1230 | 9.68 |
| 16 | 316 | 1406 | 11.06 |
| 18 | 356 | 1582 | 12.44 |
| 20 | 395 | 1758 | 13.82 |
| 22 | 435 | 1934 | 15.21 |
| 24 | 474 | 2110 | 16.58 |
| Mesh | # of Elements | BL Levels | BL min (mm) |
|---|---|---|---|
| Coarse | 151,200 | 5 | 0.1504 |
| Medium | 252,720 | 9 | 0.0538 |
| Fine | 512,730 | 14 | 0.0203 |
| Extra fine | 1,041,692 | 21 | 0.0051 |
| Mesh | TAWSS Result (Pa) Error (%) | OSI Result Error (%) | RRT Result (Pa−1) Error (%) | |||
|---|---|---|---|---|---|---|
| Coarse | 0.604379 | 5.79% | 0.152441 | 7.36% | 3.350175 | −3.40% |
| Medium | 0.630215 | 1.76% | 0.160095 | 2.71% | 3.273128 | −1.02% |
| Fine | 0.639206 | 0.36% | 0.163306 | 0.76% | 3.245296 | −0.16% |
| Extra fine | 0.641492 | - | 0.164552 | - | 3.240018 | - |
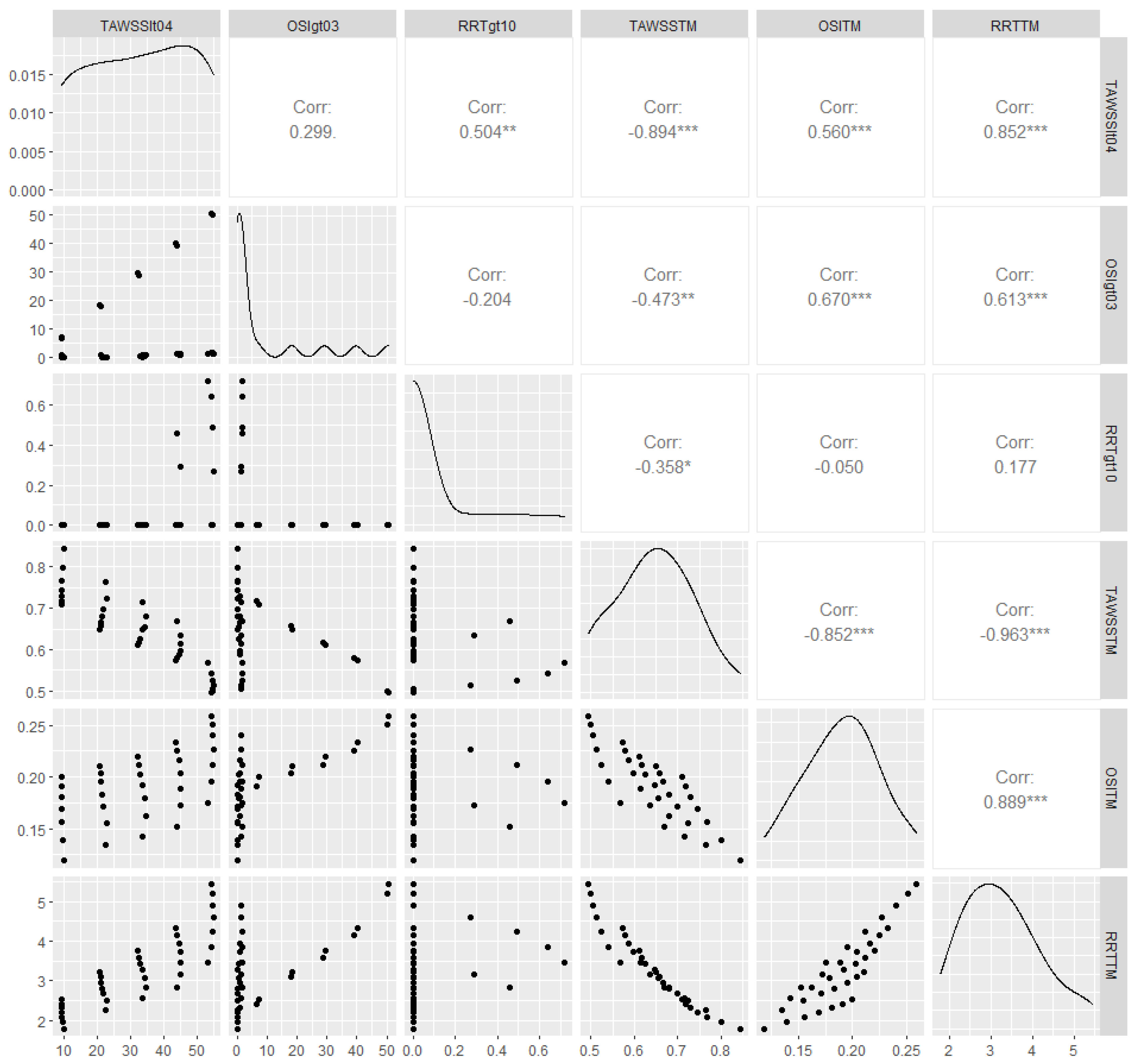
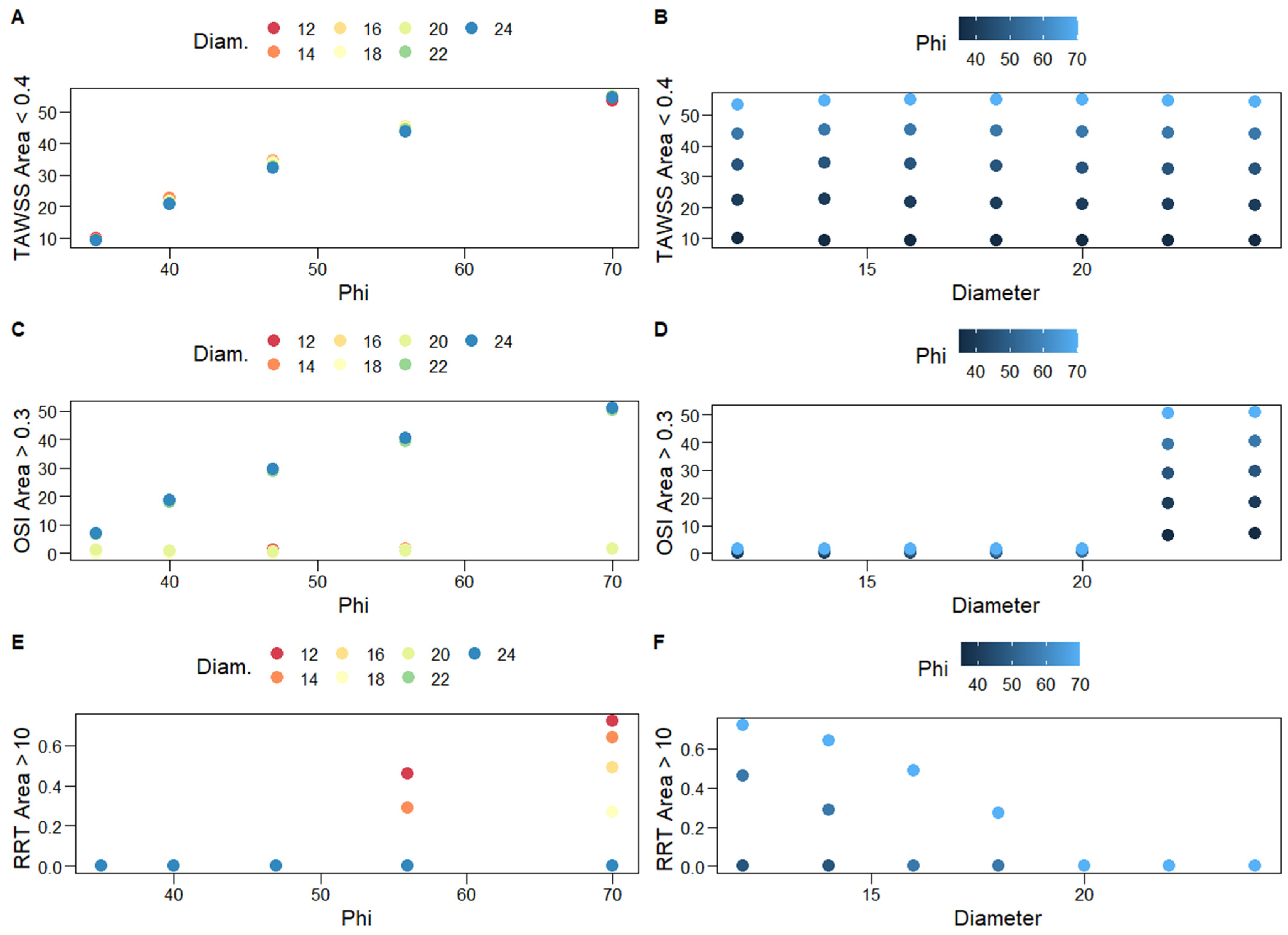
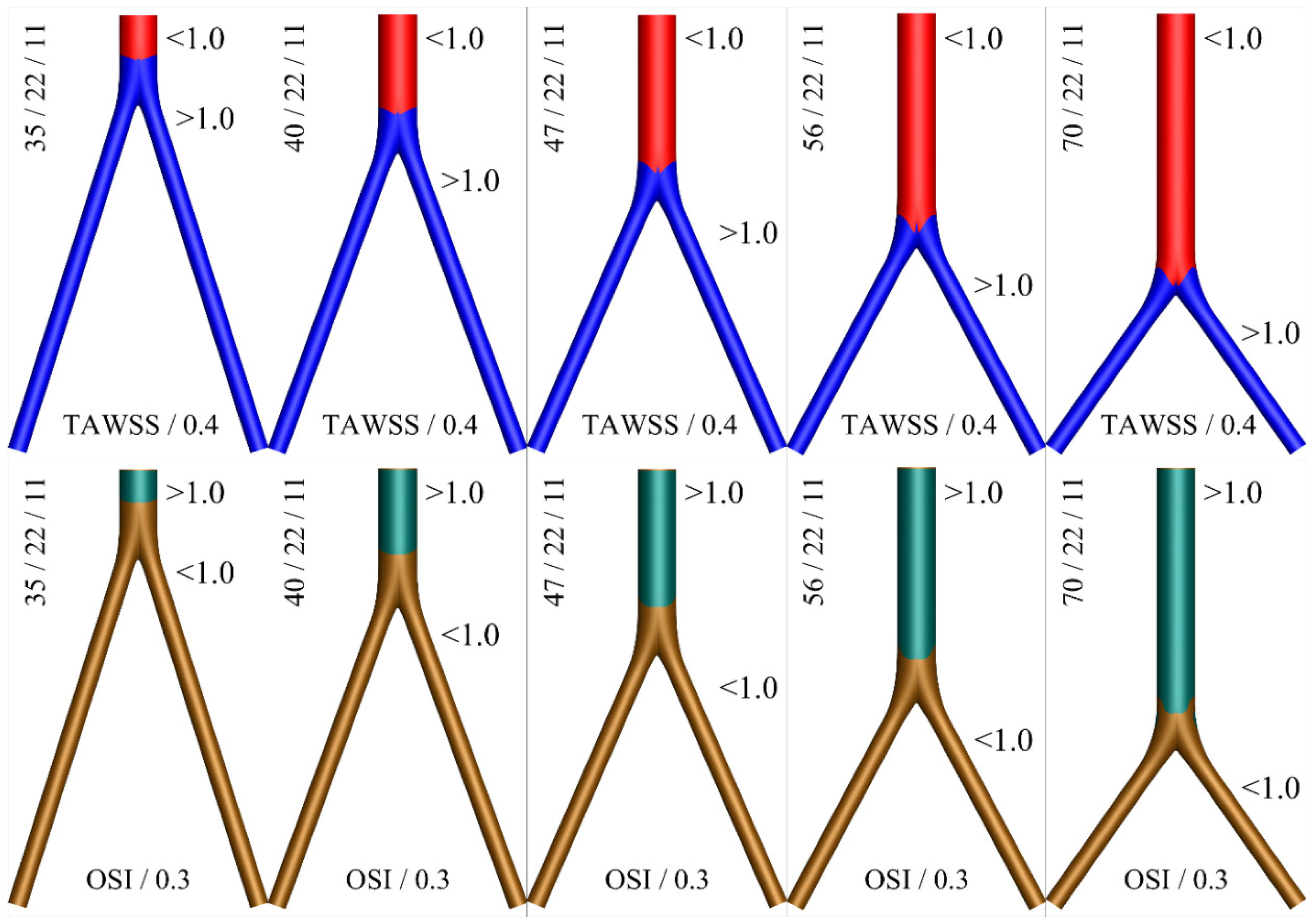
| φ | D/d | TAWSS TM | % Area with TAWSS < 0.4 Pa | OSI TM | % Area with OSI > 0.3 | RRT TM | % Area with RRT > 10 Pa−1 |
|---|---|---|---|---|---|---|---|
| 35° | 12/6 mm | 0.845 | 9.87 | 0.119 | 0.00 | 1.792 | 0.00 |
| 14/7 mm | 0.799 | 9.42 | 0.139 | 0.00 | 1.955 | 0.00 | |
| 16/8 mm | 0.767 | 9.22 | 0.156 | 0.00 | 2.087 | 0.00 | |
| 18/9 mm | 0.745 | 9.18 | 0.169 | 0.00 | 2.204 | 0.00 | |
| 20/10 mm | 0.729 | 9.15 | 0.181 | 1.07 | 2.315 | 0.00 | |
| 22/11 mm | 0.718 | 9.13 | 0.191 | 6.64 | 2.416 | 0.00 | |
| 24/12 mm | 0.709 | 9.12 | 0.200 | 7.08 | 2.522 | 0.00 | |
| 40° | 12/6 mm | 0.764 | 22.54 | 0.135 | 0.31 | 2.270 | 0.00 |
| 14/7 mm | 0.724 | 22.74 | 0.155 | 0.00 | 2.500 | 0.00 | |
| 16/8 mm | 0.698 | 21.79 | 0.171 | 0.00 | 2.668 | 0.00 | |
| 18/9 mm | 0.679 | 21.27 | 0.183 | 0.00 | 2.813 | 0.00 | |
| 20/10 mm | 0.666 | 21.02 | 0.195 | 0.81 | 2.959 | 0.00 | |
| 22/11 mm | 0.657 | 20.88 | 0.204 | 17.95 | 3.091 | 0.00 | |
| 24/12 mm | 0.650 | 20.81 | 0.211 | 18.53 | 3.216 | 0.00 | |
| 47° | 12/6 mm | 0.716 | 33.72 | 0.143 | 1.14 | 2.554 | 0.00 |
| 14/7 mm | 0.679 | 34.53 | 0.162 | 0.91 | 2.833 | 0.00 | |
| 16/8 mm | 0.655 | 34.18 | 0.179 | 0.45 | 3.073 | 0.00 | |
| 18/9 mm | 0.648 | 33.56 | 0.192 | 0.00 | 3.268 | 0.00 | |
| 20/10 mm | 0.626 | 32.94 | 0.203 | 0.54 | 3.436 | 0.00 | |
| 22/11 mm | 0.617 | 32.54 | 0.212 | 28.73 | 3.594 | 0.00 | |
| 24/12 mm | 0.611 | 32.31 | 0.220 | 29.57 | 3.746 | 0.00 | |
| 56° | 12/6 mm | 0.669 | 44.04 | 0.152 | 1.53 | 2.844 | 0.46 |
| 14/7 mm | 0.635 | 45.13 | 0.172 | 1.50 | 3.168 | 0.29 | |
| 16/8 mm | 0.613 | 45.13 | 0.189 | 1.34 | 3.466 | 0.00 | |
| 18/9 mm | 0.597 | 44.93 | 0.204 | 1.03 | 3.728 | 0.00 | |
| 20/10 mm | 0.587 | 44.56 | 0.216 | 0.90 | 3.949 | 0.00 | |
| 22/11 mm | 0.579 | 44.13 | 0.225 | 39.25 | 4.140 | 0.00 | |
| 24/12 mm | 0.573 | 43.75 | 0.233 | 40.22 | 4.322 | 0.00 | |
| 70° | 12/6 mm | 0.567 | 53.40 | 0.175 | 1.55 | 3.447 | 0.72 |
| 14/7 mm | 0.541 | 54.51 | 0.195 | 1.59 | 3.850 | 0.64 | |
| 16/8 mm | 0.524 | 54.90 | 0.212 | 1.58 | 4.231 | 0.49 | |
| 18/9 mm | 0.512 | 54.95 | 0.227 | 1.50 | 4.587 | 0.27 | |
| 20/10 mm | 0.504 | 54.85 | 0.240 | 1.50 | 4.910 | 0.00 | |
| 22/11 mm | 0.499 | 54.67 | 0.251 | 50.31 | 5.202 | 0.00 | |
| 24/12 mm | 0.495 | 54.42 | 0.259 | 50.77 | 5.445 | 0.00 |
| TAWSS TM | % Area with TAWSS < 0.4 Pa | OSI TM | % Area with OSI > 0.3 | |
|---|---|---|---|---|
| β0 | 1.634 (0.179) | −94.764 (8.472) | −0.072 (0.026) | 150.991 (49.801) |
| β1 | −0.036 (0.010) | - | 1.561 (0.218) | −16.064 (4.581) |
| β2 | −0.017 (0.005) | 1.946 (0.307) | 0.117 (0.032) | −1.364 (0.776) |
| β3 | 0.592 (0.209) | −12.016 (7.247) | −0.281 (0.046) | 377.692 (104.973) |
| β4 | 0.080 (0.040) | −26.717 (2.327) | - | - |
| β5 | 0.135 (0.087) | 6.466 (4.625) | 0.022 (0.016) | 97.158 (50.264) |
| ΔAICc | 0 | 2.537 | 2.708 | 2.695 |
| GoF | 0.982 | 0.973 | 0.994 | 0.778 |
| GoFφ | 0.811 | 0.962 | 0.302 | 0.043 |
| GOFD | 0.104 | 0.021 | 0.630 | 0.568 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tzirakis, K.; Kamarianakis, Y.; Kontopodis, N.; Ioannou, C.V. Selection of Bifurcated Grafts’ Dimensions during Aorto-Iliac Vascular Reconstruction Based on Their Hemodynamic Performance. Bioengineering 2023, 10, 776. https://doi.org/10.3390/bioengineering10070776
Tzirakis K, Kamarianakis Y, Kontopodis N, Ioannou CV. Selection of Bifurcated Grafts’ Dimensions during Aorto-Iliac Vascular Reconstruction Based on Their Hemodynamic Performance. Bioengineering. 2023; 10(7):776. https://doi.org/10.3390/bioengineering10070776
Chicago/Turabian StyleTzirakis, Konstantinos, Yiannis Kamarianakis, Nikolaos Kontopodis, and Christos V. Ioannou. 2023. "Selection of Bifurcated Grafts’ Dimensions during Aorto-Iliac Vascular Reconstruction Based on Their Hemodynamic Performance" Bioengineering 10, no. 7: 776. https://doi.org/10.3390/bioengineering10070776
APA StyleTzirakis, K., Kamarianakis, Y., Kontopodis, N., & Ioannou, C. V. (2023). Selection of Bifurcated Grafts’ Dimensions during Aorto-Iliac Vascular Reconstruction Based on Their Hemodynamic Performance. Bioengineering, 10(7), 776. https://doi.org/10.3390/bioengineering10070776









