Machine Learning Techniques for the Performance Enhancement of Multiple Classifiers in the Detection of Cardiovascular Disease from PPG Signals
Abstract
1. Introduction
Review of Previous Work
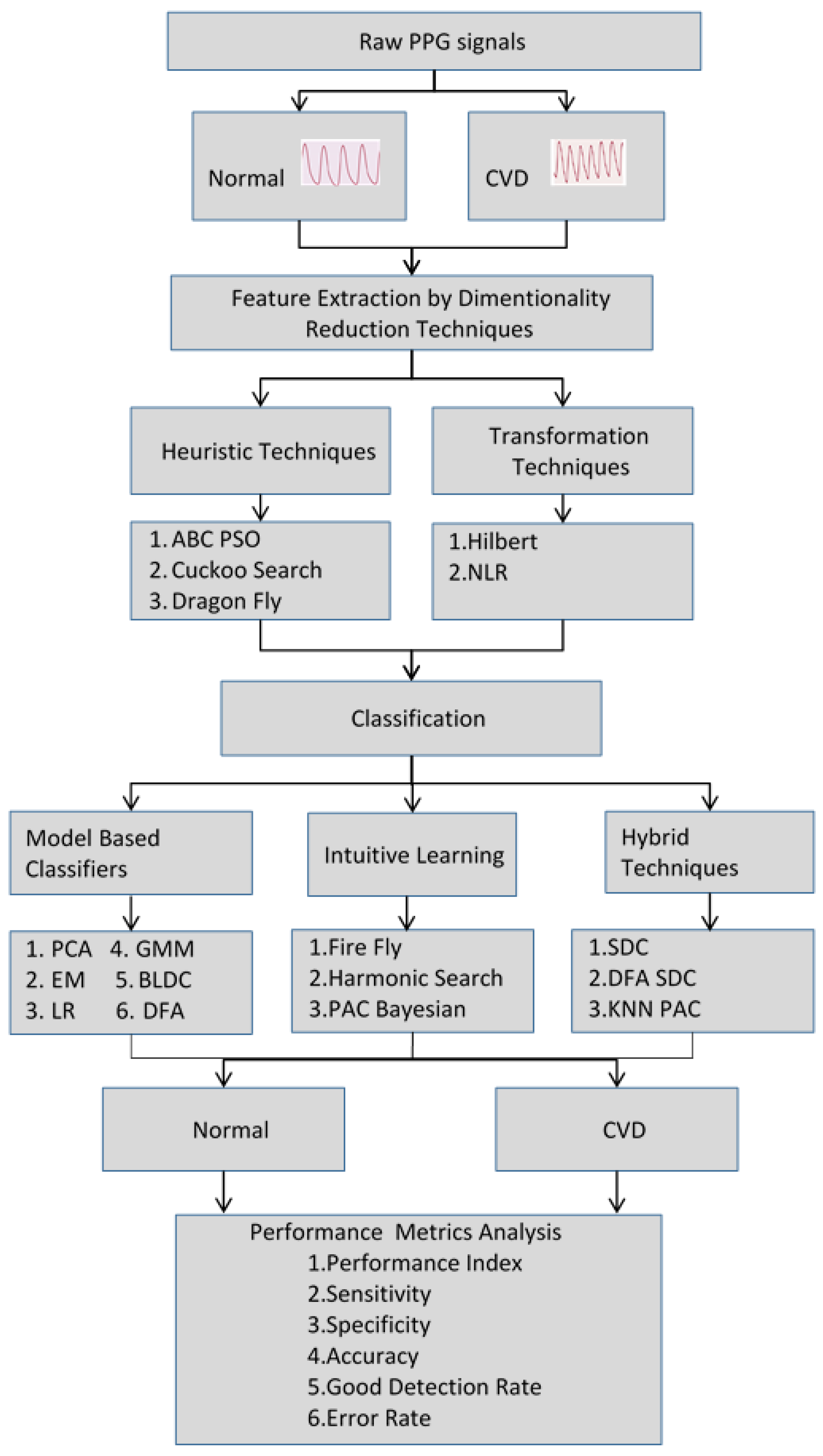
2. Methodology
3. Dimensionality Reduction Methods
3.1. Hilbert Transform
3.2. Nonlinear Regression
3.3. ABC-PSO
- 1.
- Initialization of the swarm.
- 2.
- Velocity and position of the particle are updated by performing the employed bee phase.
- 3.
- The local best position of a particle is updated by finding its new position by performing the onlooker bee phase.
- 4.
- If the highest value of the trial counter for any food source is higher than the limit, a scout bee will search for a new food source site.
- 5.
- At this point, instead of using scout bees, the PSO algorithm is used to look for new food sources.
- 6.
- Particles with random placements are used to initialize the population of new food sources.
- 7.
- The fitness value is determined for all particles for the specific objective function.
- 8.
- The fitness function is used to select the optimal set of features. The expression for the fitness function is as follows:where is the classifier performance in subset ; is the feature subset length; is the total number of features; and is the classification quality.
- 9.
- The number of particles that are currently present is set as .
- 10.
- A new set of particles is created by adding velocity to the initial particle, and a fitness value is calculated for the same.
- 11.
- A new is discovered between the two particle sets by comparing the fitness values of each particle to one another.
- 12.
- The least fitness value is determined by comparing the two sets of particles, and the corresponding particle is then referred to as the .
- 13.
- Simultaneously, in the next iteration, the update in the velocity ( and position is conducted as follows:The maximum step size that a particle can take in each iteration is influenced by the acceleration coefficients and .
- 14.
- The PSO iterations are continued until convergence is reached.
- 15.
- The finest food source is identified and remembered.
- 16.
- The process can be performed as many times as necessary to fully satisfy the stopping criteria.
3.4. Cuckoo Search
- At a certain time, every cuckoo bird lays one egg and dumps it in an arbitrary selected host nest.
- The subsequent generation will carry the top-quality eggs, which are present in the best host nests.
- There are only fixed quantities of host nests available, and a host bird can realize a cuckoo’s egg with a probability of . In this instance, a cuckoo’s egg in the host nest may be thrown away by the host bird or it abandons the nest and creates an entirely new nest in a different location.
- Create a population of N host nests at the beginning.
- Randomly select the host nest X.
- Lay the egg in the selected host nest X.
- Compare the fitness of the cuckoo’s egg with the host egg’s fitness.
- If the fitness of the cuckoo’s egg is better than the host egg’s fitness, replace the egg in nest X with the cuckoo’s egg.
- Abandon the nest if the host bird notices and build a new one.
- Repeat steps 2–6 until the termination criteria are met.
3.5. Dragonfly
- 1.
- Separation: This indicates the static avoidance of flies colliding with other flies in the area. It is calculated aswhere denotes the separation motion of the individual.
- 2.
- Alignment: This signifies the velocity matching among individual flies within the same group. It is denoted aswhere denotes the velocity of the individual.
- 3.
- Cohesiveness: This denotes the tendency of individual flies to move to the center of swarms. The estimation of this is given by
- 4.
- Attraction towards the nourishment source is estimated aswhere denotes the nourishment source of the individual and is the position of the nourishment source.
- 5.
- Diversion: This represents the distance outwards to the enemy. It is calculated aswhere denotes the individual enemy’s position and denotes the enemy’s position.
3.6. Statistical Analysis of Dimensionally Reduced PPG Signals
4. Classifiers for Detection of CVD
4.1. PCA as a Classifier
4.2. Expectation Maximization as a Classifier
- E step (expectation): calculate the Q function:
- M step (maximization): compute the maximum:where ““ denotes the iteration number. In the E-step, for each test point, the likelihood is computed from the individual cluster, and the calculation of the respective probability is carried out by assigning the test point to the corresponding cluster based on the maximum probability. All parameters are updated in the M step. This algorithm is repeated until it reaches convergence.
4.3. Logistic Regression as a Classifier
4.4. Gaussian Mixture Model (GMM) as a Classifier
- E step: the posterior probability, , is evaluated at iterations as
- M step: utilizing the probabilities evaluated from the E step, the parameters , are updated at iterations:
4.5. Bayesian Linear Discriminant Analysis as a Classifier
4.6. Firefly Algorithm as a Classifier
- All fireflies considered here are unisex in nature, and along these lines, one firefly will be attractive to other fireflies irrespective of sex.
- The attractive feature of a particular firefly varies with respect to its intelligence. Thus, for any two fireflies, the brighter firefly effectively pulls in the darker firefly. Assuming there are no fireflies brighter than a particular firefly, at that point, that specific firefly will move arbitrarily.
- When the distance from the firefly increases, the brightness or light intensity of a firefly will decrease because the light is captured as it passes through the air. Subsequently, the engaging quality or intelligence of a particular firefly, , seen by firefly “” is characterized aswhere β is the light ingestion coefficient of a particular medium, signifies the brightness of firefly ” at , and r indicates the Euclidean distance between firefly “ and firefly :where and are the individual areas of fireflies “ and , respectively. If firefly is the brighter one, then its amount of attractiveness directs the movement of the specific firefly “” as per the accompanying condition:where is the randomization parameter, and rand denotes a random number taken from a uniform distribution that lies in the range between −1 and +1, inclusively. Firefly can effectively move towards firefly based on the second term in the above equation.
4.7. Harmonic Search as a Classifier
- 1.
- Problem Definition and HS Parameter InitializationAn unconstrained optimization problem is described as the minimization or maximization of the objective function, , given as follows:where denotes the decision variable set; is the set of all possible values of every decision variable; and and represent the upper and lower bounds of the decision variable.
- 2.
- Initialization of the Harmony MemoryIn this stage, the harmony memory (HM) is initialized. All decision variables in the HM are kept as matrices. The opening harmony memory is created from a uniform random distribution of values that are constrained by the parameters and .
- 3.
- Improvisation of a New HarmonyThe HM is utilized in this process to create a new harmony.
- 4.
- Updating the Harmony MemoryThe HM is updated with the new harmony vector and the minimal harmony vector is deleted from the HM if the new improvised harmony vector is superior to the minimum harmony vector in the HM.
- 5.
- Verification of the Terminating CriterionWhen the termination criterion is satisfied, the iterations are terminated. If not, steps 3 and 4 are repeated until the allotted number of iterations has been reached.
4.8. Detrend Fluctuation Analysis as a Classifier
4.9. Probably Approximately Correct (PAC) Bayesian Learning Method as a Classifier
4.10. KNN-PAC Bayesian Learning Method as a Classifier
4.11. Softmax Discriminant Classifier (SDC) as a Classifier
4.12. Detrend with SDC as a Classifier
5. Results and Discussion
5.1. Training and Testing of the Classifiers
5.2. Selection of the Optimal Parameters for the Classifiers
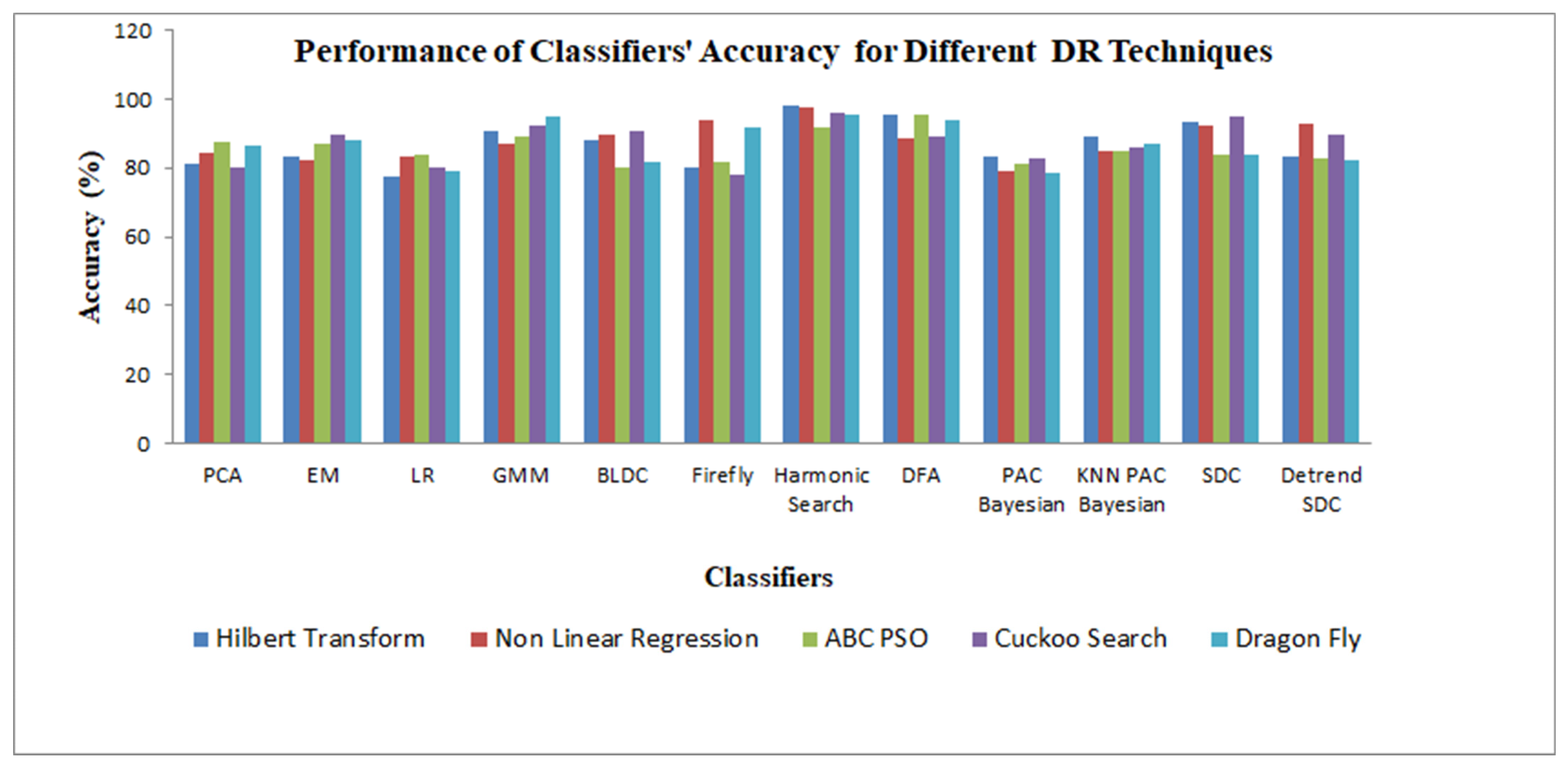
5.3. Performance Metrics of the Classifiers
5.4. Summary of Previous Works on the Detection of CVD Classes
5.5. Computational Complexity Analysis of the Classifiers
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Pilt, K.; Meigas, K.; Ferenets, R.; Kaik, J. Photoplethysmographic signal processing using adaptive sum comb filter for pulse delay measurement. Est. J. Eng. 2010, 16, 78–94. [Google Scholar] [CrossRef]
- Giannetti, S.M.; Dotor, M.L.; Silveira, J.P.; Golmayo, D.; Miguel-Tobal, F.; Bilbao, A.; Galindo, M.; Martín-Escudero, P. Heuristic algorithm for photoplethysmographic heart rate tracking during maximal exercise test. J. Med. Biol. Eng. 2012, 32, 181–188. [Google Scholar] [CrossRef]
- Al-Fahoum, A.S.; Al-Zaben, A.; Seafan, W. A multiple signal classification approach for photoplethysmography signals in healthy and athletic subjects. Int. J. Biomed. Eng. Technol. 2015, 17, 1–23. [Google Scholar] [CrossRef]
- Sukor, J.A.; Redmond, S.J.; Lovell, N.H. Signal quality measures for pulse oximetry through waveform morphology analysis. Physiol. Meas. 2011, 32, 369–384. [Google Scholar] [CrossRef]
- Di, U.; Te, A.; De, J. Awareness of Heart Disease Prevention among Patients Attending a Specialist Clinic in Southern Nigeria. Int. J. Prev. Treat. 2012, 1, 40–43. [Google Scholar]
- Tun, H.M. Photoplethysmography (PPG) Scheming System Based on Finite Impulse Response (FIR) Filter Design in Biomedical Applications. Int. J. Electr. Electron. Eng. Telecommun. 2021, 10, 272–282. [Google Scholar] [CrossRef]
- Ram, M.R.; Madhav, K.V.; Krishna, E.H.; Komalla, N.R.; Reddy, K.A. A novel approach for motion artifact reduction in PPG signals based on AS-LMS adaptive filter. IEEE Trans. Instrum. Meas. 2011, 61, 1445–1457. [Google Scholar] [CrossRef]
- Luke, A.; Shaji, S.; Menon, K.U. Motion artifact removal and feature extraction from PPG signals using efficient signal processing algorithms. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics (ICACCI), Bangalore, India, 19–22 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 624–630. [Google Scholar] [CrossRef]
- Otsuka, T.; Kawada, T.; Katsumata, M.; Ibuki, C. Utility of second derivative of the finger photoplethysmogram for the estimation of the risk of coronary heart disease in the general population. Circ. J. 2006, 70, 304–310. [Google Scholar] [CrossRef]
- Shintomi, A.; Izumi, S.; Yoshimoto, M.; Kawaguchi, H. Effectiveness of the heartbeat interval error and compensation method on heart rate variability analysis. Healthc. Technol. Lett. 2022, 9, 9–15. [Google Scholar] [CrossRef]
- Moraes, J.L.; Rocha, M.X.; Vasconcelos, G.G.; Vasconcelos Filho, J.E.; De Albuquerque, V.H.; Alexandria, A.R. Advances in photopletysmography signal analysis for biomedical applications. Sensors 2018, 18, 1894. [Google Scholar] [CrossRef]
- Hwang, S.; Seo, J.; Jebelli, H.; Lee, S. Feasibility analysis of heart rate monitoring of construction workers using a photoplethysmography (PPG) sensor embedded in a wristband-type activity tracker. Autom. Constr. 2016, 71, 372–381. [Google Scholar] [CrossRef]
- Moshawrab, M.; Adda, M.; Bouzouane, A.; Ibrahim, H.; Raad, A. Smart Wearables for the Detection of Cardiovascular Diseases: A Systematic Literature Review. Sensors 2023, 23, 828. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef]
- Kumar, P.S.; Harikumar, R. Performance Comparison of EM, MEM, CTM, PCA, ICA, entropy and MI for photoplethysmography signals. Biomed. Pharmacol. J. 2015, 8, 413–418. [Google Scholar] [CrossRef]
- Almarshad, M.A.; Islam, S.; Al-Ahmadi, S.; BaHammam, A.S. Diagnostic Features and Potential Applications of PPG Signal in Healthcare: A Systematic Review. Healthcare 2022, 10, 547. [Google Scholar] [CrossRef]
- Yousefi, M.R.; Khezri, M.; Bagheri, R.; Jafari, R. Automatic detection of premature ventricular contraction based on photoplethysmography using chaotic features and high order statistics. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ukil, A.; Bandyoapdhyay, S.; Puri, C.; Pal, A.; Mandana, K. Cardiac condition monitoring through photoplethysmogram signal denoising using wearables: Can we detect coronary artery disease with higher performance efficacy? In Proceedings of the Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 281–284. [Google Scholar] [CrossRef]
- Almanifi, O.R.A.; Khairuddin, I.M.; Razman, M.A.M.; Musa, R.M.; Majeed, A.P.A. Human activity recognition based on wrist PPG via the ensemble method. ICT Express 2022, 8, 513–517. [Google Scholar] [CrossRef]
- Paradkar, N.; Chowdhury, S.R. Coronary artery disease detection using photoplethysmography. In Proceedings of the 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; pp. 100–103. [Google Scholar] [CrossRef]
- Neha; Kanawade, R.; Tewary, S.; Sardana, H.K. Neha; Kanawade, R.; Tewary, S.; Sardana, H.K. Photoplethysmography based arrhythmia detection and classification. In Proceedings of the 6th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 7–8 March 2019; pp. 944–948. [Google Scholar] [CrossRef]
- Prabhakar, S.K.; Rajaguru, H.; Lee, S.W. Metaheuristic-based dimensionality reduction and classification analysis of PPG signals for interpreting cardiovascular disease. IEEE Access 2019, 7, 165181–165206. [Google Scholar] [CrossRef]
- Sadad, T.; Bukhari, S.A.C.; Munir, A.; Ghani, A.; El-Sherbeeny, A.M.; Rauf, H.T. Detection of Cardiovascular Disease Based on PPG Signals Using Machine Learning with Cloud Computing. Comput. Intell. Neurosci. 2022, 2022, 1672677. [Google Scholar] [CrossRef]
- Karlen, W.; Turner, M.; Cooke, E.; Dumont, G.; Ansermino, J.M. CapnoBase: Signal database and tools to collect, share and annotate respiratory signals. In Proceedings of the 2010 Annual Meeting of the Society for Technology in Anesthesia, West Palm Beach, FL, USA, 13–16 January 2010; Society for Technology in Anesthesia: Milwaukee, WI, USA, 2010; p. 27. [Google Scholar]
- Velliangiri, S.; Alagumuthukrishnan, S.J. A review of dimensionality reduction techniques for efficient computation. Procedia Comput. Sci. 2019, 165, 104–111. [Google Scholar] [CrossRef]
- Van Der Maaten, L.; Postma, E.; Van den Herik, J. Dimensionality reduction: A comparative. J. Mach. Learn Res. 2009, 10, 13. [Google Scholar]
- Rajaguru, H.; Prabhakar, S.K. PPG signal analysis for cardiovascular patient using correlation dimension and Hilbert transform based classification. In New Trends in Computational Vision and Bioinspired Computing: ICCVBIC 2018; Springer: Cham, Switzerland, 2020; pp. 1103–1110. [Google Scholar] [CrossRef]
- Benitez, D.; Gaydecki, P.A.; Zaidi, A.; Fitzpatrick, A.P. The use of the Hilbert transform in ECG signal analysis. Comput. Biol. Med. 2001, 31, 399–406. [Google Scholar] [CrossRef] [PubMed]
- Smyth, G.K. Nonlinear regression. Encycl. Environ. Metr. 2002, 3, 1405–1411. [Google Scholar]
- Khuat, T.T.; Le, M.H. A novel hybrid ABC-PSO algorithm for effort estimation of software projects using agile methodologies. J. Intell. Syst. 2018, 27, 489–506. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Esmael, B.; Arnaout, A.; Fruhwirth, R.; Thonhauser, G. A statistical feature-based approach for operations recognition in drilling time series. Int. J. Comput. Inf. Syst. Ind. Manag. Appl. 2012, 4, 100–108. [Google Scholar]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. -Heart Circ. Physiol. 2000, 278, H2039–H2049. [Google Scholar] [CrossRef]
- Dai, J.J.; Lieu, L.; Rocke, D. Dimension reduction for classification with gene expression microarray data. Stat. Appl. Genet. Mol. Biol. 2006, 5, 1–19. [Google Scholar] [CrossRef]
- Fan, X.; Yuan, Y.; Liu, J.S. The EM algorithm and the rise of computational biology. Stat. Sci. 2010, 25, 476–491. [Google Scholar] [CrossRef]
- Li, G. Application of finite mixture of logistic regression for heterogeneous merging behavior analysis. J. Adv. Transp. 2018, 2018, 1436521. [Google Scholar] [CrossRef]
- Li, R.; Perneczky, R.; Yakushev, I.; Foerster, S.; Kurz, A.; Drzezga, A.; Kramer, S. Alzheimer’s Disease Neuroimaging Initiative. Gaussian mixture models and model selection for [18F] fluorodeoxyglucose positron emission tomography classification in Alzheimer’s disease. PLoS ONE 2015, 10, e0122731. [Google Scholar] [CrossRef]
- Fonseca, P.; Den Teuling, N.; Long, X.; Aarts, R.M. Cardiorespiratory sleep stage detection using conditional random fields. IEEE J. Biomed. Health Inform. 2016, 21, 956–966. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.S. Firefly algorithm, stochastic test functions and design optimization. Int. J. Bioinspired Comput. 2010, 2, 78–84. [Google Scholar] [CrossRef]
- Bharanidharan, N.; Rajaguru, H. Classification of dementia using harmony search optimization technique. In Proceedings of the IEEE Region 10 Humanitarian Technology Conference (R10-HTC), Malambe, Sri Lanka, 6–8 December 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Berthouze, L.; Farmer, S.F. Adaptive time-varying detrended fluctuation analysis. J. Neurosci. Methods 2012, 209, 178–188. [Google Scholar] [CrossRef]
- Guedj, B. A primer on PAC-Bayesian learning. arXiv 2019, arXiv:1901.05353. [Google Scholar]
- Aci, M.; Inan, C.; Avci, M. A hybrid classification method of k nearest neighbor, Bayesian methods and genetic algorithm. Expert Syst. Appl. 2010, 37, 5061–6067. [Google Scholar] [CrossRef]
- Rajaguru, H.; Prabhakar, S.K. Softmax discriminant classifier for detection of risk levels in alcoholic EEG signals. In Proceedings of the International Conference on Computing Methodologies and Communication (ICCMC), Erode, India, 18–19 July 2017; pp. 989–991. [Google Scholar] [CrossRef]
- Soltane, M.; Ismail, M.; Rashid, Z.A. Artificial Neural Networks (ANN) approach to PPG signal classification. Int. J. Comput. Inf. Sci. 2004, 2, 58–65. [Google Scholar]
- Hosseini, Z.S.; Zahedi, E.; Attar, H.M.; Fakhrzadeh, H.; Parsafar, M.H. Discrimination between different degrees of coronary artery disease using time-domain features of the finger photoplethysmogram in response to reactive hyperemia. Biomed. Signal Process. Control 2015, 18, 282–292. [Google Scholar] [CrossRef]
- Shobitha, S.; Sandhya, R.; Ali, M.A. Recognizing cardiovascular risk from photoplethysmogram signals using ELM. In Proceedings of the Second International Conference on Cognitive Computing and Information Processing (CCIP), Mysore, India, 12–13 August 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Prabhakar, S.K.; Rajaguru, H. Performance analysis of GMM classifier for classification of normal and abnormal segments in PPG signals. In Proceedings of the 16th International Conference on Biomedical Engineering: ICBME 2016, Singapore, 7–10 December 2016; Springer: Singapore, 2017; pp. 73–79. [Google Scholar] [CrossRef]
- Miao, K.H.; Miao, J.H. Coronary heart disease diagnosis using deep neural networks. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 1–8. [Google Scholar] [CrossRef]
- Hao, L.; Ling, S.H.; Jiang, F. Classification of cardiovascular disease via a new softmax model. In Proceedings of the 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, USA, 18–21 July 2018; pp. 486–489. [Google Scholar] [CrossRef]
- Ramachandran, D.; Thangapandian, V.P.; Rajaguru, H. Computerized approach for cardiovascular risk level detection using photoplethysmography signals. Measurement 2020, 150, 107048. [Google Scholar] [CrossRef]
- Prabhakar, S.K.; Rajaguru, H.; Kim, S.H. Fuzzy-inspired photoplethysmography signal classification with bioinspired optimization for analyzing cardiovascular disorders. Diagnostics 2020, 10, 763. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhou, B.; Jiang, Z.; Chen, X.; Li, Y.; Tang, M.; Miao, F. Multiclass Arrhythmia Detection and Classification from Photoplethysmography Signals Using a Deep Convolutional Neural Network. J. Am. Heart Assoc. 2022, 11, e023555. [Google Scholar] [CrossRef] [PubMed]
- Ihsan, M.F.; Mandala, S.; Pramudyo, M. Study of Feature Extraction Algorithms on Photoplethysmography (PPG) Signals to Detect Coronary Heart Disease. In Proceedings of the International Conference on Data Science and Its Applications (ICoDSA), Bandung, Indonesia, 6–7 July 2022; pp. 300–304. [Google Scholar] [CrossRef]
- Al Fahoum, A.S.; Abu Al-Haija, A.O.; Alshraideh, H.A. Identification of Coronary Artery Diseases Using Photoplethysmography Signals and Practical Feature Selection Process. Bioengineering 2023, 10, 249. [Google Scholar] [CrossRef]
- Rajaguru, H.; Shankar, M.G.; Nanthakumar, S.P.; Murugan, I.A. Performance analysis of classifiers in detection of CVD using PPG signals. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2023; Volume 2725, p. 020002. [Google Scholar] [CrossRef]
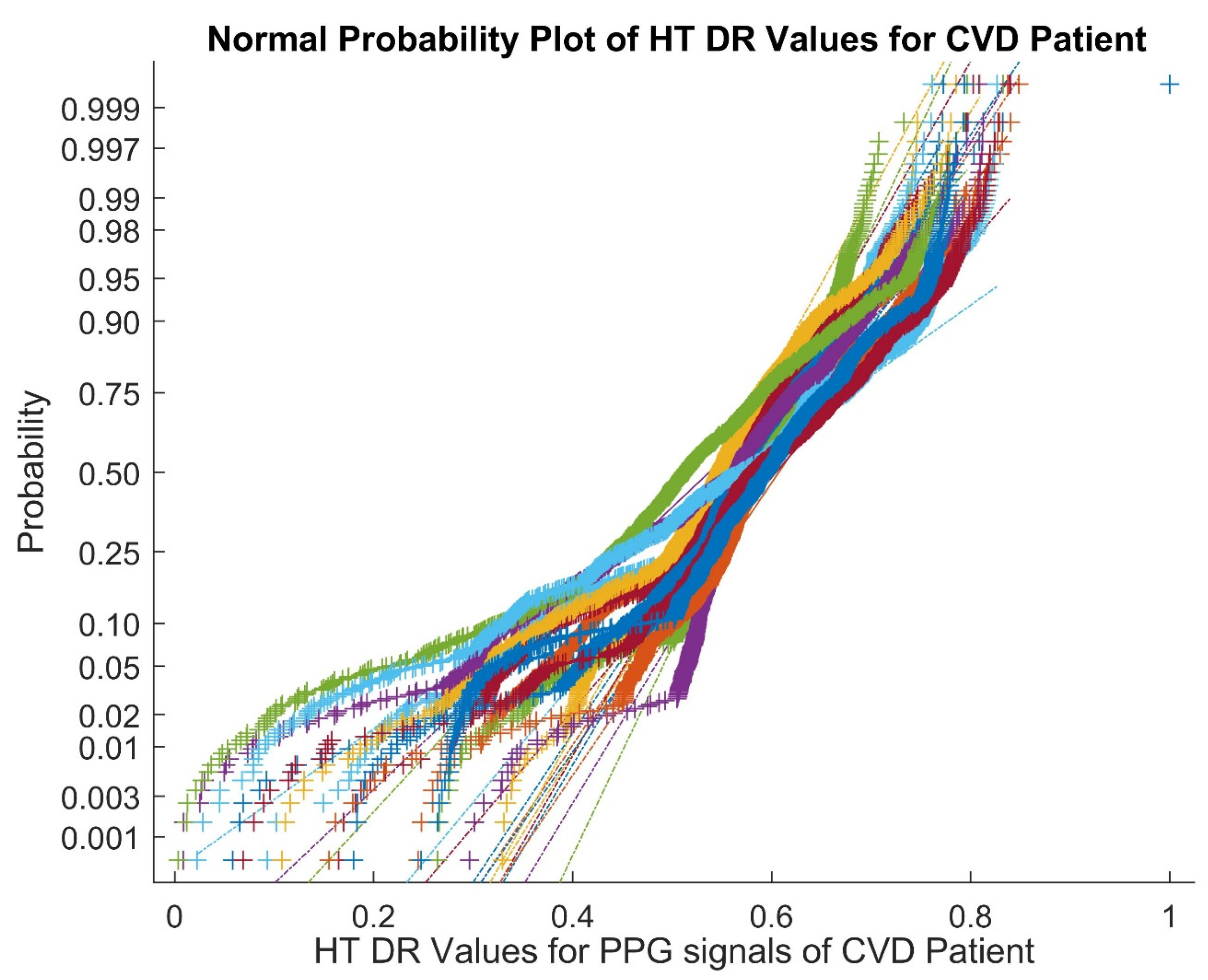
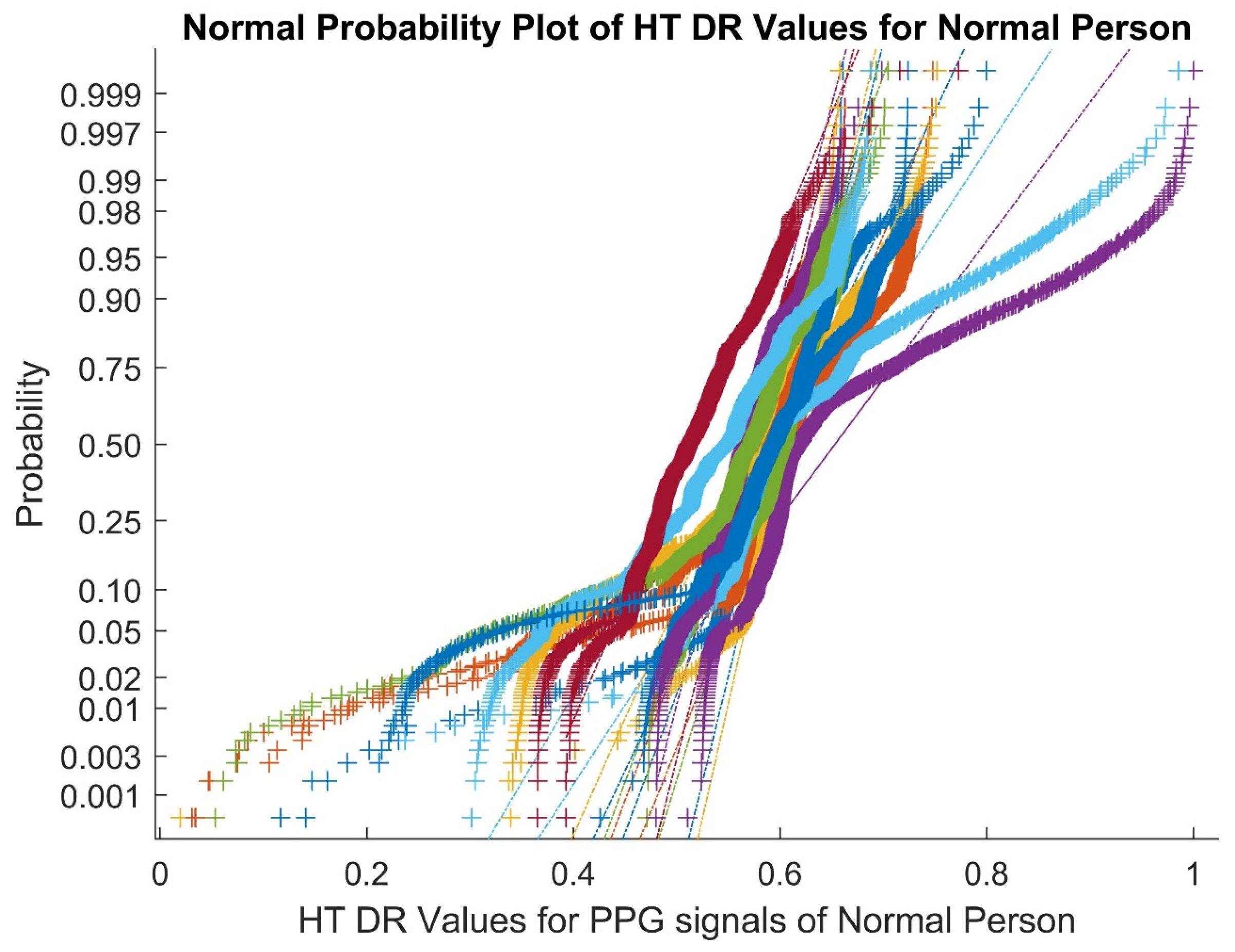

| Statistical Parameters | Dimensionality Reduction Techniques | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hilbert Transform | NLR | ABC PSO | Cuckoo Search | Dragonfly | ||||||
| Normal | CVD | Normal | CVD | Normal | CVD | Normal | CVD | Normal | CVD | |
| Mean | 2.0611 | 5.457 | 2.126 | 117.469 | 0.08886 | 0.7939 | 0.5176 | 11.622 | 0.7803 | −5.461 |
| Variance | 0.0706 | 1.162 | 23.056 | 225,124.7 | 0.0105 | 0.3412 | 0.0463 | 93.9237 | 411.1297 | 274.941 |
| Skewness | −1.118 | −0.8151 | 3.2789 | 5.769 | −0.1046 | −0.0888 | 0.1411 | −0.1172 | −0.0015 | −0.0084 |
| Kurtosis | 5.626 | 1.638 | 14.59 | 46.05 | 0.2226 | 0.0991 | −0.4971 | −1.6769 | −1.0065 | −0.74424 |
| PCC | 0.3687 | 0.2332 | 0.01 | 0.0063 | −0.0215 | 0.0134 | 0.2319 | 0.24 | −0.1541 | 0.0775 |
| Sample Entropy | 9.7695 | 9.9328 | 6.9142 | 7.3959 | 9.9494 | 9.9473 | 9.9494 | 4.9919 | 9.9499 | 9.9522 |
| CCA | 0.5425 | 0.2198 | 0.1066 | 0.3674 | 0.4621 | |||||
| Classifiers | Optimal Parameters of the Classifiers |
|---|---|
| Principal component analysis (PCA) | Decorrelated Eigen vector , and a threshold value of 0.72 with the training of trial and error method with MSE of (10)−5 or a maximum iteration of 1000—whichever happens first. |
| Expectation maximization | Test point likelihood probability 0.15, cluster probability of 0.6, with a convergence rate of 0.6. Criterion: MSE |
| Logistic regression | Threshold . Criterion: MSE |
| Gaussian mixture model (GMM) | Mean, covariance of the input samples and tuning parameter is EM steps. Criterion: MSE |
| Bayesian linear discriminant analysis (BLDC) | Prior probability P(x): 0.5, class mean and . Criterion: MSE |
| Firefly algorithm classifier | = 0.1, = 0.65 initial conditions, with an MSE of (10)−5 or maximum iteration of 1000—whichever happens first. Criterion: MSE |
| Harmonic search | Class harmony is fixed at target values for the classes 0.85 and 0.1. The upper and lower bounds are adjusted with a step size of ∆w of 0.004. The final harmony aggregation is attained with an MSE of (10)−5 or a maximum iteration of 1000—whichever happens first. Criterion: MSE |
| Detrend fluctuation analysis (DFA) | The initial values for = 10000, = 1000, and n = 100 are set to find F(n). Criterion: MSE |
| Probably approximately correct (PAC) Bayesian learning method | P(z), class probability: 0.5, class mean: 0.8,0.1; γ = 0.13, Criterion: MSE |
| KNN-PAC Bayesian learning method | Number of clusters = 2 with PAC Bayesian variables. Criterion: MSE |
| Softmax discriminant classifier (SDC) | = 0.5 along with mean of each class target values as 0.1 and 0.85. |
| Detrend with SDC | Cascaded condition of DFA with SDC classifiers with parameters as mentioned above. |
| Classifiers | Category | Hilbert Transform | NLR | ABC PSO | Cuckoo | Dragonfly |
|---|---|---|---|---|---|---|
| PCA | CVD | 2.81 × 10−5 | 7.84 × 10−6 | 2.50 × 10−7 | 6.60 × 10−4 | 1.44 × 10−6 |
| Normal | 3.06 × 10−4 | 2.79 × 10−4 | 2.40 × 10−4 | 3.72 × 10−5 | 1.21 × 10−4 | |
| EM | CVD | 1.60 × 10−5 | 3.97 × 10−5 | 1.44 × 10−4 | 3.24 × 10−6 | 7.74 × 10−5 |
| Normal | 2.28 × 10−4 | 6.24 × 10−5 | 8.10 × 10−7 | 3.03 × 10−5 | 2.50 × 10−7 | |
| Logistic regression | CVD | 9.03 × 10−5 | 8.27 × 10−5 | 1.09 × 10−5 | 3.61 × 10−5 | 6.24 × 10−5 |
| Normal | 3.23 × 10−4 | 1.84 × 10−5 | 2.56 × 10−4 | 4.84 × 10−4 | 1.33 × 10−4 | |
| GMM | CVD | 1.44 × 10−6 | 4.41 × 10−6 | 6.40 × 10−5 | 4.84 × 10−6 | 6.76 × 10−6 |
| Normal | 2.70 × 10−5 | 6.56 × 10−5 | 3.60 × 10−7 | 1.09 × 10−5 | 3.60 × 10−7 | |
| Bayesian LDC | CVD | 2.92 × 10−5 | 2.50 × 10−5 | 5.49 × 10−5 | 1.00 × 10−6 | 2.22 × 10−5 |
| Normal | 1.45 × 10−5 | 4.00 × 10−6 | 7.57 × 10−5 | 3.03 × 10−5 | 3.06 × 10−4 | |
| Firefly | CVD | 4.41 × 10−4 | 6.25 × 10−6 | 8.84 × 10−5 | 6.40 × 10−5 | 8.41 × 10−6 |
| Normal | 3.36 × 10−5 | 1.44 × 10−6 | 3.25 × 10−5 | 4.20 × 10−4 | 9.61 × 10−6 | |
| Harmonic search | CVD | 1.60 × 10−7 | 4.90 × 10−7 | 3.61 × 10−6 | 3.24 × 10−6 | 5.29 × 10−6 |
| Normal | 9.00 × 10−8 | 3.24 × 10−6 | 6.76 × 10−6 | 1.60 × 10−7 | 4.90 × 10−7 | |
| DFA (weighted) | CVD | 1.60 × 10−7 | 2.56 × 10−6 | 4.00 × 10−8 | 1.30 × 10−5 | 2.50 × 10−7 |
| Normal | 6.25 × 10−6 | 5.04 × 10−5 | 7.84 × 10−6 | 2.03 × 10−5 | 6.76 × 10−6 | |
| PAC Bayesian learning | CVD | 4.90 × 10−7 | 3.35 × 10−4 | 3.06 × 10−4 | 1.68 × 10−5 | 5.78 × 10−5 |
| Normal | 2.89 × 10−4 | 5.04 × 10−5 | 2.70 × 10−5 | 1.19 × 10−4 | 3.03 × 10−4 | |
| KNN-PAC Bayesian | CVD | 7.84 × 10−6 | 8.41 × 10−6 | 6.25 × 10−6 | 1.00 × 10−6 | 8.41 × 10−6 |
| Normal | 2.40 × 10−5 | 1.32 × 10−4 | 1.96 × 10−4 | 1.10 × 10−4 | 4.76 × 10−5 | |
| SDC | CVD | 2.89 × 10−6 | 4.84 × 10−6 | 1.21 × 10−4 | 1.44 × 10−6 | 3.69 × 10−4 |
| Normal | 8.41 × 10−6 | 1.15 × 10−5 | 1.31 × 10−5 | 2.57 × 10−6 | 1.16 × 10−5 | |
| Detrend SDC | CVD | 2.40 × 10−4 | 8.10 × 10−7 | 3.06 × 10−4 | 1.02 × 10−5 | 4.41 × 10−4 |
| Normal | 1.69 × 10−5 | 1.75 × 10−5 | 1.76 × 10−5 | 1.85 × 10−5 | 1.86 × 10−5 |
| Actual Classification Class Output | Predicted Classification Class Output | |
|---|---|---|
| CVD | Normal | |
| CVD | TP | FN |
| Normal | FP | TN |
| Classifiers | TP | TN | FP | FN |
|---|---|---|---|---|
| PCA | 10,080 | 7920 | 7200 | 4320 |
| EM | 8640 | 7920 | 7200 | 5760 |
| Logistic regression | 11,520 | 7920 | 7200 | 2880 |
| GMM | 12,960 | 10,800 | 4320 | 1440 |
| Bayesian LDC | 10,080 | 12,240 | 2880 | 4320 |
| Firefly | 7200 | 10,800 | 4320 | 7200 |
| Harmonic search | 14,400 | 14,400 | 720 | 0 |
| DFA (weighted) | 13,680 | 12,960 | 2160 | 720 |
| PAC Bayesian learning | 11,520 | 7920 | 7200 | 2880 |
| KNN-PAC Bayesian | 7920 | 7920 | 7200 | 6480 |
| SDC | 12,960 | 12,960 | 2160 | 1440 |
| Detrend SDC | 7200 | 11,520 | 3600 | 7200 |
| Classifiers | PI (%) | Sensitivity (%) | Specificity (%) | Accuracy (%) | GDR (%) | Error Rate (%) |
|---|---|---|---|---|---|---|
| PCA | 30.975 | 60.725 | 100 | 80.36 | 60.72 | 39.28 |
| EM | 72.6 | 94.01 | 85.42 | 89.715 | 73.425 | 20.57 |
| Logistic regression | 30.175 | 60.125 | 100 | 80.065 | 60.125 | 39.875 |
| GMM | 81.395 | 100 | 84.38 | 92.19 | 81.415 | 15.625 |
| Bayesian LDC | 75.205 | 81.255 | 100 | 90.63 | 81.255 | 18.745 |
| Firefly | 20.76 | 56.15 | 100 | 78.275 | 56.15 | 43.855 |
| Harmonic search | 91.29 | 92.185 | 100 | 96.095 | 92.19 | 7.81 |
| DFA (weighted) | 71.915 | 77.995 | 100 | 89 | 77.995 | 22.005 |
| PAC Bayesian learning | 48.605 | 67.1 | 100 | 82.84 | 67.085 | 32.915 |
| KNN-PAC Bayesian | 56.255 | 77.93 | 95.835 | 86.09 | 73.385 | 26.235 |
| SDC | 89.015 | 94.665 | 95.315 | 94.99 | 89.495 | 10.02 |
| Detrend SDC | 75.635 | 88.55 | 91.15 | 89.85 | 77.79 | 20.315 |
| Classifiers | Performance Metrics | Hilbert | NLR | ABC PSO | Cuckoo | Dragonfly |
|---|---|---|---|---|---|---|
| PCA | PI | 35.69 | 47.195 | 55.145 | 30.975 | 55.215 |
| Error rate | 37.78 | 31.07 | 25.1 | 39.28 | 26.69 | |
| Accuracy | 81.11 | 84.265 | 87.45 | 80.36 | 86.655 | |
| GDR | 62.22 | 68.935 | 74.9 | 60.72 | 73.31 | |
| EM | PI | 47.1 | 44.285 | 55.41 | 72.6 | 60.925 |
| Error rate | 33.35 | 35.545 | 26.11 | 20.57 | 23.3 | |
| Accuracy | 83.335 | 82.225 | 86.95 | 89.715 | 88.35 | |
| GDR | 44.485 | 64.455 | 55.57 | 73.425 | 61.05 | |
| Logistic regression | PI | 17.07 | 48.955 | 46.195 | 30.175 | 27.255 |
| Error rate | 45.245 | 32.86 | 31.98 | 39.875 | 41.93 | |
| Accuracy | 77.38 | 83.575 | 84.015 | 80.065 | 79.035 | |
| GDR | 54.755 | 51.13 | 66.125 | 60.125 | 45.555 | |
| GMM | PI | 75.445 | 59.205 | 64.685 | 81.395 | 88.815 |
| Error rate | 18.68 | 26.43 | 22.13 | 15.625 | 9.76 | |
| Accuracy | 90.66 | 86.79 | 88.935 | 92.19 | 95.12 | |
| GDR | 81.32 | 72.615 | 64.905 | 81.415 | 88.945 | |
| Bayesian LDC | PI | 68.635 | 73.285 | 34.145 | 75.205 | 37.65 |
| Error ate | 24.345 | 20.315 | 39.58 | 18.745 | 36.74 | |
| Accuracy | 87.83 | 89.845 | 80.21 | 90.63 | 81.63 | |
| GDR | 75.655 | 78.795 | 60.42 | 81.255 | 63.26 | |
| Firefly | PI | 31.72 | 86.855 | 40.715 | 20.76 | 80.075 |
| Error rate | 39.23 | 11.715 | 36.525 | 43.855 | 16.595 | |
| Accuracy | 80.39 | 94.145 | 81.74 | 78.275 | 91.7 | |
| GDR | 60.77 | 87.04 | 40.755 | 56.15 | 81.85 | |
| Harmonic search | PI | 96.485 | 95.35 | 82.65 | 91.29 | 89.405 |
| Error rate | 3.38 | 4.425 | 16.405 | 7.81 | 9.375 | |
| Accuracy | 98.31 | 97.79 | 91.805 | 96.095 | 95.315 | |
| GDR | 96.55 | 95.575 | 83.595 | 92.19 | 90.625 | |
| Detrend fluctuation analysis (weighted) | PI | 89.57 | 66.12 | 89.65 | 71.915 | 87.29 |
| Error rate | 9.11 | 23.235 | 8.85 | 22.005 | 12.495 | |
| Accuracy | 95.445 | 88.38 | 95.575 | 89 | 93.76 | |
| GDR | 90.89 | 76.765 | 91.15 | 77.995 | 87.505 | |
| PAC Bayesian learning | PI | 44.95 | 26.885 | 35.82 | 48.605 | 25.285 |
| Error rate | 32.96 | 41.635 | 37.715 | 32.915 | 42.39 | |
| Accuracy | 83.525 | 79.22 | 81.14 | 82.84 | 78.7 | |
| GDR | 64.74 | 58.365 | 62.285 | 67.085 | 46.055 | |
| KNN-PAC Bayesian | PI | 71.875 | 49.755 | 50.005 | 56.255 | 63.69 |
| Error rate | 21.48 | 30.47 | 29.95 | 26.235 | 25.45 | |
| Accuracy | 89.26 | 84.765 | 85.025 | 86.09 | 87.275 | |
| GDR | 78.52 | 69.535 | 70.05 | 73.385 | 74.55 | |
| SDC | PI | 84.215 | 81.175 | 48.41 | 89.015 | 43.41 |
| Error rate | 13.535 | 15.755 | 31.77 | 10.02 | 32.915 | |
| Accuracy | 93.23 | 92.125 | 84.115 | 94.99 | 83.615 | |
| GDR | 86.465 | 83.23 | 68.23 | 89.495 | 67.09 | |
| Detrend SDC | PI | 45.635 | 83.395 | 42.93 | 75.635 | 39.775 |
| Error rate | 33.825 | 14.84 | 34.655 | 20.315 | 35.585 | |
| Accuracy | 83.095 | 92.585 | 82.675 | 89.85 | 82.215 | |
| GDR | 66.175 | 84.875 | 65.345 | 77.79 | 64.42 |
| Sl.no | Authors | Features | Classifier | Accuracy (%) |
|---|---|---|---|---|
| 1 | Soltane et al. [47] 2004 | Time and frequency domain features | Artificial neural network | 94.70% |
| 2 | Hosseini et al. [48] 2015 | Time domain features | K-nearest neighbor | 81.50% |
| 3 | Shobita et al. [49] 2016 | Time domain features | Extreme learning machine | 82.50% |
| 4 | Prabhakaret al. [50] 2017 | Statistical features +SVD | GMM | 98.97% |
| 5 | Miao and Miao [51] 2018 | Time domain features | Deep neural networks | 83.67% |
| 6 | Hao et al. [52] 2018 | Statistical features | Softmax regression model | 94.44% |
| 7 | Divya et al. [53] 2019 | SVD + statistical features + wavelets | SDC | 97.88% |
| GMM | 96.64% | |||
| 8 | Prabhakar et al. [54] 2020 | Fuzzy-inspired statistical features | SVM–RBF (kernel) for CVD | 95.05% |
| RBF neural network-for normal | 94.79% | |||
| 9 | Liu et al. [55] 2022 | Time domain features | Deep convolutional neural network | 85% |
| 10 | Ihsan et al. [56] 2022 | HRV features and time domain features | Decision tree classifier | 94.4% |
| 11 | Al Fahoum et al. [57] 2023 | Time domain features | Naive Bayes | 94.44% in first stage 89.37% in second stage |
| 12 | Rajaguru et al. [58] 2023 | Statistical features | Linear regression | 65.85% |
| 13 | As reported in this paper | Hilbert transform | Harmonic search classifier | 98.31% |
| Classifiers | Optimization Techniques | ||||
|---|---|---|---|---|---|
| Hilbert | NLR | ABC PSO | Cuckoo | Dragonfly | |
| PCA | |||||
| EM | |||||
| Logistic regression | |||||
| GMM | |||||
| Bayesian LDC | |||||
| Firefly | |||||
| Harmonic search | |||||
| DFA (weighted) | |||||
| PAC Bayesian l earning | |||||
| KNN-PAC Bayesian | |||||
| SDC | |||||
| Detrend SDC | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palanisamy, S.; Rajaguru, H. Machine Learning Techniques for the Performance Enhancement of Multiple Classifiers in the Detection of Cardiovascular Disease from PPG Signals. Bioengineering 2023, 10, 678. https://doi.org/10.3390/bioengineering10060678
Palanisamy S, Rajaguru H. Machine Learning Techniques for the Performance Enhancement of Multiple Classifiers in the Detection of Cardiovascular Disease from PPG Signals. Bioengineering. 2023; 10(6):678. https://doi.org/10.3390/bioengineering10060678
Chicago/Turabian StylePalanisamy, Sivamani, and Harikumar Rajaguru. 2023. "Machine Learning Techniques for the Performance Enhancement of Multiple Classifiers in the Detection of Cardiovascular Disease from PPG Signals" Bioengineering 10, no. 6: 678. https://doi.org/10.3390/bioengineering10060678
APA StylePalanisamy, S., & Rajaguru, H. (2023). Machine Learning Techniques for the Performance Enhancement of Multiple Classifiers in the Detection of Cardiovascular Disease from PPG Signals. Bioengineering, 10(6), 678. https://doi.org/10.3390/bioengineering10060678









