Monocular 3D Human Pose Markerless Systems for Gait Assessment
Abstract
1. Introduction
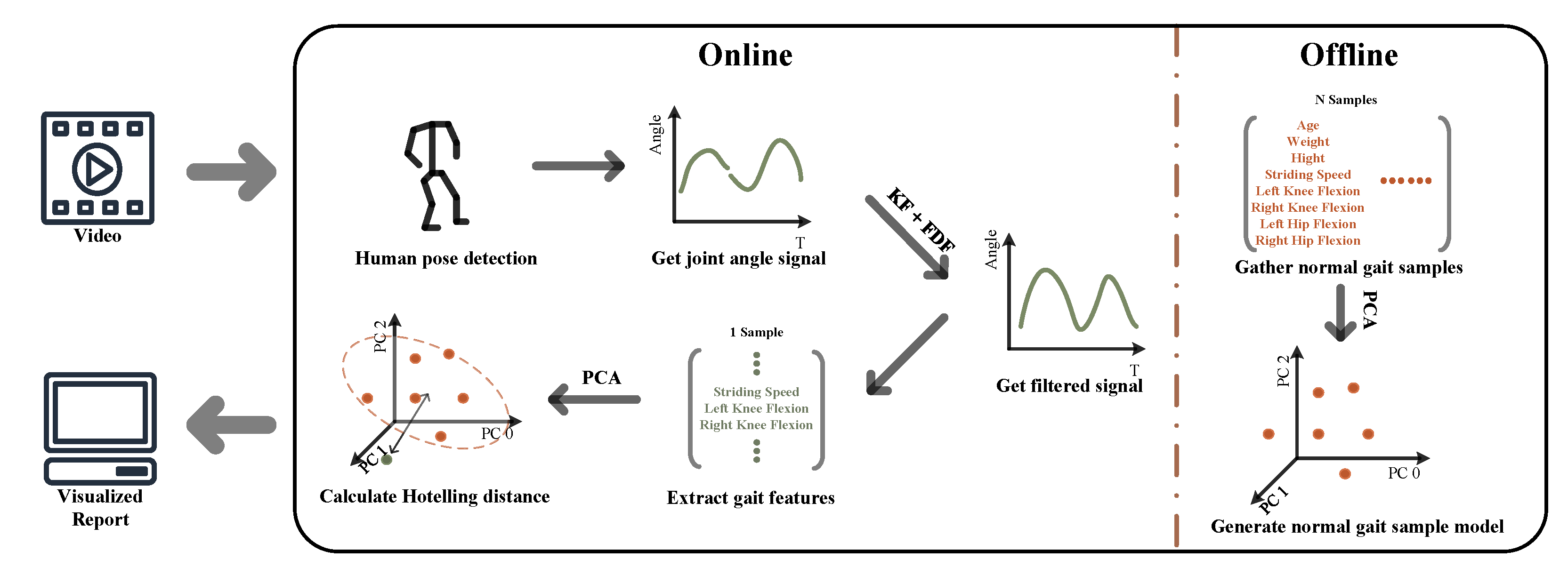
2. Methodology
- 1.
- Generating gait signals by computing joint angles.
- 2.
- Processing gait signals to complement the missing signals and removing any noise from the signals.
- 3.
- Creating a feature model by extracting the discrete gait parameters from gait signals.
2.1. Generate Gait Signals
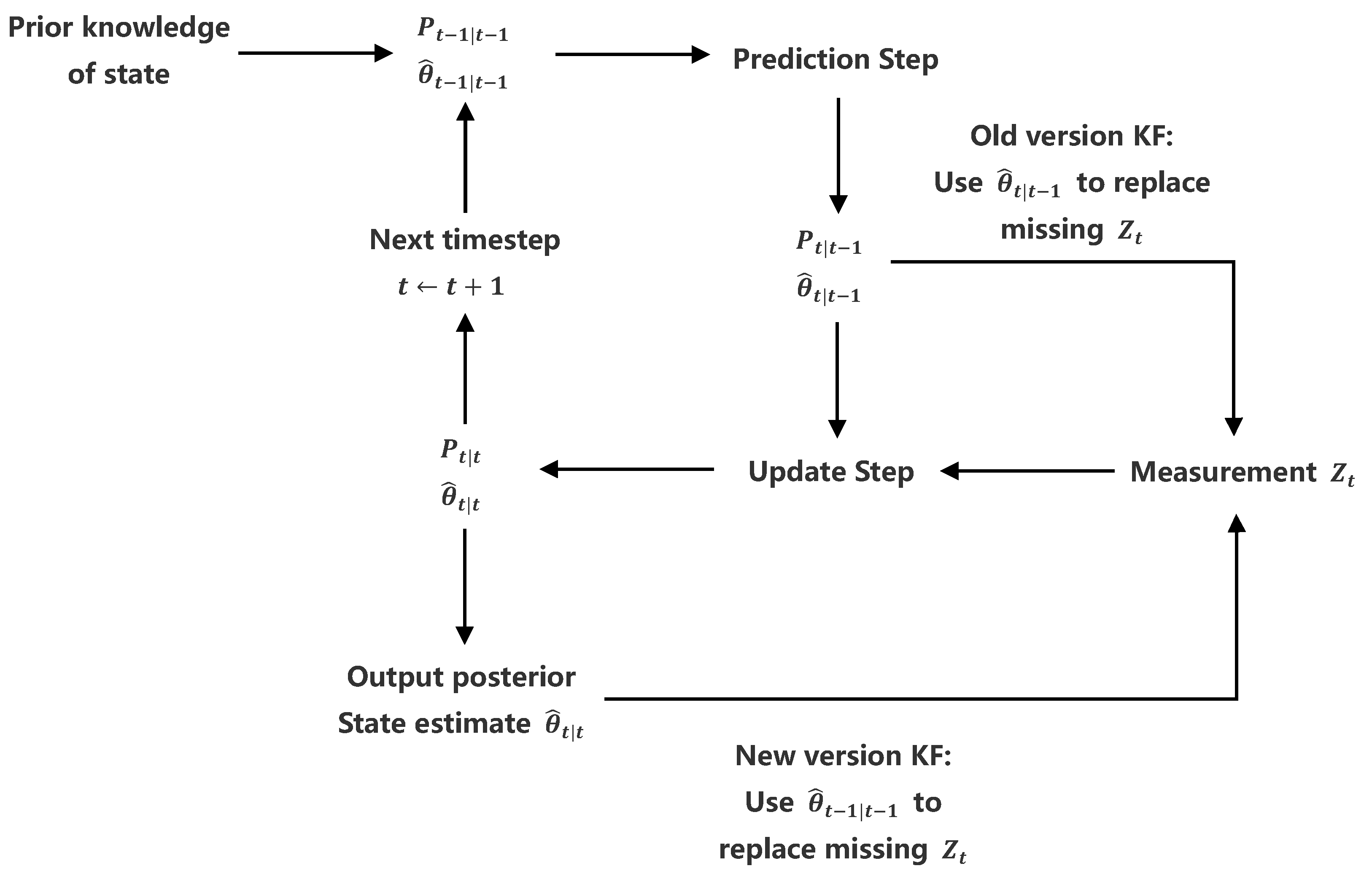
2.2. Post-Process Gait Signals
2.3. Gait Parameters Analysis
3. Experiment Results
3.1. Evaluation Metrics
3.2. Datasets
3.3. Hyper-Parameters Setting
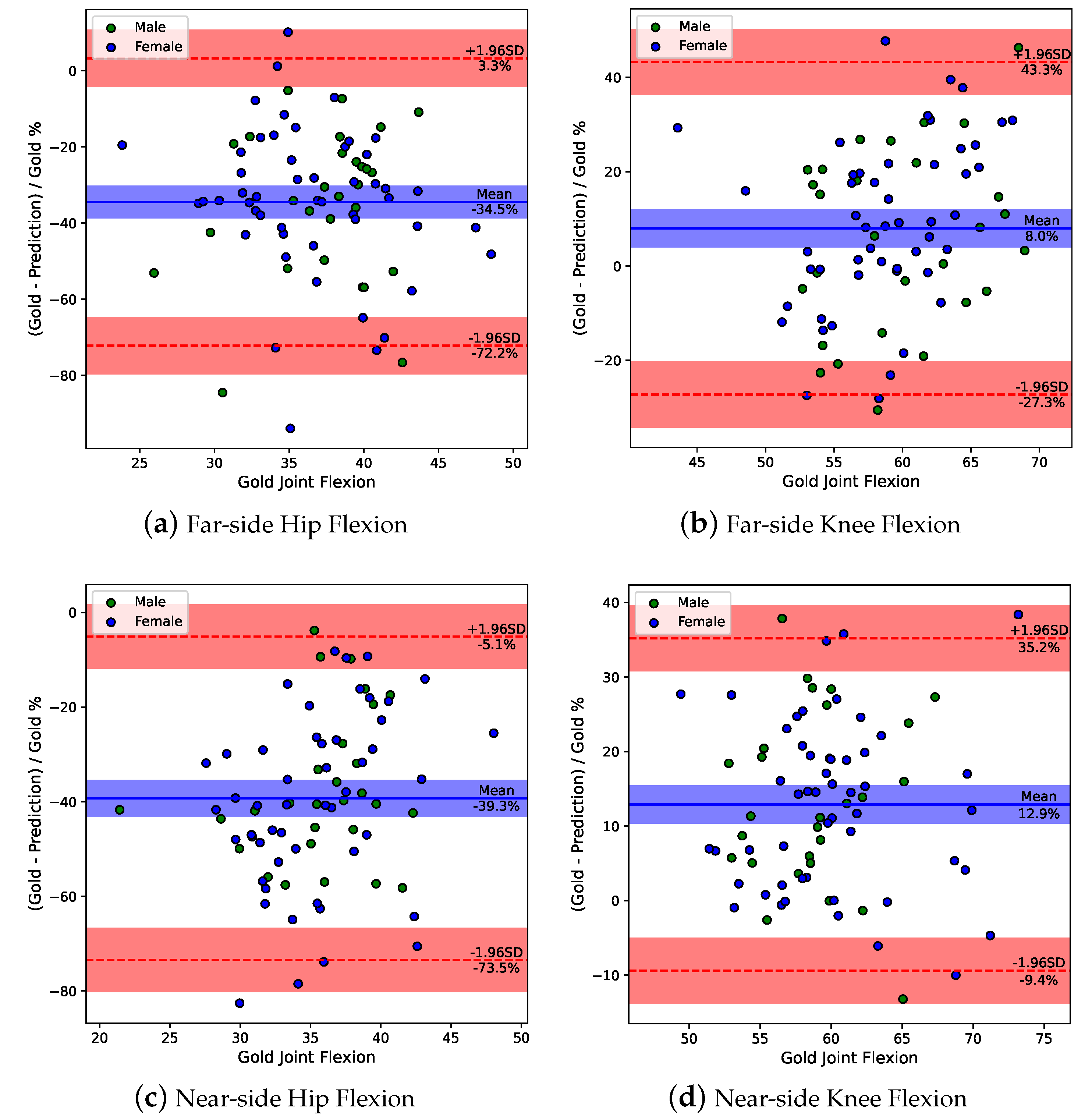
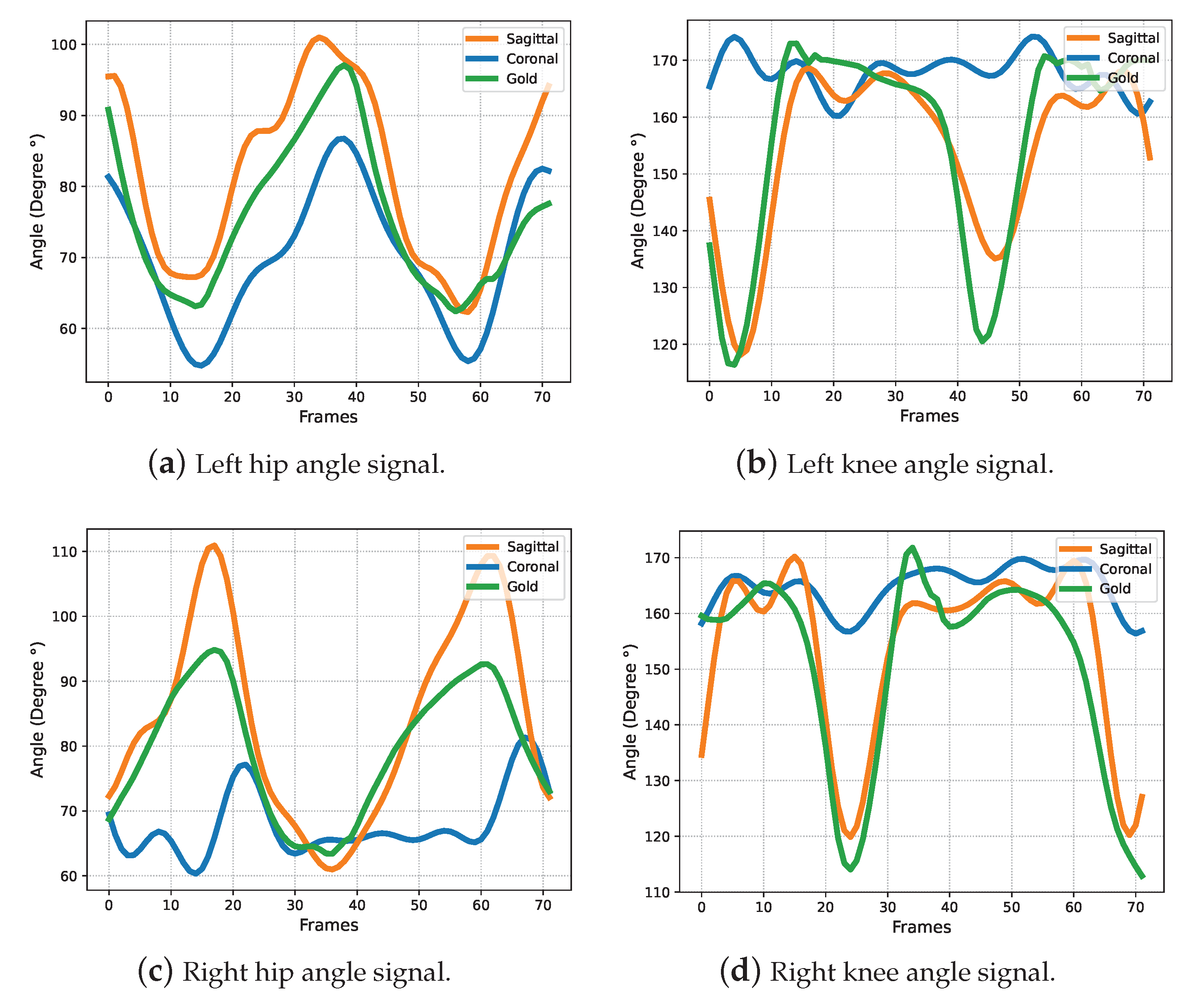
3.4. System Performance Evaluation
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Biggs, P.; Holsgaard-Larsen, A.; Holt, C.A.; Naili, J.E. Gait function improvements, using Cardiff Classifier, are related to patient-reported function and pain following hip arthroplasty. J. Orthop. Res. 2022, 40, 1182–1193. [Google Scholar] [CrossRef]
- Green, D.J.; Panizzolo, F.A.; Lloyd, D.G.; Rubenson, J.; Maiorana, A.J. Soleus Muscle as a Surrogate for Health Status in Human Heart Failure. Exerc. Sport Sci. Rev. 2016, 44, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Sliwinski, M.; Sisto, S. Gait, quality of life, and their association following total hip arthroplasty. J. Geriatr. Phys. Ther. 2006, 29, 8–15. [Google Scholar]
- Brandes, M.; Schomaker, R.; Möllenhoff, G.; Rosenbaum, D. Quantity versus quality of gait and quality of life in patients with osteoarthritis. Gait Posture 2008, 28, 74–79. [Google Scholar] [CrossRef]
- Chia, K.; Fischer, I.; Thomason, P.; Graham, H.K.; Sangeux, M. A Decision Support System to Facilitate Identification of Musculoskeletal Impairments and Propose Recommendations Using Gait Analysis in Children With Cerebral Palsy. Front. Bioeng. Biotechnol. 2020, 8, 529415. [Google Scholar] [CrossRef]
- Liew, B.X.W.; Rügamer, D.; Zhai, X.; Wang, Y.; Morris, S.; Netto, K. Comparing shallow, deep, and transfer learning in predicting joint moments in running. J. Biomech. 2021, 129, 110820. [Google Scholar] [CrossRef] [PubMed]
- Topley, M.; Richards, J.G. A comparison of currently available optoelectronic motion capture systems. J. Biomech. 2020, 106, 109820. [Google Scholar] [CrossRef]
- Muro-de-la Herran, A.; García-Zapirain, B.; Méndez-Zorrilla, A. Gait analysis methods: An overview of wearable and non-wearable systems, highlighting clinical applications. Sensors 2014, 14, 3362–3394. [Google Scholar] [CrossRef]
- Boukhennoufa, I.; Zhai, X.; Utti, V.; Jackson, J.; McDonald-Maier, K.D. Wearable sensors and machine learning in post-stroke rehabilitation assessment: A systematic review. Biomed. Signal Process. Control. 2022, 71, 103197. [Google Scholar] [CrossRef]
- Fernández-González, P.; Koutsou, A.; Cuesta-Gómez, A.; Carratalá-Tejada, M.; Miangolarra-Page, J.C.; Molina-Rueda, F. Reliability of kinovea® software and agreement with a three-dimensional motion system for gait analysis in healthy subjects. Sensors 2020, 20, 3154. [Google Scholar] [CrossRef]
- D’Antonio, E.; Taborri, J.; Mileti, I.; Rossi, S.; Patane, F. Validation of a 3D Markerless System for Gait Analysis Based on OpenPose and Two RGB Webcams. IEEE Sensors J. 2021, 21, 17064–17075. [Google Scholar] [CrossRef]
- Ye, M.; Yang, C.; Stankovic, V.; Stankovic, L.; Kerr, A. A Depth Camera Motion Analysis Framework for Tele-rehabilitation: Motion Capture and Person-Centric Kinematics Analysis. IEEE J. Sel. Top. Signal Process. 2016, 10, 877–887. [Google Scholar] [CrossRef]
- Needham, L.; Evans, M.; Cosker, D.P.; Wade, L.; McGuigan, P.M.; Bilzon, J.L.; Colyer, S.L. The accuracy of several pose estimation methods for 3D joint centre localisation. Sci. Rep. 2021, 11, 20673. [Google Scholar] [CrossRef] [PubMed]
- Liang, S.; Zhang, Y.; Diao, Y.; Li, G.; Zhao, G. The reliability and validity of gait analysis system using 3D markerless pose estimation algorithms. Front. Bioeng. Biotechnol. 2022, 10, 857975. [Google Scholar] [CrossRef]
- Zhu, X.; Boukhennoufa, I.; Liew, B.; McDonald-Maier, K.D.; Zhai, X. A Kalman Filter based Approach for Markerless Pose Tracking and Assessment. In Proceedings of the 2022 27th International Conference on Automation and Computing (ICAC), Bristol, UK, 1–3 September 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Bazarevsky, V.; Grishchenko, I.; Raveendran, K.; Zhu, T.; Zhang, F.; Grundmann, M. BlazePose: On-device Real-time Body Pose tracking. arXiv 2020, arXiv:2006.10204. Available online: http://xxx.lanl.gov/abs/2006.10204 (accessed on 25 April 2023).
- Cao, Z.; Hidalgo Martinez, G.; Simon, T.; Wei, S.; Sheikh, Y.A. OpenPose: Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 43, 172–186. [Google Scholar] [CrossRef]
- Bittner, M.; Yang, W.T.; Zhang, X.; Seth, A.; van Gemert, J.; van der Helm, F.C. Towards Single Camera Human 3D-Kinematics. Sensors 2022, 23, 341. [Google Scholar] [CrossRef]
- Mroz, S.; Baddour, N.; McGuirk, C.; Juneau, P.; Tu, A.; Cheung, K.; Lemaire, E. Comparing the quality of human pose estimation with blazepose or openpose. In Proceedings of the 2021 4th International Conference on Bio-Engineering for Smart Technologies (BioSMART), Paris, France, 8–10 December 2021; IEEE: New York, NY, USA, 2021; pp. 1–4. [Google Scholar]
- Ghorbani, S.; Mahdaviani, K.; Thaler, A.; Kording, K.; Cook, D.J.; Blohm, G.; Troje, N.F. MoVi: A large multi-purpose human motion and video dataset. PLoS ONE 2021, 16, e0253157. [Google Scholar] [CrossRef] [PubMed]
- Welch, G.F. Kalman Filter. In Computer Vision: A Reference Guide; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–3. [Google Scholar] [CrossRef]
- HandWiki. Kalman Filter. HandWiki. 2022. Available online: https://handwiki.org/wiki/Kalman_filter (accessed on 25 April 2023).
- De Groote, F.; De Laet, T.; Jonkers, I.; De Schutter, J. Kalman smoothing improves the estimation of joint kinematics and kinetics in marker-based human gait analysis. J. Biomech. 2008, 41, 3390–3398. [Google Scholar] [CrossRef]
- Błażkiewicz, M.; Lace, K.L.V.; Hadamus, A. Gait symmetry analysis based on dynamic time warping. Symmetry 2021, 13, 836. [Google Scholar] [CrossRef]
- Yu, X.; Xiong, S. A dynamic time warping based algorithm to evaluate Kinect-enabled home-based physical rehabilitation exercises for older people. Sensors 2019, 19, 2882. [Google Scholar] [CrossRef] [PubMed]
- Mansournia, M.A.; Waters, R.; Nazemipour, M.; Bland, M.; Altman, D.G. Bland-Altman methods for comparing methods of measurement and response to criticisms. Glob. Epidemiol. 2021, 3, 100045. [Google Scholar] [CrossRef]
- Vesna, I. Understanding Bland Altman Analysis. Biochem. Medica 2009, 19, 10–16. [Google Scholar]
- Gu, X.; Deligianni, F.; Lo, B.; Chen, W.; Yang, G.Z. Markerless gait analysis based on a single RGB camera. In Proceedings of the 2018 IEEE 15th International Conference on Wearable and Implantable Body Sensor Networks, BSN 2018, Las Vegas, NV, USA, 4–7 March 2018; pp. 42–45. [Google Scholar] [CrossRef]
- Nagymáté, G.; Kiss, R.M. Affordable gait analysis using augmented reality markers. PLoS ONE 2019, 14, e0212319. [Google Scholar] [CrossRef] [PubMed]


| Subject | Gender | Age | Cut Interval | Subject | Gender | Age | Cut Interval |
|---|---|---|---|---|---|---|---|
| 3 | male | 26 | (900, 950) | 48 | female | 18 | (4700, 4760) |
| 4 | male | 26 | (1335, 1390) | 49 | female | 23 | (1700, 1810) |
| 5 | male | 23 | (836, 890) | 50 | female | 18 | (1900, 1990) |
| 8 | female | 22 | (2020, 2100) | 51 | female | 18 | (2360, 2420) |
| 10 | female | 24 | (680, 770) | 53 | female | 23 | (2550, 2650) |
| 11 | male | 27 | (4194, 4277) | 54 | female | 18 | (990, 1060) |
| 12 | female | 26 | (3465, 3535) | 55 | female | 20 | (4370, 4420) |
| 13 | male | 26 | (2365, 2420) | 56 | female | 19 | (3500, 3560) |
| 15 | male | 21 | (3460, 3530) | 57 | female | 17 | (640, 720) |
| 16 | female | 26 | (210, 280) | 58 | female | 18 | (3680, 3760) |
| 17 | female | 26 | (2590, 2660) | 59 | female | 18 | (3920, 3990) |
| 18 | male | 25 | (1132, 1212) | 60 | male | 21 | (2930, 3020) |
| 19 | male | 18 | (3250, 3320) | 61 | female | 18 | (1850, 1925) |
| 20 | male | 29 | (690, 760) | 62 | female | 17 | (3710, 3770) |
| 22 | male | 28 | (1218, 1284) | 64 | female | 18 | (3600, 3680) |
| 23 | male | 25 | (2095, 2140) | 65 | female | 19 | (3940, 4020) |
| 24 | female | 20 | (1130, 1220) | 66 | female | 18 | (2020, 2100) |
| 25 | female | 21 | (2920, 2970) | 67 | female | 18 | (4410, 4490) |
| 26 | male | 24 | (3690, 3780) | 68 | female | 20 | (2870, 2930) |
| 27 | male | 23 | (3465, 3552) | 69 | female | 19 | (1310, 1390) |
| 28 | male | 25 | (2605, 2675) | 70 | female | 17 | (820, 890) |
| 30 | female | 19 | (4310, 4380) | 71 | male | 18 | (360, 420) |
| 31 | male | 28 | (3305, 3375) | 72 | female | 20 | (3760, 3830) |
| 32 | female | 20 | (3740, 3805) | 73 | female | 18 | (500, 580) |
| 33 | male | 21 | (290, 350) | 74 | female | 19 | (2020, 2100) |
| 34 | female | 21 | (680, 740) | 75 | male | 19 | (1720, 1780) |
| 35 | male | 29 | (4508, 4588) | 76 | female | 19 | (3340, 3440) |
| 36 | male | 29 | (860, 920) | 77 | female | 19 | (1650, 1730) |
| 37 | male | 21 | (4610, 4690) | 78 | female | 18 | (730, 790) |
| 38 | female | 32 | (250, 350) | 79 | female | 19 | (3780, 3840) |
| 39 | female | 21 | (410, 475) | 80 | female | 19 | (2560, 2620) |
| 40 | female | 21 | (3866, 3950) | 81 | female | 18 | (3990, 4060) |
| 41 | male | 28 | (1860, 1910) | 82 | female | 17 | (2420, 2520) |
| 42 | male | 21 | (2020, 2080) | 84 | female | 20 | (3130, 3190) |
| 43 | male | 21 | (2460, 2540) | 85 | female | 19 | (2880, 2970) |
| 44 | female | 20 | (2710, 2770) | 86 | female | 18 | (2180, 2250) |
| 45 | female | 18 | (480, 550) | 87 | male | 18 | (1830, 1890) |
| 46 | male | 21 | (2960, 3040) | 88 | female | 19 | (3390, 3460) |
| 47 | male | 18 | (5200, 5255) | 89 | female | 21 | (3580, 3650) |
| Far-Side (Knee & Hip) | Near-Side (Knee & Hip) | ||||
|---|---|---|---|---|---|
| DTW | PE | DTW | PE | ||
| 0.001 | 0.001 | 9.88 | 80.92% | 5.39 | 45.37% |
| 10 | 10 | 7.75 | 61.64% | 5.30 | 44.89% |
| 10 | 1 | 7.72 | 58.85% | 5.36 | 42.86% |
| 10 | 0.1 | 7.77 | 58.49% | 5.38 | 42.57% |
| 1 | 1 | 7.75 | 62.18% | 5.31 | 44.99% |
| 1 | 0.1 | 7.70 | 58.89% | 5.36 | 42.88% |
| 1 | 0.01 | 7.76 | 58.49% | 5.38 | 42.57% |
| 0.1 | 0.1 | 7.64 | 62.55% | 5.34 | 45.18% |
| 0.1 | 0.01 | 7.65 | 58.85% | 5.37 | 42.91% |
| 0.1 | 0.001 | 7.76 | 58.48% | 5.38 | 42.57% |
| 0.01 | 0.01 | 7.52 | 62.46% | 5.37 | 45.32% |
| 0.01 | 0.001 | 7.62 | 58.72% | 5.37 | 42.94% |
| 0.01 | 0.0001 | 7.75 | 58.46% | 5.38 | 42.57% |
| 0.001 | 0.001 | 7.50 | 62.16% | 5.39 | 45.37% |
| 0.001 | 0.0001 | 7.60 | 58.62% | 5.38 | 42.95% |
| Method | Far-Side | Near-Side | Average | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Knee | Hip | Knee | Hip | |||||||
| DTW | PE | DTW | PE | DTW | PE | DTW | PE | DTW | PE | |
| 5.08 | 36.11% | 4.85 | 45.00% | 2.91 | 18.27% | 2.48 | 27.15% | 3.83 | 31.63% | |
| 4.17 | 25.81% | 3.46 | 32.88% | 2.94 | 17.33% | 2.43 | 25.57% | 3.25 | 25.40% | |
| Original signal | 4.59 | 25.93% | 4.05 | 37.71% | 2.95 | 17.90% | 2.98 | 27.77% | 3.64 | 27.32% |
| Gender | PC | Explained Variance | Cosine Similarity | |
|---|---|---|---|---|
| Predictions | Gold-Standard | |||
| Female | 0 | 26.45% | 30.11% | 0.89 |
| 1 | 18.64% | 17.61% | 0.78 | |
| 2 | 13.86% | 16.07% | 0.83 | |
| 3 | 12.13% | 11.08% | 0.71 | |
| Male | 0 | 25.61% | 38.12% | 0.65 |
| 1 | 21.55% | 21.01% | 0.72 | |
| 2 | 17.13% | 13.42% | 0.15 | |
| 3 | 12.20% | 10.61% | 0.13 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Boukhennoufa, I.; Liew, B.; Gao, C.; Yu, W.; McDonald-Maier, K.D.; Zhai, X. Monocular 3D Human Pose Markerless Systems for Gait Assessment. Bioengineering 2023, 10, 653. https://doi.org/10.3390/bioengineering10060653
Zhu X, Boukhennoufa I, Liew B, Gao C, Yu W, McDonald-Maier KD, Zhai X. Monocular 3D Human Pose Markerless Systems for Gait Assessment. Bioengineering. 2023; 10(6):653. https://doi.org/10.3390/bioengineering10060653
Chicago/Turabian StyleZhu, Xuqi, Issam Boukhennoufa, Bernard Liew, Cong Gao, Wangyang Yu, Klaus D. McDonald-Maier, and Xiaojun Zhai. 2023. "Monocular 3D Human Pose Markerless Systems for Gait Assessment" Bioengineering 10, no. 6: 653. https://doi.org/10.3390/bioengineering10060653
APA StyleZhu, X., Boukhennoufa, I., Liew, B., Gao, C., Yu, W., McDonald-Maier, K. D., & Zhai, X. (2023). Monocular 3D Human Pose Markerless Systems for Gait Assessment. Bioengineering, 10(6), 653. https://doi.org/10.3390/bioengineering10060653