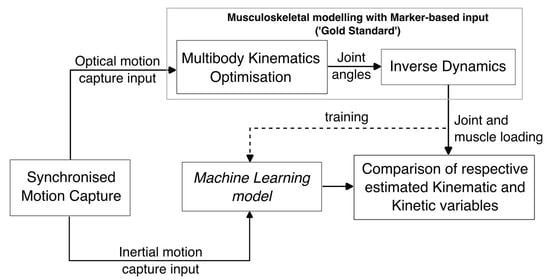
Machine Learning for Optical Motion Capture-Driven Musculoskeletal Modelling from Inertial Motion Capture Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
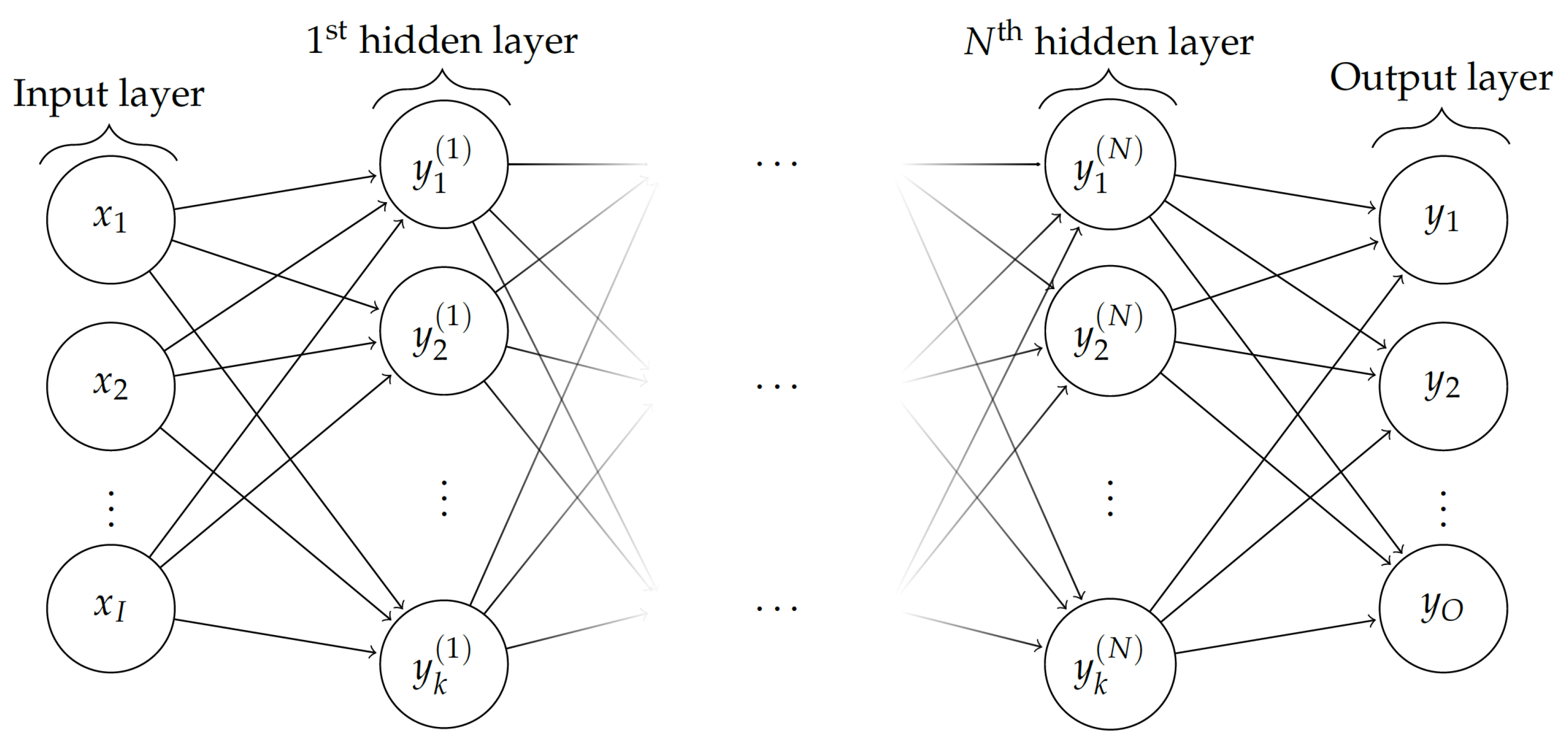
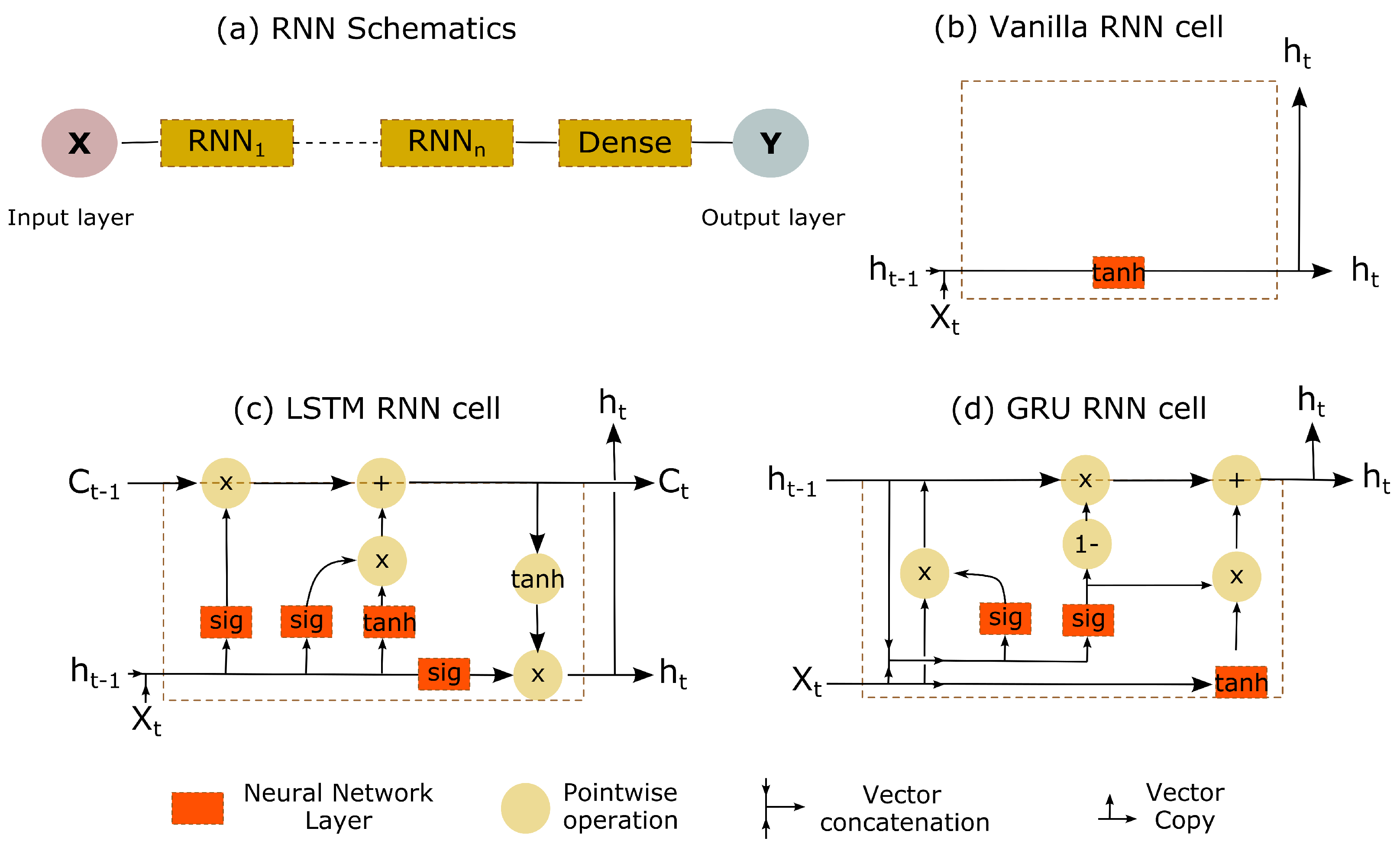
2.2. Supervised Learning
- The time feature, normalised between zero and one, indicates the proportion of total time taken to complete the task at the subject’s chosen pace.
- Muscles are typically discretised into numerous muscle bundles in MSK models. MSK model outputs for muscle activations and muscle forces comprise features for the four considered superficial muscle groups, i.e., (a) Biceps Brachii, (b) Pectoralis major (Clavicle part), (c) Brachioradialis, and (d) Deltoid (Medial) [49]. The ‘maximum envelope’ of the tendon forces of specified bundles forming a certain muscle was calculated for further analysis. Muscle activation measures the force in a selected muscle relative to its strength.
- We have used many-to-one RNN architecture, which uses multiple previous inputs for an output; therefore, we transformed the time-series data into a sub-time-series of t frames by sliding across the original time-series in a step of one. Thus, the input of the RNN is , where t was taken as 10.
2.3. Validation and Train–Test Split
2.4. Error Metrics
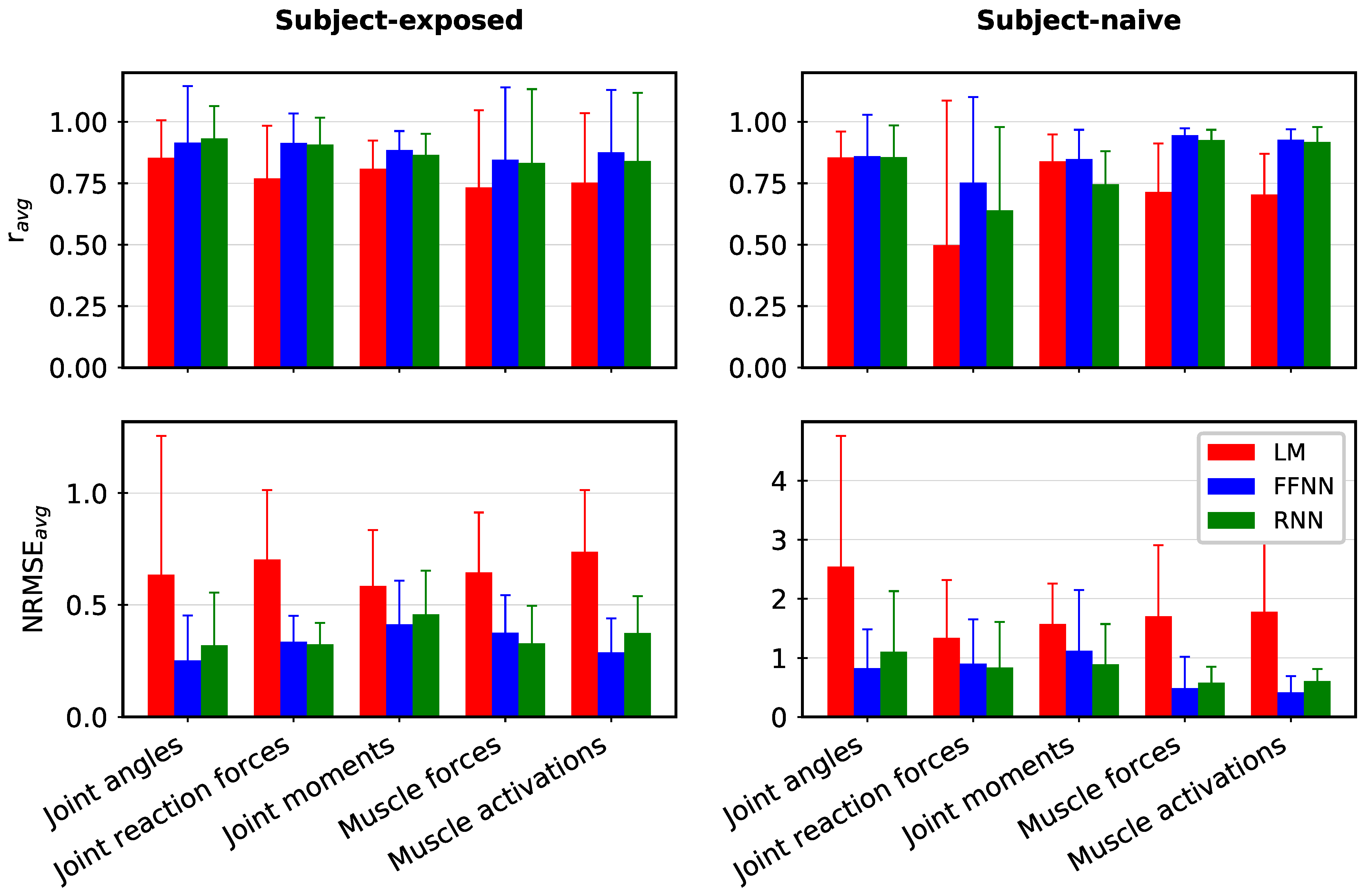
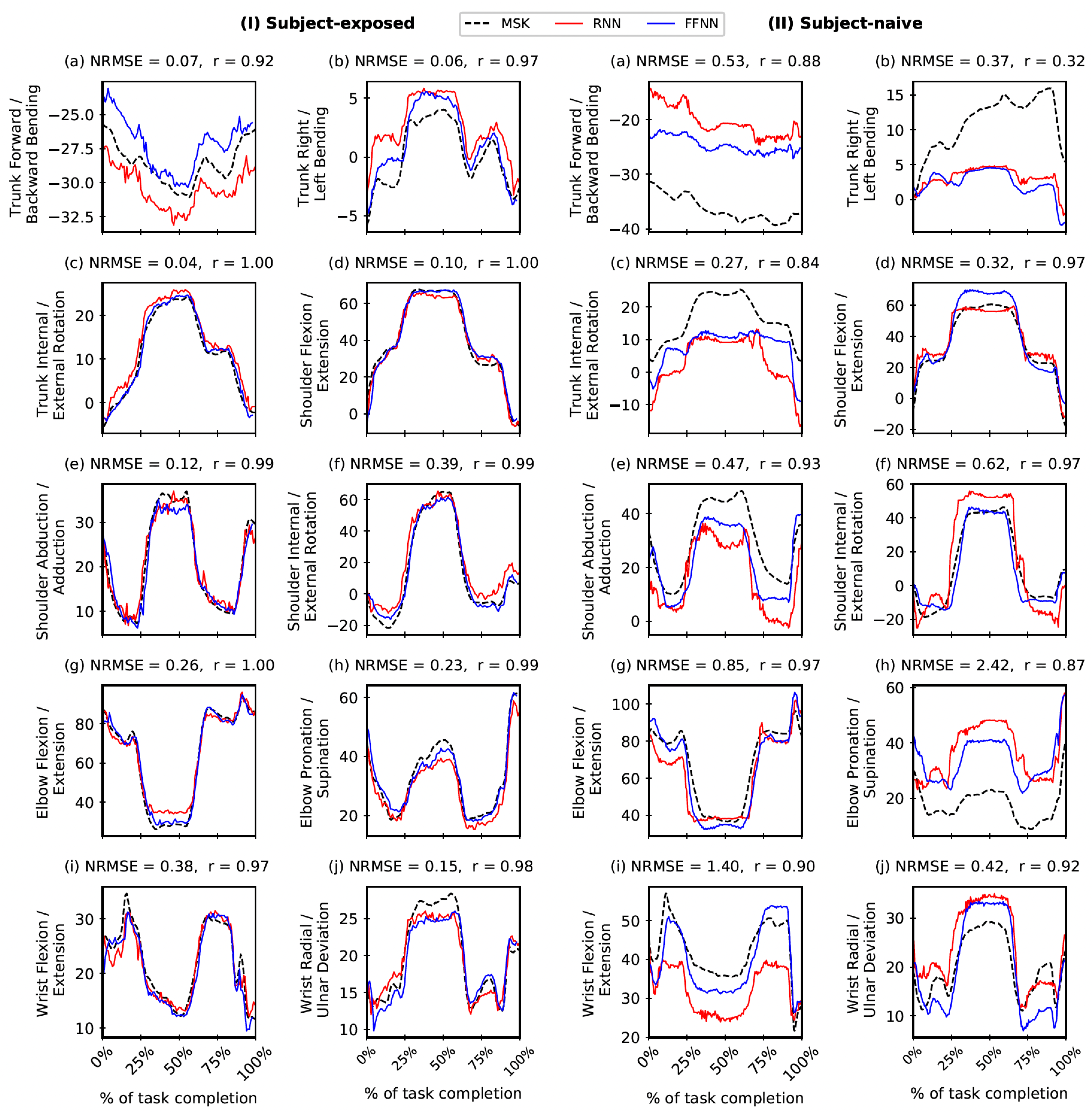
3. Results
4. Discussion
5. Study Limitations
6. Recommended Future Work
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rau, G.; Disselhorst-Klug, C.; Schmidt, R. Movement biomechanics goes upwards: From the leg to the arm. J. Biomech. 2000, 33, 1207–1216. [Google Scholar] [CrossRef] [PubMed]
- Anglin, C.; Wyss, U. Review of arm motion analyses. J. Eng. Med. 2000, 214, 541–555. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, A.; McLean, S.; Herzog, W.; van den Bogert, A.J. Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 2007, 22, 131–154. [Google Scholar] [CrossRef] [PubMed]
- Killen, B.A.; Falisse, A.; De Groote, F.; Jonkers, I. In Silico-Enhanced Treatment and Rehabilitation Planning for Patients with Musculoskeletal Disorders: Can Musculoskeletal Modelling and Dynamic Simulations Really Impact Current Clinical Practice? Appl. Sci. 2020, 10, 7255. [Google Scholar] [CrossRef]
- Smith, S.H.; Coppack, R.J.; van den Bogert, A.J.; Bennett, A.N.; Bull, A.M. Review of musculoskeletal modelling in a clinical setting: Current use in rehabilitation design, surgical decision making and healthcare interventions. Clin. Biomech. 2021, 83, 105292. [Google Scholar] [CrossRef]
- Fregly, B.J. A Conceptual Blueprint for Making Neuromusculoskeletal Models Clinically Useful. Appl. Sci. 2021, 11, 2037. [Google Scholar] [CrossRef]
- Zhou, H.; Hu, H. Human motion tracking for rehabilitation—A survey. Biomed. Signal Process. Control 2008, 3, 1–18. [Google Scholar] [CrossRef]
- Cappozzo, A.; Della Croce, U.; Leardini, A.; Chiari, L. Human movement analysis using stereophotogrammetry: Part 1: Theoretical background. Gait Posture 2005, 21, 186–196. [Google Scholar]
- Jung, E.; Lin, C.; Contreras, M.; Teodorescu, M. Applied Machine Learning on Phase of Gait Classification and Joint-Moment Regression. Biomechanics 2022, 2, 44–65. [Google Scholar] [CrossRef]
- Iosa, M.; Picerno, P.; Paolucci, S.; Morone, G. Wearable inertial sensors for human movement analysis. Expert Rev. Med. Devices 2016, 13, 641–659. [Google Scholar] [CrossRef]
- Picerno, P.; Iosa, M.; D’Souza, C.; Benedetti, M.G.; Paolucci, S.; Morone, G. Wearable inertial sensors for human movement analysis: A five-year update. Expert Rev. Med. Devices 2021, 18, 1–16. [Google Scholar] [CrossRef]
- Verheul, J.; Nedergaard, N.J.; Vanrenterghem, J.; Robinson, M.A. Measuring biomechanical loads in team sports—From lab to field. Sci. Med. Footb. 2020, 4, 246–252. [Google Scholar] [CrossRef]
- Saxby, D.J.; Killen, B.A.; Pizzolato, C.; Carty, C.; Diamond, L.; Modenese, L.; Fernandez, J.; Davico, G.; Barzan, M.; Lenton, G.; et al. Machine learning methods to support personalized neuromusculoskeletal modelling. Biomech. Model. Mechanobiol. 2020, 19, 1169–1185. [Google Scholar] [CrossRef] [PubMed]
- Arac, A. Machine learning for 3D kinematic analysis of movements in neurorehabilitation. Curr. Neurol. Neurosci. Rep. 2020, 20, 1–6. [Google Scholar] [CrossRef]
- Frangoudes, F.; Matsangidou, M.; Schiza, E.C.; Neokleous, K.; Pattichis, C.S. Assessing Human Motion During Exercise Using Machine Learning: A Literature Review. IEEE Access 2022, 10, 86874–86903. [Google Scholar] [CrossRef]
- Damsgaard, M.; Rasmussen, J.; Christensen, S.T.; Surma, E.; De Zee, M. Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 2006, 14, 1100–1111. [Google Scholar] [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Karatsidis, A.; Jung, M.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Veltink, P.H.; Andersen, M.S. Musculoskeletal model-based inverse dynamic analysis under ambulatory conditions using inertial motion capture. Med. Eng. Phys. 2019, 65, 68–77. [Google Scholar] [CrossRef] [PubMed]
- Konrath, J.M.; Karatsidis, A.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Andersen, M.S. Estimation of the knee adduction moment and joint contact force during daily living activities using inertial motion capture. Sensors 2019, 19, 1681. [Google Scholar] [CrossRef] [PubMed]
- Nagaraja, V.H.; Cheng, R.; Kwong, E.M.T.; Bergmann, J.H.; Andersen, M.S.; Thompson, M.S. Marker-based vs. Inertial-based Motion Capture: Musculoskeletal Modelling of Upper Extremity Kinetics. In Proceedings of the ISPO Trent International Prosthetics Symposium (TIPS) 2019, ISPO, Manchester, UK, 20–22 March 2019; pp. 37–38. [Google Scholar]
- Larsen, F.G.; Svenningsen, F.P.; Andersen, M.S.; De Zee, M.; Skals, S. Estimation of spinal loading during manual materials handling using inertial motion capture. Ann. Biomed. Eng. 2020, 48, 805–821. [Google Scholar] [CrossRef]
- Skals, S.; Bláfoss, R.; Andersen, L.L.; Andersen, M.S.; de Zee, M. Manual material handling in the supermarket sector. Part 2: Knee, spine and shoulder joint reaction forces. Appl. Ergon. 2021, 92, 103345. [Google Scholar] [CrossRef] [PubMed]
- Di Raimondo, G.; Vanwanseele, B.; Van der Have, A.; Emmerzaal, J.; Willems, M.; Killen, B.A.; Jonkers, I. Inertial Sensor-to-Segment Calibration for Accurate 3D Joint Angle Calculation for Use in OpenSim. Sensors 2022, 22, 3259. [Google Scholar] [CrossRef] [PubMed]
- Philp, F.; Freeman, R.; Stewart, C. An international survey mapping practice and barriers for upper-limb assessments in movement analysis. Gait Posture 2022, 96, 93–101. [Google Scholar] [CrossRef] [PubMed]
- Halilaj, E.; Rajagopal, A.; Fiterau, M.; Hicks, J.L.; Hastie, T.J.; Delp, S.L. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 2018, 81, 1–11. [Google Scholar] [CrossRef]
- Xiang, L.; Wang, A.; Gu, Y.; Zhao, L.; Shim, V.; Fernandez, J. Recent Machine Learning Progress in Lower Limb Running Biomechanics with Wearable Technology: A Systematic Review. Front. Neurorobot. 2022, 16, 913052. [Google Scholar] [CrossRef]
- Cronin, N.J. Using deep neural networks for kinematic analysis: Challenges and opportunities. J. Biomech. 2021, 123, 110460. [Google Scholar] [CrossRef]
- Amrein, S.; Werner, C.; Arnet, U.; de Vries, W.H. Machine-Learning-Based Methodology for Estimation of Shoulder Load in Wheelchair-Related Activities Using Wearables. Sensors 2023, 23, 1577. [Google Scholar] [CrossRef]
- Lee, C.J.; Lee, J.K. Inertial Motion Capture-Based Wearable Systems for Estimation of Joint Kinetics: A Systematic Review. Sensors 2022, 22, 2507. [Google Scholar] [CrossRef]
- Sharma, R.; Dasgupta, A.; Cheng, R.; Mishra, C.; Nagaraja, V.H. Machine Learning for Musculoskeletal Modeling of Upper Extremity. IEEE Sens. J. 2022, 22, 18684–18697. [Google Scholar] [CrossRef]
- Wouda, F.J.; Giuberti, M.; Bellusci, G.; Maartens, E.; Reenalda, J.; Van Beijnum, B.J.F.; Veltink, P.H. Estimation of vertical ground reaction forces and sagittal knee kinematics during running using three inertial sensors. Front. Physiol. 2018, 9, 218. [Google Scholar] [CrossRef]
- Fernandez, J.; Dickinson, A.; Hunter, P. Population based approaches to computational musculoskeletal modelling. Biomech. Model Mechanobiol. 2020, 19, 1165–1168. [Google Scholar] [CrossRef] [PubMed]
- Sohane, A.; Agarwal, R. Knee Muscle Force Estimating Model Using Machine Learning Approach. Comput. J. 2022, 65, 1167–1177. [Google Scholar] [CrossRef]
- Mubarrat, S.T.; Chowdhury, S. Convolutional LSTM: A deep learning approach to predict shoulder joint reaction forces. Comput. Methods Biomech. Biomed. Eng. 2023, 26, 65–77. [Google Scholar] [CrossRef] [PubMed]
- Cleather, D.J. Neural network based approximation of muscle and joint contact forces during jumping and landing. J. Hum. Perform. Health 2019, 1, f1–f13. [Google Scholar]
- Giarmatzis, G.; Zacharaki, E.I.; Moustakas, K. Real-Time Prediction of Joint Forces by Motion Capture and Machine Learning. Sensors 2020, 20, 6933. [Google Scholar] [CrossRef] [PubMed]
- Mundt, M.; Koeppe, A.; David, S.; Witter, T.; Bamer, F.; Potthast, W.; Markert, B. Estimation of gait mechanics based on simulated and measured IMU data using an artificial neural network. Front. Bioeng. Biotechnol. 2020, 8, 41. [Google Scholar] [CrossRef]
- Mundt, M.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of ground reaction force and joint moments based on optical motion capture data during gait. Med. Eng. Phys. 2020, 86, 29–34. [Google Scholar] [CrossRef]
- Mundt, M.; Thomsen, W.; Witter, T.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of lower limb joint angles and moments during gait using artificial neural networks. Med. Biol. Eng. Comput. 2020, 58, 211–225. [Google Scholar] [CrossRef]
- Nagaraja, V.; Bergmann, J.; Andersen, M.S.; Thompson, M. Compensatory Movements Involved During Simulated Upper Limb Prosthetic Usage: Reach Task vs. Reach-to-Grasp Task. In Proceedings of the XV ISB International Symposium on 3-D Analysis of Human Movement, ISB, Salford, UK, 3–6 July 2018. [Google Scholar]
- Nagaraja, V.H.; Bergmann, J.H.; Andersen, M.S.; Thompson, M.S. Comparison of a Scaled Cadaver-Based Musculoskeletal Model With a Clinical Upper Extremity Model. J. Biomech. Eng. 2023, 145, 041012. [Google Scholar] [CrossRef]
- Vicon Motion Systems. Plug-In Gait Reference Guide—Vicon Documentation. Available online: https://docs.vicon.com/display/Nexus212/Plug-in+Gait+Reference+Guide (accessed on 6 February 2023).
- Paulich, M.; Schepers, M.; Rudigkeit, N.; Bellusci, G. Xsens MTw Awinda: Miniature Wireless Inertial-Magnetic Motion Tracker for Highly Accurate 3D Kinematic Applications; Xsens: Enschede, The Netherlands, 2018; pp. 1–9. [Google Scholar]
- Xsens MVN User Manual. 2021. Available online: https://www.xsens.com/hubfs/Downloads/usermanual/MVN_User_Manual.pdf (accessed on 6 February 2023).
- Xsens. Syncronising Xsens Systems with Vicon Nexus. 2020. Available online: https://www.xsens.com/hubfs/Downloads/plugins%20%20tools/SynchronisingXsenswithVicon.pdf (accessed on 6 February 2023).
- Vicon Nexus™ 2.5 Manual. What’s New in Vicon Nexus 2.5—Nexus 2.5 Documentation. 2016. Available online: https://docs.vicon.com/display/Nexus25/PDF+downloads+for+Vicon+Nexus?preview=/50888706/50889382/ViconNexusWhatsNew25.pdf (accessed on 6 February 2023).
- Motion Lab Systems. C3D.ORG—The Biomechanics Standard File Format. Available online: https://www.c3d.org (accessed on 6 February 2023).
- MVN Analyze. Available online: https://www.movella.com/products/motion-capture/mvn-analyze#overview (accessed on 6 February 2023).
- Harthikote Nagaraja, V. Motion Capture and Musculoskeletal Simulation Tools to Measure Prosthetic Arm Functionality. Ph.D. Thesis, Department of Engineering Science, University of Oxford, Oxford, UK, 2019. [Google Scholar]
- Moisio, K.C.; Sumner, D.R.; Shott, S.; Hurwitz, D.E. Normalization of joint moments during gait: A comparison of two techniques. J. Biomech. 2003, 36, 599–603. [Google Scholar] [CrossRef]
- Derrick, T.R.; van den Bogert, A.J.; Cereatti, A.; Dumas, R.; Fantozzi, S.; Leardini, A. ISB recommendations on the reporting of intersegmental forces and moments during human motion analysis. J. Biomech. 2020, 99, 109533. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 20 April 2023).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Rane, L.; Ding, Z.; McGregor, A.H.; Bull, A.M. Deep learning for musculoskeletal force prediction. Ann. Biomed. Eng. 2019, 47, 778–789. [Google Scholar] [CrossRef]
- Bicer, M.; Phillips, A.T.; Melis, A.; McGregor, A.H.; Modenese, L. Generative Deep Learning Applied to Biomechanics: A New Augmentation Technique for Motion Capture Datasets. J. Biomech. 2022, 144, 111301. [Google Scholar] [CrossRef] [PubMed]
- Leardini, A.; Chiari, L.; Della Croce, U.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 3. Soft tissue artifact assessment and compensation. Gait Posture 2005, 21, 212–225. [Google Scholar] [CrossRef]
- Chiari, L.; Della Croce, U.; Leardini, A.; Cappozzo, A. Human movement analysis using stereophotogrammetry: Part 2: Instrumental errors. Gait Posture 2005, 21, 197–211. [Google Scholar] [CrossRef]
- Camomilla, V.; Dumas, R.; Cappozzo, A. Human movement analysis: The soft tissue artefact issue. J. Biomech. 2017, 62, 1. [Google Scholar] [CrossRef] [PubMed]
- Hicks, J.L.; Uchida, T.K.; Seth, A.; Rajagopal, A.; Delp, S.L. Is my model good enough? Best practices for verification and validation of musculoskeletal models and simulations of movement. J. Biomech. Eng. 2015, 137, 020905. [Google Scholar] [CrossRef]
- Wang, J.M.; Hamner, S.R.; Delp, S.L.; Koltun, V. Optimizing locomotion controllers using biologically-based actuators and objectives. ACM Trans. Graph. TOG 2012, 31, 1–11. [Google Scholar] [CrossRef]
- Miller, R.H.; Umberger, B.R.; Hamill, J.; Caldwell, G.E. Evaluation of the minimum energy hypothesis and other potential optimality criteria for human running. Proc. R. Soc. Biol. Sci. 2012, 279, 1498–1505. [Google Scholar] [CrossRef]
- Van den Bogert, A.J.; Geijtenbeek, T.; Even-Zohar, O.; Steenbrink, F.; Hardin, E.C. A real-time system for biomechanical analysis of human movement and muscle function. Med. Biol. Eng. Comput. 2013, 51, 1069–1077. [Google Scholar] [CrossRef]
- Pizzolato, C.; Reggiani, M.; Modenese, L.; Lloyd, D. Real-time inverse kinematics and inverse dynamics for lower limb applications using OpenSim. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 436–445. [Google Scholar] [CrossRef]
- Pizzolato, C.; Reggiani, M.; Saxby, D.J.; Ceseracciu, E.; Modenese, L.; Lloyd, D.G. Biofeedback for gait retraining based on real-time estimation of tibiofemoral joint contact forces. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1612–1621. [Google Scholar] [CrossRef] [PubMed]
- Lund, M.E.; de Zee, M.; Andersen, M.S.; Rasmussen, J. On validation of multibody musculoskeletal models. J. Eng. Med. 2012, 226, 82–94. [Google Scholar] [CrossRef]
- Wagner, D.W.; Stepanyan, V.; Shippen, J.M.; DeMers, M.S.; Gibbons, R.S.; Andrews, B.J.; Creasey, G.H.; Beaupre, G.S. Consistency among musculoskeletal models: Caveat utilitor. Ann. Biomed. Eng. 2013, 41, 1787–1799. [Google Scholar] [CrossRef]
- Cereatti, A.; Bonci, T.; Akbarshahi, M.; Aminian, K.; Barré, A.; Begon, M.; Benoit, D.L.; Charbonnier, C.; Dal Maso, F.; Fantozzi, S.; et al. Standardization proposal of soft tissue artefact description for data sharing in human motion measurements. J. Biomech. 2017, 62, 5–13. [Google Scholar] [CrossRef] [PubMed]
- Fregly, B.J.; Besier, T.F.; Lloyd, D.G.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’lima, D.D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef]
- Kinney, A.L.; Besier, T.F.; D’Lima, D.D.; Fregly, B.J. Update on grand challenge competition to predict in vivo knee loads. J. Biomech. Eng. 2013, 135. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, G.; Graichen, F.; Bender, A.; Kääb, M.; Rohlmann, A.; Westerhoff, P. In vivo glenohumeral contact forces—Measurements in the first patient 7 months postoperatively. J. Biomech. 2007, 40, 2139–2149. [Google Scholar] [CrossRef]
- Westerhoff, P.; Graichen, F.; Bender, A.; Halder, A.; Beier, A.; Rohlmann, A.; Bergmann, G. In vivo measurement of shoulder joint loads during activities of daily living. J. Biomech. 2009, 42, 1840–1849. [Google Scholar] [CrossRef] [PubMed]
- Nikooyan, A.A.; Veeger, H.; Westerhoff, P.; Graichen, F.; Bergmann, G.; Van der Helm, F. Validation of the Delft Shoulder and Elbow Model using in-vivo glenohumeral joint contact forces. J. Biomech. 2010, 43, 3007–3014. [Google Scholar] [CrossRef] [PubMed]
- Skals, S.; Bláfoss, R.; Andersen, M.S.; de Zee, M.; Andersen, L.L. Manual material handling in the supermarket sector. Part 1: Joint angles and muscle activity of trapezius descendens and erector spinae longissimus. Appl. Ergon. 2021, 92, 103340. [Google Scholar] [CrossRef]
- Skals, S.; Bláfoss, R.; de Zee, M.; Andersen, L.L.; Andersen, M.S. Effects of load mass and position on the dynamic loading of the knees, shoulders and lumbar spine during lifting: A musculoskeletal modelling approach. Appl. Ergon. 2021, 96, 103491. [Google Scholar] [CrossRef] [PubMed]
- Bassani, G.; Filippeschi, A.; Avizzano, C.A. A Dataset of Human Motion and Muscular Activities in Manual Material Handling Tasks for Biomechanical and Ergonomic Analyses. IEEE Sens. J. 2021, 21, 24731–24739. [Google Scholar] [CrossRef]
- Mathis, A.; Schneider, S.; Lauer, J.; Mathis, M.W. A primer on motion capture with deep learning: Principles, pitfalls, and perspectives. Neuron 2020, 108, 44–65. [Google Scholar] [CrossRef]
- Winter, D.A. Biomechanics and Motor Control of Human Movement; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ponvel, P.; Singh, D.K.A.; Beng, G.K.; Chai, S.C. Factors affecting upper extremity kinematics in healthy adults: A systematic review. Crit. Rev. Phys. Rehabil. Med. 2019, 31, 101–123. [Google Scholar] [CrossRef]
- Horsak, B.; Pobatschnig, B.; Schwab, C.; Baca, A.; Kranzl, A.; Kainz, H. Reliability of joint kinematic calculations based on direct kinematic and inverse kinematic models in obese children. Gait Posture 2018, 66, 201–207. [Google Scholar] [CrossRef]
- Peters, A.; Galna, B.; Sangeux, M.; Morris, M.; Baker, R. Quantification of soft tissue artifact in lower limb human motion analysis: A systematic review. Gait Posture 2010, 31, 1–8. [Google Scholar] [CrossRef]
- Lamberto, G.; Martelli, S.; Cappozzo, A.; Mazzà, C. To what extent is joint and muscle mechanics predicted by musculoskeletal models sensitive to soft tissue artefacts? J. Biomech. 2017, 62, 68–76. [Google Scholar] [CrossRef]
- Muller, A.; Pontonnier, C.; Dumont, G. Uncertainty propagation in multibody human model dynamics. Multibody Syst. Dyn. 2017, 40, 177–192. [Google Scholar] [CrossRef]
- Aizawa, J.; Masuda, T.; Hyodo, K.; Jinno, T.; Yagishita, K.; Nakamaru, K.; Koyama, T.; Morita, S. Ranges of active joint motion for the shoulder, elbow, and wrist in healthy adults. Disabil. Rehabil. 2013, 35, 1342–1349. [Google Scholar] [CrossRef]
- Cheng, R.; Nagaraja, V.H.; Bergmann, J.H.; Thompson, M.S. Motion Capture Analysis & Plotting Assistant: An Opensource Framework to Analyse Inertial-Sensor-based Measurements. In Proceedings of the ISPO Trent International Prosthetics Symposium (TIPS) 2019, ISPO, Manchester, UK, 20–22 March 2019; pp. 156–157. [Google Scholar]
- Cheng, R.; Nagaraja, V.H.; Bergmann, J.H.; Thompson, M.S. An Opensource Framework to Analyse Marker-based and Inertial-Sensor-based Measurements: Motion Capture Analysis & Plotting Assistant (MCAPA) 2.0. In Proceedings of the BioMedEng, London, UK, 5–6 September 2019. [Google Scholar]
- Carnegie Mellon University—CMU Graphics Lab—Motion Capture Library. 2003. Available online: http://mocap.cs.cmu.edu (accessed on 6 February 2023).
- Mundt, M.; Johnson, W.R.; Potthast, W.; Markert, B.; Mian, A.; Alderson, J. A Comparison of Three Neural Network Approaches for Estimating Joint Angles and Moments from Inertial Measurement Units. Sensors 2021, 21, 4535. [Google Scholar] [CrossRef] [PubMed]
- Mathis, A.; Mamidanna, P.; Cury, K.M.; Abe, T.; Murthy, V.N.; Mathis, M.W.; Bethge, M. DeepLabCut: Markerless pose estimation of user-defined body parts with deep learning. Nat. Neurosci. 2018, 21, 1281–1289. [Google Scholar] [CrossRef] [PubMed]


| Output | Weight | Optimizer | Batch-Size | Epoch | Activation | Number of | Hidden | Learning | Dropout |
|---|---|---|---|---|---|---|---|---|---|
| Initialization | Function | Nodes | Layers | Rate | Probability | ||||
| Hyperparameters explored | |||||||||
| He normal, | RMSProp, | 64, | 50, | ReLU, | 200 to 1800 | 2, 4, 6, | 0.001, | 0, 0.2 | |
| Random normal, | SGD, | 256, | 100, | sigmoid, | with increments | 8, 10 | 0.005 | ||
| Xavier normal | Adam | 1028 | 200 | tanh | of 200 | ||||
| Optimal hyperparameters | |||||||||
| Subject-exposed settings | |||||||||
| Muscle forces | Random normal | SGD | 64 | 50 | ReLU | 400 | 8 | 0.005 | 0.0 |
| Muscle activations | Xavier normal | Adam | 256 | 100 | ReLU | 1000 | 6 | 0.005 | 0.0 |
| Joint angles | Random normal | Adam | 256 | 200 | ReLU | 200 | 2 | 0.001 | 0.0 |
| Joint reaction forces | Xavier normal | Adam | 256 | 100 | ReLU | 200 | 8 | 0.005 | 0.0 |
| Joint moments | Xavier normal | Adam | 64 | 50 | sigmoid | 1400 | 2 | 0.001 | 0.2 |
| Subject-naive settings | |||||||||
| Muscle forces | Xavier normal | SGD | 64 | 200 | ReLU | 1200 | 8 | 0.005 | 0.2 |
| Muscle activations | Random normal | Adam | 256 | 200 | ReLU | 1200 | 6 | 0.001 | 0.2 |
| Joint angles | Random normal | Adam | 256 | 100 | ReLU | 800 | 4 | 0.005 | 0.0 |
| Joint reaction forces | Random normal | Adam | 256 | 50 | ReLU | 800 | 8 | 0.001 | 0.0 |
| Joint moments | Xavier normal | Adam | 64 | 50 | sigmoid | 1800 | 2 | 0.001 | 0.2 |
| Output | RNN Cell | Optimizer | Batch-Size | Epoch | Activation | Number of | RNN | Dropout | Learning |
|---|---|---|---|---|---|---|---|---|---|
| Function | Nodes | Layers | Probability | Rate | |||||
| Hyperparameters explored for RNN | |||||||||
| Vanilla, LSTM, | Adam, | 64, | 50, | ReLU, | 128, | 1, 2, | 0.1, 0.2 | 0.001, | |
| GRU, B-Vanilla, | SGD, | 128, | 100, | sigmoid, | 256, | 3, 4 | 0.005 | ||
| B-LSTM, B-GRU | RMSProp | 256 | 200 | tanh | 512 | ||||
| Optimal hyperparameters | |||||||||
| Subject-exposed settings | |||||||||
| Muscle forces | LSTM | RMSprop | 64 | 100 | tanh | 256 | 1 | 0.1 | 0.001 |
| Muscle activations | LSTM | RMSprop | 64 | 50 | sigmoid | 128 | 3 | 0.1 | 0.001 |
| Joint angles | B-LSTM | Adam | 256 | 200 | sigmoid | 256 | 1 | 0.2 | 0.001 |
| Joint reaction forces | LSTM | RMSprop | 128 | 50 | sigmoid | 128 | 2 | 0.1 | 0.001 |
| Joint moments | B-LSTM | RMSprop | 64 | 100 | sigmoid | 256 | 1 | 0.1 | 0.001 |
| Subject-naive settings | |||||||||
| Muscle forces | GRU | Adam | 256 | 100 | ReLU | 512 | 3 | 0.2 | 0.001 |
| Muscle activations | LSTM | RMSprop | 128 | 100 | tanh | 512 | 2 | 0.1 | 0.001 |
| Joint angles | B-LSTM | Adam | 64 | 50 | tanh | 256 | 1 | 0.2 | 0.001 |
| Joint reaction forces | LSTM | Adam | 64 | 50 | ReLU | 128 | 4 | 0.1 | 0.001 |
| Joint moments | GRU | Adam | 128 | 100 | sigmoid | 256 | 2 | 0.2 | 0.005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dasgupta, A.; Sharma, R.; Mishra, C.; Nagaraja, V.H. Machine Learning for Optical Motion Capture-Driven Musculoskeletal Modelling from Inertial Motion Capture Data. Bioengineering 2023, 10, 510. https://doi.org/10.3390/bioengineering10050510
Dasgupta A, Sharma R, Mishra C, Nagaraja VH. Machine Learning for Optical Motion Capture-Driven Musculoskeletal Modelling from Inertial Motion Capture Data. Bioengineering. 2023; 10(5):510. https://doi.org/10.3390/bioengineering10050510
Chicago/Turabian StyleDasgupta, Abhishek, Rahul Sharma, Challenger Mishra, and Vikranth Harthikote Nagaraja. 2023. "Machine Learning for Optical Motion Capture-Driven Musculoskeletal Modelling from Inertial Motion Capture Data" Bioengineering 10, no. 5: 510. https://doi.org/10.3390/bioengineering10050510
APA StyleDasgupta, A., Sharma, R., Mishra, C., & Nagaraja, V. H. (2023). Machine Learning for Optical Motion Capture-Driven Musculoskeletal Modelling from Inertial Motion Capture Data. Bioengineering, 10(5), 510. https://doi.org/10.3390/bioengineering10050510