Direct Multi-Material Reconstruction via Iterative Proximal Adaptive Descent for Spectral CT Imaging
Abstract
1. Introduction
2. Materials and Methods
2.1. Multi-Material, Non-Linear forward Projection Model
2.2. Optimization Model and Algorithm
| Algorithm 1 Iterative Proximal Adaptive Descent Algorithm (IPAD) |
| Input: such that the constant Initialization: While , via (8)–(11). via (12)–(13). . End while Output: |
2.3. Convergence Analysis
3. Results
3.1. Algorithm Investigation
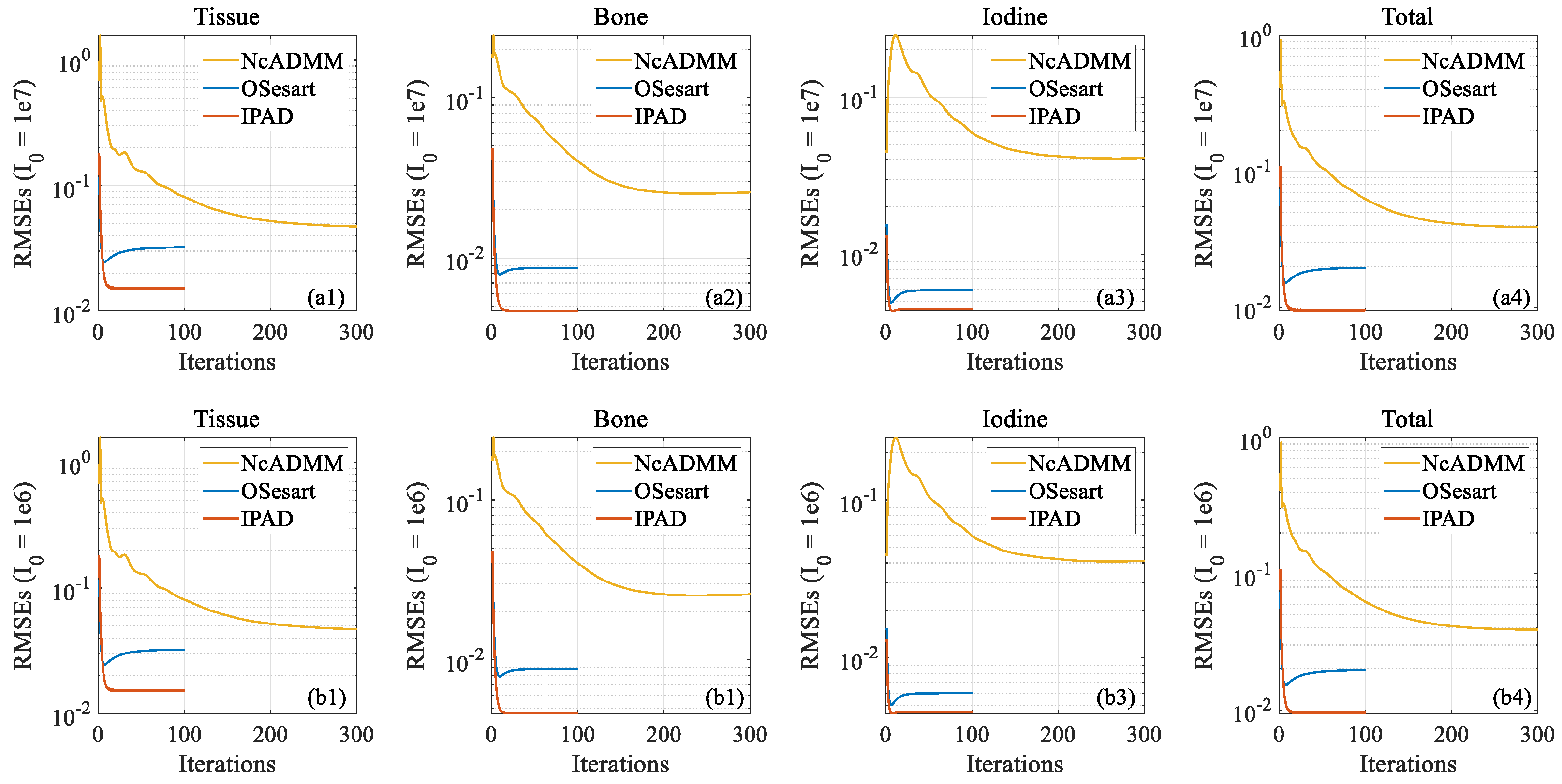
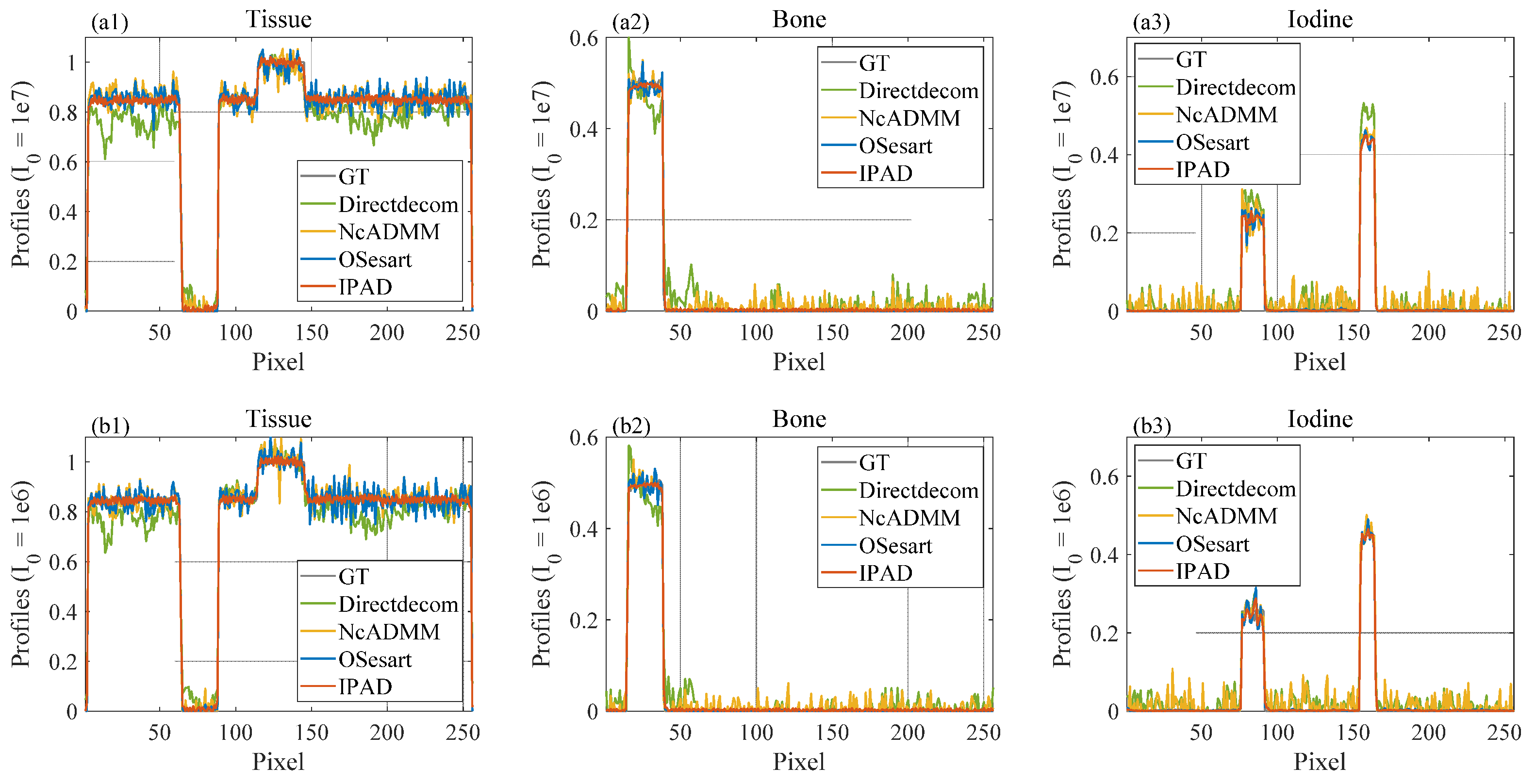
3.1.1. Noise-Free Simulation
3.1.2. Performance under Different Noise Levels
3.2. Comparison Experiments
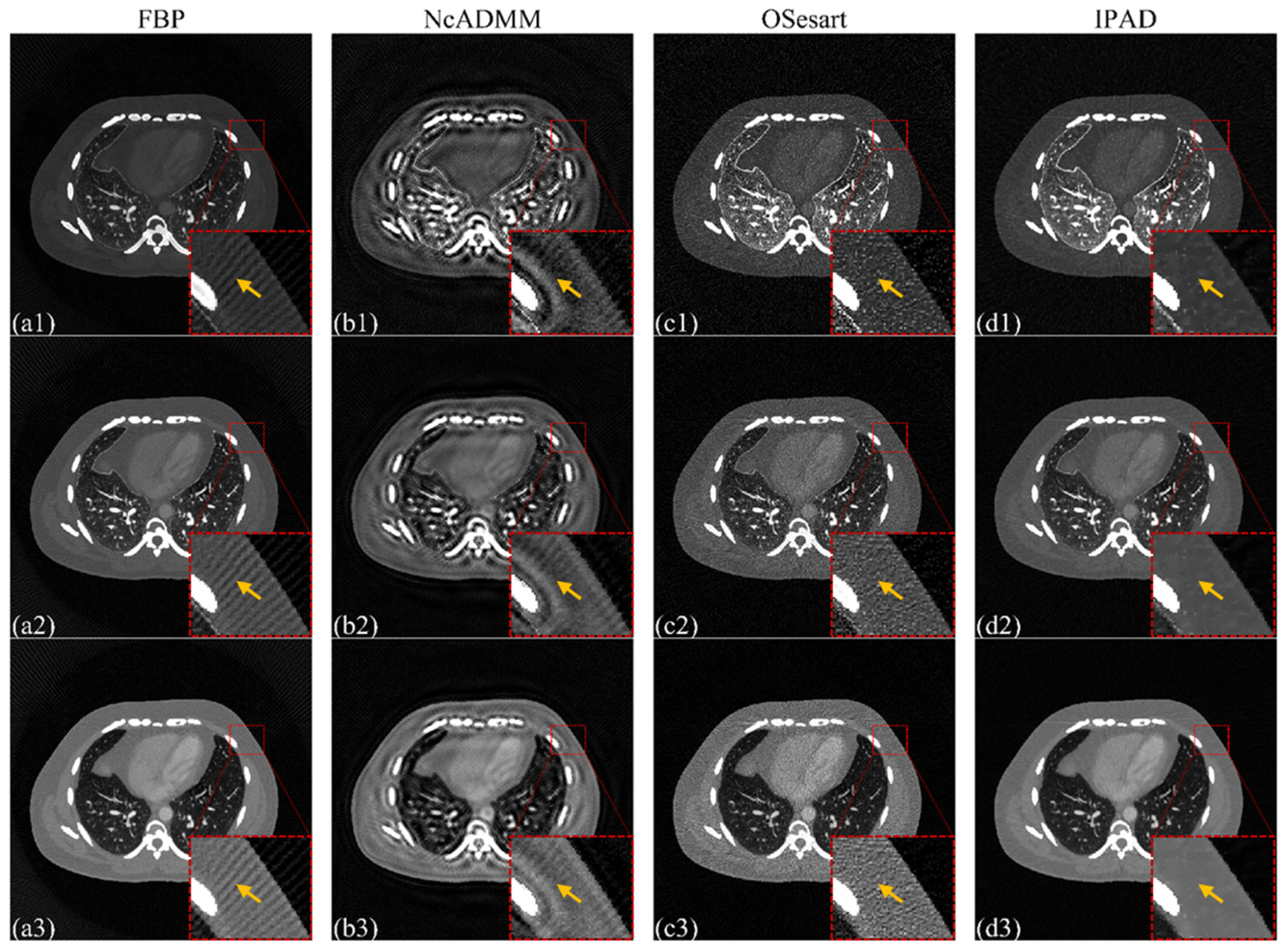
3.3. Thorax Dataset Verification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Solving Scheme for Proximal Step
Appendix B. Proof of Lemma 1
Appendix C. Proof of Theorem 1
References
- Brandelik, S.C.; Skornitzke, S.; Mokry, T.; Sauer, S.; Stiller, W.; Nattenmüller, J.; Kauczor, H.U.; Weber, T.F.; Do, T.D. Quantitative and qualitative assessment of plasma cell dyscrasias in dual-layer spectral CT. Eur. Radiol. 2021, 31, 7664–7673. [Google Scholar] [CrossRef] [PubMed]
- Demirler Simsir, B.; Danse, E.; Coche, E. Benefit of dual-layer spectral CT in emergency imaging of different organ systems. Clin. Radiol. 2020, 75, 886–902. [Google Scholar] [CrossRef] [PubMed]
- Daoud, B.; Cazejust, J.; Tavolaro, S.; Durand, S.; Pommier, R.; Hamrouni, A.; Bornet, G. Could Spectral CT Have a Potential Benefit in Coronavirus Disease (COVID-19)? AM J. Roentgenol. 2020, 216, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Agostini, A.; Floridi, C.; Borgheresi, A.; Badaloni, M.; Esposto Pirani, P.; Terilli, F.; Ottaviani, L.; Giovagnoni, A. Proposal of a low-dose, long-pitch, dual-source chest CT protocol on third-generation dual-source CT using a tin filter for spectral shaping at 100 kVp for CoronaVirus Disease 2019 (COVID-19) patients: A feasibility study. Radiol. Med. 2020, 125, 365–373. [Google Scholar] [CrossRef]
- Taguchi, K.; Iwanczyk, J.S. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Med. Phys. 2013, 40, 100901. [Google Scholar] [CrossRef]
- Anderson, N.G.; Butler, A.P.; Scott, N.J.A.; Cook, N.J.; Butzer, J.S.; Schleich, N.; Firsching, M.; Grasset, R.; de Ruiter, N.; Campbell, M.; et al. Spectroscopic (multi-energy) CT distinguishes iodine and barium contrast material in MICE. Eur. Radiol. 2010, 20, 2126–2134. [Google Scholar] [CrossRef]
- Noh, J.; Fessler, J.A.; Kinahan, P.E. Statistical Sinogram Restoration in Dual-Energy CT for PET Attenuation Correction. IEEE T Med. Imaging 2009, 28, 1688–1702. [Google Scholar] [CrossRef]
- Alvarez, R.E. Estimator for photon counting energy selective x-ray imaging with multibin pulse height analysis. Med. Phys. 2011, 38, 2324–2334. [Google Scholar] [CrossRef]
- Niu, T.; Dong, X.; Petrongolo, M.; Zhu, L. Iterative image-domain decomposition for dual-energy CT. Med. Phys. 2014, 41, 041901. [Google Scholar] [CrossRef]
- Maaß, C.; Baer, M.; Kachelrieß, M. Image-based dual energy CT using optimized precorrection functions: A practical new approach of material decomposition in image domain. Med. Phys. 2009, 36, 3818–3829. [Google Scholar] [CrossRef]
- Ding, Q.; Niu, T.; Zhang, X.; Long, Y. Image-domain multimaterial decomposition for dual-energy CT based on prior information of material images. Med. Phys. 2018, 45, 3614–3626. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, R.E.; Macovski, A. Energy-selective reconstructions in X-ray computerised tomography. Phys. Med. Biol. 1976, 21, 733–744. [Google Scholar] [CrossRef] [PubMed]
- Sawatzky, A.; Xu, Q.; Schirra, C.O.; Anastasio, M.A. Proximal ADMM for Multi-Channel Image Reconstruction in Spectral X-ray CT. IEEE T Med. Imaging 2014, 33, 1657–1668. [Google Scholar] [CrossRef] [PubMed]
- Schlomka, J.P.; Roessl, E.; Dorscheid, R.; Dill, S.; Martens, G.; Istel, T.; Bäumer, C.; Herrmann, C.; Steadman, R.; Zeitler, G.; et al. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Phys. Med. Biol. 2008, 53, 4031–4047. [Google Scholar] [CrossRef]
- Zou, Y.; Silver, M. Analysis of Fast kV-Switching in Dual Energy CT Using a Pre-Reconstruction Decomposition Technique; SPIE: Bellingham, DC, USA, 2008; Volume 6913. [Google Scholar]
- Faby, S.; Kuchenbecker, S.; Sawall, S.; Simons, D.; Schlemmer, H.-P.; Lell, M.; Kachelrieß, M. Performance of today’s dual energy CT and future multi energy CT in virtual non-contrast imaging and in iodine quantification: A simulation study. Med. Phys. 2015, 42, 4349–4366. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhao, X.; Zhang, P. An Extended Algebraic Reconstruction Technique (E-ART) for Dual Spectral CT. IEEE T Med. Imaging 2015, 34, 761–768. [Google Scholar] [CrossRef]
- Hu, J.; Zhao, X.; Wang, F. An extended simultaneous algebraic reconstruction technique (E-SART) for X-ray dual spectral computed tomography. Scanning 2016, 38, 599–611. [Google Scholar] [CrossRef]
- Zhao, S.; Pan, H.; Zhang, W.; Xia, D.; Zhao, X. An oblique projection modification technique (OPMT) for fast multispectral CT reconstruction. Phys. Med. Biol. 2021, 66, 065003. [Google Scholar] [CrossRef]
- Zhang, W.; Zhao, S.; Pan, H.; Zhao, Y.; Zhao, X. An iterative reconstruction method based on monochromatic images for dual energy CT. Med. Phys. 2021, 48, 6437–6452. [Google Scholar] [CrossRef]
- Xu, Q.; Mou, X.; Tang, S.; Hong, W.; Zhang, Y.; Luo, T. Implementation of Penalized-Likelihood Statistical Reconstruction for Polychromatic Dual-Energy CT; SPIE: Bellingham, DC, USA, 2009. [Google Scholar]
- Long, Y.; Fessler, J.A. Multi-Material Decomposition Using Statistical Image Reconstruction for Spectral CT. IEEE T Med. Imaging 2014, 33, 1614–1626. [Google Scholar] [CrossRef] [PubMed]
- Weidinger, T.; Buzug, T.M.; Flohr, T.; Kappler, S.; Stierstorfer, K. Polychromatic Iterative Statistical Material Image Reconstruction for Photon-Counting Computed Tomography. Int. J. Biomed. Imaging 2016, 2016, 5871604. [Google Scholar] [CrossRef]
- Mechlem, K.; Ehn, S.; Sellerer, T.; Braig, E.; Münzel, D.; Pfeiffer, F.; Noël, P.B. Joint Statistical Iterative Material Image Reconstruction for Spectral Computed Tomography Using a Semi-Empirical Forward Model. IEEE T Med. Imaging 2018, 37, 68–80. [Google Scholar] [CrossRef]
- Foygel Barber, R.; Sidky, E.Y.; Gilat Schmidt, T.; Pan, X. An algorithm for constrained one-step inversion of spectral CT data. Phys. Med. Biol. 2016, 61, 3784–3818. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Jørgensen, J.H.; Pan, X. Convex optimization problem prototyping for image reconstruction in computed tomography with the Chambolle-Pock algorithm. Phys. Med. Biol. 2012, 57, 3065–3091. [Google Scholar] [CrossRef] [PubMed]
- Barber, R.F.; Sidky, E.Y. Convergence for nonconvex ADMM, with applications to CT imaging. arXiv 2021, arXiv:2006.07278v2. [Google Scholar]
- Schmidt, T.G.; Sammut, B.A.; Barber, R.F.; Pan, X.; Sidky, E.Y. Addressing CT metal artifacts using photon-counting detectors and one-step spectral CT image reconstruction. Med. Phys. 2022, 49, 3021–3040. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Rodet, T.; Legoupil, S.; Mohammad-Djafari, A. A full-spectral Bayesian reconstruction approach based on the material decomposition model applied in dual-energy computed tomography. Med. Phys. 2013, 40, 111916. [Google Scholar] [CrossRef]
- Xu, Q.; Sawatzky, A.; Anastasio, M.A.; Schirra, C.O. Sparsity-regularized image reconstruction of decomposed K-edge data in spectral CT. Phys. Med. Biol. 2014, 59, N65–N79. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Sidky, E.Y.; Xia, D.; Pan, X. Image reconstruction and scan configurations enabled by optimization-based algorithms in multispectral CT. Phys. Med. Biol. 2017, 62, 8763–8793. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, Z.; Xia, D.; Sidky, E.Y.; Pan, X. Non-convex primal-dual algorithm for image reconstruction in spectral CT. Comput. Med. Imag. Grap 2021, 87, 101821. [Google Scholar] [CrossRef]
- Zhang, W.; Cai, A.; Zheng, Z.; Wang, L.; Liang, N.; Li, L.; Yan, B.; Hu, G. A Direct Material Reconstruction Method for DECT Based on Total Variation and BM3D Frame. IEEE Access. 2019, 7, 138579–138592. [Google Scholar] [CrossRef]
- Erdogan, H.; Fessler, J.A. Ordered subsets algorithms for transmission tomography. Phys. Med. Biol. 1999, 44, 2835–2851. [Google Scholar] [CrossRef] [PubMed]
- Attouch, H.; Bolte, J.; Svaiter, B.F. Convergence of descent methods for semi-algebraic and tame problems: Proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 2013, 137, 91–129. [Google Scholar] [CrossRef]
- Zhou, W.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE T Image Process 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Poludniowski, G.; Landry, G.; DeBlois, F.; Evans, P.M.; Verhaegen, F. SpekCalc: A program to calculate photon spectra from tungsten anode x-ray tubes. Phys. Med. Biol. 2009, 54, N433–N438. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, H.; Wang, L.; Wang, X.; Hu, X.; Cai, A.; Li, L.; Niu, T.; Yan, B. Image domain dual material decomposition for dual-energy CT using butterfly network. Med. Phys. 2019, 46, 2037–2051. [Google Scholar] [CrossRef] [PubMed]
- Lehtinen, J.; Munkberg, J.; Hasselgren, J.; Laine, S.; Karras, T.; Aittala, M.; Aila, T. Noise2Noise: Learning Image Restoration without Clean Data. arXiv 2018, arXiv:1803.04189. [Google Scholar]
- Fang, W.; Wu, D.; Kim, K.; Kalra, M.K.; Singh, R.; Li, L.; Li, Q. Iterative material decomposition for spectral CT using self-supervised Noise2Noise prior. Phys. Med. Biol. 2021, 66, 155013. [Google Scholar] [CrossRef]
- Wu, W.; Hu, D.; Niu, C.; Broeke, L.V.; Butler, A.P.; Cao, P.; Atlas, J.; Chernoglazov, A.; Vardhanabhuti, V.; Wang, G. Deep learning based spectral CT imaging. Neural Netw. 2021, 144, 342–358. [Google Scholar] [CrossRef]
- Wu, W.; Hu, D.; Niu, C.; Yu, H.; Vardhanabhuti, V.; Wang, G. DRONE: Dual-domain residual-based optimization network for sparse-view CT reconstruction. IEEE Trans. Med. Imaging 2021, 40, 3002–3014. [Google Scholar] [CrossRef]
- Dong, Y. Weak convergence of an extended splitting method for monotone inclusions. J. Global Optim. 2021, 79, 257–277. [Google Scholar] [CrossRef]






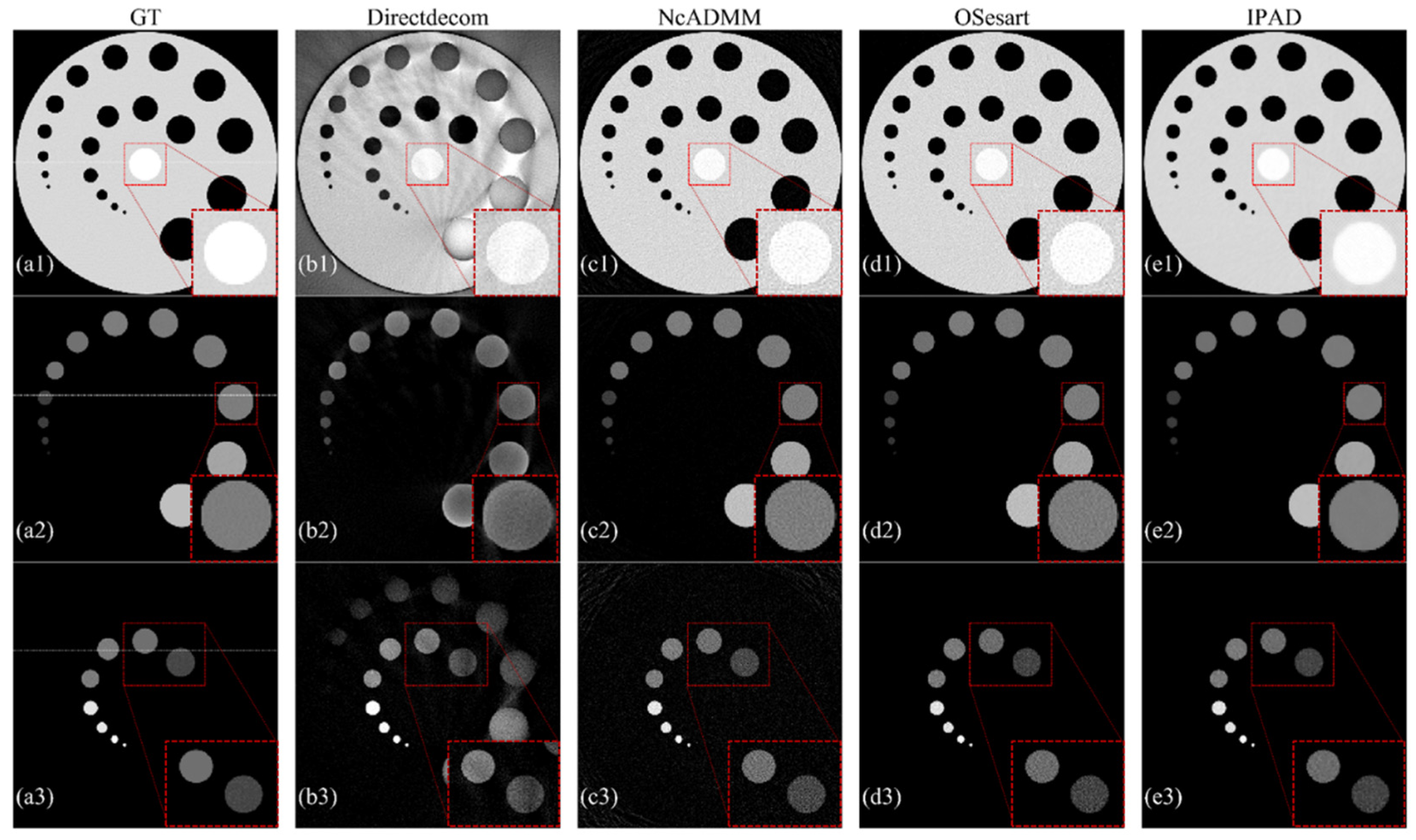
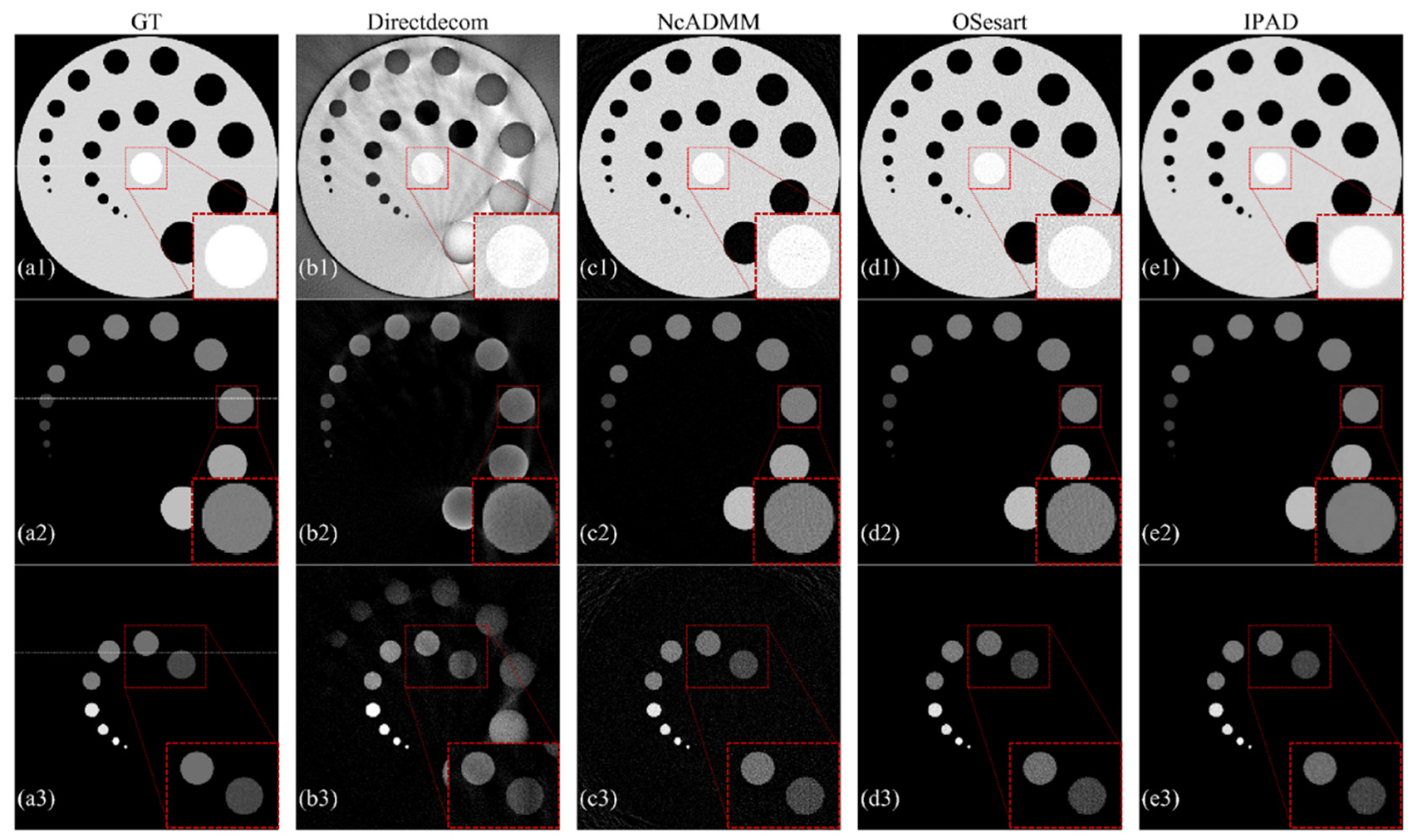

| Noisy (I0 = 1 × 107) | Noisy (I0 = 1 × 106) | ||||||
|---|---|---|---|---|---|---|---|
| Algorithm | Materials | PSNR | SSIM | RMSE | PSNR | SSIM | RMSE |
| Directdecom | Tissue | 11.970 | 0.454 | 0.252 | 11.626 | 0.443 | 0.262 |
| Bone | 23.009 | 0.269 | 7.07 × 10−2 | 23.582 | 0.320 | 6.62 × 10−2 | |
| Iodine | 23.620 | 0.326 | 6.59 × 10−2 | 24.818 | 0.371 | 5.74 × 10−2 | |
| Averaged | 19.533 | 0.350 | 0.130 | 20.009 | 0.378 | 0.129 | |
| NcADMM | Tissue | 26.609 | 0.505 | 4.67 × 10−2 | 26.611 | 0.505 | 4.67 × 10−2 |
| Bone | 31.546 | 0.618 | 2.65 × 10−2 | 31.472 | 0.614 | 2.67 × 10−2 | |
| Iodine | 27.213 | 0.357 | 4.36 × 10−2 | 27.134 | 0.353 | 4.4 × 10−2 | |
| Averaged | 28.456 | 0.493 | 3.89 × 10−2 | 28.406 | 0.491 | 3.91 × 10−2 | |
| OSesart | Tissue | 29.836 | 0.669 | 3.22 × 10−2 | 29.819 | 0.668 | 3.23 × 10−2 |
| Bone | 41.236 | 0.968 | 8.72 × 10−3 | 41.176 | 0.967 | 8.74 × 10−3 | |
| Iodine | 44.609 | 0.983 | 5.91 × 10−3 | 44.455 | 0.983 | 6.02 × 10−3 | |
| Averaged | 38.560 | 0.873 | 1.56 × 10−2 | 38.483 | 0.873 | 1.57 × 10−2 | |
| IPAD | Tissue | 34.846 | 0.787 | 1.81 × 10−2 | 34.818 | 0.787 | 1.82 × 10−2 |
| Bone | 45.287 | 0.951 | 5.41 × 10−3 | 45.420 | 0.950 | 5.42 × 10−3 | |
| Iodine | 47.643 | 0.986 | 4.11 × 10−3 | 47.426 | 0.987 | 4.31 × 10−3 | |
| Averaged | 42.592 | 0.908 | 9.2 × 10−3 | 42.555 | 0.908 | 9.3 × 10−3 | |
| Computation Costs | NcADMM | OSesart | IPAD |
|---|---|---|---|
| Time (unit: second) | 64.898 | 24.451 | 25.520 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Cai, A.; Liang, N.; Wang, S.; Zheng, Z.; Li, L.; Yan, B. Direct Multi-Material Reconstruction via Iterative Proximal Adaptive Descent for Spectral CT Imaging. Bioengineering 2023, 10, 470. https://doi.org/10.3390/bioengineering10040470
Yu X, Cai A, Liang N, Wang S, Zheng Z, Li L, Yan B. Direct Multi-Material Reconstruction via Iterative Proximal Adaptive Descent for Spectral CT Imaging. Bioengineering. 2023; 10(4):470. https://doi.org/10.3390/bioengineering10040470
Chicago/Turabian StyleYu, Xiaohuan, Ailong Cai, Ningning Liang, Shaoyu Wang, Zhizhong Zheng, Lei Li, and Bin Yan. 2023. "Direct Multi-Material Reconstruction via Iterative Proximal Adaptive Descent for Spectral CT Imaging" Bioengineering 10, no. 4: 470. https://doi.org/10.3390/bioengineering10040470
APA StyleYu, X., Cai, A., Liang, N., Wang, S., Zheng, Z., Li, L., & Yan, B. (2023). Direct Multi-Material Reconstruction via Iterative Proximal Adaptive Descent for Spectral CT Imaging. Bioengineering, 10(4), 470. https://doi.org/10.3390/bioengineering10040470






