Author Contributions
Conceptualization, F.E., N.O.V.P., C.P.U., and A.W.; methodology, F.E.; software, F.E.; validation, F.E.; formal analysis, F.E.; investigation, F.E. and A.W.; resources—computing resources and analysis tools, F.E.; resources—laboratory samples, E.C. and H.P.T.N.; resources, N.O.V.P.; data curation, E.C.; writing—original draft preparation, F.E.; writing—review and editing, F.E., N.O.V.P., C.P.U., and A.W.; visualization, F.E.; supervision, A.W.; funding acquisition, N.O.V.P. and C.P.U. All authors have read and agreed to the published version of the manuscript.
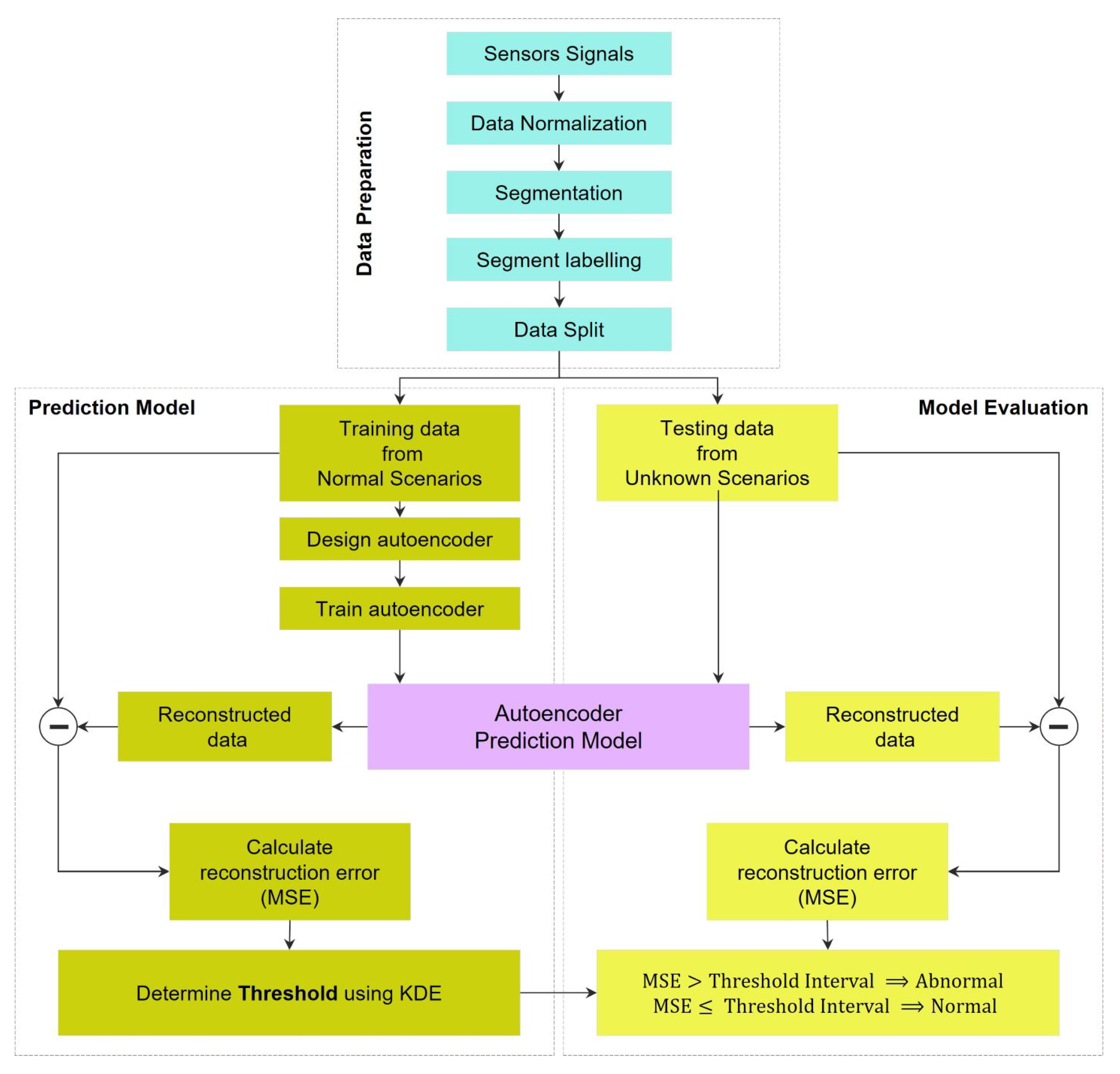
Figure 1.
Framework of the presented automated anomaly detection using autoencoder-based neural networks.
Figure 1.
Framework of the presented automated anomaly detection using autoencoder-based neural networks.
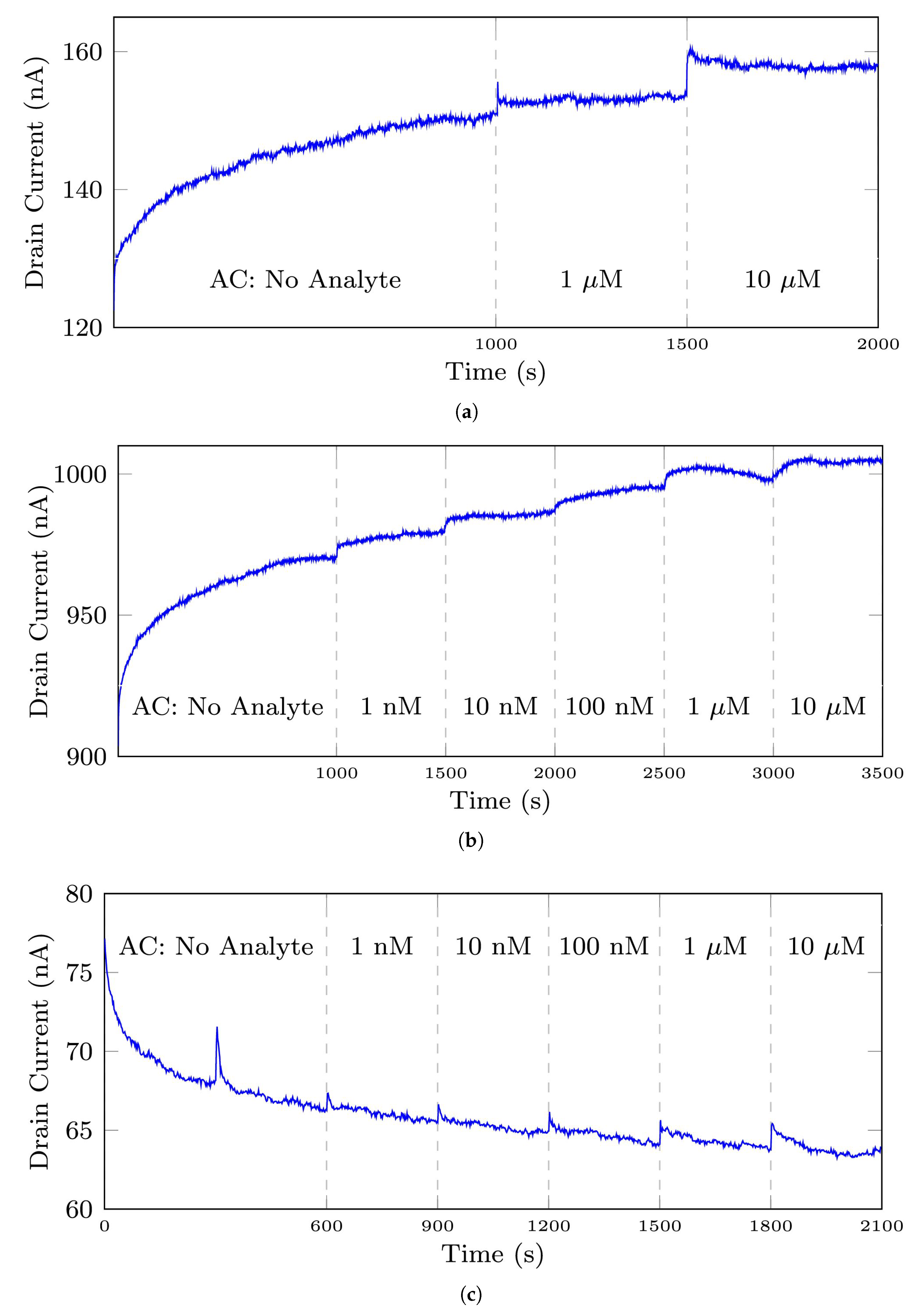
Figure 2.
The typical and normal signals measured by biosensors, (a) the 35-mer adenosine signal with initial AC of 1 M, (b) the 35-mer adenosine signal with initial AC of 1 nM, (c) the 31-mer oestradiol signal, (d) the 35-mer oestradiol signal. AC refers to the analyte concentration in this paper.
Figure 2.
The typical and normal signals measured by biosensors, (a) the 35-mer adenosine signal with initial AC of 1 M, (b) the 35-mer adenosine signal with initial AC of 1 nM, (c) the 31-mer oestradiol signal, (d) the 35-mer oestradiol signal. AC refers to the analyte concentration in this paper.
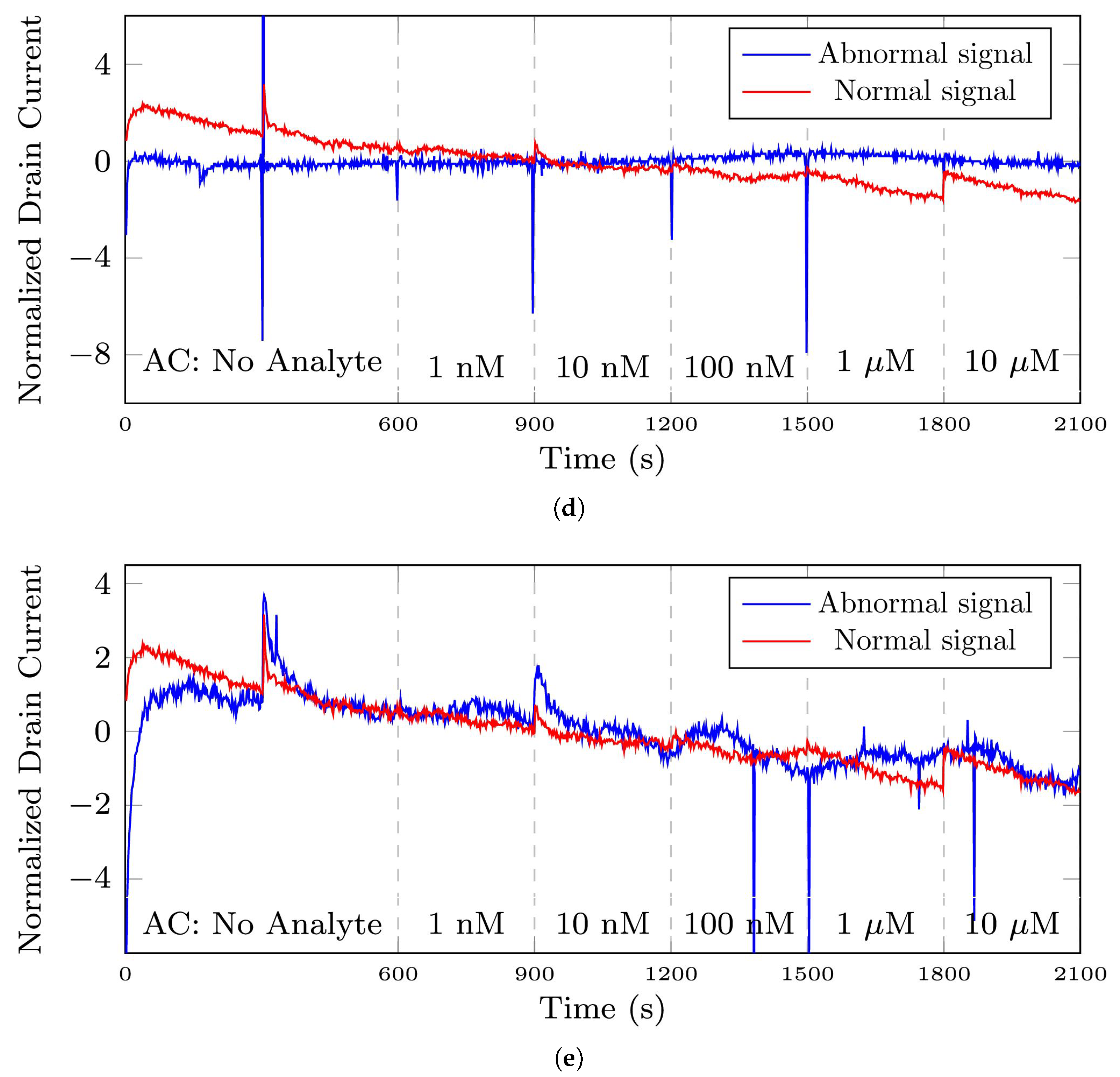
Figure 3.
The plots depict the differences between a normal signal and abnormal signals from the 35-mer oestradiol dataset. Note that regarding this dataset, analyte concentration (AC) refers to the volume of oestradiol in the sensor’s well. (a) a signal with normal sensing behavior, (b) a signal with abnormal time points in A, B, C, and D, (c) a signal containing abnormal time interval presented in the pink square area, (d) an abnormal time series registered by a broken transistor, (e) an abnormal time series that did not show sensing the changes in analyte concentration.
Figure 3.
The plots depict the differences between a normal signal and abnormal signals from the 35-mer oestradiol dataset. Note that regarding this dataset, analyte concentration (AC) refers to the volume of oestradiol in the sensor’s well. (a) a signal with normal sensing behavior, (b) a signal with abnormal time points in A, B, C, and D, (c) a signal containing abnormal time interval presented in the pink square area, (d) an abnormal time series registered by a broken transistor, (e) an abnormal time series that did not show sensing the changes in analyte concentration.
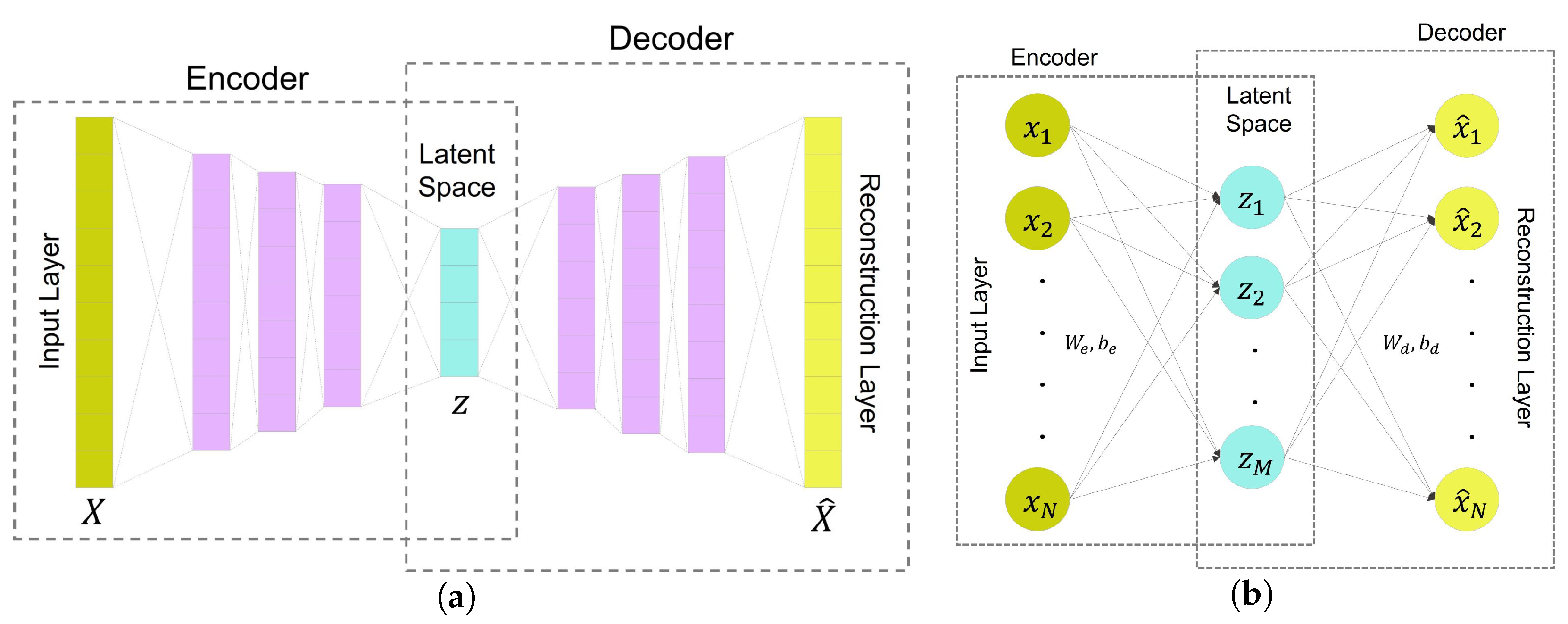
Figure 4.
Autoencoder neural networks with their component modules: (a) Ilustration of an autoencoder-based network, (b) A vanilla autoencoder, Note that the FC layer refers to the fully connected layer.
Figure 4.
Autoencoder neural networks with their component modules: (a) Ilustration of an autoencoder-based network, (b) A vanilla autoencoder, Note that the FC layer refers to the fully connected layer.
Figure 5.
Illustration of an LSTM unit, the building block of LSTM networks. Note that and refer to logistic sigmoid and hyperbolic tangent functions, respectively. Moreover, ⊕ and ⊙ point to addition and Hadamard product, also known as element-wise multiplication, respectively.
Figure 5.
Illustration of an LSTM unit, the building block of LSTM networks. Note that and refer to logistic sigmoid and hyperbolic tangent functions, respectively. Moreover, ⊕ and ⊙ point to addition and Hadamard product, also known as element-wise multiplication, respectively.
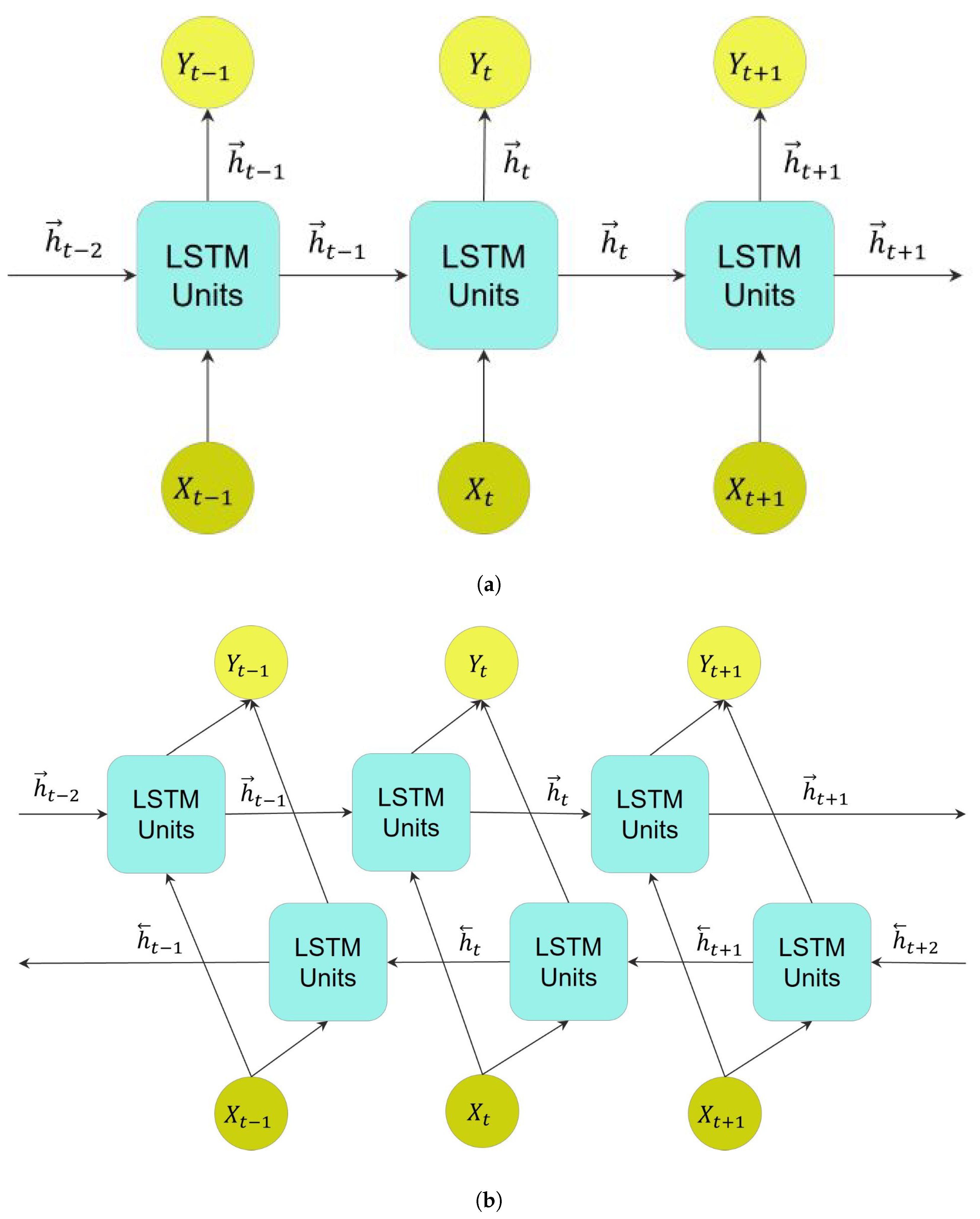
Figure 6.
Unfolded LSTM layers in three consecutive time steps depict the flow of information in these layers, where X and Y refer to the input and output of these layers, respectively. (a) A ULSTM layer, where refers to the forward state, positive direction, in this layer. (b) A BLSTM layer, where and refer to forward and backward states, respectively.
Figure 6.
Unfolded LSTM layers in three consecutive time steps depict the flow of information in these layers, where X and Y refer to the input and output of these layers, respectively. (a) A ULSTM layer, where refers to the forward state, positive direction, in this layer. (b) A BLSTM layer, where and refer to forward and backward states, respectively.
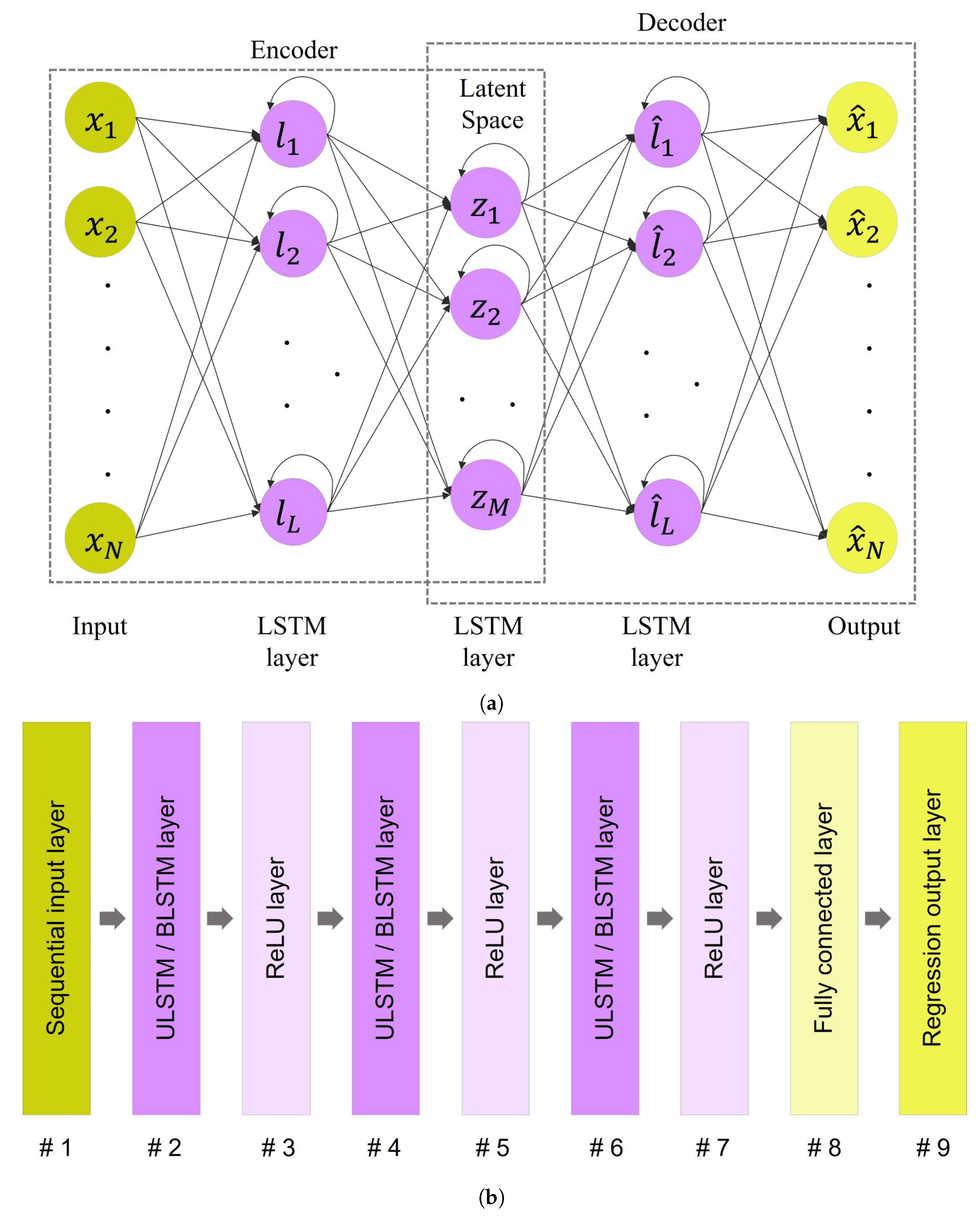
Figure 7.
The architecture of LSTM autoencoder: (a) A simplified schematic of an LSTM-based autoencoder that both encoder and decoder modules include two LSTM layers. The length of the first and last layers, N, is identical to the length of the input sequence. The number of LSTM units in layers 2 and 4 equals L; the dimension of these layers. Similarly, there are M LSTM units in the third layer. (b) Structure of LSTM autoencoder networks. Note that a ULSTM autoencoder and a BLSTM autoencoder differed in their LSTM layers. The former used the unidirectional LSTM layers, while the former used the bidirectional LSTM layers in their structures.
Figure 7.
The architecture of LSTM autoencoder: (a) A simplified schematic of an LSTM-based autoencoder that both encoder and decoder modules include two LSTM layers. The length of the first and last layers, N, is identical to the length of the input sequence. The number of LSTM units in layers 2 and 4 equals L; the dimension of these layers. Similarly, there are M LSTM units in the third layer. (b) Structure of LSTM autoencoder networks. Note that a ULSTM autoencoder and a BLSTM autoencoder differed in their LSTM layers. The former used the unidirectional LSTM layers, while the former used the bidirectional LSTM layers in their structures.
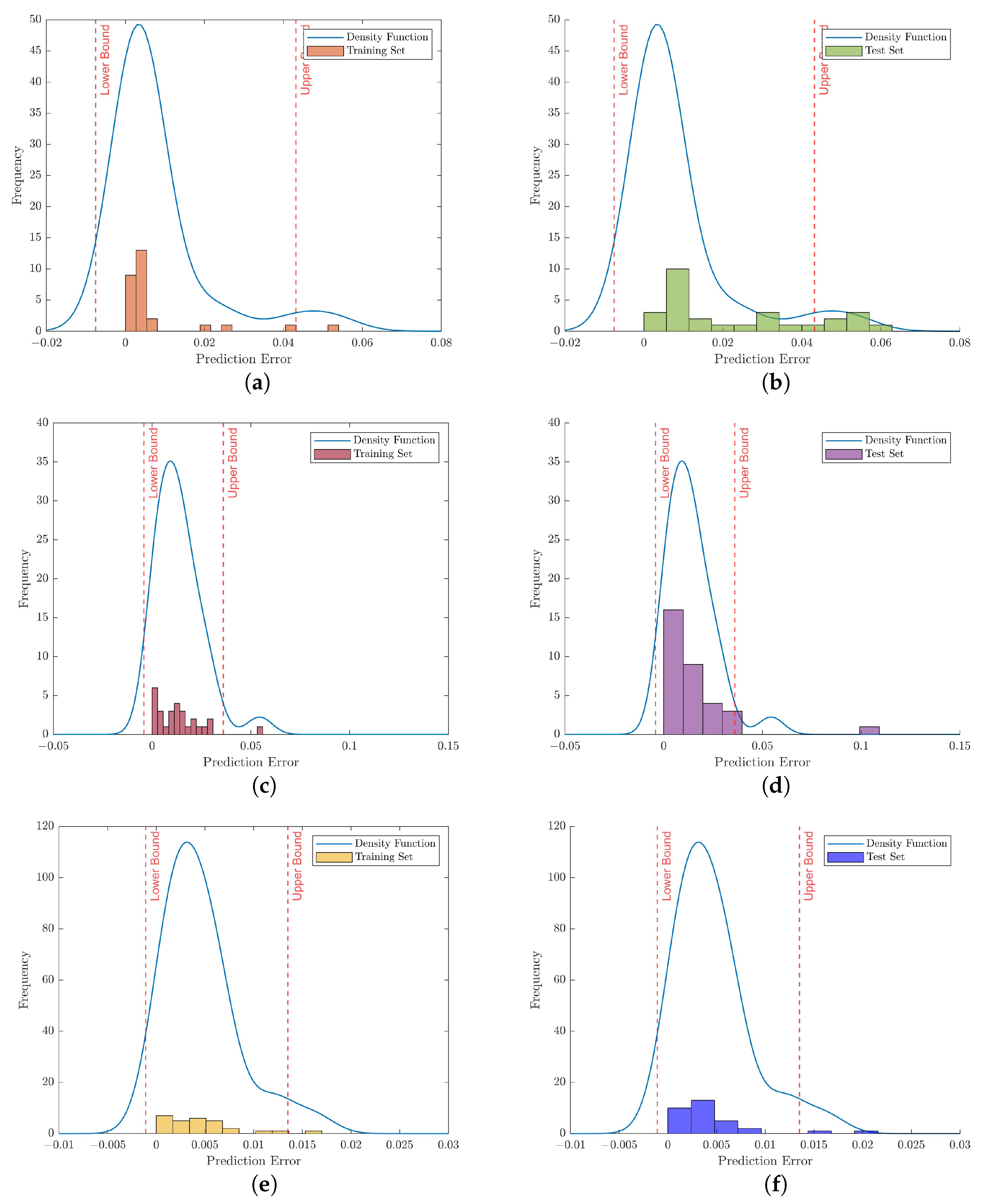
Figure 8.
Illustration of anomaly detection based on the prediction error which was estimated by KDE regarding the 35-mer adenosine data set. Note that the histograms on the left column show the reconstruction errors related to the training set with different autoencoder networks. Similarly, the histograms on the right column depict the prediction errors for samples in the test set. (a) Trained by vanilla autoencoder, (b) Tested by vanilla autoencoder, (c) Trained by ULSTM autoencoder, (d) Tested by ULSTM network, (e) Trained by BLSTM autoencoder, (f) Tested by BLSTM network.
Figure 8.
Illustration of anomaly detection based on the prediction error which was estimated by KDE regarding the 35-mer adenosine data set. Note that the histograms on the left column show the reconstruction errors related to the training set with different autoencoder networks. Similarly, the histograms on the right column depict the prediction errors for samples in the test set. (a) Trained by vanilla autoencoder, (b) Tested by vanilla autoencoder, (c) Trained by ULSTM autoencoder, (d) Tested by ULSTM network, (e) Trained by BLSTM autoencoder, (f) Tested by BLSTM network.
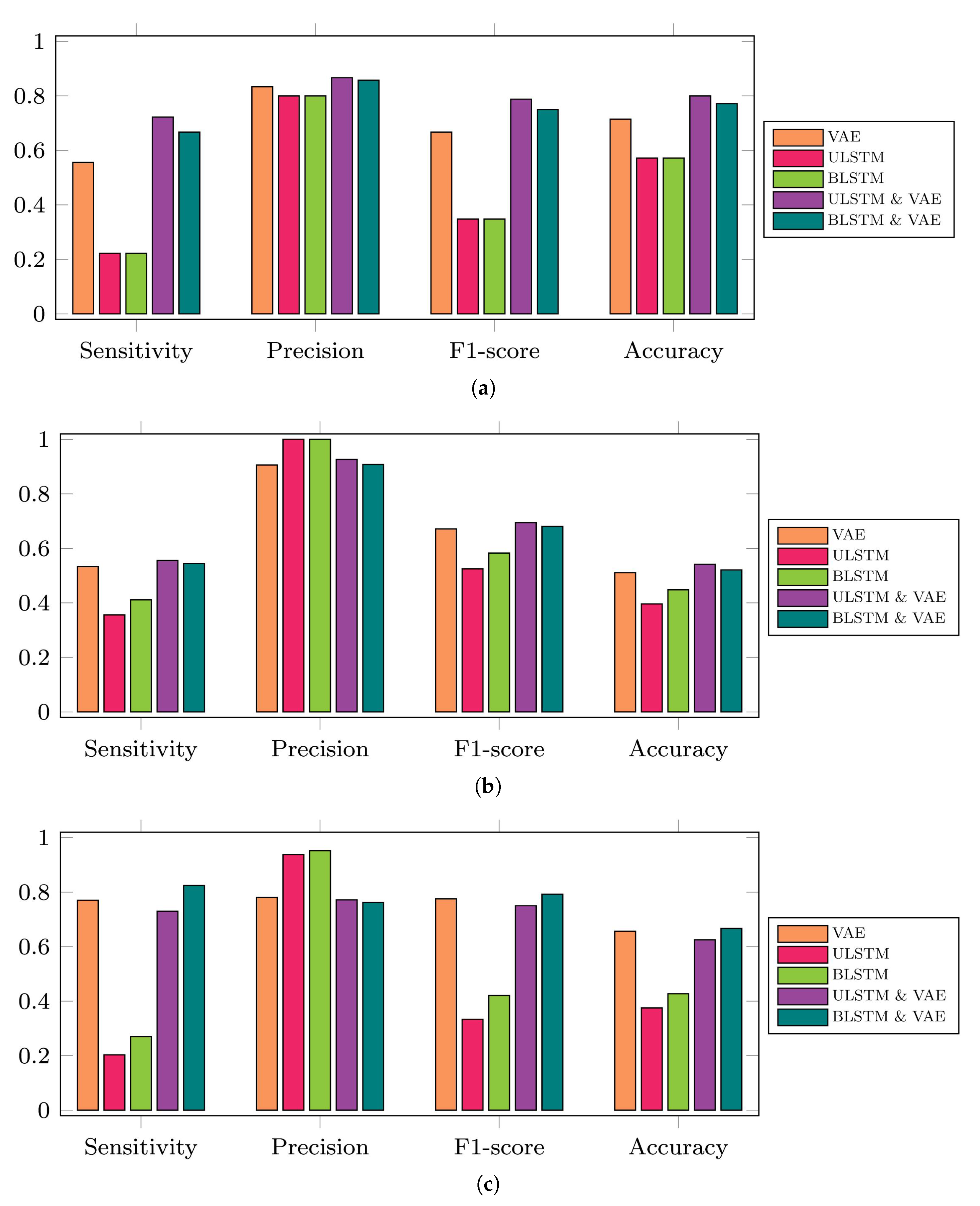
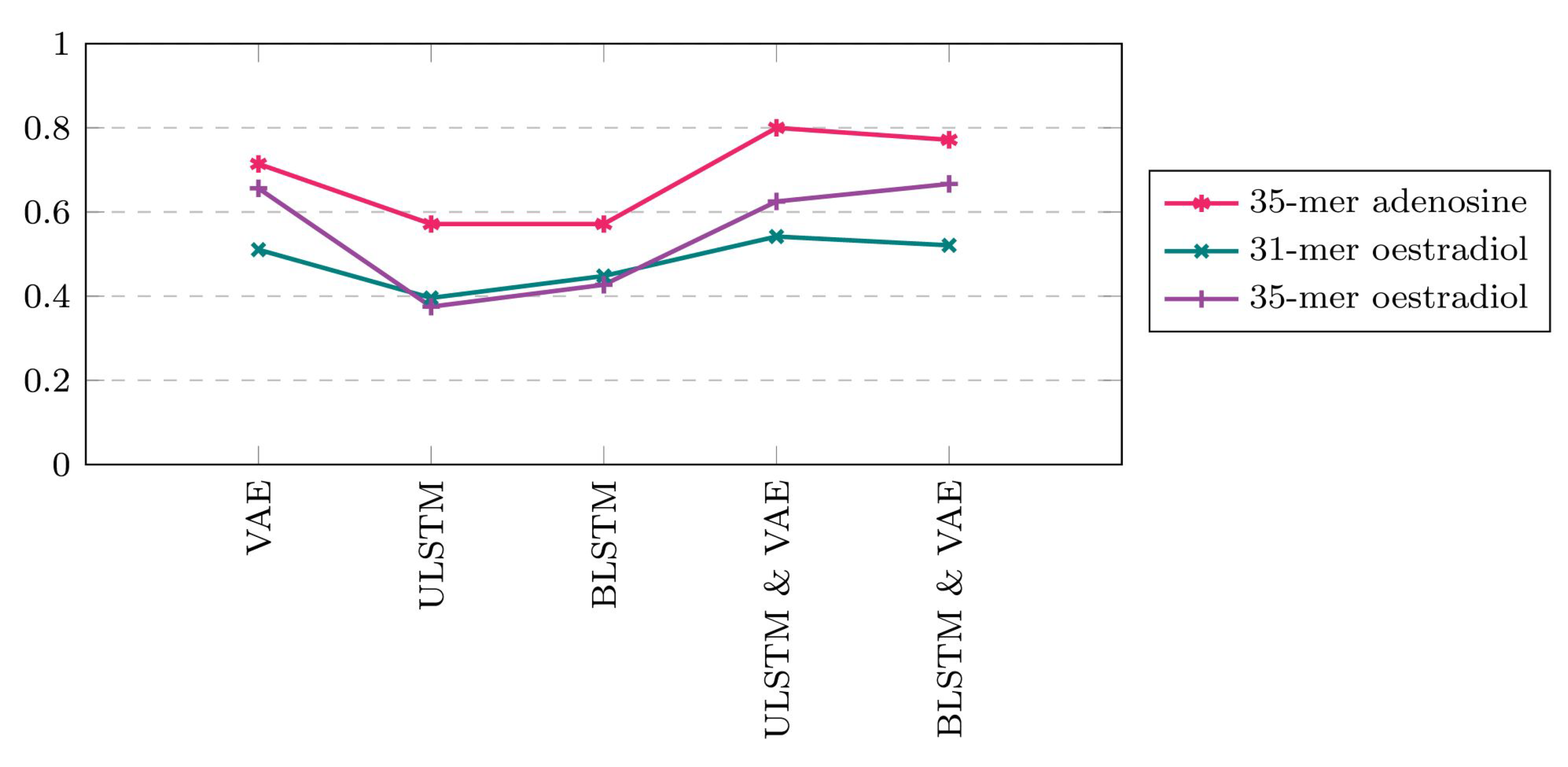
Figure 9.
Performance metrics of the five proposed prediction models regarding three available time series datasets for this study. Note that VAE in this figure refers to vanilla autoencoder and it is different from variational autoencoders in some other papers that they also used VAE as the short form of this method. In addition, ULSTM & VAE and BLSTM & VAE refer to the integrated models of LSTM and vanilla autoencoders. (a) 35-mer adenosine time series, (b) 31-mer oestradiol time series, (c) 35-mer oestradiol time series.
Figure 9.
Performance metrics of the five proposed prediction models regarding three available time series datasets for this study. Note that VAE in this figure refers to vanilla autoencoder and it is different from variational autoencoders in some other papers that they also used VAE as the short form of this method. In addition, ULSTM & VAE and BLSTM & VAE refer to the integrated models of LSTM and vanilla autoencoders. (a) 35-mer adenosine time series, (b) 31-mer oestradiol time series, (c) 35-mer oestradiol time series.
Figure 10.
Comparing the accuracy of the models on the available datasets.
Figure 10.
Comparing the accuracy of the models on the available datasets.
Table 1.
Main features of sensing protocols for drain current measurements of the adenosine and oestradiol time-series signals. The information related to the 31-mer and 35-mer oestradiol biosensors is merged into one column due to the identical sensing protocols for these biosensors.
Table 1.
Main features of sensing protocols for drain current measurements of the adenosine and oestradiol time-series signals. The information related to the 31-mer and 35-mer oestradiol biosensors is merged into one column due to the identical sensing protocols for these biosensors.
| Sensing Protocols | Adenosine Biosensor | Oestradil Biosensors |
|---|
| Analyte | adenosine | oestradiol |
| Measurement time interval | 1 s | 1.081 s with std |
| Initial analyte load time | 1000 s | 600 s |
| Time interval of analyte injection | 500 s | 300 s |
| Variation of analyte concentration | 1 pM–10 M | 1 nM–10 M |
Table 2.
The number of entire signals in available datasets.
Table 2.
The number of entire signals in available datasets.
| Dataset ID | Dataset Name | Total Signals |
|---|
| 1 | 35-mer Adenosine | 15 |
| 2 | 31-mer Oestradiol | 24 |
| 3 | 35-mer Oestradiol | 24 |
Table 3.
The number of available segments for each dataset, classified based on their analyte concentration range.
Table 3.
The number of available segments for each dataset, classified based on their analyte concentration range.
| Class ID | Analyte Concentration | Dataset ID |
|---|
| 1 | 2 | 3 |
|---|
| 1 | No Analyte | 15 | 24 | 24 |
| - | 100 pM | 1 | 0 | 0 |
| 2 | 1 nM | 5 | 24 | 24 |
| 3 | 10 nM | 7 | 24 | 24 |
| 4 | 100 nM | 9 | 24 | 24 |
| 5 | 1 M | 12 | 24 | 24 |
| 6 | 10 M | 15 | 24 | 24 |
| Total Segments | | 63 | 144 | 144 |
Table 4.
Total number of normal and abnormal segments for the available datasets.
Table 4.
Total number of normal and abnormal segments for the available datasets.
| Dataset ID | Dataset Name | Total Normal Segments | Total Abnormal Segments |
|---|
| 1 | 35-mer Adenosine | 45 | 18 |
| 2 | 31-mer Oestradiol | 54 | 90 |
| 3 | 35-mer Oestradiol | 70 | 74 |
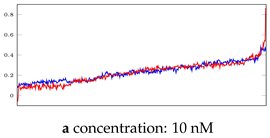
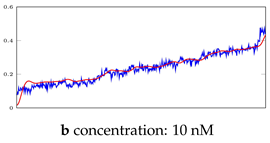
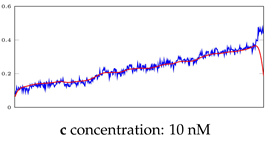
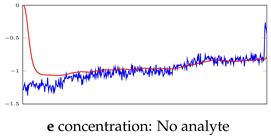
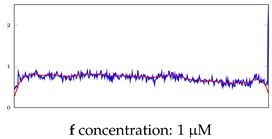
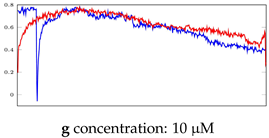
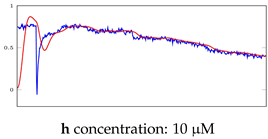
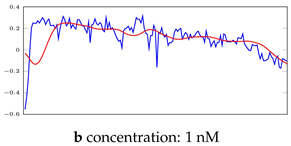
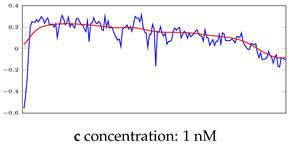
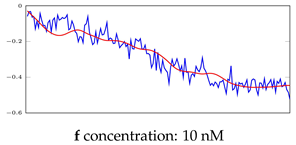
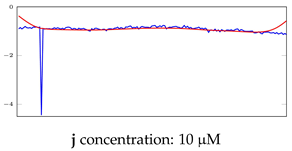
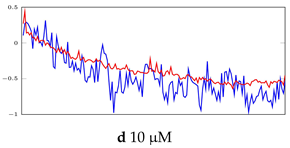
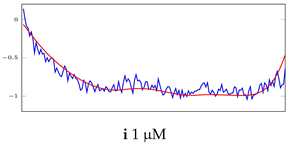
Table 5.
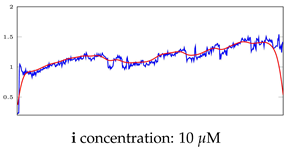
Visualization of anomaly detection for 35-mer adenosine dataset. This table shows original and reconstructed segments created by designed autoencoder networks. The blue curves were the original time series, and the red curves were the reconstructed time series.
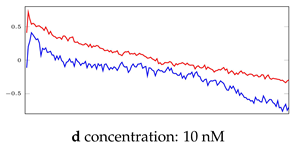
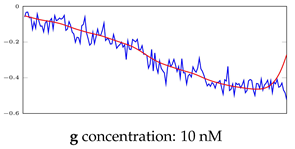
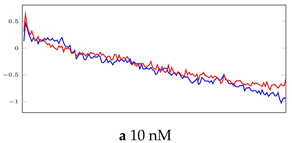
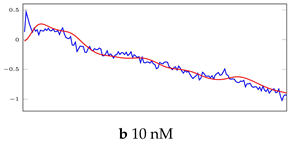
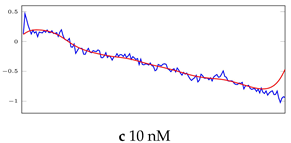
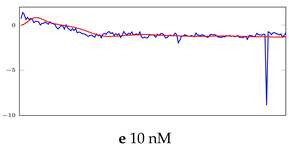
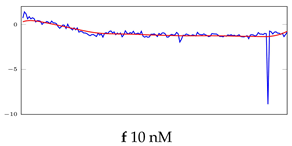
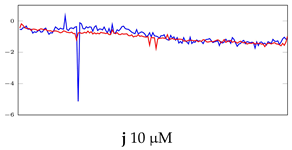
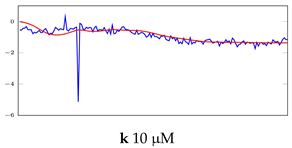
Table 6.
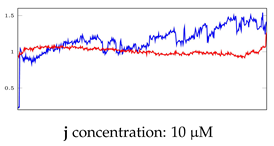
Visualization of anomaly detection for 31-mer oestradiol dataset. This table shows original and reconstructed segments created by designed autoencoder networks. The blue curves were the original time series, and the red curves were the reconstructed time series.
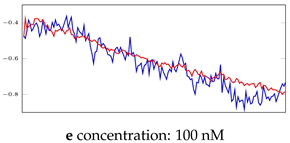
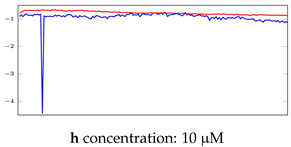
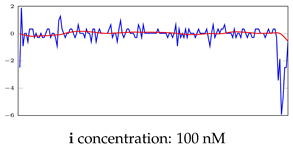
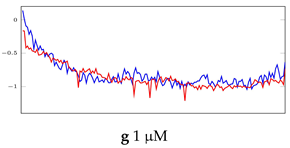
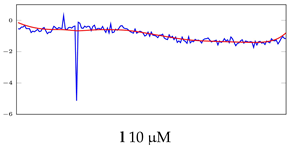
Table 7.
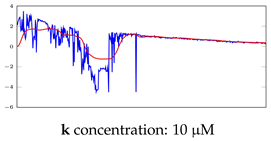
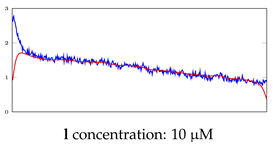
Visualization of anomaly detection for 35-mer oestradiol dataset. This table shows original and reconstructed segments created by designed autoencoder networks. The blue curves were the original time series, and the red curves were the reconstructed time series.
Table 8.
Representation of anomaly detection in the integrated autoencoder networks.
Table 8.
Representation of anomaly detection in the integrated autoencoder networks.
| LSTM Model | Vanilla Model | Integrated Models |
|---|
| Anomaly (0) | N/A 1 | Anomaly (0) |
| Normal (1) | Anomaly (0) | Anomaly (0) |
| Normal (1) | Normal (1) | Normal (1) |
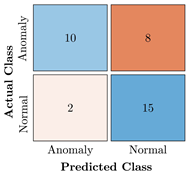
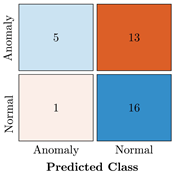
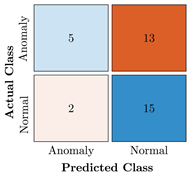
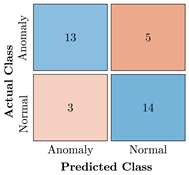
Table 9.
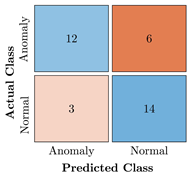
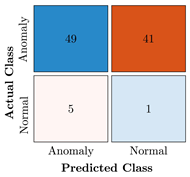
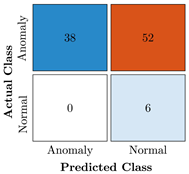
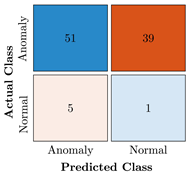
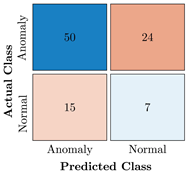
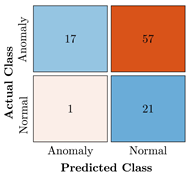
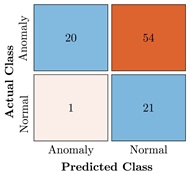
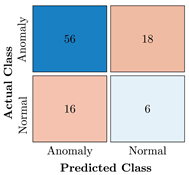
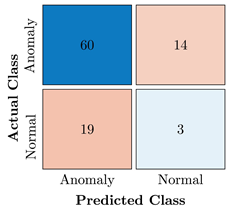
Confusion Charts for the five proposed models and three datasets.