Recent Advances in Coupled MBS and FEM Models of the Spine—A Review
Abstract
1. Introduction
2. Methods
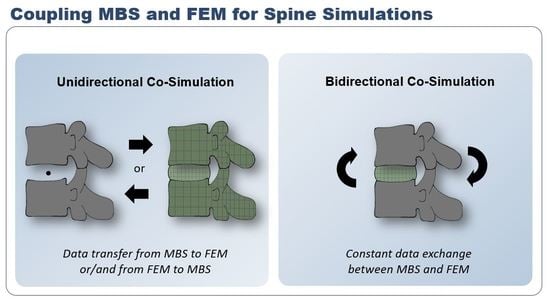
3. Unidirectional Co-Simulation of the Spine
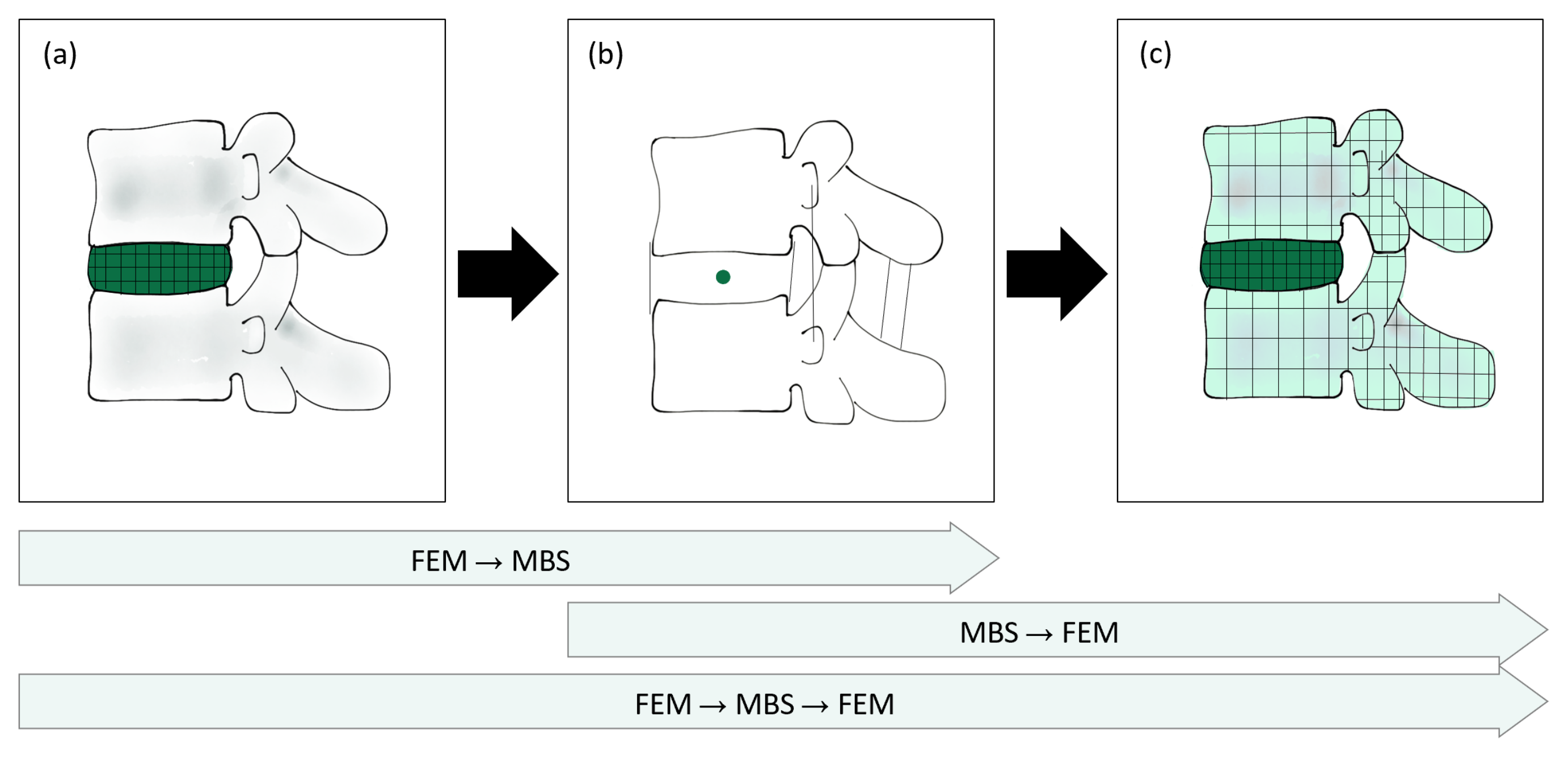
3.1. MBS → FEM
- (I)
- The first model included an initial, detailed FEM representation of the spine.
- (II)
- The second model was based on the detailed model but consisted of rigid bodies and interconnecting beam elements. It is later referred to as the musculoskeletal (MS) model.
3.2. FEM → MBS
3.3. FEM → MBS → FEM
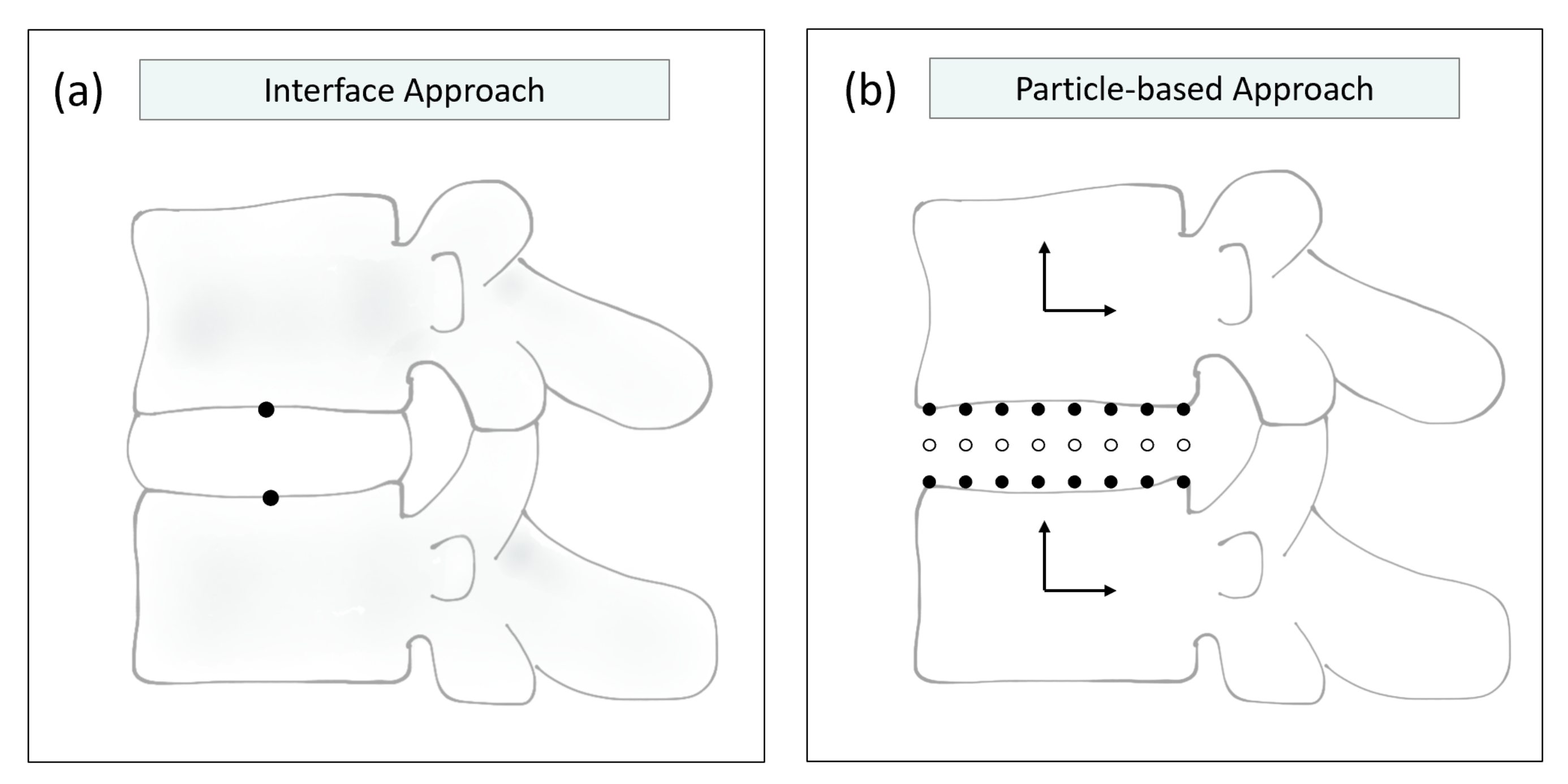
4. Bidirectional Co-Simulation of the Spine
5. Limitations and Challenges
6. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IVD | Intervertebral Disc |
| MBS | Multibody Simulation |
| FEM | Finite Element Method |
| MRI | Magnetic resonance imaging |
| DoF | Degrees of Freedom |
| BC | Boundary Conditions |
| FSU | Functional Spine Unit |
| ROM | Range of Motion |
| CAD | Computer-aided Design |
| STS | Sit-to-Stand |
| CoR | Center of Rotation |
| RP | Reference Point |
| ODE | Ordinary Differential Equation |
| VHM | Visible Human Male |
| CS | Coordinate Split |
| MSD | Multibody System Dynamics |
References
- Twomey, L.; Taylor, J. Age changes in lumbar intervertebral discs. Acta Orthop. Scand. 1985, 56, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Ball, J.R.; Harris, C.B.; Lee, J.; Vives, M.J. Lumbar Spine Injuries in Sports: Review of the Literature and Current Treatment Recommendations. Sport. Med.-Open 2019, 5, 26. [Google Scholar] [CrossRef] [PubMed]
- Stokes, I.A.; Iatridis, J.C. Mechanical conditions that accelerate intervertebral disc degeneration: Overload versus immobilization. Spine 2004, 29, 2724–2732. [Google Scholar] [CrossRef] [PubMed]
- Videman, T.; Battié, M.C.; Gibbons, L.E.; Maravilla, K.; Manninen, H.; Kaprio, J. Associations between back pain history and lumbar MRI findings. Spine 2003, 28, 582–588. [Google Scholar] [CrossRef] [PubMed]
- Actis, J.A.; Honegger, J.D.; Gates, D.H.; Petrella, A.J.; Nolasco, L.A.; Silverman, A.K. Validation of lumbar spine loading from a musculoskeletal model including the lower limbs and lumbar spine. J. Biomech. 2018, 68, 107–114. [Google Scholar] [CrossRef]
- Bassani, T.; Casaroli, G.; Galbusera, F. Dependence of lumbar loads on spinopelvic sagittal alignment: An evaluation based on musculoskeletal modeling. PLoS ONE 2019, 14, e0207997. [Google Scholar] [CrossRef]
- Beaucage-Gauvreau, E.; Robertson, W.S.P.; Brandon, S.C.E.; Fraser, R.; Freeman, B.J.C.; Graham, R.B.; Thewlis, D.; Jones, C.F. Validation of an OpenSim full-body model with detailed lumbar spine for estimating lower lumbar spine loads during symmetric and asymmetric lifting tasks. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 451–464. [Google Scholar] [CrossRef]
- Bruno, A.G.; Bouxsein, M.L.; Anderson, D.E. Development and Validation of a Musculoskeletal Model of the Fully Articulated Thoracolumbar Spine and Rib Cage. J. Biomech. Eng. 2015, 137, 081003. [Google Scholar] [CrossRef]
- Christophy, M.; Faruk Senan, N.A.; Lotz, J.C.; O’Reilly, O.M. A musculoskeletal model for the lumbar spine. Biomech. Model. Mechanobiol. 2012, 11, 19–34. [Google Scholar] [CrossRef]
- Dao, T.T.; Pouletaut, P.; Charleux, F.; Lazàry, A.; Eltes, P.; Varga, P.P.; Ho Ba Tho, M.C. Multimodal medical imaging (CT and dynamic MRI) data and computer-graphics multi-physical model for the estimation of patient specific lumbar spine muscle forces. Data Knowl. Eng. 2015, 96-97, 3–18. [Google Scholar] [CrossRef]
- de Zee, M.; Hansen, L.; Wong, C.; Rasmussen, J.; Simonsen, E.B. A generic detailed rigid-body lumbar spine model. J. Biomech. 2007, 40, 1219–1227. [Google Scholar] [CrossRef] [PubMed]
- Fasser, M.R.; Jokeit, M.; Kalthoff, M.; Gomez Romero, D.A.; Trache, T.; Snedeker, J.G.; Farshad, M.; Widmer, J. Subject-Specific Alignment and Mass Distribution in Musculoskeletal Models of the Lumbar Spine. Front. Bioeng. Biotechnol. 2021, 9, 721042. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.K.; Zhang, Y. Estimation of lumbar spinal loading and trunk muscle forces during asymmetric lifting tasks: Application of whole-body musculoskeletal modelling in OpenSim. Ergonomics 2017, 60, 563–576. [Google Scholar] [CrossRef] [PubMed]
- Raabe, M.E.; Chaudhari, A.M.W. An investigation of jogging biomechanics using the full-body lumbar spine model: Model development and validation. J. Biomech. 2016, 49, 1238–1243. [Google Scholar] [CrossRef] [PubMed]
- Bayoglu, R.; Galibarov, P.E.; Verdonschot, N.; Koopman, B.; Homminga, J. Twente Spine Model: A thorough investigation of the spinal loads in a complete and coherent musculoskeletal model of the human spine. Med. Eng. Phys. 2019, 68, 35–45. [Google Scholar] [CrossRef]
- Favier, C.D.; Finnegan, M.E.; Quest, R.A.; Honeyfield, L.; McGregor, A.H.; Phillips, A.T.M. An open-source musculoskeletal model of the lumbar spine and lower limbs: A validation for movements of the lumbar spine. Comput. Methods Biomech. Biomed. Eng. 2021, 24, 1310–1325. [Google Scholar] [CrossRef]
- Hajihosseinali, M.; Arjmand, N.; Shirazi-Adl, A.; Farahmand, F.; Ghiasi, M.S. A novel stability and kinematics-driven trunk biomechanical model to estimate muscle and spinal forces. Med. Eng. Phys. 2014, 36, 1296–1304. [Google Scholar] [CrossRef]
- Han, K.S.; Rohlmann, A.; Yang, S.J.; Kim, B.S.; Lim, T.H. Spinal muscles can create compressive follower loads in the lumbar spine in a neutral standing posture. Med. Eng. Phys. 2011, 33, 472–478. [Google Scholar] [CrossRef]
- Petit, Y.; Aubin, C.E.; Labelle, H. Patient-specific mechanical properties of a flexible multi-body model of the scoliotic spine. Med. Biol. Eng. Comput. 2004, 42, 55–60. [Google Scholar] [CrossRef]
- Senteler, M.; Weisse, B.; Rothenfluh, D.A.; Snedeker, J.G. Intervertebral reaction force prediction using an enhanced assembly of OpenSim models. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 538–548. [Google Scholar] [CrossRef]
- Ignasiak, D.; Dendorfer, S.; Ferguson, S.J. Thoracolumbar spine model with articulated ribcage for the prediction of dynamic spinal loading. J. Biomech. 2016, 49, 959–966. [Google Scholar] [CrossRef] [PubMed]
- Rupp, T.K.; Ehlers, W.; Karajan, N.; Günther, M.; Schmitt, S. A forward dynamics simulation of human lumbar spine flexion predicting the load sharing of intervertebral discs, ligaments, and muscles. Biomech. Model. Mechanobiol. 2015, 14, 1081–1105. [Google Scholar] [CrossRef] [PubMed]
- Pearcy, M.J.; Bogduk, N. Instantaneous axes of rotation of the lumbar intervertebral joints. Spine 1988, 13, 1033–1041. [Google Scholar] [CrossRef] [PubMed]
- Han, K.S.; Zander, T.; Taylor, W.R.; Rohlmann, A. An enhanced and validated generic thoraco-lumbar spine model for prediction of muscle forces. Med. Eng. Phys. 2012, 34, 709–716. [Google Scholar] [CrossRef] [PubMed]
- Peloquin, J.M.; Yoder, J.H.; Jacobs, N.T.; Moon, S.M.; Wright, A.C.; Vresilovic, E.J.; Elliott, D.M. Human L3L4 intervertebral disc mean 3D shape, modes of variation, and their relationship to degeneration. J. Biomech. 2014, 47, 2452–2459. [Google Scholar] [CrossRef] [PubMed]
- Sekuboyina, A.; Rempfler, M.; Valentinitsch, A.; Menze, B.H.; Kirschke, J.S. Labeling Vertebrae with Two-dimensional Reformations of Multidetector CT Images: An Adversarial Approach for Incorporating Prior Knowledge of Spine Anatomy. Radiol. Artif. Intell. 2020, 2, e190074. [Google Scholar] [CrossRef] [PubMed]
- Lavecchia, C.E.; Espino, D.M.; Moerman, K.M.; Tse, K.M.; Robinson, D.; Lee, P.V.S.; Shepherd, D.E.T. Lumbar model generator: A tool for the automated generation of a parametric scalable model of the lumbar spine. J. R. Soc. Interface 2018, 15, 20170829. [Google Scholar] [CrossRef]
- Schmidt, H.; Heuer, F.; Drumm, J.; Klezl, Z.; Claes, L.; Wilke, H.J. Application of a calibration method provides more realistic results for a finite element model of a lumbar spinal segment. Clin. Biomech. 2007, 22, 377–384. [Google Scholar] [CrossRef]
- Dauvilliers, F.; Bendjellal, F.; Weiss, M.; Lavaste, F.; Tarriere, C. Development of a Finite Element Model of the Neck. In Proceedings of the 38th Stapp Car Crash Conference, Fort Lauderdale, FL, USA, 31 October–4 November 1994. [Google Scholar] [CrossRef]
- Chetoui, M.A.; Boiron, O.; Ghiss, M.; Dogui, A.; Deplano, V. Assessment of intervertebral disc degeneration-related properties using finite element models based on H-weighted MRI data. Biomech. Model. Mechanobiol. 2019, 18, 17–28. [Google Scholar] [CrossRef]
- Sen, S.; Jacobs, N.T.; Boxberger, J.I.; Elliott, D.M. Human annulus fibrosus dynamic tensile modulus increases with degeneration. Mech. Mater. 2012, 44, 93–98. [Google Scholar] [CrossRef]
- Iatridis, J.C.; Setton, L.A.; Foster, R.J.; Rawlins, B.A.; Weidenbaum, M.; Mow, V. Degeneration affects the anisotropic and nonlinear behaviors of human anulus fibrosus in compression. J. Biomech. 1998, 31, 535–544. [Google Scholar] [CrossRef] [PubMed]
- Massey, C.J.; van Donkelaar, C.C.; Vresilovic, E.; Zavaliangos, A.; Marcolongo, M. Effects of aging and degeneration on the human intervertebral disc during the diurnal cycle: A finite element study. J. Orthop. Res. 2012, 30, 122–128. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.G.; Wang, Y.H.; Wu, J.H.; Guan, J.J.; Mao, N.F.; Lu, C.W.; Lv, R.X.; Ding, M.C.; Shi, Z.C.; Cai, B. Study of Double-level Degeneration of Lower Lumbar Spines by Finite Element Model. World Neurosurg. 2016, 86, 294–299. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, W.; Karajan, N.; Markert, B. An extended biphasic model for charged hydrated tissues with application to the intervertebral disc. Biomech. Model. Mechanobiol. 2009, 8, 233–251. [Google Scholar] [CrossRef]
- Azari, F.; Arjmand, N.; Shirazi-Adl, A.; Rahimi-Moghaddam, T. A combined passive and active musculoskeletal model study to estimate L4-L5 load sharing. J. Biomech. 2018, 70, 157–165. [Google Scholar] [CrossRef]
- Esat, V.; Acar, M. Viscoelastic finite element analysis of the cervical intervertebral discs in conjunction with a multi-body dynamic model of the human head and neck. Proc. Inst. Mech. Eng. Part-J. Eng. Med. 2009, 223, 249–262. [Google Scholar] [CrossRef] [PubMed]
- Esat, V.; van Lopik, D.W.; Acar, M. Combined multi-body dynamic and Fe models of human head and neck. In IUTAM Symposium on Impact Biomechanics: From Fundamental Insights to Applications; Springer: Dordrecht, The Netherlands, 2005; Volume 124, pp. 91–100. [Google Scholar]
- Kamal, Z.; Rouhi, G.; Arjmand, N.; Adeeb, S. A stability-based model of a growing spine with adolescent idiopathic scoliosis: A combination of musculoskeletal and finite element approaches. Med. Eng. Phys. 2019, 64, 46–55. [Google Scholar] [CrossRef]
- Khoddam-Khorasani, P.; Arjmand, N.; Shirazi-Adl, A. Trunk Hybrid Passive–Active Musculoskeletal Modeling to Determine the Detailed T12–S1 Response Under In Vivo Loads. Ann. Biomed. Eng. 2018, 46, 1830–1843. [Google Scholar] [CrossRef]
- Liu, T.; El-Rich, M. Effects of nucleus pulposus location on spinal loads and joint centers of rotation and reaction during forward flexion: A combined finite element and Musculoskeletal study. J. Biomech. 2020, 104, 109740. [Google Scholar] [CrossRef]
- Liu, T.; Khalaf, K.; Naserkhaki, S.; El-Rich, M. Load-sharing in the lumbosacral spine in neutral standing & flexed postures - A combined finite element and inverse static study. J. Biomech. 2018, 70, 43–50. [Google Scholar] [CrossRef]
- Meszaros, L.; Hammer, M.; Riede, J.; Pivonka, P.; Little, J.; Schmitt, S. Simulating subject-specific spine mechanics: An integrated finite element and neuro-musculoskeletal modelling framework. In Proceedings of the XXVIII Congress of the International Society of Biomechanics, Stockholm, Sweden, 25–29 July 2021. [Google Scholar]
- Karajan, N.; Rohrle, O.; Ehlers, W.; Schmitt, S. Linking continuous and discrete intervertebral disc models through homogenisation. Biomech. Model. Mechanobiol. 2013, 12, 453–466. [Google Scholar] [CrossRef] [PubMed]
- Knapik, G.G.; Mendel, E.; Marras, W.S. Use of a personalized hybrid biomechanical model to assess change in lumbar spine function with a TDR compared to an intact spine. Eur. Spine J. 2012, 21 (Suppl. S5), S641–S652. [Google Scholar] [CrossRef] [PubMed]
- Monteiro, N.M.B.; da Silva, M.P.T.; Folgado, J.; Melancia, J.P.L. Structural analysis of the intervertebral discs adjacent to an interbody fusion using multibody dynamics and finite element cosimulation. Multibody Syst. Dyn. 2011, 25, 245–270. [Google Scholar] [CrossRef]
- Remus, R.; Lipphaus, A.; Neumann, M.; Bender, B. Calibration and validation of a novel hybrid model of the lumbosacral spine in ArtiSynth-The passive structures. PLoS ONE 2021, 16, e0250456. [Google Scholar] [CrossRef]
- Cheng, E.J.; Brown, I.E.; Loeb, G.E. Virtual muscle: A computational approach to understanding the effects of muscle properties on motor control. J. Neurosci. Methods 2000, 101, 117–130. [Google Scholar] [CrossRef]
- Du, C.F.; Mo, Z.J.; Tian, S.; Wang, L.Z.; Fan, J.; Liu, S.Y.; Fan, Y.B. Biomechanical investigation of thoracolumbar spine in different postures during ejection using a combined finite element and multi-body approach. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 1121–1131. [Google Scholar] [CrossRef]
- Agur, A.M.R.; Dalley, A.F. Grant Atlas of Anatomy, 10th ed.; Williams and Wilkins: Baltimore, MD, USA, 2009. [Google Scholar]
- Henao, J.; Aubin, C.E.; Labelle, H.; Arnoux, P.J. Patient-specific finite element model of the spine and spinal cord to assess the neurological impact of scoliosis correction: Preliminary application on two cases with and without intraoperative neurological complications. Comput. Methods Biomech. Biomed. Eng. 2016, 19, 901–910. [Google Scholar] [CrossRef]
- Aubin, C.E.; Labelle, H.; Chevrefils, C.; Desroches, G.; Clin, J.; Boivin, A. Preoperative planning simulator for spinal deformity surgeries. Spine 2008, 33, 2143–2152. [Google Scholar] [CrossRef]
- Honegger, J.D.; Actis, J.A.; Gates, D.H.; Silverman, A.K.; Munson, A.H.; Petrella, A.J. Development of a multiscale model of the human lumbar spine for investigation of tissue loads in people with and without a transtibial amputation during sit-to-stand. Biomech. Model. Mechanobiol. 2021, 20, 339–358. [Google Scholar] [CrossRef]
- Campbell, J.Q.; Coombs, D.J.; Rao, M.; Rullkoetter, P.J.; Petrella, A.J. Automated finite element meshing of the lumbar spine: Verification and validation with 18 specimen-specific models. J. Biomech. 2016, 49, 2669–2676. [Google Scholar] [CrossRef]
- Wilke, H.J.; Neef, P.; Caimi, M.; Hoogland, T.; Claes, L.E. New in vivo measurements of pressures in the intervertebral disc in daily life. Spine 1999, 24, 755–762. [Google Scholar] [CrossRef] [PubMed]
- Shirazi-Adl, A.; Ahmed, A.M.; Shrivastava, S.C. Mechanical Response of a Lumbar Motion Segment in Axial Torque Alone and Combined with Compression. Spine 1986, 11, 914–927. [Google Scholar] [CrossRef]
- Shirazi-Adl, A.; Parnianpour, M. Nonlinear response analysis of the human ligamentous lumbar spine in compression. On mechanisms affecting the postural stability. Spine 1993, 18, 147–158. [Google Scholar] [CrossRef] [PubMed]
- Kiefer, A.; Shirazi-Adl, A.; Parnianpour, M. Synergy of the human spine in neutral postures. Eur. Spine J. 1998, 7, 471–479. [Google Scholar] [CrossRef]
- Kiefer, A.; Shirazi-Adl, A.; Parnianpour, M. Stability of the human spine in neutral postures. Eur. Spine J. 1997, 6, 45–53. [Google Scholar] [CrossRef]
- Shirazi-Adl, A.; Sadouk, S.; Parnianpour, M.; Pop, D.; El-Rich, M. Muscle force evaluation and the role of posture in human lumbar spine under compression. Eur. Spine J. 2002, 11, 519–526. [Google Scholar] [CrossRef]
- Arjmand, N.; Shirazi-Adl, A. Biomechanics of Changes in Lumbar Posture in Static Lifting. Spine 2005, 30, 2648. [Google Scholar] [CrossRef]
- Arjmand, N.; Gagnon, D.; Plamondon, A.; Shirazi-Adl, A.; Larivière, C. Comparison of trunk muscle forces and spinal loads estimated by two biomechanical models. Clin. Biomech. 2009, 24, 533–541. [Google Scholar] [CrossRef]
- Rajaee, M.A.; Arjmand, N.; Shirazi-Adl, A. A novel coupled musculoskeletal finite element model of the spine - Critical evaluation of trunk models in some tasks. J. Biomech. 2021, 119, 110331. [Google Scholar] [CrossRef] [PubMed]
- Kumaran, Y.; Shah, A.; Katragadda, A.; Padgaonkar, A.; Zavatsky, J.; McGuire, R.; Serhan, H.; Elgafy, H.; Goel, V.K. Iatrogenic muscle damage in transforaminal lumbar interbody fusion and adjacent segment degeneration: A comparative finite element analysis of open and minimally invasive surgeries. Eur. Spine J. 2021, 30, 2622–2630. [Google Scholar] [CrossRef] [PubMed]
- Shah, A.; Kumaran, Y.; Zavatsky, J.; McGuire, R.; Serhan, H. Development of a Novel Finite Element Model of a Thoracolumbar Spine with Ribcage and Muscle Forces to Simulate Scenarios Closer to in Vivo. In Proceedings of the ORS 2020 Annual Meeting, Phoenix, AZ, USA, 8–11 February 2020. [Google Scholar]
- Little, J.P.; Adam, C.J. Geometric sensitivity of patient-specific finite element models of the spine to variability in user-selected anatomical landmarks. Comput. Methods Biomech. Biomed. Eng. 2013, 18, 676–688. [Google Scholar] [CrossRef] [PubMed]
- Ackerman, M.J. The Visible Human Project: A resource for education. Acad Med. 1999, 74, 667–670. [Google Scholar] [CrossRef] [PubMed]
- Rohlmann, A.; Bauer, L.; Zander, T.; Bergmann, G.; Wilke, H.J. Determination of trunk muscle forces for flexion and extension by using a validated finite element model of the lumbar spine and measured in vivo data. J. Biomech. 2006, 39, 981–989. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, H.; Heuer, F.; Simon, U.; Kettler, A.; Rohlmann, A.; Claes, L.; Wilke, H.J. Application of a new calibration method for a three-dimensional finite element model of a human lumbar annulus fibrosus. Clin. Biomech. 2006, 21, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Tseng, F.C.; Hulbert, G.M. A gluing algorithm for network-distributed multibody dynamics simulation. Multibody Syst. Dyn. 2001, 6, 377–396. [Google Scholar] [CrossRef]
- Yen, J.; Petzold, L.R. An efficient Newton-type iteration for the numerical solution of highly oscillatory constrained multibody dynamic systems. Siam J. Sci. Comput. 1998, 19, 1513–1534. [Google Scholar] [CrossRef]
- Wang, J.Z.; Ma, Z.D.; Hulbert, G.M. A gluing algorithm for distributed simulation of multibody systems. Nonlinear Dyn. 2003, 34, 159–188. [Google Scholar] [CrossRef]
- Dicko, A.H.; Tong-Yette, N.; Gilles, B.; Faure, F.; Palombi, O. Construction and validation of a hybrid lumbar spine model for the fast evaluation of intradiscal pressure and mobility. Int. Sci. Index Med. Health Sci. 2015, 9, 134–145. [Google Scholar]
- Stavness, I.; Lloyd, J.E.; Payan, Y.; Fels, S. Coupled hard-soft tissue simulation with contact and constraints applied to jaw-tongue-hyoid dynamics. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 367–390. [Google Scholar] [CrossRef]
- Remus, R.; Uttich, E.; Bender, B. Sensitivity of biomechanical responses in path optimized follower loads considering the lumbosacral load sharing. In Proceedings of the XXVIII Congress of the International Society of Biomechanics, Stockholm, Sweden, 25–29 July 2021. [Google Scholar]
- Remus, R.; Lipphaus, A.; Hoffmann, A.; Neumann, M.; Bender, B. An inverse dynamic active hybrid model to predict effects of the intra-abdominal pressure on the lumbar spine. In Proceedings of the 27th Congress of the European Society of Biomechanics, Porto, Portugal, 26–29 June 2022. [Google Scholar]
- Mueller, M.; Gross, M. Interactive Virtual Materials. In Proceedings of the Graphics Interface 2004 Conference, London, ON, Canada, 17–19 May 2004. [Google Scholar]
| MBS Solver 1 | FEM Solver | Execution Order | Transferred Data | Software Structure | Model Geometry | |
|---|---|---|---|---|---|---|
| Esat et al., 2005, 2009 [37,38] | visualNastran 4D from MSC Software | Marc/Mentat from MSC Software. | MBS → FEM | Two time-dependent sagittal forces and one sagittal moment at each IVD → BC | Distinct software, manual transfer | Literature |
| Du et al., 2014 [49] | Hypermesh | Hypermesh (Altair Engineering) | MBS → FEM | Time-dependent translation & rotation at hip joint & T9 endplate → BC | Distinct software, manual transfer | Literature |
| Henao et al., 2016 [51] | ADAMS [52] | RADIOSSTM (Altair Engineering) | MBS → FEM | Displacement of vertebrae | Distinct software, manual transfer | Patient-specific/Literature |
| Honegger et al., 2021 [53] | OpenSim | Abaqus | MBS → FEM | Time-dependent joint angles and muscle forces | Distinct software, manual transfer | Preexisting FEM model fitted to patient-specific geometry |
| Kamal et al., 2019 [39] | Matlab | Abaqus | MBS → FEM | Resulting muscle forces and reaction moments as distributed pressure and shear stress | Distinct software, manual transfer | CT-based |
| Azari et al., 2018, Khoddam-Khorasani et al., 2018, Rajaee et al., 2021 [36,40,63] | Abaqus/Matlab | Abaqus/In-house | MBS → FEM | Mostly static muscle forces and moments | Distinct software/One software incorporating muscles and detailed passive elements | CT-based |
| Karajan et al., 2013 [44] | Not mentioned | Not mentioned | FEM → MBS | IVD displacement → bushing component definition | Distinct software, manual transfer | Simplified as cylinders |
| Kumaran et al., 2021 [64] | OpenSim | Abaqus | FEM → MBS → FEM | FEM → MBS: ROM MBS → FEM: Muscle forces | Distinct software, manual transfer | Literature |
| Liu et al., 2018,2020 [41,42] | Anybody | Abaqus/Hypermesh | FEM → MBS → FEM | FEM → MBS: Joint stiffness curves of IVDs MBS → FEM: Reaction moment, ligament and muscle forces at T12-L1 joint | Distinct software, manual transfer by trial-and-error | ˙Default Anybody data/Literature |
| Meszaros et al., 2021 [43] | VHM | Abaqus | FEM → MBS → FEM | FEM → MBS: IVD response as mechanical parameters MBS → FEM: Time-dependent muscle, tendon & ligament forces | Distinct software, manual transfer | VHM for MBS, patient-specific & VHM-based FEM (morphed) |
| MBS Solver | FEM Solver | Execution Order | Transferred Data | Software Structure | Model Geometry | |
|---|---|---|---|---|---|---|
| Monteiro et al., 2011 [46] | Abaqus | Apollo (Fortran) | constant | Displacements in MBS ↔ reaction forces and moments in FEM | Single software | Literature |
| Dicko et al., 2015 [73] | Not mentioned | Not mentioned | constant | Integrated approach based on particles | Single software | Literature |
| Remus et al., 2021 [47] | ArtiSynth | ArtiSynth | constant | Integrated approach based on particles | Single software | Literature (VHM) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nispel, K.; Lerchl, T.; Senner, V.; Kirschke, J.S. Recent Advances in Coupled MBS and FEM Models of the Spine—A Review. Bioengineering 2023, 10, 315. https://doi.org/10.3390/bioengineering10030315
Nispel K, Lerchl T, Senner V, Kirschke JS. Recent Advances in Coupled MBS and FEM Models of the Spine—A Review. Bioengineering. 2023; 10(3):315. https://doi.org/10.3390/bioengineering10030315
Chicago/Turabian StyleNispel, Kati, Tanja Lerchl, Veit Senner, and Jan S. Kirschke. 2023. "Recent Advances in Coupled MBS and FEM Models of the Spine—A Review" Bioengineering 10, no. 3: 315. https://doi.org/10.3390/bioengineering10030315
APA StyleNispel, K., Lerchl, T., Senner, V., & Kirschke, J. S. (2023). Recent Advances in Coupled MBS and FEM Models of the Spine—A Review. Bioengineering, 10(3), 315. https://doi.org/10.3390/bioengineering10030315