Effects of Pulsed Radiofrequency Source on Cardiac Ablation
Abstract
:1. Introduction
2. Methodology
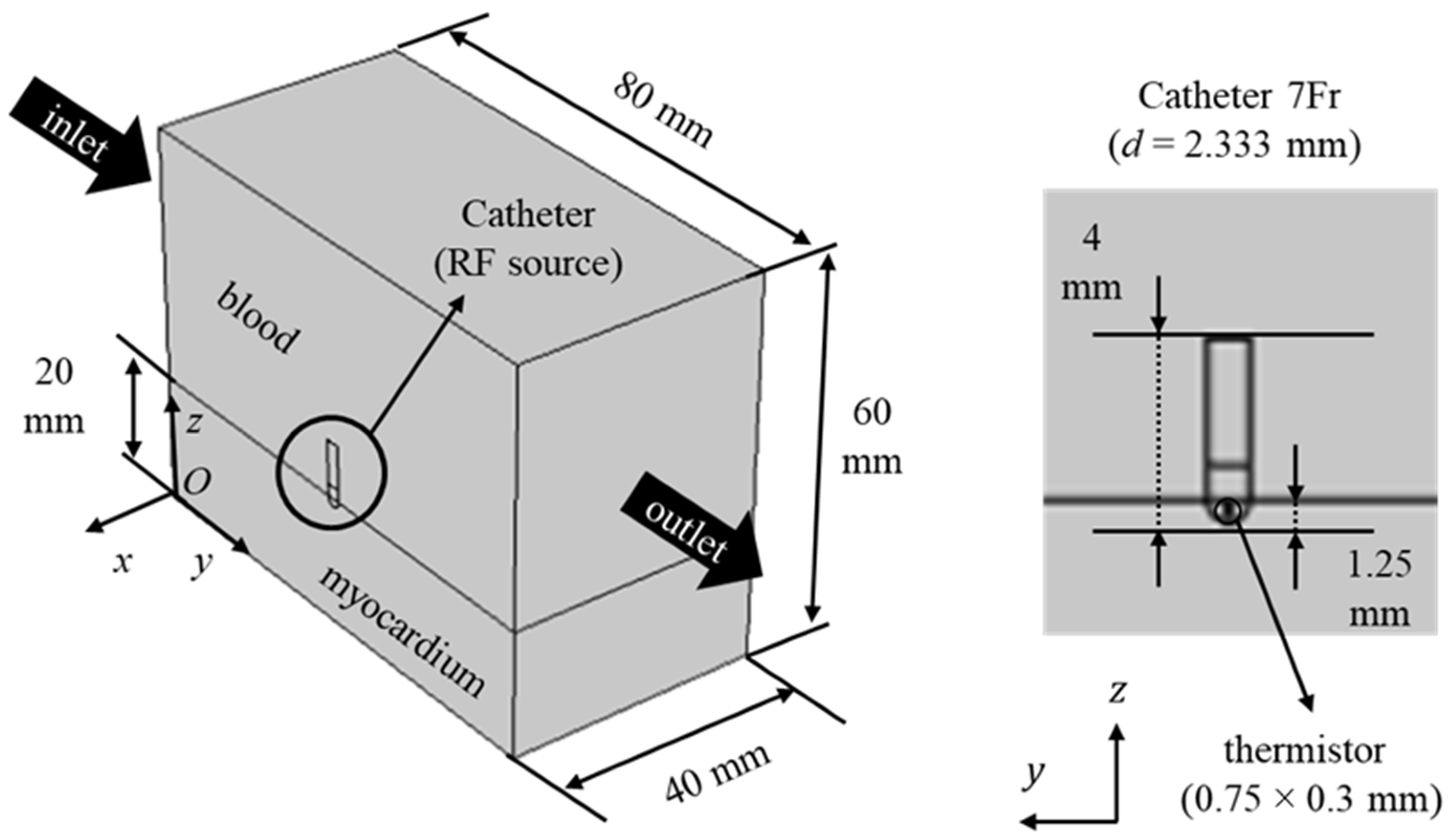
2.1. Geometry and Governing Equations
2.2. Boundary Conditions and Thermophysical Properties
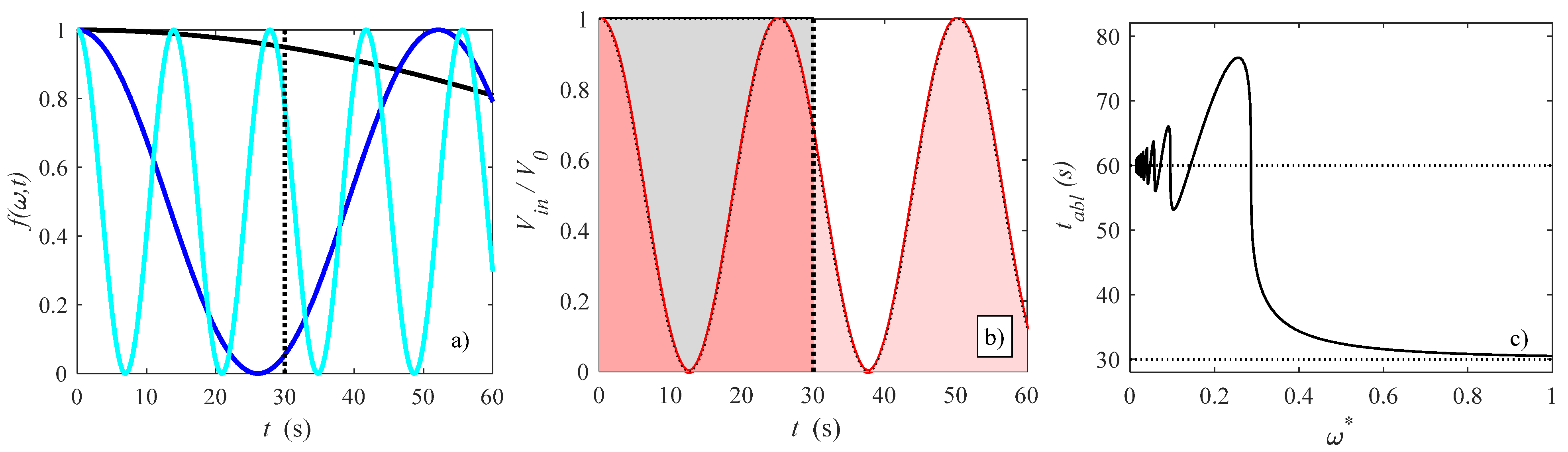
2.3. Modulated Heat Transfer Modeling
2.4. Numerical Modeling and Validation
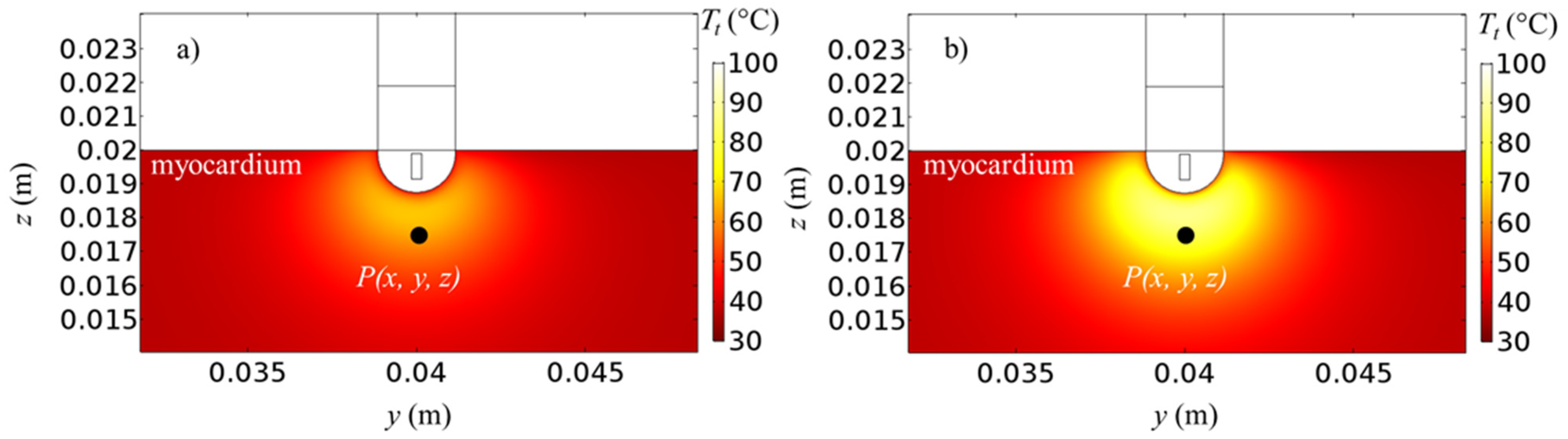
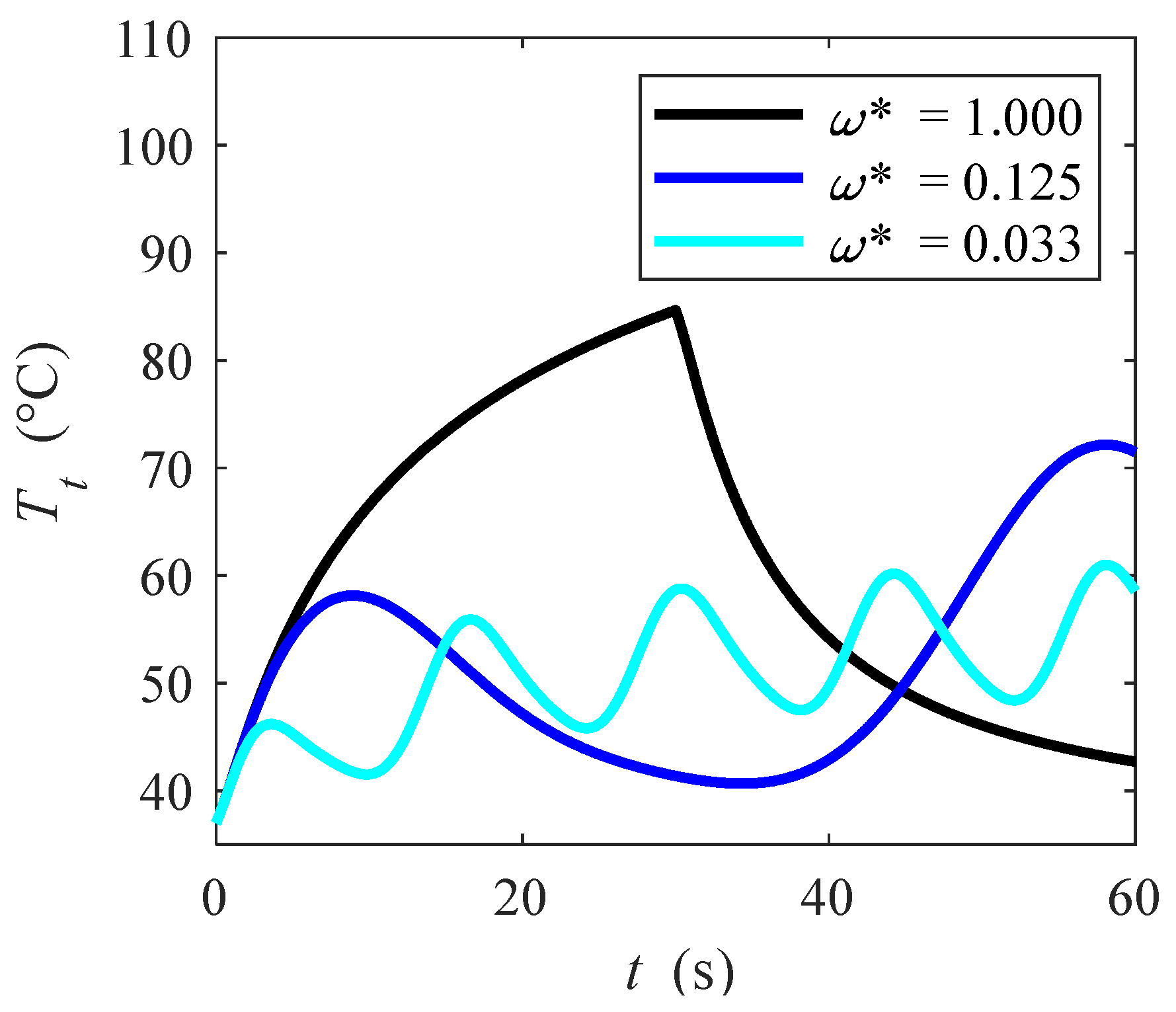
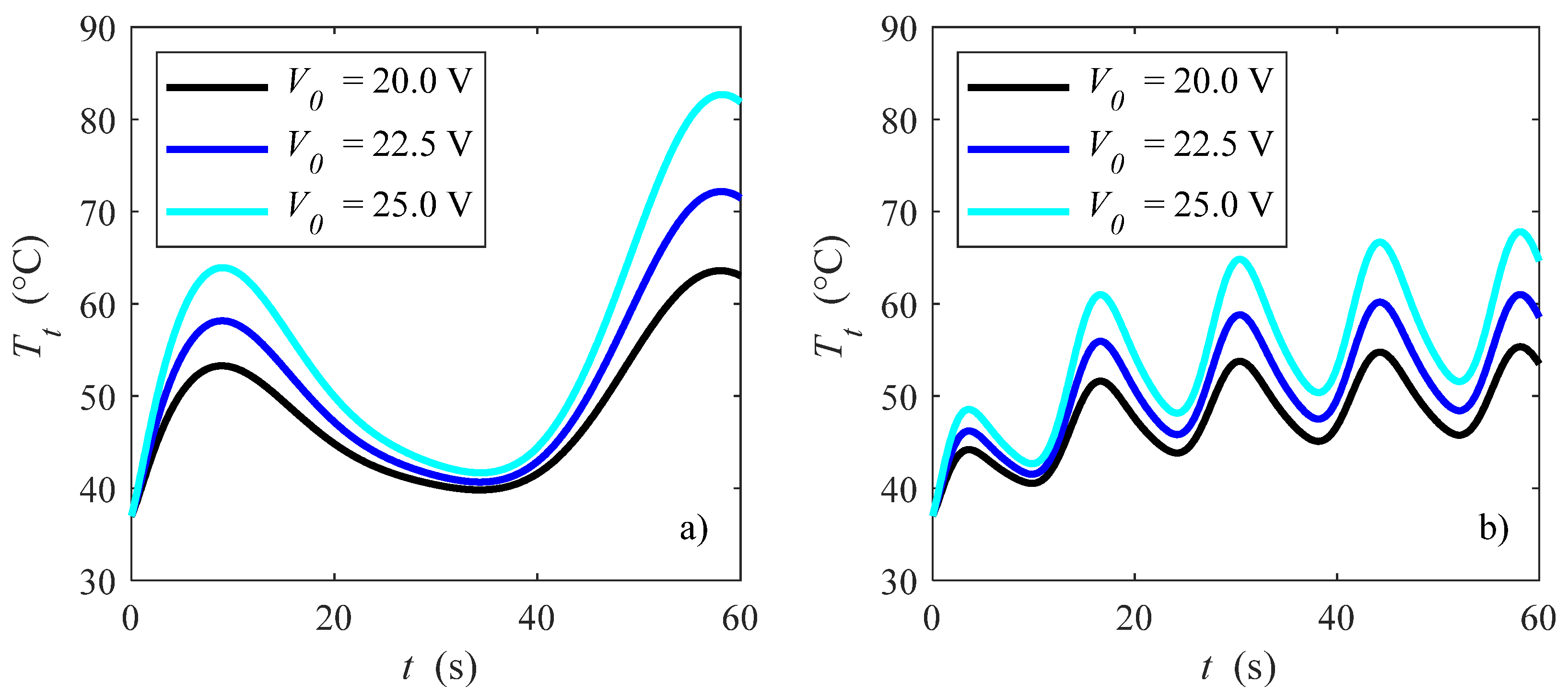
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| CH2O | water content |
| C | heat capacity (J kg−1 K−1) |
| E | electric field (V m−1) |
| hc | interfacial heat transfer coefficient (W m−2 K−1) |
| k | thermal conductivity (W m−1 K−1) |
| K | permeability (m−2) |
| p | pressure (Pa) |
| heat rate (W) | |
| radiofrequency heat generation (W m−3) | |
| Sv | specific surface area (m−1) |
| t | time (s) |
| T | temperature (K) |
| u | velocity vector (m s−1) |
| V | voltage (V) |
| x, y, z | cartesian coordinates (m) |
| Greek letters | |
| ε | porosity |
| λ | water latent heat of vaporization (J kg−1) |
| μ | viscosity (Pa s) |
| ρ | density (kg m−3) |
| σ | electric conductivity (S m−1) |
| ω | angular frequency (rad s−1) |
| Subscripts | |
| 0 | reference |
| abl | ablation |
| b | blood |
| c | catheter |
| g | gas |
| eff | effective |
| ev | evaporation |
| in | inlet |
| l | liquid |
| t | tissue |
References
- Goldberg, S.N. Radiofrequency tumor ablation: Principles and techniques. In Multi-Treatment Modalities of Liver Tumours; Habib, N.A., Ed.; Springer: New York, NY, USA, 2002; pp. 87–118. [Google Scholar]
- Haines, D.E.; Watson, D.D. Tissue heating during radiofrequency catheter ablation: A thermodynamic model and observations in isolated perfused and superfused canine right ventricular free wall. Pace 1989, 12, 962–976. [Google Scholar] [PubMed]
- Labonté, S.; Stanislaw, W.; Stuchly, S. Radio-frequency ablation of the myocardium: A numerical model. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 31 October–3 November 1991. [Google Scholar]
- Shahidi, A.V.; Savard, P. A finite element model for radiofrequency ablation of the myocardium. IEEE Trans. Biomed. Eng. 1994, 41, 963–968. [Google Scholar] [PubMed]
- Woo, E.J.; Tungjitkusolmun, S.; Cao, H.; Tsai, J.Z.; Webster, J.G.; Vorperian, V.R.; Will, J.A. A new catheter design using needle electrode for subendocardial RF ablation of ventricular muscles: Finite element analysis and in vitro experiments. IEEE Trans. Biomed. Eng. 2000, 47, 23–31. [Google Scholar]
- Tungjitkusolmun, S.; Haemmerich, D.; Cao, H.; Tsai, J.Z.; Choy, Y.B.; Vorperian, V.R.; Webster, J.G. Modeling bipolar phase-shifted multielectrode catheter ablation. IEEE Trans. Biomed. Eng. 2002, 49, 10–17. [Google Scholar]
- Lai, Y.C.; Choy, Y.B.; Haemmerich, D.; Vorperian, V.R.; Webster, J.G. Lesion size estimator of cardiac radiofrequency ablation at different common locations with different tip temperatures. IEEE Trans. Biomed. Eng. 2004, 51, 1859–1864. [Google Scholar] [CrossRef]
- González-Suárez, A.; Berjano, E. Comparative analysis of different methods of modeling the thermal effect of circulating blood flow during RF cardiac ablation. IEEE Trans. Biomed. Eng. 2015, 63, 250–259. [Google Scholar]
- Parés, C.; Berjano, E.; González-Suárez, A. Effect of intracardiac blood flow pulsatility during radiofrequency cardiac ablation: Computer modeling study. Int. J. Hyperth. 2021, 38, 316–325. [Google Scholar]
- Pérez, J.J.; Nadal, E.; Berjano, E.; González-Suárez, A. Computer modeling of radiofrequency cardiac ablation including heartbeat-induced electrode displacement. Comput. Biol. Med. 2022, 144, 105346. [Google Scholar]
- Iasiello, M.; Andreozzi, A.; Bianco, N.; Vafai, K. The porous media theory applied to radiofrequency catheter ablation. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 2669–2681. [Google Scholar]
- Wang, K.; Tavakkoli, F.; Wang, S.; Vafai, K. Analysis and analytical characterization of bioheat transfer during radiofrequency ablation. J. Biomech. 2015, 48, 930–940. [Google Scholar] [CrossRef]
- Sluijter, M.E. Non-thermal radiofrequency procedures in the treatment spinal pain. In Proceedings of the Pain in Europe: 2nd Annual Congress of the European Federation of IASP Chapters, Barcelona, Spain, 24–27 September 1997. [Google Scholar]
- Sluijter, M.E. The role of radiofrequency in failed back surgery patients. Curr. Rev. Pain 2000, 4, 49–53. [Google Scholar]
- Bedoya, M.; del Rio, A.M.; Chiang, J.; Brace, C.L. Microwave ablation energy delivery: Influence of power pulsing on ablation results in an ex vivo and in vivo liver model. Med. Phys. 2014, 41, 123301. [Google Scholar]
- Goldberg, S.N.; Stein, M.C.; Gazelle, G.S.; Sheiman, R.G.; Kruskal, J.B.; Clouse, M.E. Percutaneous radiofrequency tissue ablation: Optimization of pulsed-radiofrequency technique to increase coagulation necrosis. J. Vasc. Interv. Radiol. 1999, 10, 907–916. [Google Scholar]
- Fukushima, T.; Ikeda, K.; Kawamura, Y.; Sorin, Y.; Hosaka, T.; Kobayashi, M.; Saitoh, S.; Sezaki, H.; Akuta, N.; Suzuki, F.; et al. Randomized controlled trial comparing the efficacy of impedance control and temperature control of radiofrequency interstitial thermal ablation for treating small hepatocellular carcinoma. Oncology 2015, 89, 47–52. [Google Scholar] [CrossRef]
- Zhang, B.; Moser, M.A.; Zhang, E.M.; Luo, Y.; Zhang, W. Numerical analysis of the relationship between the area of target tissue necrosis and the size of target tissue in liver tumours with pulsed radiofrequency ablation. Int. J. Hyperth. 2015, 31, 715–725. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Numerical analysis of the pulsating heat source effects in a tumor tissue. Comput. Methods Programs Biomed. 2021, 200, 105887. [Google Scholar] [CrossRef]
- Tucci, C.; Trujillo, M.; Berjano, E.; Iasiello, M.; Andreozzi, A.; Vanoli, G.P. Pennes’ bioheat equation vs. porous media approach in computer modeling of radiofrequency tumor ablation. Sci. Rep. 2021, 11, 1–13. [Google Scholar]
- Radosevic, A.; Prieto, D.; Burdío, F.; Berjano, E.; Prakash, P.; Trujillo, M. Short pulsed microwave ablation: Computer modeling and ex vivo experiments. Int. J. Hyperth. 2021, 38, 409–420. [Google Scholar] [CrossRef]
- Sánchez-Muñoz, E.J.; Berjano, E.; González-Suárez, A. Computer simulations of consecutive radiofrequency pulses applied at the same point during cardiac catheter ablation: Implications for lesion size and risk of overheating. Comput. Methods Programs Biomed. 2022, 220, 106817. [Google Scholar]
- Jain, M.K.; Wolf, P.D. A three-dimensional finite element model of radiofrequency ablation with blood flow and its experimental validation. Ann. Biomed. Eng. 2000, 28, 1075–1084. [Google Scholar] [CrossRef]
- Schutt, D.; Berjano, E.J.; Haemmerich, D. Effect of electrode thermal conductivity in cardiac radiofrequency catheter ablation: A computational modeling study. Int. J. Hyperth. 2009, 25, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Iasiello, M.; Andreozzi, A.; Bianco, N.; Vafai, K. The Porous Media Theory Applied to Radio Frequency Catheter Ablation. In Proceedings of the ICCHMT XI International Conference on Computational Heat, Mass and Momentum Transfer, Cracow, Poland, 21–24 May 2018. [Google Scholar]
- Payne, S.; Flanagan, R.; Pollari, M.; Alhonnoro, T.; Bost, C.; O’Neill, D.; Peng, T.; Stiegler, P. Image-based multi-scale modelling and validation of radio-frequency ablation in liver tumours. Philos. Trans. R. Soc. A 2011, 369, 4233–4254. [Google Scholar]
- Lamien, B.; Varon, L.A.; Orlande, H.R.; Elicabe, G.E. State estimation in bioheat transfer: A comparison of particle filter algorithms. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 615–638. [Google Scholar]
- Paruch, M. Identification of the cancer ablation parameters during RF hyperthermia using gradient, evolutionary and hybrid algorithms. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 674–697. [Google Scholar] [CrossRef]
- Iasiello, M.; Vafai, K.; Andreozzi, A.; Bianco, N. Analysis of non-Newtonian effects within an aorta-iliac bifurcation region. J. Biomech. 2017, 64, 153–163. [Google Scholar]
- Huyghe, J.M.; Arts, T.; Van Campen, D.H.; Reneman, R.S. Porous medium finite element model of the beating left ventricle. Am. J. Physiol. Heart Circ. Physiol. 1992, 262, H1256–H1267. [Google Scholar] [CrossRef]
- Michler, C.; Cookson, A.N.; Chabiniok, R.; Hyde, E.; Lee, J.; Sinclair, M.; Sochi, T.; Goyal, A.; Vigueras, G.; Nordsletten, D.A.; et al. A computationally efficient framework for the simulation of cardiac perfusion using a multi-compartment Darcy porous-media flow model. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 217–232. [Google Scholar] [CrossRef]
- Alves, J.R.; de Queiroz, R.A.; dos Santos, R.W. Simulation of cardiac perfusion by contrast in the myocardium using a formulation of flow in porous media. J. Comput. Appl. Math. 2016, 295, 13–24. [Google Scholar]
- Khaled, A.R.; Vafai, K. The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transf. 2003, 46, 4989–5003. [Google Scholar]
- Khanafer, K.; Vafai, K. The role of porous media in biomedical engineering as related to magnetic resonance imaging and drug delivery. Heat Mass Transf. 2006, 42, 939–953. [Google Scholar]
- Nakayama, A.; Kuwahara, F. A general bioheat transfer model based on the theory of porous media. Int. J. Heat Mass Transf. 2008, 51, 3190–3199. [Google Scholar]
- Coccarelli, A.; Prakash, A.; Nithiarasu, P. A novel porous media-based approach to outflow boundary resistances of 1D arterial blood flow models. Biomech. Model. Mechanobiol. 2019, 18, 939–951. [Google Scholar]
- Amiri, A.; Vafai, K. Analysis of Dispersion Effects and Non-Thermal Equilibrium Non-Darcian, Variable Porosity Incompressible Flow Through Porous Medium. Int. J. Heat Mass Transf. 1994, 37, 939–954. [Google Scholar]
- Alazmi, B.; Vafai, K. Constant Wall Heat Flux Boundary Conditions in Porous Media Under Local Thermal Non-Equilibrium Conditions. Int. J. Heat Mass Transf. 2002, 45, 3071–3087. [Google Scholar] [CrossRef]
- Alazmi, B.; Vafai, K. Analysis of Variable Porosity, Thermal Dispersion and Local Thermal Non-Equilibrium on Free Surface Flows Through Porous Media. J. Heat Transf. 2004, 126, 389–399. [Google Scholar] [CrossRef]
- Ouyang, X.; Vafai, K.; Jiang, P. Analysis of Thermally Developing Flow in Porous Media under Local Thermal Non-Equilibrium Conditions. Int. J. Heat Mass Transf. 2013, 67, 768–775. [Google Scholar]
- Whitaker, S. Advances in theory of fluid motion in porous media. Ind. Eng. Chem. Res. 1969, 61, 14–28. [Google Scholar]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Bioheat transfer in a spherical biological tissue: A comparison among various models. J. Phys. Conf. Ser. 2019, 1224, 012001. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling heat transfer in tumors: A review of thermal therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar]
- Labonte, S. Numerical model for radio-frequency ablation of the endocardium and its experimental validation. IEEE Trans. Biomed. Eng. 1994, 41, 108–115. [Google Scholar]
- Abraham, J.P.; Stark, J.; Gorman, J.; Sparrow, E.; Minkowycz, W.J. Tissue burns due to contact between a skin surface and highly conducting metallic media in the presence of inter-tissue boiling. Burns 2019, 45, 369–378. [Google Scholar] [CrossRef]
- Abraham, J.P.; Sparrow, E.M. A thermal-ablation bioheat model including liquid-to-vapor phase change, pressure- and necrosis-dependent perfusion, and moisture-dependent properties. Int. J. Heat Mass Transf. 2007, 50, 2537–2544. [Google Scholar] [CrossRef]
- Ramadhyani, S.; Abraham, J.P.; Sparrow, E.M. A mathematical model to predict tissue temperatures and necrosis during microwave thermal ablation of the prostate. In Advances in Numerical Heat Transfer, 1st ed.; Minkowycz, W.J., Sparrow, E.M., Abraham, J.P., Eds.; CRC Press: Boca Raton, FL, USA, 2009; Volume 3, pp. 357–384. [Google Scholar]
- Pop, M.; Ghugre, N.R.; Ramanan, V.; Morikawa, L.; Stanisz, G.; Dick, A.J.; Wright, G.A. Quantification of fibrosis in infarcted swine hearts by ex vivo late gadolinium-enhancement and diffusion-weighted MRI methods. Phys. Med. Biol. 2013, 58, 5009. [Google Scholar] [PubMed]
- Yuan, P. Numerical analysis of temperature and thermal dose response of biological tissues to thermal non-equilibrium during hyperthermia therapy. Med. Eng. Phys. 2008, 30, 135–143. [Google Scholar] [CrossRef] [PubMed]
- Jain, M.K.; Wolf, P.D. Temperature-controlled and constant-power radio-frequency ablation: What affects lesion growth? IEEE Trans. Biomed. Eng. 1999, 46, 1405–1412. [Google Scholar] [CrossRef]
- Jain, M.K.; Tomassoni, G.; Riley, R.E.; Wolf, P.D. Effect of skin electrode location on radiofrequency ablation lesions: An in vivo and a three-dimensional finite element study. J. Cardiovasc. Electrophysiol. 1998, 9, 1325–1335. [Google Scholar]
- Panescu, D.; Whayne, J.G.; Fleischman, S.D.; Mirotznik, M.S.; Swanson, D.K.; Webster, J.G. Three-dimensional finite element analysis of current density and temperature distributions during radio-frequency ablation. IEEE Trans. Biomed. Eng. 1995, 42, 879–890. [Google Scholar] [PubMed]
- Tungjitkusolmun, S.; Vorperian, V.R.; Bhavaraju, N.; Cao, H.; Tsai, J.Z.; Webster, J.G. Guidelines for predicting lesion size at common endocardial locations during radio-frequency ablation. IEEE Trans. Biomed. Eng. 2001, 48, 194–201. [Google Scholar] [PubMed]
- Seo, C.H.; Stephens, D.; Cannata, J.; Dentinger, A.; Lin, F.; Park, S.; Wildes, D.; Thomenius, K.; Chen, P.; Nguyen, T.; et al. Monitoring radiofrequency catheter ablation using thermal strain imaging. In Proceedings of the IEEE International Ultrasonics Symposium, San Diego, CA, USA, 11–14 October 2010. [Google Scholar]
- Dinerman, J.L.; Berger, R.D.; Calkins, H. Temperature monitoring during radiofrequency ablation. J. Cardiovasc. Electrophysiol. 1996, 7, 163–173. [Google Scholar]
- Frost, L.; Vestergaard, P.; Mosekilde, L. Hyperthyroidism and risk of atrial fibrillation or flutter: A population-based study. Arch. Intern. Med. 2004, 164, 1675–1678. [Google Scholar] [CrossRef]
- Mont, L.; Elosua, R.; Brugada, J. Endurance sport practice as a risk factor for atrial fibrillation and atrial flutter. Europace 2009, 11, 11–17. [Google Scholar] [CrossRef]
- Chamberlain, A.M.; Agarwal, S.K.; Folsom, A.R.; Duval, S.; Soliman, E.Z.; Ambrose, M.; Eberly, L.E.; Alonso, A. Smoking and incidence of atrial fibrillation: Results from the Atherosclerosis Risk in Communities (ARIC) study. Heart Rhythm 2011, 8, 1160–1166. [Google Scholar] [PubMed]
- Vlachos, K.; Mascia, G.; Martin, C.A.; Bazoukis, G.; Frontera, A.; Cheniti, G.; Letsas, K.P.; Efremidis, M.; Georgopoulos, S.; Gkalapis, C.; et al. Atrial fibrillation in Brugada syndrome: Current perspectives. J. Cardiovasc. Electrophysiol. 2020, 31, 975–984. [Google Scholar] [CrossRef]
- Platonov, P.G.; McNitt, S.; Polonsky, B.; Rosero, S.Z.; Zareba, W. Atrial fibrillation in long QT syndrome by genotype. Circ. Arrhythmia Electrophysiol. 2019, 12, e007213. [Google Scholar]
- Mascia, G.; Giaccardi, M. A new era in zero X-ray ablation. Arrhythmia Electrophysiol. Rev. 2020, 9, 121–127. [Google Scholar] [CrossRef]
- Carpeggiani, C.; Kraft, G.; Caramella, D.; Semelka, R.; Picano, E. Radioprotection (un) awareness in cardiologists, and how to improve it. Int. J. Cardiovasc. Imaging 2012, 28, 1369–1374. [Google Scholar] [CrossRef] [PubMed]
- Sarkozy, A.; De Potter, T.; Heidbuchel, H.; Ernst, S.; Kosiuk, J.; Vano, E.; Picano, E.; Arbelo, E.; Tedrow, U. Occupational radiation exposure in the electrophysiology laboratory with a focus on personnel with reproductive potential and during pregnancy: A European Heart Rhythm Association (EHRA) consensus document endorsed by the Heart Rhythm Society (HRS). Europace 2017, 19, 1909–1922. [Google Scholar] [PubMed]


| Element (Material) | σ (S/m) | k (W/m K) | ρc (MJ/m3 K) | K · 1011 (m2) | ε | hc (W/m2 K) | Sv (1/mm) |
|---|---|---|---|---|---|---|---|
| Electrode (Pt-Ir) | 4.6∙106 | 71 | 2.838 | ||||
| Thermistor (Glass Fiber) | 1.0∙10−5 | 0.038 | 0.027 | ||||
| Catheter (Polyurethane) | 1.0∙10−5 | 0.026 | 0.073 | ||||
| Cardiac chamber (Blood) | 0.667 | 0.541 | 4.180 | ||||
| Myocardium (Tissue/Blood) | Equation (10)/ 0.667 | Equation (11)/ 0.541 | Equation (12) | 5.6 | 0.10 | 170 | 50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iasiello, M.; Andreozzi, A.; Bianco, N.; Vafai, K. Effects of Pulsed Radiofrequency Source on Cardiac Ablation. Bioengineering 2023, 10, 227. https://doi.org/10.3390/bioengineering10020227
Iasiello M, Andreozzi A, Bianco N, Vafai K. Effects of Pulsed Radiofrequency Source on Cardiac Ablation. Bioengineering. 2023; 10(2):227. https://doi.org/10.3390/bioengineering10020227
Chicago/Turabian StyleIasiello, Marcello, Assunta Andreozzi, Nicola Bianco, and Kambiz Vafai. 2023. "Effects of Pulsed Radiofrequency Source on Cardiac Ablation" Bioengineering 10, no. 2: 227. https://doi.org/10.3390/bioengineering10020227
APA StyleIasiello, M., Andreozzi, A., Bianco, N., & Vafai, K. (2023). Effects of Pulsed Radiofrequency Source on Cardiac Ablation. Bioengineering, 10(2), 227. https://doi.org/10.3390/bioengineering10020227









