Planar Elliptical Inductor Design for Wireless Implantable Medical Devices
Abstract
1. Introduction
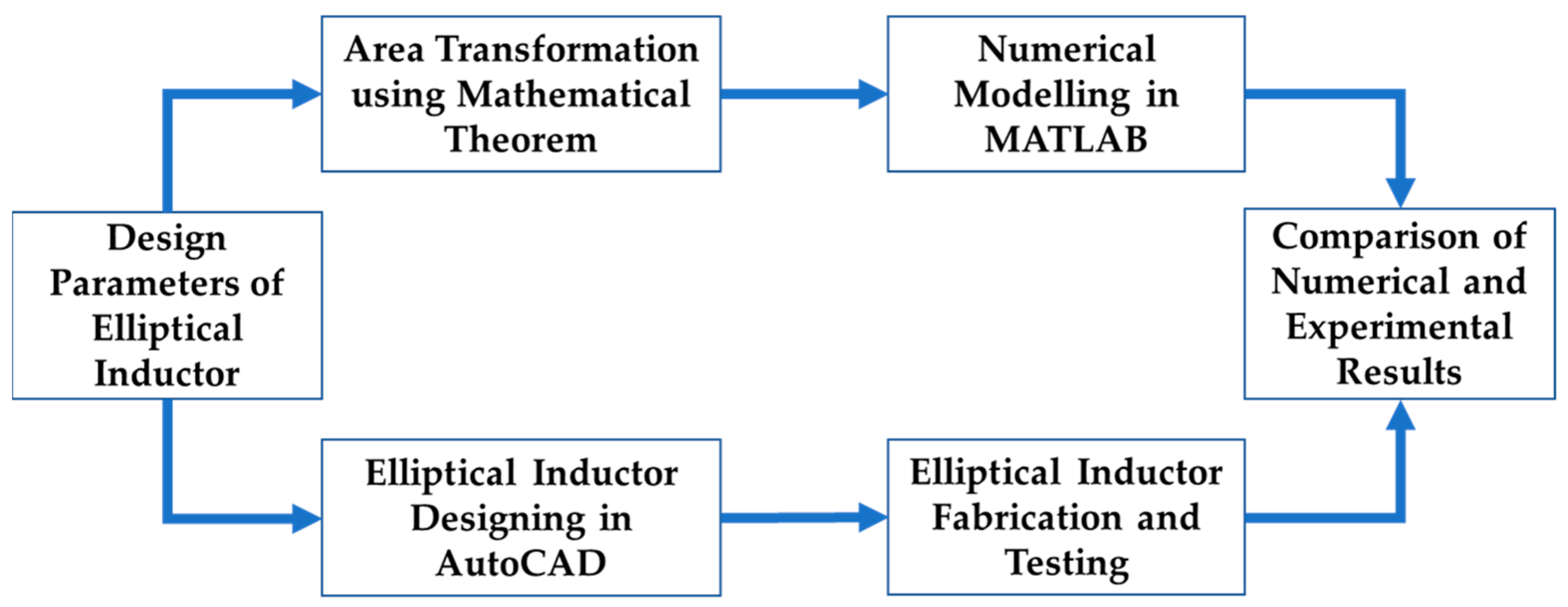
2. Materials and Methods
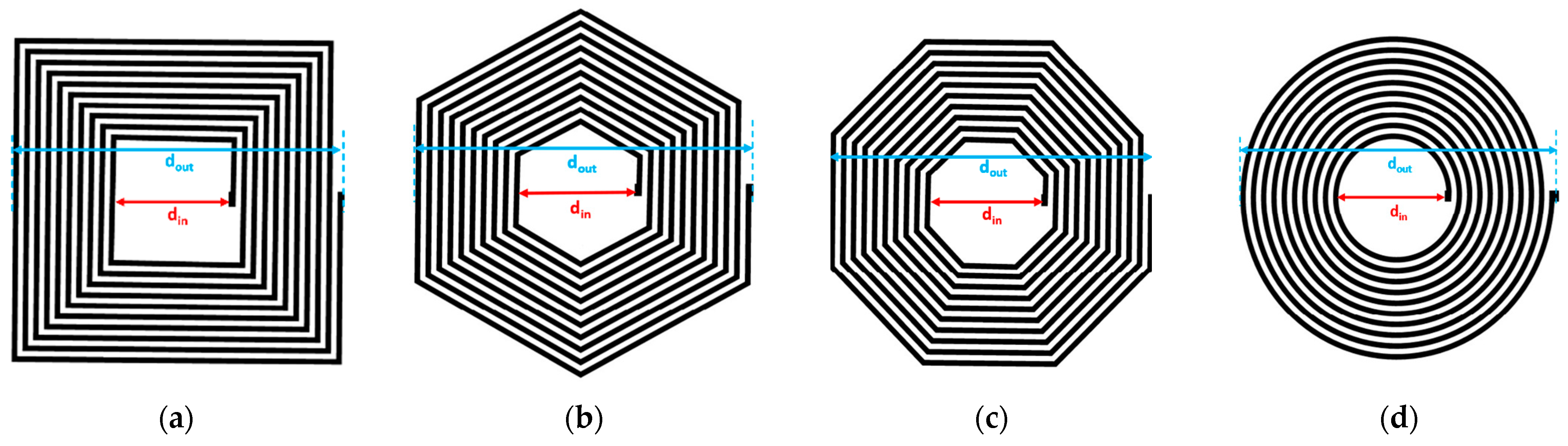
2.1. Planar Inductor Design
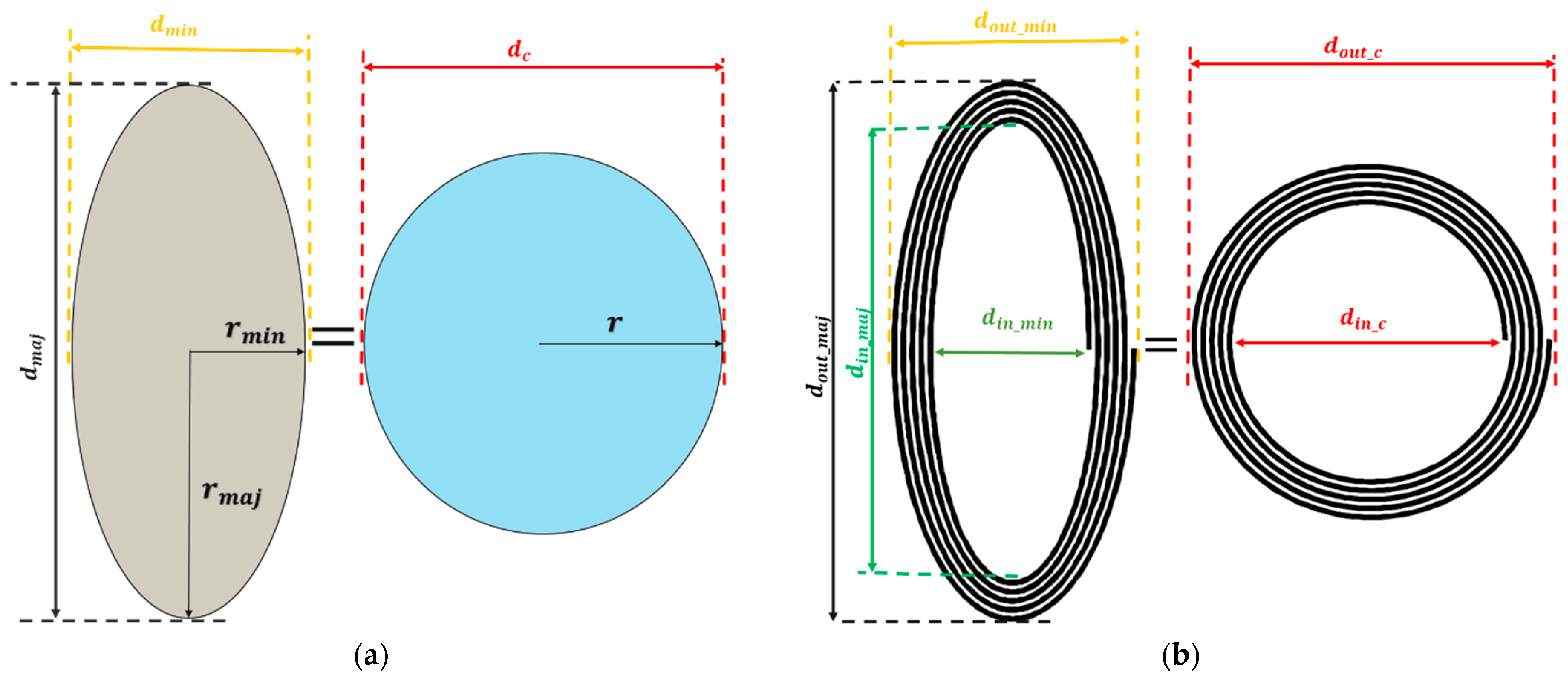
2.2. Area Transformation Technique to Model Elliptical Planar Inductor
2.3. Parasitic Components
2.4. Fabrication
2.5. Device Validation
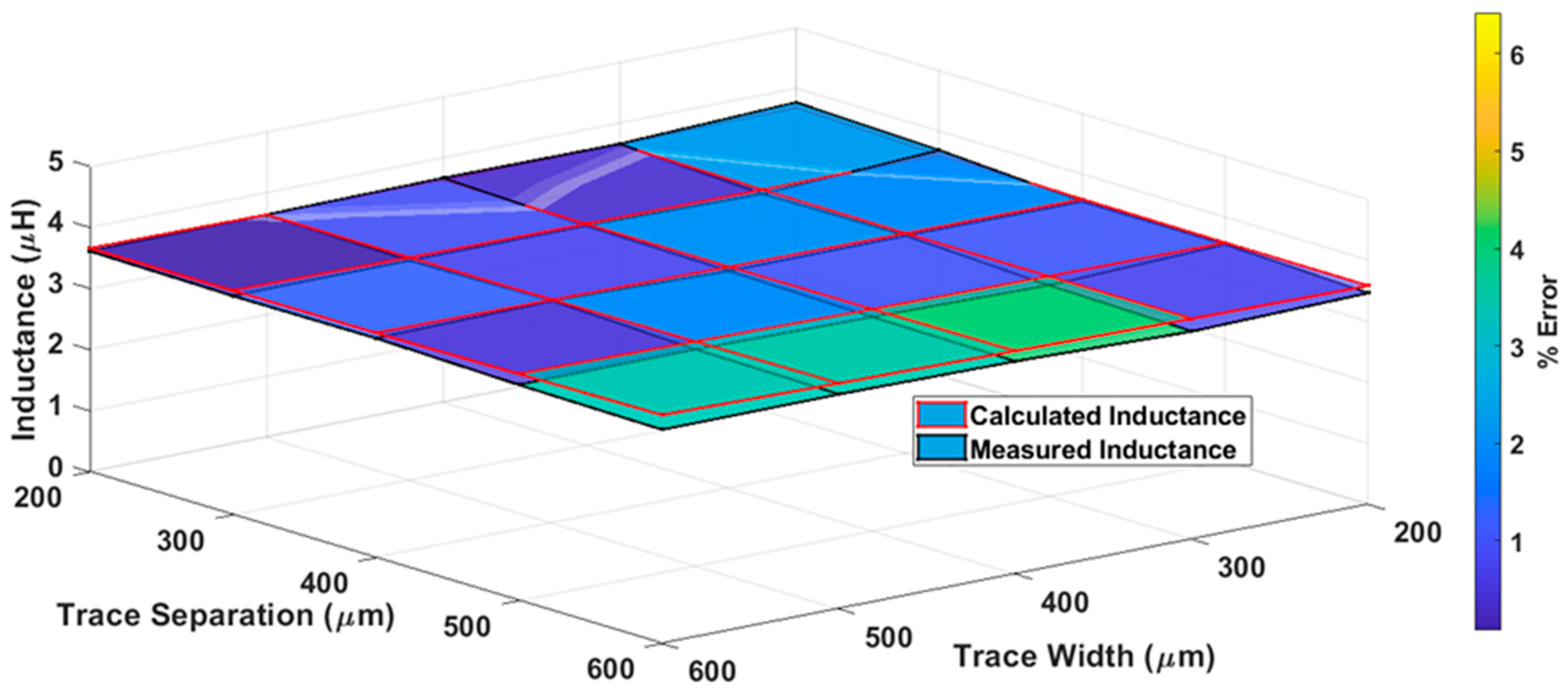
3. Results
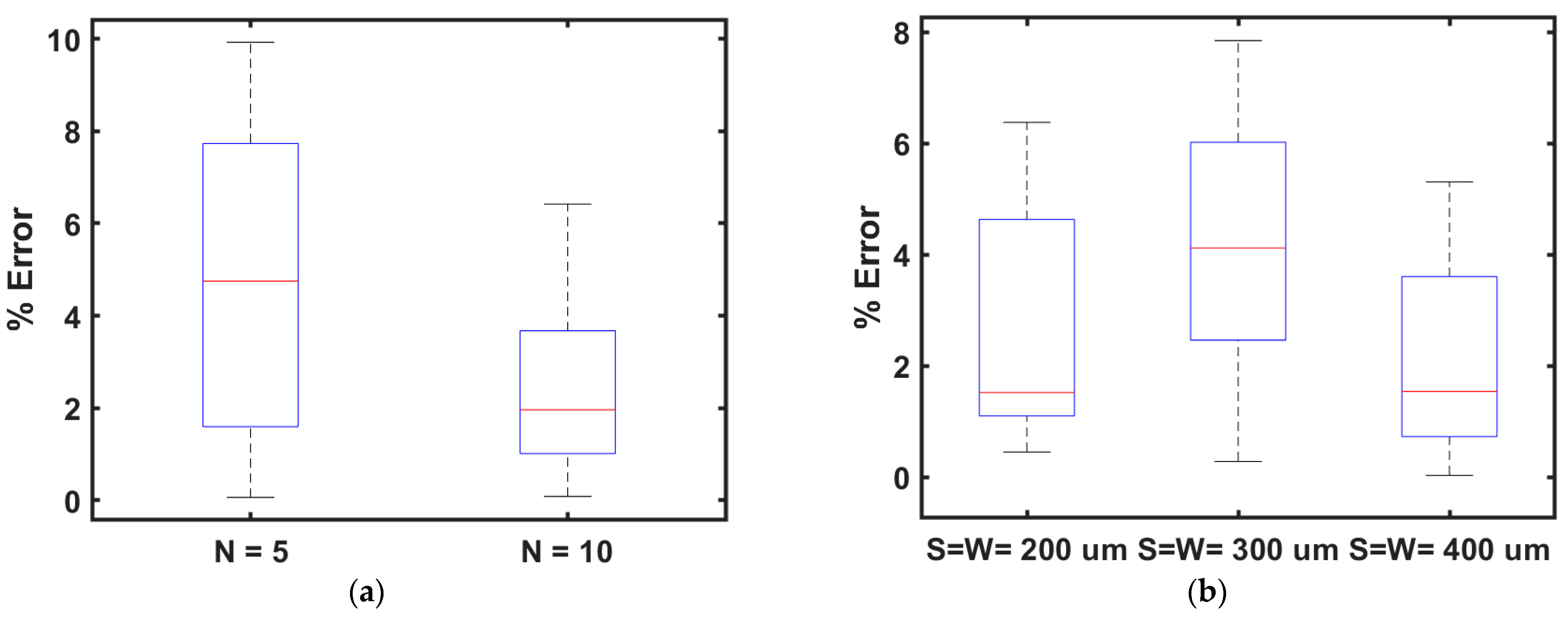
3.1. Estimation Results for Varying Trace Separation (S) and Trace Width (W) While Keeping the Ratio (R) between the Inner Minor Diameter to Inner Major Diameter Constant
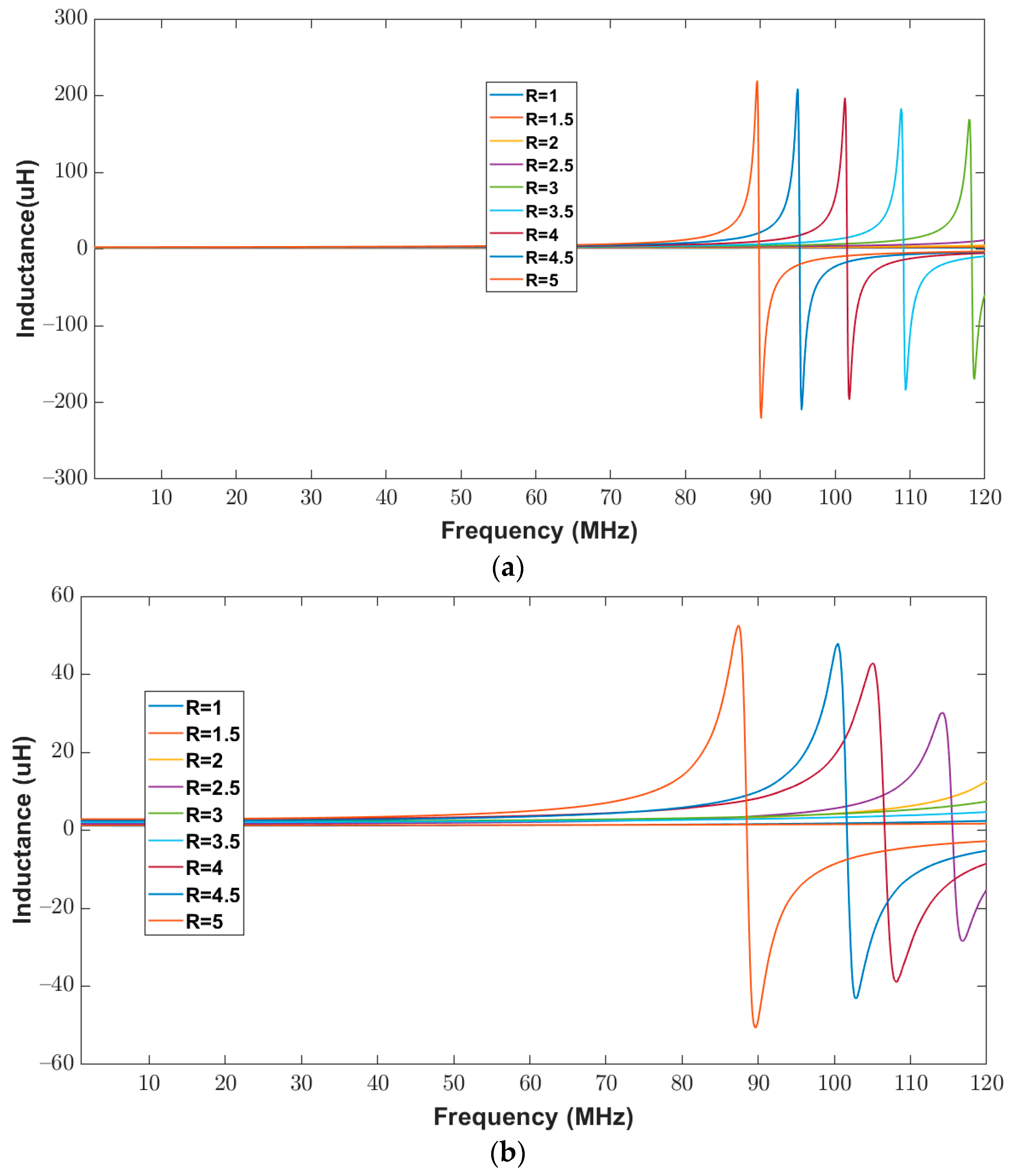
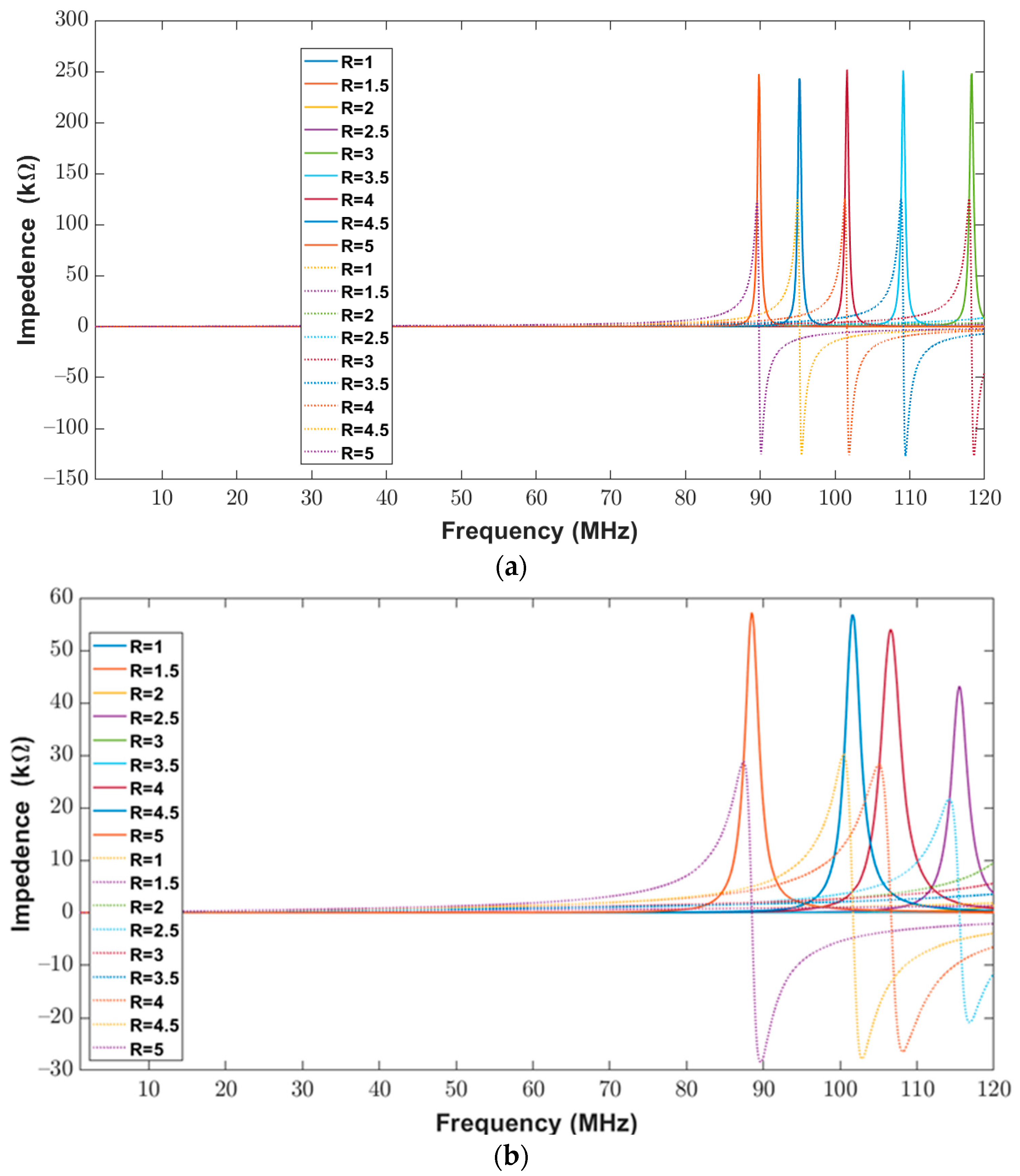
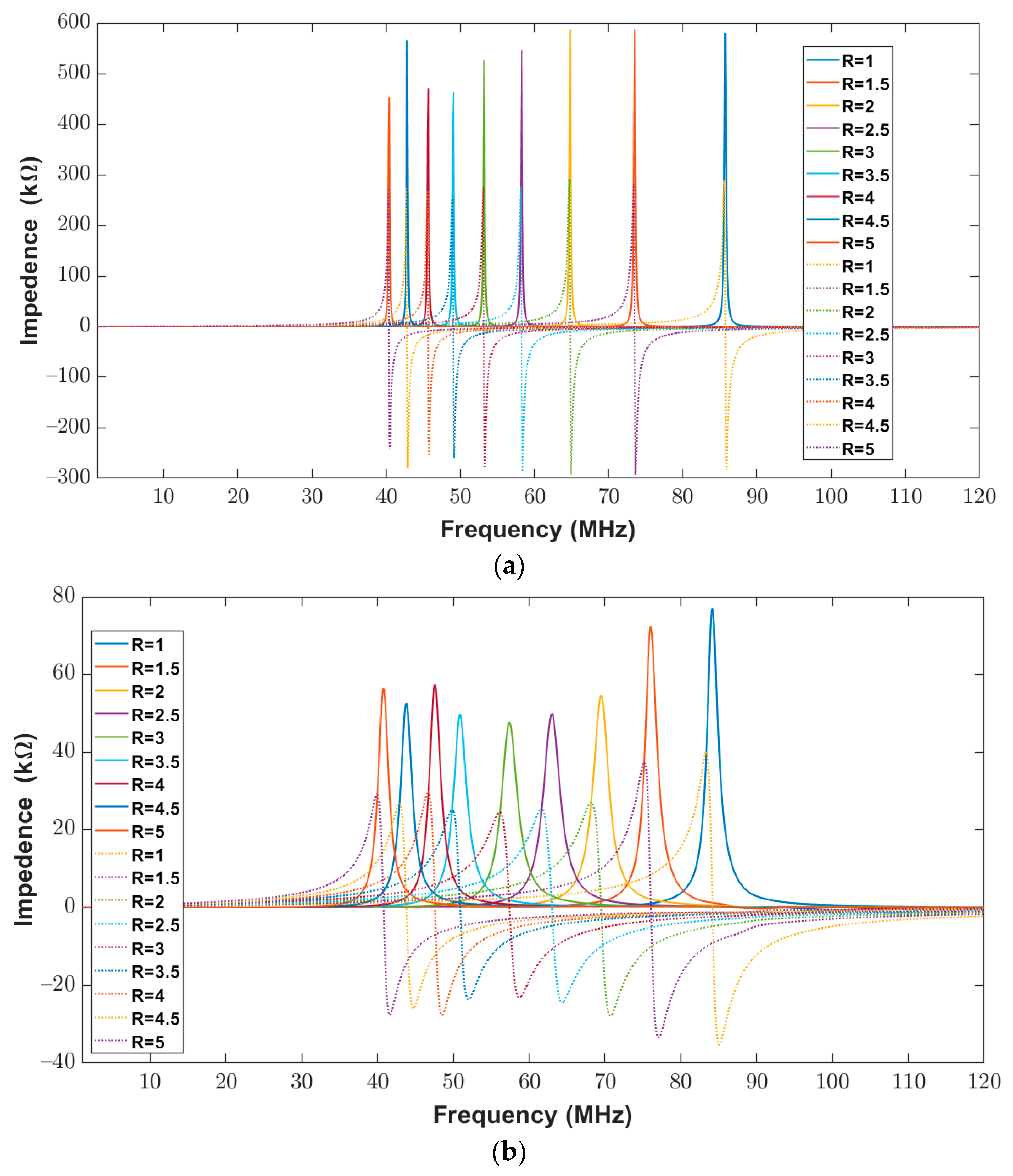
3.2. Estimation Results for Varying Ratios of Inner Minor Diameter to the Inner Major Diameter between 1 to 5 While Keeping Trace Separation and Width Fixed at 200 μm
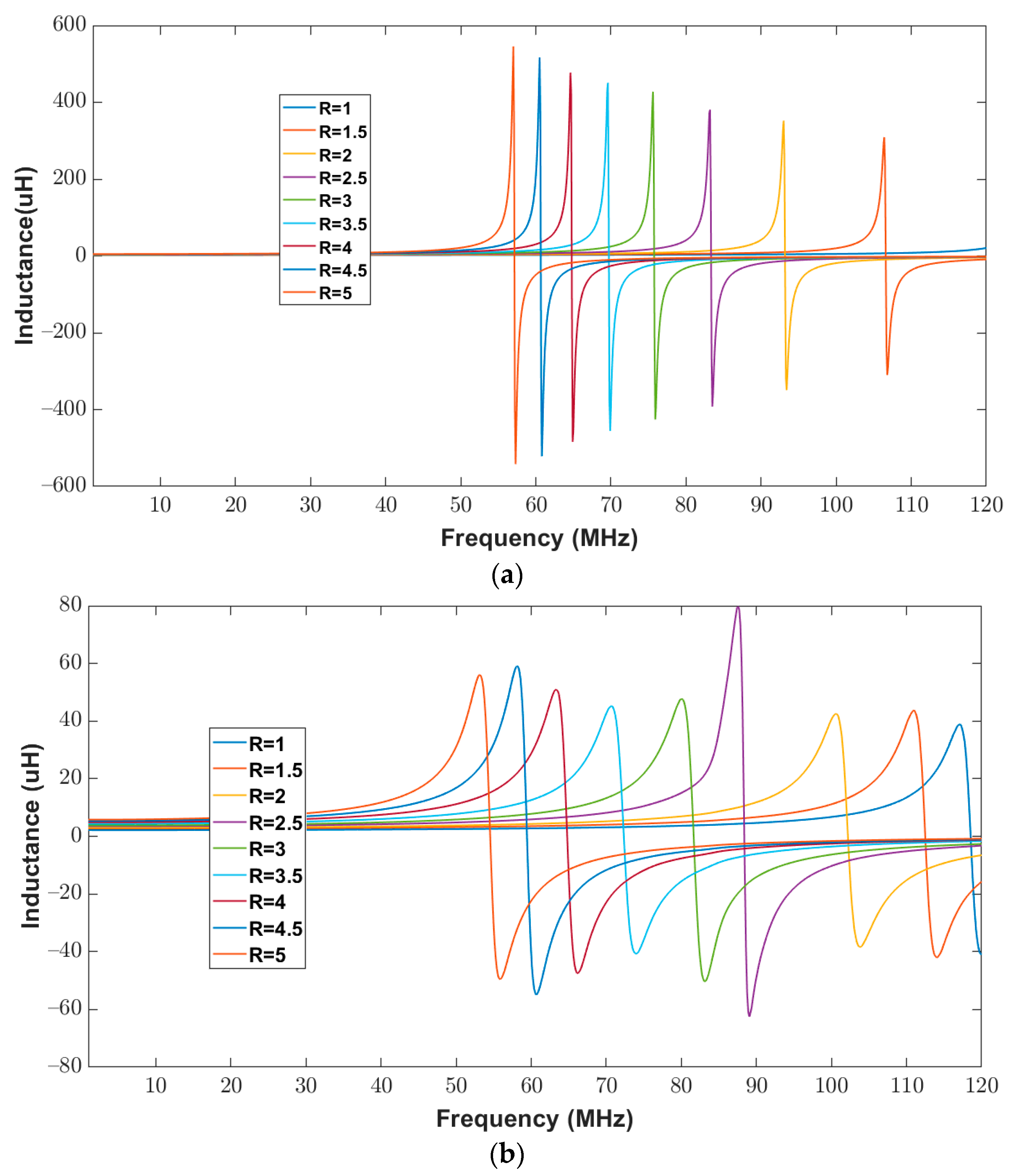
3.3. Estimation Results for Varying Ratios of Inner Minor Diameter to the Inner Major Diameter between 1 to 5 While Keeping Trace Separation and Width Fixed at 300 μm
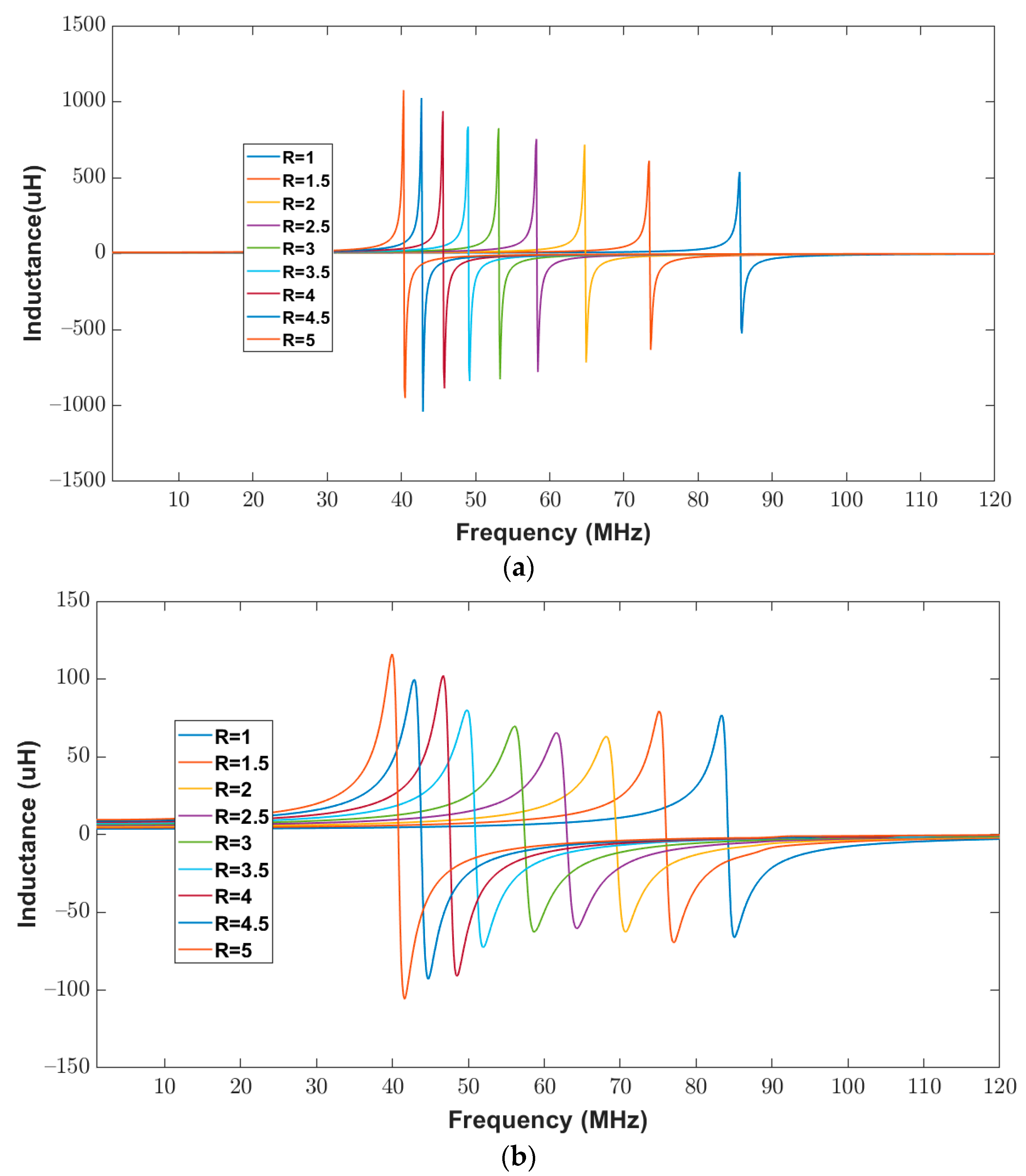
3.4. Estimation Results for Varying Ratios of Inner Minor Diameter to the Inner Major Diameter between 1 to 5 While Keeping Trace Separation and Width Fixed at 400 μm
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teaw, E.; Hou, G.; Gouzman, M.; Tang, K.W.; Kesluk, A.; Kane, M.; Farrell, J.A. Wireless Health Monitoring System. In Proceedings of the 2005 IEEE Conference on Information Acquisition, Hong Kong, China, 27 June–3 July 2005; pp. 312–317. [Google Scholar]
- Yazdandoost, K.Y.; Kohno, R. Wireless Communications for Body Implanted Medical Device. In Proceedings of the 2007 Asia-Pacific Microwave Conference, Bangkok, Thailand, 11–14 December 2007. [Google Scholar] [CrossRef]
- Ammarullah, M.I.; Santoso, G.; Sugiharto, S.; Supriyono, T.; Kurdi, O.; Tauviqirrahman, M.; Winarni, T.I.; Jamari, J. Tresca stress study of CoCrMo-on-CoCrMo bearings based on body mass index using 2D computational model. J. Tribol. 2022, 33, 31–38. [Google Scholar]
- Nelson, B.D.; Karipott, S.S.; Wang, Y.; Ong, K.G. Wireless Technologies for Implantable Devices. Sensors 2020, 20, 4604. [Google Scholar] [CrossRef]
- Molosky, V. The Influence of Identifiable Personality Traits on Nurses’ Intention to Use Wireless Implantable Medical Devices. Ph.D. Thesis, Nova Southeastern University, Fort Lauderdale, FL, USA, 2019. [Google Scholar]
- Kanaan, A.I.; Sabaawi, A.M. Implantable Wireless Systems: A Review of Potentials and Challenges. Antenna Syst. 2021. [Google Scholar] [CrossRef]
- Soliman, M.; Chowdhury, M.; Khandakar, A.; Islam, M.; Qiblawey, Y.; Musharavati, F.; Nezhad, E.Z. Review on Medical Implantable Antenna Technology and Imminent Research Challenges. Sensors 2021, 21, 3163. [Google Scholar] [CrossRef] [PubMed]
- Farooq, M.; Amin, B.; Kraśny, M.J.; Elahi, A.; Rehman, M.R.U.; Wijns, W.; Shahzad, A. An Ex Vivo Study of Wireless Linkage Distance between Implantable LC Resonance Sensor and External Readout Coil. Sensors 2022, 22, 8402. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.; Yan, Y.; Deng, Y.; Yang, Q.; Zhao, J.; Seo, M.; Bai, W.; MacEwan, M.R.; Huang, Y.; Ray, W.Z.; et al. Bioresorbable Wireless Sensors as Temporary Implants for In Vivo Measurements of Pressure. Adv. Funct. Mater. 2020, 30. [Google Scholar] [CrossRef]
- Park, J.; Kim, J.-K.; Patil, S.J.; Park, J.-K.; Park, S.; Lee, D.-W. A Wireless Pressure Sensor Integrated with a Biodegradable Polymer Stent for Biomedical Applications. Sensors 2016, 16, 809. [Google Scholar] [CrossRef] [PubMed]
- Takahata, K.; DeHennis, A.; Wise, K.; Gianchandani, Y. A wireless microsensor for monitoring flow and pressure in a blood vessel utilizing a dual-inductor antenna stent and two pressure sensors. In Proceedings of the 17th IEEE International Conference on Micro Electro Mechanical Systems. Maastricht MEMS 2004 Technical Digest, Maastricht, The Netherlands, 25–29 January 2004. [Google Scholar] [CrossRef]
- Lu, D.; Yan, Y.; Avila, R.; Kandela, I.; Stepien, I.; Seo, M.; Bai, W.; Yang, Q.; Li, C.; Haney, C.R.; et al. Bioresorbable, wireless, passive sensors as temporary implants for monitoring regional body temper-ature. Adv. Healthc. Mater. 2020, 9, 2000942. [Google Scholar] [CrossRef]
- Chen, L.Y.; Tee, C.K.; Chortos, A.; Schwartz, G.; Tse, V.; Lipomi, D.J.; Wong, H.S.P.; McConnell, M.; Bao, Z. Continuous wireless pressure monitoring and mapping with ultra-small passive sensors for health monitoring and critical care. Nat. Commun. 2014, 5, 5028. [Google Scholar] [CrossRef]
- Raju, S.; Wu, R.; Chan, M.; Yue, C.P. Modeling of Mutual Coupling Between Planar Inductors in Wireless Power Applications. IEEE Trans. Power Electron. 2013, 29, 481–490. [Google Scholar] [CrossRef]
- Schormans, M.; Valente, V.; Demosthenous, A. Practical Inductive Link Design for Biomedical Wireless Power Transfer: A Tutorial. IEEE Trans. Biomed. Circuits Syst. 2018, 12, 1112–1130. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X.; Shokoueinejad, M.; Iskandar, B.J.; Webster, J.G.; Medow, J.E. Spiral planar coil design for the intracranial pressure sensor. Med. Devices Sens. 2018, 1, e10012. [Google Scholar] [CrossRef]
- Charkhabi, S.; Jackson, K.J.; Beierle, A.M.; Carr, A.R.; Zellner, E.M.; Reuel, N.F. Monitoring Wound Health through Bandages with Passive LC Resonant Sensors. ACS Sens. 2020, 6, 111–122. [Google Scholar] [CrossRef]
- Ong, K.; Grimes, C.; Robbins, C.; Singh, R. Design and application of a wireless, passive, resonant-circuit environmental monitoring sensor. Sens. Actuators A Phys. 2001, 93, 33–43. [Google Scholar] [CrossRef]
- Grimes, C.A.; Mungle, C.S.; Zeng, K.; Jain, M.; Dreschel, W.R.; Paulose, M.; Ong, K.G. Wireless Magnetoelastic Resonance Sensors: A Critical Review. Sensors 2002, 2, 294–313. [Google Scholar] [CrossRef]
- Farooq, M.; Iqbal, T.; Vazquez, P.; Farid, N.; Thampi, S.; Wijns, W.; Shahzad, A. Thin-film flexible wireless pressure sensor for continuous pressure monitoring in medical applications. Sensors 2020, 20, 6653. [Google Scholar] [CrossRef] [PubMed]
- Ammouri, A.; Belloumi, H.; Salah, T.B.; Kourda, F. Experimental analysis of planar spiral inductors. In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM); 2014; pp. 1–5. [Google Scholar]
- Ahn, C.; Allen, M. Micromachined planar inductors on silicon wafers for MEMS applications. IEEE Trans. Ind. Electron. 1998, 45, 866–876. [Google Scholar] [CrossRef]
- Mohan, S.S.; Hershenson, M.d.; Boyd, S.P.; Lee, T.H. Simple accurate expressions for planar spiral in-ductances. IEEE J. Solid-State Circuits 1999, 34, 1419–1424. [Google Scholar] [CrossRef]
- Mutashar, S.; Hannan, M.A.; Samad, S.A.; Hussain, A. Analysis and Optimization of Spiral Circular Inductive Coupling Link for Bio-Implanted Applications on Air and within Human Tissue. Sensors 2014, 14, 11522–11541. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.-J.; Wang, L.-F.; Dong, L.; Huang, Q.-A. LC Wireless Sensitive Pressure Sensors With Microstructured PDMS Dielectric Layers for Wound Monitoring. IEEE Sensors J. 2018, 18, 4886–4892. [Google Scholar] [CrossRef]
- Chen, P.-J.; Saati, S.; Varma, R.; Humayun, M.S.; Tai, Y.-C. Wireless Intraocular Pressure Sensing Using Microfabricated Minimally Invasive Flexible-Coiled LC Sensor Implant. J. Microelectromechanical Syst. 2010, 19, 721–734. [Google Scholar] [CrossRef]
- Greenhouse, H. Design of Planar Rectangular Microelectronic Inductors. IEEE Trans. Parts, Hybrids, Packag. 1974, 10, 101–109. [Google Scholar] [CrossRef]
- Eroglu, A. Planar Inductor Design for High Power Applications. Prog. Electromagn. Res. B 2011, 35, 53–67. [Google Scholar] [CrossRef]
- Yue, C.; Ryu, C.; Lau, J.; Lee, T.; Wong, S. A physical model for planar spiral inductors on silicon. Int. Electron Devices Meeting. Tech. Dig. 1996, 155–158. [Google Scholar] [CrossRef]
- Hurley, W.; Duffy, M. Calculation of self- and mutual impedances in planar sandwich inductors. IEEE Trans. Magn. 1997, 33, 2282–2290. [Google Scholar] [CrossRef]
- Aldoumani, M.; Yuce, B.; Zhu, D. Using the Variable Geometry in a Planar Inductor for an Optimised Performance. Electronics 2021, 10, 721. [Google Scholar] [CrossRef]
- Hussain, I.; Woo, D.-K. Self-Inductance Calculation of the Archimedean Spiral Coil. Energies 2021, 15, 253. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Zheng, J.; Chen, L.; Wu, S.; Wang, S.; Yan, Z.; Pan, X. The Effects of Position on the Wear Debris Detection with Planar Inductor. Sensors 2019, 19, 4961. [Google Scholar] [CrossRef]
- Derkaoui, M.; Benhadda, Y.; Hamid, A. Modeling and simulation of an integrated octagonal planar transformer for RF systems. SN Appl. Sci. 2020, 2, 1–14. [Google Scholar] [CrossRef]
- Gibbs, R.; Moreton, G.; Meydan, T.; Williams, P. Comparison between Modelled and Measured Magnetic Field Scans of Different Planar Coil Topologies for Stress Sensor Applications. Sensors 2018, 18, 931. [Google Scholar] [CrossRef]
- Grover, F.W. Inductance Calculations: Working Formulas and Tables; Van Nostrand: New York, NY, USA, 1946. [Google Scholar]
- Huei, S.G.; Esa, M.; Kordesh, A.V. RF spiral planar inductor designs-preliminary results. Fac. Electr. Eng. Univ. Technol. Malays. 2003. [Google Scholar]
- Crols, J.; Kinget, P.; Craninckx, J.; Steyaert, M. An analytical model of planar inductors on lowly doped silicon substrates for high frequency analog design up to 3 GHz. In Proceedings of the 1996 Symposium on VLSI Circuits. Digest of Technical Papers, Honolulu, HI, USA, 13–15 June 1996. [Google Scholar] [CrossRef]
- Dill, H.G. Designing inductors for thin film applications. Electron. Des. 1964, 52–59. [Google Scholar]
- Wheeler, H. Simple Inductance Formulas for Radio Coils. Proc. IRE 1928, 16, 1398–1400. [Google Scholar] [CrossRef]
- Salnikov, A.S.; Goryainov, A.E.; Dobush, I.M.; Kalentyev, A.A.; Garays, D.V. Approach to scalable modeling for planar inductor using EM simulation and a few samples measurement. 2017 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization for RF, Microwave, and Terahertz Applications (NEMO), Seville, Spain, 17–19 May 2017; pp. 55–57. [Google Scholar]
- Taylor, L.; Margueron, X.; Le Menach, Y.; Le Moigne, P. Numerical modelling of PCB planar inductors: Impact of 3D modelling on high-frequency copper loss evaluation. IET Power Electron. 2017, 10, 1966–1974. [Google Scholar] [CrossRef]
- Pacurar, C.; Topa, V.; Racasan, A.; Munteanu, C. Inductance calculation and layout optimization for planar spiral inductors. In Proceedings of the 2012 13th International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Brasov, Romania, 24–26 May 2012; pp. 225–232. [Google Scholar]
- Zheng, C.; Li, W.; Li, A.-L.; Zhan, Z.; Wang, L.-Y.; Sun, D.-H. Design and Manufacturing of a Passive Pressure Sensor Based on LC Resonance. Micromachines 2016, 7, 87. [Google Scholar] [CrossRef]
- Liang, Y.; Ma, M.; Zhang, F.; Liu, F.; Liu, Z.; Wang, D.; Li, Y. An LC Wireless Microfluidic Sensor Based on Low Temperature Co-Fired Ceramic (LTCC) Technology. Sensors 2019, 19, 1189. [Google Scholar] [CrossRef]
- Melati, R.; Hamid, A.; Thierry, L.; Derkaoui, M. Design of a new electrical model of a ferromagnetic planar inductor for its integration in a micro-converter. Math. Comput. Model. 2013, 57, 200–227. [Google Scholar] [CrossRef]
- Hildebrand, F.B. Advanced Calculus for Applications; Pearson College Division: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Abderahim, A.; Koularambaye, M.; Chatelon, J.P.; Capraro, S.; Piétroy, D.; Rousseau, J.J. A method to determine winding losses in integrated inductors and separate skin and proximity effects. SN Appl. Sci. 2020, 2, 1–10. [Google Scholar] [CrossRef]
- Kuhn, W.; Ibrahim, N. Analysis of current crowding effects in multiturn spiral inductors. IEEE Trans. Microw. Theory Tech. 2001, 49, 31–38. [Google Scholar] [CrossRef]
- Ammouri, A.; Ben Salah, T.; Morel, H. A spiral planar inductor: An experimentally verified physically based model for frequency and time domains. Int. J. Numer. Model. Electron. Networks, Devices Fields 2017, 31, e2272. [Google Scholar] [CrossRef]
- Islam, A.B.; Islam, S.K.; Tulip, F.S. Design and Optimization of Printed Circuit Board Inductors for Wireless Power Transfer System. Circuits Syst. 2013, 4, 237–244. [Google Scholar] [CrossRef]
- DeBoi, B.T. On the Accuracy of Impedance Measurements and the Influence of Fixturing; The University of Alabama: Tuscaloosa, AL, USA, 2019. [Google Scholar]








| Layout | ||||
|---|---|---|---|---|
| Circular | 1 | 2.46 | 0 | 0.2 |
| Octagonal | 1.07 | 2.29 | 0 | 0.19 |
| Hexagonal | 1.09 | 2.23 | 0 | 0.17 |
| Square | 1.27 | 2.07 | 0.18 | 0.13 |
| Calculated Inductance (μH) of Elliptical Inductor Models (Number of Turns (N) = 10, Major-to-Minor Ratio (R) = 3) | ||||||
|---|---|---|---|---|---|---|
| Test Parameters | Trace Separation (µm) | |||||
| 200 | 300 | 400 | 500 | 600 | ||
| Trace Width (µm) | 200 | 3.69 | 3.65 | 3.63 | 3.64 | 3.66 |
| 300 | 3.62 | 3.61 | 3.62 | 3.64 | 3.67 | |
| 400 | 3.59 | 3.60 | 3.62 | 3.65 | 3.68 | |
| 500 | 3.58 | 3.60 | 3.63 | 3.67 | 3.71 | |
| 600 | 3.58 | 3.61 | 3.65 | 3.69 | 3.74 | |
| Measured Inductance (μH) of Fabricated Elliptical Inductors (Number of Turns (N) = 10 Major-to-Minor Ratio (R) = 3) | ||||||
|---|---|---|---|---|---|---|
| Test Parameters | Trace Separation (µm) | |||||
| 200 | 300 | 400 | 500 | 600 | ||
| Trace Width (µm) | 200 | 3.77 | 3.66 | 3.67 | 3.64 | 3.61 |
| 300 | 3.69 | 3.54 | 3.59 | 3.59 | 3.58 | |
| 400 | 3.55 | 3.56 | 3.55 | 3.63 | 3.59 | |
| 500 | 3.55 | 3.45 | 3.50 | 3.54 | 3.53 | |
| 600 | 3.46 | 3.40 | 3.48 | 3.51 | 3.50 | |
| % Error in Calculated and Measured Inductances (Number of Turns (N) = 10, Major-to-Minor Ratio (R) = 3) | ||||||
|---|---|---|---|---|---|---|
| Test Parameters | Trace Separation (µm) | |||||
| 200 | 300 | 400 | 500 | 600 | ||
| Trace Width (µm) | 200 | 2.17 | 0.39 | 0.95 | 0.08 | 1.26 |
| 300 | 1.82 | 1.96 | 0.75 | 1.28 | 2.46 | |
| 400 | 1.09 | 1.03 | 1.86 | 0.47 | 2.62 | |
| 500 | 0.75 | 4.11 | 3.53 | 3.44 | 4.84 | |
| 600 | 3.31 | 5.80 | 4.59 | 4.92 | 6.42 | |
| Calculated Inductance (μH) of Elliptical Inductor Models (Number of Turns (N) = 5, Major-to-Minor Ratio (R) = 3) | ||||||
|---|---|---|---|---|---|---|
| Test Parameters | Trace Separation (µm) | |||||
| 200 | 300 | 400 | 500 | 600 | ||
| Trace Width (µm) | 200 | 1.01 | 0.982 | 0.964 | 0.953 | 0.945 |
| 300 | 0.975 | 0.958 | 0.947 | 0.940 | 0.935 | |
| 400 | 0.952 | 0.941 | 0.934 | 0.930 | 0.928 | |
| 500 | 0.935 | 0.928 | 0.924 | 0.922 | 0.922 | |
| 600 | 0.922 | 0.919 | 0.917 | 0.917 | 0.918 | |
| Measured Inductance (μH) of Fabricated Elliptical Inductors (Number of Turns (N) = 5, Major-to-Minor Ratio (R) = 3) | ||||||
|---|---|---|---|---|---|---|
| Test Parameters | Trace Separation (µm) | |||||
| 200 | 300 | 400 | 500 | 600 | ||
| Trace Width µm) | 200 | 1.00 | 0.966 | 0.938 | 0.915 | 0.933 |
| 300 | 0.916 | 0.948 | 0.884 | 0.910 | 0.896 | |
| 400 | 0.907 | 0.875 | 0.864 | 0.857 | 0.846 | |
| 500 | 0.860 | 0.836 | 0.864 | 0.851 | 0.833 | |
| 600 | 0.851 | 0.918 | 0.921 | 0.931 | 0.940 | |
| % Error in Calculated and Measured Values (Number of Turns (N) = 5, Major-to-minor ratio (R) = 3) | ||||||
|---|---|---|---|---|---|---|
| Test Parameters | Trace Separation (µm) | |||||
| 200 | 300 | 400 | 500 | 600 | ||
| Trace Width (µm) | 200 | 0.59 | 1.61 | 2.73 | 3.96 | 1.30 |
| 300 | 6.10 | 1.08 | 6.64 | 3.15 | 4.19 | |
| 400 | 4.75 | 7.02 | 7.48 | 7.81 | 8.81 | |
| 500 | 8.04 | 9.93 | 6.50 | 7.73 | 9.67 | |
| 600 | 7.75 | 0.06 | 0.45 | 1.54 | 2.36 | |
| R | % Error | ||||||
|---|---|---|---|---|---|---|---|
| 5 | 5 | 13 | 13 | 1 | 1.02 | 1.00 | 2.31 |
| 5 | 7.5 | 13 | 15.5 | 1.5 | 1.23 | 1.22 | 0.74 |
| 5 | 10 | 13 | 18 | 2 | 1.43 | 1.41 | 1.22 |
| 5 | 12.5 | 13 | 20.5 | 2.5 | 1.62 | 1.63 | 0.45 |
| 5 | 15 | 13 | 23 | 3 | 1.81 | 1.84 | 1.52 |
| 5 | 17.5 | 13 | 25.5 | 3.5 | 1.99 | 2.02 | 1.47 |
| 5 | 20 | 13 | 28 | 4 | 2.16 | 2.26 | 4.58 |
| 5 | 22.5 | 13 | 30.5 | 4.5 | 2.33 | 2.45 | 4.79 |
| 5 | 25 | 13 | 33 | 5 | 2.50 | 2.66 | 6.38 |
| R | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
|---|---|---|---|---|---|---|---|---|---|
| (MHz) | >120 | >120 | >120 | >120 | 118.2 | 109.1 | 101.6 | 95.2 | 89.8 |
| (MHz) | >120 | >120 | >120 | >120 | >120 | 115.5 | 106.4 | 101.6 | 88.4 |
| % Error | N/A | N/A | N/A | N/A | N/A | 5.87 | 4.72 | 6.72 | 1.56 |
| (mm) | (mm) | (mm) | (mm) | R | (μH) | (μH) | % Error |
|---|---|---|---|---|---|---|---|
| 10 | 10 | 22 | 22 | 1 | 1.97 | 1.85 | 6.24 |
| 10 | 15 | 22 | 27 | 1.5 | 2.41 | 2.29 | 5.19 |
| 10 | 20 | 22 | 32 | 2 | 2.83 | 2.72 | 3.72 |
| 10 | 25 | 22 | 37 | 2.5 | 3.23 | 3.14 | 2.73 |
| 10 | 30 | 22 | 42 | 3 | 3.61 | 3.62 | 0.28 |
| 10 | 35 | 22 | 47 | 3.5 | 3.98 | 4.05 | 1.66 |
| 10 | 40 | 22 | 52 | 4 | 4.34 | 4.52 | 4.12 |
| 10 | 45 | 22 | 57 | 4.5 | 4.68 | 4.96 | 5.95 |
| 10 | 50 | 22 | 62 | 5 | 5.02 | 5.41 | 7.85 |
| R | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
|---|---|---|---|---|---|---|---|---|---|
| (MHz) | >120 | 106.6 | 93.2 | 83.3 | 75.7 | 69.7 | 64.8 | 60.6 | 57.1 |
| (MHz) | 118.3 | 112.3 | 102.1 | 88.3 | 81.5 | 72.2 | 64.7 | 59.3 | 54.5 |
| % Error | N/A | 5.35 | 9.55 | 6.00 | 7.66 | 3.59 | 0.15 | 2.15 | 4.55 |
| R | % Error | ||||||
|---|---|---|---|---|---|---|---|
| 12 | 12 | 31.2 | 31.2 | 1 | 3.52 | 3.40 | 3.36 |
| 12 | 18 | 31.2 | 37.2 | 1.5 | 4.23 | 4.18 | 1.40 |
| 12 | 24 | 31.2 | 43.2 | 2 | 4.92 | 4.88 | 0.82 |
| 12 | 30 | 31.2 | 49.2 | 2.5 | 5.59 | 5.56 | 0.45 |
| 12 | 36 | 31.2 | 55.2 | 3 | 6.23 | 6.23 | 0.03 |
| 12 | 42 | 31.2 | 61.2 | 3.5 | 6.85 | 6.96 | 1.54 |
| 12 | 48 | 31.2 | 67.2 | 4 | 7.45 | 7.66 | 2.68 |
| 12 | 54 | 31.2 | 73.2 | 4.5 | 8.04 | 8.39 | 4.34 |
| 12 | 60 | 31.2 | 79.2 | 5 | 8.62 | 9.08 | 5.31 |
| R | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
|---|---|---|---|---|---|---|---|---|---|
| (MHz) | 85.7 | 73.5 | 64.8 | 58.3 | 53.2 | 49.1 | 45.7 | 42.8 | 40.4 |
| (MHz) | 84.1 | 75.9 | 69.3 | 62.9 | 57.3 | 50.7 | 47.4 | 43.7 | 40.7 |
| % Error | 1.87 | 3.27 | 6.94 | 7.89 | 7.71 | 3.26 | 3.72 | 2.10 | 0.74 |
| % Error | Average % Error and Standard Deviation of % Error for Inductance | |||||
|---|---|---|---|---|---|---|
| W and S Varied from 200 μm to 600 μm and R = 3 | R Varied between 1 to 5 for N = 10 | Overall | ||||
| N = 5 | N = 10 | S = W = 200 μm | S = W = 300 μm | S = W = 400 μm | ||
| Average | 4.85 | 2.47 | 3.61 | 4.19 | 2.22 | 3.47 |
| Standard Deviation | 3.18 | 1.80 | 2.11 | 2.39 | 1.82 | 2.26 |
| Technique | Methodology/Expression/Simulator | Limitations | % Error |
|---|---|---|---|
| [37] | is the self-inductance of the single current-carrying electrode, W and t are the trace thickness and width, and l is the length of the conductor, Where gmd is the geometric mean distance between two conductors and can be computed using the below equation. P is the pitch of the coil. | Only suitable when the number of turns is an integer Not suitable for quarter turn Only suitable for symmetrical inductors Perform complex computation It takes a long time to evaluate the inductance. | 12.9 |
| Wheeler Expression [40] | Here r | Only accurate for circular solenoid coils Error increases with the increase in trace width | 5–20 |
| Modified Wheeler Expression [23] | Where are geometry dependent | Only suitable for symmetrical inductors | 9.8 |
| Current Sheet Expression [23] | Where is geometry dependent | then the error is 8% | 9.9 |
| Monomial Expression [23] | Here and β are geometry dependent | Only suitable for symmetrical inductors | 9 |
| Crols Expression [38] | Where and φ are geometry dependent | Only tested for a square planar model with very few samples | 10–20 |
| 3D Finite Element Simulators [31,32,33] | ANSYS Maxwell, COMSOL Multiphysics, etc. | Computationally intensive Long run times Need to implement the inductor design each time | Low |
| This study | Here is geometry dependent | Less accurate when the inductance is <1 μH | 5 * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Farooq, M.; Amin, B.; Elahi, A.; Wijns, W.; Shahzad, A. Planar Elliptical Inductor Design for Wireless Implantable Medical Devices. Bioengineering 2023, 10, 151. https://doi.org/10.3390/bioengineering10020151
Farooq M, Amin B, Elahi A, Wijns W, Shahzad A. Planar Elliptical Inductor Design for Wireless Implantable Medical Devices. Bioengineering. 2023; 10(2):151. https://doi.org/10.3390/bioengineering10020151
Chicago/Turabian StyleFarooq, Muhammad, Bilal Amin, Adnan Elahi, William Wijns, and Atif Shahzad. 2023. "Planar Elliptical Inductor Design for Wireless Implantable Medical Devices" Bioengineering 10, no. 2: 151. https://doi.org/10.3390/bioengineering10020151
APA StyleFarooq, M., Amin, B., Elahi, A., Wijns, W., & Shahzad, A. (2023). Planar Elliptical Inductor Design for Wireless Implantable Medical Devices. Bioengineering, 10(2), 151. https://doi.org/10.3390/bioengineering10020151








