Enhancing COVID-19 Classification Accuracy with a Hybrid SVM-LR Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Support Vector Machine (SVM)
2.2. Logistic Regression (LR)
2.3. Proposed Hybrid Model
2.4. Statistical Performance Criteria
2.5. Data
3. Results and Discussion
4. Conclusions
5. Limitation of the Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sethi, J.K.; Mittal, M. Efficient weighted naive bayes classifiers to predict air quality index. Earth Sci. Inform. 2022, 15, 541–552. [Google Scholar] [CrossRef]
- Foo, L.K.; Chua, S.L.; Ibrahim, N. Attribute Weighted Naive Bayes Classifier. CMC-Comput. Mater. Contin. 2022, 71, 1945–1957. [Google Scholar] [CrossRef]
- Jahangiri, M.; Khodadi, E.; Rahim, F.; Saki, N.; Malehi, A.S. Decision-tree-based methods for differential diagnosis of thalassemia trait from iron deficiency anemia. Expert Syst. 2017, 34, e12201. [Google Scholar] [CrossRef]
- Asteris, P.G.; Rizal, F.I.M.; Koopialipoor, M.; Roussis, P.C.; Ferentinou, M.; Armaghani, D.J.; Gordan, B. Slope Stability Classification under Seismic Conditions Using Several Tree-Based Intelligent Techniques. Appl. Sci. 2022, 12, 1753. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, A.; Bi, W.H.; Ma, J.W. A greedy belief rule base generation and learning method for classification problem. Appl. Soft Comput. 2021, 98, 106856. [Google Scholar] [CrossRef]
- Ouyang, T.H.; Zhang, X.H. DBSCAN-based granular descriptors for rule-based modeling. Soft Comput. 2022, 26, 13249–13262. [Google Scholar] [CrossRef]
- Guenther, N.; Schonlau, M. Support vector machines. Stata J. 2016, 16, 917–937. [Google Scholar] [CrossRef]
- Pernes, D.; Fernande, K.; Cardoso, J.S. Directional Support Vector Machines. Appl. Sci. 2019, 9, 725. [Google Scholar] [CrossRef]
- Milosevic, N.; Rackovic, M. Classification Based on Missing Features in Deep Convolutional Neural Networks. Neural Netw. World 2019, 29, 221–234. [Google Scholar] [CrossRef]
- Melin, P.; Monica, J.C.; Sanchez, D.; Castillo, O. Multiple Ensemble Neural Network Models with Fuzzy Response Aggregation for Predicting COVID-19 Time Series: The Case of Mexico. Healthcare 2020, 8, 181. [Google Scholar] [CrossRef]
- Murua, A.; Wicker, N. Fast Approximate Complete-data k-nearest-neighbor Estimation. Austrian J. Stat. 2020, 49, 18–30. [Google Scholar] [CrossRef]
- Cao, M.W.; Jia, W.; Lv, Z.H.; Xie, W.J.; Zheng, L.P.; Liu, X.P. Two-Pass K Nearest Neighbor Search for Feature Tracking. IEEE Access 2018, 6, 72939–72951. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, R.; Wang, H.S. Logistic Regression with Network Structure. Stat. Sin. 2020, 30, 673–693. [Google Scholar] [CrossRef]
- Shin, B.; Lee, S. Robust logistic regression with shift parameter estimation. J. Stat. Comput. Simul. 2023, 93, 2625–2641 . [Google Scholar] [CrossRef]
- Charan, G.V.S.; Kumar, N.S. Analysis and Comparison for Innovative Prediction Technique of COVID-19 using Logistic Regression algorithm over Support Vector Machine Algorithm with Improved Accuracy. J. Pharm. Negat. Results 2022, 13, 461–469. [Google Scholar] [CrossRef]
- Pavithraa, G.; Sivaprasad. Analysis and Comparison of Prediction of Heart Disease Using Novel Support Vector Machine and Logistic Regression Algorithm. Cardiometry 2022, 25, 783–787. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Nurul Hila, Z.; Muhamad Safiih, L. The Performance of BB-MCEWMA Model: Case Study on Sukuk Rantau Abang Capital Berhad, Malaysia. Int. J. Appl. Bus. Econ. Res. 2016, 14, 63–77. [Google Scholar]
- Nurul Hila, Z.; Muhamad Safiih, L.; Maman Abdurachman, D.; Fadhilah, Y.; Mohd Noor Afiq, R.; Aziz, D.; Yahaya, I.; Mohd Tajuddin, A. Improvement of time forecasting model using a novel hybridization of double bootstrap artificial neural network. Appl. Soft Comput. 2019, 84, 105676. [Google Scholar] [CrossRef]
- Abdullah, M.T.; Lola, M.S.; Hisham, A.E.; Sabreena, S.; Nor Fazila, C.M.; Idham, K.; Dennis, C.Y. Framework of Measures for Covid-19 Pandemic in Malaysia: Threats, Initiatives and Opportunities. J. Sustain. Sci. Manag. 2022, 17, 6–16. [Google Scholar] [CrossRef]
- Wan Mohamad Nawi, W.I.; Abdul Hamid, A.A.; Lola, M.S.; Zakaria, S.; Aruchunan, E.; Gobithaasan, R.U.; Zainuddin, N.H.; Mustafa, W.A.; Abdullah, M.L.; Mokhtar, N.A.; et al. Developing forecasting model for future pandemic applications based on COVID-19 data 2020–2022. PLoS ONE 2023, 18, e0285407. [Google Scholar] [CrossRef]
- Abdul Hamid, A.A.; Wan Mohamad Nawi, W.I.; Lola, M.S.; Mustafa, W.A.; Abdul Malik, S.M.; Zakaria, S.; Aruchunan, E.; Zainuddin, N.H.; Gobithaasan, R.U.; Abdullah, M.T. Improvement of time forecasting models using machine learning for future pandemic applications based on COVID-19 data 2020–2022. Diagnostics 2023, 13, 1121. [Google Scholar] [CrossRef]
- Naeem, M.; Yu, J.; Aamir, M.; Khan, S.A.; Adeleye, O.; Khan, Z. Comparative analysis of machine learning approaches to analyse and predict the COVID-19 outbreak. Peer J. Comput. Sci. 2021, 17, e746. [Google Scholar] [CrossRef]
- Ahmadini, A.A.H.; Naeem, M.; Aamir, M.; Dewan, R.; Alshqaq, S.S.A.; Mashwani, W.K. Analysis and Forecast of the Number of Deaths, Recovered Cases, and Confirmed Cases from COVID-19 for the Top Four Affected Countries Using Kalman Filter. Front. Phys. 2021, 9, 629320. [Google Scholar] [CrossRef]
- Lee, J.W.; Lee, J.B.; Park, M.; Song, S.H. An extensive comparison of recent classification tools applied to microarray data. Comput. Stat. Data Anal. 2005, 48, 869–885. [Google Scholar] [CrossRef]
- Verplancke, T.; Van, L.S.; Benoit, D.; Vansteelandt, S.; Depuydt, P.; De, T.F.; Decruyenaere, J. Support vector machine versus logistic regression modeling for prediction of hospital mortality in critically ill patients with haematological malignancies. BMC Med. Inf. Decis. Mak 2008, 8, 56. [Google Scholar] [CrossRef] [PubMed]
- Shou, T.; Hsiao, Y.; Huang, Y. Comparative analysis of logistic regression, support vector machine and artificial neural network for the differential diagnosis of benign and malignant solid breast tumors by the use of three-dimensional power doppler. Korean J. Radiol. 2009, 10, 464–471. [Google Scholar]
- Westreich, D.; Lessler, J.; Jonsson, M. Propensity score estimation: Neural networks, support vector machines, decision trees (CART), and meta-classifiers as alternatives to logistic regression. J. Clin. Epidemiol. 2010, 63, 826–833. [Google Scholar] [CrossRef]
- Austin, P.C.; Steyerberg, E.W. Events per variable (EPV) and the relative performance of different strategies for estimating the out-of-sample validity of logistic regression models. Stat. Methods Med. Res. 2014, 26, 796–808. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Song, K.; Choi, B.W. How to Develop, Validate, and Compare Clinical Prediction Models Involving Radiological Parameters: Study Design and Statistical Methods. Korean J. Radiol. 2016, 17, 339–350. [Google Scholar] [CrossRef]
- Peduzzi, P.; Concato, J.; Holford, T.R. Importance of events per independent variable in proportional hazards analysis. J. Clin. Epidemiol. 1995, 48, 1495–1501. [Google Scholar] [CrossRef] [PubMed]
- Peduzzi, P.; Concato, J.; Kemper, E. A simulation study of the number of events per variable in logistic regression analysis. J. Clin. Epidemiol. 1996, 49, 1373–1379. [Google Scholar] [CrossRef]
- Lola, M.S.; Zainuddin, N.H.; Ramlee, M.N.; Na’eim, M.; Rahman, A.; Abdullah, M.T. Improvement of Estimation Based on Small Number of Events Per Variable (EPV) using Bootstrap Logistics Regression Model. Malays. J. Fundam. Appl. Sci. 2017, 13, 693–704. [Google Scholar] [CrossRef]
- Zien, A. Engineering support vector machine kernels that recognize translation initiation sites. Bioinformatics 2000, 16, 799–807. [Google Scholar] [CrossRef]
- Siriyasatien, P.; Phumee, A.; Ongruk, P.; Jampachaisri, K.; Kesorn, K. Analysis of significant factors for dengue fever incidence prediction. BMC Bioinform. 2016, 17, 166. [Google Scholar] [CrossRef] [PubMed]
- Joachims, T. Text categorization with support vector machines. In Proceedings of the 10th European Conference on Machine Learning, Chemnitz, Germany, 21–23 April 1998. [Google Scholar]
- Ge, M.; Du, R.; Zhang, G.C. Fault diagnosis using support vector machine with an application in sheet metal stamping operations. Mech. Syst. Signal Process. 2004, 18, 143–159. [Google Scholar] [CrossRef]
- Wu, H.; Lu, H.Q.; Ma, S.D. Ordinal regression in content-based image retrieval. J. Softw. 2004, 15, 1336–1344. [Google Scholar]
- Moulin, L.S.; Silva, A.P.; El-Sharkawi, M.A. Support vector machines for transient stability analysis of large-scale power systems. IEEE Trans. Power Syst. 2004, 19, 818–825. [Google Scholar] [CrossRef]
- Gestel, T.V.; Suykens, J.K.; Gaestaens, D.E. Financial time series prediction using least squares support vector machines within the evidence framework. IEEE Trans. Neural Netw. 2001, 12, 809–821. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Classification by pairwise coupling. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Carroll, R.J.; Pederson, S. On robustness in the logistic regression model. J. R. Stat. Soc. Ser. B (Methodol.) 1993, 55, 693–706. [Google Scholar] [CrossRef]
- Razali, M.R.; Lola, M.S.; Abd, M.E.; Djauhari, M.A. A Hybrid Logistic Regression Model with a Bootstrap Approach to Improve the Accuracy of the Performance of Jellyfish Collagen Data. J. Sustain. Sci. Manag. 2021, 16, 191–203. [Google Scholar] [CrossRef]
- Baratloo, A.; Hosseini, M.; Negida, A.; El Ashal, G. Part 1: Simple Definition and Calculation of Accuracy, Sensitivity and Specificity. Emergency 2015, 3, 48–49. [Google Scholar] [PubMed]
- Nurul Hila, Z.; Muhamad Safiih, L.; Nur Shazrahanim, K. Modelling Moving Centerline Exponentially Weighted Moving Average (MCEMA) with bootstrap approach: Case study on sukuk musyarakah of Rantau Abang Capital Berhad, Malaysia. Int. J. Appl. Bus. Econ. Res. 2016, 14, 621–638. [Google Scholar]
- Kwekha-Rashid, A.S.; Abduljabbar, H.N.; Alhayani, B. Coronavirus disease (COVID-19) cases analysis using machine-learning applications. Appl. Nanosci. 2023, 13, 2013–2025. [Google Scholar] [CrossRef]
- Kushwaha, S.; Bahl, S.; Bagha, A.K.; Parmar, K.S.; Javaid, M.; Haleem, A.; Singh, R.P. Significant applications of machine learning for COVID-19 pandemic. J. Ind. Integr. Manag. 2020, 5, 453–479. [Google Scholar] [CrossRef]
- Heidari, A.; Jafari Navimipour, N.; Unal, M.; Toumaj, S. Machine learning applications for COVID-19 outbreak management. Neural Comput. Appl. 2022, 34, 15313–15348. [Google Scholar] [CrossRef] [PubMed]
- Medina, M.A. Preliminary Estimate of COVID-19 Case Fatality Rate in the Philippines Using Linear Regression Analysis. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3569248 (accessed on 7 April 2020).
- Rustam, F.; Reshi, A.A.; Mehmood, A.; Ullah, S.; On, B.W.; Aslam, W.; Choi, G.S. COVID-19 Future Forecasting Using Supervised Machine Learning Models. IEEE Access 2022, 8, 101489–101499. [Google Scholar] [CrossRef]
- Anastassopoulou, C.; Russo, L.; Tsakris, A.; Siettos, C. Data-based analysis, modelling and forecasting of the COVID-19 outbreak. PLoS ONE 2020, 15, e0230405. [Google Scholar] [CrossRef]
- Verity, L.C.; Robert, I.O.; Peter, D.; Charles, W.; Natsuko, W.; Gina, I.; Cuomo, D. Estimates of the Severity of Coronavirus Disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Razali, N.M.; Wa, H.Y.B. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- Mirri, S.; Delnevo, G.; Roccetti, M. Is a COVID-19 second wave possible in Emilia-Romagna (Italy)? Forecasting a future outbreak with particulate pollution and machine learning. Computation 2020, 8, 74. [Google Scholar] [CrossRef]

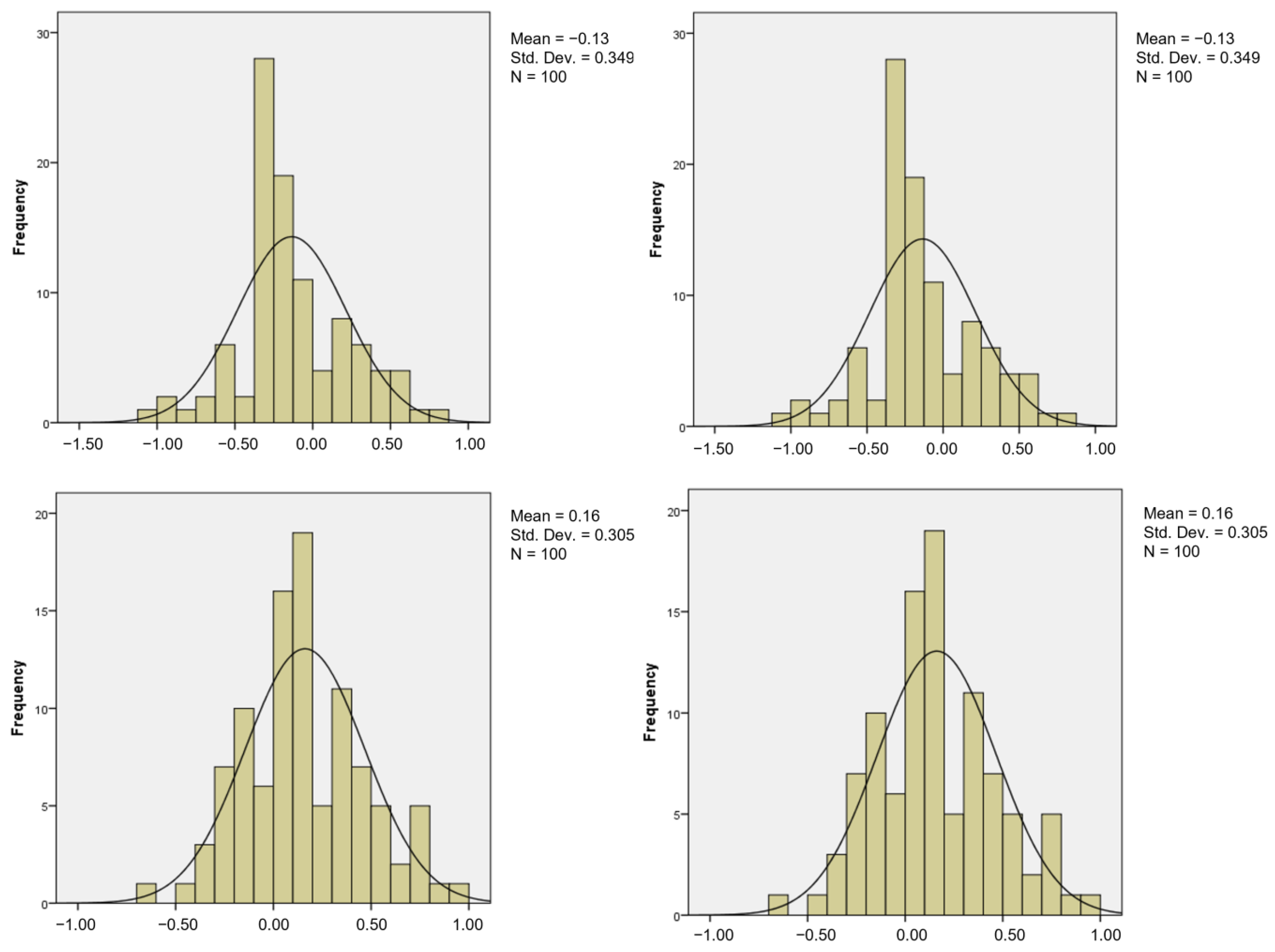
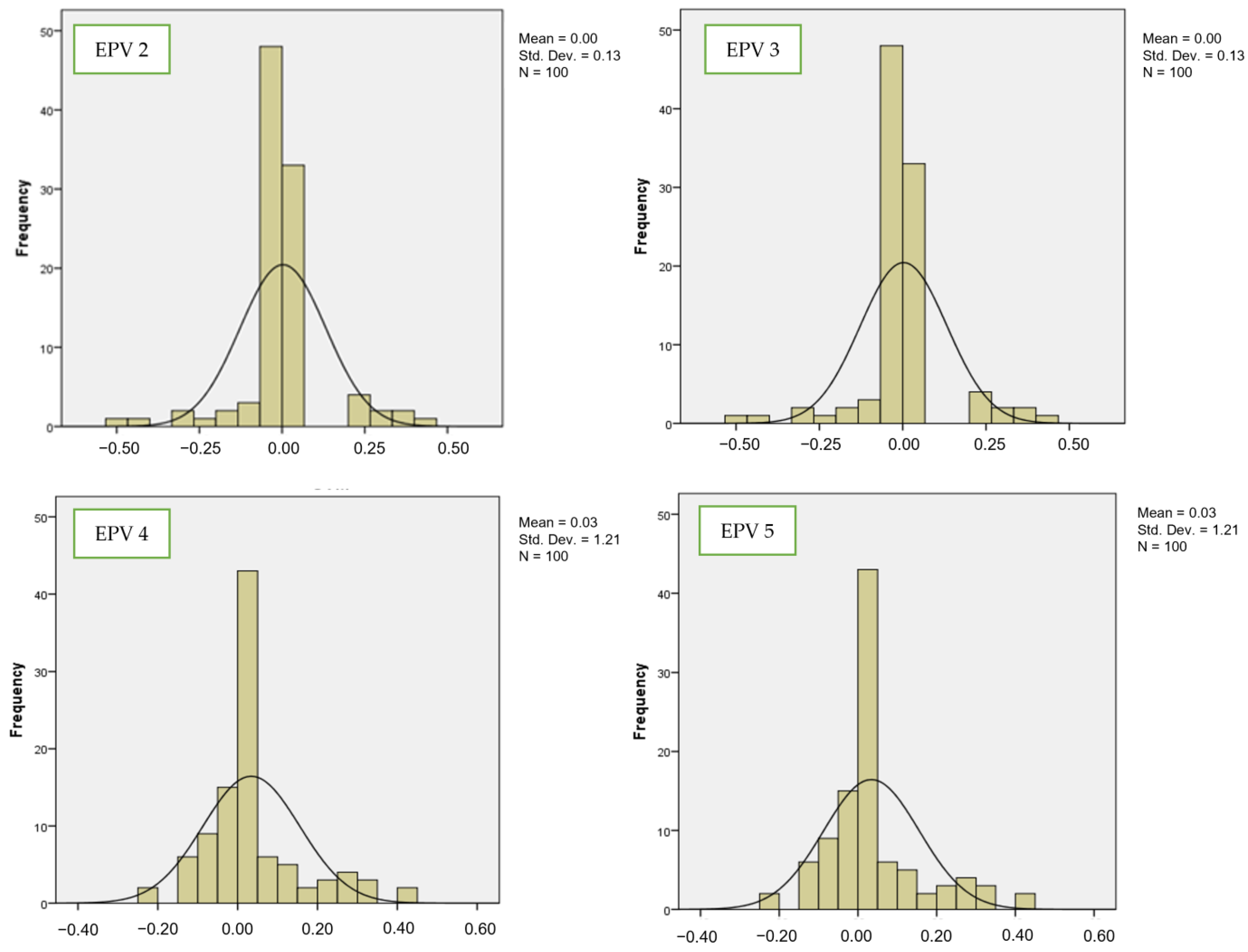
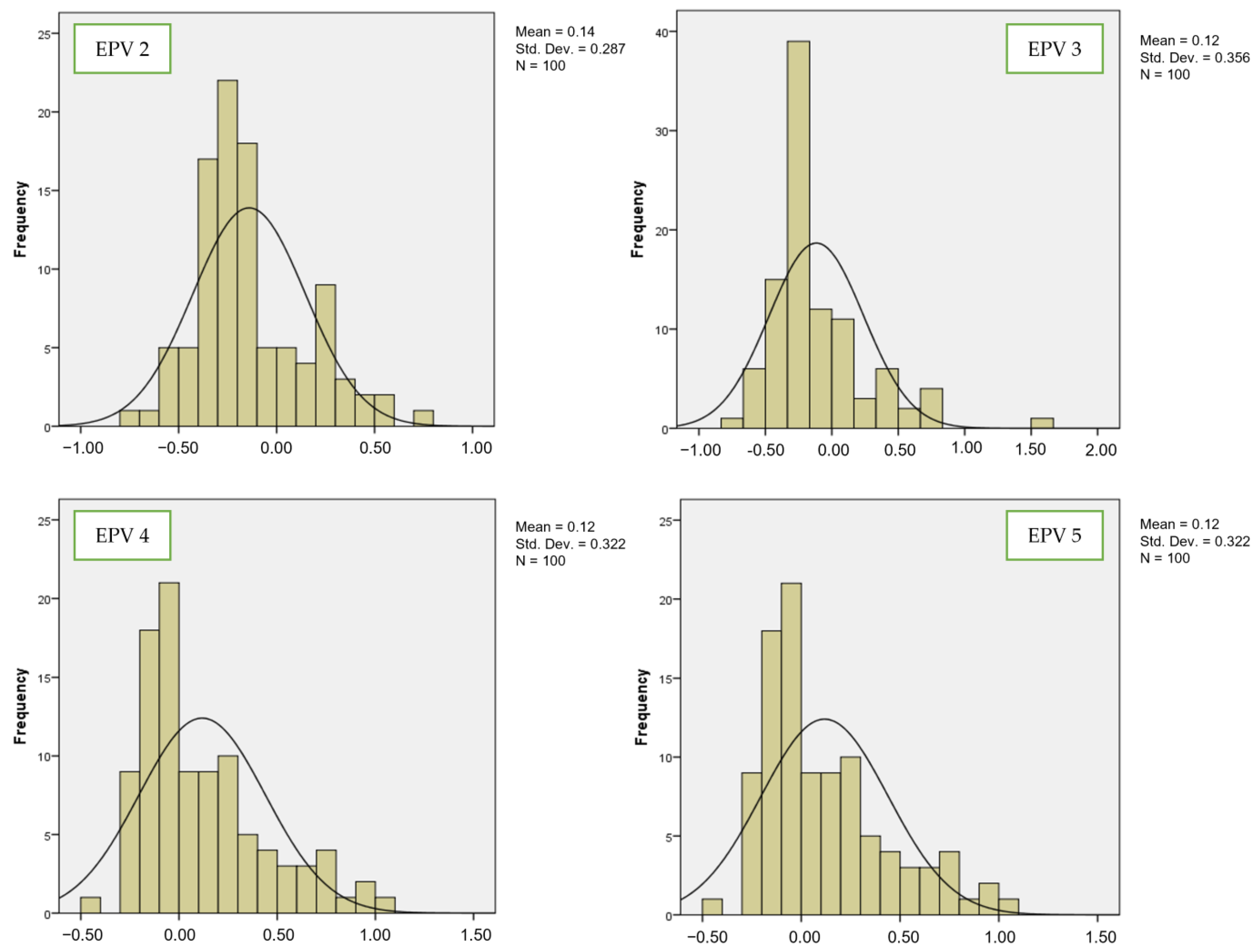


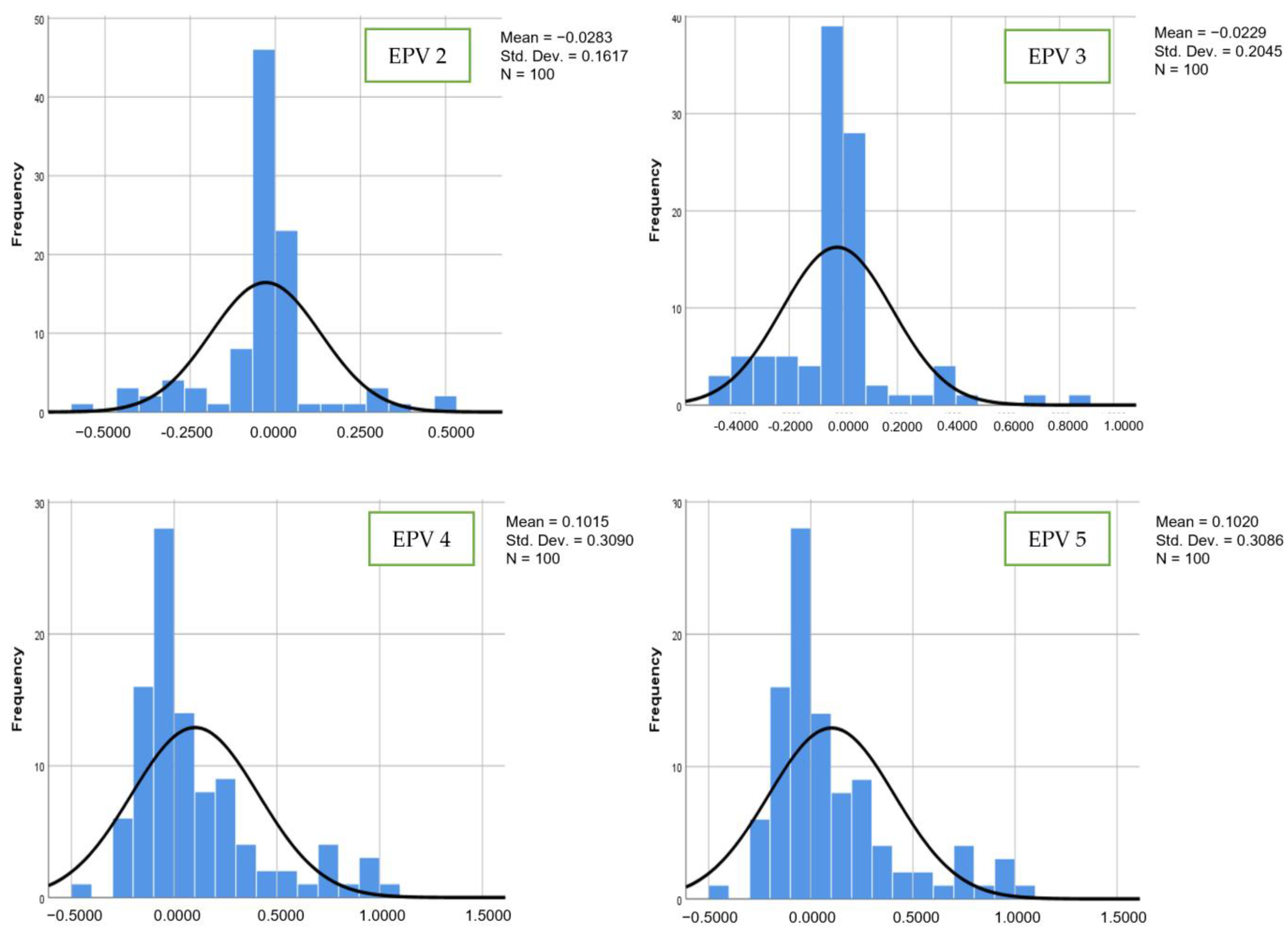

| Chi-Square | Significant p-Value | Interpretation |
|---|---|---|
| 150.627 | 0.000 | model significant |
| EPV 2 | EPV 3 | |||||
| LR | SVM | Hybrid | LR | SVM | Hybrid | |
| Accuracy | 0.8649 | 0.8538 | 0.8684 | 0.8642 | 0.8538 | 0.8691 |
| RMSE | 0.1351 | 0.1462 | 0.1316 | 0.1358 | 0.1462 | 0.1309 |
| MSE | 0.3539 | 0.3660 | 0.3485 | 0.3558 | 0.3668 | 0.3485 |
| EPV 4 | EPV 5 | |||||
| LR | SVM | Hybrid | LR | SVM | Hybrid | |
| Accuracy | 0.8622 | 0.8540 | 0.8684 | 0.8678 | 0.8549 | 0.8715 |
| RMSE | 0.1378 | 0.1460 | 0.1316 | 0.1322 | 0.1451 | 0.1285 |
| MSE | 0.3596 | 0.3670 | 0.3496 | 0.3523 | 0.3665 | 0.3469 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nordin, N.I.; Mustafa, W.A.; Lola, M.S.; Madi, E.N.; Kamil, A.A.; Nasution, M.D.; K. Abdul Hamid, A.A.; Zainuddin, N.H.; Aruchunan, E.; Abdullah, M.T. Enhancing COVID-19 Classification Accuracy with a Hybrid SVM-LR Model. Bioengineering 2023, 10, 1318. https://doi.org/10.3390/bioengineering10111318
Nordin NI, Mustafa WA, Lola MS, Madi EN, Kamil AA, Nasution MD, K. Abdul Hamid AA, Zainuddin NH, Aruchunan E, Abdullah MT. Enhancing COVID-19 Classification Accuracy with a Hybrid SVM-LR Model. Bioengineering. 2023; 10(11):1318. https://doi.org/10.3390/bioengineering10111318
Chicago/Turabian StyleNordin, Noor Ilanie, Wan Azani Mustafa, Muhamad Safiih Lola, Elissa Nadia Madi, Anton Abdulbasah Kamil, Marah Doly Nasution, Abdul Aziz K. Abdul Hamid, Nurul Hila Zainuddin, Elayaraja Aruchunan, and Mohd Tajuddin Abdullah. 2023. "Enhancing COVID-19 Classification Accuracy with a Hybrid SVM-LR Model" Bioengineering 10, no. 11: 1318. https://doi.org/10.3390/bioengineering10111318
APA StyleNordin, N. I., Mustafa, W. A., Lola, M. S., Madi, E. N., Kamil, A. A., Nasution, M. D., K. Abdul Hamid, A. A., Zainuddin, N. H., Aruchunan, E., & Abdullah, M. T. (2023). Enhancing COVID-19 Classification Accuracy with a Hybrid SVM-LR Model. Bioengineering, 10(11), 1318. https://doi.org/10.3390/bioengineering10111318








