Effect of Ligament Fibers on Dynamics of Synthetic, Self-Oscillating Vocal Folds in a Biomimetic Larynx Model
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthetic Larynx Model
2.2. Biomimetic Functionality
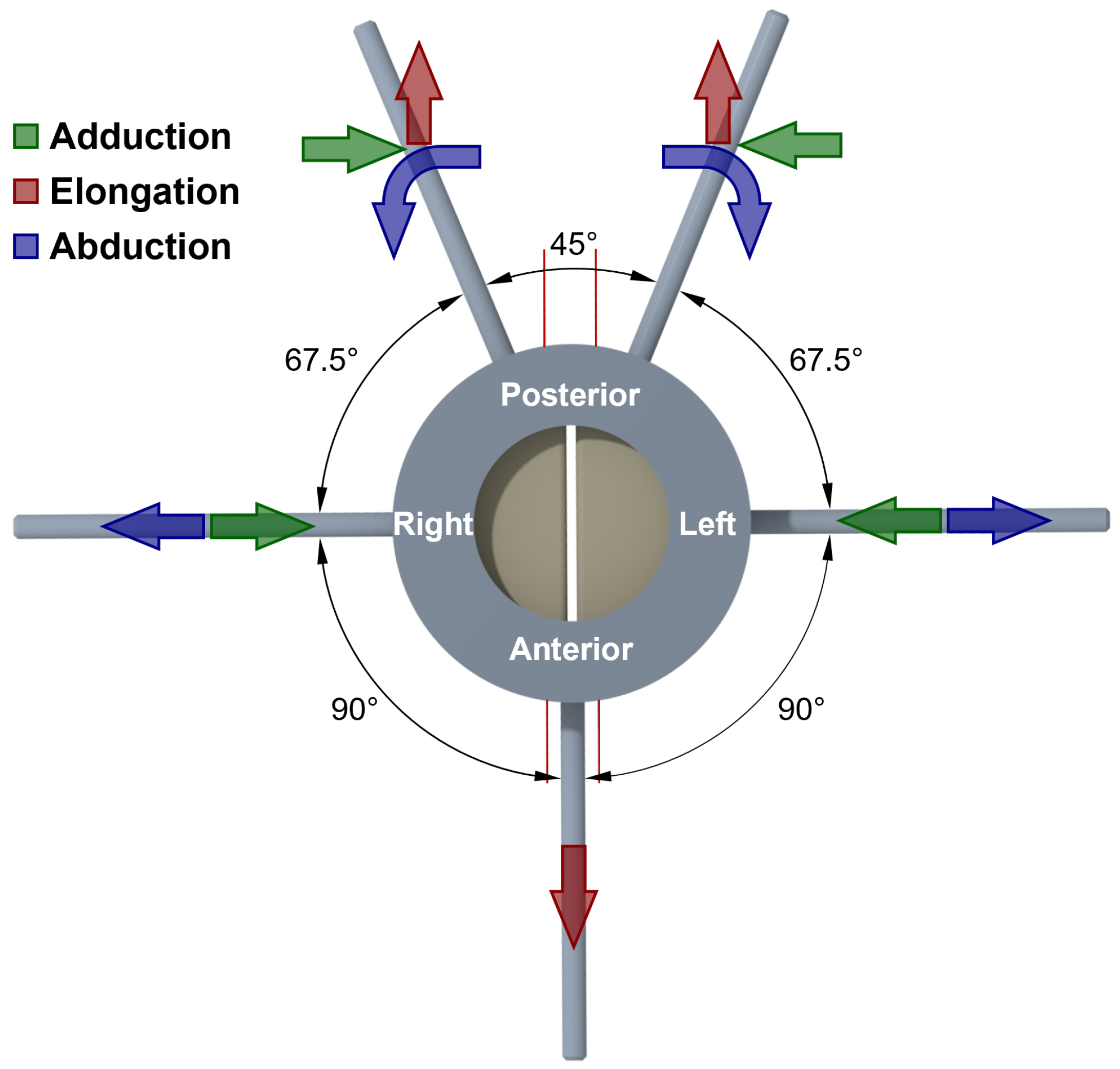
2.3. Fiber Guidance and Tensioning System
2.4. Measurement Setup and Data Acquisition
2.5. Data Processing and Analysis
| Parameter | Abbreviation/Unit | Description/Range | Reference |
|---|---|---|---|
| (a) Glottal dynamic parameters | |||
| Glottis gap index | /AU | 0: full closure/[0, 1] | [59] |
| Closing quotient | /AU | 1: completely open/[0, 1] | [60] |
| Amplitude periodicity | /AU | 1: periodic/[0, 1] | [61] |
| Time periodicity | /AU | 1: periodic/[0, 1] | [61] |
| Phase asymmetry index | /AU | 0: symmetric/[0, 1] | [61] |
| Amplitude symmetry index | /AU | 1: symmetric/[0, 1] | [62] |
| (b) Acoustic parameters | |||
| Harmonics-to-noise ratio | /dB | Higher is better * | [63] |
| Normalized noise energy | /dB | Smaller is better * | [64] |
| Cepstral peak prominance | /dB | Higher is better * | [65] |
| Shimmer | /% | Smaller is better * | [66] |
| Jitter | /% | Smaller is better * | [66] |
2.6. Measuring Protocol
- Relax the translation stage to 0 mm to ensure the fibers are in a completely tension-free state with no force applied.
- Adduct the vocal folds until complete glottal closure is achieved.
- Take a reference measurement of the subglottal pressure with the flow completely switched off.
- Manually increase the flow rate until the oscillation onset flow is identified, which is the point at which the synthetic vocal folds begin to oscillate stably.
- Record the first measurement at the onset of oscillation.
- Iteratively increase the flow rate by increments of 10 SLM until reaching the maximum flow rate of 200 SLM.
- Switch off the flow.
- Increase the fiber tension by elongating the fiber by 5 mm.
- Establish complete glottis closure if not already closed.
- Repeat the procedure starting from identifying the onset flow (step 4).
3. Results and Discussion
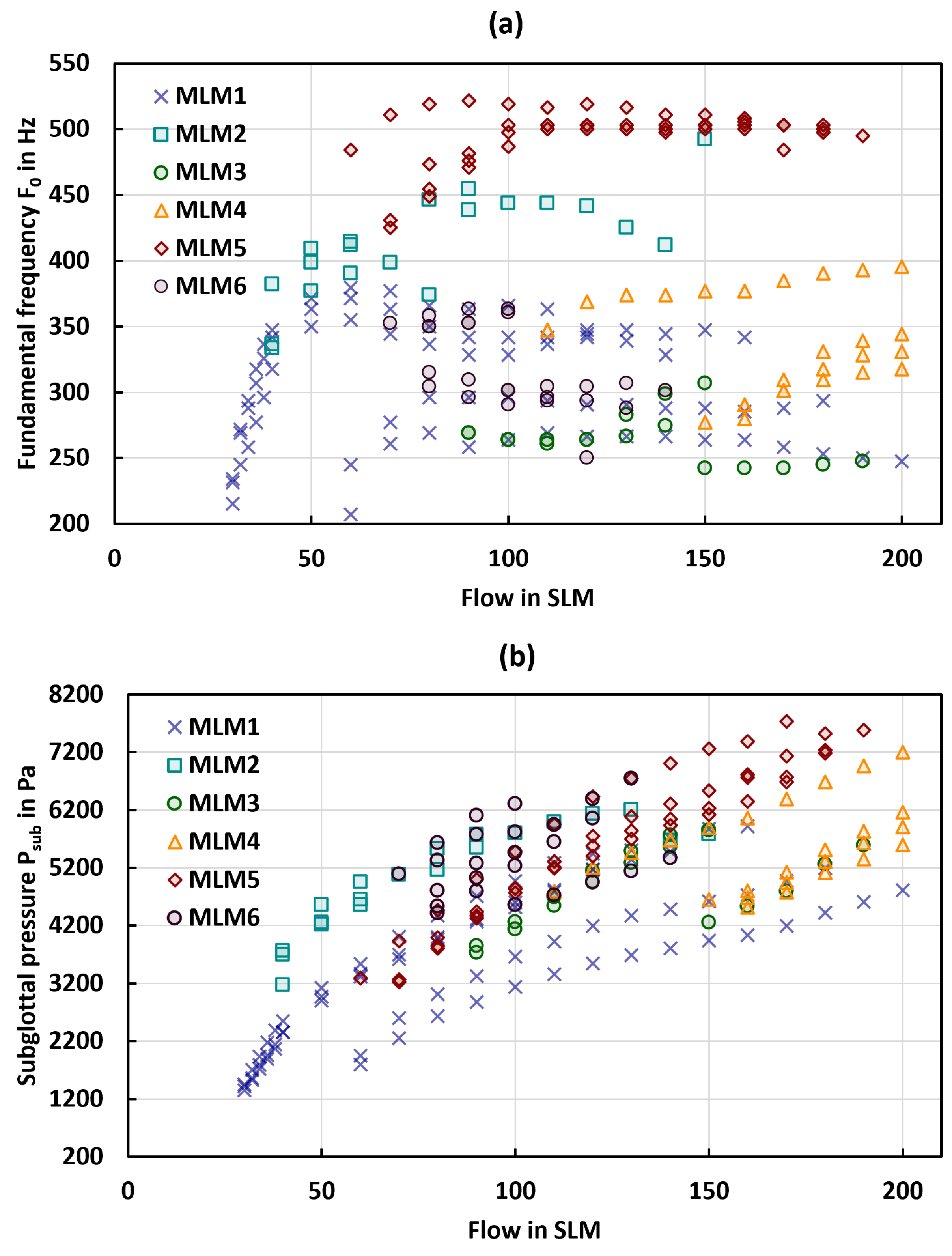
3.1. General Phonation Parameters
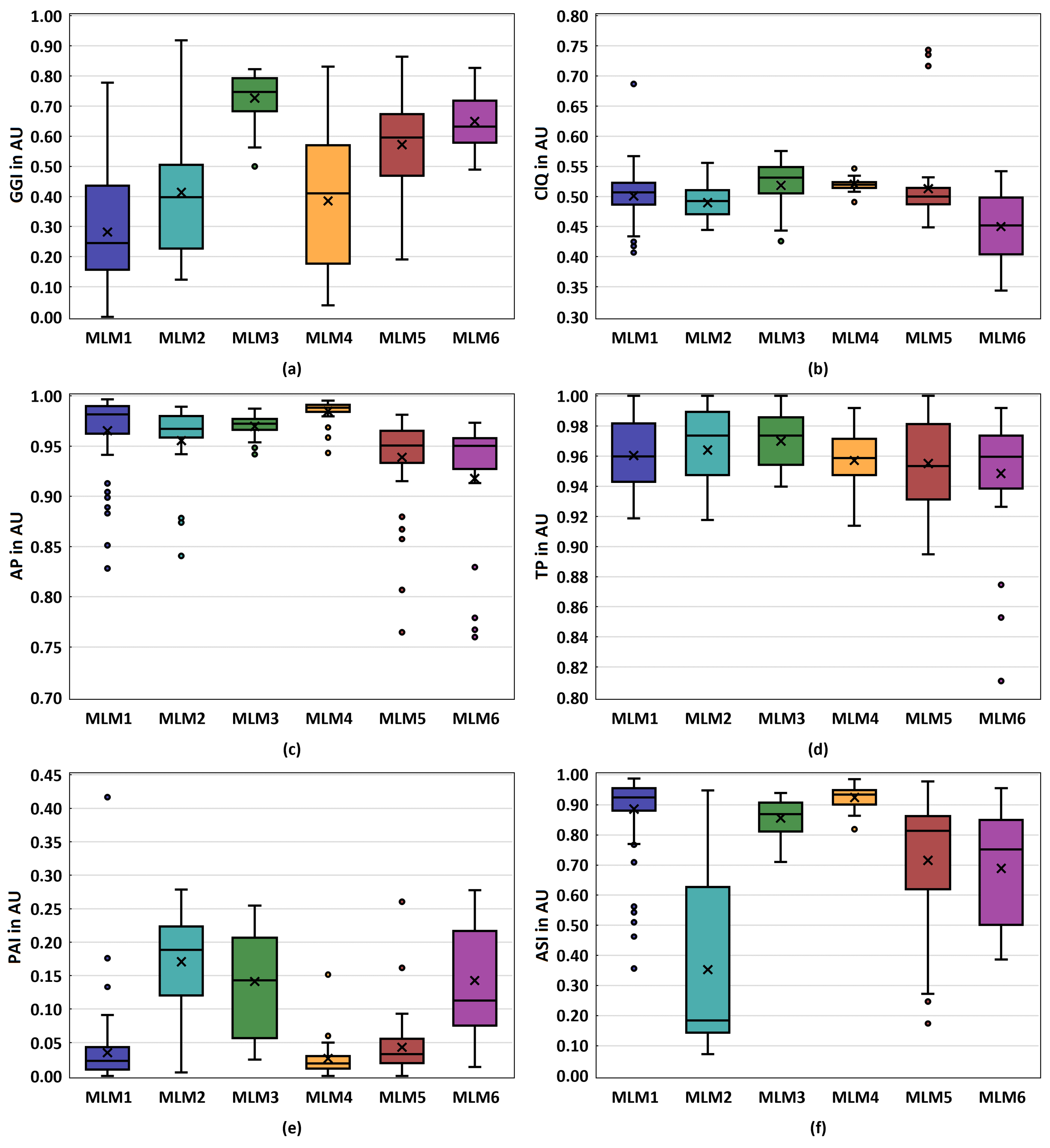
3.2. Glottal Dynamic Parameters
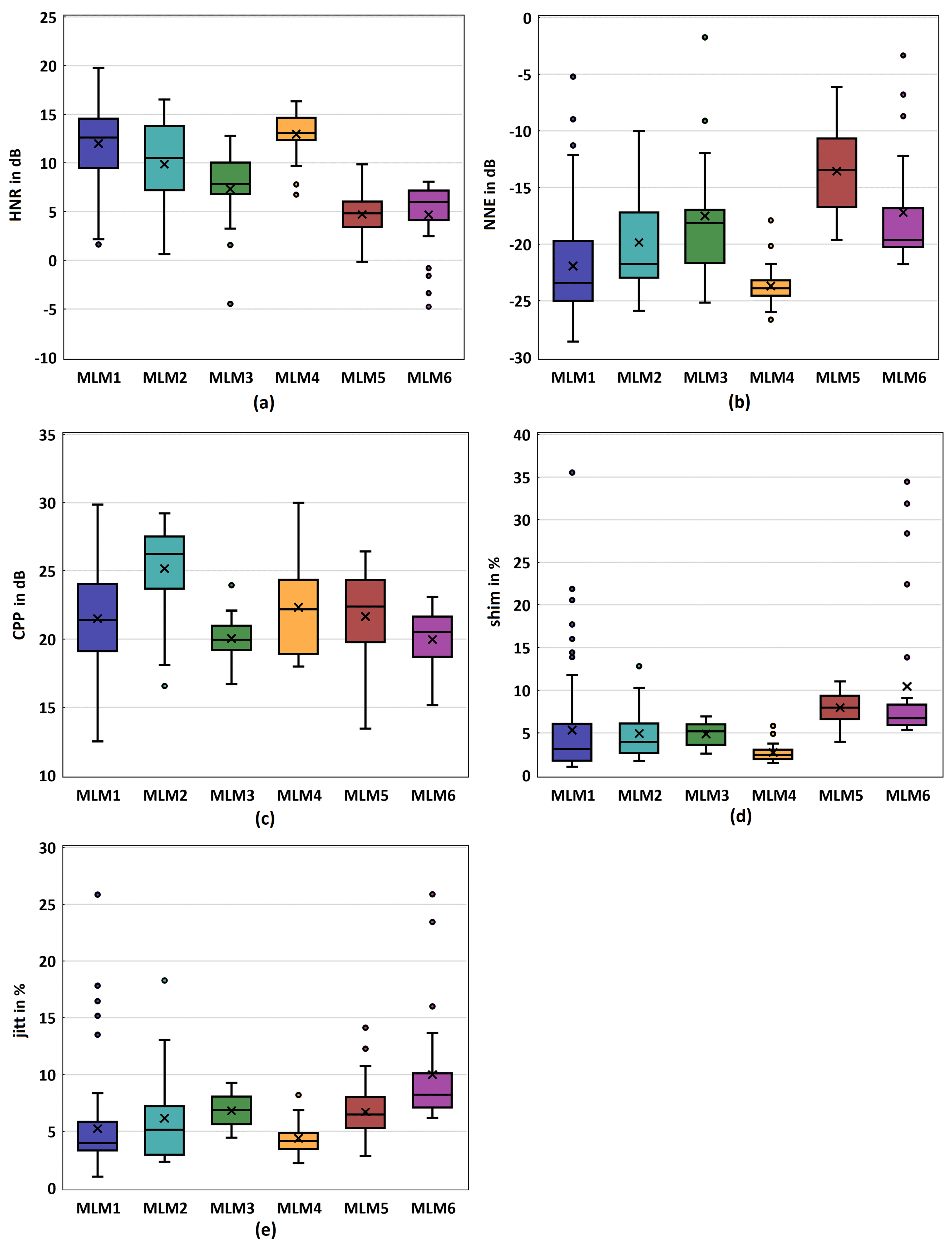
3.3. Acoustic Parameters
3.4. Evaluation of Reproduction Characteristics of the Larynx Model
3.5. Influence of Fiber Tension
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Den Berg, J.; Tan, T.S. Results of experiments with human larynxes. Pract. Oto-Rhino-Laryngol. 1959, 21, 425–450. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.; Son, Y.I.; So, Y.K.; Byun, H.; Lee, E.K.; Yun, Y.S. Posterior glottic gap and age as factors predicting voice outcome of injection laryngoplasty in patients with unilateral vocal fold paralysis. J. Laryngol. Otol. 2012, 126, 260–266. [Google Scholar] [CrossRef] [PubMed]
- Morrison, M.D.; Rammage, L.A.; Belisle, G.M.; Pullan, C.B.; Nichol, H. Muscular tension dysphonia. J. Otolaryngol. 1983, 12, 302–306. [Google Scholar] [PubMed]
- Nguyen, D.D.; Kenny, D.T.; Tran, N.D.; Livesey, J.R. Muscle tension dysphonia in Vietnamese female teachers. J. Voice Off. J. Voice Found. 2009, 23, 195–208. [Google Scholar] [CrossRef] [PubMed]
- Bhatt, J.; Verma, S. Management of glottal insufficiency. Otorinolaringologia 2014, 64, 101–107. [Google Scholar]
- Stevens, K.N. Acoustic Phonetics, 1. Paperback ed.; Number 30 in Current Studies in Linguistics Series; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Patel, R.R.; Dixon, A.; Richmond, A.; Donohue, K.D. Pediatric high speed digital imaging of vocal fold vibration: A normative pilot study of glottal closure and phase closure characteristics. Int. J. Pediatr. Otorhinolaryngol. 2012, 76, 954–959. [Google Scholar] [CrossRef]
- Fritzen, B.; Hammarberg, B.; Gauffin, J.; Karlsson, I.; Sundberg, J. Breathiness and insufficient vocal fold closure. J. Phon. 1986, 14, 549–553. [Google Scholar] [CrossRef]
- Cielo, C.A.; Schwarz, K.; Finger, L.S.; Lima, J.M.; Christmann, M.K. Glottal Closure in Women with No Voice Complaints or Laryngeal Disorders. Int. Arch. Otorhinolaryngol. 2019, 23, e384–e388. [Google Scholar] [CrossRef]
- Schneider, B.; Bigenzahn, W. Influence of glottal closure configuration on vocal efficacy in young normal-speaking women. J. Voice 2003, 17, 468–480. [Google Scholar] [CrossRef]
- Berry, D.A.; Montequin, D.W.; Tayama, N. High-speed digital imaging of the medial surface of the vocal folds. J. Acoust. Soc. Am. 2001, 110, 2539–2547. [Google Scholar] [CrossRef]
- Döllinger, M.; Tayama, N.; Berry, D.A. Empirical Eigenfunctions and medial surface dynamics of a human vocal fold. Methods Inf. Med. 2005, 44, 384–391. [Google Scholar] [PubMed]
- Boessenecker, A.; Berry, D.A.; Lohscheller, J.; Eysholdt, U.; Doellinger, M. Mucosal wave properties of a human vocal fold. Acta Acust. United Acust. 2007, 93, 815–823. [Google Scholar]
- Kniesburges, S.; Thomson, S.L.; Barney, A.; Triep, M.; Sidlof, P.; Horáčcek, J.; Brücker, C.; Becker, S. In vitro experimental investigation of voice production. Curr. Bioinform. 2011, 6, 305–322. [Google Scholar] [CrossRef]
- Spencer, M.; Siegmund, T.; Mongeau, L. Determination of superior surface strains and stresses, and vocal fold contact pressure in a synthetic larynx model using digital image correlation. J. Acoust. Soc. Am. 2008, 123, 1089–1103. [Google Scholar] [CrossRef]
- Motie-Shirazi, M.; Zañartu, M.; Peterson, S.D.; Mehta, D.D.; Hillman, R.E.; Erath, B.D. Collision Pressure and Dissipated Power Dose in a Self-Oscillating Silicone Vocal Fold Model With a Posterior Glottal Opening. J. Speech Lang. Hear. Res. 2022, 65, 2829–2845. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.J.; Mongeau, L. Verification of two minimally invasive methods for the estimation of the contact pressure in human vocal folds during phonation. J. Acoust. Soc. Am. 2011, 130, 1618–1627. [Google Scholar] [CrossRef]
- Horáček, J.; Bula, V.; Radolf, V.; Šidlof, P. Impact stress in a self-oscillating model of human vocal folds. Adv. Vib. Eng. 2016, 13. [Google Scholar]
- Motie-Shirazi, M.; Zañartu, M.; Peterson, S.D.; Mehta, D.D.; Kobler, J.B.; Hillman, R.E.; Erath, B.D. Toward Development of a Vocal Fold Contact Pressure Probe: Sensor Characterization and Validation Using Synthetic Vocal Fold Models. Appl. Sci. 2019, 9, 3002. [Google Scholar] [CrossRef]
- Motie-Shirazi, M.; Zañartu, M.; Peterson, S.D.; Erath, B.D. Vocal fold dynamics in a synthetic self-oscillating model: Contact pressure and dissipated-energy dose. J. Acoust. Soc. Am. 2021, 150, 478–489. [Google Scholar] [CrossRef]
- Weiss, S.; Sutor, A.; Rupitsch, S.J.; Kniesburges, S.; Doellinger, M.; Lerch, R. Development of a small film sensor for the estimation of the contact pressure of artificial vocal folds. J. Acoust. Soc. Am. 2013, 133, 3618. [Google Scholar] [CrossRef]
- Neubauer, J.; Zhang, Z.; Miraghaie, R.; Berry, D.A. Coherent structures of the near field flow in a self-oscillating physical model of the vocal folds. J. Acoust. Soc. Am. 2007, 121, 1102–1118. [Google Scholar] [CrossRef] [PubMed]
- Popolo, P.S.; Titze, I.R. Qualification of a quantitative laryngeal imaging system using videostroboscopy and videokymography. Ann. Otol. Rhinol. Laryngol. 2008, 117, 404–412. [Google Scholar] [CrossRef] [PubMed]
- Semmler, M.; Kniesburges, S.; Birk, V.; Ziethe, A.; Patel, R.; Dollinger, M. 3D Reconstruction of Human Laryngeal Dynamics Based on Endoscopic High-Speed Recordings. IEEE Trans. Med. Imaging 2016, 35, 1615–1624. [Google Scholar] [CrossRef] [PubMed]
- Semmler, M.; Kniesburges, S.; Parchent, J.; Jakubaß, B.; Zimmermann, M.; Bohr, C.; Schützenberger, A.; Döllinger, M. Endoscopic Laser-Based 3D Imaging for Functional Voice Diagnostics. Appl. Sci. 2017, 7, 600. [Google Scholar] [CrossRef]
- Thomson, S.L.; Mongeau, L.; Frankel, S.H. Aerodynamic transfer of energy to the vocal folds. J. Acoust. Soc. Am. 2005, 118, 1689–1700. [Google Scholar] [CrossRef] [PubMed]
- Motie-Shirazi, M.; Zañartu, M.; Peterson, S.D.; Erath, B.D. Vocal fold dynamics in a synthetic self-oscillating model: Intraglottal aerodynamic pressure and energy. J. Acoust. Soc. Am. 2021, 150, 1332–1345. [Google Scholar] [CrossRef]
- Migimatsu, K.; Tokuda, I.T. Experimental study on nonlinear source-filter interaction using synthetic vocal fold models. J. Acoust. Soc. Am. 2019, 146, 983–997. [Google Scholar] [CrossRef]
- Zhang, Z.; Hieu Luu, T. Asymmetric vibration in a two-layer vocal fold model with left-right stiffness asymmetry: Experiment and simulation. J. Acoust. Soc. Am. 2012, 132, 1626–1635. [Google Scholar] [CrossRef]
- Zhang, Z.; Kreiman, J.; Gerratt, B.R.; Garellek, M. Acoustic and perceptual effects of changes in body layer stiffness in symmetric and asymmetric vocal fold models. J. Acoust. Soc. Am. 2013, 133, 453–462. [Google Scholar] [CrossRef]
- Kniesburges, S.; Lodermeyer, A.; Semmler, M.; Schulz, Y.K.; Schützenberger, A.; Becker, S. Analysis of the tonal sound generation during phonation with and without glottis closure. J. Acoust. Soc. Am. 2020, 147, 3285–3293. [Google Scholar] [CrossRef]
- Zhang, Z.; Neubauer, J.; Berry, D.A. The influence of subglottal acoustics on laboratory models of phonation. J. Acoust. Soc. Am. 2006, 120, 1558–1569. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Neubauer, J.; Berry, D.A. Influence of vocal fold stiffness and acoustic loading on flow-induced vibration of a single-layer vocal fold model. J. Sound Vib. 2009, 322, 299–313. [Google Scholar] [CrossRef]
- Zhang, Z. Restraining mechanisms in regulating glottal closure during phonation. J. Acoust. Soc. Am. 2011, 130, 4010–4019. [Google Scholar] [CrossRef] [PubMed]
- Hirano, M. Cover-body theory of vocal cord vibration. Speech Sci. 1985, 1–46. [Google Scholar]
- Murray, P.R.; Thomson, S.L. Vibratory responses of synthetic, self-oscillating vocal fold models. J. Acoust. Soc. Am. 2012, 132, 3428–3438. [Google Scholar] [CrossRef]
- Shaw, S.M.; Thomson, S.L.; Dromey, C.; Smith, S. Frequency response of synthetic vocal fold models with linear and nonlinear material properties. J. Speech Lang. Hear. Res. 2012, 55, 1395–1406. [Google Scholar] [CrossRef]
- Xuan, Y.; Zhang, Z. Influence of Embedded Fibers and an Epithelium Layer on the Glottal Closure Pattern in a Physical Vocal Fold Model. J. Speech Lang. Hear. Res. 2014, 57, 416–425. [Google Scholar] [CrossRef]
- Scherer, R.C.; Shinwari, D.; De Witt, K.J.; Zhang, C.; Kucinschi, B.R.; Afjeh, A.A. Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. J. Acoust. Soc. Am. 2001, 109, 1616–1630. [Google Scholar] [CrossRef]
- Murray, P.R.; Thomson, S.L.; Smith, M.E. A Synthetic, Self-Oscillating Vocal Fold Model Platform for Studying Augmentation Injection. J. Voice 2014, 28, 133–143. [Google Scholar] [CrossRef]
- Kniesburges, S.; Birk, V.; Lodermeyer, A.; Schützenberger, A.; Bohr, C.; Becker, S. Effect of the ventricular folds in a synthetic larynx model. J. Biomech. 2007, 55, 128–133. [Google Scholar] [CrossRef]
- Titze, I.R. Principles of Voice Production; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Min, Y.B.; Titze, I.R.; Alipour-Haghighi, F. Stress-Strain Response of the Human Vocal Ligament. Ann. Otol. Rhinol. Laryngol. 1995, 104, 563–569. [Google Scholar] [CrossRef] [PubMed]
- Titze, I.; Alipour, F. The Myoelastic-Aerodynamic Theory of Phonation; National Center for Voice and Speech: Salt Lake City, UT, USA, 2006. [Google Scholar]
- Birk, V.; Döllinger, M.; Sutor, A.; Berry, D.A.; Gedeon, D.; Traxdorf, M.; Wendler, O.; Bohr, C.; Kniesburges, S. Automated setup for ex vivo larynx experiments. J. Acoust. Soc. Am. 2017, 141, 1349–1359. [Google Scholar] [CrossRef] [PubMed]
- Semmler, M.; Berry, D.A.; Schützenberger, A.; Döllinger, M. Fluid–structure-acoustic interactions in an ex vivo porcine phonation model. J. Acoust. Soc. Am. 2021, 149, 1657–1673. [Google Scholar] [CrossRef] [PubMed]
- Jakubaß, B.; Peters, G.; Kniesburges, S.; Semmler, M.; Kirsch, A.; Gerstenberger, C.; Gugatschka, M.; Döllinger, M. Effect of functional electric stimulation on phonation in an ex vivo aged ovine model. J. Acoust. Soc. Am. 2023, 153, 2803. [Google Scholar] [CrossRef] [PubMed]
- Peters, G.; Jakubaß, B.; Weidenfeller, K.; Kniesburges, S.; Böhringer, D.; Wendler, O.; Mueller, S.K.; Gostian, A.O.; Berry, D.A.; Döllinger, M.; et al. Synthetic mucus for an ex vivo phonation setup: Creation, application, and effect on excised porcine larynges. J. Acoust. Soc. Am. 2022, 152, 3245–3259. [Google Scholar] [CrossRef] [PubMed]
- Hayes, M.H. Statistical Digital Signal Processing and Modeling; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Stoica, P.G.; Moses, R.; Stoica, P.; Moses, R.L. Spectral Analysis of Signals; Pearson: Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Kniesburges, S.; Lodermeyer, A.; Becker, S.; Traxdorf, M.; Döllinger, M. The mechanisms of subharmonic tone generation in a synthetic larynx model. J. Acoust. Soc. Am. 2016, 139, 3182–3192. [Google Scholar] [CrossRef] [PubMed]
- Kist, A.M.; Gómez, P.; Dubrovskiy, D.; Schlegel, P.; Kunduk, M.; Echternach, M.; Patel, R.; Semmler, M.; Bohr, C.; Dürr, S.; et al. A Deep Learning Enhanced Novel Software Tool for Laryngeal Dynamics Analysis. J. Speech Lang. Hear. Res. 2021, 64, 1889–1903. [Google Scholar] [CrossRef]
- Maryn, Y.; Verguts, M.; Demarsin, H.; van Dinther, J.; Gomez, P.; Schlegel, P.; Döllinger, M. Intersegmenter Variability in High-Speed Laryngoscopy-Based Glottal Area Waveform Measures. Laryngoscope 2020, 130, E654–E661. [Google Scholar] [CrossRef]
- Schlegel, P.; Semmler, M.; Kunduk, M.; Döllinger, M.; Bohr, C.; Schützenberger, A. Influence of Analyzed Sequence Length on Parameters in Laryngeal High-Speed Videoendoscopy. Appl. Sci. 2018, 8, 2666. [Google Scholar] [CrossRef]
- Karnell, M.P.; Hall, K.D.; Landahl, K.L. Comparison of fundamental frequency and perturbation measurements among three analysis systems. J. Voice 1995, 9, 383–393. [Google Scholar] [CrossRef]
- Alipour, F.; Scherer, R.C.; Finnegan, E. Pressure-flow relationships during phonation as a function of adduction. J. Voice Off. J. Voice Found. 1997, 11, 187–194. [Google Scholar] [CrossRef]
- Mehta, D.D.; Zañartu, M.; Quatieri, T.F.; Deliyski, D.D.; Hillman, R.E. Investigating acoustic correlates of human vocal fold vibratory phase asymmetry through modeling and laryngeal high-speed videoendoscopy. J. Acoust. Soc. Am. 2011, 130, 3999–4009. [Google Scholar] [CrossRef] [PubMed]
- Titze, I.R.; National Center for Voice and Speech; Workshop on Acoustic Voice Analysis. Workshop on Acoustic Voice Analysis: Summary Statement; National Center for Voice and Speech: Salt Lake City, UT, USA, 1995. [Google Scholar]
- Patel, R.; Dubrovskiy, D.; Döllinger, M. Characterizing vibratory kinematics in children and adults with high-speed digital imaging. J. Speech Lang. Hear. Res. 2014, 57, S674–S686. [Google Scholar] [CrossRef] [PubMed]
- Holmberg, E.B.; Hillman, R.E.; Perkell, J.S. Glottal airflow and transglottal air pressure measurements for male and female speakers in soft, normal, and loud voice. J. Acoust. Soc. Am. 1988, 84, 511–529. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Q.; Schutte, H.; Gu, L.; Yu, Q. An Automatic Method to Quantify the Vibration Properties of Human Vocal Folds via Videokymography. Folia Phoniatr. Logop. 2003, 55, 128–136. [Google Scholar] [CrossRef]
- Wang, S.G.; Park, H.J.; Lee, B.J.; Lee, S.M.; Ko, B.; Lee, S.M.; Park, Y.M. A new videokymography system for evaluation of the vibration pattern of entire vocal folds. Auris Nasus Larynx 2016, 43, 315–321. [Google Scholar] [CrossRef]
- Yumoto, E.; Gould, W.J.; Baer, T. Harmonics-to-noise ratio as an index of the degree of hoarseness. J. Acoust. Soc. Am. 1982, 71, 1544–1549. [Google Scholar] [CrossRef]
- Kasuya, H.; Endo, Y.; Saliu, S. Novel acoustic measurements of jitter and shimmer characteristics from pathological voice. In Proceedings of the 3rd European Conference on Speech Communication and Technology (Eurospeech 1993), Berlin, Germany, 21–23 September 1993; pp. 1973–1976. [Google Scholar] [CrossRef]
- Hillenbrand, J.; Houde, R.A. Acoustic correlates of breathy vocal quality: Dysphonic voices and continuous speech. J. Speech Lang. Hear. Res. 1996, 39, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Bielamowicz, S.; Kreiman, J.; Gerratt, B.R.; Dauer, M.S.; Berke, G.S. Comparison of voice analysis systems for perturbation measurement. J. Speech Lang. Hear. Res. 1996, 39, 126–134. [Google Scholar] [CrossRef]
- Chan, R.W.; Rodriguez, M.L. A simple-shear rheometer for linear viscoelastic characterization of vocal fold tissues at phonatory frequencies. J. Acoust. Soc. Am. 2008, 124, 1207–1219. [Google Scholar] [CrossRef]
- Alipour, F.; Vigmostad, S. Measurement of Vocal Folds Elastic Properties for Continuum Modeling. J. Voice 2012, 26, 816.e21–816.e29. [Google Scholar] [CrossRef] [PubMed]
- Chhetri, D.K.; Zhang, Z.; Neubauer, J. Measurement of Young’s Modulus of Vocal Folds by Indentation. J. Voice 2011, 25, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Oren, L.; Dembinski, D.; Gutmark, E.; Khosla, S. Characterization of the Vocal Fold Vertical Stiffness in a Canine Model. J. Voice 2014, 28, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Dion, G.R.; Coelho, P.G.; Teng, S.; Janal, M.N.; Amin, M.R.; Branski, R.C. Dynamic nanomechanical analysis of the vocal fold structure in excised larynges: Nanomechanical Analysis of the VF Structure. Laryngoscope 2017, 127, E225–E230. [Google Scholar] [CrossRef] [PubMed]
- Chan, R.W.; Titze, I.R. Viscoelastic shear properties of human vocal fold mucosa: Measurement methodology and empirical results. J. Acoust. Soc. Am. 1999, 106, 2008–2021. [Google Scholar] [CrossRef] [PubMed]
- Chan, R.W.; Fu, M.; Young, L.; Tirunagari, N. Relative Contributions of Collagen and Elastin to Elasticity of the Vocal Fold Under Tension. Ann. Biomed. Eng. 2007, 35, 1471–1483. [Google Scholar] [CrossRef]
- Zemlin, W.R. Speech and Hearing Science: Anatomy and Physiology, 3rd ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Sundberg, J.; Fahlstedt, E.; Morell, A. Effects on the glottal voice source of vocal loudness variation in untrained female and male voices. J. Acoust. Soc. Am. 2005, 117, 879–885. [Google Scholar] [CrossRef]
- Jones, S.M.; Garrett, C. Laryngeal Endoscopy and Voice Therapy; OCLC: 956917938; Compton: Oxford, UK, 2016. [Google Scholar]
- Echternach, M.; Sundberg, J.; Baumann, T.; Markl, M.; Richter, B. Vocal tract area functions and formant frequencies in opera tenors’ modal and falsetto registers. J. Acoust. Soc. Am. 2011, 129, 3955–3963. [Google Scholar] [CrossRef]
- Sundberg, J.; Titze, I.; Scherer, R. Phonatory control in male singing: A study of the effects of subglottal pressure, fundamental frequency, and mode of phonation on the voice source. J. Voice 1993, 7, 15–29. [Google Scholar] [CrossRef]
- Baken, R.J.; Orlikoff, R.F. Clinical Measurement of Speech and Voice, 2nd ed.; Delmar Cengage Learning: Clifton Park, NJ, USA, 2010. [Google Scholar]
- Fulcher, L.; Lodermeyer, A.; Kähler, G.; Becker, S.; Kniesburges, S. Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements. Appl. Sci. 2019, 9, 2755. [Google Scholar] [CrossRef]
- Döllinger, M.; Berry, D.A.; Kniesburges, S. Dynamic vocal fold parameters with changing adduction in ex vivo hemilarynx experiments. J. Acoust. Soc. Am. 2016, 139, 2372–2385. [Google Scholar] [CrossRef]
- Alipour, F.; Scherer, R.C. Effects of oscillation of a mechanical hemilarynx model on mean transglottal pressures and flows. J. Acoust. Soc. Am. 2001, 110, 1562–1569. [Google Scholar] [CrossRef]
- Falk, S.; Kniesburges, S.; Schoder, S.; Jakubaß, B.; Maurerlehner, P.; Echternach, M.; Kaltenbacher, M.; Döllinger, M. 3D-FV-FE Aeroacoustic Larynx Model for Investigation of Functional Based Voice Disorders. Front. Physiol. 2021, 12, 616985. [Google Scholar] [CrossRef] [PubMed]
- Kunduk, M.; Doellinger, M.; McWhorter, A.J.; Lohscheller, J. Assessment of the variability of vocal fold dynamics within and between recordings with high-speed imaging and by phonovibrogram. Laryngoscope 2010, 120, 981–987. [Google Scholar] [CrossRef] [PubMed]
- Södersten, M.; Hertegård, S.; Hammarberg, B. Glottal closure, transglottal airflow, and voice quality in healthy middle-aged women. J. Voice 1995, 9, 182–197. [Google Scholar] [CrossRef] [PubMed]
- Semmler, M.; Kniesburges, S.; Pelka, F.; Ensthaler, M.; Wendler, O.; Schützenberger, A. Influence of Reduced Saliva Production on Phonation in Patients With Ectodermal Dysplasia. J. Voice 2021, S089219972100206X. [Google Scholar] [CrossRef]
- Schlegel, P.; Kunduk, M.; Stingl, M.; Semmler, M.; Döllinger, M.; Bohr, C.; Schützenberger, A. Influence of spatial camera resolution in high-speed videoendoscopy on laryngeal parameters. PLoS ONE 2019, 14, e0215168. [Google Scholar] [CrossRef]
- Schützenberger, A.; Kunduk, M.; Döllinger, M.; Alexiou, C.; Dubrovskiy, D.; Semmler, M.; Seger, A.; Bohr, C. Laryngeal High-Speed Videoendoscopy: Sensitivity of Objective Parameters towards Recording Frame Rate. BioMed Res. Int. 2016, 2016, 4575437. [Google Scholar] [CrossRef]
- Zhang, Z. Compensation Strategies in Voice Production With Glottal Insufficiency. J. Voice 2019, 33, 96–102. [Google Scholar] [CrossRef]
- Graham, E.; Angadi, V.; Sloggy, J.; Stemple, J. Contribution of Glottic Insufficiency to Perceived Breathiness in Classically Trained Singers. Med. Probl. Perform. Artist. 2016, 31, 179–184. [Google Scholar] [CrossRef]
- Schlegel, P.; Kniesburges, S.; Dürr, S.; Schützenberger, A.; Döllinger, M. Machine learning based identification of relevant parameters for functional voice disorders derived from endoscopic high-speed recordings. Sci. Rep. 2020, 10, 10517. [Google Scholar] [CrossRef] [PubMed]
- Bonilha, H.S.; Deliyski, D.D.; Whiteside, J.P.; Gerlach, T.T. Vocal Fold Phase Asymmetries in Patients With Voice Disorders: A Study Across Visualization Techniques. Am. J.-Speech-Lang. Pathol. 2012, 21, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Van Den Berg, J.; Zantema, J.T.; Doornenbal, P. On the Air Resistance and the Bernoulli Effect of the Human Larynx. J. Acoust. Soc. Am. 1957, 29, 626–631. [Google Scholar] [CrossRef]
- Colton, R.H. Physiological mechanisms of vocal frequency control: The role of tension. J. Voice 1988, 2, 208–220. [Google Scholar] [CrossRef]
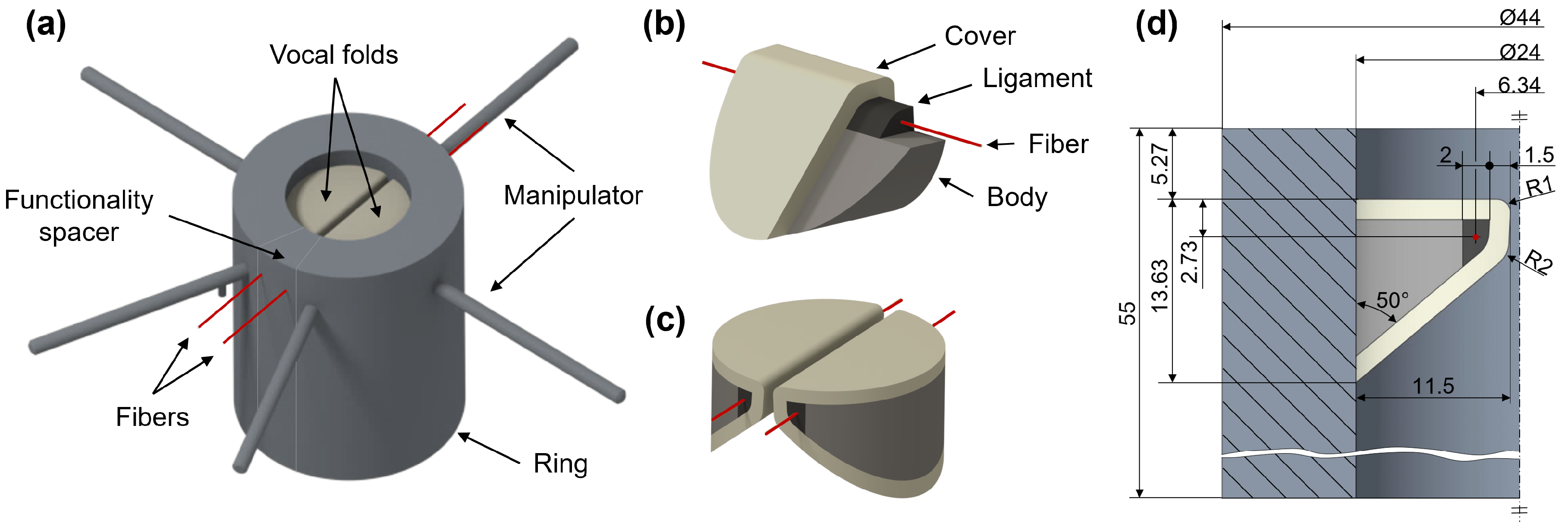


| Larynx Elements | Silicone | Mixing Ratio Part A:Part B:Thinner | Young’s Modulus in |
|---|---|---|---|
| Ring | Dragon Skin 10 Slow | 1:1:0 | 151 |
| Functionality spacer | Ecoflex 00-30 | 1:1:2.5 | 6 * |
| Body | Ecoflex 00-30 | 1:1:2 | 8.2 |
| Ligament | Ecoflex 00-30 | 1:1:0 | 60 |
| Cover | Ecoflex 00-30 | 1:1:4 | 2.5 |
| Model | Fiber | |||||
|---|---|---|---|---|---|---|
| Material |
Diameter
in mm |
Break Resistance
in kg |
E
-Modulus *
in GPa |
E
-Modulus *
in GPa | tan * | |
| MLM1 ** | PVDF | 0.108 | 1.18 | 2.91 | 0.08 | 0.03 |
| (0.07) | (0.01) | (0.00) | ||||
| MLM2 | PA 6.6 | 0.12 | 1.4 | 2.39 | 0.16 | 0.07 |
| (0.04) | (0.00) | (0.00) | ||||
| MLM3 | PA 6.6 | 0.125 | 1.82 | - | - | - |
| MLM4 | PA 6.6 | 0.18 | 2.5 | 1.19 | 0.12 | 0.10 |
| (0.03) | (0.00) | (0.00) | ||||
| MLM5 | PA 6.6 | 0.25 | 5.3 | 1.82 | 0.16 | 0.09 |
| (0.38) | (0.03) | (0.00) | ||||
| MLM6 | PA 6.6 | 0.3 | 7.9 | 1.71 | 0.12 | 0.07 |
| (0.10) | (0.01) | (0.00) | ||||
| MLM1 (N = 76) | MLM2 (N = 20) | MLM3 (N = 18) | MLM4 (N = 26) | MLM5 (N = 48) | MLM6 (N = 25) | |
|---|---|---|---|---|---|---|
| (a) Phonation onset | ||||||
| mean in Hz | 226.63 (13.55) | 371.44 (31.71) | 260.19 (12.68) | 298.77 (28.42) | 453.54 (25.92) | 328.82 (22.38) |
| mean in Pa | 1593.66 (235.96) | 4375.36 (906.12) | 3944.00 (223.64) | 4661.83 (100.76) | 3444.03 (318.67) | 4789.36 (325.45) |
| mean flow rate in SLM | 42 (14.69) | 66 (38.78) | 110 (28.28) | 145 (20.61) | 70 (7.07) | 82 (9.79) |
| (b) All recordings | ||||||
| mean in Hz | 306.42 (43.66) | 411.28 (38.46) | 264.82 (17.65) | 337.18 (36.87) | 496.32 (20.55) | 318.36 (30.43) |
| max in Hz | 379.52 | 492.57 | 306.84 | 395.67 | 522.18 | 363.37 |
| min in Hz | 207.25 | 333.76 | 242.24 | 277.23 | 425.28 | 250.32 |
| mean in Pa | 3595.90 (1281.65) | 5026.83 (863.09) | 4872.53 (642.95) | 5549.97 (708.14) | 5702.86 (1245.18) | 5405.57 (614.18) |
| max in Pa | 5918.14 | 6206.71 | 5851.08 | 7200.75 | 7737.04 | 6745.46 |
| min in Pa | 1350.85 | 3172.69 | 3733.03 | 4515.16 | 3221.27 | 4417.77 |
| MLM1 | MLM2 | MLM3 | MLM4 | MLM5 | MLM6 | |
|---|---|---|---|---|---|---|
| N | ++ | - | - - | o+ | + | o- |
| range | ++ | + | - - | o+ | - | o- |
| o- | ++ | - | - - | o+ | + | |
| GGI | ++ | o+ | - - | + | o- | - |
| ClQ | ++ | + | o- | - | o+ | - - |
| AP | o+ | o- | + | ++ | - | - - |
| TP | o+ | + | ++ | o- | - | - - |
| PAI | + | - - | o- | ++ | o+ | - |
| ASI | + | - - | o+ | ++ | o- | - |
| HNR | + | o+ | o- | ++ | - | - - |
| NNE | + | o+ | o- | ++ | - - | - |
| CPP | o+ | ++ | - | + | o- | - - |
| shim | + | o+ | o- | ++ | - - | - |
| jitt | ++ | o+ | - | + | o- | - - |
| Score | 70 | 54 | 39 | 65 | 39 | 27 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tur, B.; Gühring, L.; Wendler, O.; Schlicht, S.; Drummer, D.; Kniesburges, S. Effect of Ligament Fibers on Dynamics of Synthetic, Self-Oscillating Vocal Folds in a Biomimetic Larynx Model. Bioengineering 2023, 10, 1130. https://doi.org/10.3390/bioengineering10101130
Tur B, Gühring L, Wendler O, Schlicht S, Drummer D, Kniesburges S. Effect of Ligament Fibers on Dynamics of Synthetic, Self-Oscillating Vocal Folds in a Biomimetic Larynx Model. Bioengineering. 2023; 10(10):1130. https://doi.org/10.3390/bioengineering10101130
Chicago/Turabian StyleTur, Bogac, Lucia Gühring, Olaf Wendler, Samuel Schlicht, Dietmar Drummer, and Stefan Kniesburges. 2023. "Effect of Ligament Fibers on Dynamics of Synthetic, Self-Oscillating Vocal Folds in a Biomimetic Larynx Model" Bioengineering 10, no. 10: 1130. https://doi.org/10.3390/bioengineering10101130
APA StyleTur, B., Gühring, L., Wendler, O., Schlicht, S., Drummer, D., & Kniesburges, S. (2023). Effect of Ligament Fibers on Dynamics of Synthetic, Self-Oscillating Vocal Folds in a Biomimetic Larynx Model. Bioengineering, 10(10), 1130. https://doi.org/10.3390/bioengineering10101130






