Abstract
High spatio-temporal resolution and accurate long-term rainfall estimates are critical in sustainable water resource planning and management, assessment of climate variability and extremes, and hydro-meteorology-related water system decisions. The recent advent of improved higher-resolution open-access satellite-based rainfall products has emerged as a viable complementary to ground-based observations that can often not capture the rainfall variability on a spatial scale. In a developing country such as Nepal, where the rain-gauge monitoring network is sparse and unevenly distributed, satellite rainfall estimates are crucial. However, substantial errors associated with such satellite rainfall estimates pose a challenge to their application, particularly in complex orographic regions such as Nepal. Therefore, these precipitation products must be validated before practical usage to check their accuracy and occurrence consistency. This study aims to assess the reliability of the Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) product against ground-based observations from 1986 to 2015 in five medium-sized river basins in Nepal, namely, Babai, Bagmati, Kamala, Kankai, and the West Rapti river basin. A set of continuous evaluation metrics (correlation coefficient, root mean square error, relative bias, and Kling-Gupta efficiency) were used in analyzing the accuracy of CHIRPS and categorical metrics (probability of detection, critical success index, false alarm ratio, and frequency bias index). The Probability of Detection and Critical Success Index values were found to be considerably low (<0.4 on average), while the false alarm ratio was significant (>0.4 on average). It was found that CHIRPS showed better performance in seasonal and monthly time scales with high correlation and indicated greater consistency in non-monsoon seasons. Rainfall amount (less than 10 mm and greater than 150 mm) and rainfall frequency was underestimated by CHIRPS in all basins, while the overestimated rainfall was between 10 and 100 mm in all basins except Kamala. Additionally, CHIRPS overestimated dry days and maximum consecutive dry days in the study area. Our study suggests that CHIRPS rainfall products cannot supplant the ground-based observations but complement rain-gauge networks. However, the reliability of this product in capturing local extreme events (such as floods and droughts) seems less prominent. A high-quality rain gauge network is essential to enhance the accuracy of satellite estimations.
1. Introduction
Rainfall is one of the crucial components of the global hydrologic cycle [1,2]. The spatial and temporal variation of rainfall amount and rainfall rate modulate the Earth’s ecosystem, hydrology, and climate system [3]. Therefore, high-resolution, accurate rainfall estimates are crucial for managing hydro-meteorological hazards, planning water resource infrastructures, and adapting to likely climate changes [3,4,5,6,7]. Further, monitoring and understanding the rainfall variability is filled with challenges and uncertainties [8]. The standard rainfall measurement technique uses a ground rain gauge, which is an accurate approach [9,10]. However, the network of these ground rainfall stations is insufficient and randomly distributed [11], in particular in developing countries, such as Nepal [12].
A realistic portrayal of the rainfall behavior of a region needs a dense network of rain gauges. It also demands higher monitoring costs, which is challenging in the case of developing countries. Although weather radars can fill the data gaps between gauges, they are expensive [13]. In addition, radars have limitations due to errors from beam blockage, range effects, and the imperfect relationship between rainfall and backscatter [8,9]. With the significant development of remote sensing technology, satellite-based rainfall estimation is emerging as an alternative source of rainfall data [9]. The satellite sensors can estimate the rainfall data of remote regions with a good temporal and spatial resolution overcoming the limitations of ground-based observations [14,15]. These remotely sensed estimates are blended with ground-based observations to reduce biases [16,17,18]. Several gridded global precipitation datasets exist [19]. Some popular multi-satellite-based rainfall products are the Tropical Rainfall Measure Mission (TRMM), Multi-satellite Precipitation Analysis (TMPA; [20]), the Integrated Multi-Satellite Retrievals for Global Precipitation Measurement (GPM) mission (IMERG; [21]), the Precipitation Estimation from Remotely Sensed Information using Artificial Neural Network (PERSIANN; [22]), Climate Hazards Group Infrared Precipitation with Stations (CHIRPS; [23]), the Modern-Era Retrospective Analysis for Research and Applications (MERRA; [24]), the Climate Prediction Center Morphing method (CMORPH; [25]), the Global Satellite Mapping of Precipitation (GSMaP; [26]), and the Multi-Source Weighted-Ensemble Precipitation (MSWEP; [27]).
In most cases, rainfall data obtained from the in situ rain gauges are spatially sparse, particularly in less-developed regions. Weather radar can give rainfall information at a high spatio-temporal resolution and has a real-time monitoring ability. Still, its coverage is limited over high mountainous areas and rough terrain [28]. Similarly, satellite-derived rainfall estimates have several errors because of a weak connection between satellite signals and rainfall rate [29]. All rainfall data, whether from a ground observation, weather radar, or satellite product, have some degree of uncertainty and are subject to bias [30]. Therefore, the satellite rainfall product should be compared and validated with ground observations for certain applications. A few studies [31,32,33,34] have compared satellite products with ground measurements in Nepal. A study by Duncan and Biggs [35] assessed the accuracy of TRMM satellite estimates by comparing them with the APHRODITE data. They found the TRMM satellite products overestimated rainfall, and a high error was observed mainly during the monsoon season. Further, they reported that the extreme events, the number of rainy days, and the intensity of rainfall during the monsoon seasons were inadequately detected. Similarly, four satellite products, i.e., TRMM, GSMaP, CMORPH, and PERSIANN, were evaluated by Krakauer et al. [36] over mountainous terrains in Nepal. Among these, TRMM showed better consistency with the ground observations than the rest of the satellite products. TMPA and IMERG satellite products were evaluated in the Himalayan regions of Nepal in a study by Sharma et al. [33], where IMERG products performed better for daily time steps than TMPA for monthly time steps. Sharma et al. [33] reported that the IMERG product effectively captured extreme events, i.e., floods and droughts. A recent study by Talchabhadel et al. [12] reported the applicability of all three products of the IMERG run (i.e., IMERG Early, Late, and Final) by employing several extreme rainfall indices across Nepal.
Past studies were mainly focused on TRMM, PERSIANN, IMERG, and GSMaP for evaluating satellite precipitation products over ground observations [33]. CHIRPS has a spatial resolution of ~5 Km, and it would be helpful to evaluate the use of CHIRPS products in hydrologic modeling and water resources planning, management, and decisions. The CHIRPS product has been used globally and regionally for several applications, including forecasting [37], agriculture [38], and drought monitoring [39]. Further, there have been few comprehensive studies using CHIRPS data in Nepal. For instance, Shrestha et al. [39] evaluated the performance of CHIRPS products monthly for three decades (1981–2010) in the Koshi basin of Nepal using ground measurements. CHIRPS products performed better in low-elevation regions compared to high-elevation regions. Talchabhadel et al. [34] used high-resolution products, including CHIRPS, to force a hydrologic model in a medium-sized river basin in western Nepal. Similarly, Khatakho et al. [40] used several products, including CHIRPS, in the Karnali River basin, one of the major river basins of Nepal. Lamichhane et al. [41] used CHIRPS data to characterize the hydrometeorology of a high mountain river basin to look at transboundary multihazard dynamics in Tibet (China) and Nepal.
More validation is needed to better understand the applicability of the CHIRPS product [9]. Thus, this study aims to evaluate the performance of CHIRPS rainfall data by comparing it with ground station rainfall data from the Department of Hydrology and Meteorology (DHM), Nepal. We evaluate magnitude agreement and occurrence consistency against the ground rainfall data over medium-sized river basins in Nepal. Water availability in medium-sized rivers is highly dependent on rainfall occurrence and magnitude. As these river basins have almost negligible snow components, the rainfall to runoff dynamic is highly correlated with rainfall across the basin. Our study aims to answer three major questions: (1) How well does the CHIRPS product capture rainfall amount?; (2) What type of rainfall in what regions are best represented by the CHIRPS data?; and (3) Does the CHIRPS product capture the local extremes?
2. Materials and Methods
2.1. Study Area
Nepal is a landlocked country surrounded between the Himalayas and the Gangetic plain. It comprises the Himalayas in the north, mountains/hills in the mid, and lowlands in the south [35]. The topography and climatic features vary significantly from north to south, causing high rainfall variation throughout Nepal [42]. The study domain includes Nepal’s five different basins (West Rapti, Babai, Bagmati, Kankai, and Kamala), as shown in Figure 1. These five basins are categorized as medium-sized basins based on their area and origin [43]. The summary information, including location, catchment area, and elevation of all basins, are tabulated in Table 1.
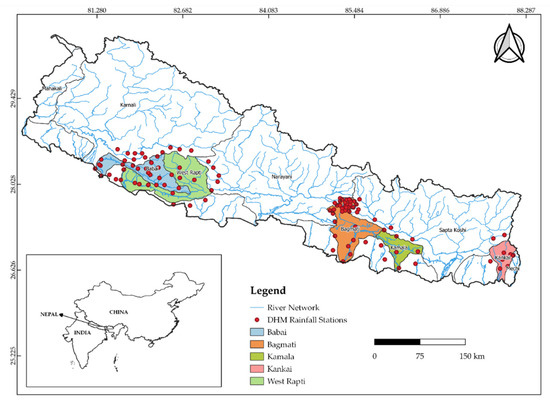
Figure 1.
The study area map comprising of Babai, Bagmati, Kamala, Kankai, and West Rapti river basins.

Table 1.
Summary information on basins.
There are mainly four different seasons, i.e., pre-monsoon (March–May), monsoon (June–September), post-monsoon (October–November), and winter (December–February). The average annual rainfall in five basins ranges from 1300 to 1800 mm per year, with an average of about 1500 mm per year, where the summer monsoon rainfall accounts for more than 80% of total annual rainfall. Table 1 briefly describes the basins considered in this study, including the number of meteorological stations.
2.2. Datasets
2.2.1. Rain Gauge Data
The daily rainfall observations of 119 meteorological stations were obtained from the Department of Hydrology and Meteorology (DHM), Nepal. The data were collected for the study period of 30 years, from January 1986 to December 2015. Manual rain gauges are dominant, so there may be human or instrumental errors. The altitude varies between 80 and 2314 m above sea level (masl). The monthly, seasonal, and annual rainfall values were accumulated from daily observations to validate the CHIRPS rainfall data.
2.2.2. Satellite Data from CHIRPS
Climate Hazards Group Infrared Precipitation with Stations (CHIRPS) environmental record is a new precipitation dataset developed by the US Geological Survey (USGS) and the Climate Hazards Group at the University of California, Santa Barbara (UCSB). Pentad is the main computational time step of CHIRPS data that can be disaggregated into the daily time step using the daily Coupled Forecast System (CFS), which is at a resolution of 0.05 [23]. Further, the CHIRPS datasets are aggregated to monthly and decadal timesteps. Further, CHIRPS is a blended product of the Climate Hazards Precipitation Climatology (CHPClim), TIR (Thermal Infrared) satellite observations, atmospheric model rainfall fields from the NOAA (National Oceanic and Atmospheric Administration) Climate Forecast System, version 2 (CFSv2), the TRMM (Tropical Rainfall Measuring Mission) 3B42 product from NASA, and in situ rainfall observations from national and regional meteorological services [23,47].
2.3. Methodology
Validation of CHIRPS products was conducted for the study period (1986–2015), considering 119 rain gauge stations in 5 different basins and their performances for detecting extreme hydrological events, such as droughts and floods were evaluated [33]. Rainfall interpolation was less preferred in the study area due to complex topography and the uneven distribution of ground-based rain gauge stations [33,48]. The CHIRPS products were extracted for the point-based station locations rather than interpolating the rain gauge measurements into grids [47]. Comparing CHIRPS products and rain gauge observations was performed at three temporal scales, i.e., monthly, seasonal, and annual. The daily rainfall data were aggregated on monthly, seasonal, and annual scales. The comparison was also extended to four different seasons, as mentioned above. Spatial and temporal consistencies were evaluated by comparing the monthly, seasonal, and annual rainfall datasets for all five basins and are represented by scatterplots. Error evaluation was conducted on a basin-scale through boxplots. Spatial maps for different statistical metrics for different basins were prepared using the Quantum Geographic Information System (QGIS).
2.3.1. Distribution Pattern of Daily Rainfall
Based on the rainfall amount per day, the rainfall rate was categorized into five different classes, similar to Prajapati et al. [49], as shown in Table 2. The percentages of rainfall contribution to total annual rainfall by different rainfall rate classes per year were calculated for all stations. Further, the percentages of frequency of rainy days of different rainfall rate classes to total annual rainy days were calculated for all stations. A combo-chart of a bar graph and a line graph was prepared to demonstrate the relationship between average daily rainfall and rainfall frequency of various rainfall rate classes for each basin. Dry days (DD) refers to the days when all the stations in the basin measure zero rainfall per day, and the number of maximum consecutive dry days is known as maximum consecutive dry days (MCDD). The temporal variations of DD and MCDD for both CHIRPS product and rain gauge observations for all five basins were evaluated and presented through line plots.

Table 2.
Classification of rainfall rate based on rainfall amount per day (mm) [49].
2.3.2. Statistical Metrics
Two types of statistics were used to examine the satellite products: continuous evaluation statistics and categorical evaluation statistics. The discrepancy between satellite estimates and observations was measured using continuous statistics, while the precipitation detection capabilities were assessed using categorical validation statistics.
Continuous Evaluation Statistics
The performance of the CHIRPS product versus the ground rain gauge observations was evaluated through four statistics metrics (i) correlation coefficient (R), (ii) root mean square error (RMS), (iii) relative bias (BIAS), and (iv) Kling-Gupta Efficiency (KGE). These metrics were calculated using the following formulae:
where Ci and Di are the values of CHIRPS rainfall data and DHM rain gauge observations for the ith rain station, respectively. The mean values of the CHIRPS rainfall data and DHM rain gauge observations were represented by and , respectively. The total number of rain gauges is denoted by n.
where R is a Pearson correlation coefficient, β is the bias ratio, and γ is the variability ratio. R was calculated to evaluate how well the CHIRPS rainfall estimates correlate with the observed rainfall values of DHM rain gauges. The absolute error between two rainfall datasets was represented by RMS error values. The degree of overestimation or underestimation between satellite product and ground-based rain gauge data was measured through BIAS. The optimal value for correlation coefficient and KGE is 1, and the minimum value of RMS error denotes a good fit. Ideally, the PBIAS value is close to 0. A higher negative value of PBIAS indicates underestimation, and a higher positive value indicates overestimation by CHIRPS.
Categorical Validation Statistics
In this study, four categorical validation statistics, the probability of detection (POD), critical success index (CSI), false alarm ratio (FAR), and frequency bias index (FBI), were used to determine the rainfall detection capacity of the CHIRPS product in comparison with DHM observations. At first, the rainfall detection of CHIRPS with DHM was compared. When both CHIRPS and DHM show a daily rainfall greater or equal to 1 mm, the detection is considered to be “a”. In contrast, if the CHIRPS product cannot detect rainfall during non-rainy days detected by the DHM, the detection is “b”. Likewise, when the CHIRPS product does not detect rainy days based on DHM, the detection is regarded as “c”. Finally, if CHIRPS and DHM show a daily rainfall of less than 1 mm, the detection is “d”. Then, categorical validation statistics were calculated based on the formulas given in Table 3.

Table 3.
Categorical validation statistics for rainfall detection evaluation.
POD was calculated to quantify the proportion of correctly predicted rainfall. CSI evaluates the proportion of predicted rainfall events that are estimated correctly, FAR indicates the proportion of false alarms by the satellite product, and the FBI determines whether the satellite rainfall estimates underestimate or overestimate the rainfall events.
3. Results and Discussion
3.1. Analysis of Rainfall Detection Capacity
The POD values for all basins were low, with median values ranging between 0.32 and 0.38, indicating CHIRPS’ inability to detect the rainfall events in the entire study area (Figure 2). In particular, the Kankai basin shows comparatively higher POD values (median = 0.38) than the other four basins. The maximum POD was found to be 0.49 in the Kamala basin; this implies that CHIRPS detects less than 49% of the rainfall events in the study area. Likewise, the CSI values were not very promising as none of the basins had values above 0.36. The CSI values were considerably greater for the Kankai basin (median = 0.31). In contrast, CSI values for three basins (Babai, Bagmati, and Kankai) were almost similar, with a median of 0.26.
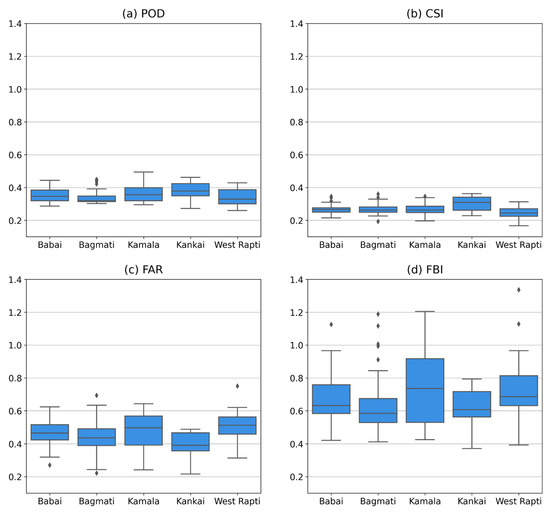
Figure 2.
Performance of rainfall detection capacity of CHIRPS product with respect to rain gauge observations during 1986–2015 for all five basins, i.e., West Rapti (WR), Babai (BB), Bagmati (BM), Kankai (KK), and Kamala (KM).
All the basins showed noteworthy false alarms, with values in the range of 0.22 to 0.75, while the FAR for the Kankai basin was comparatively small (median = 0.39). Similar findings were observed in studies by Talchabhadel et al. [34] in the West Rapti River basin and in the Tibetan Plateau and its surroundings by Tan et al. [50]. Paredes-Trejo et al. [51] also mentioned that CHIRPS satellites tend to distinguish poorly between rainfall and non-rainfall events. Over the orographic regions, CHIRPS is unable to capture rainfall events, and rainfall is often confused with warm orographic rains and extreme cold surfaces [52,53].
In general, the performance of CHIRPS was observed to be slightly better in the Kankai basin. In addition, the median of FAR values of CHIRPS seems to be high (>0.4) in the remaining four basins, with the highest in West Rapti, followed by Kamala, Babai, and Bagmati basins, which might be because of the over-detection of rainfall events by the satellite product. Similar findings were observed in a study by Ayehu et al. [9] in the Upper Blue Nile Basin of Ethiopia and by Mu et al. [54] over the southwestern Brazilian Amazon. The process of developing the CHIRPS product requires the calibration of infrared cold cloud duration rainfall estimates using TRMM multi-satellite precipitation analysis (TMPA 3B42). In this process, there might be the probability of generating too much light rain, resulting in the overestimation of rainy days by CHIRPS [9,23]. Further, the CHIRPS algorithm depends on training data from TRMM with a 0.25° resolution. When averaging the training data over a large scale, the occurrence of rainfall events increases [51]. Regarding the FBI, the underestimation of rainfall by CHIRPS based on DHM observations was noted, with the median for all basins ≤ 0.73.
Based on the categorical evaluation statistics findings, the CHIRPS rainfall estimates in the study area are not very reliable with respect to the DHM observations; therefore, some adjustments or corrections should be made before its application.
3.2. Temporal Evaluation of Rainfall Product
Figure 3 (left column) shows the scatter plots for statistical metrics (R, RMS, BIAS, and KGE) used to evaluate the performance of CHIRPS versus the observations made by rain gauges over different timescales from January 1986 to December 2015. Different colors indicate different time scales and seasons in the plots. CHIRPS performs well for the seasonal (R = 0.95) and monthly (R = 0.87) time scales with higher average values of R in comparison to the annual time scale (R = 0.31) (Figure 3). The reason for the good performance of the CHIRPS dataset might be the inclusion of station data in it [23]. The errors at the monthly scale are approximately symmetrical and cancel each other out after aggregation resulting in a higher correlation at the seasonal scale [55]. The average values from RMS at annual, seasonal, and monthly timescales for all basins were 490.19 (ranging from 394 to 586.32 mm), 221.3 (ranging from 189 to 257.71 mm), and 95.28 mm (ranging from 84.3 to 107.64 mm), respectively. In addition, the CHIRPS product underestimates rainfall over the annual, seasonal, and monthly timescales in all basins with an average BIAS of −6.63% (ranging from −7.95% to −4.30%) except in the Babai basin (+12.7%). Similar to the R-value, on average, the scatter plot of KGE shows a good agreement for the seasonal (KGE = 0.76) and monthly (KGE = 0.72) time scales, whereas a poor relation is seen for the annual time scale with an average KGE value of 0.21.
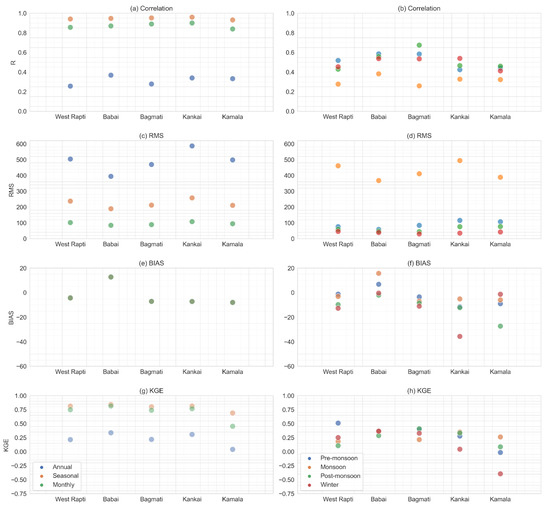
Figure 3.
Scatter plots of R, RMS, BIAS, and KGE for different time scales (a,c,e,g) and different seasons (b,d,f,h) for rainfall from CHIRPS versus rain gauge observations during 1986–2015.
Similarly, the performance evaluations of CHIRPS versus rain gauge observations through statistical metrics for the four seasons are shown in Figure 3 (right column). The rainfall estimate of monsoon from CHIRPS has the least agreement with rain gauge observations of rainfall amount with an average R-value of 0.31 (ranging from 0.26 to 0.38). The average R-values at pre-monsoon, post-monsoon, and winter seasons for all basins were 0.51 (ranging from 0.42 to 0.58), 0.52 (ranging from 0.43 to 0.67), and 0.49 (ranging from 0.41 to 0.54), respectively. The maximum RMSE appears in monsoon with an average value of 424.2 mm (ranging from 367.52 to 493.88 mm). When the rainfall increases, the RMSE value tends to be higher [56]. In comparison to the monsoon, CHIRPS has lower RMSE values in other seasons, with an average of 88.1 (ranging from 58.3 to 115.46 mm), 60.29 (ranging from 44.01 to 76.61 mm), and 38.17 mm (ranging from 29.83 to 45.55 mm), respectively. The average BIAS values for pre-monsoon, monsoon, post-monsoon, and winter are −3.71% (ranging from −8.98% to 6.75%), −1.07% (ranging from −6.98% to 15.67%), −11.93% (ranging from −27.31% to −2.02%), and −12.24% (ranging from −35.67% to −0.45%), respectively. Comparatively, the likely explanation for a BIAS value being higher in the winter season is because of the high number of cloudy days and no to very little rainfall during that period [57]. In addition, the value of KGE ranged from 0.25 to 0.45 in pre-monsoon, 0.14 to 0.30 in monsoon, 0.14 to 0.42 in post-monsoon, and 0.05 to 0.36 in winter seasons. The lower KGE score could be attributed to uncertainties in rain gauge-based estimates due to limited gauge density in the basins [58]).
We found that the RMS values of the non-monsoon periods were less than those of the monsoon period, whereas the R-values of the non-monsoon periods were higher than the monsoon period. These results indicate greater consistency between CHIRPS and rain gauge observations during non-monsoon periods. Prajapati et al. [49] observed similar findings in the Karnali River basin, where satellite-based rainfall products (including CHIRPS) showed better performance in dry seasons compared to wet seasons compared to the ground-based observations. The probable reason for better performance in the non-monsoon months might be less cloud cover, which helps increase the visibility of satellite sensors. Moreover, the results showed that CHIRPS could effectively capture the seasonal patterns of rainfall characteristics over the study area.
3.3. Spatial Distribution of Statistical Metrics
The annual and seasonal scale spatial distribution between CHIRPS satellite product and in situ rain gauge observation are presented in Figure 4, Figure 5, Figure 6 and Figure 7 for statistical metrics R, RMSE, percent bias, and KGE, respectively. Figure 4 displays the spatial variations of R over the five basins of Nepal. The CHIRPS data showed a better correlation for the northern part (Kathmandu Valley) of the Bagmati Basin. However, most rain gauges are concentrated on the northern side of the basin [59], so a spatial estimation of the entire basin is quite challenging. Further, weakly positive (negative) linear relationships were observed in all seasons in isolated parts. Further, the northern part of the Kamala basin has a comparatively good correlation in pre-monsoon, post-monsoon, and winter seasons compared to the south-eastern parts. In other basins, no significant spatial variability was observed.
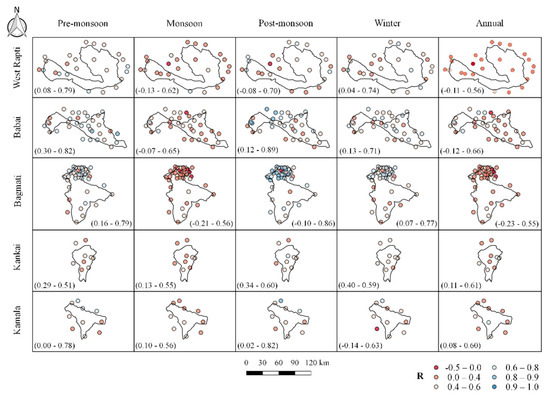
Figure 4.
Spatial distributions of R between the CHIRPS product and rain gauge observation at the seasonal and annual scales.
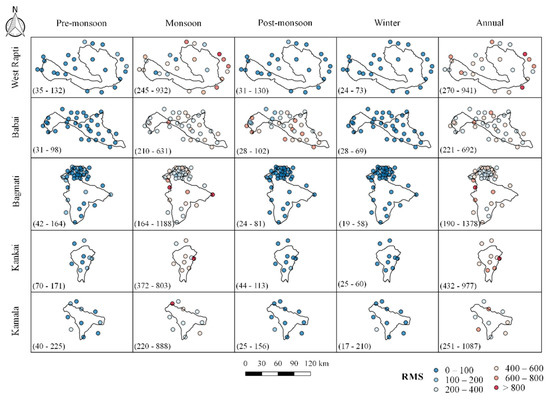
Figure 5.
Spatial distributions of RMS between the CHIRPS product and rain gauge observation at the seasonal and annual scales.
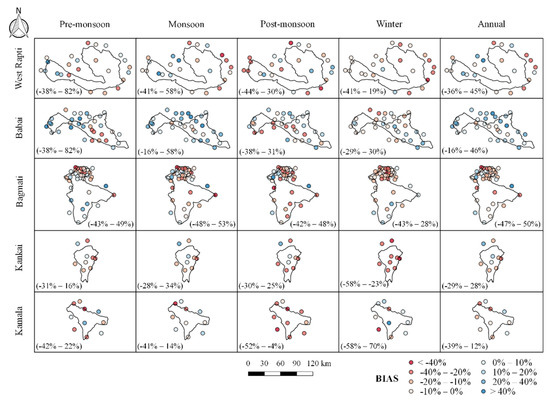
Figure 6.
Spatial distributions of BIAS between the CHIRPS product and rain gauge observation at the seasonal and annual scales.
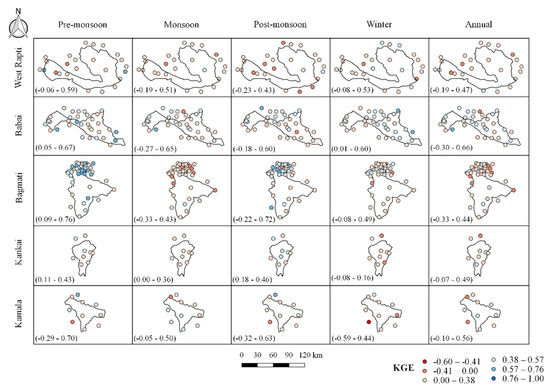
Figure 7.
Spatial distributions of KGE between the CHIRPS product and rain gauge observation at the seasonal and annual scales.
Figure 5 shows the spatial variations of RMSE. No significant trend in the spatial variation of RMSE was seen in all basins. A high RMSE value was seen in the north-eastern part (mainly) of the West Rapti River basin, mostly during the monsoon season. The probable reason can be explained by the fact that satellites are unable to measure extreme precipitation in these areas. In contrast, lower RMSE was obtained in other seasons, which could be related to the increased frequency of no rainfall recorded by both CHIRPS and ground-based observations [60]. In terms of PBIAS, a mix of over and underestimation (Figure 6) was observed in the study area. Among all basins, rain gauge observations of the Babai basin showed good agreement with CHIRPS data. The increase in PBIAS by around 20% could be attributable to the varied topography, which includes flat and elevated regions, resulting in a difference in the performance of satellites even over short distances. Moreover, a challenge that prevails is accurate satellite rainfall estimates over mountainous terrain due to the orographic effect [53]. Figure 7 shows the spatial distribution of KGE. The KGE value for the pre-monsoon period ranged from 0.09 to 0.76 (median = 0.44), 0.04 to 0.67 (median = 0.35), −0.29 to 0.70 (median = 0.25), 0.11 to 0.43 (median = 0.25), and −0.05 to 0.59 (median = 0.27) for Bagmati, Babai, Kamala, Kankai, and West Rapti, respectively. The negative KGE values indicate the poor performance of the satellite products in some stations. The lowest average KGE value was seen in the Kankai (0.05) and Kamala basins (0.09), both in the winter seasons, while the highest was seen in the Bagmati river basin (0.44) in the pre-monsoon season.
3.4. Distribution Pattern of Daily Rainfall
CHIRPS was also analyzed to evaluate the performance of different rain intensities on an annual scale. The amount and frequency (number of days) of rainfall contributed, in percentage (% of total annual rainfall), by various rainfall rate classes for both CHIRPS and rain gauge observations are shown in Figure 8 for all basins. Even though the average rainfall frequency of class ‘A’ for all basins was 55%, it contributed only 15% of total rainfall. Class ‘B’ contributed around 56% of total rainfall, although class ‘B’ frequency was about 39%. While class ‘C’ only had a frequency of around 5%, it contributed about 20% of total rainfall. Extreme rainfall events in classes ‘D’ and ‘E’ were infrequent (around 1%), contributing about 8% to total rainfall. Figure 8 demonstrates that half of all rainy days were class ‘A’ (light rain), contributing less than one-fifth of total rainfall. Around one-third of total rainfall was contributed by classes ‘B’ and ‘C’, whereas the frequency of these classes was about 45% of the total number of rainy days.
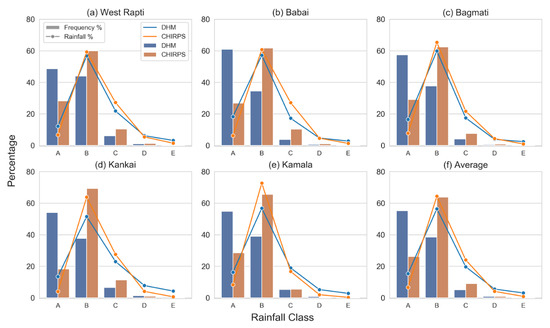
Figure 8.
Contribution of rainfall frequency (%) and cumulative rainfall (%) of CHIRPS and rain gauge observations (DHM) for various classes of rainfall rate at different basins, (a) West Rapti, (b) Babai, (c) Bagmati, (d) Kankai, (e) Kamala, and (f) Average. A description of different classes is shown in Table 2.
Both rainfall frequencies and amounts of class ‘A’ and class ‘E’ were underestimated by CHIRPS for all the basins. The average rainfall frequencies and amounts of class ‘A’ and class ‘E’ for rain gauge observations were more than double CHIRPS for all the basins. This shows that CHIRPS could not detect extreme rainfall events of greater than 150 mm per day and light rainfall events of less than 10 mm per day and determine the rainfall amount of those events. Moreover, CHIRPS should be avoided for drought monitoring as it underestimates rainfall frequency and amount of class ‘A’. The underestimation of class ‘A’ rainfall might be due to the sensors’ inability to track localized light rainfall as their spatial resolution is much smaller than the point locations of rain gauges [52]. CHIRPS overestimated both rainfall frequencies and amounts of class ‘B’ and ‘C’ in all the basins except the rainfall amount of class ‘C’ in the Kamala basin. This suggests that CHIRPS might be useful for monitoring the floods caused by high rainfall events with rainfall intensity of less than 100 mm per day. In the case of class ‘D’, CHIRPS underestimated the rainfall amount in all basins except Bagmati. The rainfall frequencies of class ‘D’ were overestimated by CHIRPS in all basins except Kamala and Kankai. In the case of rainfall frequency, there were high differences (greater than 25%) between the percentage contribution of CHIRPS and rain gauge for classes ‘A’ and ‘B’. In contrast, the differences were smaller (less than 4%) for other classes. Similarly, the percentage differences for rainfall amount were slightly higher (around 8%) for classes ‘A’ and ‘B’ compared to other classes (less than 5%). Smaller basins, i.e., Kankai and Kamala, had larger percentage differences for class ‘B’ rainfall amounts than other larger basins. The results indicated that CHIRPS was better at reporting the rainfall amounts than the occurrence of rainfall. This might be because the rainfall amount represents the cumulative sum of rainfall on an annual scale, and the frequency represents the number of rainy days [61]. In general, the performance of CHIRPS improves significantly with temporal aggregation [55].
Figure 9 shows the temporal distribution of dry days (DD) and maximum consecutive dry days (MCDD) in different basins for the study period (1986–2015). The average number of DD for CHIRPS and DHM rain gauge observations were 226 (ranging from 209 to 246) and 98 (ranging from 77 to 118), respectively. Similarly, the average numbers of MCDD for CHIRPS and DHM rain gauge observations were 34 (ranging from 25 to 54) and 22 (ranging from 16 to 33), respectively. The CHIRPS product overestimated DD and MCDD by around 130 % and 55 %, respectively. For the first fifteen years (1986–2000), the average number of DD was 110, which decreased by −23% to 85 during 2001–2015 for DHM rain gauge observations. In the case of CHIRPS products, it decreased by only −7% from 235 (1986–2000) to 218 (2001–2015). The number of MCDD was decreasing for DHM observations (−10%). In contrast, it increased for CHIRPS products (14%) in the second half of the study period compared to the first one. It is worth noting that there was a significant decrease in the number of DD in all the basins. The results concluded that CHIRPS products are not useful for estimating the number of rainy days.
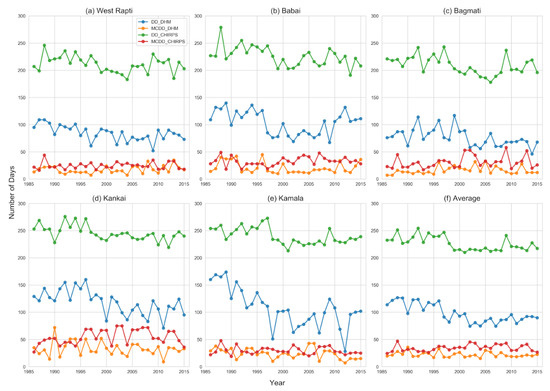
Figure 9.
Line plots of temporal distribution (1986–2015) of dry days of DHM (DD_DHM: blue), dry days of CHIRPS (DD_CHIRPS: green), maximum consecutive dry days of DHM (MCDD_DHM: orange), and maximum consecutive dry days of CHIRPS (MCDD_CHIRPS: red) for (a) West Rapti basin, (b) Babai basin, (c) Bagmati basin, (d) Kankai basin, (e) Kamala basin, and (f) Average of all five basins.
Our findings show the potential application of CHIRPS for monitoring the spatio-temporal rainfall variability in Nepal to fill the data gaps of ground-based rain gauge networks. Both ground-based rain gauge and satellite data have their limitations. Rain gauge data may have several drawbacks, such as missing data, mechanical and manual measurement errors, etc. In contrast, satellite data may have errors due to changes in orbit or detection devices, the presence of contaminants in the atmosphere, etc. [30]. Satellite data cannot supplant the rain gauge observations but rather supplement them, and the lack of long-term rain gauge observations poses significant challenges when validating data from satellite estimates [62,63]. Hence, the existing rain gauge network is still inadequate and should be expanded, considering the diverse topography. We should consider the results of the performance evaluation of satellite data through statistical metrics before its application. In general, satellite data with high R and low RMS are chosen. The underestimations of rainfall events and amounts are not preferred for flood predictions and hydrological studies, whereas the overestimations are less preferred for drought monitoring [47].
4. Conclusions
In this study, the rainfall estimates from a satellite product (CHIRPS) were compared and evaluated with ground-based observations (DHM) over five medium-sized basins—West Rapti, Babai, Bagmati, Kankai, and Kamala—from 1986 to 2015. Both continuous and categorical evaluation statistics were used to analyze the performance of CHIRPS at different time scales—monthly, seasonal, and annual. Notably lower POD values (<0.38) and CSI values (<0.36), significant false alarms, and underestimation of rainfall were observed in all basins. The categorical evaluation statistics suggest that the ability of the CHIRPS product to estimate rainfall is not reliable compared to in situ rain gauge observations, demanding certain adjustments/corrections in the CHIRPS datasets before its operational use.
The rainfall estimates of CHIRPS showed a better agreement with ground-based observations in terms of both R and KGE for seasonal (R = 0.95, KGE = 0.76) and monthly (R = 0.87, KGE = 0.72) time scales than for the annual time scale (R = 0.31, KGE = 0.21). CHIRPS underestimated the rainfall throughout the study area over all time scales, as the average BIAS value was −6.63%. A higher consistency was observed between the CHIRPS product and ground-based observations during the non-monsoon periods with greater R-values (0.41 to 0.67) and remarkably lower RMS values (29.83 to 115.46 mm). In summary, CHIRPS was found to effectively record the seasonal variation of rainfall in the study area.
In all basins, the average number and frequency of rainfall less than 10 mm (class A) and higher than 150 mm (class E) of the in situ observations were double CHIRPS observations, indicating the inability of CHIRPS to detect slight rainfall and severe rainfall events. Furthermore, the rainfall frequencies and amounts were underestimated by CHIRPS for class A and overestimated for rainfall events of 10 to 100 mm per day (class B and C). In general, CHIRPS can be used to monitor flooding events triggered by rainfall of less than 100 mm per day, whereas it is not appropriate to monitor drought scenarios.
This study concludes that the CHIRPS can serve as an alternative to monitor the spatio-temporal variation of rainfall, complement existing ground-based stations, and fulfill the existing data gaps. Our study can serve as a reference for CHIRPS users to evaluate the performance of CHIRPS regarding ground-based observations.
Author Contributions
Conceptualization, R.P. and R.T., methodology, R.P and R.T., formal analysis, S.U., P.S., S.D., and H.L. data curation, R.P., writing—original draft preparation, S.U. and P.S.; writing—review and editing, R.P., S.S., and R.T.; Supervision, R.P. and R.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
We would like to thank the Department of Hydrology and Meteorology (DHM), Nepal, for providing rainfall data. We would also like to thank John Gardner at the University of Pittsburgh, USA, for his valuable comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The Changing Character of Precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the Global Water Budget and Its Annual Cycle Using Observational and Model Data. J. Hydrometeorol. 2007, 8, 758–769. [Google Scholar] [CrossRef]
- Chen, F.; Li, X. Evaluation of IMERG and TRMM 3B43 Monthly Precipitation Products over Mainland China. Remote Sens. 2016, 8, 472. [Google Scholar] [CrossRef]
- Chen, S.; Hong, Y.; Cao, Q.; Gourley, J.J.; Kirstetter, P.-E.; Yong, B.; Tian, Y.; Zhang, Z.; Shen, Y.; Hu, J.; et al. Similarity and Difference of the Two Successive V6 and V7 TRMM Multisatellite Precipitation Analysis Performance over China. J. Geophys. Res. Atmos. 2013, 118, 13–060. [Google Scholar] [CrossRef]
- Habib, E.; Haile, A.T.; Tian, Y.; Joyce, R.J. Evaluation of the High-Resolution CMORPH Satellite Rainfall Product Using Dense Rain Gauge Observations and Radar-Based Estimates. J. Hydrometeorol. 2012, 13, 1784–1798. [Google Scholar] [CrossRef]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Hydrologic Evaluation of Satellite and Reanalysis Precipitation Datasets over a Mid-Latitude Basin. Atmos. Res. 2015, 164–165, 37–48. [Google Scholar] [CrossRef]
- Tang, L.; Tian, Y.; Yan, F.; Habib, E. An Improved Procedure for the Validation of Satellite-Based Precipitation Estimates. Atmos. Res. 2015, 163, 61–73. [Google Scholar] [CrossRef]
- Davids, J.C.; Devkota, N.; Pandey, A.; Prajapati, R.; Ertis, B.A.; Rutten, M.M.; Lyon, S.W.; Bogaard, T.A.; van de Giesen, N. Soda Bottle Science—Citizen Science Monsoon Precipitation Monitoring in Nepal. Front. Earth Sci. 2019, 7, 46. [Google Scholar] [CrossRef]
- Ayehu, G.T.; Tadesse, T.; Gessesse, B.; Dinku, T. Validation of New Satellite Rainfall Products over the Upper Blue Nile Basin, Ethiopia. Atmos. Meas. Tech. 2018, 11, 1921–1936. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Karki, R.; Parajuli, B. Intercomparison of Precipitation Measured between Automatic and Manual Precipitation Gauge in Nepal. Measurement 2017, 106, 264–273. [Google Scholar] [CrossRef]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, How Much of the Earth’s Surface Is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Sharma, S.; Khadka, N.; Hamal, K.; Karki, S.; Thapa, B.R. An Outlook on the Applicability of Satellite Precipitation Products for Monitoring Extreme Precipitation Events in Nepal Himalaya. Weather 2022, 64, 108–109. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Ghimire, G.R.; Sharma, S.; Dahal, P.; Panthi, J.; Baniya, R.; Pudashine, J.; Thapa, B.R.; Shakti, P.C.; Parajuli, B. Weather Radar in Nepal: Opportunities and Challenges in a Mountainous Region. Weather 2022, 77, 160–164. [Google Scholar] [CrossRef]
- Pan, X.; Li, X.; Yang, K.; He, J.; Zhang, Y.; Han, X. Comparison of Downscaled Precipitation Data over a Mountainous Watershed: A Case Study in the Heihe River Basin. J. Hydrometeorol. 2014, 15, 1560–1574. [Google Scholar] [CrossRef]
- Dumont, M.; Saadi, M.; Oudin, L.; Lachassagne, P.; Nugraha, B.; Fadillah, A.; Bonjour, J.-L.; Muhammad, A.; Hendarmawan; Dörfliger, N.; et al. Assessing Rainfall Global Products Reliability for Water Resource Management in a Tropical Volcanic Mountainous Catchment. J. Hydrol. Reg. Stud. 2022, 40, 101037. [Google Scholar] [CrossRef]
- Chua, Z.-W.; Kuleshov, Y.; Watkins, A.B.; Choy, S.; Sun, C. A Two-Step Approach to Blending GSMaP Satellite Rainfall Estimates with Gauge Observations over Australia. Remote Sens. 2022, 14, 1903. [Google Scholar] [CrossRef]
- Verdin, A.; Rajagopalan, B.; Kleiber, W.; Funk, C. A Bayesian Kriging Approach for Blending Satellite and Ground Precipitation Observations. Water Resour. Res. 2015, 51, 908–921. [Google Scholar] [CrossRef]
- Xie, P.; Xiong, A.-Y. A Conceptual Model for Constructing High-Resolution Gauge-Satellite Merged Precipitation Analyses. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Sun, Q.; Miao, C.; Duan, Q.; Ashouri, H.; Sorooshian, S.; Hsu, K. A Review of Global Precipitation Data Sets: Data Sources, Estimation, and Intercomparisons. Rev. Geophys. 2018, 56, 79–107. [Google Scholar] [CrossRef]
- Liu, Z. Comparison of Versions 6 and 7 3-Hourly TRMM Multi-Satellite Precipitation Analysis (TMPA) Research Products. Atmos. Res. 2015, 163, 91–101. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and Sampling Uncertainties: A Rain Gauge Perspective. J. Geophys. Res. 2008, 113, D11102. [Google Scholar] [CrossRef]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Comparison of PERSIANN and V7 TRMM Multi-Satellite Precipitation Analysis (TMPA) Products with Rain Gauge Data over Iran. Int. J. Remote Sens. 2013, 34, 8156–8171. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A Method That Produces Global Precipitation Estimates from Passive Microwave and Infrared Data at High Spatial and Temporal Resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Adler, R.F.; Kubota, T.; Ushio, T. Evaluation of GSMaP Precipitation Estimates over the Contiguous United States. J. Hydrometeorol. 2010, 11, 566–574. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; de Roo, A. MSWEP: 3-Hourly 0.25° Global Gridded Precipitation (1979–2015) by Merging Gauge, Satellite, and Reanalysis Data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.-S.; Nasrollahi, N.; Hsu, K.; Sorooshian, S. Evaluation of Satellite-Based Precipitation Estimation over Iran. J. Arid Environ. 2013, 97, 205–219. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of Satellite-Based Precipitation Products over Sparsely Gauged African River Basins. J. Hydrometeorol. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Akinyemi, D.F.; Ayanlade, O.S.; Nwaezeigwe, J.O.; Ayanlade, A. A Comparison of the Accuracy of Multi-Satellite Precipitation Estimation and Ground Meteorological Records Over Southwestern Nigeria. Remote Sens. Earth Syst. Sci. 2020, 3, 1–12. [Google Scholar] [CrossRef]
- Subba, S.; Ma, Y.; Ma, W. Spatial and Temporal Analysis of Precipitation Extremities of Eastern Nepal in the Last Two Decades (1997–2016). J. Geophys. Res. Atmos. 2019, 124, 7523–7539. [Google Scholar] [CrossRef]
- Sunilkumar, K.; Yatagai, A.; Masuda, M. Preliminary Evaluation of GPM-IMERG Rainfall Estimates Over Three Distinct Climate Zones With APHRODITE. Earth Sp. Sci. 2019, 6, 1321–1335. [Google Scholar] [CrossRef]
- Sharma, S.; Khadka, N.; Hamal, K.; Shrestha, D.; Talchabhadel, R.; Chen, Y. How Accurately Can Satellite Products (TMPA and IMERG) Detect Precipitation Patterns, Extremities, and Drought Across the Nepalese Himalaya? Earth Sp. Sci. 2020, 7, e2020EA001315. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Aryal, A.; Kawaike, K.; Yamanoi, K.; Nakagawa, H.; Bhatta, B.; Karki, S.; Thapa, B.R. Evaluation of Precipitation Elasticity Using Precipitation Data from Ground and Satellite-Based Estimates and Watershed Modeling in Western Nepal. J. Hydrol. Reg. Stud. 2021, 33, 100768. [Google Scholar] [CrossRef]
- Duncan, J.M.A.; Biggs, E.M. Assessing the Accuracy and Applied Use of Satellite-Derived Precipitation Estimates over Nepal. Appl. Geogr. 2012, 34, 626–638. [Google Scholar] [CrossRef]
- Krakauer, N.Y.; Pradhanang, S.M.; Lakhankar, T.; Jha, A.K. Evaluating Satellite Products for Precipitation Estimation in Mountain Regions: A Case Study for Nepal. Remote Sens. 2013, 5, 4107–4123. [Google Scholar] [CrossRef]
- Harrison, L.; Landsfeld, M.; Husak, G.; Davenport, F.; Shukla, S.; Turner, W.; Peterson, P.; Funk, C. Advancing Early Warning Capabilities with CHIRPS-Compatible NCEP GEFS Precipitation Forecasts. Sci. Data 2022, 9, 375. [Google Scholar] [CrossRef]
- Gummadi, S.; Dinku, T.; Shirsath, P.B.; Kadiyala, M.D.M. Evaluation of Multiple Satellite Precipitation Products for Rainfed Maize Production Systems over Vietnam. Sci. Rep. 2022, 12, 485. [Google Scholar] [CrossRef]
- Shrestha, N.K.; Qamer, F.M.; Pedreros, D.; Murthy, M.S.R.; Wahid, S.M.; Shrestha, M. Evaluating the Accuracy of Climate Hazard Group (CHG) Satellite Rainfall Estimates for Precipitation Based Drought Monitoring in Koshi Basin, Nepal. J. Hydrol. Reg. Stud. 2017, 13, 138–151. [Google Scholar] [CrossRef]
- Khatakho, R.; Talchabhadel, R.; Thapa, B.R. Evaluation of Different Precipitation Inputs on Streamflow Simulation in Himalayan River Basin. J. Hydrol. 2021, 599, 126390. [Google Scholar] [CrossRef]
- Lamichhane, S.; Aryal, K.R.; Talchabhadel, R.; Thapa, B.R.; Adhikari, R.; Khanal, A.; Pandey, V.P.; Gautam, D. Assessing the Prospects of Transboundary Multihazard Dynamics: The Case of Bhotekoshi–Sunkoshi Watershed in Sino–Nepal Border Region. Sustainability 2021, 13, 3670. [Google Scholar] [CrossRef]
- Prajapati, R.; Upadhyay, S.; Talchabhadel, R.; Thapa, B.R.; Ertis, B.; Silwal, P.; Davids, J.C. Investigating the Nexus of Groundwater Levels, Rainfall and Land-Use in the Kathmandu Valley, Nepal. Groundw. Sustain. Dev. 2021, 14, 100584. [Google Scholar] [CrossRef]
- Pandey, V.P.; Manandhar, S.; Kazama, F. Water Poverty Situation of Medium-Sized River Basins in Nepal. Water Resour. Manag. 2012, 26, 2475–2489. [Google Scholar] [CrossRef]
- Mishra, Y.; Babel, M.S.; Nakamura, T.; Mishra, B. Impacts of Climate Change on Irrigation Water Management in the Babai River Basin, Nepal. Hydrology 2021, 8, 85. [Google Scholar] [CrossRef]
- Bastola, S.; Lee, S.; Shin, Y.; Jung, Y. An Assessment of Environmental Impacts on the Ecosystem Services: Study on the Bagmati Basin of Nepal. Sustainability 2020, 12, 8186. [Google Scholar] [CrossRef]
- Silwal, C.B.; Pathak, D.; Adhikari, D.; Adhikari, T.R. Climate Change and Its Possible Impact in Groundwater Resource of the Kankai River Basin, East Nepal Himalaya. Climate 2020, 8, 137. [Google Scholar] [CrossRef]
- Dembélé, M.; Zwart, S.J. Evaluation and Comparison of Satellite-Based Rainfall Products in Burkina Faso, West Africa. Int. J. Remote Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef]
- Monsieurs, E.; Kirschbaum, D.B.; Tan, J.; Maki Mateso, J.-C.; Jacobs, L.; Plisnier, P.-D.; Thiery, W.; Umutoni, A.; Musoni, D.; Bibentyo, T.M.; et al. Evaluating TMPA Rainfall over the Sparsely Gauged East African Rift. J. Hydrometeorol. 2018, 19, 1507–1528. [Google Scholar] [CrossRef]
- Prajapati, R.; Silwal, P.; Duwal, S.; Shrestha, S.; Kafle, A.S.; Talchabhadel, R.; Kumar, S. Detectability of Rainfall Characteristics over a Mountain River Basin in the Himalayan Region from 2000 to 2015 Using Ground- and Satellite-Based Products. Theor. Appl. Climatol. 2021, 147, 185–204. [Google Scholar] [CrossRef]
- Tan, X.; Ma, Z.; He, K.; Han, X.; Ji, Q.; He, Y. Evaluations on Gridded Precipitation Products Spanning More than Half a Century over the Tibetan Plateau and Its Surroundings. J. Hydrol. 2020, 582, 124455. [Google Scholar] [CrossRef]
- Paredes-Trejo, F.J.; Barbosa, H.A.; Lakshmi Kumar, T.V. Validating CHIRPS-Based Satellite Precipitation Estimates in Northeast Brazil. J. Arid Environ. 2017, 139, 26–40. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; van der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of Satellite Rainfall Estimates for Drought and Flood Monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Dinku, T.; Ceccato, P.; Connor, S.J. Challenges of Satellite Rainfall Estimation over Mountainous and Arid Parts of East Africa. Int. J. Remote Sens. 2011, 32, 5965–5979. [Google Scholar] [CrossRef]
- Mu, Y.; Biggs, T.; Shen, S.S.P. Satellite-Based Precipitation Estimates Using a Dense Rain Gauge Network over the Southwestern Brazilian Amazon: Implication for Identifying Trends in Dry Season Rainfall. Atmos. Res. 2021, 261, 105741. [Google Scholar] [CrossRef]
- Mastrantonas, N.; Bhattacharya, B.; Shibuo, Y.; Rasmy, M.; Espinoza-Dávalos, G.; Solomatine, D. Evaluating the Benefits of Merging Near-Real-Time Satellite Precipitation Products: A Case Study in the Kinu Basin Region, Japan. J. Hydrometeorol. 2019, 20, 1213–1233. [Google Scholar] [CrossRef]
- Mitra, A.K.; Iyengar, G.R.; Durai, V.R.; Sanjay, J.; Krishnamurti, T.N.; Mishra, A.; Sikka, D.R. Experimental Real-Time Multi-Model Ensemble (MME) Prediction of Rainfall during Monsoon 2008: Large-Scale Medium-Range Aspects. J. Earth Syst. Sci. 2011, 120, 27–52. [Google Scholar] [CrossRef]
- Saeidizand, R.; Sabetghadam, S.; Tarnavsky, E.; Pierleoni, A. Evaluation of CHIRPS Rainfall Estimates over Iran. Q. J. R. Meteorol. Soc. 2018, 144, 282–291. [Google Scholar] [CrossRef]
- Prakash, S. Performance Assessment of CHIRPS, MSWEP, SM2RAIN-CCI, and TMPA Precipitation Products across India. J. Hydrol. 2019, 571, 50–59. [Google Scholar] [CrossRef]
- Prajapati, R.; Talchabhadel, R.; Silwal, P.; Upadhyay, S.; Ertis, B.; Thapa, B.R.; Davids, J.C. Less Rain and Rainy Days—Lessons from 45 Years of Rainfall Data (1971–2015) in the Kathmandu Valley, Nepal. Theor. Appl. Climatol. 2021, 145, 1369–1383. [Google Scholar] [CrossRef]
- Miri, M.; Masoudi, R.; Raziei, T. Performance Evaluation of Three Satellites-Based Precipitation Data Sets Over Iran. J. Indian Soc. Remote Sens. 2019, 47, 2073–2084. [Google Scholar] [CrossRef]
- Nandargi, S.; Mulye, S.S. Relationships between Rainy Days, Mean Daily Intensity, and Seasonal Rainfall over the Koyna Catchment during 1961. Sci. World J. 2012, 2012, 894313. [Google Scholar] [CrossRef] [PubMed]
- Aliyar, Q.; Dhungana, S.; Shrestha, S. Spatio-Temporal Trend Mapping of Precipitation and Its Extremes across Afghanistan (1951–2010). Theor. Appl. Climatol. 2022, 147, 605–626. [Google Scholar] [CrossRef]
- Muthoni, F.K.; Odongo, V.O.; Ochieng, J.; Mugalavai, E.M.; Mourice, S.K.; Hoesche-Zeledon, I.; Mwila, M.; Bekunda, M. Long-Term Spatial-Temporal Trends and Variability of Rainfall over Eastern and Southern Africa. Theor. Appl. Climatol. 2019, 137, 1869–1882. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).