Abstract
The presence of dust on the snowpack accelerates snowmelt. This has been observed through snowpack and hydrometeorological measurements at a small study watershed in southwestern Colorado. For a 13-year period, we quantified the annual dust-enhanced energy absorption (DEAE) and used this information to model the snowpack melt-out under observed (with dust present) and clean conditions (no dust). We determine the difference in snow cover duration between actual (dust present) and simulated ideal (clean) snowpack (ΔSAG) to characterize the shifts in melt timing for each year. We compute the center of mass of runoff (tQ50) as a characteristic of snowmelt. DEAE, ΔSAG and tQ50 vary from year to year, and are dictated by the quantity of snow accumulation, and to a lesser extent the number of dust events, the annual dust loading, and springtime snowfall.
1. Introduction
Shortwave radiation provides most of the energy for melt in continental mountain snowpacks [1,2]. Deposition of light absorbing particulates (LAPs), such as dust, ash, black carbon, needles and tree litter, onto the snowpack reduces its albedo (reflectance as measured by the ratio of incoming vs. reflected shortwave radiation) and alters the snowpack energy balance [2,3,4,5,6,7,8,9,10,11,12]. Airborne dust from deserts deposited on a Colorado snowpack [13] have been shown to reduce the surface albedo [14], especially in the visible portion of the shortwave radiation spectrum (Figure 1). This reduction in albedo accelerated the timing of snowmelt by 18 to 51 days [2,15]. Across much of the Upper Colorado River Basin (UCRB), the transport of aeolian dust is a regular occurrence [16,17], particularly onto the snowpack [18,19,20]. Thus, streamflow forecasting in the UCRB benefits from incorporating albedo reduction resulting from aeolian dust deposition.
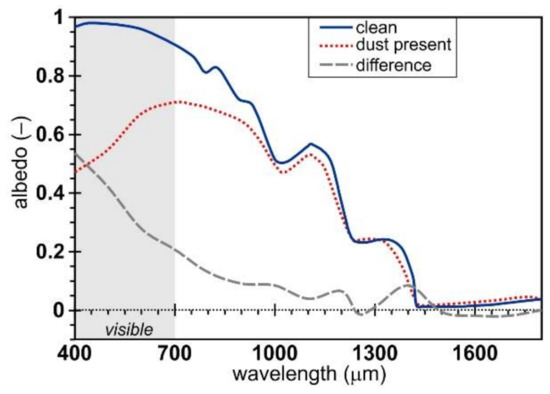
Figure 1.
Clean vs. dust present albedo and the difference between the two albedos for modeled clean snow and measured snow, as a function of wavelength with a dust concentration of 0.37 mg/g (data from Painter et al. [21]).
Current National Weather Service (NWS) Upper Colorado River Basin streamflow forecasting is based on a coupled temperature-index snowmelt model (SNOW-17) [22] and soil moisture model (Sac-SMA) [23]. Temperature-index models have a limited ability to account for the radiation components of continental mountain snowpack energy balance [24,25]. The combination of dust loading with variations in magnitude of snow water equivalent (SWE) and meteorological factors each season modifies snowpack energy balance and introduces variations in melt timing [13,26]. These variations may cause considerable uncertainty in operational streamflow forecasting [27]. Changes in the timing of snowmelt will alter streamflow characteristics [28], particularly with the interplay of a changing climate [29,30,31]. Here, we present patterns of dust loading and snowpack energy absorption over 13 years to better characterize the magnitude of dust influence on snowmelt timing.
Understanding how snow accumulation amounts [32,33] and snowmelt rates [34] influence streamflow timing is important for hydrologists for runoff forecasting [35,36]. Various metrics have been used to simplify the assessment of runoff timing. The simplest being the center of mass of runoff for a water year (WY, from 1 October to 30 September in the U.S.), which is the date when 50% of the annual runoff volume (tQ50) has passed the gauge [37,38]. For snow dominated systems, tQ50 is used to represent the peak of a snowmelt input into a stream [33,39,40], and tQ20 has been used to show the beginning of snowmelt [38].
We determine the patterns of additional snowpack energy absorption and snow melt acceleration due to dust over 13 years (2007 to 2019) at a small study basin in the San Juan Mountains. The specific objectives of this paper are as follows: (1) compare the shortwave radiation, snowpack, and runoff characteristics for a light (2015) and heavy (2009) dust year; (2) quantify dust-enhanced absorbed energy (DEAE) for each year; (3) determine the difference in snow cover duration between the actual (dust present) and simulated ideal (clean) snowpack to characterize the shifts in melt timing for each year; (4) determine the timing of subsequent snowmelt streamflow in terms of the occurrence of the center of mass of the runoff; and (5) assess potential drivers of interannual patterns in snow melt acceleration and runoff characteristics due to dust loading, snowpack characteristics, and meteorology. The term DEAE is used here to define the additional shortwave radiation added, rather than the term radiative forcing or RF used by Skiles et al. [15], as the authors feel that RF implies all shortwave radiation, regardless of the presence of dust or not. The snow cover duration in objective 3 is assessed using the date of complete snowmelt, or snow-all-gone (SAG).
2. Study Site and Datasets
2.1. Study Basin and Automated Data
We examined dust and snowpack characteristics over 13 WYs from 2007 through 2019 at a study site in the San Juan Mountains of southwestern Colorado. Senator Beck Study Basin (SBB) is a 2.91 km2 continental high-elevation (3362 to 4118 m) research watershed that sits at the headwaters of the Uncompahgre River [41] in the UCRB (Figure 2). Two micrometeorological towers measure data including radiation fluxes and energy balance summarized in 1-h, 3-h, and 24-h arrays, with a period of record from 2005 to present. The towers are located at 3371 m (Swamp Angel Study Plot, SASP) and 3714 m (Senator Beck Study Plot, SBSP) representing the two principal terrains of the study basin (subalpine forest and alpine tundra, respectively) [41]. Manual snow profile assessments are collected at both sites approximately weekly during ablation within an undisturbed study plot directly alongside each automated tower, and those measurements are archived by the Center for Snow and Avalanche Studies (CSAS) <https://www.snowstudies.org> (accessed 20 December 2021).
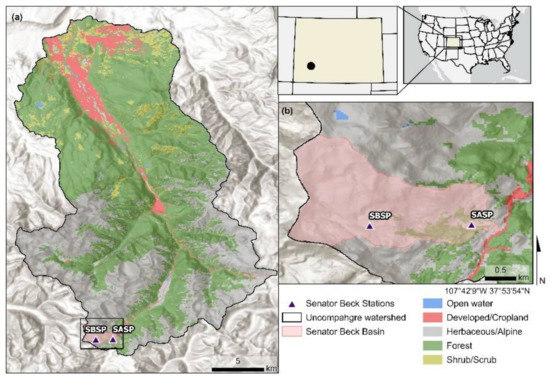
Figure 2.
Location map of (a) the Uncompahgre River at Ouray and (b) Senator Beck Basin within the state of Colorado (middle-upper inset with the study basins identified by the black dot), within the U.S. (right-upper inset). The locations of SBSP and SASP are illustrated within SBB in (b). The 10-m digital elevation model was obtained from the National Elevation Dataset via the USDA-NRCS Geospatial Data Gateway (https://datagateway.nrcs.usda.gov/, accessed on 1 March 2021) and the land cover data are the 2016 National Land Cover Database (https://www.mrlc.gov/, accessed on 1 March 2021).
2.2. Snowpack Development and Dust Timing
Peak SWE for WY2007 to 2019, estimated using snow depth from CSAS and snowpack density from the nearby snow telemetry (SNOTEL) station, ranged from 543 mm (WY2018) to 936 mm (WY2011) with an average peak SWE of 719 mm (Figure 3a). The average date of peak SWE for the period was 13 April, with earliest peak SWE occurring on 18 March in WY2012 and latest peak SWE on 1 May in both WY2011 and WY2019 (Figure 3a). Date of peak SWE for each individual WY is the defining threshold to characterize precipitation quantities (Figure 3b) and dust events (Figure 3c) as pre- or post-peak SWE. The timing of dust deposition during snowpack development is connected to potential dust-enhanced energy absorption, as the nominal depth of shortwave radiation penetration into the snowpack is around 30 cm [21]. Later-season dust events can remain closer to the snow surface and have an earlier effect on snow albedo [2,21]. The timing and magnitude of snowfall events is directly connected to snowmelt timing and magnitude, which are influenced by the presence of dust at the study site [14,20,26,27,42].
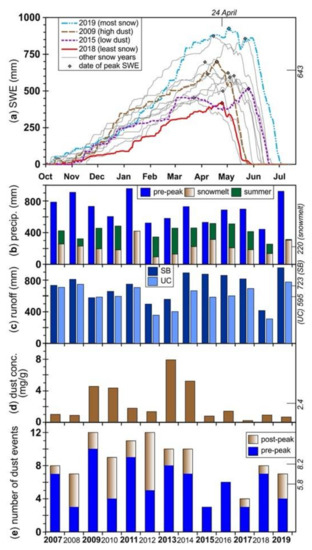
Figure 3.
Snow and related data from WY2007 to WY2019 illustrating (a) daily SWE from Red Mountain Pass SNOTEL highlighting WY2019 as the maximum peak SWE, WY2009 as a high dust year, WY2015 as a low dust year, and WY2018 as the minimum peak SWE for the period of record (other years are in grey), (b) annual total precipitation at SASP divided as pre-peak SWE, and post-peak SWE divided into during and after (summer) snowmelt, (c) the annual runoff volume at SBB and the Uncompahgre River (UC), (d) the year-end dust concentrations, and (e) the number of dust events recorded at SASP observed pre- and post-peak SWE. The mean for each time series is noted on the top or right vertical axis.
2.3. CSAS Snow Stake Data
Snow accumulation, wind redistribution, and heterogeneous snowmelt can change the gradient of the snow surface around the towers [21]. Therefore, assuming a level snow surface and calculating snow albedo with uncorrected visible incoming shortwave radiation (HK-IN, called irradiance by Painter et al. [21]) can be erroneous. To estimate the local slope and aspect of the changing snow surface, CSAS staff manually recorded snow depths from the snow stake arrays at both SASP and SBSP from WY2006 to WY2012. The SASP site had four stakes arranged around the central tower whereas the SBSP had six stakes due to greater snow surface variability from stronger wind redistribution [21]. We determined the plane of best fit to these snow depth arrays to use in combination with seasonal solar position to correct albedo incident angle.
2.4. CSAS Snow Pit Data
In addition to the automated continuous micrometeorological tower data, CSAS staff collect approximately weekly manual measurements of snow profile characteristics at both sites. These profile assessments consist of excavating a snow pit to the ground and collecting a temperature profile, describing snowpack stratigraphy (including layer interval, grain shape and size) and liquid water content, and measuring bulk SWE using methods described in Elder et al. [43] (also see [41]). Bulk snow density is calculated from the depth and SWE measurements. If dust layers are present, dust stratigraphy (depth, number of layers) is measured, and dust characteristics (approximate grain size, color) are recorded (see [41]). CSAS assigns numbers to each perceptible dust layer within the snowpack to allow tracking throughout accumulation and ablation. Bulk dust samples (all layers merged or ALM) are collected towards the end of each snow season.
2.5. SNOTEL Site and Data
Daily SWE and snow depth data were retrieved from the Red Mountain Pass (RMP) SNOTEL station from the Natural Resources Conservation Service (NRCS) <https://www.nrcs.usda.gov> (accessed 20 January 2022). RMP is located approximately 1.8 km SSW of the study basin at 3413 m elevation in a forested clearing with a western aspect. Bulk snow density was calculated at RMP and used to derive daily SWE at SASP from the measured depth, as density is less spatially variable than SWE or snow depth [44,45,46].
2.6. Streamflow Data
Water level is gauged hourly at a broad-crested weir at the outlet of SBB, starting prior to onset of snowmelt input and late into the fall [41]. These water level data are converted into hourly streamflow using a rating curve based on field measurements of streamflow and concurrent water level measurements <https://www.snowstudies.org> (accessed 20 December 2021). Here, mean daily streamflow data were used. A similar method is used by the U.S. Geological Survey (USGS) to compute streamflow on the 199 km2 Uncompahgre River at Ouray station (USGS number 09146020) (Figure 2a). This station was used instead of the downstream Uncompahgre River at Ridgway (station number 09146200) since the former (at Ouray) is entirely within the persistent seasonal snow zone [26,47]. Data were obtained from the USGS National Water Information System <https://nwis.waterdata.usgs.gov/nwis> (accessed 25 January 2022).
3. Methods
3.1. Albedo Correction
Calculating snow albedo with uncorrected radiation flux measurements assumes a level snow surface, which can be erroneous given wind redistribution, snow accumulation patterns, and heterogenous snowmelt [21]. We retrieved the slope and aspect of the snow surface from snow stake array observations (Figure A1). Such data were available from 2007 to 2012; since they were not available from 2013 to 2019, approximation from the first time period were applied to the second time period (Appendix A; Figure A2). The time series of slope and aspect was linearly interpolated between each weekly set of measurements to approximate a daily snow surface [21]. In addition to the geometric correction of a non-level snow surface, we corrected for seasonally shifting solar position (see Appendix A). Of the two sites, the alpine site (SBSP) has a more continuous record of incoming shortwave radiation (HK-in) since it experiences higher wind speeds which regularly clear the snow off the up-facing pyranometers [41]. When HK-in data from the sub-alpine site (SASP) were not available, they were estimated as the ratio of the outgoing shortwave radiation (HK-out) at SASP to the albedo of the alpine site (αalpine) [15].
3.2. Dust Concentration
Total dust concentrations were determined from the ALM samples collected towards the end of each ablation season. Bulk samples were processed by the U.S. Geological Survey of Colorado to yield dust loading and geochemical properties [48]. Dust loading (in mg/g) was transformed to end-of-year dust concentration using the 3 cm × 0.5 m2 sample volume [2] and the bulk snow density observed on the collection date.
Dust detection is accomplished by tracking the weather forecast for wind or storm events that may be conducive to dust mobilization in the source regions (see https://www.codos.org, accessed on 1 March 2022). During these events, the Colorado dust-on-snow (CODOS) program views camera images located in these areas for the presence of dust. These cameras are operated by the department of transportation in their respective states (Colorado, Utah, Arizona and New Mexico). As well, the USGS’s dust detection camera network that has six cameras deployed in identified dust producing areas of the southwest U.S. (https://gec.cr.usgs.gov/dustdetection/, accessed on 1 March 2022). Concurrently, satellite imagery products that are designed to detect airborne dust are inspected by CODOS for mobilization and spatial extent of a dust event. Another valuable tool are observations from citizen scientists communicating with CODOS via email or social media.
3.3. Absorbed Energy Calculations
There is an interaction with the acceleration of grain growth and the earlier exposure of darker substrate [49], but the greater divergence of LAP-influenced snow surface albedo from that of clean snow occurs within the visible spectrum [50] (Figure 1). Thus, we calculated the DEAE based on snow surface albedo within visible wavelengths. The visible DEAE (DEAEVIS in W/m2) at the surface was calculated as the product of the incoming shortwave radiation in the visible portion of the spectrum (HK-in-VIS) and the difference between broadband HK-in and NIR/SWIR HK-in (ΔVIS) [15]. This difference (ΔVIS) was computed from the observed visible albedo for dust-free or clean snow (αVIS-clean) at the study site (assigned a value of 0.92 by Skiles et al. [15]) minus the visible albedo estimated from tower measurements (αVIS-measured). This study also used an αVIS-clean of 0.92 for fresh snow.
Previous studies also calculated the additional NIR/SWIR energy absorption due to dust based on an empirical relation to grain coarsening in the absence of dust developed with two years of dust and snow observations in the study basin [2]. The total energy absorbed from the combined direct visible effect and indirect NIR/SWIR effect was identified as dust radiative forcing [2,15,20]. Daily mean visible DEAE is calculated from 1 April to help estimate the SAG for each year, and springtime incoming shortwave radiation and precipitation are totaled over the same interval. While dust-enhanced energy absorption may begin earlier in the season, this period captures typical snowpack ablation from peak SWE to complete melt-out when DEAE has the greatest effect on melt timing.
3.4. Snow Energy Balance Model
We used the point-based snow energy balance SNOBAL to model hypothetical snowpack at the sub-alpine site under actual hourly conditions (dust present) and snowpack with the dust effect removed (clean) to understand differences in melt timing, since this is the same model previously used at this site by Skiles et al. [15]. SNOBAL approximates the snowpack as two layers: the upper 25 cm layer exchanges energy with the atmosphere, and the underlying remainder of the snowpack acts as an energy and mass storage layer [51,52]. We ran the model for each spring melt season at the sub-alpine site using data from manual snow assessments and automated tower collection. The starting snow conditions of each model run were determined from the field measurements collected closest in time to 13 April (average date of peak SWE for the study plot). The model calculated hourly changes in snow state variables using observed hourly forcing variables (Table A1) and precipitation inputs. Dust present model runs were completed with actual recorded conditions. Clean model runs modified the hourly net shortwave radiation inputs by subtracting the DEAE on an hourly time step. For all runs, total precipitation mass recorded by an electronic weighing gauge at the sub-alpine site was partitioned into rain or snow based on dewpoint temperature, as defined by Susong et al. [53] in SNOBAL [52] (Table A2).
Percentage of precipitation falling as snow and fresh snow density were assigned based on specific quantities (Table A2). All model runs set soil temperature to 0°C since soil temperatures are generally ~0 °C at time of peak snow accumulation and are considered to have a relatively negligible contribution to snowpack energy balance [51]. Snow surface aerodynamic roughness (z0) was set to 0.001 m [54] for all model runs based on the determination of Skiles et al. [15] who found the model results not highly sensitive to reasonable z0 values (<0.005 m).
The accuracy of modeled SWE was assessed by comparing dust present SWE to two observations of SWE: derived and manually measured. Derived SWE is a combination of the calculated daily bulk snow density at Red Mountain Pass SNOTEL and the observed daily snow depth at the study site. The manual measurements of SWE were collected on an approximately weekly basis by CSAS staff during snow pit assessments. The difference in melt-out dates (ΔSAG) between the modeled dust present scenario and the modeled clean scenario is a measure of melt acceleration due to amount of DEAE, since the two scenarios are otherwise modeled with identical snow state variables and meteorological inputs.
3.5. Timing of Snowmelt Runoff
While the tQ50 is often computed based on the entire WY [33,34,39,40,55], others have examined a shorter time period since fall and winter streamflow often varies much less than the snowmelt contribution [32]; Bryant et al. [27] used the period from 1 January to 30 September while Dudley et al. [56] used 1 January to 31 July. Here, we computed tQ50 for 1 January to 30 September to compare results to Bryant et al. [27].
At Senator Beck Basin, streamflow gauging begins in March, prior to the onset of melt observed at the SNOTEL station (Figure 3a) when baseflow is the only contribution to streamflow. The exception was 2019 when streamflow monitoring started after the onset of melt, due to the large amount of snow as illustrated in Figure 3a [57]. The median baseflow is 0.0022 m3/s (0.066 mm/d) at the start of stream gauging (this is less than 0.5% of the median peak flow at SBB 0.48 m3/s). The ungauged portion of the hydrograph (i.e., before gauging begins in March) at SBB was estimated from the Uncompahgre River at Ouray time series using a quadratic fit (R2 = 0.80); the minimum daily flow was set to 0.002 mm/d, as streamflow has been observed over the entire year [57].
3.6. Drivers of Dust Present vs. the Clean Snow Energy Balance Model
As summarized above, SNOBAL requires much data preparation. Thus, to consider using DEAE or ΔSAG as decision variables for operational streamflow forecasting models, we assessed their potential drivers. Six variables were individually compared to DEAE and ΔSAG: the concentration of dust (measured in mg/g), the number of dust events (as a count), the cumulative incoming shortwave radiation from 1 April to SAG (in MJ/m2), the total precipitation from April 1st to SAG (in mm), the 1 April SWE (in mm), and the percentage of the dust events that occurred after peak SWE. For each of these evaluations, outlier years were identified and assessed as to why they were outliers based on dust, snowpack and meteorology of that year. The cross-correlation between the variables was computed to evaluate any redundancy among variables. A multi-variate linear regression was used due to the limited number of study years (e.g., Fassnacht et al. [58]) compared to other methods where more data are available [59]. Variables were standardized by dividing each annual value by the largest observed quantity in the 13-year time series. Using the linear regression approach, the magnitude of coefficient will represent the relative importance of each variable.
4. Results
4.1. Light and Heavy Dust Years
Over the 13 study years, peak SWE, precipitation quantities, number of dust events, and the cumulative concentration of dust varied (Figure 3; Table A3). Two years were chosen to illustrate the inter-annual differences from 1 April through to 31 May (Figure 4): WY2015 had low dust deposition (0.79 mg/g) and the shortest ΔSAG (11 days) and WY2009 had the most dust deposition (4.55 mg/g) and a long ΔSAG (31 days) (Figure 3). While WY2015 had less than the 13-year average peak SWE, peak SWE occurred the latest due to snow accumulation in May (Figure 3a and Figure 4b). Conversely peak SWE in WY2009 was larger than average (Figure 3a) but melt-out occurred much more rapidly than other years (Figure 3a and Figure 4d). The mean daily incoming shortwave radiation was similar for both focus years (dotted orange lines in Figure 4a vs. Figure 4c), but the DEAE was much greater in 2009 (1 April to SAG mean of 46.9 W/m2, Figure 4c) than 2015 (1 April to 31 May at a mean of 25.5 W/m2, Figure 4a). In 2015, there were only three dust deposition events (in April) and they were buried by numerous snowfalls (Figure 4a,b). There were ten dust deposition events in 2009, prior to peak SWE, and then two more once the melt began (Figure 4c). The presence of dust in 2009 yielded a lower albedo (mean of 0.42 in the visible from 1 April to SAG) than in 2015 (mean of 0.52 in the visible over the same period) (Figure 4c vs. Figure 4a). Further, once the snowpack is fully melting, i.e., SWE is continuously decreasing, the melt rate in 2009 (mean of 39.1 mm/d) is almost twice that of 2015 (mean of 23.8 mm/d); even when the increase in SWE on 7 June 2015 is disregarded, the mean melt is 26.2 mm/d.
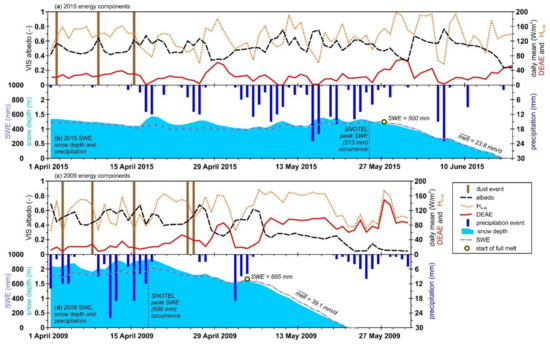
Figure 4.
Summary of April through SAG illustrating (a,c) snow surface albedo (black dashed), daily mean DEAE (red), incoming shortwave radiation in the visible portion of the spectrum (orange dotted), and the occurrence of dust events (brown lines), and (b,d) snow depth (solid blue), daily precipitation inputs (blue vertical bars), and estimated SWE (dash-dot blue). The date and amount (in parentheses) of peak SWE at the nearby SNOTEL station is shown with a fine black dashed line. The date when the snowpack begins to melt consistently is denoted by a yellow circle and the estimated SWE at that time is stated. The average melt per day from that point to SAG is stated as . (a,b) represent WY2015 with the shortest ΔSAG (11 days), the fewest dust events (3) and a low end-of-year dust concentration (0.79 mg/g); (c,d) represent WY2009 with the longest ΔSAG (31 days), the most dust events (12), and a high end-of-year dust concentration (4.55 mg/g).
4.2. Daily Mean Visible DEAE
For WY2007 to WY2019, the daily mean visible DEAE was 39.8 W/m2 during ablation and ranged from 31 W/m2 (WY2015) to 50 W/m2 (WY2019) (Figure 5a; Table A3). The large DEAE in WY2019 corresponds to a high peak SWE (Figure 3a) and a long period of snowmelt that occurred later (Figure 5b). Although melt started later in WY2015 due to late season snowfall (Figure 4b), peak SWE was low (Figure 3a) and the melt period was the shortest (Figure 5b) yielding the lowest DEAE; the last dust event in 2015 occurred 42 days prior to peak SWE (Figure 4a) and the total dust concentration was the lowest over the period of record (Figure 3c).
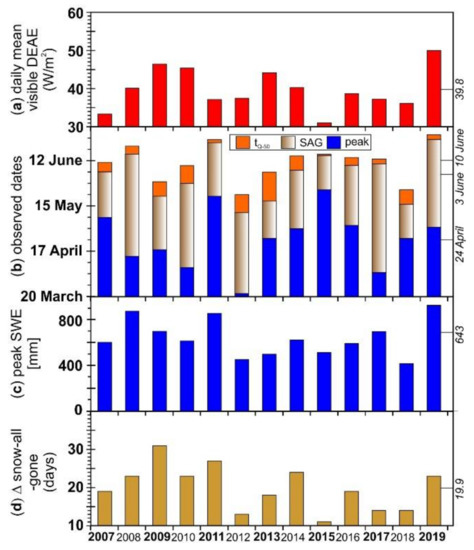
Figure 5.
Annual (a) estimated daily mean visible dust enhanced energy absorbed (DEAE), (b) observed peak SWE (Figure 3a) and snow-all-gone (SAG) date, (c) peak SWE, and (d) modeled difference in SAG (ΔSAG) for a clean vs. dust present snowpack. The mean for each time series is noted on the right vertical axis.
4.3. Modeled SWE and Snow Cover Duration
Overall, SNOBAL simulated observed SWE well (Figure 6). The difference between modeled and derived SWE (from CSAS snow depth and SNOTEL density) is 34 mm greater than between modeled and manually measured SWE (statistics beside the legend in Figure 6). Typically, model comparisons are poorer for shorter timesteps than for longer timesteps [60]; the derived SWE data had a daily time step while the manually measured SWE had approximately a weekly time step. However, the modeled SWE under actual (dust present) conditions (red lines in Figure 6) matches the seasonal patterns of manually measured bulk SWE (black points in Figure 6) fairly well, in particular capturing late-season melt rates. Modeled clean snowpack has slower melt rates than modeled dust present snowpack (Figure 6). Some divergence between modeled and observed SWE is more apparent in years with late-season precipitation events during snowmelt (e.g., WY2013 in Figure 6g and WY2016 in Figure 6j). For all years, the derived SWE is consistently lower than manually measured SWE at the snow pits (with an average difference of 93 mm).
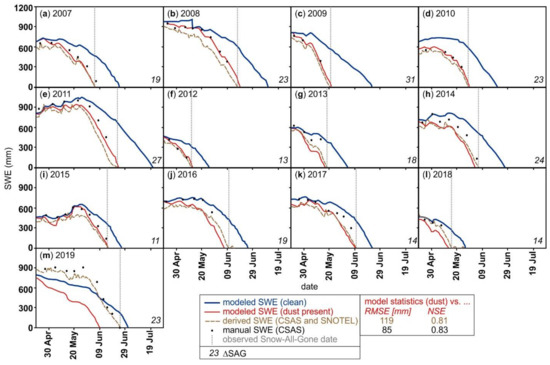
Figure 6.
Modeled and observed SWE from mid-April to snowpack disappearance curves for snowmelt season (a–m) 2007 to 2019. SWE is simulated using the SNOBAL model for clean conditions (blue), dust-present conditions (red). Derived SWE is calculated from observed snow density at Red Mountain Pass SNOTEL and observed snow depth at CSAS study plot (dashed brown lines), and manually measured bulk SWE (black points). The date of the observed snow-all-gone is presented as a dotted vertical grey line. The modeled dust present vs. clean (ΔSAG) is presented in the lower right corner of each figure. The statistics of the model dust-present SWE vs. the derived and manual SWE observations are presented beside the legend as root mean square error (RMSE) and the Nash–Sutcliffe Efficiency (NSE) coefficient.
Snow-all-gone was modeled to occur later than observed for the first six study years and later for the last seven (Figure 6; Table A3). Simulations for 8 years modeled that dust present SAG was less than 2 days different than observed SAG, with 3 years being within 3 days (WY2008, WY2014, WY2018). There was a 3.5 difference in modeled vs. observed melt-out for WY2016 (Figure 6j); the outlier was WY2019 which modeled melt-out 16 days earlier than observed (Figure 6m). The greatest degree of melt acceleration due to the presence of dust was in WY2009 (31 days earlier; also see Figure 4c,d) and the least melt acceleration was in WY2015 (11 days earlier; also see Figure 4a,b), with an average of about 20 days (Figure 5d).
4.4. Streamflow Timing
The streamflow on the Uncompahgre River at Ouray (Figure 7a) has similar patterns as the Senator Beck Basin (Figure 7b), except that there is a greater runoff volume from the smaller basin (SBB). The inter-annual variability shows early peak flows in dusty years (2009) and low snow years (2018), with late peak flows in low dust years (2015) and high snow years (2019), due to early and late melt, respectively. The timing of tQ50 varies by 35 days at SBB (22 May in 2012 to 28 June in 2019) (Figure 7d and Table A3). The tQ50 occurs 2 to 10 days earlier on the Uncompahgre River at Ouray compared to SBB (Figure 7c).
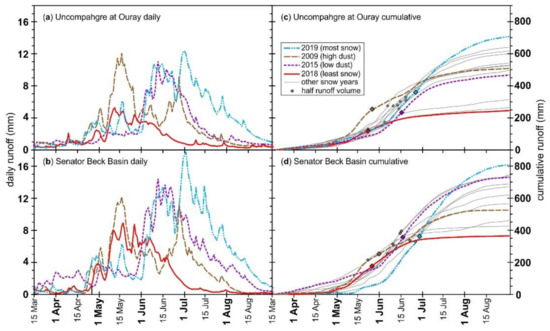
Figure 7.
Daily runoff for the two extreme snow year (low 2018 and high 2019) and the two focus years (shortest ΔSAG 2015 and longest ΔSAG 2009) at the (a) Uncompahgre River at Ouray and (b) Senator Beck Basin streamflow gauging stations, and cumulative runoff for all years at (c) Uncompahgre River at Ouray and (d) Senator Beck Basin. The cumulative runoff plots include the half runoff volume date (tQ50).
4.5. Drivers of DEAE, ΔSAG and tQ50
Daily mean visible DEAE is driven by a variety of factors (Figure 8 and Table 1). There is some correlation (R2 = 0.22) with dust concentration (Figure 8a), but as mentioned above, WY2019 is an outlier in terms of modeled vs. observed melt-out date (Figure 6m). Removing WY2019 improves the correlation (R2 = 0.55). The number of dust events and cumulative springtime (1 April to SAG) precipitation each correlate to DEAE (Figure 8b and 8e, respectively) when WY2019 is not considered. While both related to energy, there is no correlation between DEAE and cumulative springtime incoming shortwave radiation (Figure 8c), with or without WY2019. Overall, the strongest correlation for a single variable and DEAE is 1 April SWE (R2 = 0.41; Figure 8c), but WY2019 drives much of the correlation; excluding that year reduces the explained variance by almost half (R2 = 0.23).
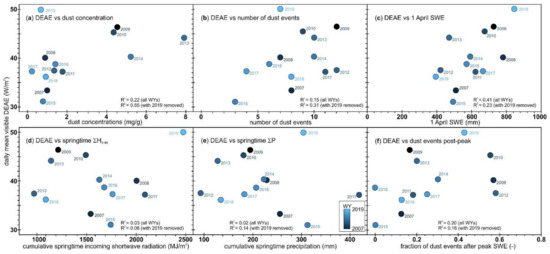
Figure 8.
Comparison of daily mean visible dust-enhanced energy absorption (DEAE), as a function of (a) end-of-year dust concentration, (b) number of dust events, (c) 1 April SWE, (d) cumulative springtime (1 April to SAG) incoming shortwave radiation, (e) cumulative springtime (1 April to SAG) precipitation, and (f) the fraction of the dust events after peak SWE.

Table 1.
Cross-correlation as the coefficient of determination (R) between climate variables (HK-IN is the incoming shortwave radiation, dust conc. = concentration, ΣP is cumulative from 1 April to SAG), daily mean DEAE, and ΔSAG. The values of R are given rather than R2 to indicate the sign of the correlation. Note: # is used to denote correlations where R2 > 0.29, and * where R2 > 0.5.
The average between modeled dust present vs. clean (ΔSAG) is significantly (p < 0.05) correlated to DEAE (R2 = 0.38; Table 1). The SWE amount of 1 April explained the most variance of all variables (R2 = 0.43; Table 1; Figure 9c). The number of dust events (R2 = 0.29; Figure 9b and Table 1) is more correlated to ΔSAG than the dust concentration (R2 = 0.14; Figure 9a and Table 1). For each dust variable, one dusty year was an obvious outlier; when the dust concentration in WY2013 (largest end-of-year dust concentration) was excluded the explained variance almost increased threefold (R2 = 0.39; Figure 9a). When the number of dust events in WY2012 (with most events post-peak SWE) was excluded, the explained variance more than doubled (R2 = 0.63; Figure 9b). Cumulative springtime (1 April to SAG) incoming shortwave radiation (HK-IN) and ΔSAG (Figure 9d) have little correlation (R2 = 0.08; Table 1) for all years. The extreme years (Figure 4) influenced the correlation between HK-IN and ΔSAG; exclusion of WY2009 increased R2 to 0.31, and exclusion of WY2009 and WY2015 increased R2 to 0.47 (Figure 9d). Cumulative springtime precipitation (ΣP) and ΔSAG (Figure 9e) have no significant correlation for all years (0.13). As with HK-IN, WY2009 and WY2015 were outliers for the correlation between ΣP and ΔSAG; exclusion of WY2015 increased R2 to 0.35, and exclusion of WY2009 and WY2015 increased R2 to 0.62 (Figure 9d).
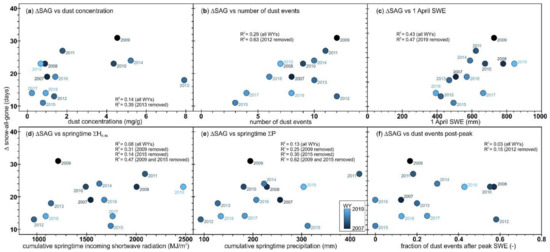
Figure 9.
Comparison of snow cover duration difference in terms of modeled snow disappearance for clean vs. dust-present (actual) conditions as the change in snow-all-gone (ΔSAG) date, as a function of (a) end-of-year dust concentration, (b) number of dust events, (c) 1 April SWE, (d) cumulative springtime (1 April to SAG) incoming shortwave radiation, (e) cumulative springtime (1 April to SAG) precipitation, and (f) the fraction of the dust events after peak SWE.
Similar to the correlations shown for DEAE or ΔSAG, 1 April SWE explains a significant amount of the inter-annual differences in tQ50 (Figure 10c). However, tQ50 is poorly correlated to DEAE or ΔSAG (Table 1). The correlation of dust concentration (Figure 10a) and number of dust events (Figure 10b) improves when specific outliers are removed, and there is limited correlation to the fraction of dust events after peak SWE (Figure 10f). Cumulative springtime incoming shortwave radiation explains 93% of the variance in tQ50 (Figure 10d) while cumulative springtime precipitation alone explains 66% of the variance (Figure 10e).
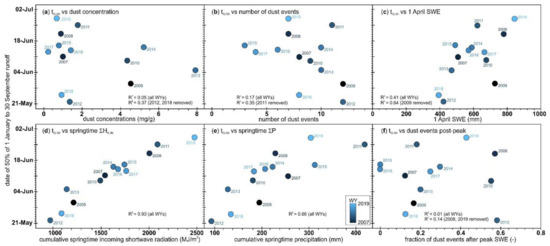
Figure 10.
Comparison of half flow date (tQ50), as a function of (a) end-of-year dust concentration, (b) number of dust events, (c) 1 April SWE, (d) cumulative springtime (1 April to SAG) incoming shortwave radiation, (e) cumulative springtime (1 April to SAG) precipitation, and (f) the fraction of the dust events after peak SWE.
While some variables, such as 1 April SWE, have a significant correlation with DEAE or ΔSAG, individually they explain less than 50% (Table 1; Figure A3). There is cross-correlation between some variables, specifically HK-IN vs. ΣP (R2 = 0.62) and HK-IN vs. 1 April SWE (R2 = 0.51) (Table 1). Thus, HK-IN was excluded in the multi-variate regression (Table 2). For DEAE, the optimal model (Figure A3a) included 1 April SWE, dust concentration, ΣP, and then number of dust events; adding the fraction of number of dust events after peak SWE did not improve the correlation (Table 2). Based on the magnitude of the standardized coefficients, a majority of the variance was explained by 1 April SWE (58%). Cumulative springtime precipitation (Figure 8d) decreased DEAE in the regression, i.e., had a negative coefficient.

Table 2.
Progression of multi-variate linear regression as the R2 values increased between mean daily DEAE (left side of table), ΔSAG (middle), tQ50 (right side) and the independent variables from Table 1, plus the fraction of dust events that occurred after peak SWE (Figure 3d). The standard error (with units of W/m2 for DEAE, days for ΔSAG, tQ50 as day of year) and the Nash–Sutcliffe Efficiency (NSE) coefficient are included. The optimal models are presented in bold face (four variables for DEAE, five for ΔSAG, and four for tQ50). The coefficients were derived from standardizing the independent variables to a value between 0 and 1. All regressions are significant at p < 0.05.
The optimal ΔSAG model also included the percentage of number of dust events (the five variables included on the right side of Table 2) and explained almost all of the inter-annual variability (Figure A3b). The model statistics are similar without the percentage of the number of dust events (the four variables included on the right side of Table 2). However, this is because ΔSAG is modeled better WY2008 and WY2010 with four variables but does not perform quite as well for the shortest and longest (Figure 4) ΔSAG (Figure A3b).
Cumulative springtime (1 April to SAG) incoming shortwave radiation explains almost all of the variation (R2 = 0.93) in tQ50 (Figure 10d). Excluding this variable (HK-IN), the correlation with multiple variables yielded similar statistics as DEAE (Table 2), with the same R2 (0.80), a slightly improved NSE (0.86) and the same four variables. Adding the fraction of dust events after peak SWE (5th variable) reduced the R2 and increased the standard error. For tQ50, cumulative springtime precipitation was most important (largest coefficient), followed by 1 April SWE, and number of dust events. The number of dust events was negatively correlated with tQ50 (Figure 10c).
5. Discussion
5.1. Inter-Annual Variability
The snowpack (Figure 3a) [61,62], snowfall (Figure 3b) [63], the quantity of dust deposited onto the snowpack (Figure 3c) [16], and the number of dust events (Figure 3d) all vary inter-annually [21]. After peak SWE, the timing of dust events (Figure 3) and snowfall events influence melt characteristics (Figure 4) [15]. Specifically, the amount of additional shortwave radiation increases (Figure 5a) due to decreased albedo (Figure 4) from dust (Figure 1) [15]. This enhanced melt also hastens disappearance of the snowpack, or SAG (Figure 6) [2], and yields earlier snowmelt runoff [14,20,26,27,42]. At this study site [64] and another small watershed in Northern Colorado [65], the timing of SAG has been directly linked to the date of peak streamflow. Future conditions could be quite different than recent observations [14], with warming causing earlier snowmelt [31]. The increased dust deposition and the corresponding decreased albedo (Figure 4) could offset less incoming shortwave radiation [29] if melting occurred early in the year.
5.2. DEAE Computation
DEAE calculations for all years relied on a snow surface correction to albedo which was observed for WY2007 to 2012 and approximated for WY2013 to 2019 (Appendix A). Generally, the incoming visible shortwave radiation calculated with the approximated snow surface correction compared well to the HK-IN with the observed correction (RMSE of 8 W/m2). The greatest difference was in May of WY2008 which had high SWE and above-average spring wind speed creating a complex snow surface not fully represented by the approximated value (Figure A1). We investigated the effect of under-estimation and over-estimation of HK-IN on a high-dust year (WY2013) and found that daily mean visible DEAE could range from 39.5 to 45.5 W/m2. A similar investigation of a low-dust year (WY2017) found a range from 32.5 to 38 W/m2. Despite the potential scale of uncertainty for daily mean visible DEAE calculations for WY2013 to WY2019, the overall pattern of DEAE response to increases in dust concentration would remain a logarithmic correlation. The DEAE data were used with the SNOBAL model, and while there was a large difference between observed and modeled SAG for 2019 (Figure 6m) (there was a 3.5-day difference in 2016), the model results for other 5 years were as good as the first 6 years (WY2007 to 2012).
The magnitude of our DEAE calculations (Table A3) compares well to other regional studies across the Upper Colorado River. Remote sensing of particulate-enhanced energy absorption from four days in WY2011 over the Uncompahgre Basin found the average instantaneous pixel value ranged from about 50 W/m2 in mid-May to 200 W/m2 in mid-June [66]. This range is likely in part due to their inclusion of all light-absorbing impurities, assumption of homogeneous snow grain size, and spatial variability due to resolution (13.8 m pixel size). We found hourly visible DEAE to range up to 234 W/m2 during June of WY2011. Additionally, Bryant et al. [27] retrieved daily mean radiative forcing from dust in the visible spectrum only and found a range from 20 to 80 W/m2 (over WY2000 to WY2010).
At SASP, Skiles et al. [15,20] and Skiles and Painter [67] computed a mean daily DEAE that had the same inter-annual pattern for seven overlapping years (WY2007 to WY2013), especially compared to dust concentrations (Figure 8a). However, this study yielded on average 28% lower (range of 22 to 38%) DEAE than Skiles and Painter [67]. Subsequently, Skiles and Painter [67] computed a mean DEAE of about 30 W/m2 for 2013 compared to the previous estimate of 65 W/m2 and the estimate here of 44 W/m2 (Figure 5; Table A3). These differences are due in part to a different date over which the mean daily DEAE was computed (here 1 April to SAG and Skiles et al. [15,20] used 15 April to SAG); HK-IN is less, and dust is typically less present (albedo is higher) over the first two weeks of April yielding a lower DEAE. We used an earlier start date than Skiles et al. [15,20], since peak SWE occurred prior to 15 April in 4 of the 13 years. Further, the specific snowpack albedo formulation will influence DEAE. Skiles and Painter [68] used a more detailed snowpack albedo model (the snow, ice, and aerosol radiative model or SNICAR, [69] coupled to the multilayer snow model SNOWPACK (see [70] and subsequent papers), but this still tended to over-estimate albedo by about 0.04 compared to measured values (mean of 0.64). Specifically, modeled albedo decay was too slow while fresh snow albedo was too low, which has been shown using a simple albedo model calibrated with SASP data that divides and treats visible (400 to 700 nm) and NIR/SWIR (700 to 2500 nm) wavelengths separately [71]. This is relevant since changes in broadband snow albedo are controlled by the dust-induced decrease in the visible portion of the spectrum more than NIR/SWIR (Figure 1), such as during the highest dust-loading year on record (WY2013; Figure 3c) [11]. A new version of SNICAR [72] may improve albedo modeling.
5.3. Modeling of Snow Cover
The inter-annual modeled difference between SAG for dust present and clean snow conditions follows a similar pattern to DEAE (Figure 5a vs. Figure 5d) with a significant (p < 0.05) R2 of 0.38 (Table 1). As with DEAE, the seven overlapping years investigated by Skiles and Painter [67] yielded on average 40% longer ΔSAG, but with wider range from 15 to 63%. The shorter ΔSAG modeled here are partially a function of lower DEAE values and modeling assumptions. Estimates of ΔSAG rely on the accurate representation of snowpack evolution by the energy balance model SNOBAL [52]. Rather than simulating the snowpack for the entire winter, modeling focused on the melting of the snowpack. Simulations started with observed snowpack state variables in approximately isothermal conditions at approximately peak SWE and ran through to SAG [73]; this reduces divergence between the modeled and observed snowpack [74] and reduces errors associated with the model energy and mass transfers. The energy balance simulation of accumulation is complex [75] and is subject to greater uncertainty due to rapidly changing or inconsistent early-season snow state variables, such as snow depth.
Two consistent approximations made across all SNOBAL runs may have influenced ΔSAG results. First, a maximum hard-coded model upper limit on net shortwave radiation (HK*) of 800 W/m2 [51] could affect melt rate. While the mean springtime HK* was less than 500 W/m2, each year a maximum springtime net shortwave radiation greater than 800 W/m2 was computed on a few days for the dust present model runs [76]. This limit does not accurately represent the radiation-dominated continental climate of the San Juan Mountains, which experience relatively high incoming shortwave radiation compared to other climates such as the cloudy Pacific Northwest [21].
Second, the SWE of spring snowfall seems to be consistently under-estimated resulting in either divergence between modeled and observed SWE (e.g., WY2011) or greater inaccuracy in modeled SAG (e.g., WY2019) (Figure 6). Since there was a 16-day difference in observed vs. modeled SAG for 2019 (Figure 6m), it could be acceptable to remove this year from subsequent analyses (Figure 8a). The model runs were initiated with state variables from a snow plot several meters away from the tower that supplied subsequent forcing variables, thus some divergence in SWE may be due to spatial variability of snow depth [18,77]. However, the prevalence of the under-estimation indicates a systemic error in precipitation inputs [78,79,80]. Precipitation is partitioned to rain or snow in SNOBAL based on dewpoint temperature and the snow percentages (Table A2) estimated from monitoring in the California Sierra Nevada [52,53]. The dewpoint temperature is computed from daily maximum and minimum temperatures and may not capture the dewpoint temperature at the specific time of a precipitation event, as the model has an hourly timestep, especially in a semi-arid environment [81]. Based on air temperature only, there is variability in the temperature threshold between snow and rain among different climates [82,83]. In the semi-arid the continental climate of Colorado, snow can fall at warmer air temperatures than in more humid or maritime environments [84,85]. Additionally, the fresh snow density partitioning in SNOBAL (Table A2) is based on SNOTEL stations in the Wasatch Range of Utah [52]. These densities may not represent the higher elevation, semi-arid climate of the Colorado where fresh snow can have lighter density compared to wetter environments [86,87].
Overall, the limit on net shortwave radiation and the underestimation of precipitation inputs may counteract one another yielding a smaller net combined effect on ΔSAG. The upper threshold on net shortwave radiation restricts the energy available to the modeled snowpack, slowing melt rates, and lengthening snow persistence. However, the underestimation of precipitation inputs results in lower bulk SWE which would have shorter snow cover duration regardless of dust presence.
5.4. Streamflow Timing
While this paper did not compare modeled streamflow for dust present (i.e., observed) conditions vs. clean (i.e., dust removed from the modeled snowpack) conditions (e.g., Bryant et al. [27]), we see differences in tQ50 based on the inter-annual in the quantity of dust that is present (Figure 6c,d). On the Uncompahgre (Figure 7c) and the Senator Beck Basin (Figure 7d), tQ50 was four and five days later, respectively, for a high dust year (WY2009) than a low snow year (WY2018). A low snowpack (e.g., WY2012 and WY2018) begins to melt sooner than an average snowpack (Figure 5b), and the streamflow, such as measured by tQ50, respond (Figure 7). The timing of peak flow, which is not the same at tQ50 (see the orange bars in Figure 3b), has been seen to correspond well with SAG (Figure 3b) [65,66]. Conversely, the response of streamflow for a low dust year (WY2015) and a high snow year (WY2019) is less similar; the latter tQ50 was 12 days later (Figure 7c,d).
The spatial distribution of dust is also important [19,27]. This may be less important for SBB than the Uncompahre watershed due to the size difference (2.91 vs. 199 km2) and spatial variability in dust [26]. However, even in the small SBB, there is spatial variability in melt patterns due to variability in terrain and its influence on HK* [25], and differences in snowmelt in the alpine (SBSP) vs. sub-alpine (SASP) [64], which all impact streamflow characteristics. For streamflow modeling, especially for forecasting, it is important to include the influence of dust [27].
5.5. Drivers of DEAE, Snow Cover Duration and Flow Characteristics
For six years (WY2005 to WY2010), DEAE was shown to be highly correlated in a log-linear manner to dust concentration [15], while we found a weak linear correlation between DEAE and dust concentration that became significant when 2019 was excluded (Figure 8a). We found 1 April SWE to have the strongest correlation with DEAE (Figure 7c and Figure A3a), but it still only explained about 40% of the variability (Table 1). A multi-variate linear regression increased the explained variance to 80% when three other variables were included (Table 2). The single variable correlations are not expected to be strong as they simplify complex snowpack processes [51,52] interacting with dust being deposited, buried by new snow (Figure 4), and then reappearing near or at the snow surface [11,69]. The bulk dust samples collected towards the end of each snow season are from all layers combined and do not consider when the dust event occur; some years all dust is deposited prior to peak SWE (e.g., WY2015 and W2016; Figure 3d). Light does penetrate into the snowpack, but this can vary from several to 10 s of cm [88,89], the deeper burial of dust delays its effect on surface albedo [11]. Further, the presence of LAPs decreases the penetration depth of light [90], which could confound the computation of albedo [71]. The presence of dust only represents a portion of the decrease in albedo, primarily in the visible portion of the spectrum (Figure 1), as albedo decrease also corresponds to the increase in snow grain size [12] and the presence of liquid water.
Less dust and/or more springtime precipitation can yield a higher albedo (Figure 4a,b), which reduces the daily mean visible DEAE (Figure 7), but as the snowmelt season progresses the incoming shortwave radiation increases (Figure 8d) which can increase DEAE. These can combine to change the timing of SAG (Figure 6). While cumulative springtime precipitation is poorly correlated to DEAE and ΔSAG (Figure 8e and Figure 9e), the direction of the correlation is opposite (Table 1 and Table 2). The number of dust events influences ΔSAG more than the dust concentration (Table 2).
Low SWE produces a shorter snow persistence regardless of dust (Figure 9c), which results in lower ΔSAG [15], as seen in WY2012 and WY2013 (Figure 6f,g and Figure 9c) and in the multi-variate regression (Table 2). WY2015 (Figure 4a,b) and WY2017 are low-dust years (Figure 3c) which received enough late-season precipitation (Figure 3b) to lengthen snow cover duration and increase the cumulative HK-IN values while keeping ΔSAG short (Figure 9d). The late-season snowfall events, such as in WY2105, not only bury exposed dust but also increase albedo [72] (Figure 4b) and reduces HK-IN (Figure 4a) due to the presence of cloud cover. Conversely, greater SWE accumulation allows for a longer period of dust influence, leading to greater divergence in snow cover duration (Figure 9c) [2]. Melt rates are a function of the total energy balance. Here, we focus on the change in the shortwave radiation component; when dust is present and the albedo is lower, even if melt occurs earlier and there is less incoming shortwave radiation, melt rates are accelerated (Figure 4b vs. Figure 4d).
While dust on its own does not correlate with the tQ50 (Figure 10a,b, Table 1), the number of dust events is about half as important as cumulative precipitation in the optimal multi-variate regression (Table 2). However, cumulative precipitation itself explains two-thirds of the variance (Figure 10e, Table 1 and Table 2). More significantly, HK-IN explains almost all (R2 = 0.93) of the variance with tQ50, and ΣP is strongly correlated with HK-IN (R2 = 0.62 in Table 1); the more precipitation in the spring, typically as snow (Figure 4b), then HK-IN is greater as the sun is higher in the sky, and tQ50, the later, since snowmelt contributes to streamflow longer [34]. Additionally, tQ50 and SAG are highly correlated (Figure 5c; R2 = 0.94), as expected. However, this sequence of processes does not relate back to dust related variables, specifically DEAE is not correlated to HK-IN (Figure 8d) and ΔSAG is poorly correlated to HK-IN (Figure 9d).
5.6. Implications and Uses of This Work
We found that deposited dust layers can increase the mean visible energy absorbed by the snowpack up to an additional 51 W/m2 per day during an ablation season in the UCRB, accelerating melt from at least 11 days to as many as 31 days when only considering energy in the visible spectrum. Previous studies have found melt advanced up to 51 days when also considering NIR/SWIR effects [15]. Projected warming in the southwestern USA will increase potential drought, disturbance, and desertification [91] which can lead to increased dust loading of southwestern Colorado snowpack. Further investigation of the impact of dust on snowpack energy balance is needed since the connection between dust loading and melt acceleration is not direct.
Dust-enhanced radiative forcing has potentially shortened snow cover in southwestern Colorado by up to 51 days [15] accelerating timing of snowmelt runoff in the region [14,42]. Accounting for the dust-enhanced radiative effect on the snowpack energy balance will likely reduce the uncertainty of runoff predictions [25]. However, continued investigation of interannual and sub-seasonal patterns of dust loading is necessary to better inform operational snowmelt projections in the UCRB. Our results indicate that dust concentration magnitude is not directly responsible for accelerated melt rates and that sub-seasonal combinations of SWE magnitude, irradiance, and precipitation all influence snow cover duration. Daily analysis of dust, snow, and climate dynamics by Skiles and Painter [11] over a high-dust and low-SWE ablation season (WY2013) showed that even small dust concentrations can decrease albedo and snow depth declined 50% faster than years of similar depth and lower dust. Understanding the relation of snowpack development and dust concentration may require measurements at a finer temporal resolution than bulk seasonal averages.
While it has become common to study streamflow patterns using percentages of flow [34,37,38,39,40,56], such as tQ50, these metrics may not be appropriate for examining the correlation between snowmelt and streamflow [92]. Large individual precipitation events [33] and inter-annual variability in total streamflow volume can influence changes in the timing of tQ50 [92]. As such, other streamflow characteristics, such as the actual onset of snowmelt streamflow should be considered [93].
There is also the need by water managers to expand beyond point-based studies and ascertain melt acceleration changes across larger basins. Future calibration of remote-sensing products [26] and forecasting of melt acceleration [27] will depend on direct monitoring of snowpack energy balance at multiple locations [41]. Recommended next steps are to understand individual dust layer dynamics [68] in relation to sub-seasonal snow and climate variables, to incorporate weather forecasts into snowpack energy balance modeling [94] and develop a real-time dust-enhanced energy absorption forecast product for operational end-users. Operational streamflow forecasting is challenging [95], and snowpack and hydrological models are often too complex to be very useful in a forecast setting [96,97]. A hierarchal decision tree approach [98] could be constructed to prioritize most important variables as the snow season unfolds. This would likely require a finer temporal resolution study to examine when and under what conditions melt responds to the environmental conditions. Intra-annual or sub-seasonal variations, such as the timing of dust events (Figure 3d) seem to be crucial to be able to determine what are the most important variables to measure to better develop such as decision tree to be useful to identify if melt is expected to be accelerated.
There are ongoing efforts to enhance data information at existing stations, such as adding anemometers and four-component radiometers (shortwave and longwave incoming and outgoing) at the SNOTEL sites. New data collection systems are being implemented, such as the U.S. Geological Survey Next Generation Water Observing System <https://www.usgs.gov/mission-areas/water-resources/science/next-generation-water-observing-system-ngwos> (last accessed 10 February 2022), which includes a portion of the Upper Colorado River. Finally, new inexpensive sensors are being built in labs and deployed [99]. Inexpensive commercially available sensors are being used to measure fine scale variability [100,101] and could be deployed over larger domains.
6. Conclusions
At a site in southern Colorado, the nature of the snowpack varies due to inter-annual fluctuations, and the snowmelt characteristics are a function of the amount and timing of dust events together with spring precipitation patterns. The mean daily visible dust enhanced absorbed energy ranged from 31 to 51 W/m2. It is driven by the quantity of snow accumulation, often measured as 1 April SWE, and to a lesser extent the precipitation during snowmelt, the end-of-year dust concentration and the number of dust events per year. Snow cover duration decreased under dust present conditions for all years modeled, with the range of melt acceleration from 11 to 31 days. A more accelerated melt is partially driven by daily mean visible DEAE, but is also mostly influenced by 1 April SWE, and to a lesser extent, the number of dust events. The springtime precipitation, dust concentration, and the fraction of dust events after peak SWE had a minor influence on ΔSAG. Incorporation of individual dust layer burial depth, dispersal distance of dust layers throughout the snowpack, and the relative timing of irradiance and precipitation inputs would potentially improve simulations of snowmelt. Future development of operational streamflow forecasting for the UCRB will benefit from continued monitoring and quantification of those sub-seasonal effects.
Author Contributions
Conceptualization, S.R.F., C.R.D. and A.K.D.P.; methodology, S.R.F., C.R.D., A.K.D.P. and R.W.W.; software, C.R.D., S.R.F. and A.K.D.P.; formal analysis, S.R.F. and C.R.D.; investigation, C.R.D. and S.R.F.; data curation, J.E.D.; writing—original draft preparation, S.R.F., C.R.D., A.K.D.P.; writing—review and editing, S.R.F., A.K.D.P., R.W.W., W.E.S., J.E.D. and D.C.R.; visualization, S.R.F., C.R.D., L.G.D.; supervision, S.R.F.; project administration, S.R.F.; funding acquisition, S.R.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by U.S. Geological Survey National Institutes for Water Resources (U.S. Department of the Interior), grant number 2018CO345B project “Dirty Snow: Turning Qualitative Assessments into Quantitative Factors for the Effect of Dust on Snow Albedo and Melt Rate,” through the Colorado Water Center. The views and conclusions contained in this document are those of the authors and should not be interpreted as necessarily representing the official policies, either expressed or implied, of the U.S. Government.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All snowpack and meteorological data for SASP and SBSP are available from the Center for Snow and Avalanche Studies (CSAS) <https://www.snowstudies.org> (accessed 21 December 2021). All SNOTEL snowpack data are available from NRCS <https://www.nrcs.usda.gov> (accessed 20 January 2022). The SBB streamflow data are available from CSAS and the Uncompahgre River streamflow data are available from the USGS <https://nwis.waterdata.usgs.gov/nwis> (accessed 25 January 2022).
Acknowledgments
Stephanie Kampf and Jay Ham of Colorado State University provided reviews of the M.S. thesis on which this paper is partially based. Micah Johnson and the team at the Northwest Watershed Research Center (USDA-ARS) in Boise Idaho provided technical support for the SNOBAL modeling. Kim Wolfe of Fort Collins/Silverton shared much life wisdom with C.R.D.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Albedo Adjustment Procedures
Geometric and solar position adjustments are combined with the following relation (after Painter et al. [21]):
where β is the local solar zenith angle, θs is the solar zenith angle for the horizontal surface, Φs is the solar azimuth angle, θn is the surface slope, and Φn is the surface aspect. The scalar (Mβ) by which we corrected the measured hourly incoming shortwave radiation flux values to at-surface irradiances is (after Painter et al. [2]):
cos β = cos θs cos θn + sin θs sin θn cos {Φs − Φn}
Mβ = cos β/cos θs
Snow surface albedo was calculated from the corrected incoming shortwave radiation and observed reflected shortwave radiation flux (Figure A1). Snow stake array depth observations were only collected for WY2007-2012, so the mean slope and aspect for each calendar day were used to approximate a daily corrective Mβ value for WY2013-2019 (Figure A2). In addition to correcting for non-level snow surface, we also adjusted for snow deposition on the up-facing pyranometers. Accumulation on the up-facing pyranometers reduces the measured incoming shortwave radiation compared to the actual incoming shortwave radiation.
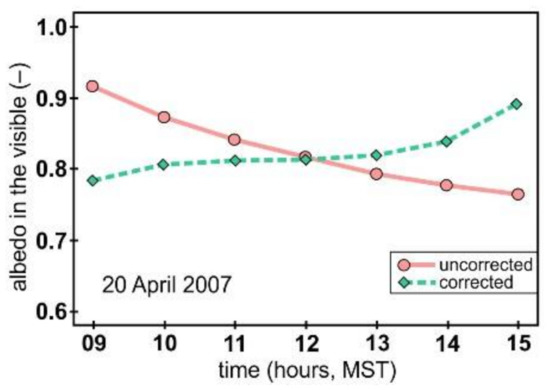
Figure A1.
Hourly snow surface albedo was corrected for a non-level snow surface and seasonally shifting solar position to capture diurnal variation.
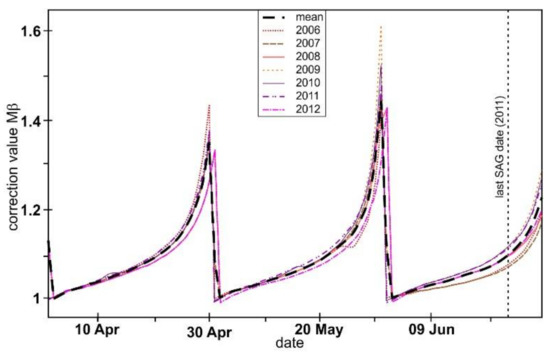
Figure A2.
Observed snow surface correction values for WY2007–2012 (color lines) and approximated surface correction value used for WY2013–2019 (black line) over ablation season (April, May, and June). Vertical dashed line is the latest observed date of SAG (WY2011) for the period.
Appendix B. Model Components
The forcing and state variable for the SNOBAL model runs are presented in Table A1. The percent of precipitation as snow and the associated fresh snow density used in the SNOBAL model runs are summarized in Table A2.

Table A1.
Required forcing variables and modeled state variables for SNOBAL (after Marks et al. [52]).
Table A1.
Required forcing variables and modeled state variables for SNOBAL (after Marks et al. [52]).
| Forcing Variables | State Variables |
|---|---|
| Net shortwave radiation (W/m2) | Snow depth (m) |
| Incoming longwave radiation (W/m2) | Snow density (kg/m3) |
| Air temperature (°C) | Snow surface layer temperature (°C) |
| Vapor pressure (Pa) | Average total snowpack temperature (°C) |
| Wind speed (m/s) | Average snow liquid water content (%) |

Table A2.
Precipitation partitioning table and fresh snow density based on dewpoint temperature (after Susong et al. [53]).
Table A2.
Precipitation partitioning table and fresh snow density based on dewpoint temperature (after Susong et al. [53]).
| Dewpoint Temperature (°C) | Percentage of Snow (%) | Snow Density (kg/m3) |
|---|---|---|
| Td < –5 | 100 | 75 |
| –5 ≤ Td < –3 | 100 | 100 |
| –3 ≤ Td < –1.5 | 100 | 150 |
| –1.5 ≤ Td < –0.5 | 100 | 175 |
| –0.5 ≤ Td < 0 | 75 | 200 |
| 0 ≤ Td < 0.5 | 25 | 250 |
| 0.5 ≥ Td | 0 | 0 |
Appendix C. Observed and Computed Annual Data
The observed and computed data are summarized in Table A3.

Table A3.
Observed (dust concentration to dust events post-peak SWE in columns 2 to 7), computed (DEAE in column 8), SNOBAL modeled (ΔSAG in column 9), and streamflow-derived (tQ50 in column 10) annual data for the 13 study years at SBB, as per the data presented in Table 1.
Table A3.
Observed (dust concentration to dust events post-peak SWE in columns 2 to 7), computed (DEAE in column 8), SNOBAL modeled (ΔSAG in column 9), and streamflow-derived (tQ50 in column 10) annual data for the 13 study years at SBB, as per the data presented in Table 1.
| WY | Dust Conc. (mg/g) | Dust Events | ΣHK-IN (MJ/m2) | Σprecip (mm) | 1 April SWE (mm) | Fraction of Dust Events Post-Peak SWE | DEAE (W/m2) | ΔSAG (Days) | tQ50 (Date) |
|---|---|---|---|---|---|---|---|---|---|
| 2007 | 1 | 8 | 1543 | 256 | 508 | 0.13 | 33.3 | 19 | 11 June |
| 2008 | 0.88 | 7 | 2004 | 229 | 780 | 0.57 | 40.1 | 23 | 21 June |
| 2009 | 4.55 | 12 | 1213 | 195 | 729 | 0.17 | 46.4 | 31 | 30 May |
| 2010 | 4.35 | 9 | 1494 | 181 | 675 | 0.56 | 45.4 | 23 | 9 June |
| 2011 | 1.78 | 11 | 2090 | 419 | 623 | 0.18 | 37.2 | 27 | 25 June |
| 2012 | 1.35 | 12 | 969 | 93 | 420 | 0.58 | 37.5 | 13 | 22 May |
| 2013 | 7.92 | 10 | 1142 | 128 | 469 | 0.20 | 44.2 | 18 | 5 June |
| 2014 | 5.22 | 10 | 1629 | 223 | 589 | 0.30 | 40.3 | 24 | 15 June |
| 2015 | 0.79 | 3 | 1744 | 313 | 493 | 0.00 | 31.0 | 11 | 16 June |
| 2016 | 1.41 | 6 | 1677 | 207 | 572 | 0.00 | 38.7 | 19 | 14 June |
| 2017 | 0.22 | 4 | 1763 | 183 | 665 | 0.25 | 37.3 | 14 | 13 June |
| 2018 | 0.92 | 8 | 1084 | 134 | 393 | 0.13 | 36.2 | 14 | 25 May |
| 2019 | 0.67 | 7 | 2477 | 304 | 843 | 0.43 | 50.0 | 23 | 28 June |
Appendix D. Model vs. Observed Model Correlation
The fit between the SWE only and optimal multi-variate linear regression models for DEAE and ΔSAG are shown in Figure A3a and A3b, respectively.
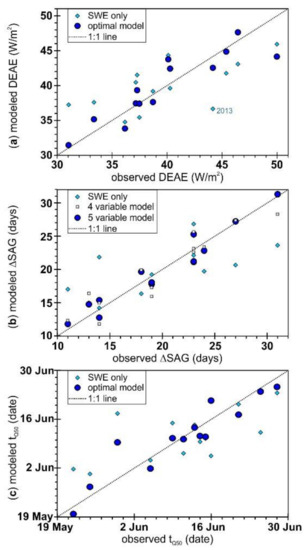
Figure A3.
Modeled vs. observed (a) DEAE, (b) ΔSAG, and (c) tQ50 for SWE only and the optimal multi-variate linear regression models (see Table 2).
References
- Bales, R.C.; Molotch, N.P.; Painter, T.H.; Dettinger, M.D.; Rice, R.; Dozier, J. Mountain hydrology of the western United States. Water Resour. Res. 2006, 42, W08432. [Google Scholar] [CrossRef]
- Painter, T.H.; Barrett, A.P.; Landry, C.C.; Neff, J.; Cassidy, M.P.; Lawrence, C.; McBride, K.E.; Farmer, G.L. Impact of disturbed desert soils on duration of mountain snow cover. Geophys. Res. Lett. 2007, 34, L12502. [Google Scholar] [CrossRef]
- Suzuki, K.; Ohta, T. Effect of Larch Forest Density on Snow Surface Energy Balance. J. Hydrometeorol. 2003, 4, 1181–1193. [Google Scholar] [CrossRef]
- Takeuchi, N.; Li, X. Characteristics of surface dust on Ürümqi Glacier No. 1 in the Tien Shan Mountains, China. Arct. Antarct. Alp. Res. 2007, 40, 744–750. [Google Scholar] [CrossRef]
- Warren, S.G.; Wiscombe, W.J. A Model for the Spectral Albedo of Snow. II: Snow Containing Atmospheric Aerosols. J. Atmos. Sci. 1980, 37, 2734–2745. [Google Scholar] [CrossRef]
- Boon, S. Snow ablation energy balance in a dead forest stand. Hydrol. Process. 2009, 23, 2600–2610. [Google Scholar] [CrossRef]
- Flanner, M.G.; Zender, C.S.; Hess, P.G.; Mahowald, N.M.; Painter, T.H.; Ramanathan, V.; Rasch, P.J. Springtime warming and reduced snow cover from carbonaceous particles. Atmos. Chem. Phys. 2009, 9, 2481–2497. [Google Scholar] [CrossRef]
- Flanner, M.G.; Liu, X.; Zhou, C.; Penner, J.E.; Jiao, C. Enhanced solar energy absorption by internally-mixed black carbon in snow grains. Atmos. Chem. Phys. Discuss. 2012, 12, 4699–4721. [Google Scholar] [CrossRef]
- Pugh, E.; Small, E. The impact of pine beetle infestation on snow accumulation and melt in the headwaters of the Colorado River. Ecohydrology 2011, 5, 467–477. [Google Scholar] [CrossRef]
- Bond, T.C.; Doherty, S.J.; Fahey, D.W.; Forster, P.M.; Berntsen, T.; DeAngelo, B.J.; Flanner, M.G.; Ghan, S.; Kärcher, B.; Koch, D.; et al. Bounding the role of black carbon in the climate system: A scientific assessment. J. Geophys. Res. Atmos. 2013, 118, 5380–5552. [Google Scholar] [CrossRef]
- Skiles, S.M.; Painter, T. Daily evolution in dust and black carbon content, snow grain size, and snow albedo during snowmelt, Rocky Mountains, Colorado. J. Glaciol. 2016, 63, 118–132. [Google Scholar] [CrossRef]
- Skiles, S.M.; Flanner, M.; Cook, J.M.; Dumott, M.; Painter, T. Radiative forcing by light-absorbing particles in snow. Nat. Clim. Change 2018, 8, 964–971. [Google Scholar] [CrossRef]
- Lawrence, C.R.; Painter, T.H.; Landry, C.C.; Neff, J.C. Contemporary geochemical composition and flux of aeolian dust to the San Juan Mountains, Colorado, United States. J. Geophys. Res. 2010, 115, G03007. [Google Scholar] [CrossRef]
- Deems, J.S.; Painter, T.H.; Barsugli, J.J.; Belnap, J.; Udall, B. Combined impacts of current and future dust deposition and re-gional warming on Colorado River Basin snow dynamics and hydrology. Hydrol. Earth Syst. Sci. 2013, 17, 4401–4413. [Google Scholar] [CrossRef]
- Skiles, S.M.; Painter, T.H.; Deems, J.S.; Bryant, A.C.; Landry, C.C. Dust radiative forcing in snow of the Upper Colorado River Basin: 2. Interannual variability in radiative forcing and snowmelt rates. Water Resour. Res. 2012, 48, W07522. [Google Scholar] [CrossRef]
- Neff, J.C.; Ballantyne, A.P.; Farmer, G.L.; Mahowald, N.M.; Conroy, J.L.; Landry, C.C.; Overpeck, J.T.; Painter, T.H.; Lawrence, C.R.; Reynolds, R.L. Increasing eolian dust deposition in the western United States linked to human activity. Nat. Geosci. 2008, 1, 189–195. [Google Scholar] [CrossRef]
- Nauman, T.W.; Duniway, M.C.; Webb, N.P.; Belnap, J. Elevated aeolian sediment transport on the Colorado Plateau, USA: The role of grazing, vehicle disturbance, and increasing aridity. Earth Surf. Process. Landf. 2018, 43, 2897–2914. [Google Scholar] [CrossRef]
- Fassnacht, S.; Williams, M.; Corrao, M. Changes in the surface roughness of snow from millimetre to metre scales. Ecol. Complex. 2009, 6, 221–229. [Google Scholar] [CrossRef]
- Painter, T.H.; Bryant, A.C.; Skiles, S.M. Radiative forcing by light absorbing impurities in snow from MODIS surface reflectance data. Geophys. Res. Lett. 2012, 39, 17502. [Google Scholar] [CrossRef]
- Skiles, S.M.; Painter, T.H.; Belnap, J.; Holland, L.; Reynolds, R.L.; Goldstein, H.L.; Lin, J. Regional variability in dust-on-snow processes and impacts in the Upper Colorado River Basin. Hydrol. Proc. 2015, 29, 5397–5413. [Google Scholar] [CrossRef]
- Painter, T.H.; Skiles, S.M.; Deems, J.; Bryant, A.C.; Landry, C.C. Dust radiative forcing in snow of the Upper Colorado River Basin: 1. A 6 year record of energy balance, radiation, and dust concentrations. Water Resour. Res. 2012, 48, W07521. [Google Scholar] [CrossRef]
- Anderson, E.A. National Weather Service River Forecast System—Snow Accumulation and Ablation Model; NOAA Technical Memorandum NWS HYDRO-17; U.S. Department of Commerce: Silver Spring, MD, USA, 1973; p. 217. [Google Scholar]
- Burnash, R.J.; Ferral, R.L.; McGuire, R.A. A Generalized Streamflow Simulation System Conceptual Modeling for Digital Computers; U.S. Department Commerce NWS and State of California Department of Water Research: Silver Spring, MD, USA, 1973. [Google Scholar]
- Franz, K.J.; Hogue, T.S.; Sorooshian, S. Operational snow modeling: Addressing the challenges of an energy balance model for National Weather Service forecasts. J. Hydrol. 2008, 360, 48–66. [Google Scholar] [CrossRef]
- Follum, M.L.; Niemann, J.D.; Fassnacht, S.R. A comparison of snowmelt-derived streamflow from temperature-index and modified-temperature-index snow models. Hydrol. Proc. 2019, 33, 3030–3045. [Google Scholar] [CrossRef]
- Painter, T.H.; Skiles, S.M.; Deems, J.S.; Brandt, W.T.; Dozier, J. Variation in Rising Limb of Colorado River Snowmelt Runoff Hydrograph Controlled by Dust Radiative Forcing in Snow. Geophys. Res. Lett. 2018, 45, 797–808. [Google Scholar] [CrossRef]
- Bryant, A.C.; Painter, T.H.; Deems, J.S.; Bender, S.M. Impact of dust radiative forcing in snow on accuracy of operational runoff prediction in the Upper Colorado River Basin. Geophys. Res. Lett. 2013, 40, 3945–3949. [Google Scholar] [CrossRef]
- Barnhart, T.B.; Molotch, N.P.; Livneh, B.; Harpold, A.A.; Knowles, J.F.; Schneider, D. Snowmelt rate dictates streamflow. Geophys. Res. Lett. 2016, 43, 8006–8016. [Google Scholar] [CrossRef]
- Musselman, K.N.; Clark, M.P.; Liu, C.; Ikeda, K.; Rasmussen, R. Slower snowmelt in a warmer world. Nat. Clim. Change 2017, 7, 214–220. [Google Scholar] [CrossRef]
- Harpold, A.A.; Brooks, P.D. Humidity determines snowpack ablation under a warming climate. Proc. Natl. Acad. Sci. USA 2018, 115, 1215–1220. [Google Scholar] [CrossRef]
- Marshall, A.M.; Abatzoglou, J.T.; Link, T.E.; Tennant, C.J. Projected Changes in Interannual Variability of Peak Snowpack Amount and Timing in the Western United States. Geophys. Res. Lett. 2019, 46, 8882–8892. [Google Scholar] [CrossRef]
- Church, B.J.E., Jr. Recent studies of snow in the United States. Q. J. R. Meteorol. Soc. 1914, 40, 43–52. [Google Scholar] [CrossRef]
- Fassnacht, S.R. Upper versus lower Colorado River sub-basin streamflow: Characteristics, runoff estimation and model simulation. Hydrol. Process. 2006, 20, 2187–2205. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Deitemeyer, D.C.; Venable, N.B.H. Capitalizing on the daily time step of snow telemetry data to model the snowmelt components of the hydrograph for small watersheds. Hydrol. Process. 2014, 28, 4654–4668. [Google Scholar] [CrossRef]
- Pagano, T.; Garen, D.; Sorooshian, S. Evaluation of Official Western, U.S. Seasonal Water Supply Outlooks, 1922–2002. J. Hydrometeorol. 2004, 5, 896–909. [Google Scholar] [CrossRef]
- Anghileri, D.; Voisin, N.; Castelletti, A.; Pinaosi, F.; Nijssen, B.; Lettenmaier, D.P. Value of long-term streamflow forecasts to reservoir operations for water supply in snow-dominated river catchments. Water Resour. Res. 2016, 52, 4209–4225. [Google Scholar] [CrossRef]
- Court, A. Measures of Streamflow Timing. J. Geophys. Res. 1962, 67, 4335–4339. [Google Scholar] [CrossRef]
- Satterlund, D.R.; Eschner, A.R. Land use, snow, and streamflow regimen in central New York. Water Resour. Res. 1965, 1, 397–405. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes toward Earlier Streamflow Timing across Western North America. J. Clim. 2005, 18, 1136–1155. [Google Scholar] [CrossRef]
- Clow, D. Changes in the Timing of Snowmelt and Streamflow in Colorado: A Response to Recent Warming. J. Clim. 2010, 23, 2293–2306. [Google Scholar] [CrossRef]
- Landry, C.C.; Buck, K.A.; Raleigh, M.S.; Clark, M.P. Mountain system monitoring at Senator Beck Basin, San Juan Mountains, Colorado: A new integrative data source to develop and evaluate models of snow and hydrologic processes. Water Resour. Res. 2014, 50, 1773–1788. [Google Scholar] [CrossRef]
- Painter, T.H.; Deems, J.; Belnap, J.; Hamlet, A.F.; Landry, C.C.; Udall, B. Response of Colorado River runoff to dust radiative forcing in snow. Proc. Natl. Acad. Sci. USA 2010, 107, 17125–17130. [Google Scholar] [CrossRef]
- Elder, K.; Cline, D.; Liston, G.E.; Armstrong, R. NASA Cold Land Processes Experiment (CLPX 2002/03): Field Measurements of Snowpack Properties and Soil Moisture. J. Hydrometeorol. 2009, 10, 320–329. [Google Scholar] [CrossRef]
- Logan, L.A. Basin-Wide Water Equivalent Estimation from Snowpack Depth Measurements. Role of Snow and Ice in Hydrology; IAHS Press: Wallingford, UK, 1973; Volume 107, pp. 864–884. [Google Scholar]
- Elder, K.; Dozier, J.; Michaelsen, J. Snow accumulation and distribution in an Alpine Watershed. Water Resour. Res. 1991, 27, 1541–1552. [Google Scholar] [CrossRef]
- López-Moreno, J.; Fassnacht, S.; Heath, J.; Musselman, K.; Revuelto, J.; Latron, J.; Morán-Tejeda, E.; Jonas, T. Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent. Adv. Water Resour. 2012, 55, 40–52. [Google Scholar] [CrossRef]
- Hammond, J.C.; Saavedra, F.A.; Kampf, S.K. Global snow zone maps and trends in snow persistence 2001–2016. Int. J. Clim. 2018, 38, 4369–4383. [Google Scholar] [CrossRef]
- Reynolds, R.L.; Goldstein, H.L.; Moskowitz, B.M.; Kokaly, R.F.; Munson, S.M.; Solheid, P.; Breit, G.N.; Lawrence, C.R.; Derry, J. Dust Deposited on Snow Cover in the San Juan Mountains, Colorado, 2011–2016: Compositional Variability Bearing on Snow-Melt Effects. J. Geophys. Res. Atmos. 2020, 125, e2019JD032210. [Google Scholar] [CrossRef]
- Hansen, J.; Nazarenko, L. Soot climate forcing via snow and ice albedos. Proc. Natl. Acad. Sci. USA 2003, 101, 423–428. [Google Scholar] [CrossRef]
- Melloh, R.A.; Hardy, J.P.; Davis, R.E.; Robinson, P.B. Spectral albedo/reflectance of littered forest snow during the melt season. Hydrol. Process. 2001, 15, 3409–3422. [Google Scholar] [CrossRef]
- Marks, D.; Dozier, J. Climate and energy exchange at the snow surface in the alpine region of the Sierra Nevada 2. Snow Cover Energy Balance. Water Resour. Res. 1992, 28, 3043–3054. [Google Scholar] [CrossRef]
- Marks, D.; Domingo, J.; Susong, D.; Link, T.; Garen, D. A spatially distributed energy balance snowmelt model for application in mountain basins. Hydrol. Process. 1999, 13, 1935–1959. [Google Scholar] [CrossRef]
- Susong, D.; Marks, D.; Garen, D. Methods for developing time-series climate surfaces to drive topographically distributed energy- and water-balance models. Hydrol. Process. 1999, 13, 2003–2021. [Google Scholar] [CrossRef]
- Fassnacht, S.R. Estimating Alter-shielded gauge snowfall undercatch, snowpack sublimation, and blowing snow transport at six sites in the coterminous USA. Hydrol. Process. 2004, 18, 3481–3492. [Google Scholar] [CrossRef]
- Stewart, I.T. Changes in snowpack and snowmelt runoff for key mountain regions. Hydrol. Process. 2009, 23, 78–94. [Google Scholar] [CrossRef]
- Dudley, R.; Hodgkins, G.; McHale, M.; Kolian, M.; Renard, B. Trends in snowmelt-related streamflow timing in the conterminous United States. J. Hydrol. 2017, 547, 208–221. [Google Scholar] [CrossRef]
- Landry, C.; (Center for Snow and Avalanche Studies, Silverton, CO, USA). Personal communication, 2015.
- Fassnacht, S.R.; Sexstone, G.A.; Kashipazha, A.H.; López-Moreno, J.I.; Jasinski, M.F.; Kampf, S.K.; Von Thaden, B.C. Deriving snow-cover depletion curves for different spatial scales from remote sensing and snow telemetry data. Hydrol. Process. 2015, 30, 1708–1717. [Google Scholar] [CrossRef]
- Hultstrand, D.M.; Fassnacht, S.R.; Stednick, J.D.; Hiemstra, C.A. Snowpack Distribution Using Topographical, Climatological and Winter Season Index Inputs. Atmosphere 2021, 13, 3. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Dressler, K.A.; Bales, R.C. Snow water equivalent interpolation for the Colorado River Basin from snow telemetry (SNOTEL) data. Water Resour. Res. 2003, 39, 1208. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Hultstrand, M. Snowpack variability and trends at long-term stations in northern Colorado, USA. Proc. Int. Assoc. Hydrol. Sci. 2015, 371, 131–136. [Google Scholar] [CrossRef]
- Fassnacht, S.; Patterson, G.; Venable, N.; Cherry, M.; Pfohl, A.; Sanow, J.; Tedesche, M. How Do We Define Climate Change? Considering the Temporal Resolution of Niveo-Meteorological Data. Hydrology 2020, 7, 38. [Google Scholar] [CrossRef]
- Doskocil, L.G.; Fassnacht, S.R.; Derry, J.E. Mystery Peaks: Estimating the Unusual Double Peak Streamflow Behavior in the Uncompahgre River Basin. Col. Water 2021, 38, 28–29. [Google Scholar]
- Sahaar, M.; Fassnacht, S.R. The Timing of Peak Streamflow in a Small River versus Snowpack Melt-out. Col. Water 2021, 38, 21–23. [Google Scholar]
- Seidel, F.C.; Rittger, K.; Skiles, S.M.; Molotch, N.P.; Painter, T.H. Case study of spatial and temporal variability of snow cover, grain size, albedo and radiative forcing in the Sierra Nevada and Rocky Mountain snowpack derived from imaging spectroscopy. Cryosphere 2016, 10, 1229–1244. [Google Scholar] [CrossRef]
- Skiles, S.M.; Painter, T.H. A 9-yr record of dust on snow in the Colorado River Basin. In Scientific Investigations Report 2015–5180, Proceedings of the 12th Biennial Conference of Research on the Colorado Plateau, Flagstaff, AZ, USA, 16–19 September 2013; Ralston, B.E., Ed.; U.S. Geological Survey: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Skiles, S.M.; Painter, T.H. Toward Understanding Direct Absorption and Grain Size Feedbacks by Dust Radiative Forcing in Snow with Coupled Snow Physical and Radiative Transfer Modeling. Water Resour. Res. 2019, 55, 7362–7378. [Google Scholar] [CrossRef]
- Flanner, M.G.; Zender, C.S.; Randerson, J.T.; Rasch, P.J. Present-day climate forcing and response from black carbon in snow. J. Geophys. Res. Atmos. 2007, 112, D11202. [Google Scholar] [CrossRef]
- Lehning, M.; Bartelt, P.; Brown, B.; Russi, T.; Stöckli, U.; Zimmerli, M. snowpack model calculations for avalanche warning based upon a new network of weather and snow stations. Cold Reg. Sci. Technol. 1999, 30, 145–157. [Google Scholar] [CrossRef]
- Reimanis, D.C. Variable Fresh Snow Albedo: How Snowpack and Sub-nivean Properties Influence Fresh Snow Reflectance. Master’s Thesis, Watershed Science, Colorado State University, Fort Collins, CO, USA, 2021. [Google Scholar]
- Flanner, M.G.; Arnheim, J.B.; Cook, J.M.; Dang, C.; He, C.; Huang, X.; Singh, D.; Skiles, S.M.; Whicker, C.A.; Zender, C.S. SNICAR-ADv3: A community tool for modeling spectral snow albedo. Geosci. Model Dev. 2021, 14, 7673–7704. [Google Scholar] [CrossRef]
- Kilmister, I.; Campbell, P.; Dee, M. Till the End; UDR GmbH: Husum, Germany, 2015. [Google Scholar]
- Martinec, J. Snowmelt—runoff model for stream flow forecasts. Hydrol. Res. 1975, 6, 145–154. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Soulis, E.D.; Kouwen, N. Algorithm application to improve weather radar snowfall estimates for winter hy-drologic modelling. Hydrol. Process. 1999, 13, 3017–3039. [Google Scholar] [CrossRef]
- Duncan, C.R. Patterns of Dust-Enhanced Absorbed Energy and Shifts in Melt Timing for Snow of Southwestern Colorado. Master’s Thesis, Watershed Science, Colorado State University, Fort Collins, CO, USA, 2020. Available online: https://hdl.handle.net/10217/211991 (accessed on 10 February 2022).
- Fassnacht, S.R.; Brown, K.S.J.; Blumberg, E.J.; López-Moreno, J.I.; Covino, T.P.; Kappas, M.; Huang, Y.; Leone, V.; Kashipazha, A.H. Distribution of snow depth variability. Front. Earth Sci. 2018, 12, 683–692. [Google Scholar] [CrossRef]
- Goodison, B.E.; Louie, P.Y.T.; Yang, D. WMO Solid Precipitation Measurement Intercomparison Final Report; WMO Instruments and Observing Methods Report, No. 67, WMO/TD No. 872; WMO: Geneva, Switzerland, 1998. [Google Scholar]
- Fassnacht, S.R. Data time step to estimate snowpack accumulation at select United States meteorological stations. Hydrol. Process. 2007, 21, 1608–1615. [Google Scholar] [CrossRef]
- Kochendorfer, J.; Nitu, R.; Wolff, M.; Mekis, E.; Rasmussen, R.; Baker, B.; Earle, M.E.; Reverdin, A.; Wong, K.; Smith, C.D.; et al. Testing and development of transfer functions for weighing precipitation gauges in WMO-SPICE. Hydrol. Earth Syst. Sci. 2018, 22, 1437–1452. [Google Scholar] [CrossRef]
- Kimball, J.S.; Running, S.W.; Nemani, R. An improved method for estimating surface humidity from daily minimum temper-ature. Agric. Forest Meteorol. 1997, 85, 87–98. [Google Scholar] [CrossRef]
- Fassnacht, S.; Soulis, E. Implications during transitional periods of improvements to the snow processes in the land surface scheme—Hydrological model WATCLASS. Atmosphere-Ocean 2002, 40, 389–403. [Google Scholar] [CrossRef]
- Rajagopal, S.; Harpold, A. Testing and Improving Temperature Thresholds for Snow and Rain Prediction in the Western United States. JAWRA J. Am. Water Resour. Assoc. 2016, 52, 1142–1154. [Google Scholar] [CrossRef]
- Fassnacht, S.R.; Venable, N.B.H.; Khishigbayar, J.; Cherry, M.L. The probability of precipitation as snow derived from daily air temperature for high elevation Areas of Colorado, United States. In Cold and Mountain Region Hydrological Systems under Climate Change: Towards Improved Projections, Proceedings of the Symposium H02, IAHS-IAPSO-IASPEI Assembly, Gothenburg, Sweden, 22–26 July 2013; IAHS: Wallingford, UK, 2013; Volume 360, pp. 65–70. [Google Scholar]
- Jennings, K.S.; Winchell, T.S.; Livneh, B.; Molotch, N.P. Spatial variation of the rain–snow temperature threshold across the Northern Hemisphere. Nat. Commun. 2018, 9, 1148. [Google Scholar] [CrossRef]
- Judson, A.; Doesken, N. Density of Freshly Fallen Snow in the Central Rocky Mountains. Bull. Am. Meteorol. Soc. 2000, 81, 1577–1587. [Google Scholar] [CrossRef]
- Meinhardt, M.; Fassnacht, S.R. Fresh snow density from the Fort Collins Colorado meteorological station and new measure-ments. Col. Water 2020, 37, 7–9. [Google Scholar] [CrossRef]
- Thomas, C.W. On the Transfer of Visible Radiation through Sea Ice and Snow. J. Glaciol. 1963, 4, 481–484. [Google Scholar] [CrossRef]
- Chan, H.G.; King, M.D.; Frey, M.M. The impact of parameterising light penetration into snow on the photochemical production of NOx and OH radicals in snow. Atmos. Chem. Phys. 2015, 15, 7913–7927. [Google Scholar] [CrossRef]
- Reay, H.J.; France, J.L.; King, M. Decreased albedo,e-folding depth and photolytic OH radical and NO2production with increasing black carbon content in Arctic snow. J. Geophys. Res. Earth Surf. 2012, 117, D00R20. [Google Scholar] [CrossRef]
- Munson, S.M.; Belnap, J.; Okin, G.S. Responses of wind erosion to climate-induced vegetation changes on the Colorado Plateau. Proc. Natl. Acad. Sci. USA 2011, 108, 3854–3859. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, P.H. Is ‘Centre of Volume’ a robust indicator of changes in snowmelt timing? Hydrol. Process. 2013, 27, 2691–2698. [Google Scholar] [CrossRef]
- Flynn, H.; MacDonald, M.; Fassnacht, S.R. Assessing Baseflow in Snow-Dominated Watersheds. Col. Water 2021, 38, 12–13. [Google Scholar] [CrossRef]
- Rasmussen, K.L.; Sexstone, G.A.; McGrath, D.; Liston, G.E.; Fassnacht, S.R.; Dougherty, E.; Kingston, A. Peering into the future: The evolution of seasonal snow in the Colorado Rocky Mountains. Col. Water 2020, 37, 9–12. [Google Scholar] [CrossRef]
- Pagano, T.C.; Wood, A.W.; Ramos, M.-H.; Cloke, H.; Pappenberger, F.; Clark, M.P.; Cranston, M.; Kavetski, D.; Mathevet, T.; Sorooshian, S.; et al. Challenges of Operational River Forecasting. J. Hydrometeorol. 2014, 15, 1692–1707. [Google Scholar] [CrossRef]
- Garousi-Nejad, I.; Tarboton, D.G. A comparison of National Water Model retrospective analysis snow outputs at snow telemetry sites across the Western United States. Hydrol. Process. 2022, 36, e14469. [Google Scholar] [CrossRef]
- Horton, P.; Schaefli, B.; Kauzlaric, M. Why do we have so many different hydrological models? A review based on the case of Switzerland. WIREs Water 2021, 9, e1574. [Google Scholar] [CrossRef]
- Jin, H.; Barry, S.; Paydar, Z.; Shao, Q.; Van Dijk, A. Decision tree based uncertainty framework for water accounting. In Proceedings of the MODSIM 2011 International Congress on Modelling and Simulation, Perth, Australia, 12–16 December 2011; pp. 3861–3867. [Google Scholar]
- Ham, J.M.; Miner, G.L.; Kluitenberg, G.J. A New Approach to Sap Flow Measurement Using 3D Printed Gauges and Open-source Electronics. In Proceedings of the American Geophysical Union Fall Meeting, San Francisco, CA, USA, 14–18 December 2015; p. H32B-04. [Google Scholar]
- Collados-Lara, A.; Fassnacht, S.R.; Pulido-Velazquez, D.; Pfohl, A.K.; Morán-Tejeda, E.; Venable, N.B.; Pardo-Igúzquiza, E.; Puntenney-Desmond, K. Intra-day variability of temperature and its near-surface gradient with elevation over mountainous terrain: Comparing MODIS land surface temperature data with coarse and fine scale near-surface measurements. Int. J. Clim. 2020, 41, E1435–E1449. [Google Scholar] [CrossRef]
- Rice, D.; Fassnacht, S.R. Does it Get Cooler Going Down the Hill? Measuring Hillslope-Scale Temperature Gradients. Col. Water 2021, 38, 16–18. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).