Flow Topology in the Confluence of an Open Channel with Lateral Drainage Pipe
Abstract
:1. Introduction
- What would be the impact of submerged lateral drainage pipe discharges into rectangular open channels on the flow topology (including maximum water height) in a CHZ for different channel widths, flow rates, Froude numbers, confluence angles, inlet pipe diameters, and lateral flows to the main channel flow ratios?
- Under what circumstances would the maximum increase in water surface elevation be confined to the desired values (e.g., 10%, or 20%)?
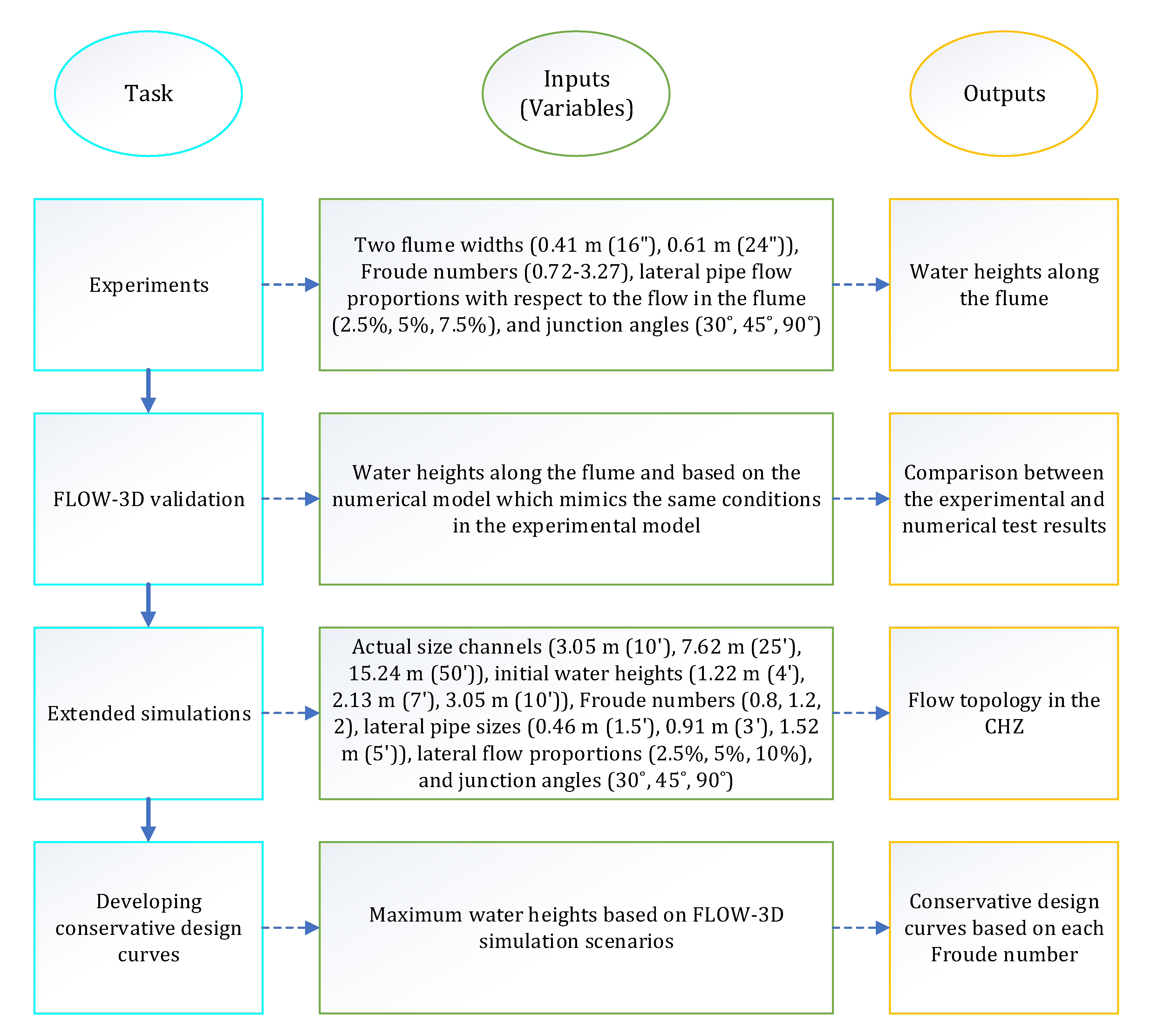
2. Materials and Methods
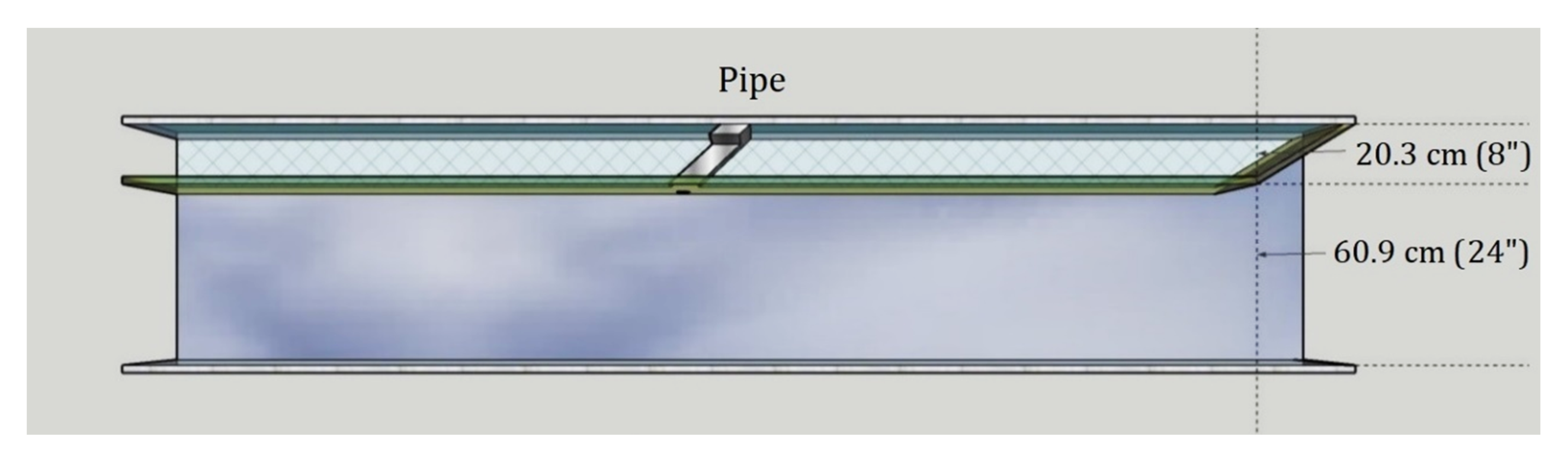
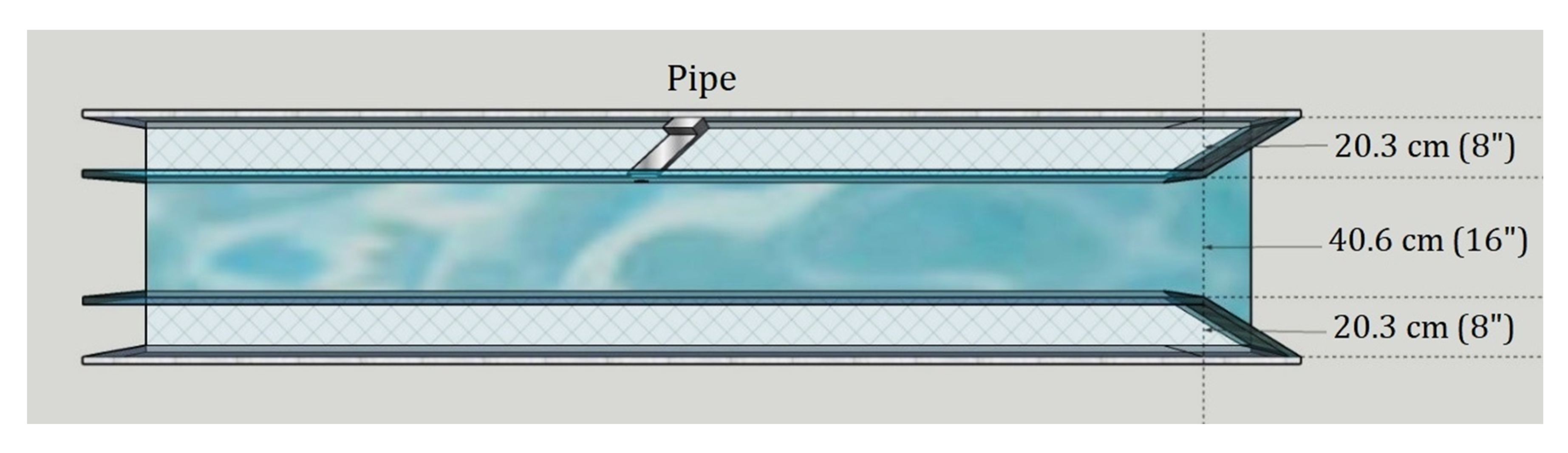
2.1. Experiments
Measurement Equipment
2.2. Numerical Modeling
2.2.1. Governing Equations
2.2.2. Momentum Equations
2.2.3. Fluid Interfaces and Free-Surfaces
3. Results and Discussion
3.1. Flume Test Results
3.1.1. Water Height Measurements
3.1.2. Water Height Ratios
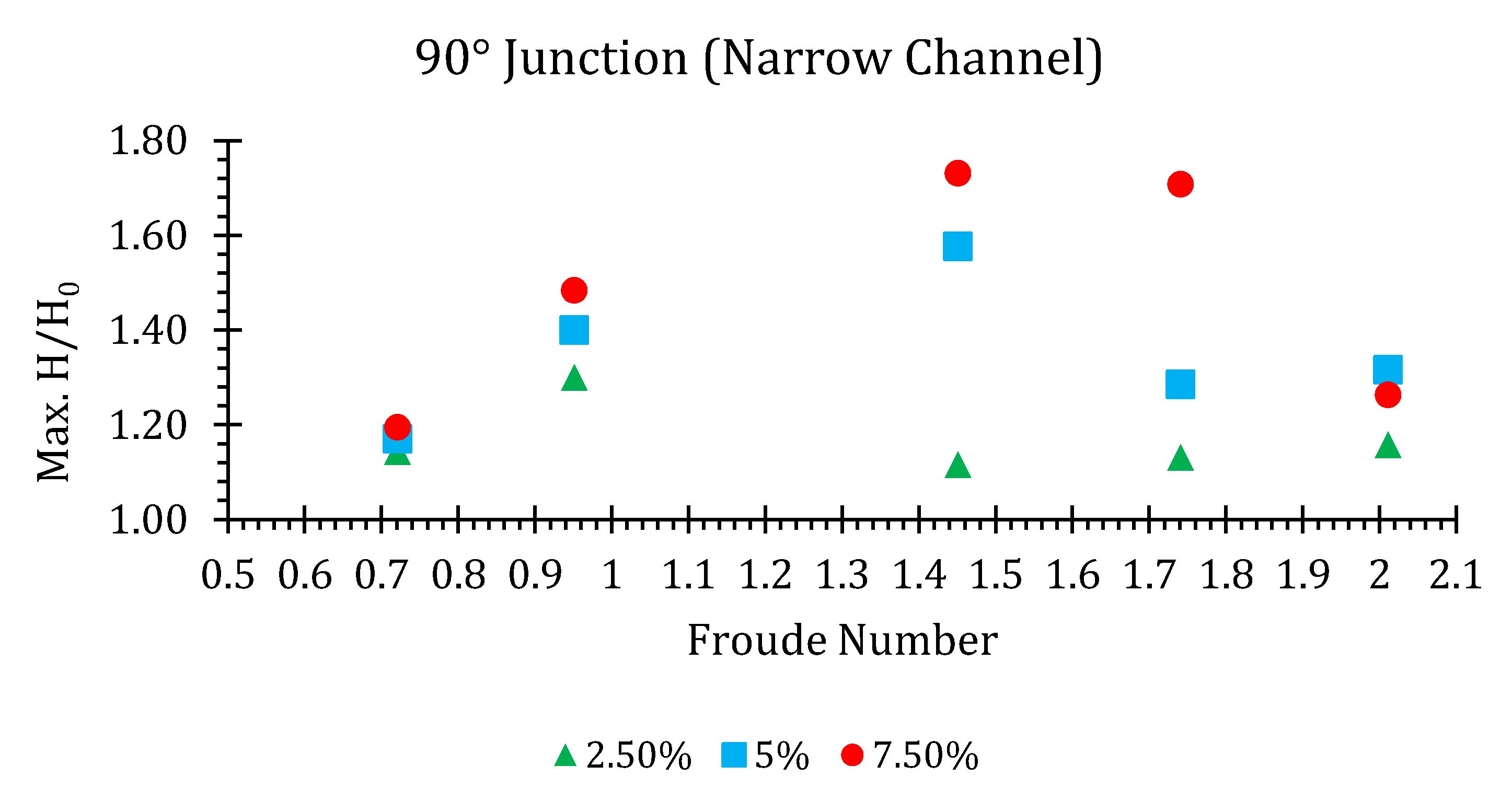
90° Junction
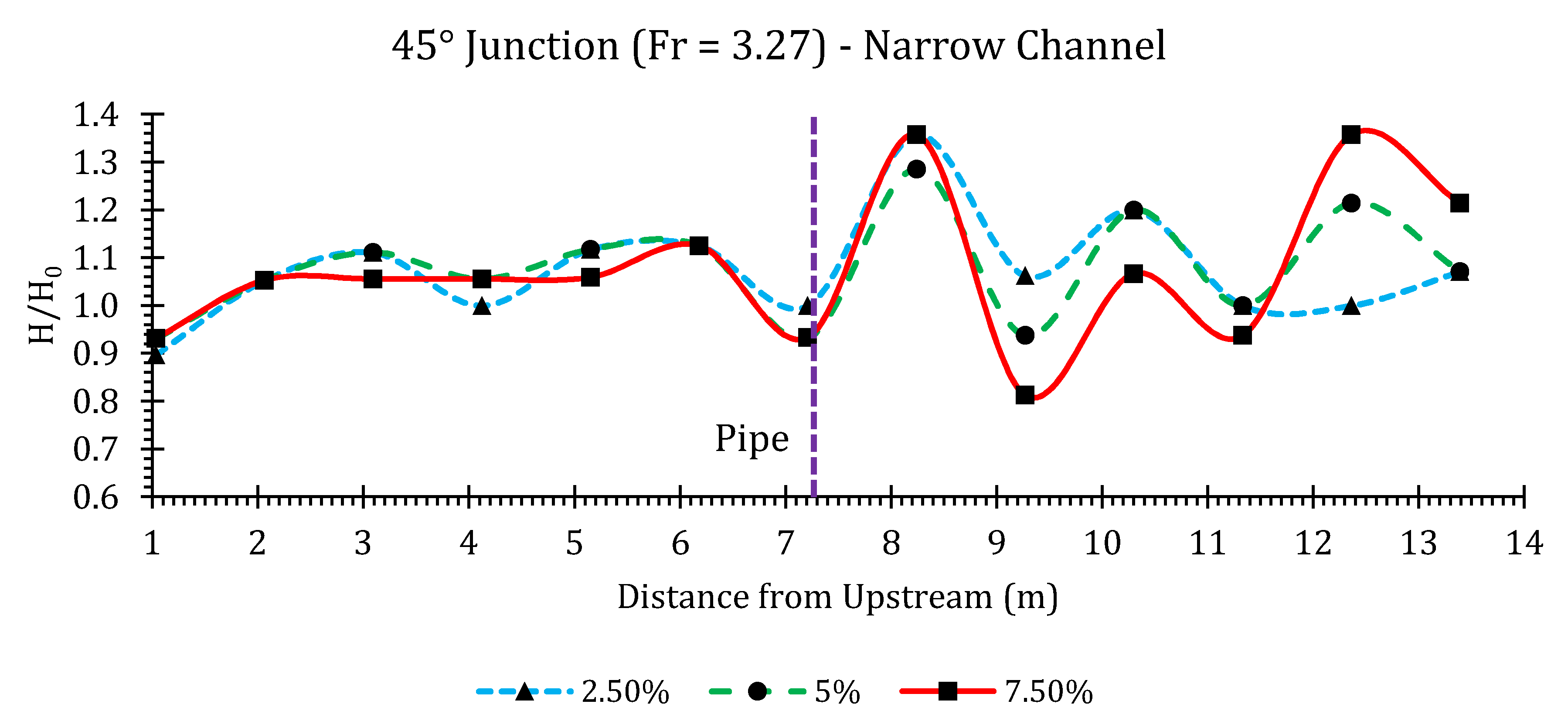
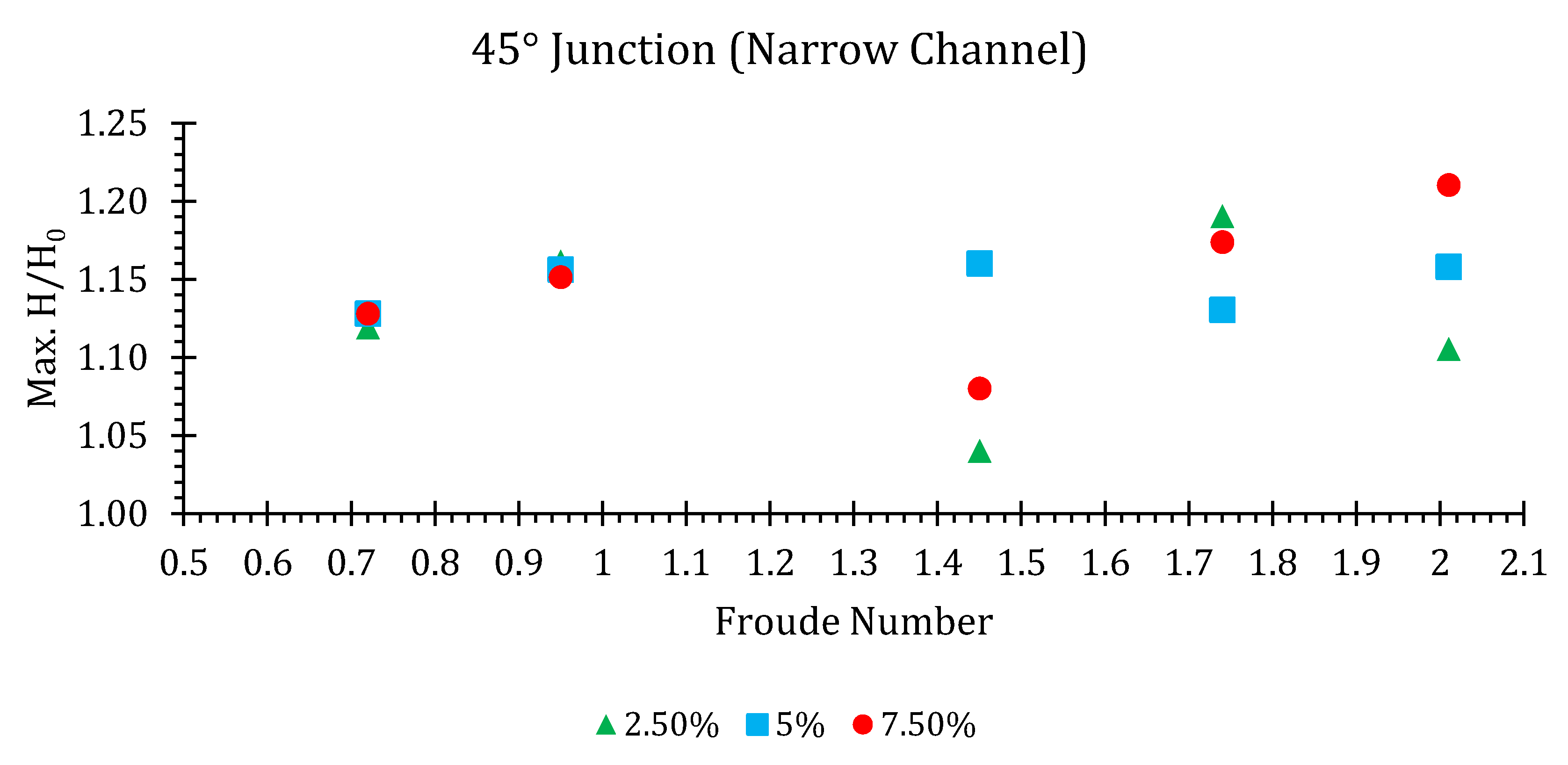
45° Junction
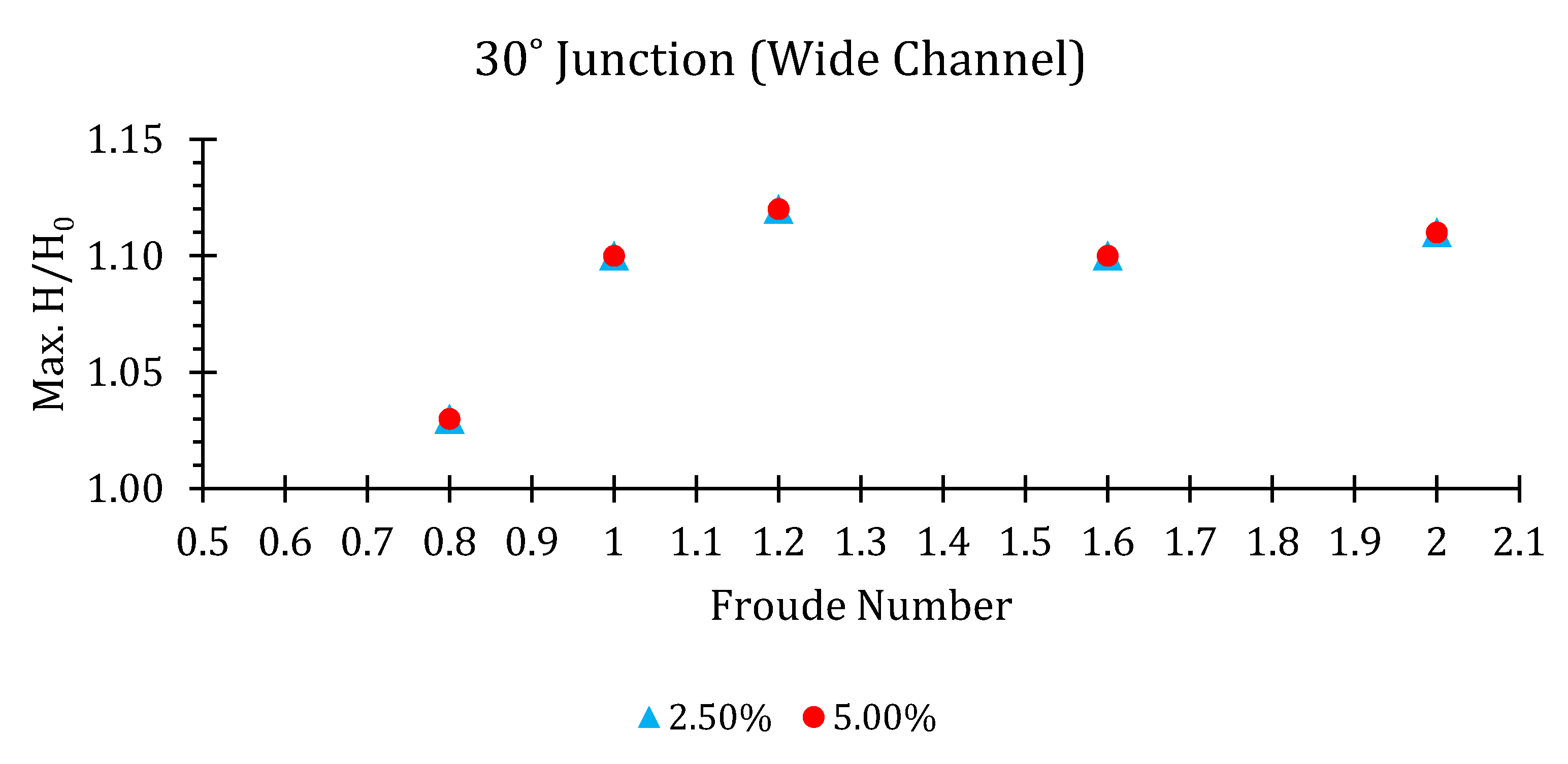
30° Junction
3.2. Numerical Model Setup
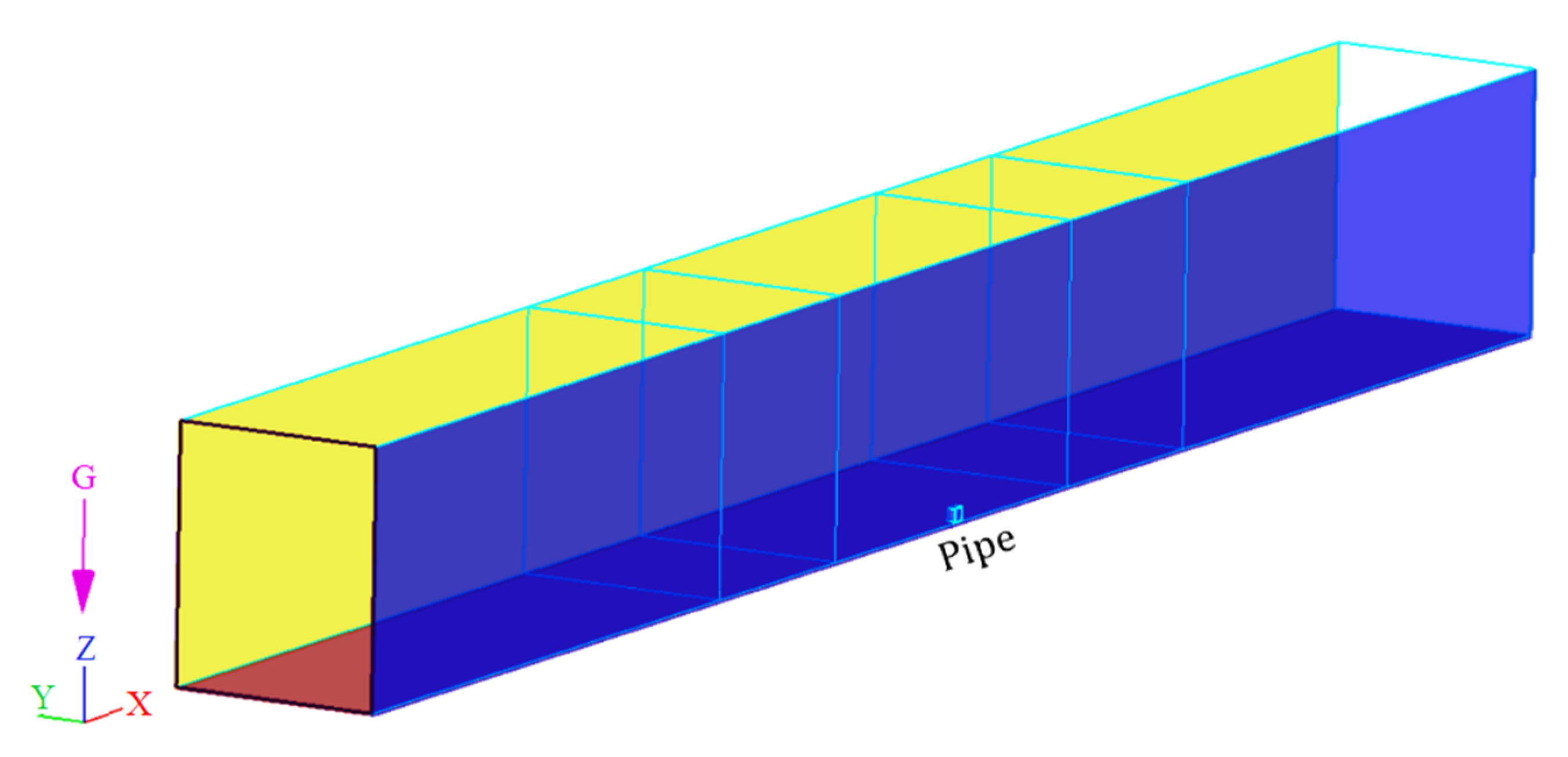
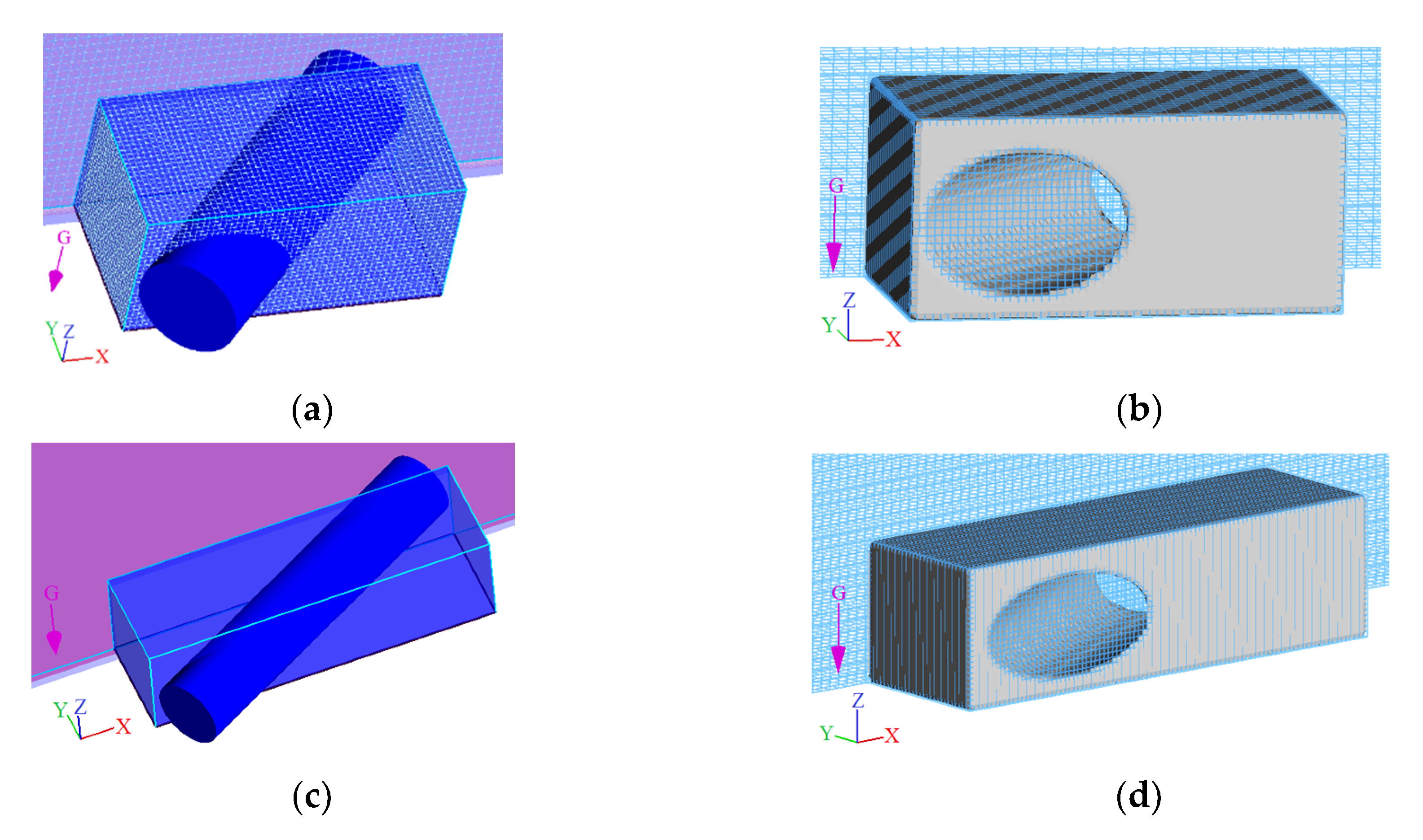
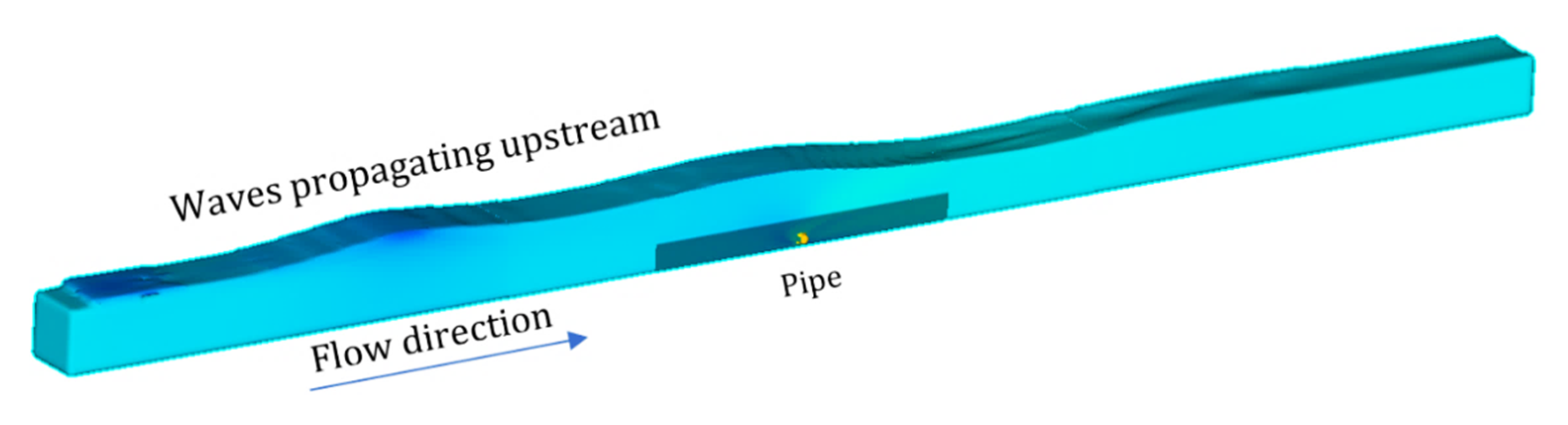
3.2.1. Geometry
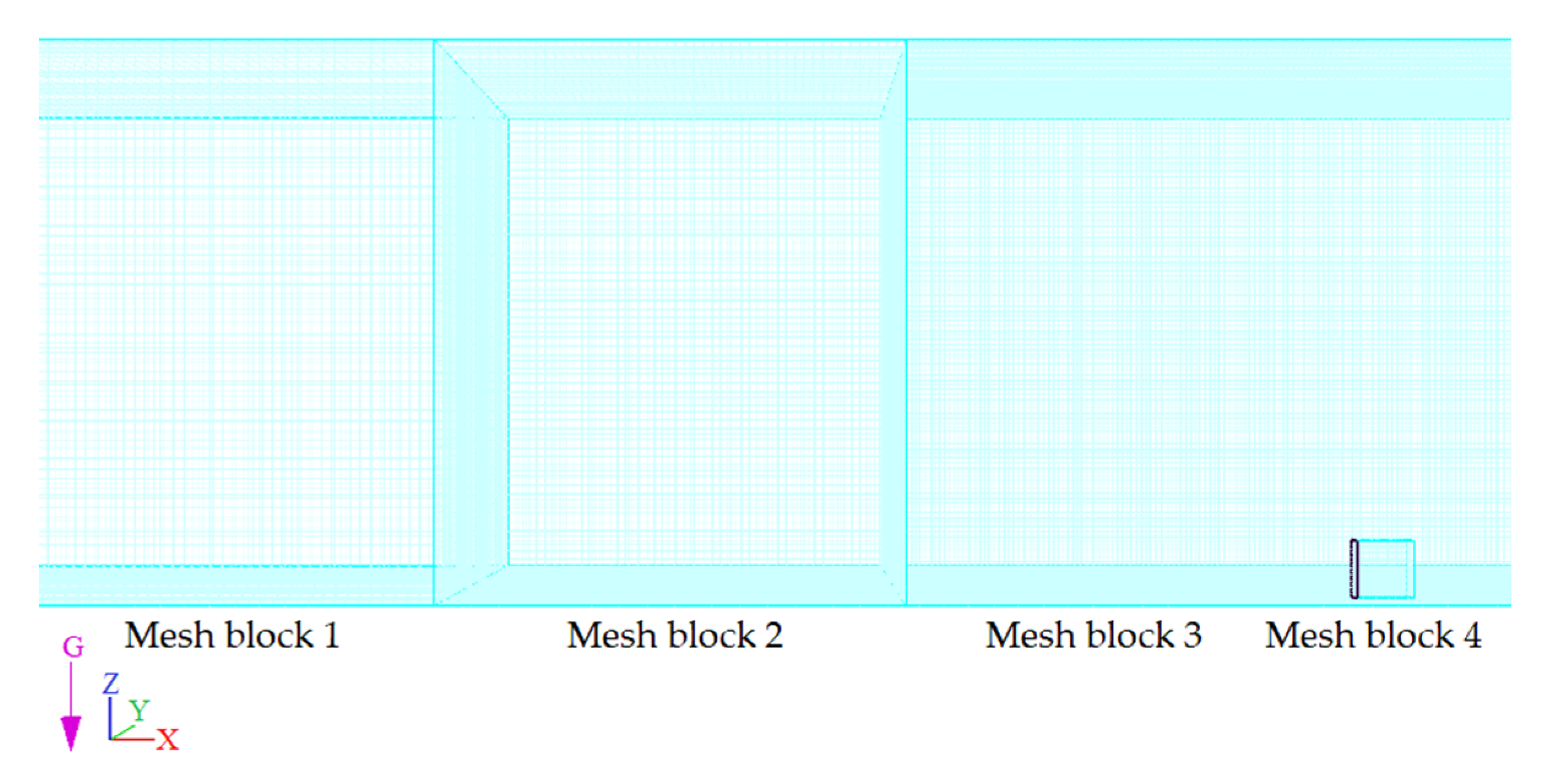
3.2.2. Meshing
3.2.3. Favor
3.2.4. Boundary Conditions
3.2.5. Initial Conditions
3.2.6. Other Considerations in Setting up the Model
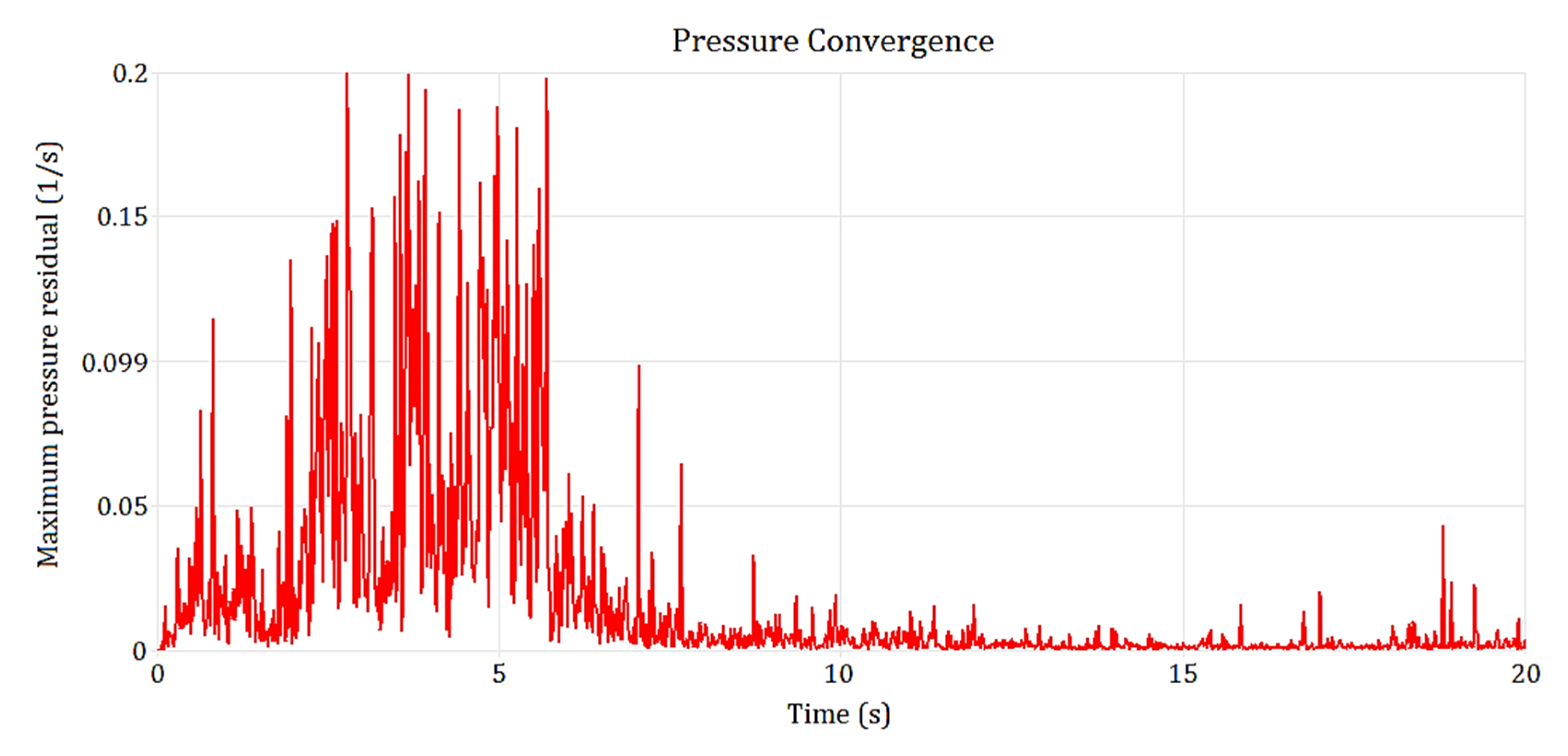
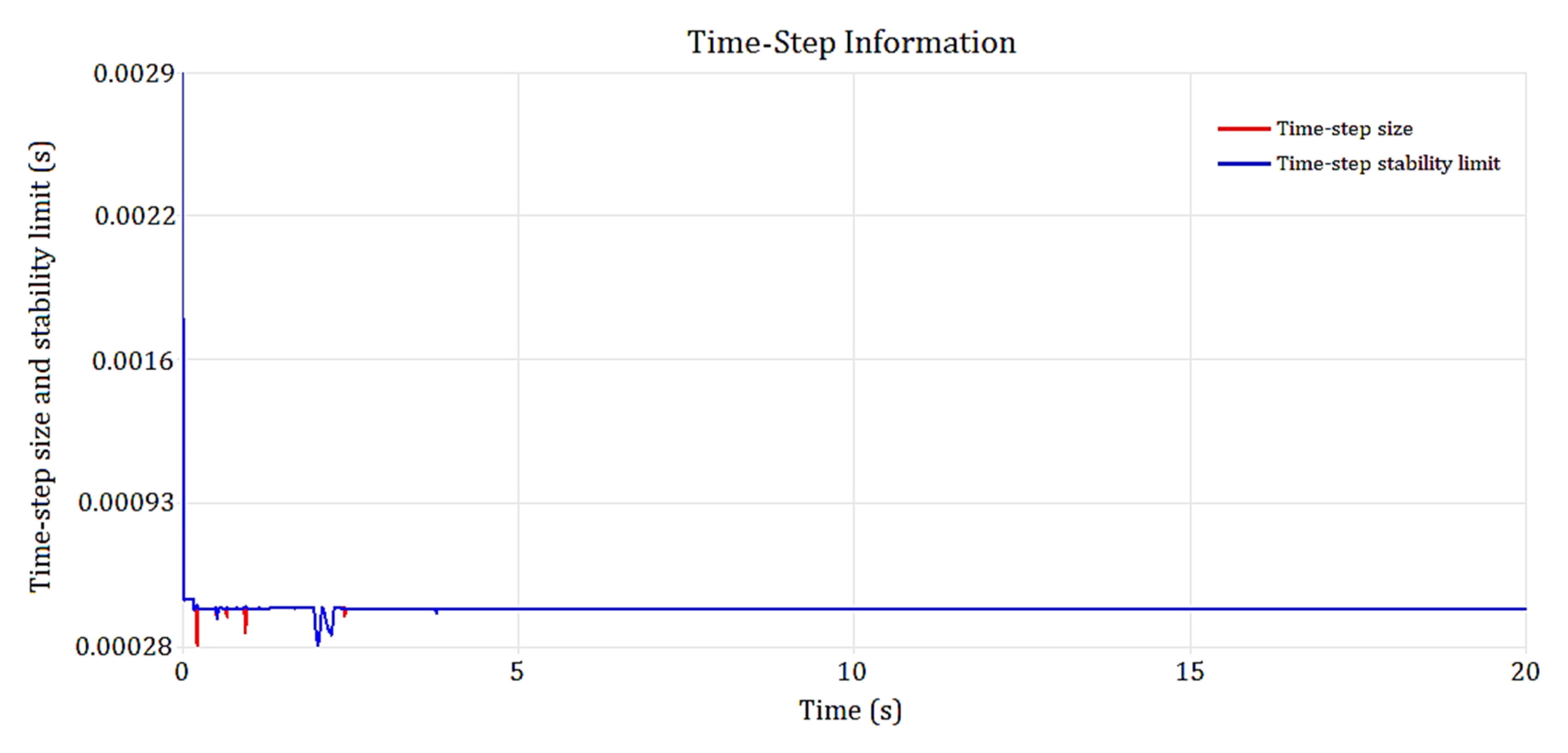
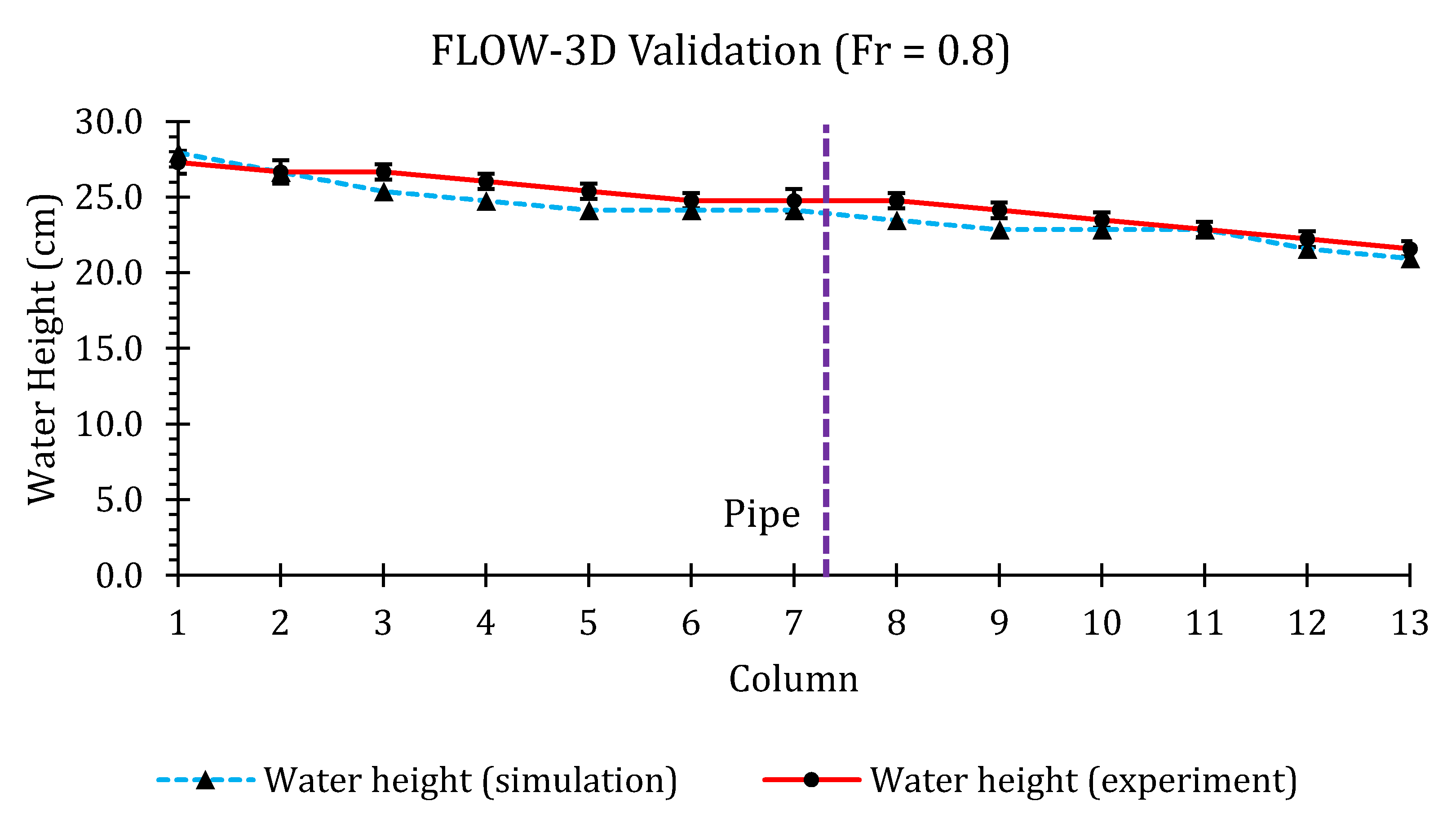
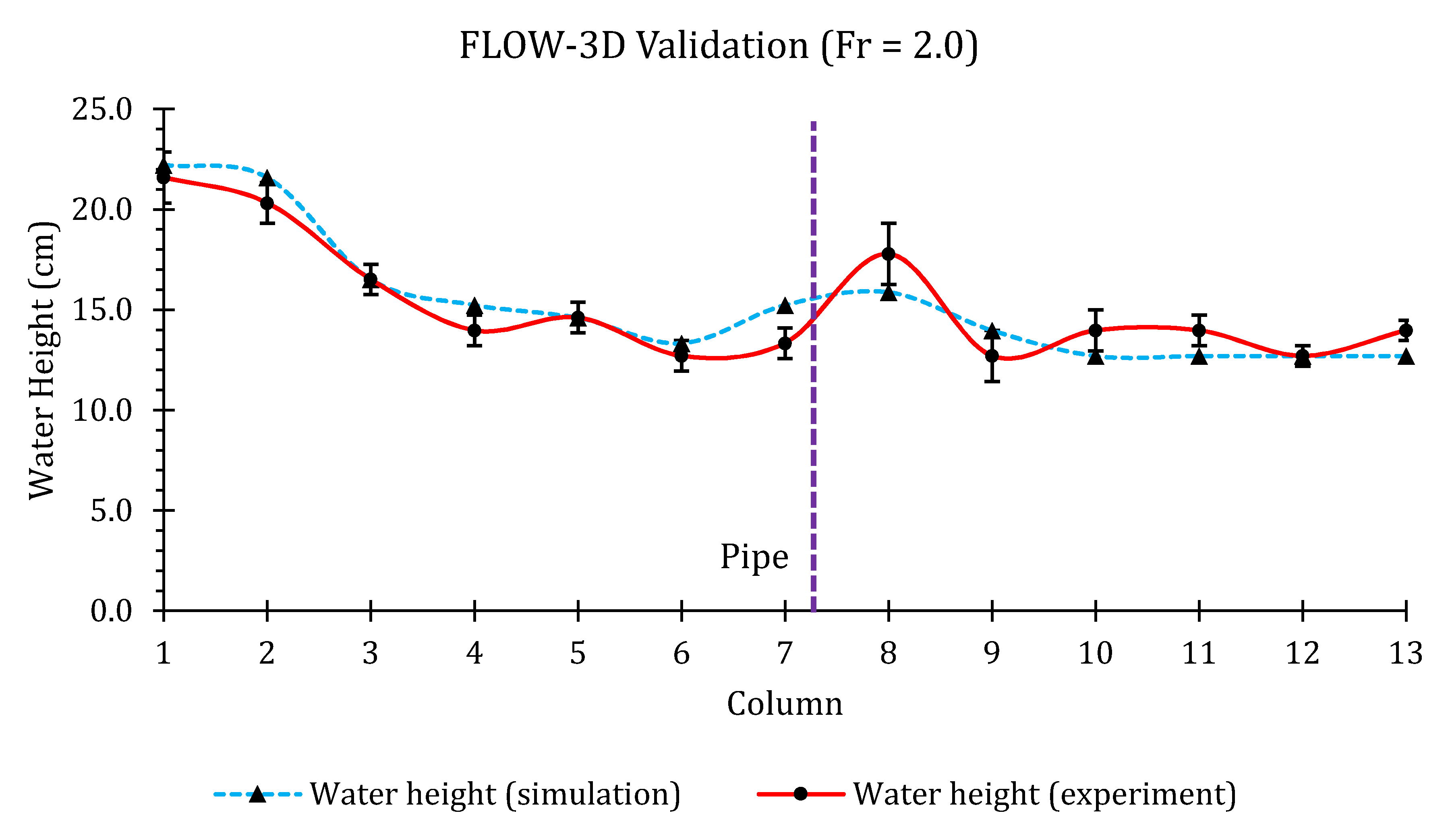
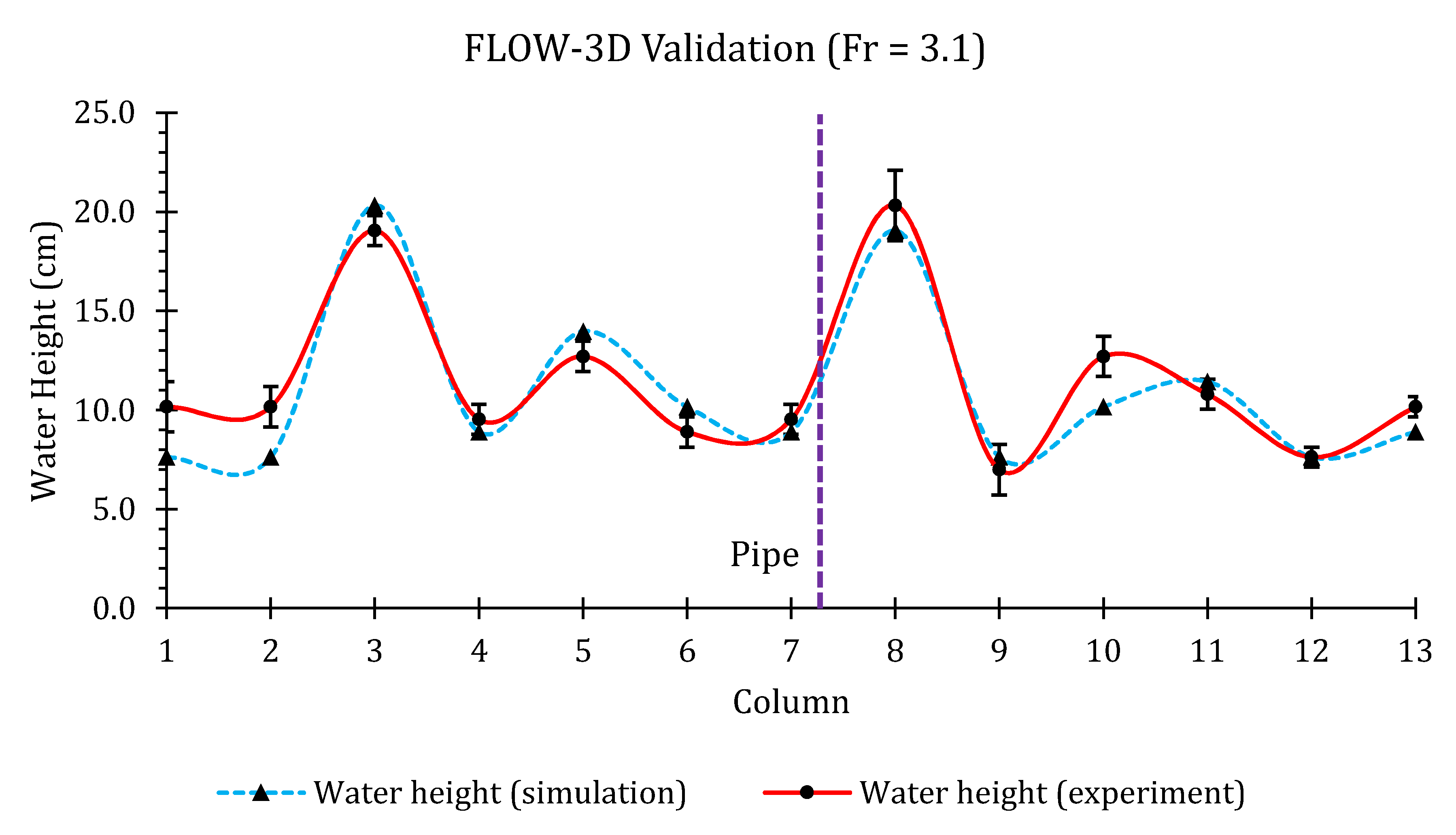
3.2.7. Convergence and Validation
3.3. Simulation Results
Surface Water Elevations and Conservative Design Curves
4. Conclusions and Recommendations
Author Contributions
Funding
Conflicts of Interest
Appendix A

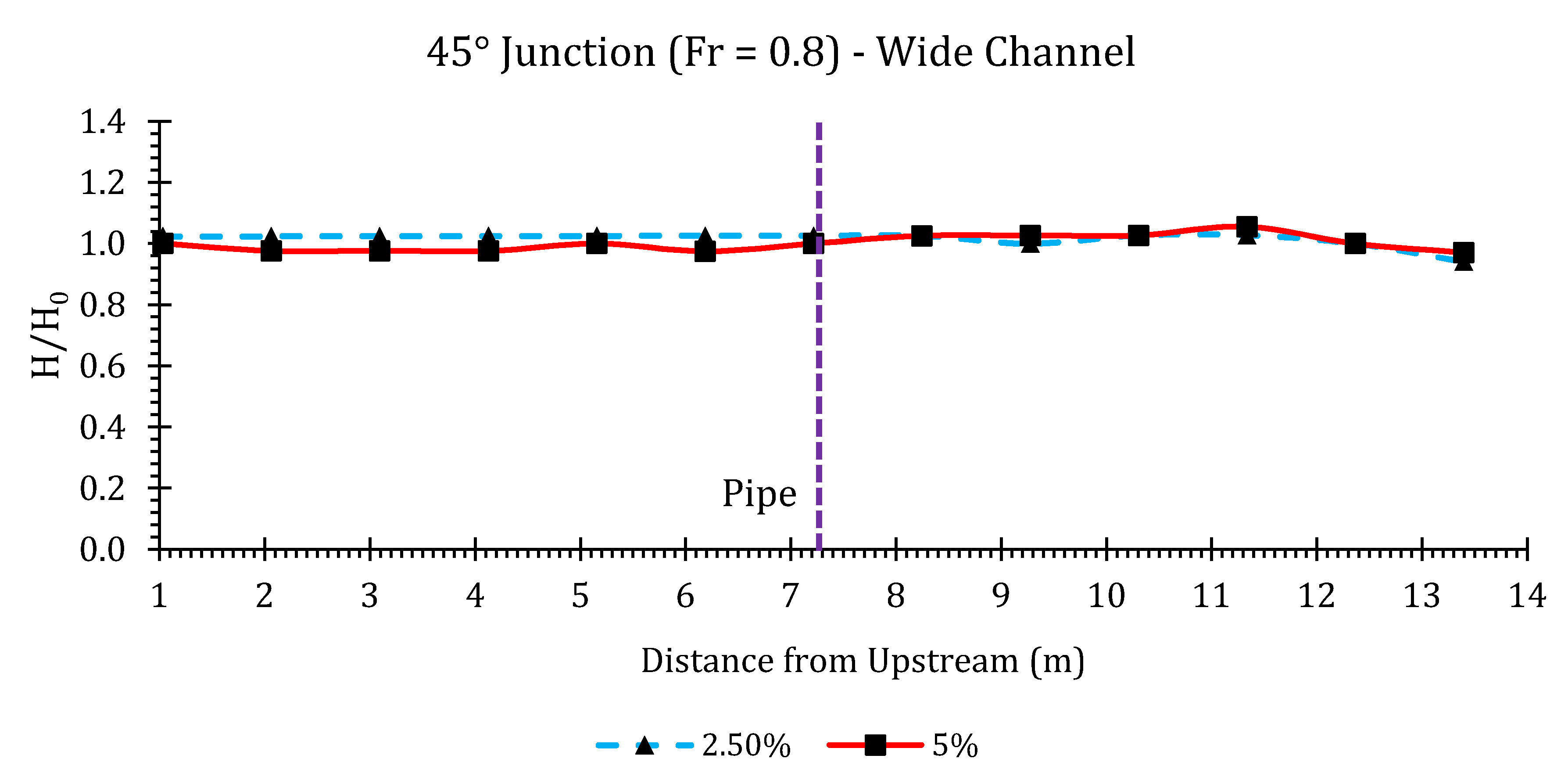
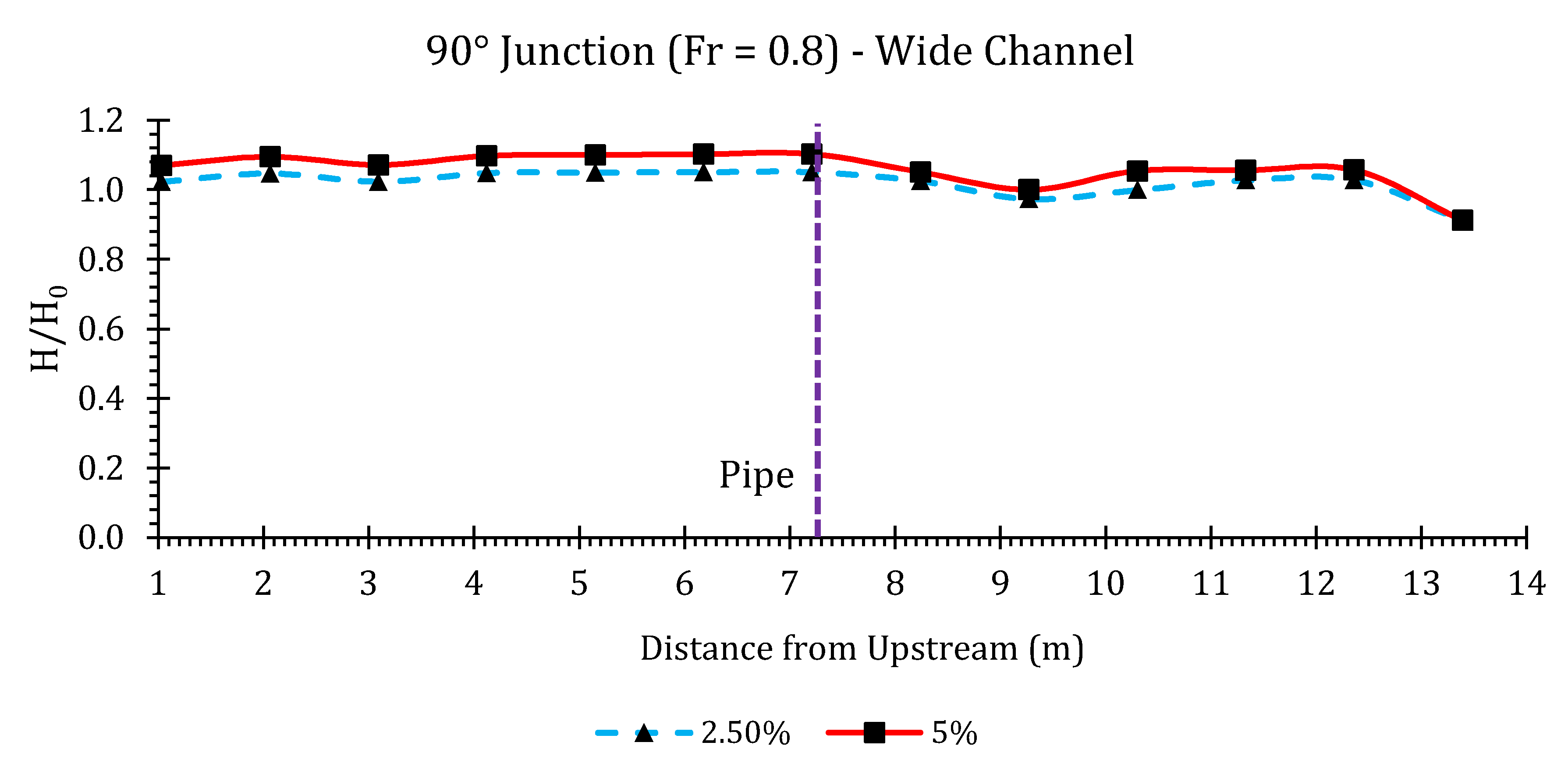
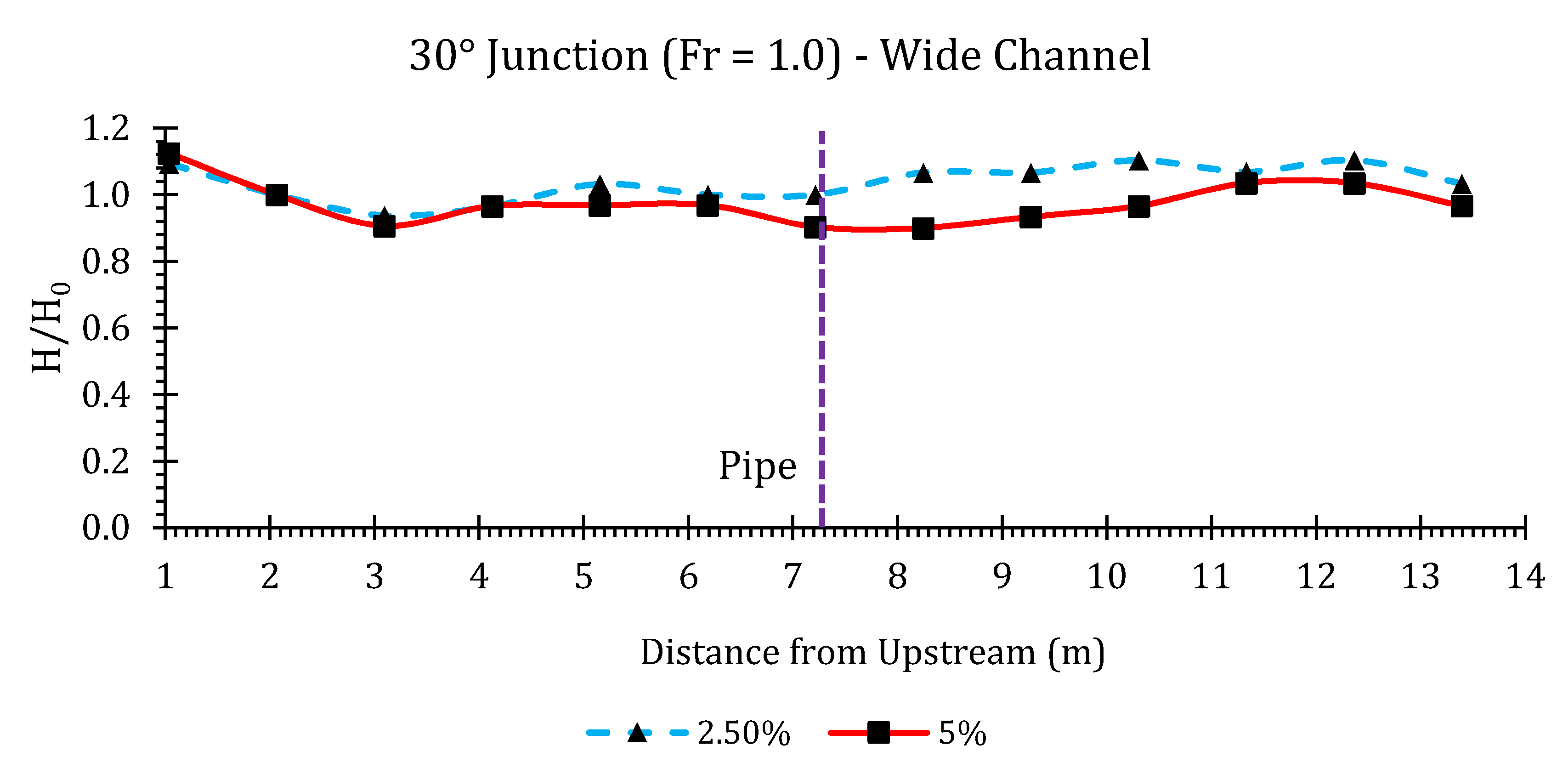
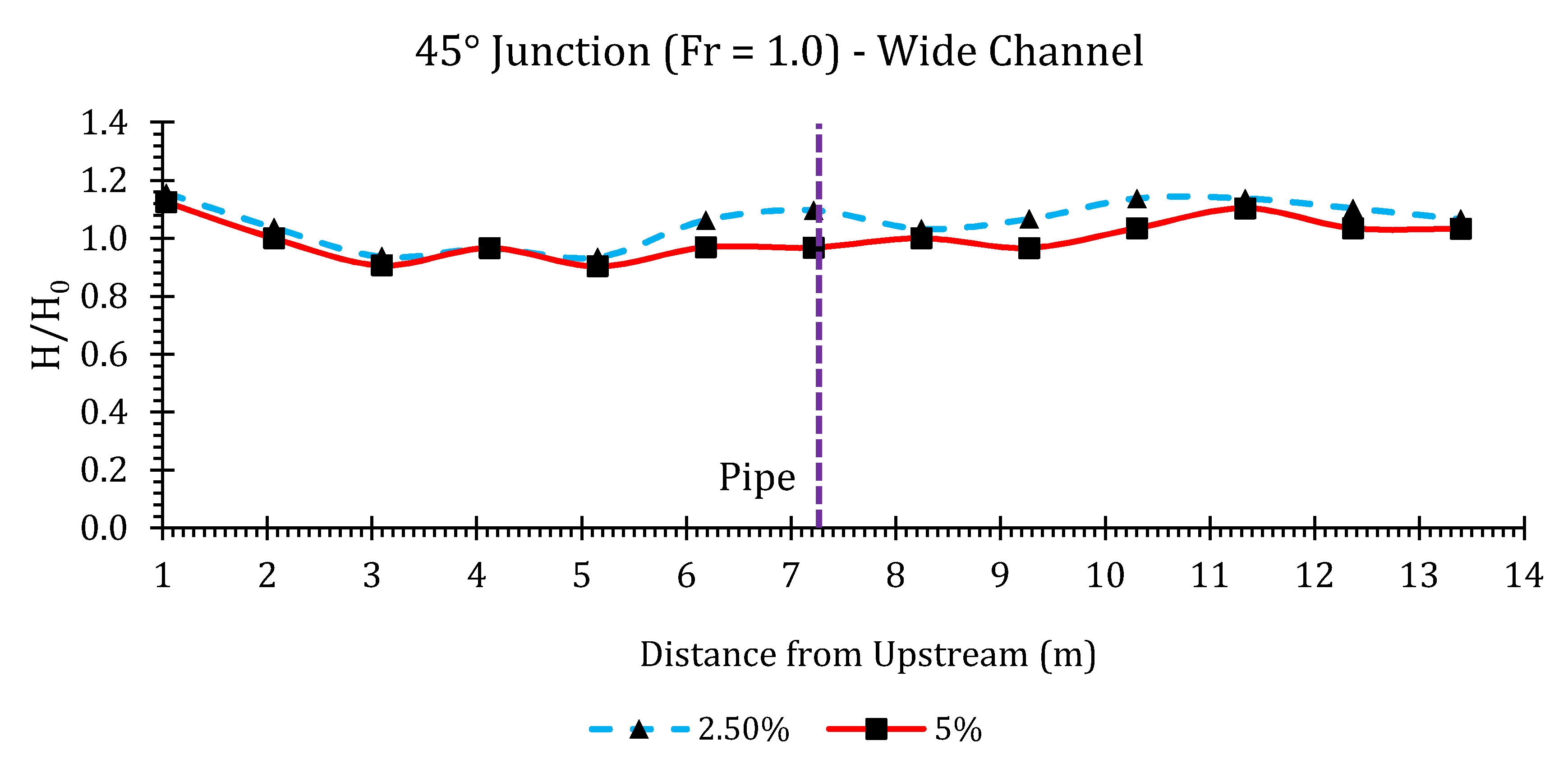
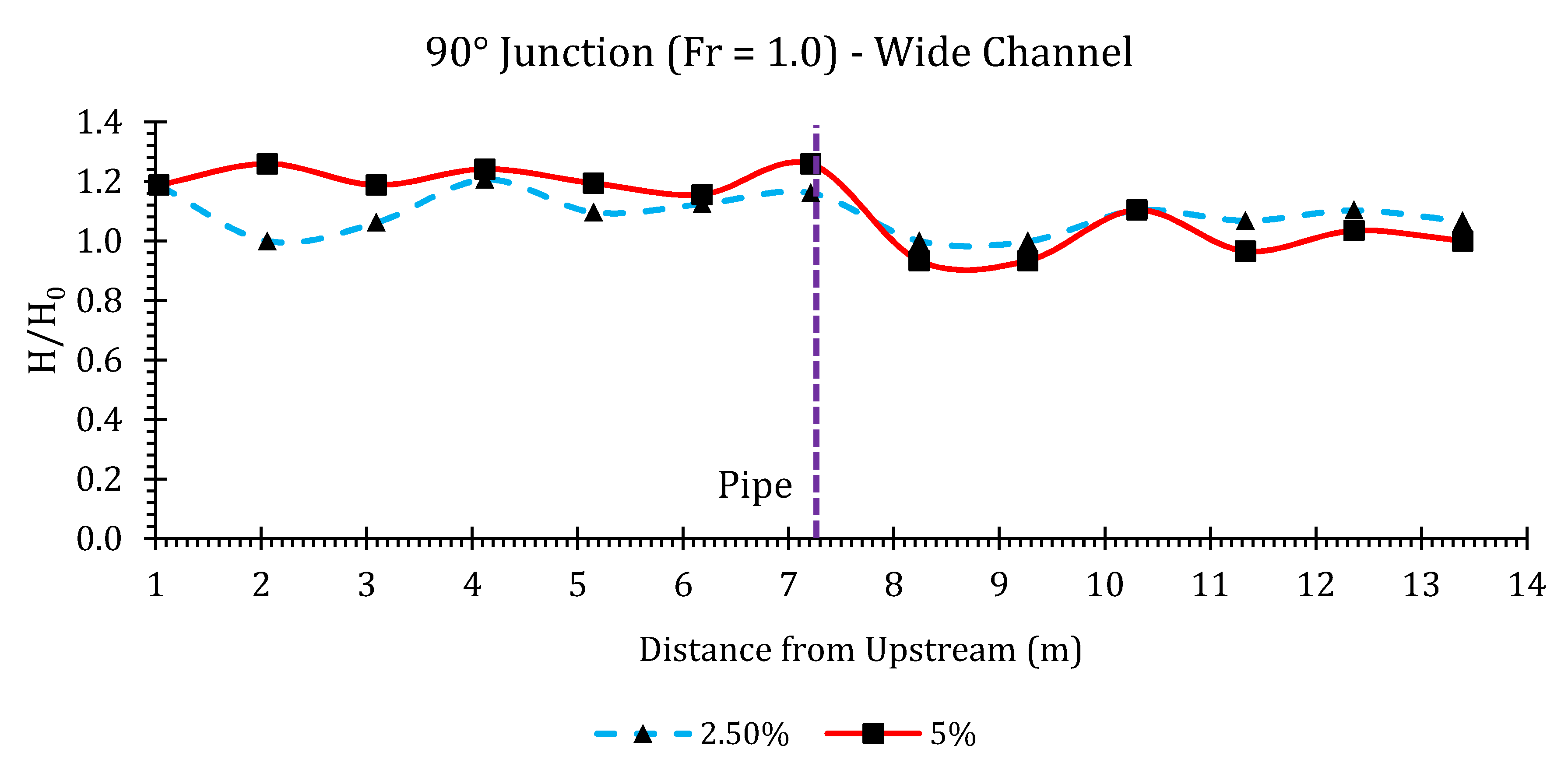
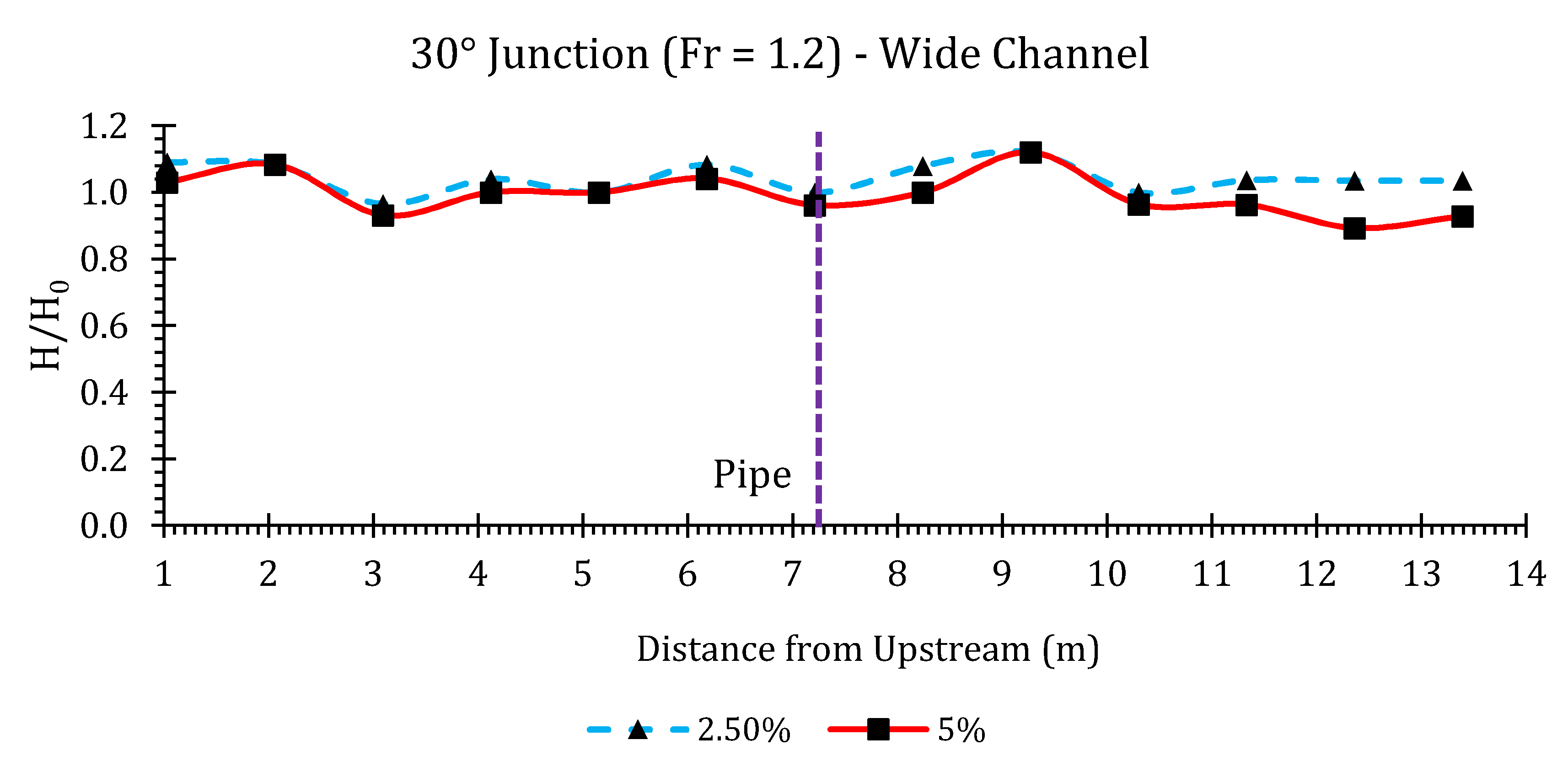
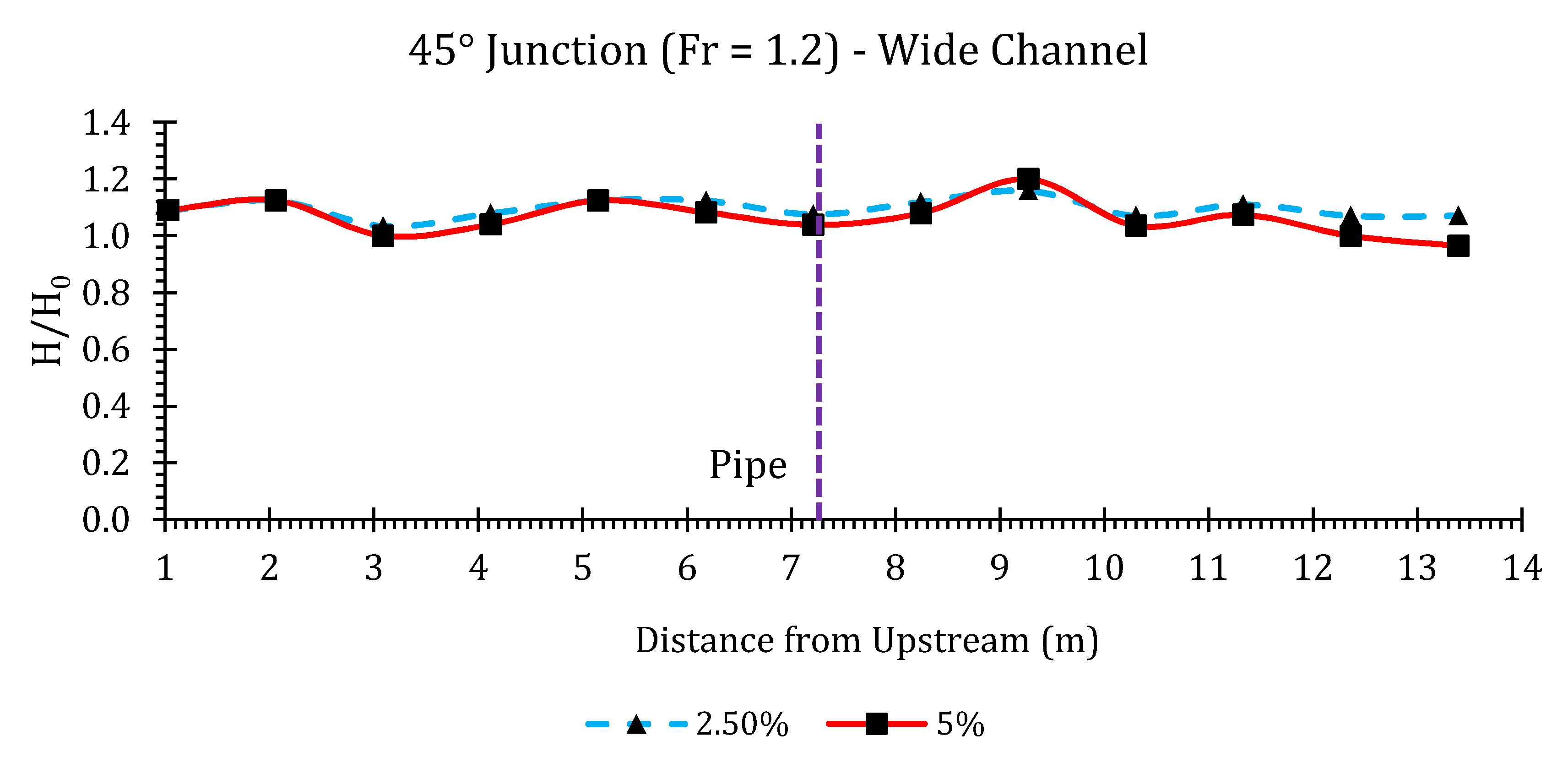
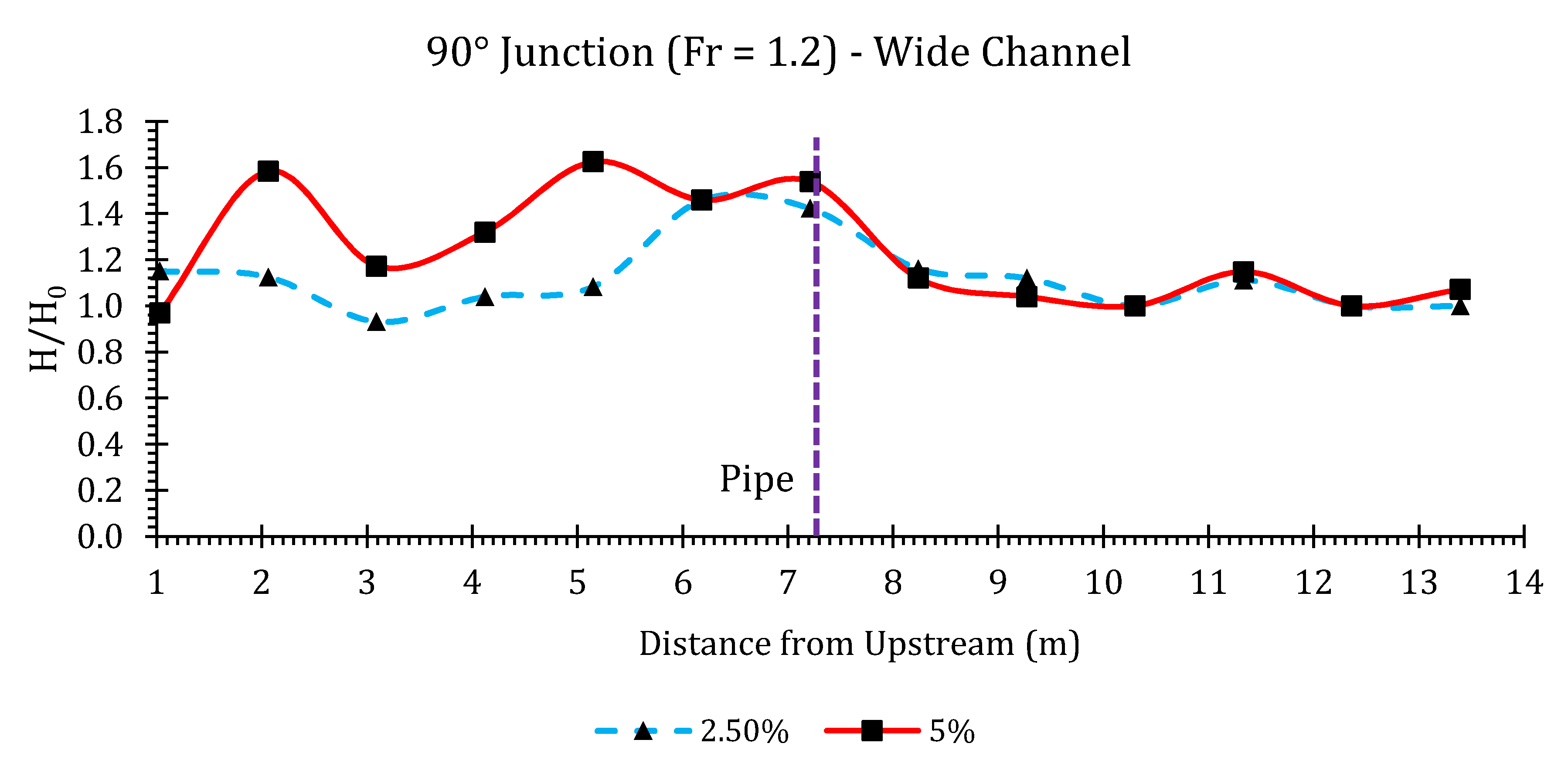
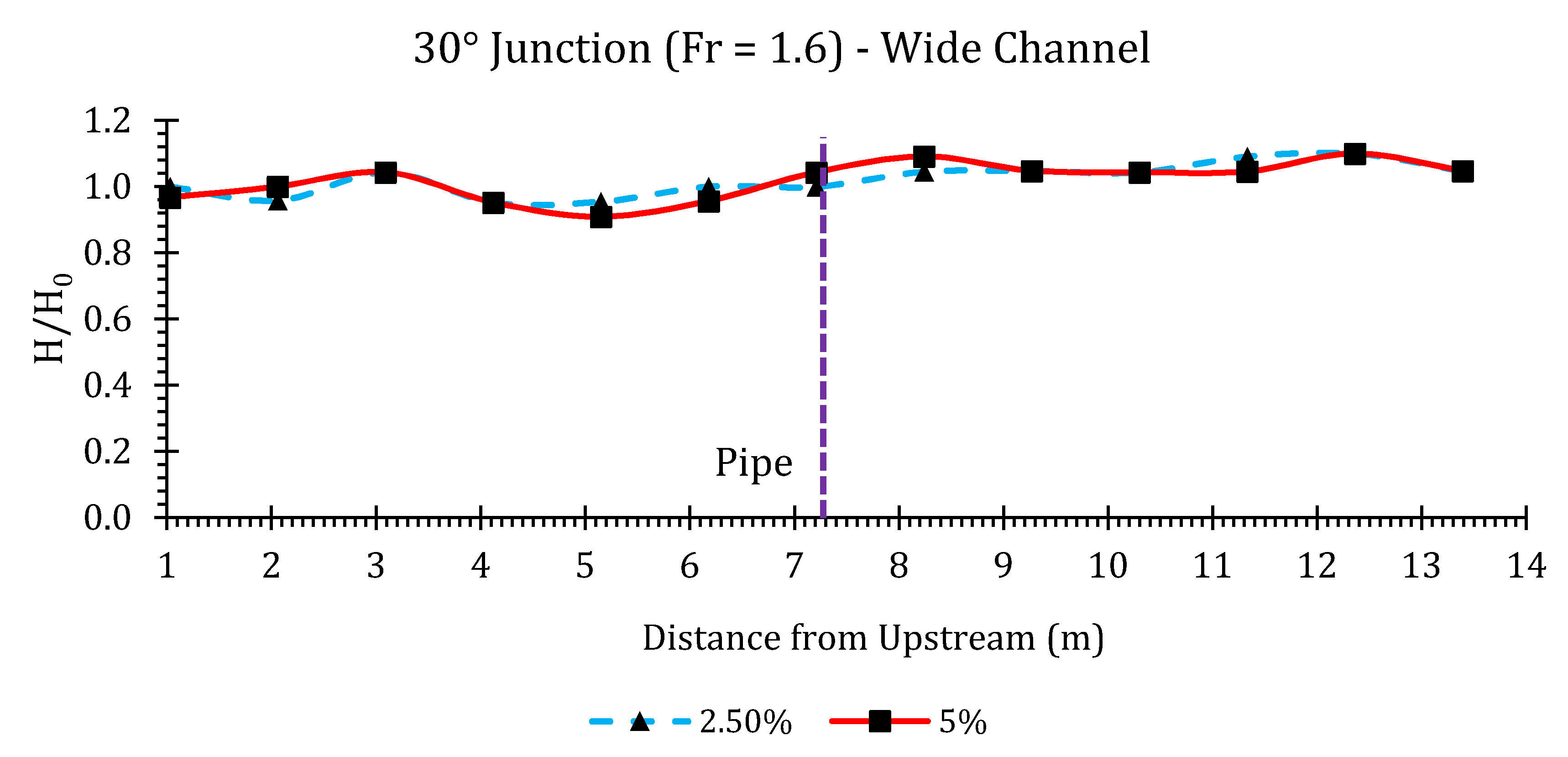
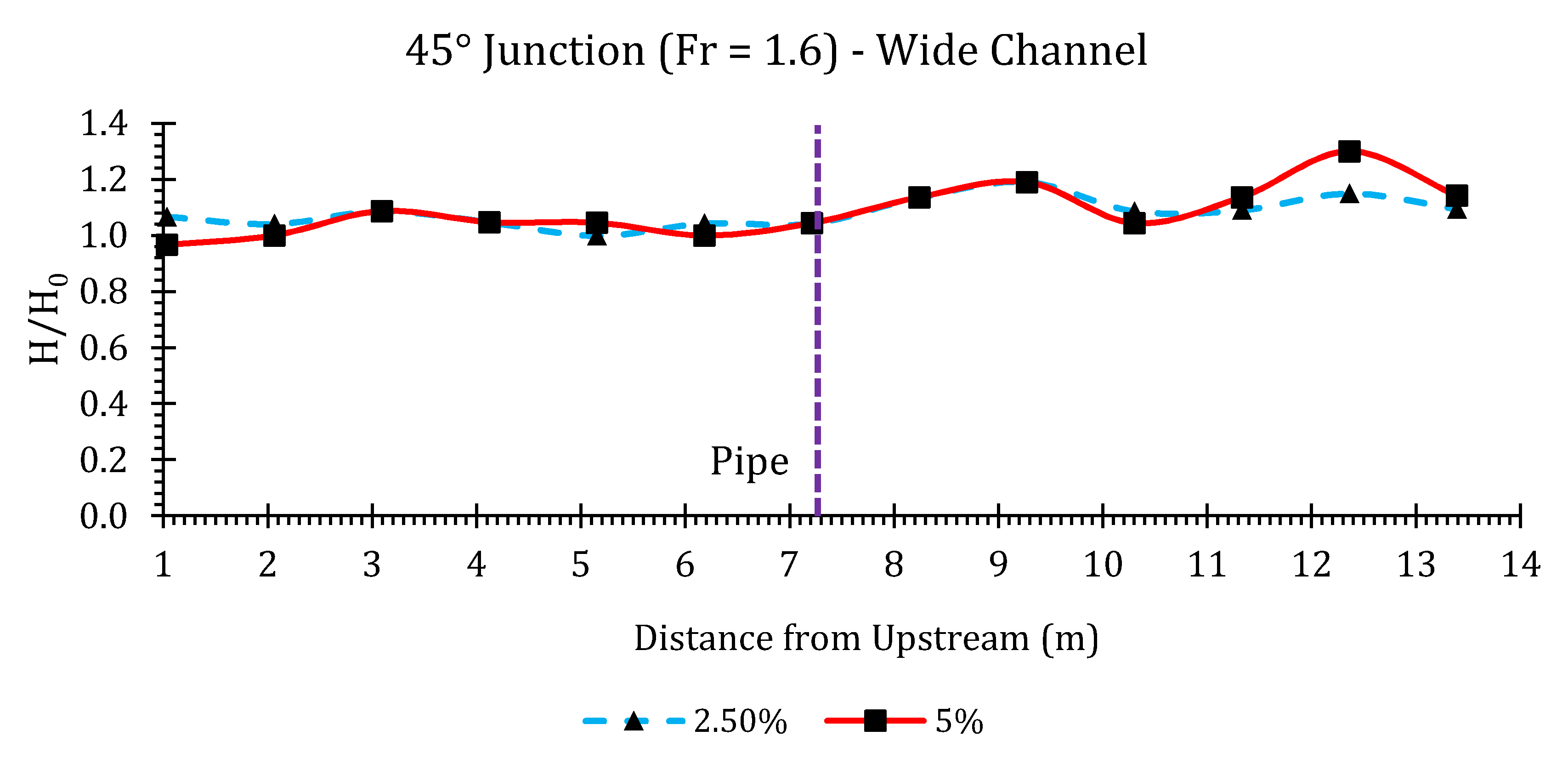
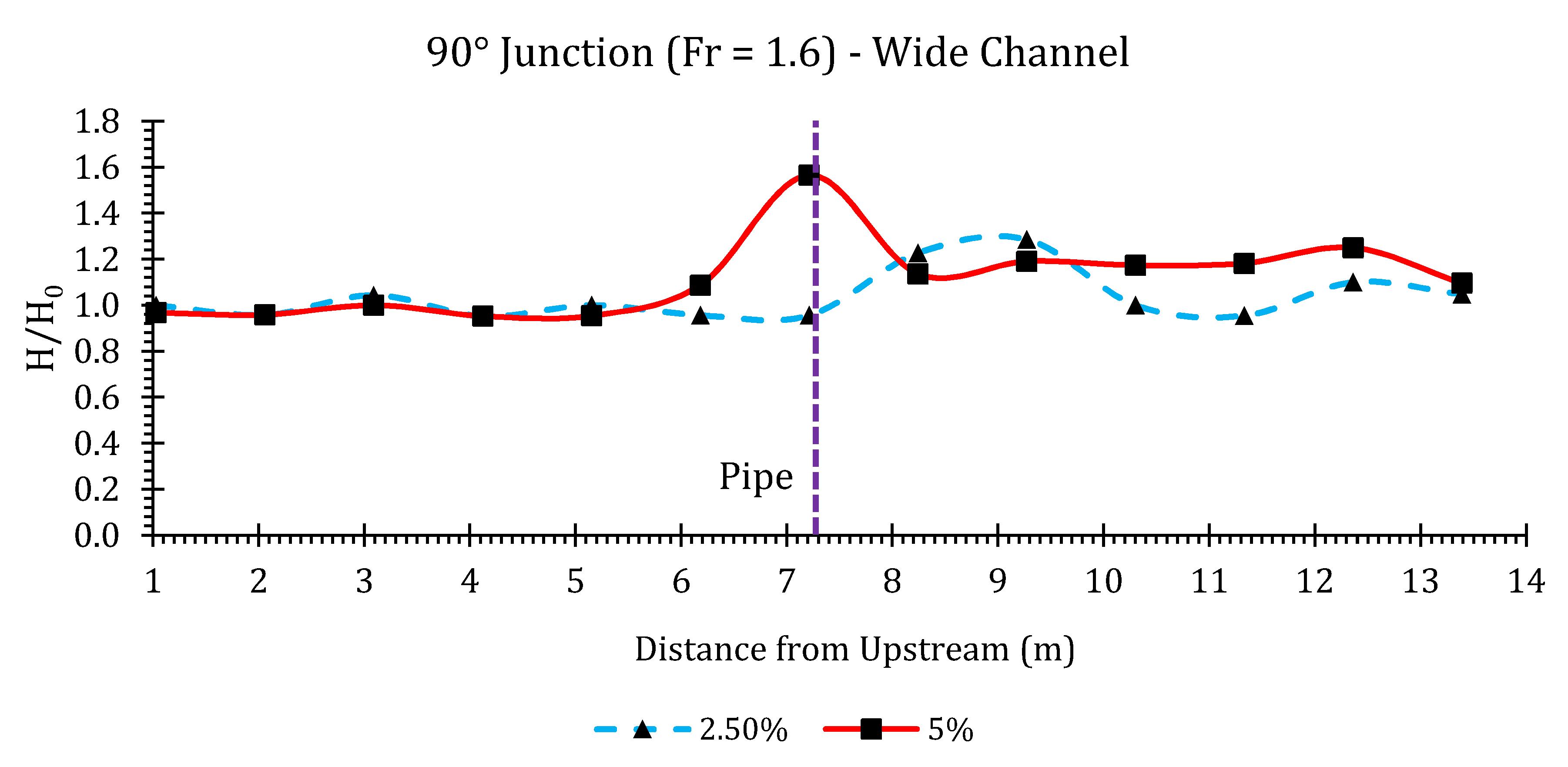
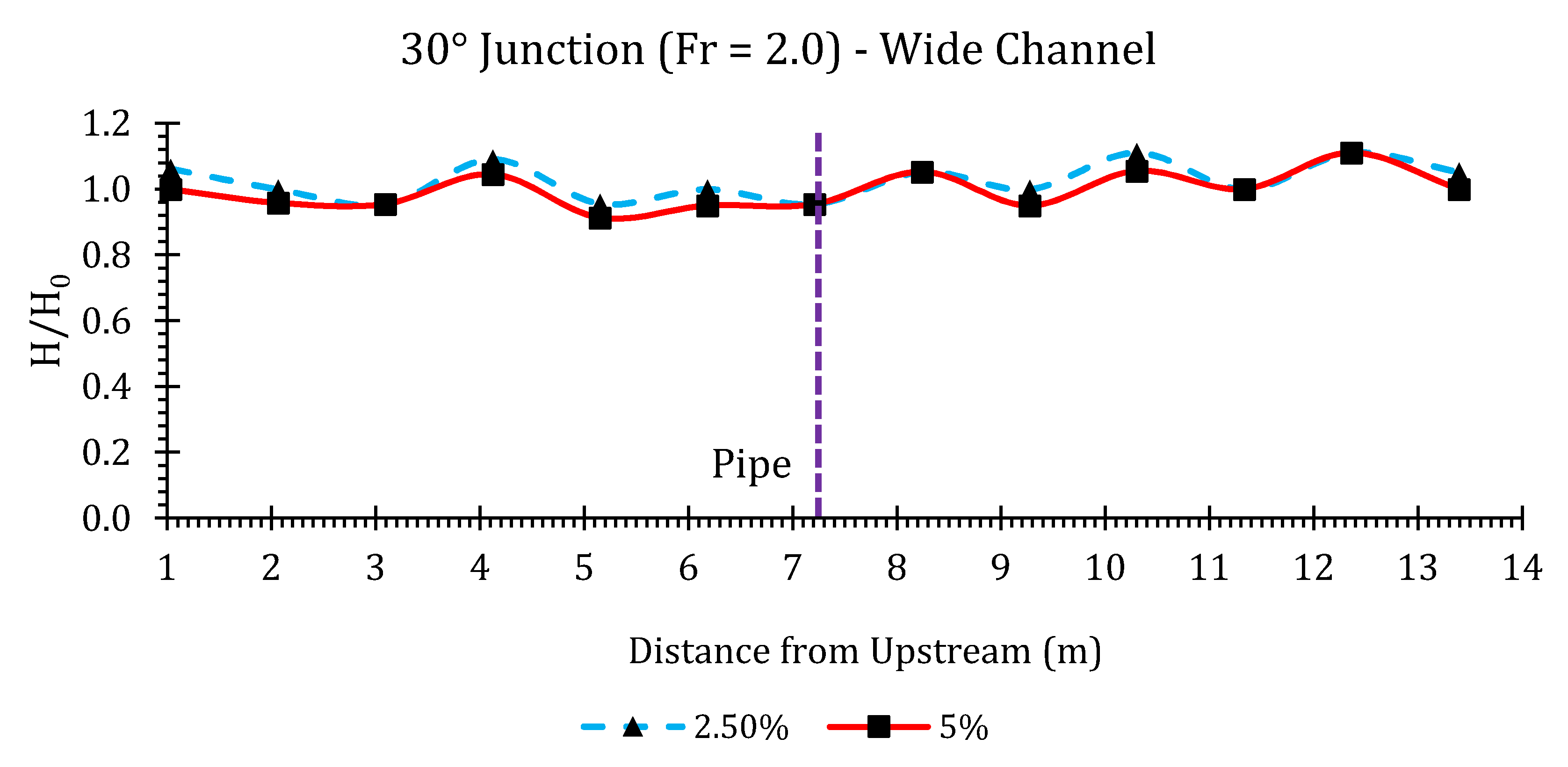
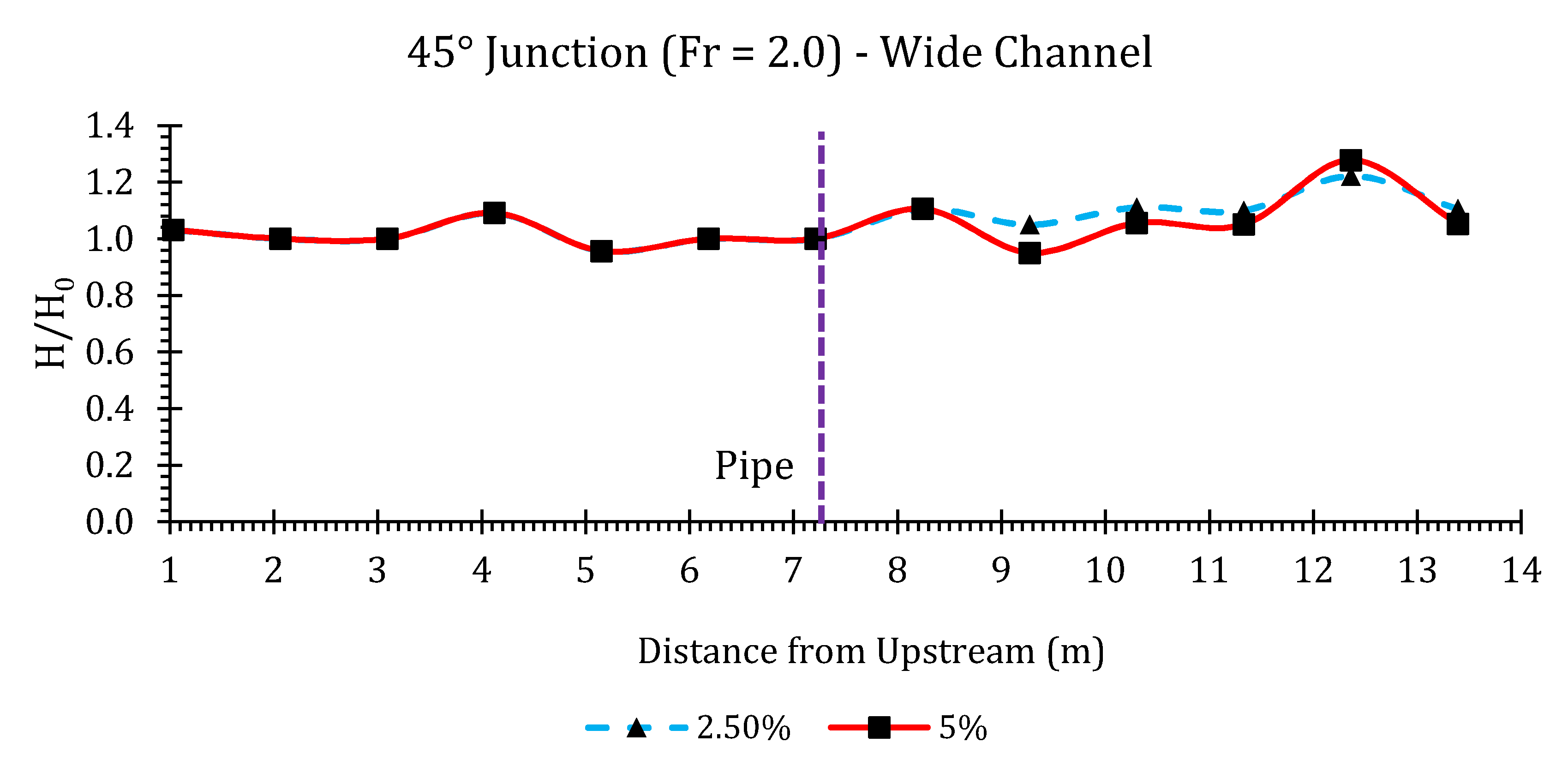
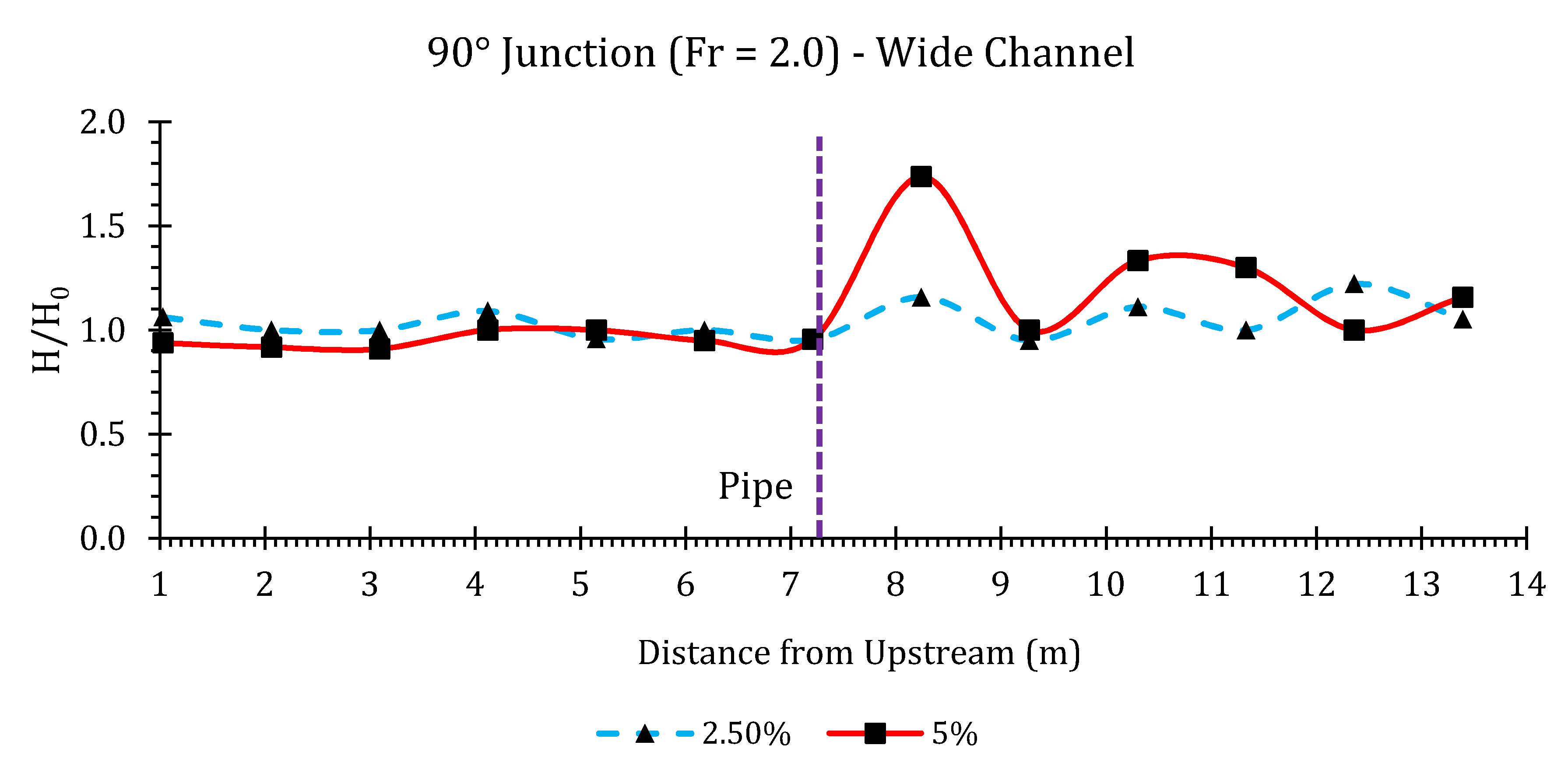
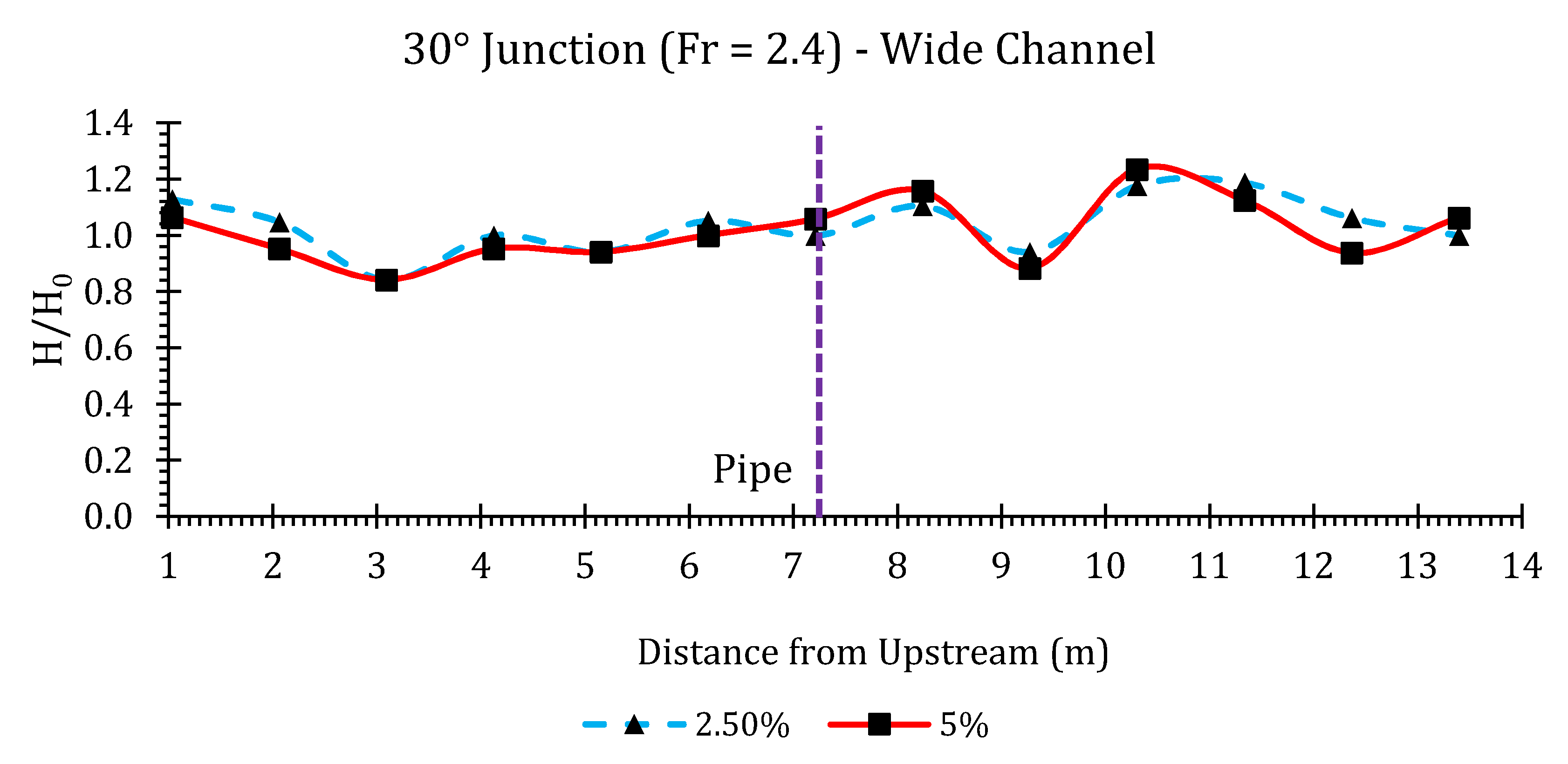
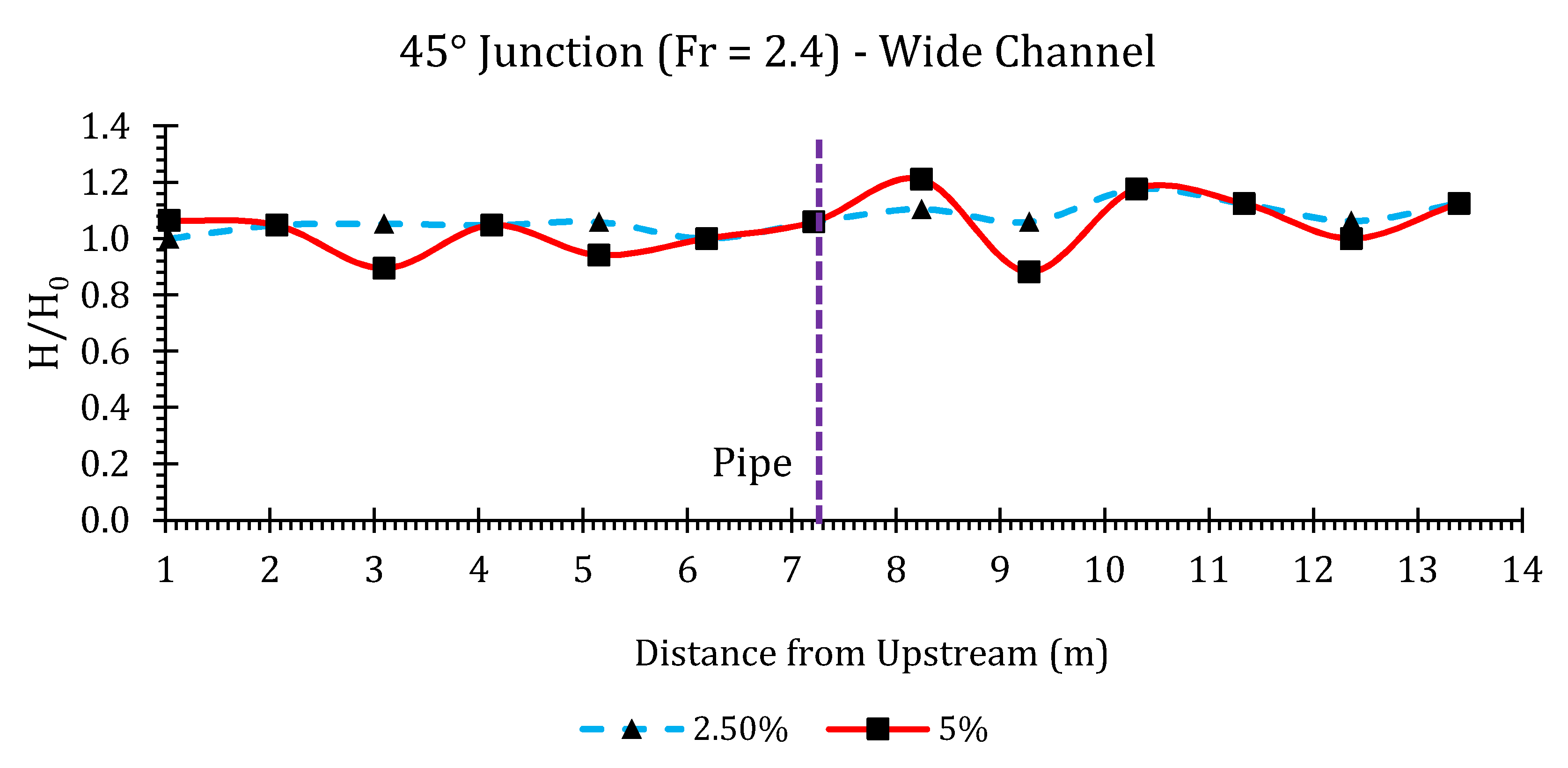

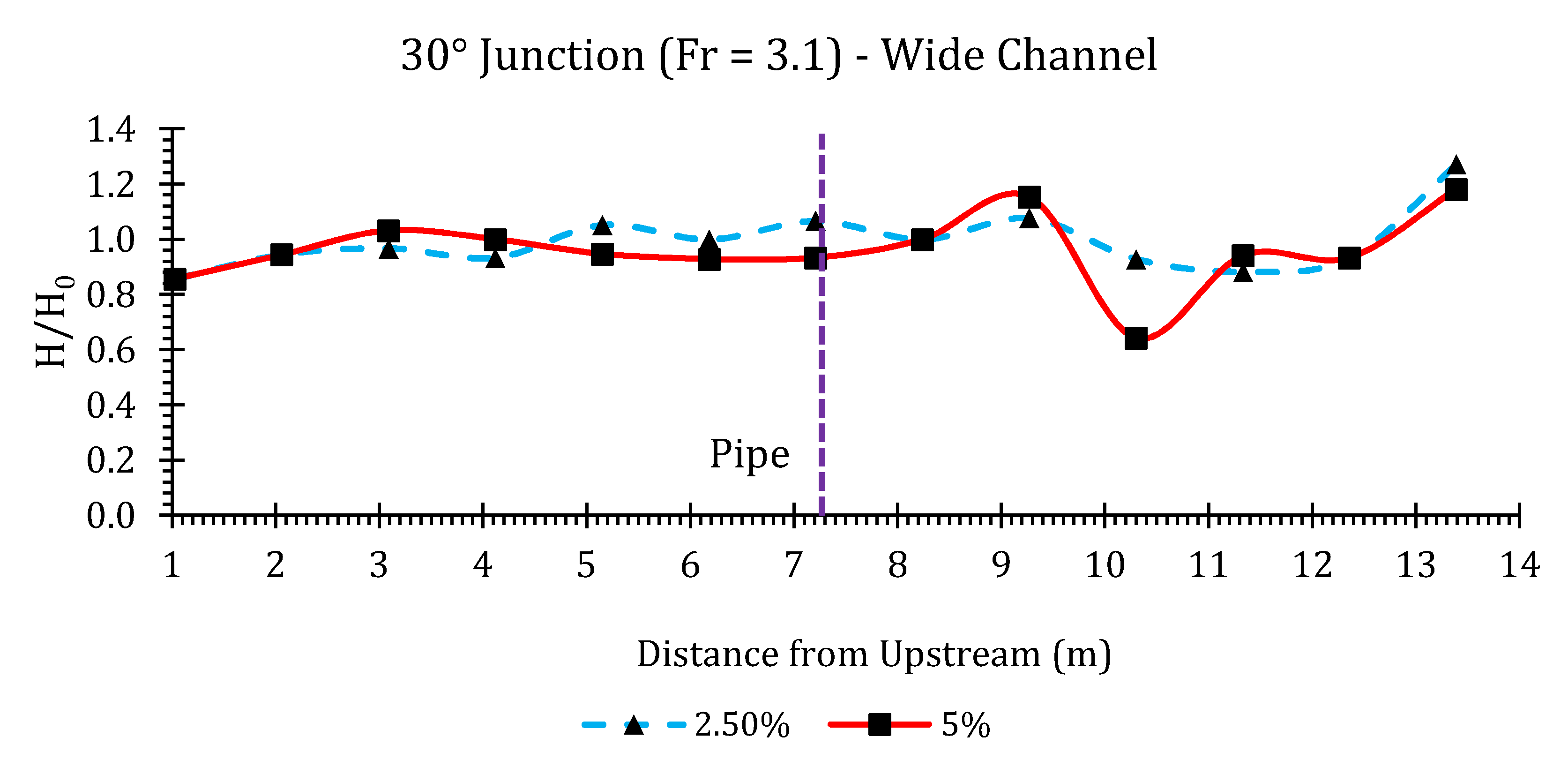
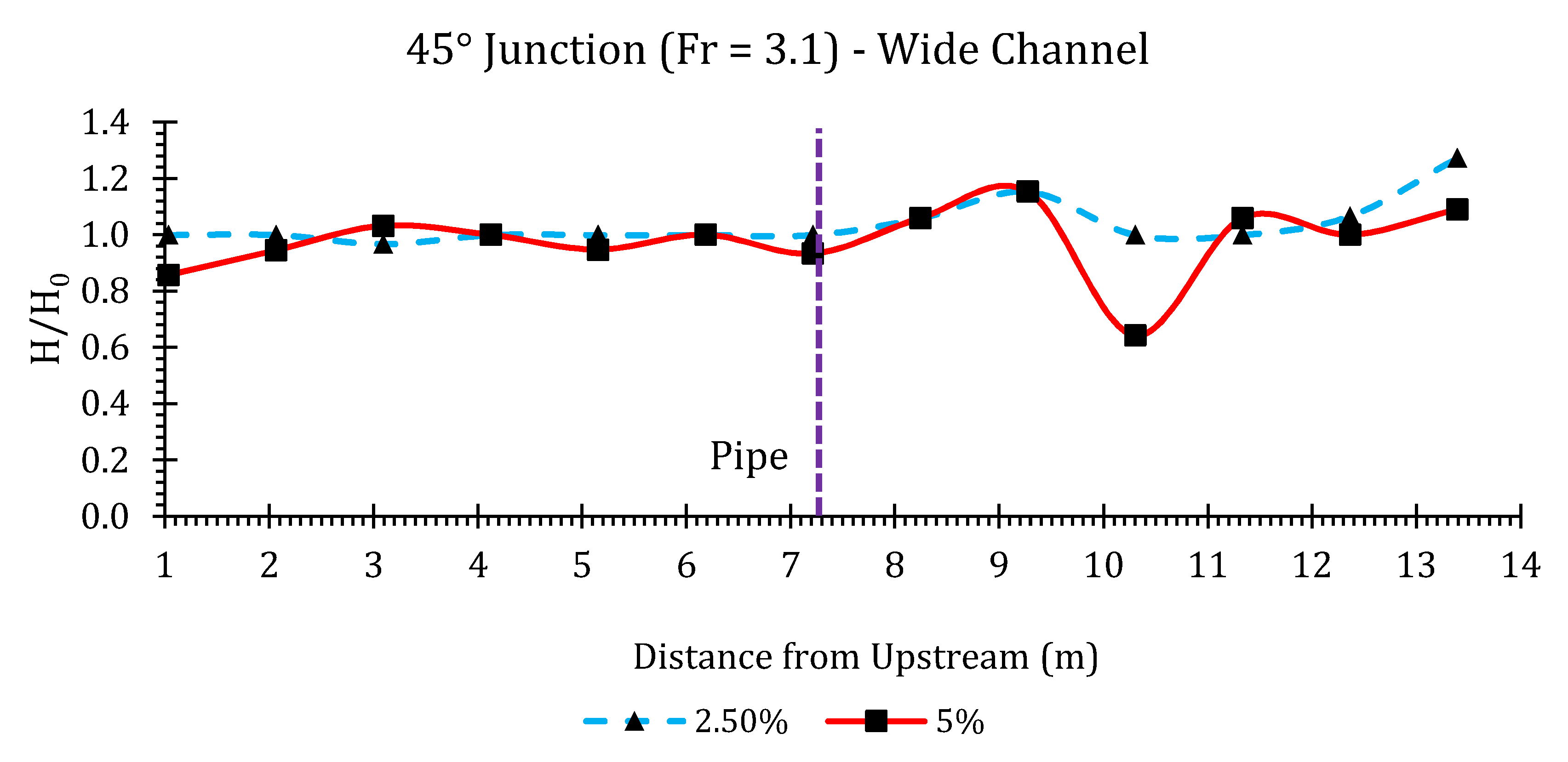
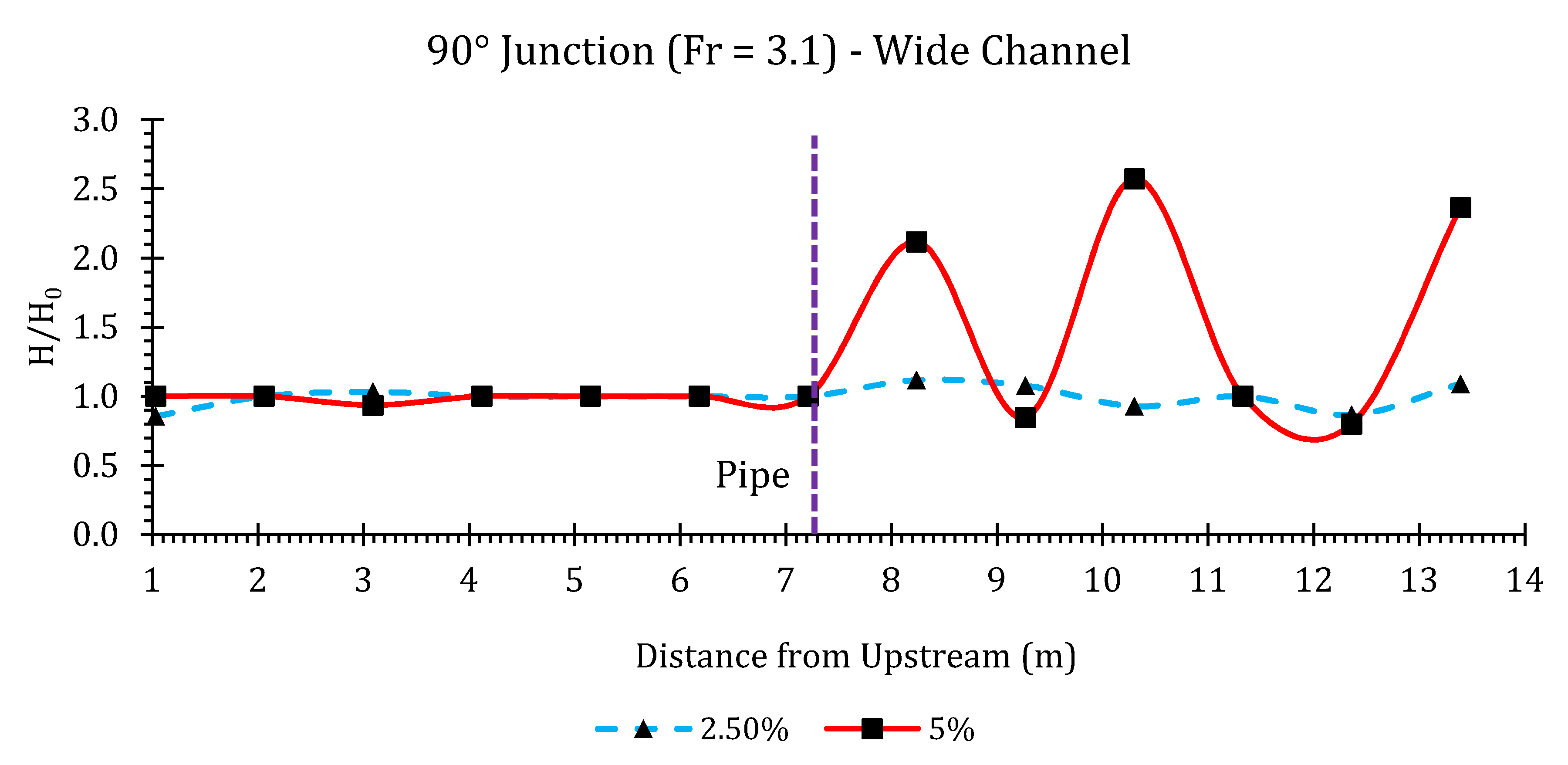
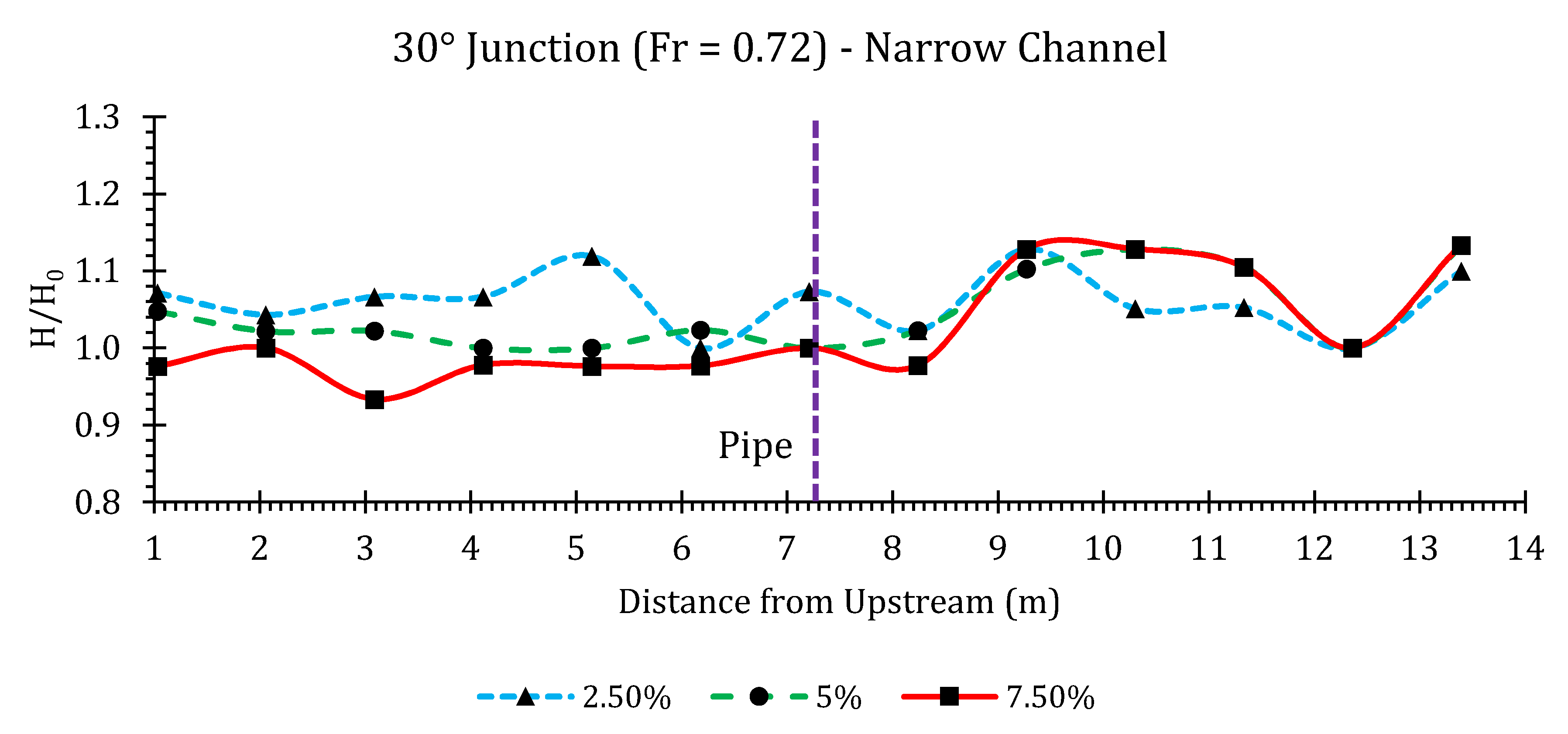
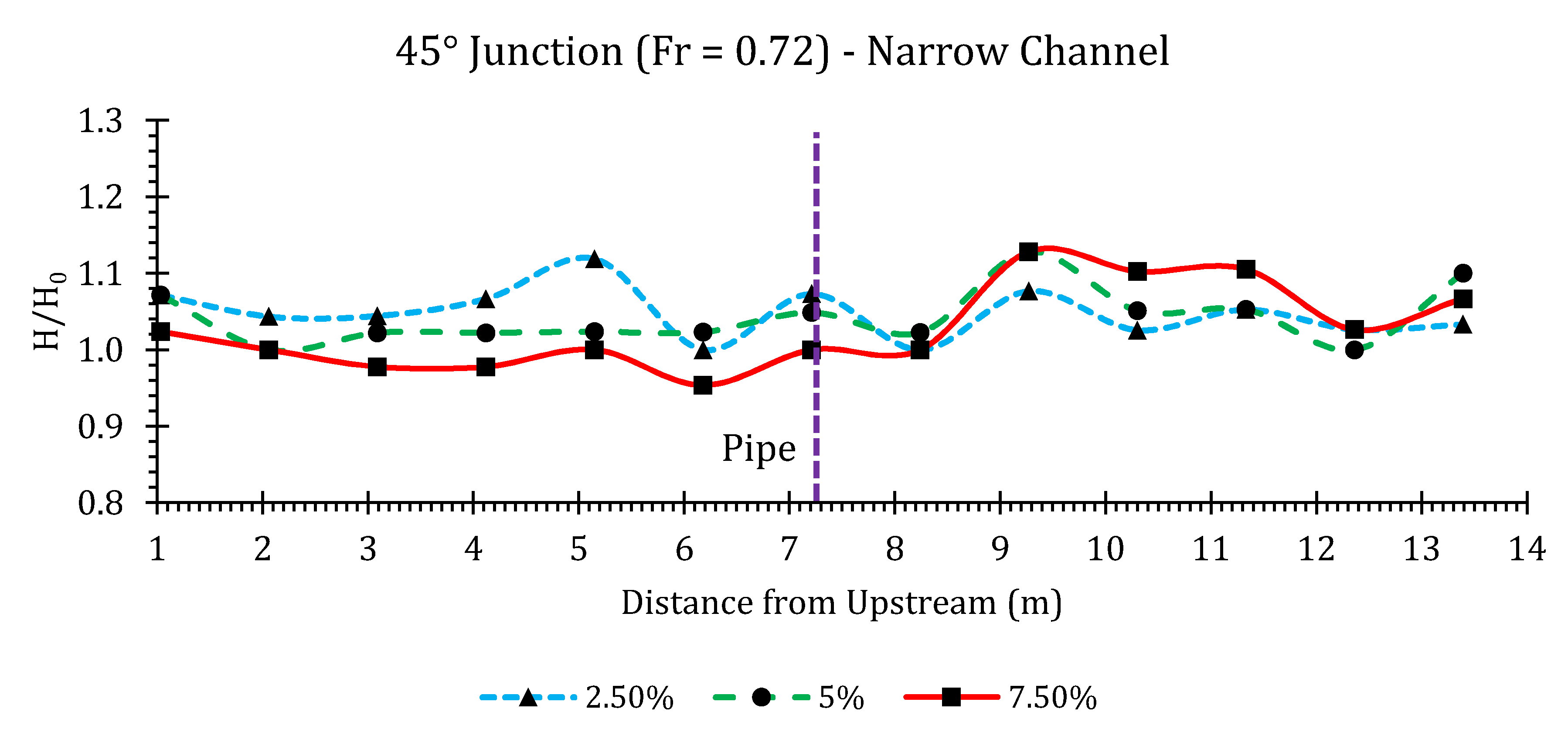
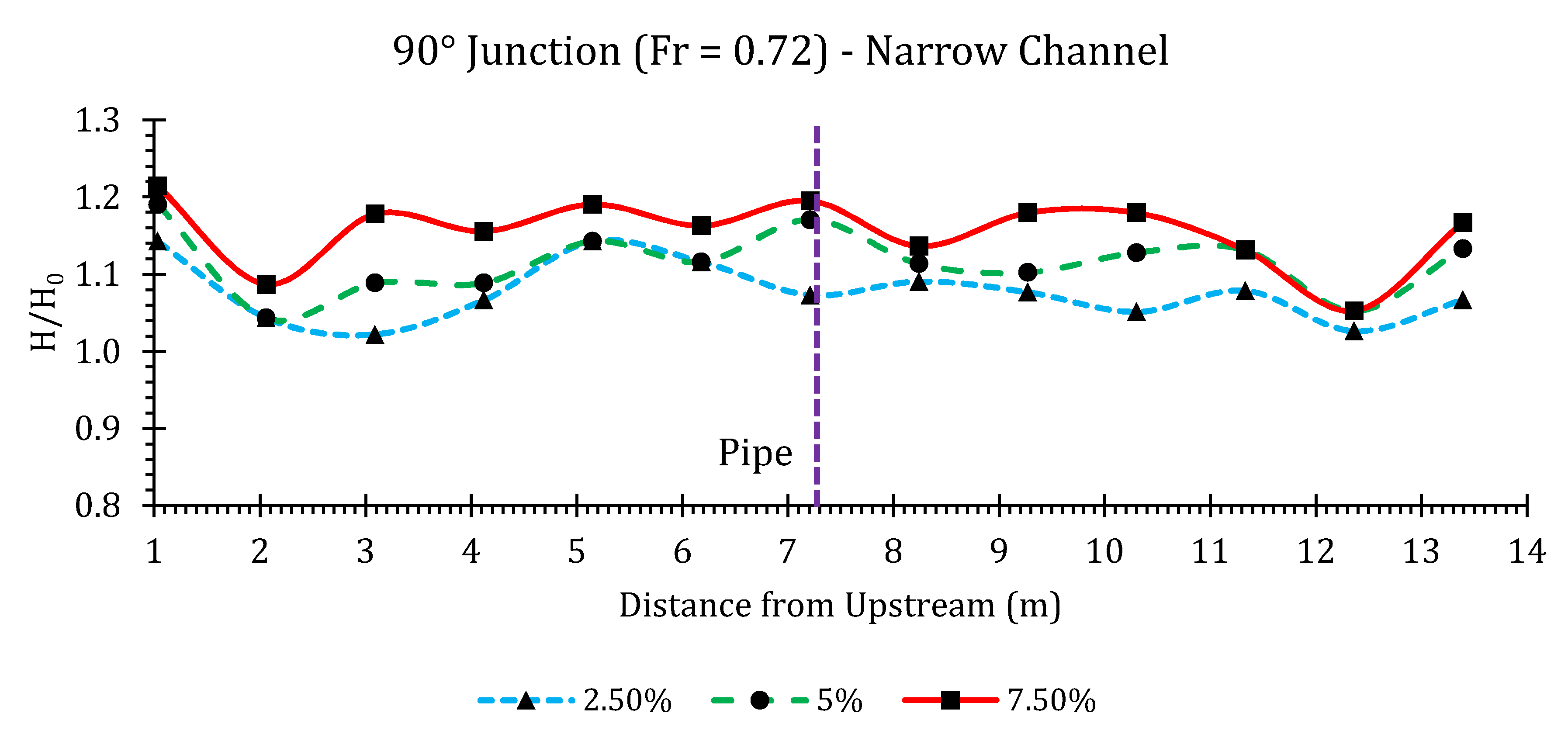
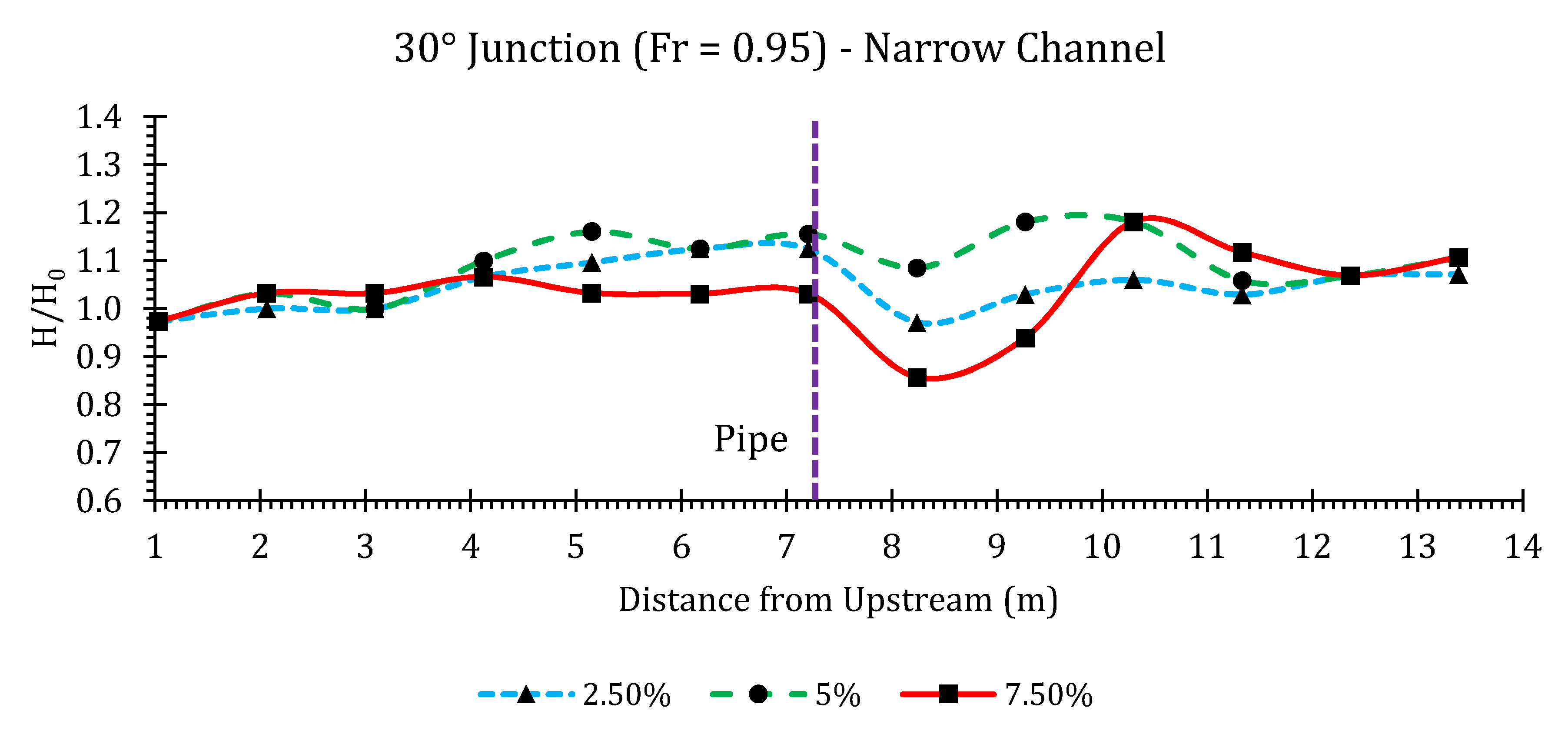
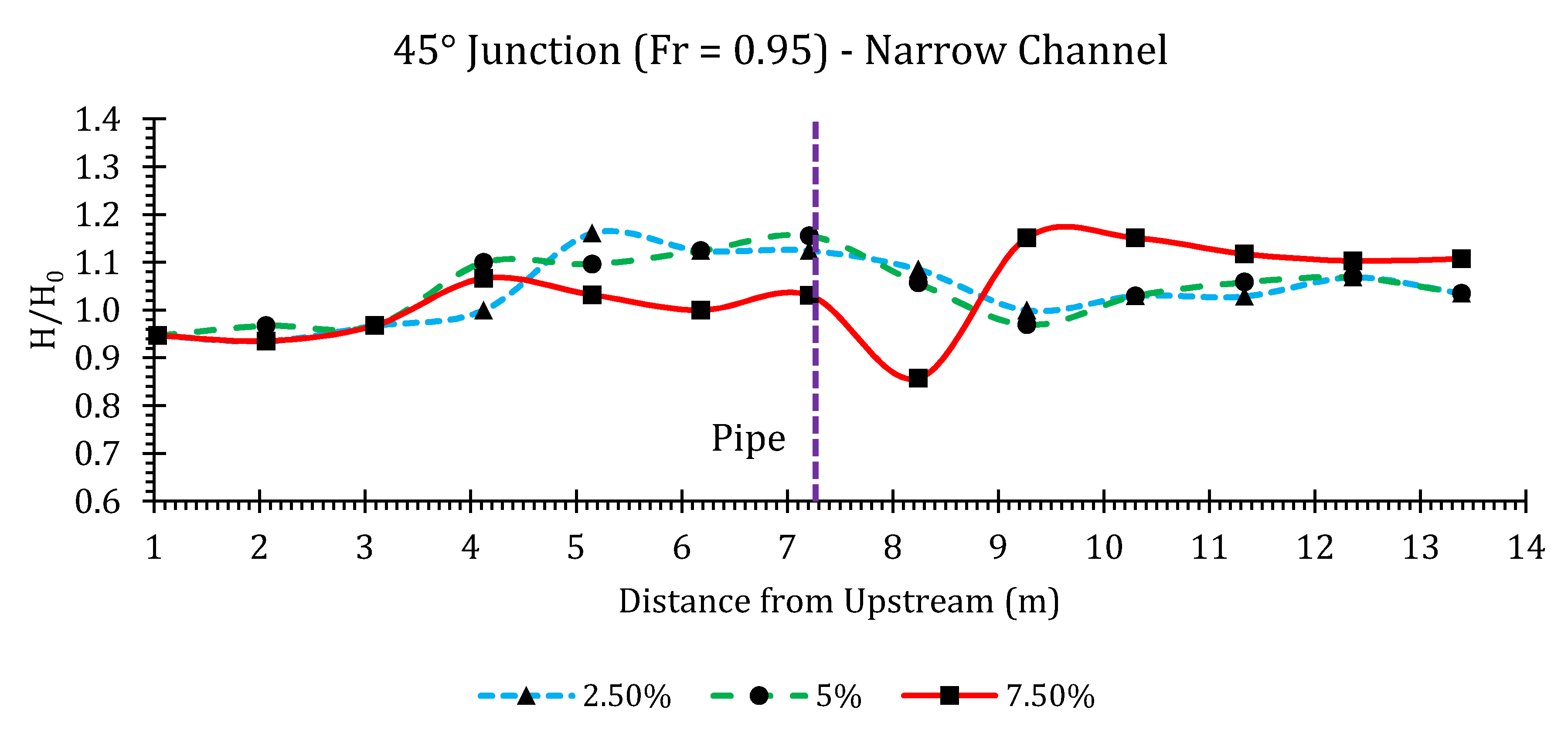
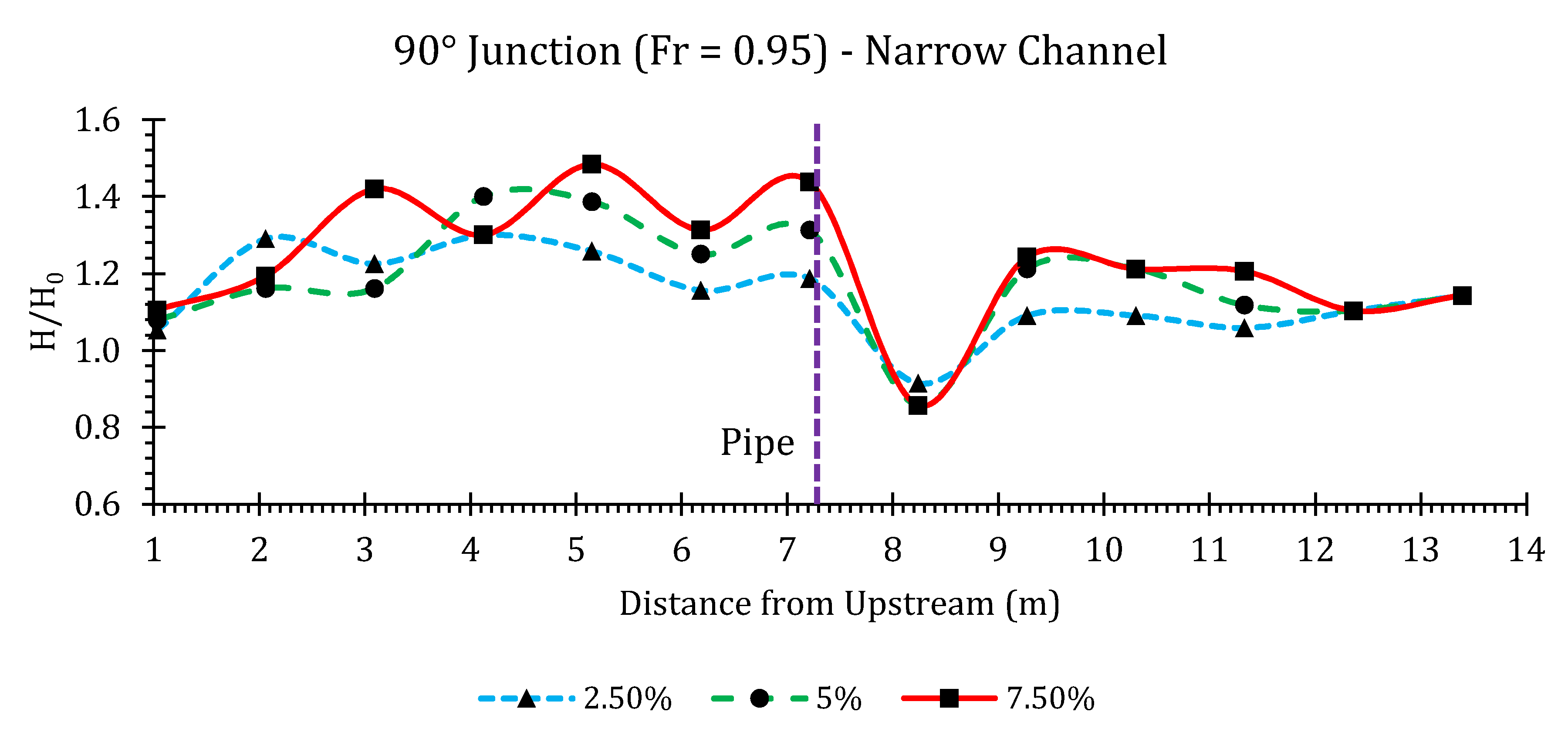
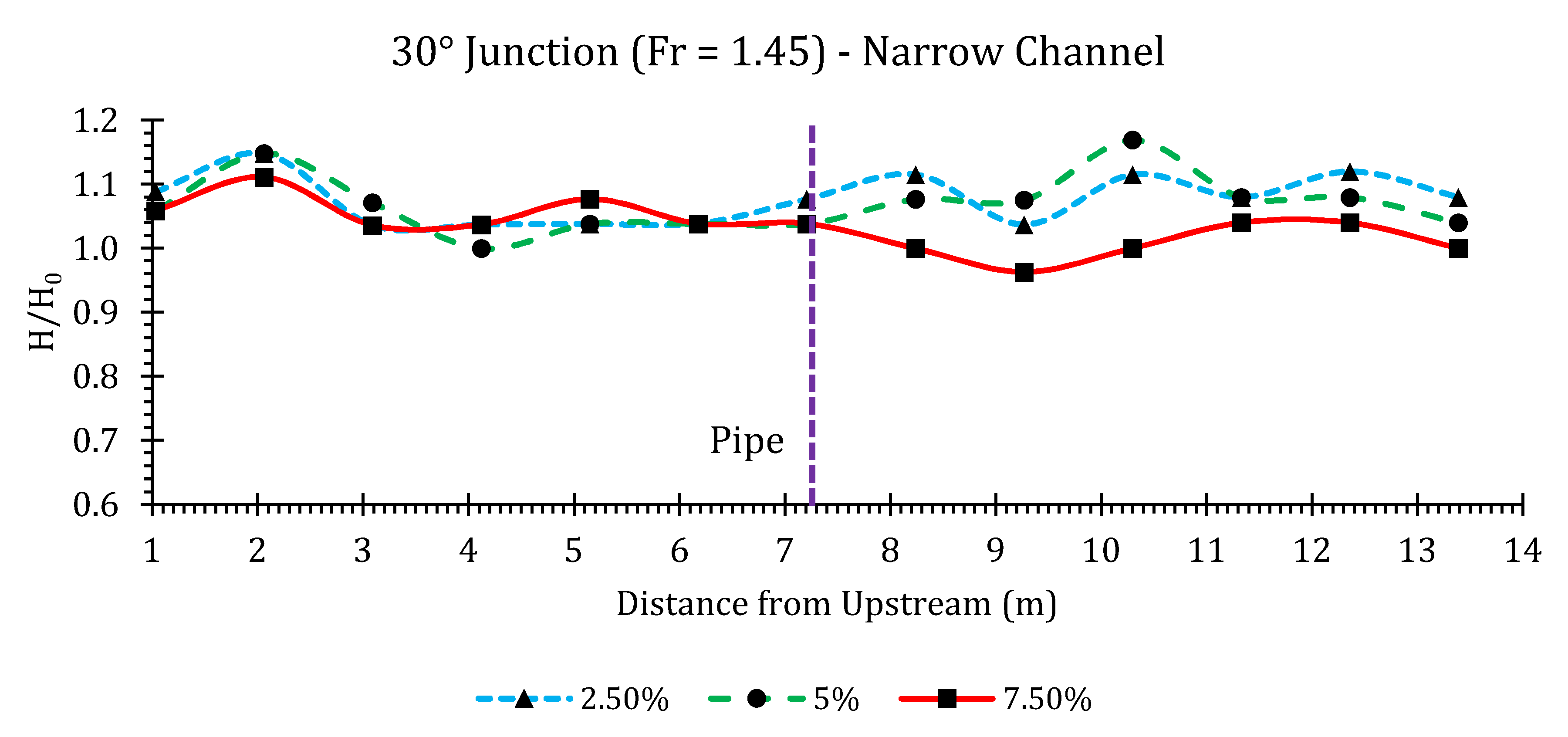
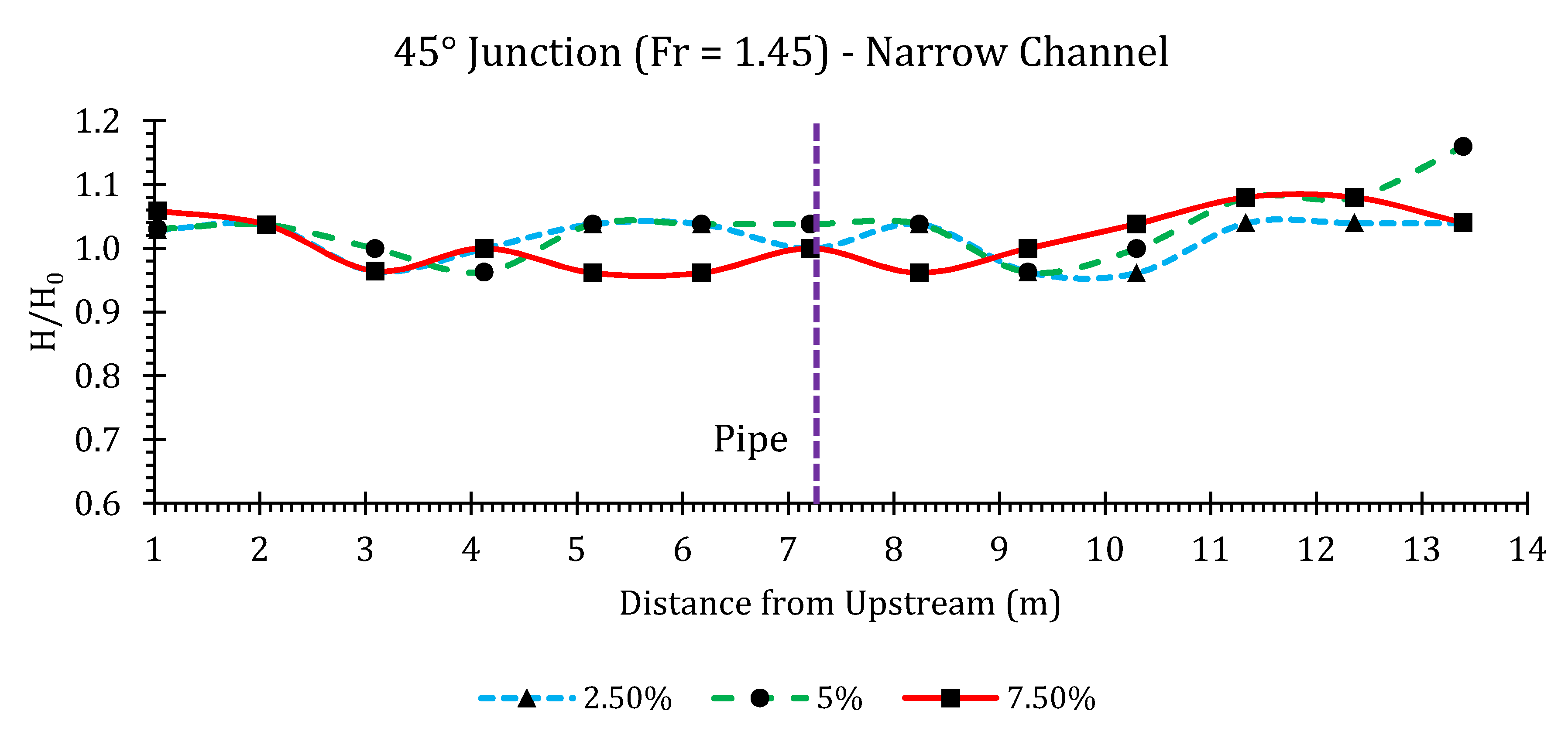
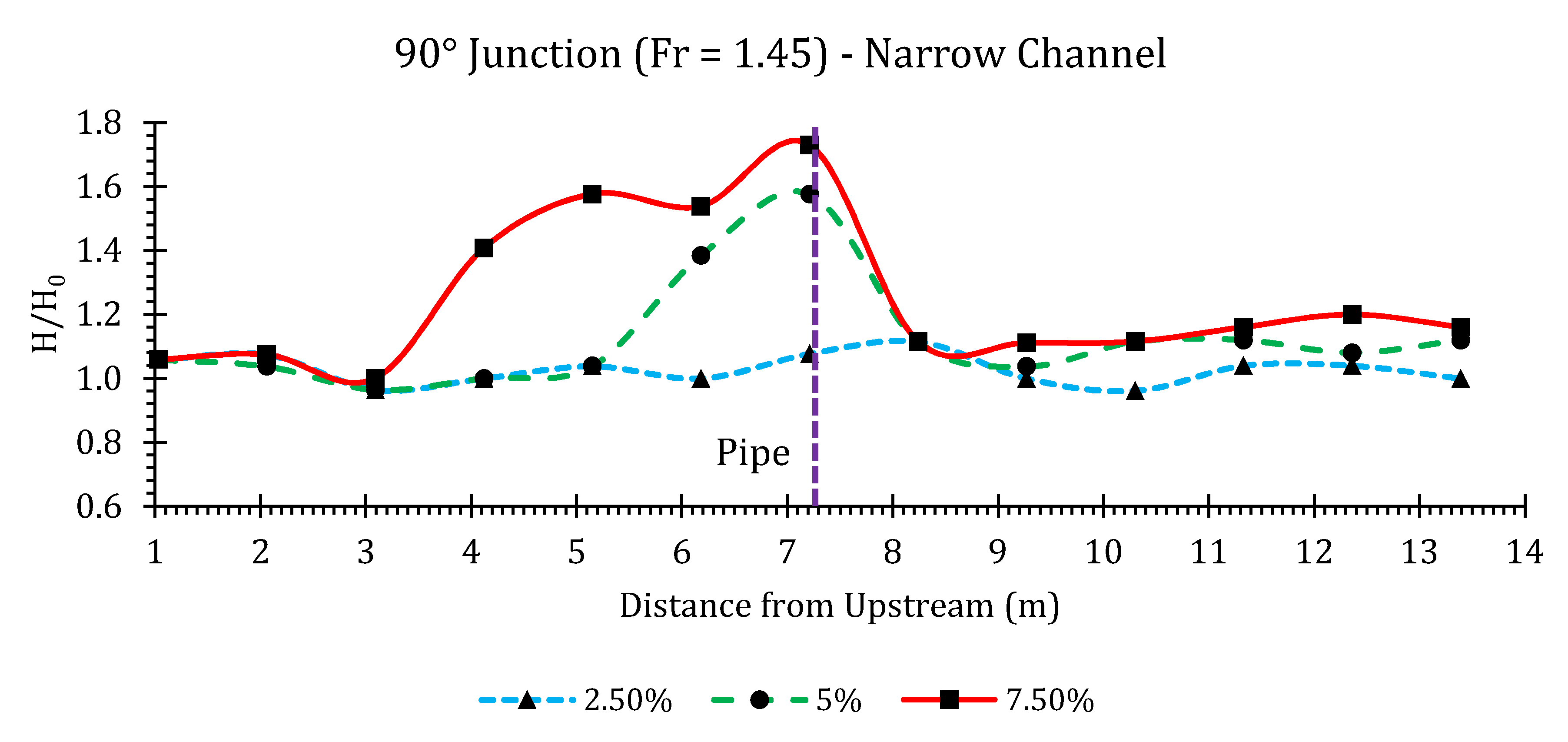
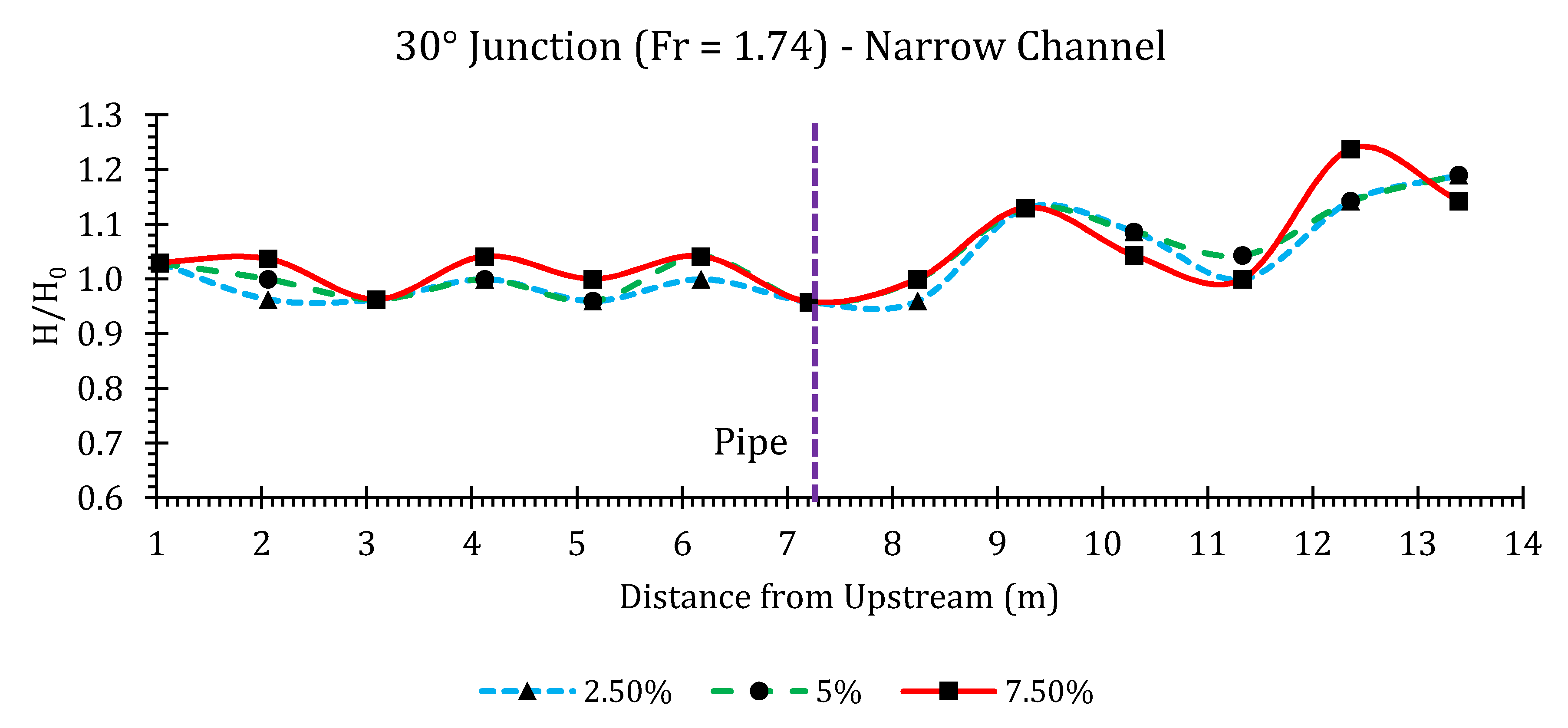
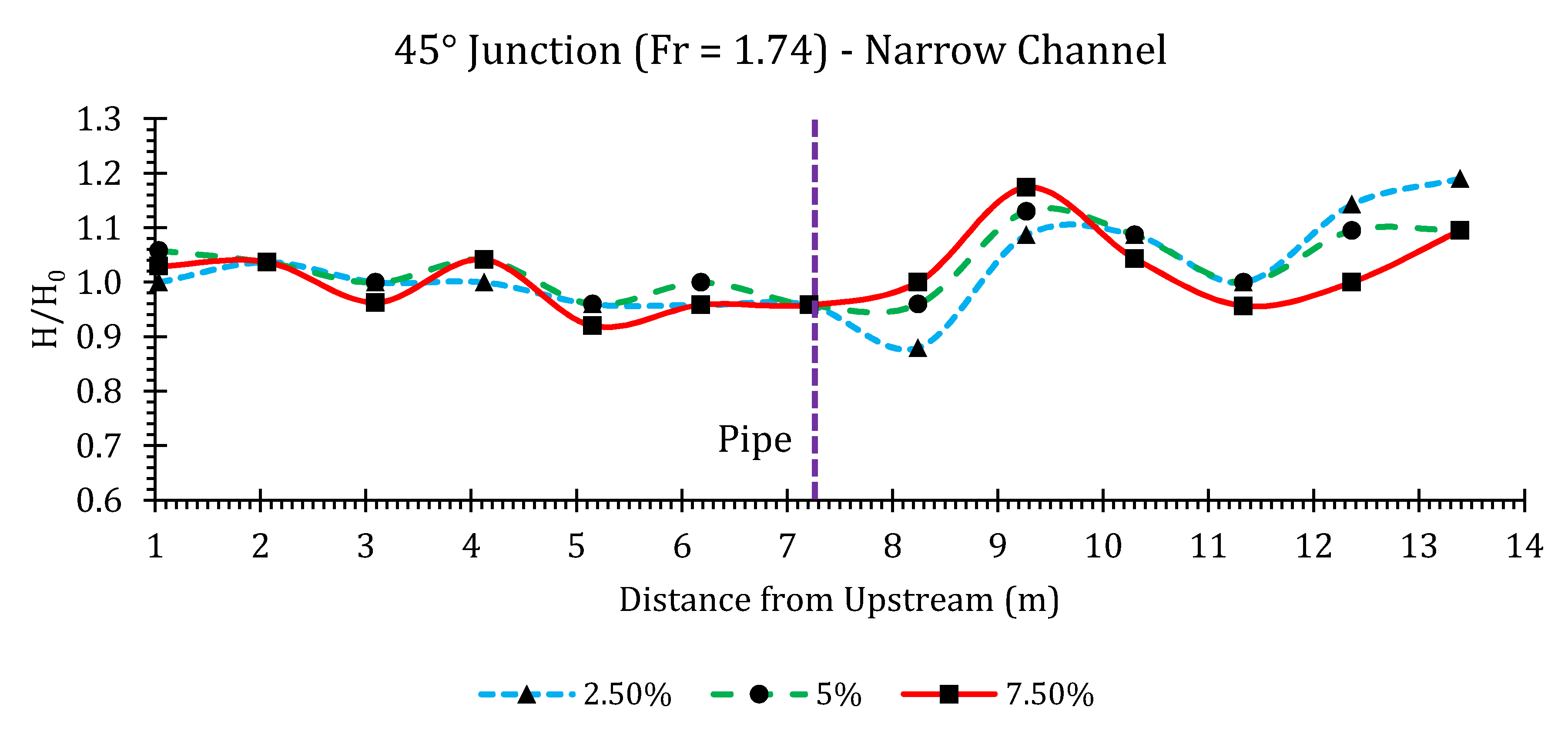
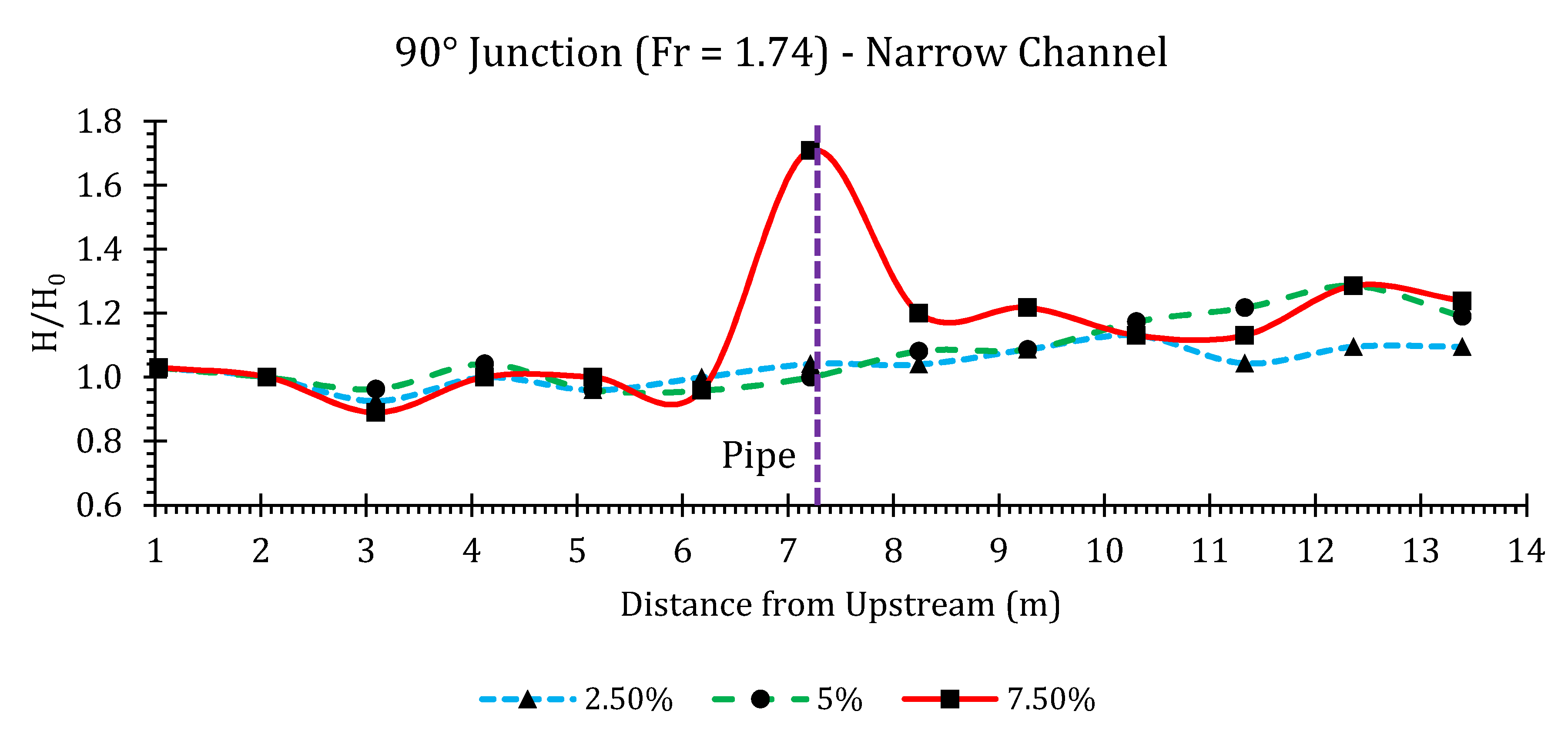
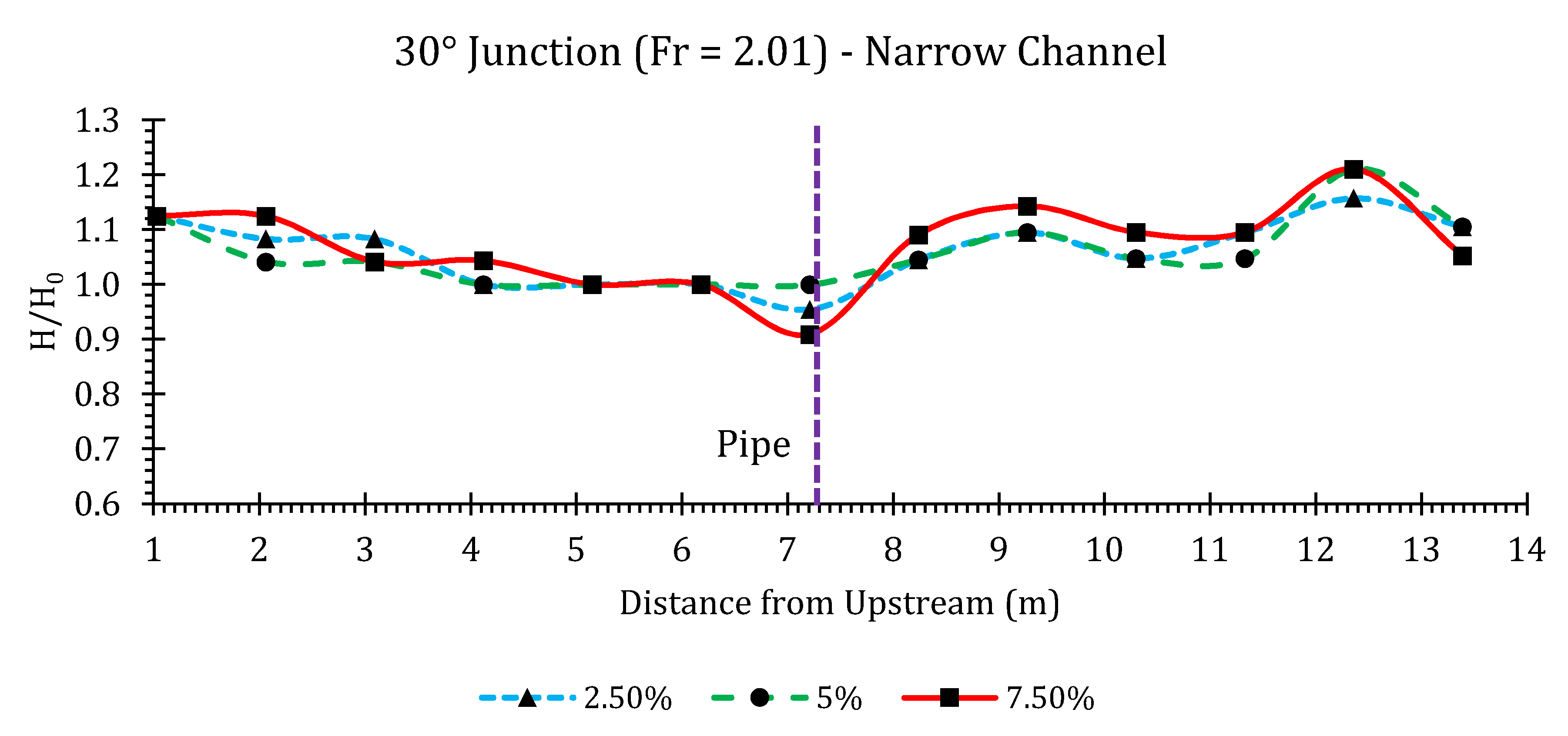
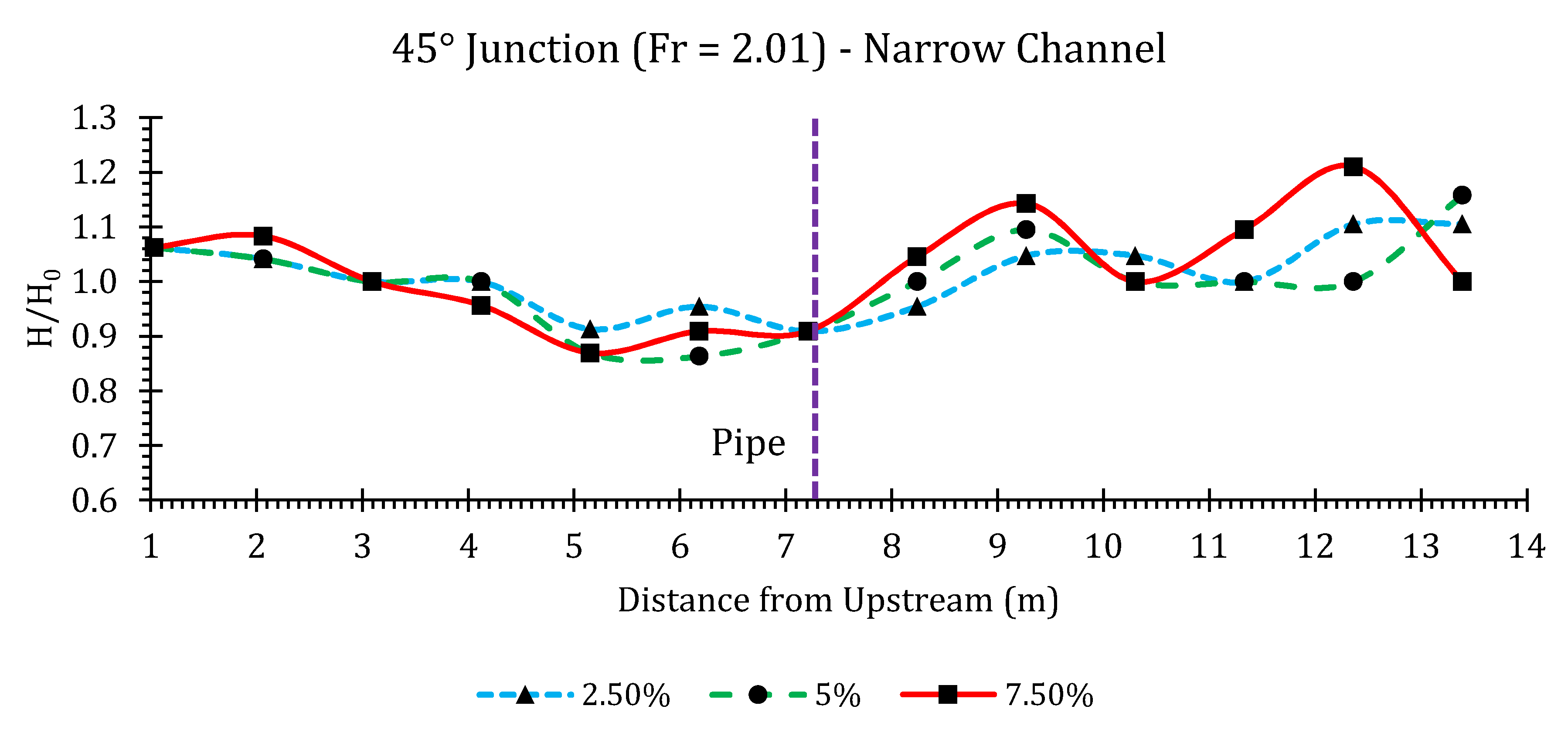
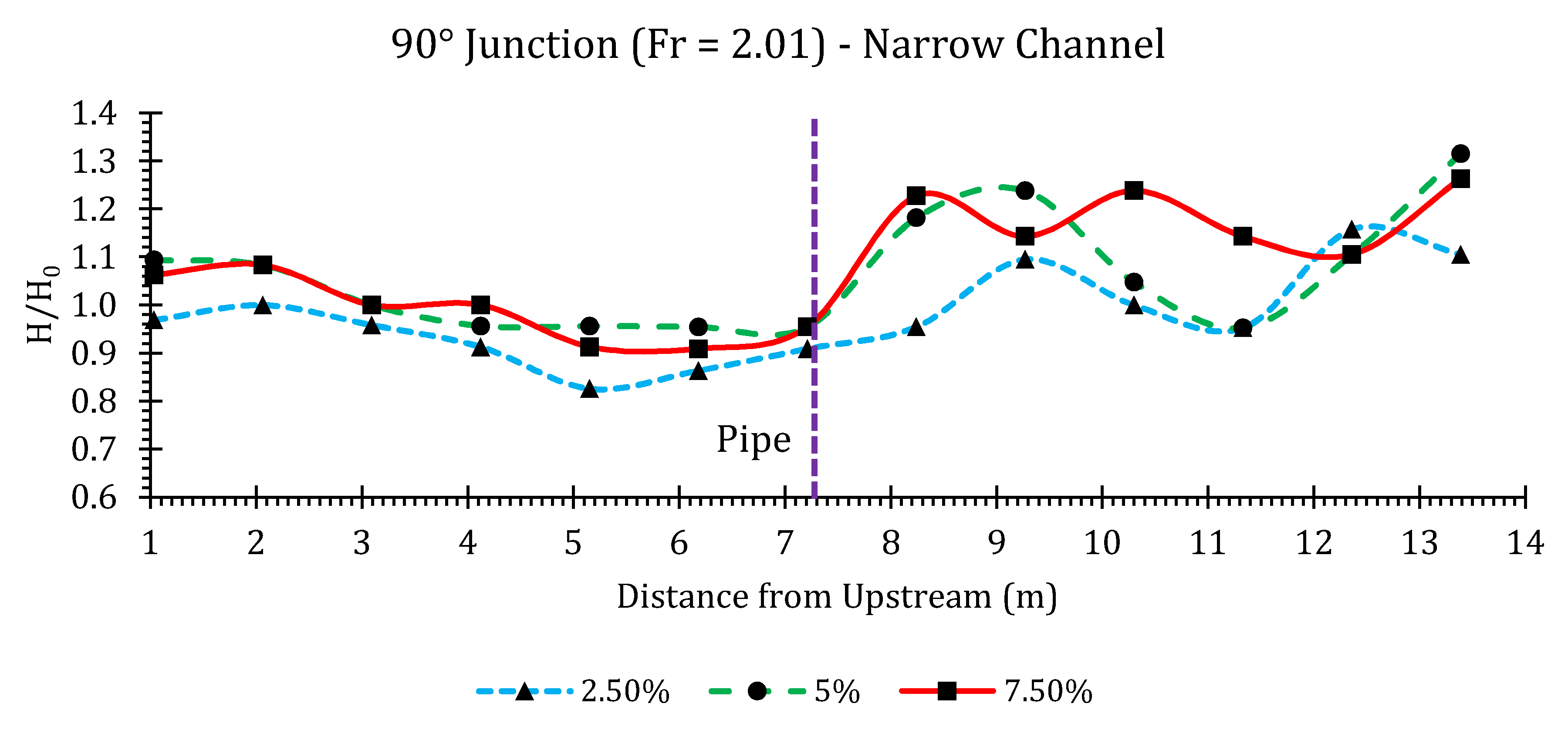
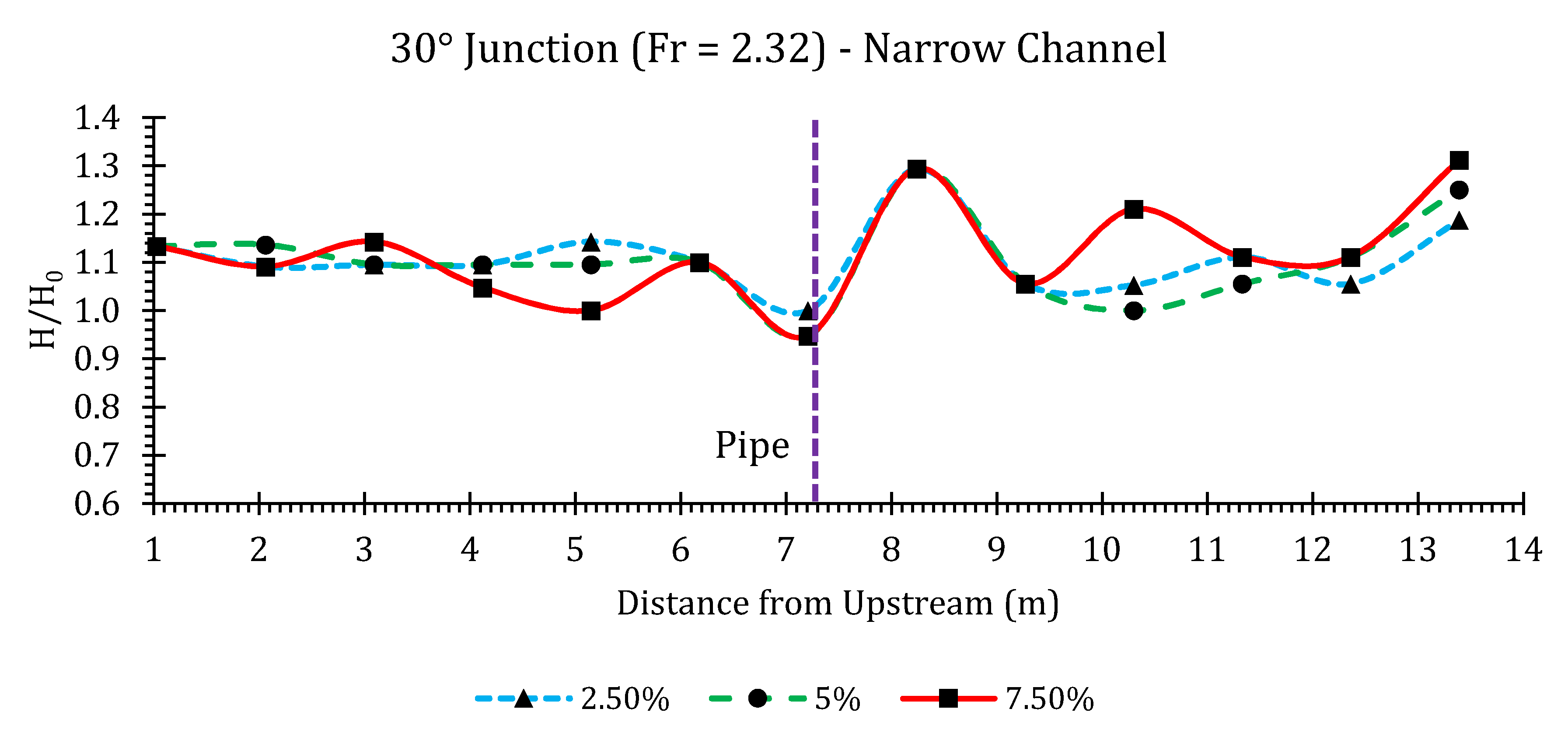
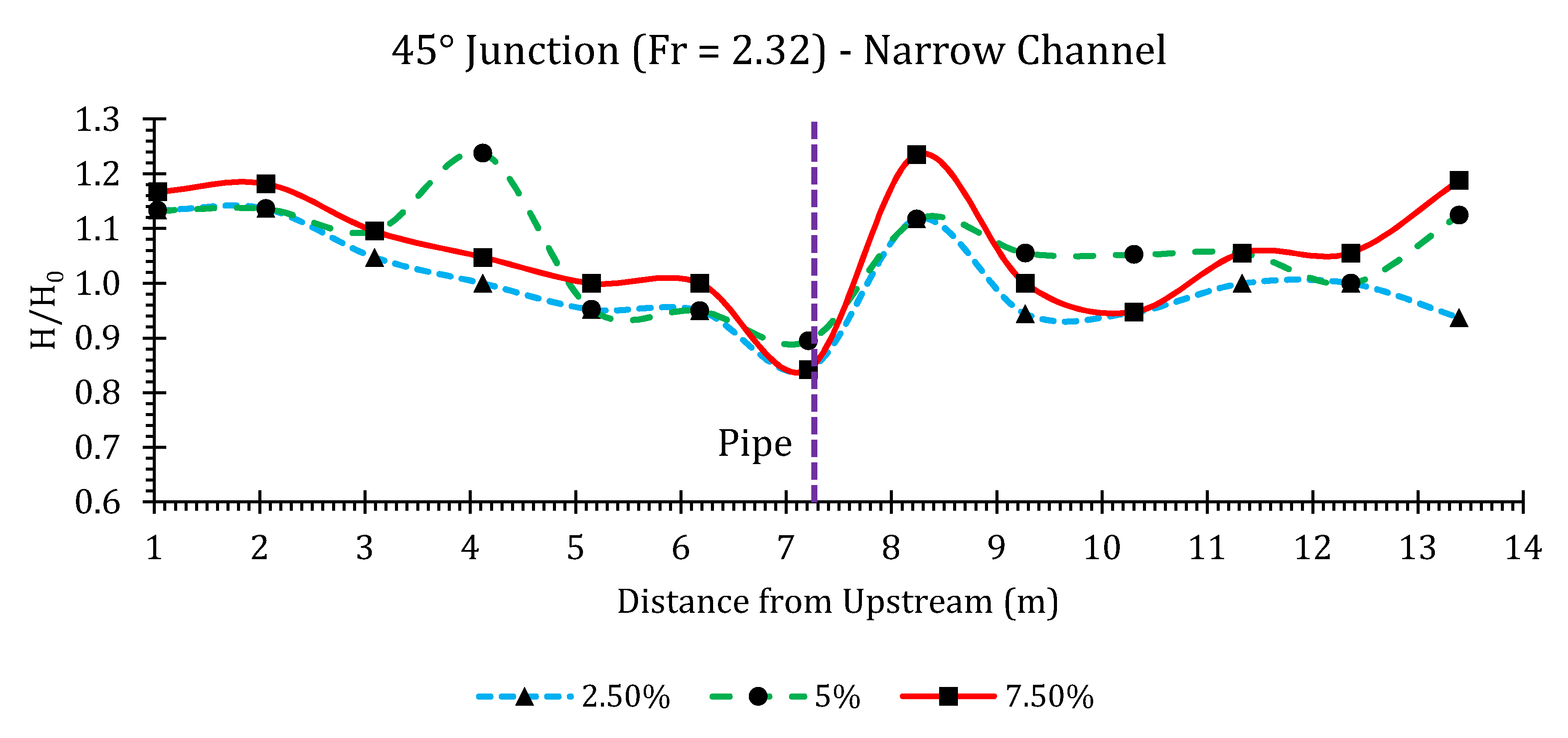

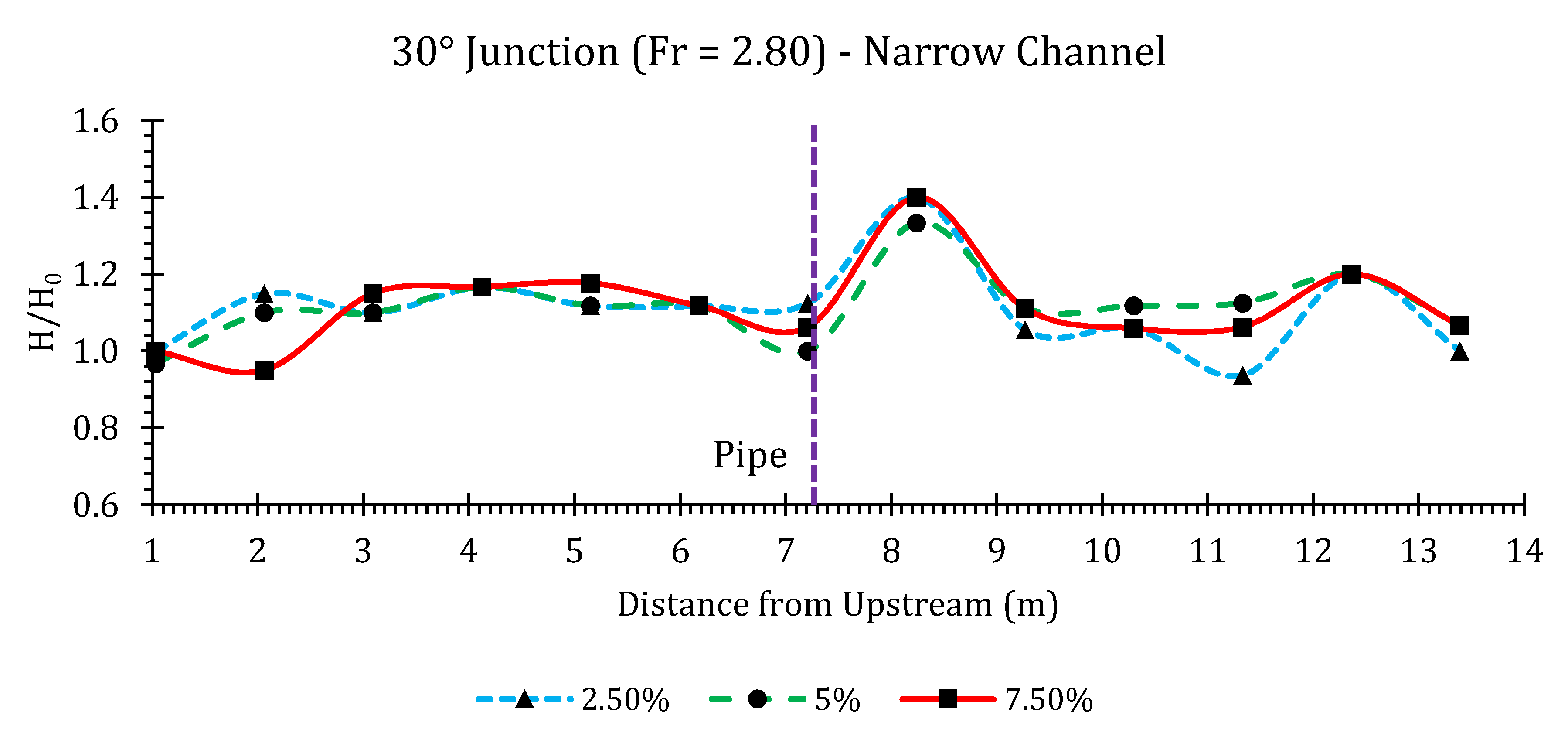
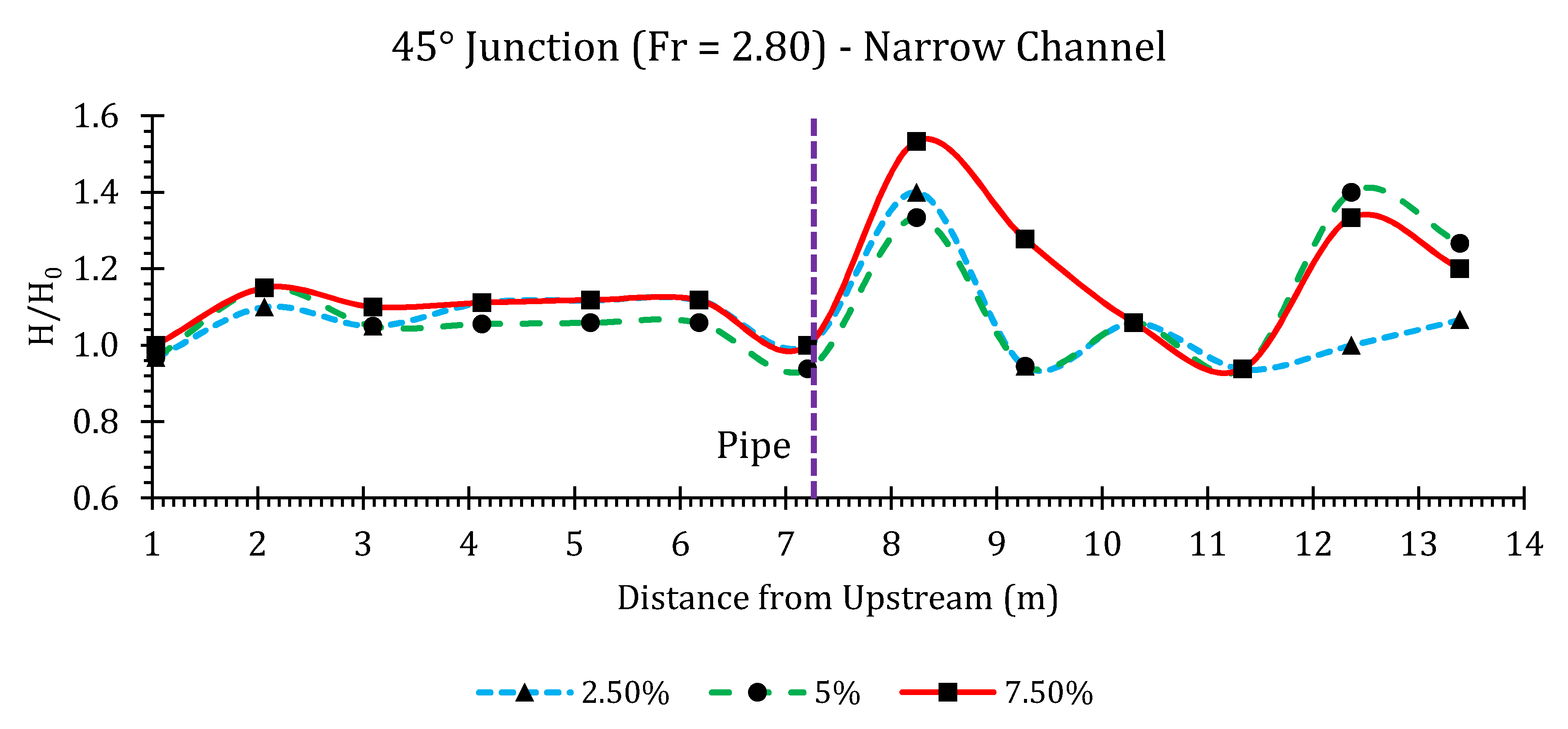
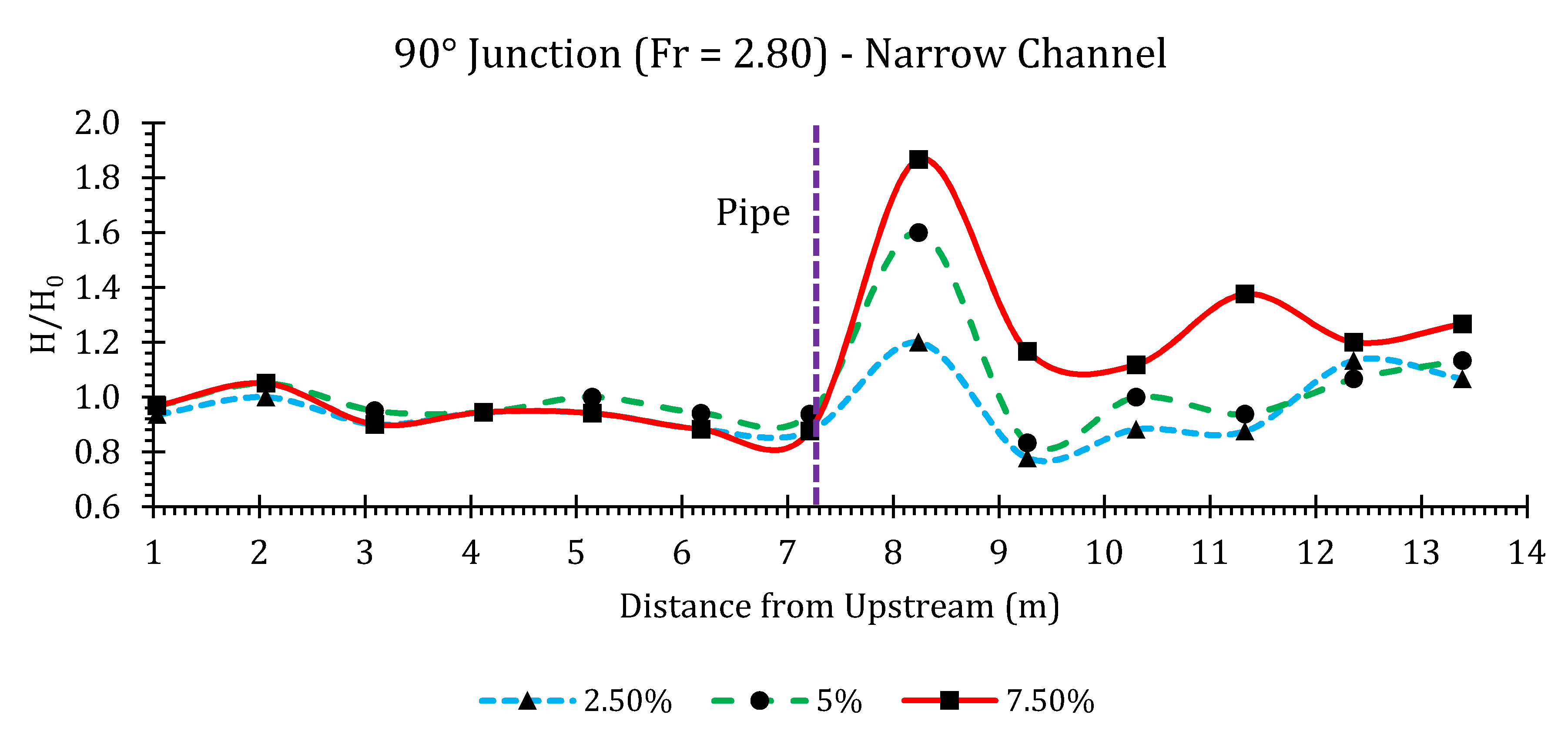
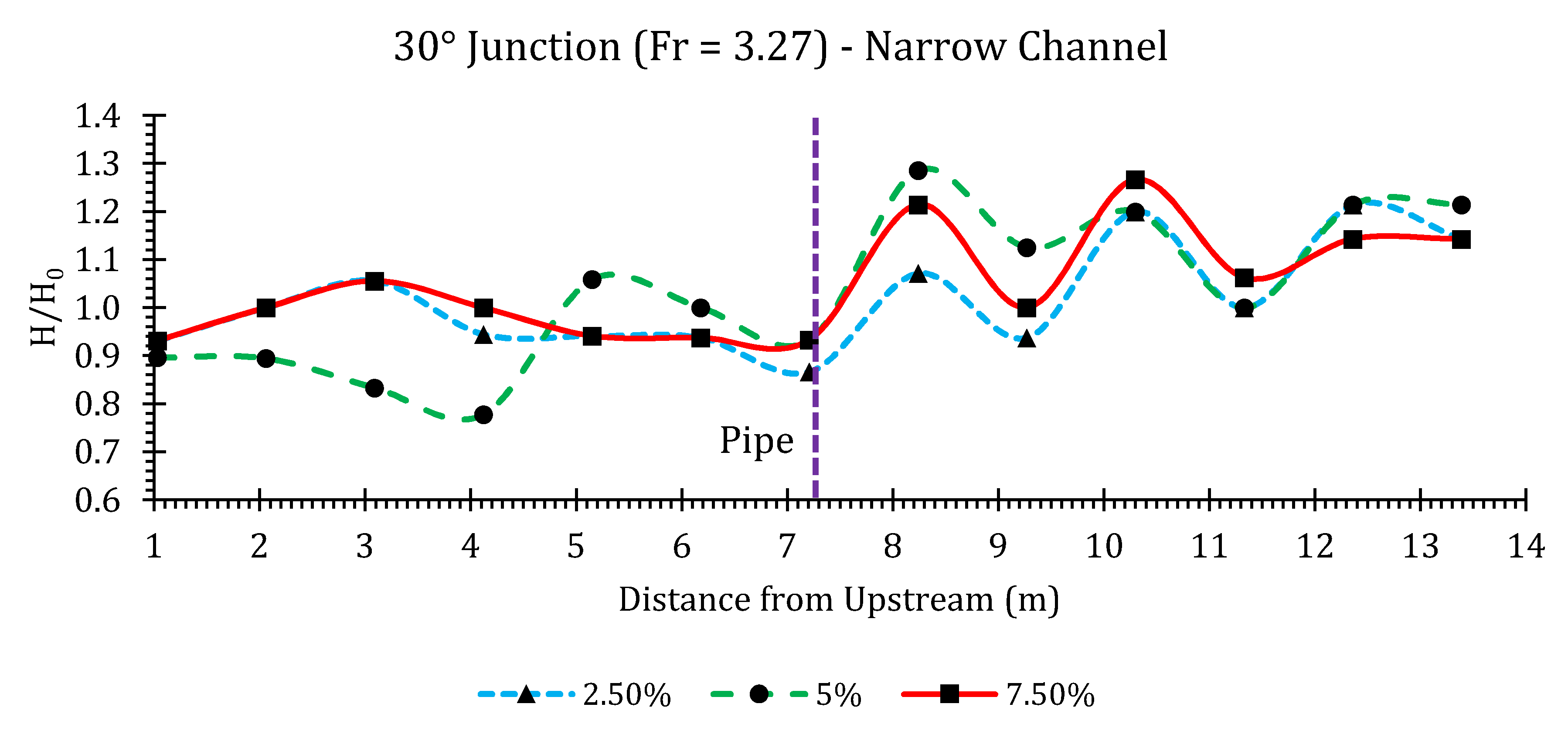

Appendix B
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.46 | 2.540 | 15.48 | 90 | 28.28 | 1.16 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.46 | 2.540 | 15.48 | 45 | 40.99 | 1.12 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.46 | 2.540 | 15.48 | 30 | 58.28 | 1.1 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 10.163 | 15.48 | 90 | 7.07 | 1.76 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 5.083 | 7.74 | 90 | 28.24 | 1.27 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 2.540 | 3.87 | 90 | 113.10 | 1.17 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 10.163 | 15.48 | 45 | 10.99 | 1.25 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 5.083 | 7.74 | 45 | 40.94 | 1.2 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 2.540 | 3.87 | 45 | 160.95 | 1.16 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 10.163 | 15.48 | 30 | 15.86 | 1.17 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 5.083 | 7.74 | 30 | 58.22 | 1.16 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 0.91 | 2.540 | 3.87 | 30 | 227.94 | 1.15 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 10.163 | 5.57 | 90 | 19.63 | 1.68 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 5.083 | 2.79 | 90 | 78.46 | 1.29 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 2.540 | 1.39 | 90 | 314.18 | 1.15 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 10.163 | 5.57 | 45 | 28.75 | 1.35 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 5.083 | 2.79 | 45 | 111.95 | 1.24 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 2.540 | 1.39 | 45 | 445.31 | 1.15 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 10.163 | 5.57 | 30 | 40.98 | 1.32 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 5.083 | 2.79 | 30 | 158.64 | 1.23 | L |
| 3.05 | 3.05 | 2 | 101.63 | 10.94 | 1.52 | 2.540 | 1.39 | 30 | 630.08 | 1.15 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.46 | 1.488 | 9.07 | 90 | 40.37 | 1.17 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.46 | 1.488 | 9.07 | 45 | 58.10 | 1.17 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.46 | 1.488 | 9.07 | 30 | 82.48 | 1.17 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 5.952 | 9.07 | 90 | 10.09 | 1.89 | W |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 2.976 | 4.54 | 90 | 40.37 | 1.32 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 1.488 | 2.27 | 90 | 161.49 | 1.19 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 5.952 | 9.07 | 45 | 15.27 | 1.26 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 2.976 | 4.54 | 45 | 58.10 | 1.18 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 1.488 | 2.27 | 45 | 229.39 | 1.18 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 5.952 | 9.07 | 30 | 21.92 | 1.18 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 2.976 | 4.54 | 30 | 82.48 | 1.18 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 0.91 | 1.488 | 2.27 | 30 | 324.72 | 1.18 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 5.952 | 3.26 | 90 | 28.04 | 1.84 | W |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 2.976 | 1.63 | 90 | 112.15 | 1.33 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 1.488 | 0.82 | 90 | 448.59 | 1.2 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 5.952 | 3.26 | 45 | 40.65 | 1.49 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 2.976 | 1.63 | 45 | 159.60 | 1.28 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 1.488 | 0.82 | 45 | 635.41 | 1.19 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 5.952 | 3.26 | 30 | 57.81 | 1.43 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 2.976 | 1.63 | 30 | 226.03 | 1.3 | L |
| 3.05 | 2.13 | 2 | 59.52 | 9.15 | 1.52 | 1.488 | 0.82 | 30 | 898.92 | 1.17 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.46 | 1.286 | 7.83 | 90 | 17.66 | 1.38 | W |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.46 | 0.643 | 3.92 | 90 | 70.65 | 1.23 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.46 | 1.286 | 7.83 | 45 | 25.98 | 1.26 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.46 | 0.643 | 3.92 | 45 | 100.91 | 1.2 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.46 | 1.286 | 7.83 | 30 | 37.06 | 1.2 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.46 | 0.643 | 3.92 | 30 | 143.03 | 1.2 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 2.571 | 3.92 | 90 | 17.66 | 1.93 | W |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 1.286 | 1.96 | 90 | 70.65 | 1.39 | W |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 0.643 | 0.98 | 90 | 282.60 | 1.17 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 2.571 | 3.92 | 45 | 25.98 | 1.53 | W |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 1.286 | 1.96 | 45 | 100.91 | 1.36 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 0.643 | 0.98 | 45 | 400.66 | 1.25 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 2.571 | 3.92 | 30 | 37.06 | 1.5 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 1.286 | 1.96 | 30 | 143.03 | 1.36 | L |
| 3.05 | 1.22 | 2 | 25.71 | 6.92 | 0.91 | 0.643 | 0.98 | 30 | 566.93 | 1.25 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.46 | 2.540 | 15.48 | 90 | 70.69 | 1.1 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.46 | 2.540 | 15.48 | 45 | 100.98 | 1.06 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.46 | 2.540 | 15.48 | 30 | 143.12 | 1.03 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 10.163 | 15.48 | 90 | 17.66 | 1.38 | W |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 5.083 | 7.74 | 90 | 70.61 | 1.19 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 2.540 | 3.87 | 90 | 282.77 | 1.1 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 10.163 | 15.48 | 45 | 25.98 | 1.15 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 5.083 | 7.74 | 45 | 100.86 | 1.11 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 2.540 | 3.87 | 45 | 400.90 | 1.1 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 10.163 | 15.48 | 30 | 37.06 | 1.08 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 5.083 | 7.74 | 30 | 142.96 | 1.07 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 0.91 | 2.540 | 3.87 | 30 | 567.28 | 1.06 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 10.163 | 5.57 | 90 | 49.07 | 1.32 | W |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 5.083 | 2.79 | 90 | 196.15 | 1.18 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 2.540 | 1.39 | 90 | 785.48 | 1.1 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 10.163 | 5.57 | 45 | 70.39 | 1.2 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 5.083 | 2.79 | 45 | 278.40 | 1.15 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 2.540 | 1.39 | 45 | 1111.84 | 1.1 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 10.163 | 5.57 | 30 | 99.86 | 1.17 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 5.083 | 2.79 | 30 | 394.04 | 1.15 | L |
| 7.62 | 3.05 | 2 | 254.09 | 10.94 | 1.52 | 2.540 | 1.39 | 30 | 1572.69 | 1.1 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.46 | 1.488 | 9.07 | 90 | 100.93 | 1.07 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.46 | 1.488 | 9.07 | 45 | 143.74 | 1.01 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.46 | 1.488 | 9.07 | 30 | 203.60 | 1.01 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 5.952 | 9.07 | 90 | 25.23 | 1.36 | W |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 2.976 | 4.54 | 90 | 100.93 | 1.14 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 1.488 | 2.27 | 90 | 403.73 | 1.07 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 5.952 | 9.07 | 45 | 36.69 | 1.11 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 2.976 | 4.54 | 45 | 143.74 | 1.09 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 1.488 | 2.27 | 45 | 571.97 | 1.07 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 5.952 | 9.07 | 30 | 52.20 | 1.11 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 2.976 | 4.54 | 30 | 203.60 | 1.08 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 0.91 | 1.488 | 2.27 | 30 | 809.20 | 1.06 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 5.952 | 3.26 | 90 | 70.09 | 1.43 | W |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 2.976 | 1.63 | 90 | 280.37 | 1.14 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 1.488 | 0.82 | 90 | 1121.48 | 1.07 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 5.952 | 3.26 | 45 | 100.13 | 1.22 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 2.976 | 1.63 | 45 | 397.50 | 1.12 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 1.488 | 0.82 | 45 | 1587.01 | 1.06 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 5.952 | 3.26 | 30 | 141.92 | 1.2 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 2.976 | 1.63 | 30 | 562.47 | 1.12 | L |
| 7.62 | 2.13 | 2 | 148.81 | 9.15 | 1.52 | 1.488 | 0.82 | 30 | 2244.70 | 1.06 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.46 | 1.286 | 7.83 | 90 | 44.16 | 1.17 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.46 | 0.643 | 3.92 | 90 | 176.63 | 1.07 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.46 | 1.286 | 7.83 | 45 | 63.45 | 1.08 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.46 | 0.643 | 3.92 | 45 | 250.79 | 1.02 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.46 | 1.286 | 7.83 | 30 | 90.04 | 1.01 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.46 | 0.643 | 3.92 | 30 | 354.98 | 1.01 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 2.571 | 3.92 | 90 | 44.16 | 1.39 | W |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 1.286 | 1.96 | 90 | 176.63 | 1.17 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 0.643 | 0.98 | 90 | 706.50 | 1.08 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 2.571 | 3.92 | 45 | 63.45 | 1.27 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 1.286 | 1.96 | 45 | 250.79 | 1.15 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 0.643 | 0.98 | 45 | 1000.14 | 1.07 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 2.571 | 3.92 | 30 | 90.04 | 1.25 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 1.286 | 1.96 | 30 | 354.98 | 1.14 | L |
| 7.62 | 1.22 | 2 | 64.28 | 6.92 | 0.91 | 0.643 | 0.98 | 30 | 1414.73 | 1.06 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.46 | 2.540 | 15.48 | 90 | 141.38 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.46 | 2.540 | 15.48 | 45 | 200.94 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.46 | 2.540 | 15.48 | 30 | 284.49 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 10.163 | 15.48 | 90 | 35.33 | 1.23 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 5.083 | 7.74 | 90 | 141.22 | 1.07 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 2.540 | 3.87 | 90 | 565.52 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 10.163 | 15.48 | 45 | 50.96 | 1.07 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 5.083 | 7.74 | 45 | 200.72 | 1.02 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 2.540 | 3.87 | 45 | 800.76 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 10.163 | 15.48 | 30 | 72.38 | 1.02 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 5.083 | 7.74 | 30 | 284.17 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 0.91 | 2.540 | 3.87 | 30 | 1132.76 | 1.01 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 10.163 | 5.57 | 90 | 98.13 | 1.24 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 5.083 | 2.79 | 90 | 392.28 | 1.08 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 2.540 | 1.39 | 90 | 1570.88 | 1.03 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 10.163 | 5.57 | 45 | 139.77 | 1.14 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 5.083 | 2.79 | 45 | 555.77 | 1.08 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 2.540 | 1.39 | 45 | 2222.55 | 1.05 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 10.163 | 5.57 | 30 | 197.98 | 1.12 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 5.083 | 2.79 | 30 | 786.29 | 1.06 | L |
| 15.24 | 3.05 | 2 | 508.15 | 10.94 | 1.52 | 2.540 | 1.39 | 30 | 3143.48 | 1.01 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.46 | 1.488 | 9.07 | 90 | 201.87 | 1.05 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.46 | 1.488 | 9.07 | 45 | 286.48 | 1.01 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.46 | 1.488 | 9.07 | 30 | 405.47 | 1.01 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 5.952 | 9.07 | 90 | 50.47 | 1.25 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 2.976 | 4.54 | 90 | 201.87 | 1.11 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 1.488 | 2.27 | 90 | 807.47 | 1.09 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 5.952 | 9.07 | 45 | 72.37 | 1.09 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 2.976 | 4.54 | 45 | 286.48 | 1.06 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 1.488 | 2.27 | 45 | 1142.93 | 1.02 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 5.952 | 9.07 | 30 | 102.67 | 1.07 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 2.976 | 4.54 | 30 | 405.47 | 1.04 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 0.91 | 1.488 | 2.27 | 30 | 1616.67 | 1.01 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 5.952 | 3.26 | 90 | 140.19 | 1.3 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 2.976 | 1.63 | 90 | 560.74 | 1.11 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 1.488 | 0.82 | 90 | 2242.96 | 1.07 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 5.952 | 3.26 | 45 | 199.25 | 1.17 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 2.976 | 1.63 | 45 | 794.01 | 1.07 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 1.488 | 0.82 | 45 | 3173.03 | 1.02 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 5.952 | 3.26 | 30 | 282.10 | 1.17 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 2.976 | 1.63 | 30 | 1123.21 | 1.08 | L |
| 15.24 | 2.13 | 2 | 297.61 | 9.15 | 1.52 | 1.488 | 0.82 | 30 | 4487.66 | 1.02 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.46 | 1.286 | 7.83 | 90 | 88.31 | 1.08 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.46 | 0.643 | 3.92 | 90 | 353.25 | 1.06 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.46 | 1.286 | 7.83 | 45 | 125.89 | 1.03 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.46 | 0.643 | 3.92 | 45 | 500.57 | 1.01 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.46 | 1.286 | 7.83 | 30 | 178.36 | 1.01 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.46 | 0.643 | 3.92 | 30 | 708.23 | 1.01 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 2.571 | 3.92 | 90 | 88.31 | 1.23 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 1.286 | 1.96 | 90 | 353.25 | 1.06 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 0.643 | 0.98 | 90 | 1413.00 | 1.03 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 2.571 | 3.92 | 45 | 125.89 | 1.15 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 1.286 | 1.96 | 45 | 500.57 | 1.04 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 0.643 | 0.98 | 45 | 1999.28 | 1.02 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 2.571 | 3.92 | 30 | 178.36 | 1.14 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 1.286 | 1.96 | 30 | 708.23 | 1.03 | L |
| 15.24 | 1.22 | 2 | 128.56 | 6.92 | 0.91 | 0.643 | 0.98 | 30 | 2827.73 | 1.01 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.46 | 1.524 | 9.29 | 90 | 28.26 | 1.2 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.46 | 1.524 | 9.29 | 45 | 40.97 | 1.2 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.46 | 1.524 | 9.29 | 30 | 58.25 | 1.2 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 6.097 | 9.29 | 90 | 7.07 | 1.78 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 3.048 | 4.64 | 90 | 28.26 | 1.43 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 1.524 | 2.32 | 90 | 113.04 | 1.18 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 6.097 | 9.29 | 45 | 10.99 | 1.26 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 3.048 | 4.64 | 45 | 40.97 | 1.23 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 1.524 | 2.32 | 45 | 160.86 | 1.15 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 6.097 | 9.29 | 30 | 15.86 | 1.22 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 3.048 | 4.64 | 30 | 58.25 | 1.2 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 0.91 | 1.524 | 2.32 | 30 | 227.81 | 1.15 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 6.097 | 3.34 | 90 | 19.63 | 1.84 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 3.048 | 1.67 | 90 | 78.50 | 1.43 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 1.524 | 0.84 | 90 | 314.00 | 1.19 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 6.097 | 3.34 | 45 | 28.75 | 1.57 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 3.048 | 1.67 | 45 | 112.02 | 1.33 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 1.524 | 0.84 | 45 | 445.06 | 1.17 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 6.097 | 3.34 | 30 | 40.98 | 1.54 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 3.048 | 1.67 | 30 | 158.73 | 1.32 | L |
| 3.05 | 3.05 | 1.2 | 60.97 | 6.56 | 1.52 | 1.524 | 0.84 | 30 | 629.73 | 1.17 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.46 | 1.785 | 10.88 | 90 | 10.10 | 1.28 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.46 | 0.893 | 5.44 | 90 | 40.38 | 1.2 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.46 | 1.785 | 10.88 | 45 | 15.28 | 1.2 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.46 | 0.893 | 5.44 | 45 | 58.11 | 1.2 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.46 | 1.785 | 10.88 | 30 | 21.92 | 1.2 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.46 | 0.893 | 5.44 | 30 | 82.50 | 1.2 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 3.571 | 5.44 | 90 | 10.10 | 1.85 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 1.785 | 2.72 | 90 | 40.38 | 1.36 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 0.893 | 1.36 | 90 | 161.54 | 1.15 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 3.571 | 5.44 | 45 | 15.28 | 1.33 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 1.785 | 2.72 | 45 | 58.11 | 1.23 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 0.893 | 1.36 | 45 | 229.45 | 1.12 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 3.571 | 5.44 | 30 | 21.92 | 1.27 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 1.785 | 2.72 | 30 | 82.50 | 1.22 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 0.91 | 0.893 | 1.36 | 30 | 324.81 | 1.11 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 3.571 | 1.96 | 90 | 28.04 | 1.87 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 1.785 | 0.98 | 90 | 112.18 | 1.35 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 0.893 | 0.49 | 90 | 448.71 | 1.15 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 3.571 | 1.96 | 45 | 40.66 | 1.66 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 1.785 | 0.98 | 45 | 159.64 | 1.31 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 0.893 | 0.49 | 45 | 635.58 | 1.13 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 3.571 | 1.96 | 30 | 57.82 | 1.63 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 1.785 | 0.98 | 30 | 226.09 | 1.31 | L |
| 3.05 | 2.13 | 1.2 | 35.71 | 5.49 | 1.52 | 0.893 | 0.49 | 30 | 899.16 | 1.13 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 1.543 | 9.41 | 90 | 4.41 | 1.65 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 0.772 | 4.70 | 90 | 17.66 | 1.2 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 0.386 | 2.35 | 90 | 70.62 | 1.08 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 1.543 | 9.41 | 45 | 7.24 | 1.1 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 0.772 | 4.70 | 45 | 25.97 | 1.07 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 0.386 | 2.35 | 45 | 100.88 | 1.03 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 1.543 | 9.41 | 30 | 10.56 | 1.03 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 0.772 | 4.70 | 30 | 37.04 | 1.03 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.46 | 0.386 | 2.35 | 30 | 142.98 | 1.03 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 1.543 | 2.35 | 90 | 17.66 | 1.78 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 0.772 | 1.18 | 90 | 70.62 | 1.28 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 0.386 | 0.59 | 90 | 282.50 | 1.09 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 1.543 | 2.35 | 45 | 25.97 | 1.52 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 0.772 | 1.18 | 45 | 100.88 | 1.25 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 0.386 | 0.59 | 45 | 400.51 | 1.08 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 1.543 | 2.35 | 30 | 37.04 | 1.48 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 0.772 | 1.18 | 30 | 142.98 | 1.25 | L |
| 3.05 | 1.22 | 1.2 | 15.43 | 4.15 | 0.91 | 0.386 | 0.59 | 30 | 566.72 | 1.07 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.46 | 1.524 | 9.29 | 90 | 70.66 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.46 | 1.524 | 9.29 | 45 | 100.92 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.46 | 1.524 | 9.29 | 30 | 143.05 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 6.097 | 9.29 | 90 | 17.66 | 1.27 | W |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 3.048 | 4.64 | 90 | 70.66 | 1.07 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 1.524 | 2.32 | 90 | 282.63 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 6.097 | 9.29 | 45 | 25.98 | 1.06 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 3.048 | 4.64 | 45 | 100.92 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 1.524 | 2.32 | 45 | 400.69 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 6.097 | 9.29 | 30 | 37.06 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 3.048 | 4.64 | 30 | 143.05 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 0.91 | 1.524 | 2.32 | 30 | 566.98 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 6.097 | 3.34 | 90 | 49.07 | 1.26 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 3.048 | 1.67 | 90 | 196.27 | 1.17 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 1.524 | 0.84 | 90 | 785.07 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 6.097 | 3.34 | 45 | 70.39 | 1.14 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 3.048 | 1.67 | 45 | 278.57 | 1.06 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 1.524 | 0.84 | 45 | 1111.26 | 1.01 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 6.097 | 3.34 | 30 | 99.87 | 1.13 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 3.048 | 1.67 | 30 | 394.27 | 1.05 | L |
| 7.62 | 3.05 | 1.2 | 152.43 | 6.56 | 1.52 | 1.524 | 0.84 | 30 | 1571.88 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.46 | 1.785 | 10.88 | 90 | 25.24 | 1.04 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.46 | 0.893 | 5.44 | 90 | 100.98 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.46 | 1.785 | 10.88 | 45 | 36.70 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.46 | 0.893 | 5.44 | 45 | 143.80 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.46 | 1.785 | 10.88 | 30 | 52.22 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.46 | 0.893 | 5.44 | 30 | 203.69 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 3.571 | 5.44 | 90 | 25.24 | 1.21 | W |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 1.785 | 2.72 | 90 | 100.98 | 1.06 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 0.893 | 1.36 | 90 | 403.91 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 3.571 | 5.44 | 45 | 36.70 | 1.04 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 1.785 | 2.72 | 45 | 143.80 | 1.02 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 0.893 | 1.36 | 45 | 572.21 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 3.571 | 5.44 | 30 | 52.22 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 1.785 | 2.72 | 30 | 203.69 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 0.91 | 0.893 | 1.36 | 30 | 809.54 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 3.571 | 1.96 | 90 | 70.12 | 1.21 | W |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 1.785 | 0.98 | 90 | 280.49 | 1.05 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 0.893 | 0.49 | 90 | 1121.96 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 3.571 | 1.96 | 45 | 100.17 | 1.15 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 1.785 | 0.98 | 45 | 397.67 | 1.04 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 0.893 | 0.49 | 45 | 1587.69 | 1.01 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 3.571 | 1.96 | 30 | 141.98 | 1.13 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 1.785 | 0.98 | 30 | 562.71 | 1.04 | L |
| 7.62 | 2.13 | 1.2 | 89.28 | 5.49 | 1.52 | 0.893 | 0.49 | 30 | 2245.66 | 1.01 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 1.543 | 9.41 | 90 | 11.04 | 1.25 | W |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 0.772 | 4.70 | 90 | 44.16 | 1.09 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 0.386 | 2.35 | 90 | 176.62 | 1.01 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 1.543 | 9.41 | 45 | 16.61 | 1.18 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 0.772 | 4.70 | 45 | 63.45 | 1.05 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 0.386 | 2.35 | 45 | 250.79 | 1.01 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 1.543 | 9.41 | 30 | 23.81 | 1.01 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 0.772 | 4.70 | 30 | 90.04 | 1.01 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.46 | 0.386 | 2.35 | 30 | 354.98 | 1.01 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 1.543 | 2.35 | 90 | 44.16 | 1.27 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 0.772 | 1.18 | 90 | 176.62 | 1.12 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 0.386 | 0.59 | 90 | 706.50 | 1.04 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 1.543 | 2.35 | 45 | 63.45 | 1.2 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 0.772 | 1.18 | 45 | 250.79 | 1.09 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 0.386 | 0.59 | 45 | 1000.14 | 1.02 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 1.543 | 2.35 | 30 | 90.04 | 1.17 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 0.772 | 1.18 | 30 | 354.98 | 1.08 | L |
| 7.62 | 1.22 | 1.2 | 38.60 | 4.15 | 0.91 | 0.386 | 0.59 | 30 | 1414.73 | 1.01 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.46 | 1.524 | 9.29 | 90 | 141.30 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.46 | 1.524 | 9.29 | 45 | 200.83 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.46 | 1.524 | 9.29 | 30 | 284.33 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 6.097 | 9.29 | 90 | 35.33 | 1.1 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 3.048 | 4.64 | 90 | 141.30 | 1.02 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 1.524 | 2.32 | 90 | 565.20 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 6.097 | 9.29 | 45 | 50.96 | 1.03 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 3.048 | 4.64 | 45 | 200.83 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 1.524 | 2.32 | 45 | 800.31 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 6.097 | 9.29 | 30 | 72.38 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 3.048 | 4.64 | 30 | 284.33 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 0.91 | 1.524 | 2.32 | 30 | 1132.13 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 6.097 | 3.34 | 90 | 98.13 | 1.1 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 3.048 | 1.67 | 90 | 392.50 | 1.02 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 1.524 | 0.84 | 90 | 1570.00 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 6.097 | 3.34 | 45 | 139.77 | 1.03 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 3.048 | 1.67 | 45 | 556.08 | 1.02 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 1.524 | 0.84 | 45 | 2221.32 | 1.01 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 6.097 | 3.34 | 30 | 197.98 | 1.05 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 3.048 | 1.67 | 30 | 786.73 | 1.02 | L |
| 15.24 | 3.05 | 1.2 | 304.83 | 6.56 | 1.52 | 1.524 | 0.84 | 30 | 3141.73 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.46 | 1.785 | 10.88 | 90 | 50.48 | 1.02 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.46 | 0.893 | 5.44 | 90 | 201.92 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.46 | 1.785 | 10.88 | 45 | 72.39 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.46 | 0.893 | 5.44 | 45 | 286.56 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.46 | 1.785 | 10.88 | 30 | 102.69 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.46 | 0.893 | 5.44 | 30 | 405.57 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 3.571 | 5.44 | 90 | 50.48 | 1.11 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 1.785 | 2.72 | 90 | 201.92 | 1.03 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 0.893 | 1.36 | 90 | 807.68 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 3.571 | 5.44 | 45 | 72.39 | 1.02 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 1.785 | 2.72 | 45 | 286.56 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 0.893 | 1.36 | 45 | 1143.24 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 3.571 | 5.44 | 30 | 102.69 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 1.785 | 2.72 | 30 | 405.57 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 0.91 | 0.893 | 1.36 | 30 | 1617.10 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 3.571 | 1.96 | 90 | 140.22 | 1.12 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 1.785 | 0.98 | 90 | 560.89 | 1.04 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 0.893 | 0.49 | 90 | 2243.57 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 3.571 | 1.96 | 45 | 199.31 | 1.06 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 1.785 | 0.98 | 45 | 794.22 | 1.02 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 0.893 | 0.49 | 45 | 3173.89 | 1.01 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 3.571 | 1.96 | 30 | 282.18 | 1.06 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 1.785 | 0.98 | 30 | 1123.52 | 1.02 | L |
| 15.24 | 2.13 | 1.2 | 178.54 | 5.49 | 1.52 | 0.893 | 0.49 | 30 | 4488.87 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 1.543 | 9.41 | 90 | 22.07 | 1.19 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 0.772 | 4.70 | 90 | 88.28 | 1.04 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 0.386 | 2.35 | 90 | 353.12 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 1.543 | 9.41 | 45 | 32.21 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 0.772 | 4.70 | 45 | 125.85 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 0.386 | 2.35 | 45 | 500.39 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 1.543 | 9.41 | 30 | 45.87 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 0.772 | 4.70 | 30 | 178.29 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.46 | 0.386 | 2.35 | 30 | 707.97 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 1.543 | 2.35 | 90 | 88.28 | 1.14 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 0.772 | 1.18 | 90 | 353.12 | 1.05 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 0.386 | 0.59 | 90 | 1412.48 | 1.02 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 1.543 | 2.35 | 45 | 125.85 | 1.05 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 0.772 | 1.18 | 45 | 500.39 | 1.02 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 0.386 | 0.59 | 45 | 1998.55 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 1.543 | 2.35 | 30 | 178.29 | 1.02 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 0.772 | 1.18 | 30 | 707.97 | 1.01 | L |
| 15.24 | 1.22 | 1.2 | 77.16 | 4.15 | 0.91 | 0.386 | 0.59 | 30 | 2826.69 | 1.01 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.46 | 2.033 | 12.39 | 90 | 7.07 | 1.33 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.46 | 1.017 | 6.20 | 90 | 28.26 | 1.17 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.46 | 2.033 | 12.39 | 45 | 10.99 | 1.1 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.46 | 1.017 | 6.20 | 45 | 40.97 | 1.1 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.46 | 2.033 | 12.39 | 30 | 15.86 | 1.1 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.46 | 1.017 | 6.20 | 30 | 58.25 | 1.1 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 4.066 | 6.20 | 90 | 7.07 | 1.71 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 2.033 | 3.10 | 90 | 28.26 | 1.39 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 1.017 | 1.55 | 90 | 113.04 | 1.19 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 4.066 | 6.20 | 45 | 10.99 | 1.36 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 2.033 | 3.10 | 45 | 40.97 | 1.31 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 1.017 | 1.55 | 45 | 160.86 | 1.18 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 4.066 | 6.20 | 30 | 15.86 | 1.32 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 2.033 | 3.10 | 30 | 58.25 | 1.29 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 0.91 | 1.017 | 1.55 | 30 | 227.81 | 1.18 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 4.066 | 2.23 | 90 | 19.63 | 1.7 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 2.033 | 1.12 | 90 | 78.50 | 1.4 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 1.017 | 0.56 | 90 | 314.00 | 1.2 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 4.066 | 2.23 | 45 | 28.75 | 1.58 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 2.033 | 1.12 | 45 | 112.02 | 1.35 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 1.017 | 0.56 | 45 | 445.06 | 1.2 | L |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 4.066 | 2.23 | 30 | 40.98 | 1.54 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 2.033 | 1.12 | 30 | 158.73 | 1.35 | W |
| 3.05 | 3.05 | 0.8 | 40.66 | 4.38 | 1.52 | 1.017 | 0.56 | 30 | 629.73 | 1.2 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 2.381 | 14.51 | 90 | 2.52 | 1.72 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 1.191 | 7.26 | 90 | 10.09 | 1.36 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 0.595 | 3.63 | 90 | 40.36 | 1.14 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 2.381 | 14.51 | 45 | 4.57 | 1.08 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 1.191 | 7.26 | 45 | 15.27 | 1.08 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 0.595 | 3.63 | 45 | 58.07 | 1.08 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 2.381 | 14.51 | 30 | 6.78 | 1.05 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 1.191 | 7.26 | 30 | 21.91 | 1.05 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.46 | 0.595 | 3.63 | 30 | 82.45 | 1.05 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 2.381 | 3.63 | 90 | 10.09 | 1.76 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 1.191 | 1.81 | 90 | 40.36 | 1.41 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 0.595 | 0.91 | 90 | 161.43 | 1.16 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 2.381 | 3.63 | 45 | 15.27 | 1.47 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 1.191 | 1.81 | 45 | 58.07 | 1.32 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 0.595 | 0.91 | 45 | 229.29 | 1.16 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 2.381 | 3.63 | 30 | 21.91 | 1.42 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 1.191 | 1.81 | 30 | 82.45 | 1.31 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 0.91 | 0.595 | 0.91 | 30 | 324.59 | 1.15 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 2.381 | 1.31 | 90 | 28.03 | 1.73 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 1.191 | 0.65 | 90 | 112.10 | 1.4 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 0.595 | 0.33 | 90 | 448.41 | 1.17 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 2.381 | 1.31 | 45 | 40.63 | 1.7 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 1.191 | 0.65 | 45 | 159.54 | 1.35 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 0.595 | 0.33 | 45 | 635.15 | 1.17 | L |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 2.381 | 1.31 | 30 | 57.78 | 1.64 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 1.191 | 0.65 | 30 | 225.94 | 1.35 | W |
| 3.05 | 2.13 | 0.8 | 23.81 | 3.66 | 1.52 | 0.595 | 0.33 | 30 | 898.55 | 1.17 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 1.028 | 6.26 | 90 | 4.42 | 1.72 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 0.514 | 3.13 | 90 | 17.67 | 1.34 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 0.257 | 1.57 | 90 | 70.69 | 1.15 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 1.028 | 6.26 | 45 | 7.25 | 1.18 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 0.514 | 3.13 | 45 | 25.99 | 1.18 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 0.257 | 1.57 | 45 | 100.97 | 1.09 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 1.028 | 6.26 | 30 | 10.57 | 1.18 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 0.514 | 3.13 | 30 | 37.08 | 1.18 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.46 | 0.257 | 1.57 | 30 | 143.11 | 1.09 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 1.028 | 1.57 | 90 | 17.67 | 1.65 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 0.514 | 0.78 | 90 | 70.69 | 1.38 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 0.257 | 0.39 | 90 | 282.76 | 1.17 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 1.028 | 1.57 | 45 | 25.99 | 1.63 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 0.514 | 0.78 | 45 | 100.97 | 1.34 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 0.257 | 0.39 | 45 | 400.88 | 1.17 | L |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 1.028 | 1.57 | 30 | 37.08 | 1.55 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 0.514 | 0.78 | 30 | 143.11 | 1.31 | W |
| 3.05 | 1.22 | 0.8 | 10.28 | 2.77 | 0.91 | 0.257 | 0.39 | 30 | 567.24 | 1.17 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.46 | 2.033 | 12.39 | 90 | 17.66 | 1.14 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.46 | 1.017 | 6.20 | 90 | 70.65 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.46 | 2.033 | 12.39 | 45 | 25.98 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.46 | 1.017 | 6.20 | 45 | 100.91 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.46 | 2.033 | 12.39 | 30 | 37.06 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.46 | 1.017 | 6.20 | 30 | 143.03 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 4.066 | 6.20 | 90 | 17.66 | 1.4 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 2.033 | 3.10 | 90 | 70.65 | 1.16 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 1.017 | 1.55 | 90 | 282.60 | 1.04 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 4.066 | 6.20 | 45 | 25.98 | 1.14 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 2.033 | 3.10 | 45 | 100.91 | 1.08 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 1.017 | 1.55 | 45 | 400.66 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 4.066 | 6.20 | 30 | 37.06 | 1.09 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 2.033 | 3.10 | 30 | 143.03 | 1.07 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 0.91 | 1.017 | 1.55 | 30 | 566.93 | 1.01 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 4.066 | 2.23 | 90 | 49.06 | 1.41 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 2.033 | 1.12 | 90 | 196.25 | 1.17 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 1.017 | 0.56 | 90 | 785.00 | 1.04 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 4.066 | 2.23 | 45 | 70.38 | 1.28 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 2.033 | 1.12 | 45 | 278.54 | 1.15 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 1.017 | 0.56 | 45 | 1111.16 | 1.04 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 4.066 | 2.23 | 30 | 99.86 | 1.26 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 2.033 | 1.12 | 30 | 394.23 | 1.13 | L |
| 7.62 | 3.05 | 0.8 | 101.66 | 4.38 | 1.52 | 1.017 | 0.56 | 30 | 1571.73 | 1.04 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 2.381 | 14.51 | 90 | 6.31 | 1.25 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 1.191 | 7.26 | 90 | 25.23 | 1.11 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 0.595 | 3.63 | 90 | 100.92 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 2.381 | 14.51 | 45 | 9.92 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 1.191 | 7.26 | 45 | 36.68 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 0.595 | 3.63 | 45 | 143.72 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 2.381 | 14.51 | 30 | 14.35 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 1.191 | 7.26 | 30 | 52.19 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.46 | 0.595 | 3.63 | 30 | 203.57 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 2.381 | 3.63 | 90 | 25.23 | 1.38 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 1.191 | 1.81 | 90 | 100.92 | 1.13 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 0.595 | 0.91 | 90 | 403.67 | 1.03 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 2.381 | 3.63 | 45 | 36.68 | 1.18 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 1.191 | 1.81 | 45 | 143.72 | 1.09 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 0.595 | 0.91 | 45 | 571.87 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 2.381 | 3.63 | 30 | 52.19 | 1.17 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 1.191 | 1.81 | 30 | 203.57 | 1.08 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 0.91 | 0.595 | 0.91 | 30 | 809.06 | 1.01 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 2.381 | 1.31 | 90 | 70.08 | 1.38 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 1.191 | 0.65 | 90 | 280.32 | 1.14 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 0.595 | 0.33 | 90 | 1121.30 | 1.04 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 2.381 | 1.31 | 45 | 100.11 | 1.3 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 1.191 | 0.65 | 45 | 397.44 | 1.13 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 0.595 | 0.33 | 45 | 1586.75 | 1.03 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 2.381 | 1.31 | 30 | 141.89 | 1.29 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 1.191 | 0.65 | 30 | 562.38 | 1.13 | L |
| 7.62 | 2.13 | 0.8 | 59.55 | 3.66 | 1.52 | 0.595 | 0.33 | 30 | 2244.32 | 1.02 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 1.028 | 6.26 | 90 | 11.05 | 1.3 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 0.514 | 3.13 | 90 | 44.20 | 1.16 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 0.257 | 1.57 | 90 | 176.82 | 1.04 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 1.028 | 6.26 | 45 | 16.63 | 1.11 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 0.514 | 3.13 | 45 | 63.52 | 1.06 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 0.257 | 1.57 | 45 | 251.06 | 1.02 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 1.028 | 6.26 | 30 | 23.83 | 1.04 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 0.514 | 3.13 | 30 | 90.14 | 1.03 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.46 | 0.257 | 1.57 | 30 | 355.37 | 1.01 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 1.028 | 1.57 | 90 | 44.20 | 1.35 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 0.514 | 0.78 | 90 | 176.82 | 1.15 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 0.257 | 0.39 | 90 | 707.28 | 1.05 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 1.028 | 1.57 | 45 | 63.52 | 1.28 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 0.514 | 0.78 | 45 | 251.06 | 1.12 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 0.257 | 0.39 | 45 | 1001.24 | 1.03 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 1.028 | 1.57 | 30 | 90.14 | 1.27 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 0.514 | 0.78 | 30 | 355.37 | 1.13 | L |
| 7.62 | 1.22 | 0.8 | 25.71 | 2.77 | 0.91 | 0.257 | 0.39 | 30 | 1416.29 | 1.01 | L |
| W (m) | H0 (m) | Fr (-) | Q Chan. (m3/s) | V Chan. (m/s) | D Pipe (m) | q Pipe (m3/s) | v Pipe (m/s) | θ Junc. (deg.) | Impact | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.46 | 2.033 | 12.39 | 90 | 35.33 | 1.03 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.46 | 1.017 | 6.20 | 90 | 141.30 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.46 | 2.033 | 12.39 | 45 | 50.96 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.46 | 1.017 | 6.20 | 45 | 200.83 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.46 | 2.033 | 12.39 | 30 | 72.38 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.46 | 1.017 | 6.20 | 30 | 284.33 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 4.066 | 6.20 | 90 | 35.33 | 1.18 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 2.033 | 3.10 | 90 | 141.30 | 1.05 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 1.017 | 1.55 | 90 | 565.20 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 4.066 | 6.20 | 45 | 50.96 | 1.04 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 2.033 | 3.10 | 45 | 200.83 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 1.017 | 1.55 | 45 | 800.31 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 4.066 | 6.20 | 30 | 72.38 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 2.033 | 3.10 | 30 | 284.33 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 0.91 | 1.017 | 1.55 | 30 | 1132.13 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 4.066 | 2.23 | 90 | 98.13 | 1.17 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 2.033 | 1.12 | 90 | 392.50 | 1.04 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 1.017 | 0.56 | 90 | 1570.00 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 4.066 | 2.23 | 45 | 139.77 | 1.1 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 2.033 | 1.12 | 45 | 556.08 | 1.03 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 1.017 | 0.56 | 45 | 2221.32 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 4.066 | 2.23 | 30 | 197.98 | 1.09 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 2.033 | 1.12 | 30 | 786.73 | 1.01 | L |
| 15.24 | 3.05 | 0.8 | 203.32 | 4.38 | 1.52 | 1.017 | 0.56 | 30 | 3141.73 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 2.381 | 14.51 | 90 | 12.61 | 1.16 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 1.191 | 7.26 | 90 | 50.45 | 1.03 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 0.595 | 3.63 | 90 | 201.79 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 2.381 | 14.51 | 45 | 18.84 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 1.191 | 7.26 | 45 | 72.34 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 0.595 | 3.63 | 45 | 286.37 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 2.381 | 14.51 | 30 | 26.96 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 1.191 | 7.26 | 30 | 102.62 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.46 | 0.595 | 3.63 | 30 | 405.30 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 2.381 | 3.63 | 90 | 50.45 | 1.18 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 1.191 | 1.81 | 90 | 201.79 | 1.07 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 0.595 | 0.91 | 90 | 807.14 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 2.381 | 3.63 | 45 | 72.34 | 1.08 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 1.191 | 1.81 | 45 | 286.37 | 1.03 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 0.595 | 0.91 | 45 | 1142.47 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 2.381 | 3.63 | 30 | 102.62 | 1.08 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 1.191 | 1.81 | 30 | 405.30 | 1.02 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 0.91 | 0.595 | 0.91 | 30 | 1616.01 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 2.381 | 1.31 | 90 | 140.13 | 1.17 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 1.191 | 0.65 | 90 | 560.51 | 1.06 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 0.595 | 0.33 | 90 | 2242.06 | 1.02 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 2.381 | 1.31 | 45 | 199.17 | 1.12 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 1.191 | 0.65 | 45 | 793.69 | 1.04 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 0.595 | 0.33 | 45 | 3171.75 | 1.01 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 2.381 | 1.31 | 30 | 281.99 | 1.12 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 1.191 | 0.65 | 30 | 1122.76 | 1.05 | L |
| 15.24 | 2.13 | 0.8 | 119.07 | 3.66 | 1.52 | 0.595 | 0.33 | 30 | 4485.85 | 1.01 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 1.028 | 6.26 | 90 | 22.09 | 1.2 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 0.514 | 3.13 | 90 | 88.36 | 1.09 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 0.257 | 1.57 | 90 | 353.44 | 1.02 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 1.028 | 6.26 | 45 | 32.24 | 1.07 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 0.514 | 3.13 | 45 | 125.96 | 1.04 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 0.257 | 1.57 | 45 | 500.85 | 1.01 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 1.028 | 6.26 | 30 | 45.91 | 1.02 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 0.514 | 3.13 | 30 | 178.45 | 1.01 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.46 | 0.257 | 1.57 | 30 | 708.62 | 1.01 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 1.028 | 1.57 | 90 | 88.36 | 1.24 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 0.514 | 0.78 | 90 | 353.44 | 1.08 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 0.257 | 0.39 | 90 | 1413.78 | 1.02 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 1.028 | 1.57 | 45 | 125.96 | 1.19 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 0.514 | 0.78 | 45 | 500.85 | 1.07 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 0.257 | 0.39 | 45 | 2000.38 | 1.01 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 1.028 | 1.57 | 30 | 178.45 | 1.16 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 0.514 | 0.78 | 30 | 708.62 | 1.01 | L |
| 15.24 | 1.22 | 0.8 | 51.40 | 2.77 | 0.91 | 0.257 | 0.39 | 30 | 2829.29 | 1.01 | L |
References
- Gurram, S.K.; Karki, K.S.; Hager, W.H. Subcritical junction flow. J. Hydraul. Eng. 1997, 123, 447–455. [Google Scholar] [CrossRef]
- Best, J.L. Flow Dynamics and Sediment Transport at River Channel Confluences. Ph.D. Thesis, University of London, London, UK, 1985. [Google Scholar]
- U.S. Army Engineer District. Supercritical Flow at Open Channel Junction; Report No. 2-100; U.S. Army Engineer District: Los Angeles, CA, USA, 1975. [Google Scholar]
- Taylor, E.H. Flow characteristics at rectangular open-channel junctions. Trans. ASCE 1944, 109, 893–902. [Google Scholar]
- Mignot, E.; Bonakdari, H.; Knothe, P.; Liperne Kouyi, G.; Bessette, A.; Riviere, N.; Bertrand-Krajewski, J.L. Experiments and 3D simulations of flow structures in junctions and their influence on location of flowmeters. Water Sci. Technol. 2012, 66, 1325–1332. [Google Scholar] [CrossRef] [PubMed]
- Constantinescu, G.; Miyawaki, S.; Rhoads, B.; Sukhodolov, A. Numerical evaluation of the effects of planform geometry and inflow conditions on flow, turbulence structure, and bed shear velocity at a stream confluence with a concordant bed. J. Geophys. Res. 2014, 119, 2079–2097. [Google Scholar] [CrossRef]
- Webber, N.B.; Greated, C.A. An investigation of flow behaviour at the junction of rectangular channels. ICE Proc. 1966, 34, 321–334. [Google Scholar] [CrossRef]
- Hsu, C.; Wu, F.; Lee, W. Flow at 90° equal-width open-channel junction. J. Hydraul. Eng. 1998, 124, 186–191. [Google Scholar] [CrossRef]
- Nedelec, Y.; Gay, B. Experimental study of a right-angled end junction between a pipe and an open channel. J. Hydraul. Eng. 2008, 134. [Google Scholar] [CrossRef]
- GREYLINE AVFM 5.0 User’s Manual (2017) [Online]. Available online: http://www.greyline.com/pdf/AVFM%205.0%20Manual.pdf (accessed on 15 February 2018).
- Lin, J.; Soong, H. Junction losses in open channel flows. Water Resour. Res. 1979, 15, 414–418. [Google Scholar] [CrossRef]
- Garcia-Navarro, M.; Saviron, J. Numerical simulation of unsteady flow at open channel junctions. J. Hydraul. Res. 1992, 30, 595–609. [Google Scholar] [CrossRef]
- Mays, L.W. Stormwater Collection Systems Design Book; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Yen, B.C. Hydraulics of sewers. Adv. Hydrosci. 1986, 14, 1122. [Google Scholar]
- Nazari-Sharabian, M.; Nazari-Sharabian, A.; Karakouzian, M.; Karami, M. Sacrificial Piles as Scour Countermeasures in River Bridges—A Numerical Study using FLOW-3D. Civ. Eng. J. 2020, 6. [Google Scholar] [CrossRef]
- Karami, M.; Kabiri-Samani, A.; Nazari-Sharabian, M.; Karakouzian, M. Investigating the Effects of Transient Flow in Concrete-Lined Pressure Tunnels and Developing a New Analytical Formula for Pressure Wave Velocity. Tunn. Undergr. Space Technol. 2019, 91, 102992. [Google Scholar] [CrossRef]
- Flow Science, Inc. Santa Fe, NM, USA. FLOW-3D® Version 12.0 User’s Manual (2018) [Online]. Available online: https://www.flow3d.com (accessed on 3 February 2019).
- Hydrologic Criteria and Drainage Design Manual (HCDDM) of the Clark County Regional Flood Control District (CCRFCD). Available online: http://www.ccrfcd.org/hcddm.htm (accessed on 3 February 2019).
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part 1: A discussion of principles. J. Hydrol. 1970, 103, 282–290. [Google Scholar] [CrossRef]
- Kenworthy, S.; Rhoads, B. Hydrologic control of spatial patterns of suspended sediment concentration at a stream confluence. J. Hydrol. 1995, 168, 251–263. [Google Scholar] [CrossRef]



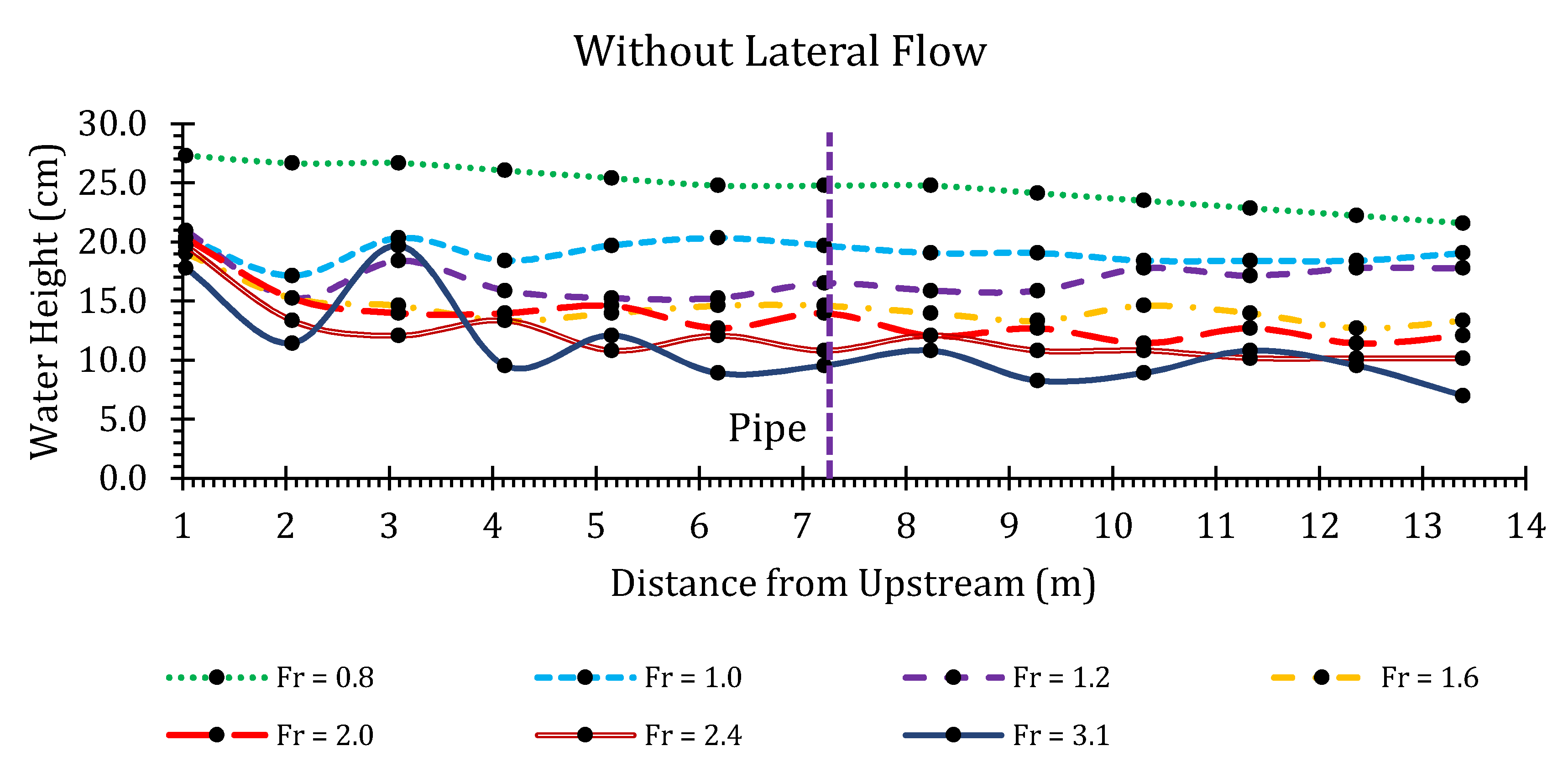
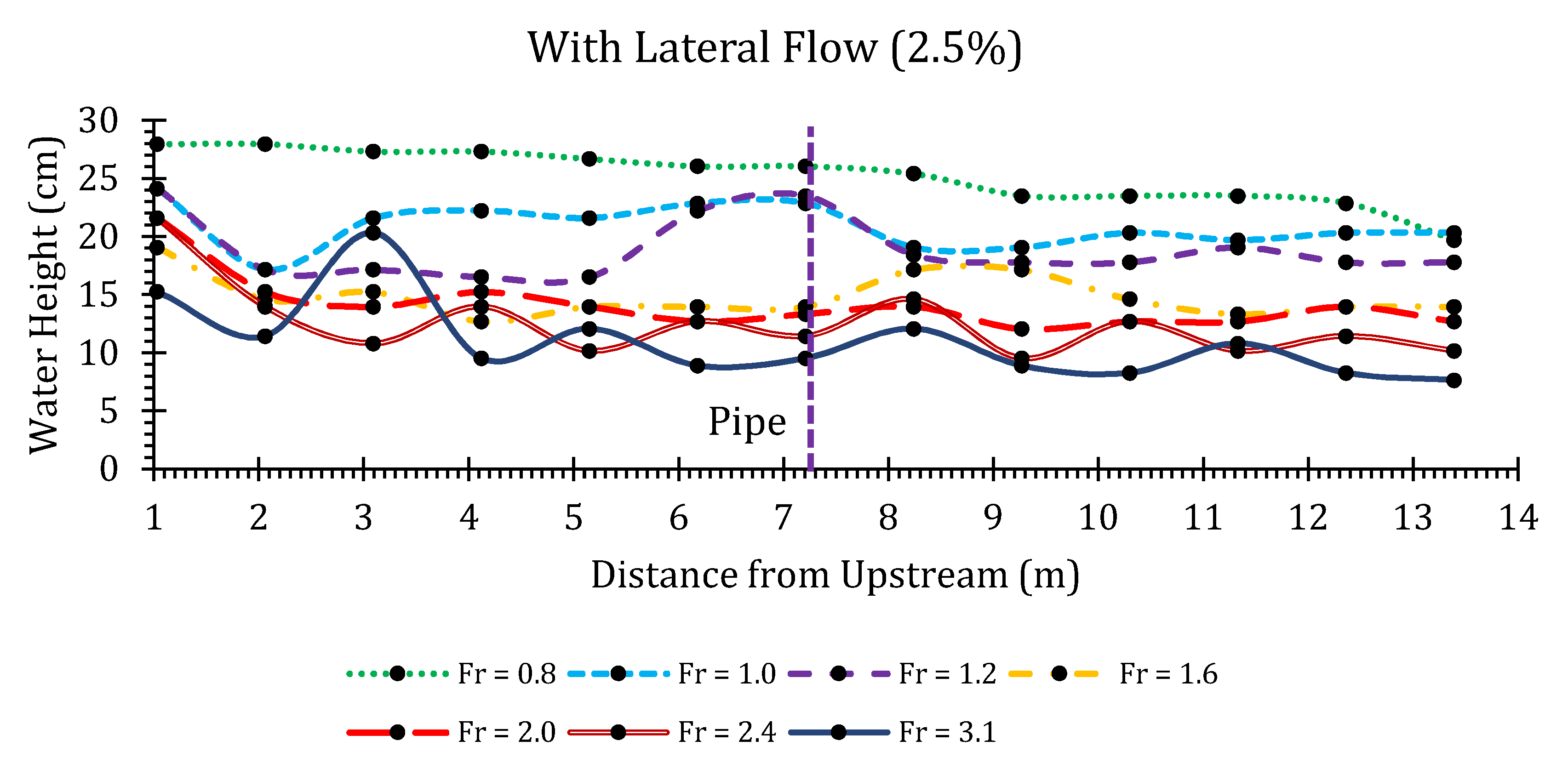
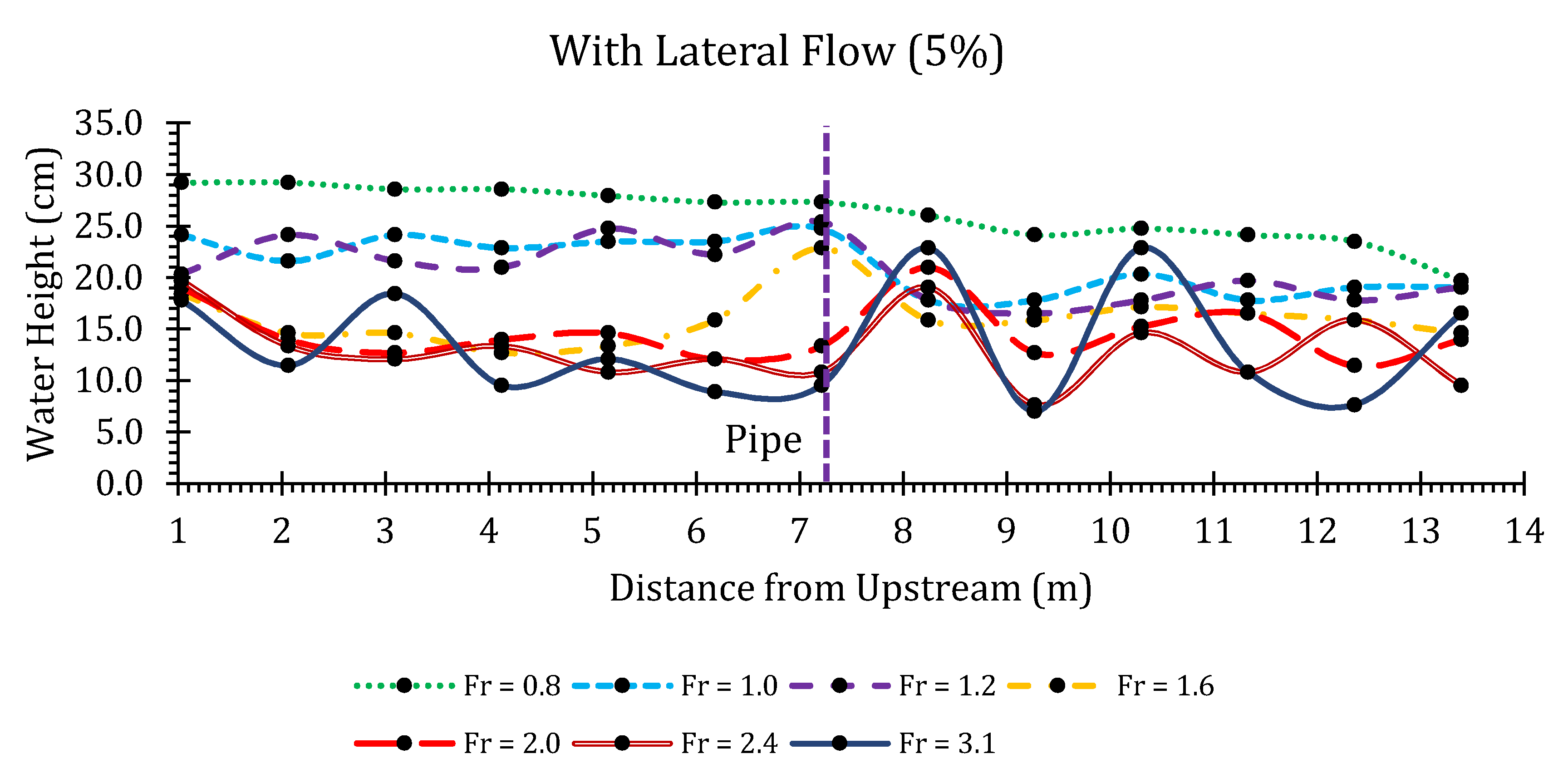
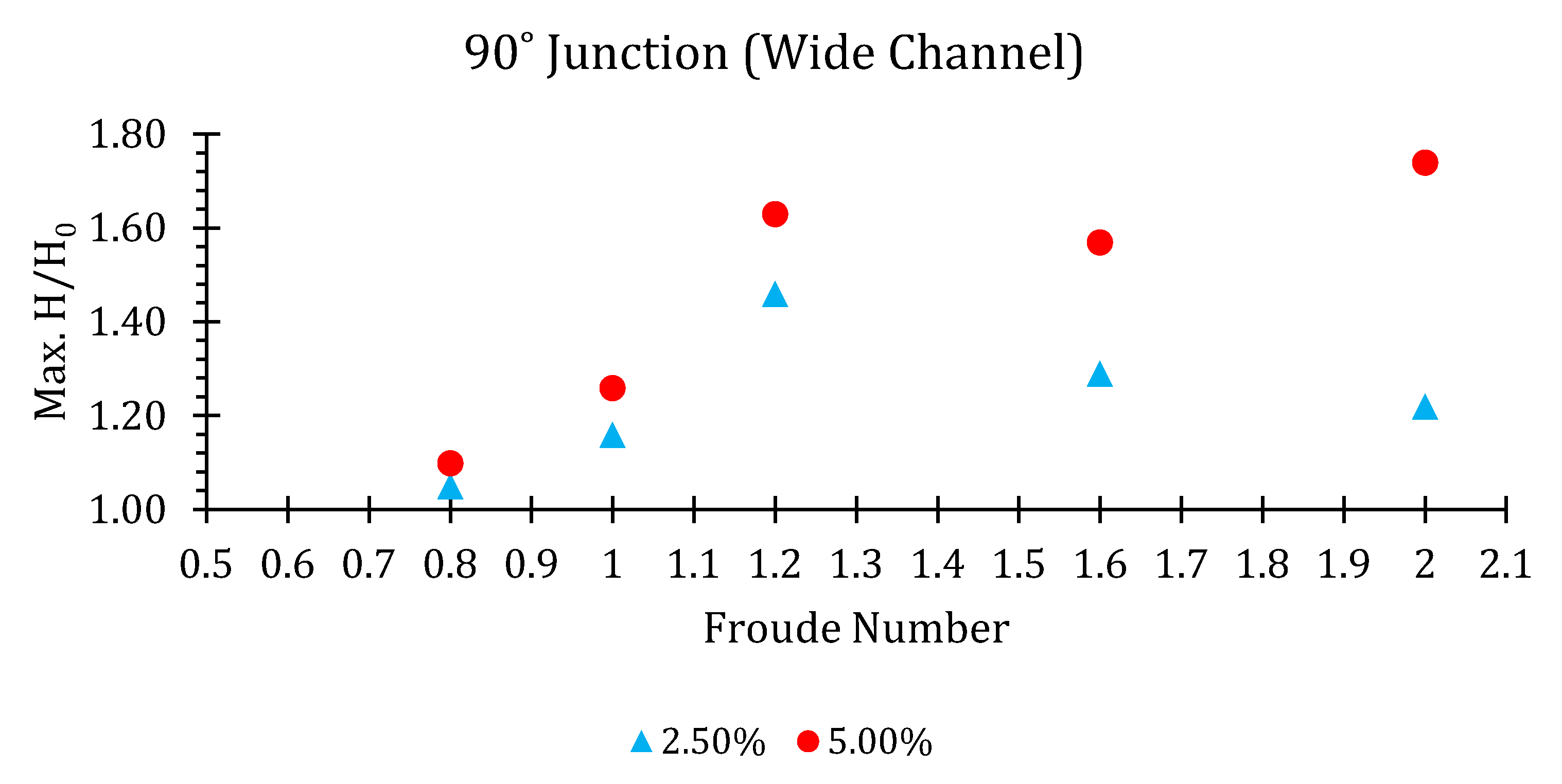




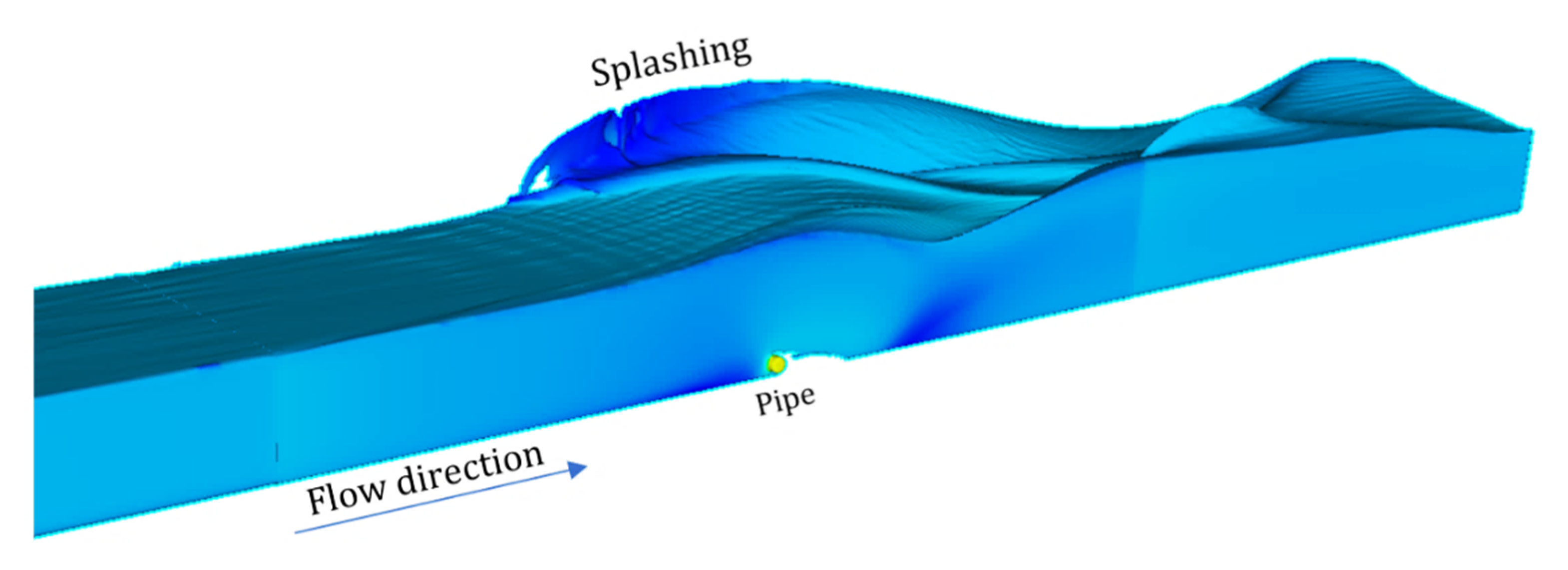
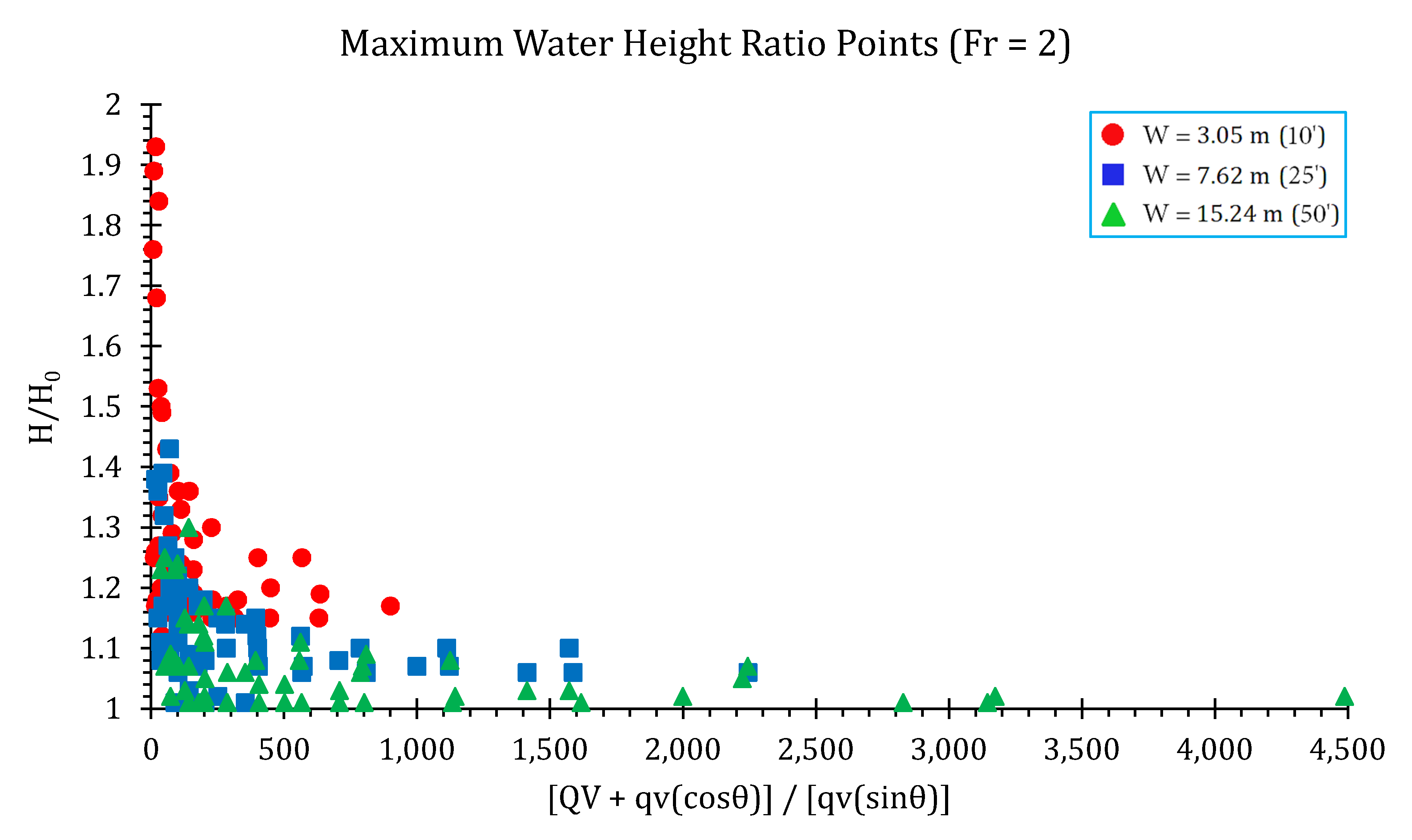
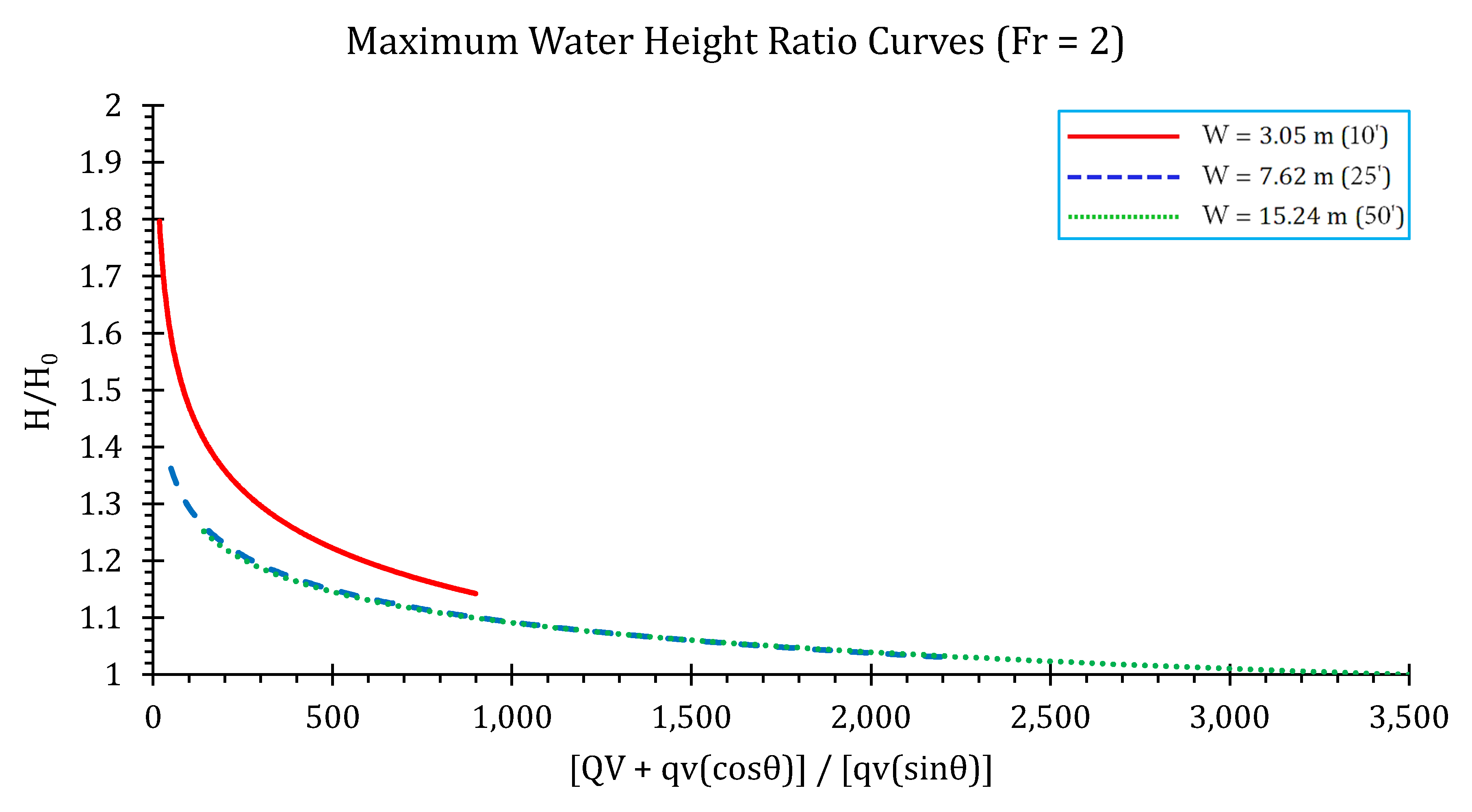
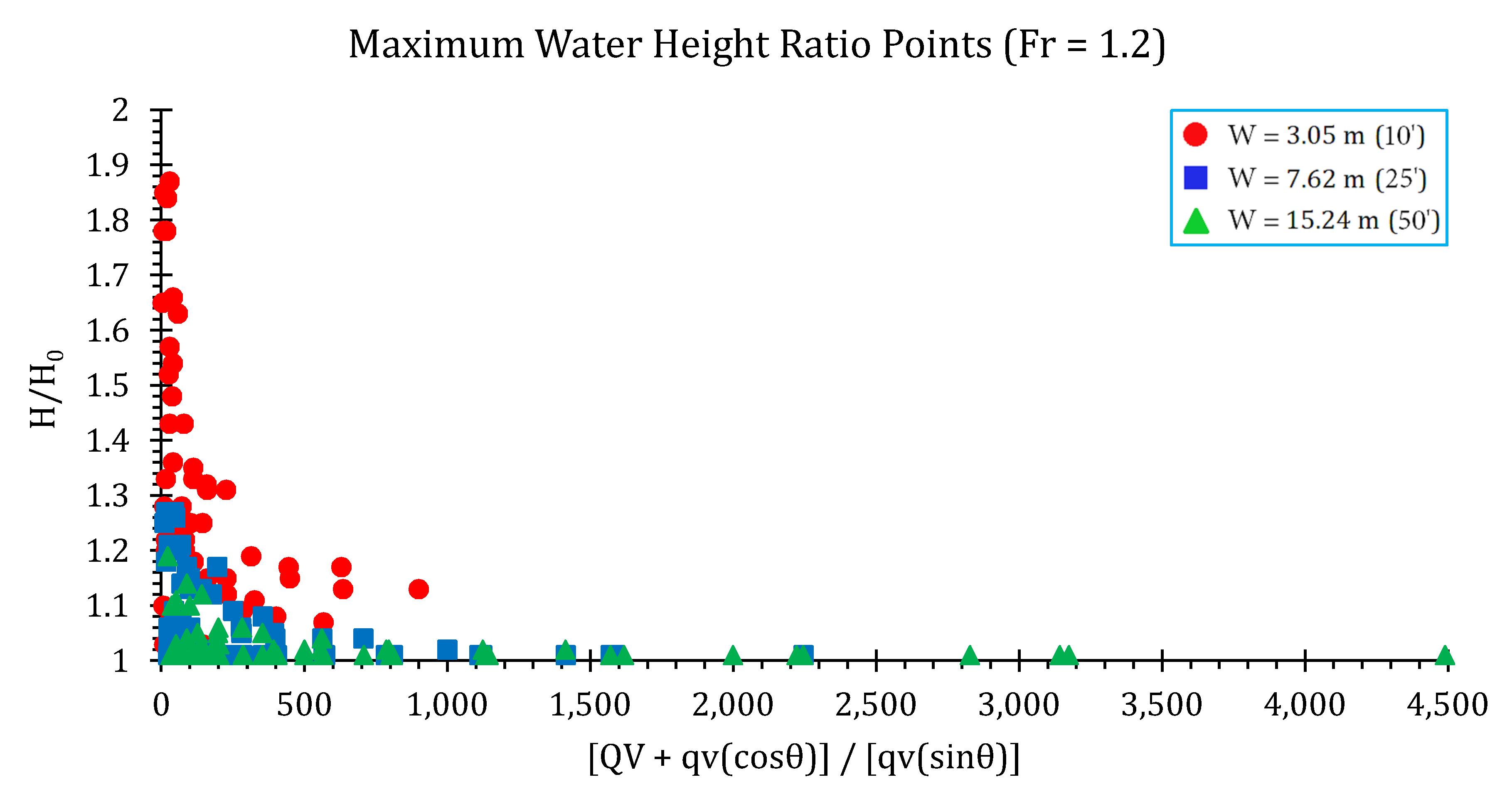
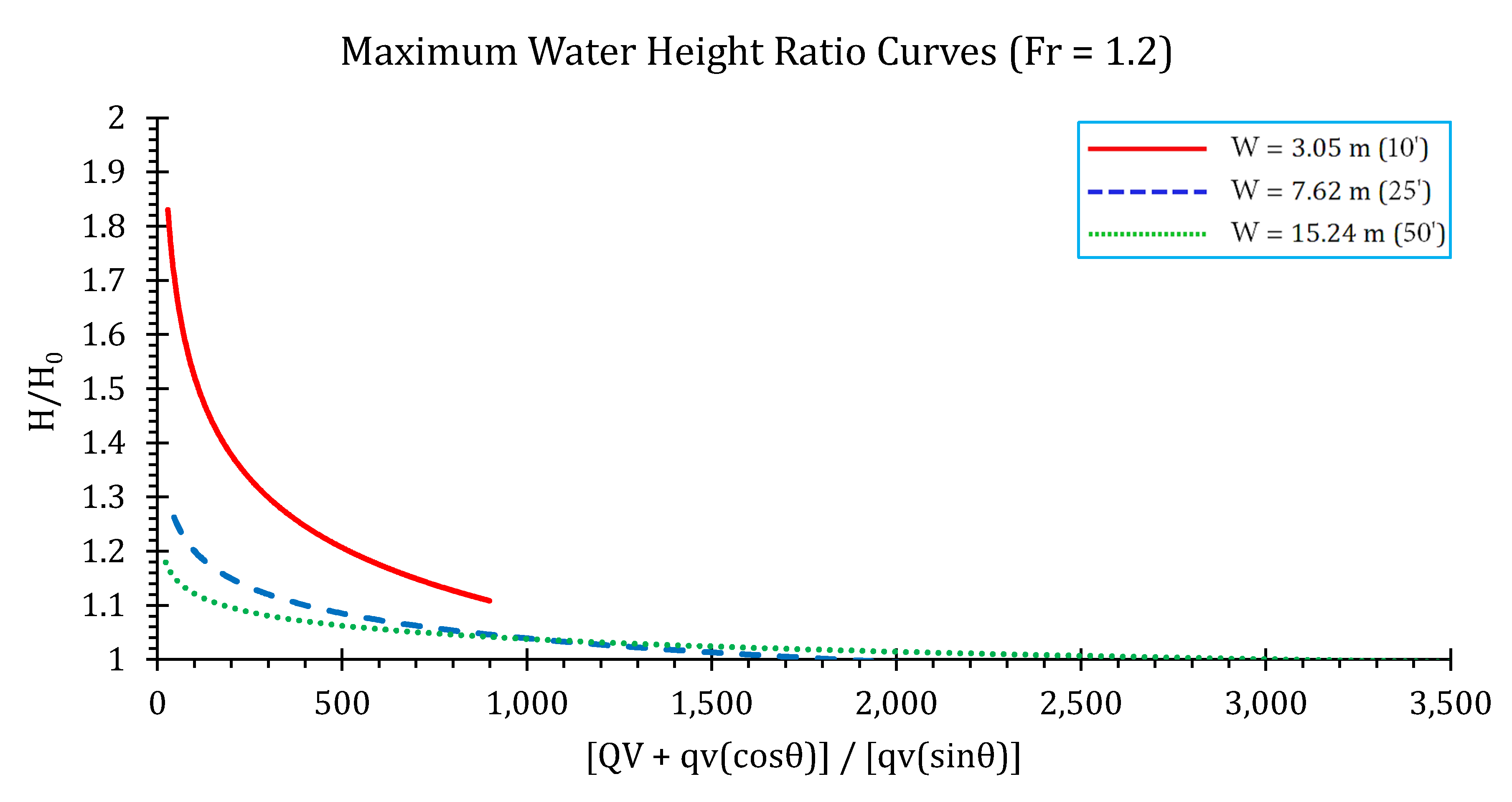
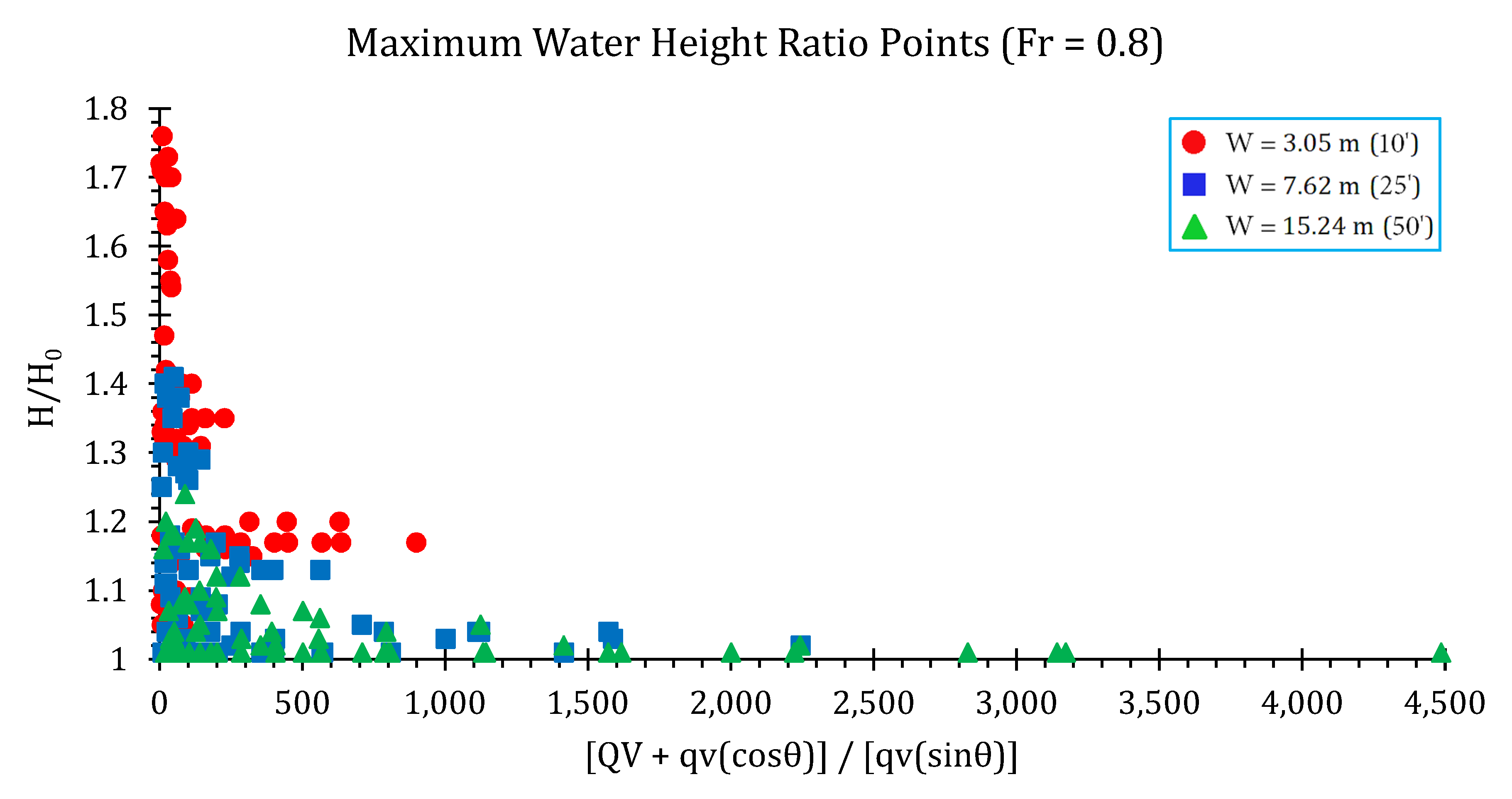
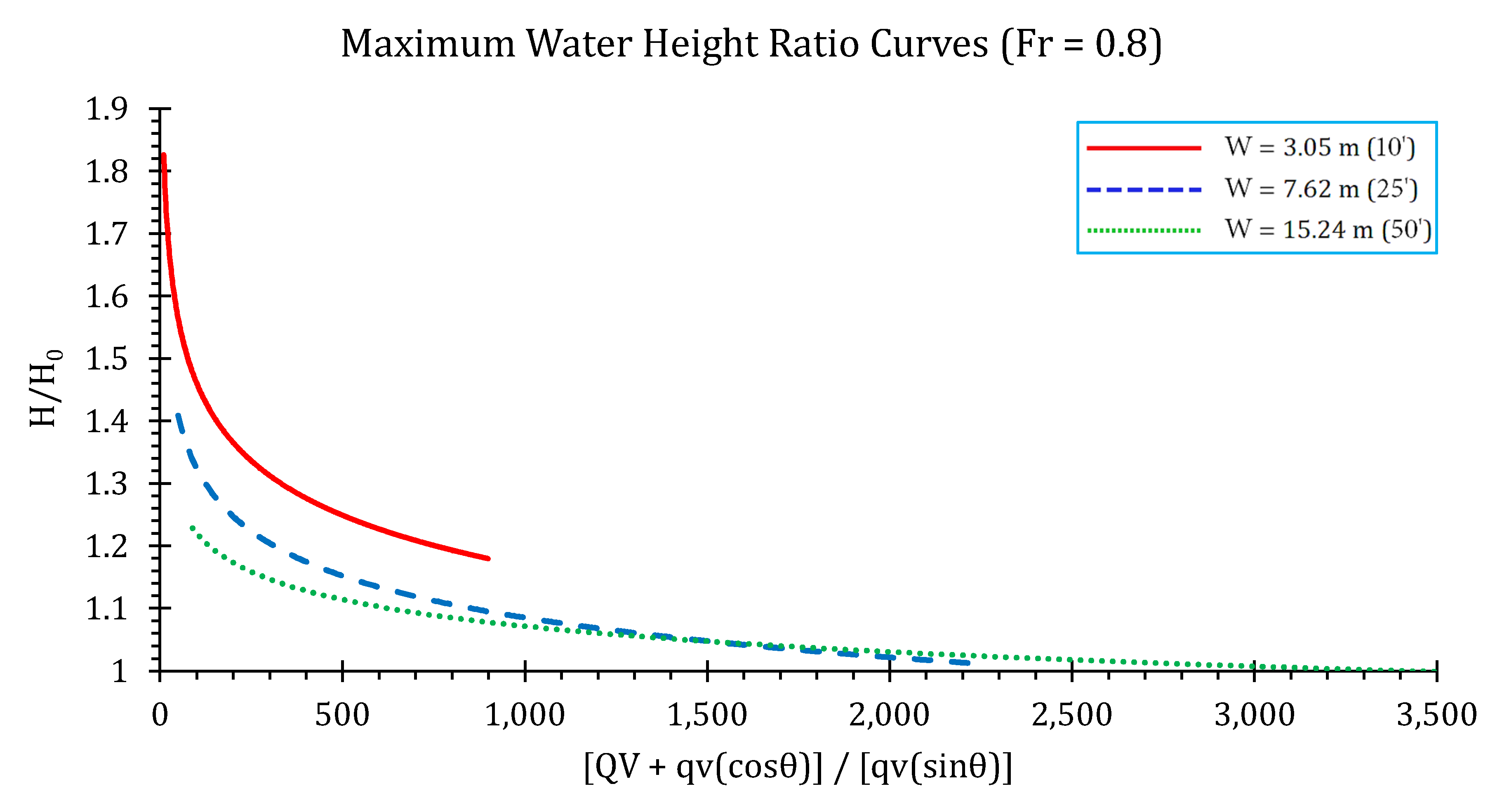
| Flume Width (m) | Flume Slope (%) | Flow Rate (m3/s) | Fr (-) | Junction Angle (degree) | Lateral Flow Proportion (%) |
|---|---|---|---|---|---|
| 0.41 (16″) | 0.00 | 0.13 | 0.72 | 30, 45, 90 | 2.5, 5.0, 7.5 |
| 0.42 | 0.12 | 0.95 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 0.68 | 0.14 | 1.45 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 0.97 | 0.14 | 1.74 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 1.68 | 0.14 | 2.01 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 2.15 | 0.13 | 2.32 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 2.60 | 0.13 | 2.80 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 3.51 | 0.13 | 3.27 | 30, 45, 90 | 2.5, 5.0, 7.5 | |
| 0.61 (24″) | 0.00 | 0.18 | 0.80 | 30, 45, 90 | 2.5, 5.0 |
| 0.44 | 0.18 | 1.0 | 30, 45, 90 | 2.5, 5.0 | |
| 0.56 | 0.18 | 1.2 | 30, 45, 90 | 2.5, 5.0 | |
| 0.89 | 0.18 | 1.6 | 30, 45, 90 | 2.5, 5.0 | |
| 1.67 | 0.18 | 2.0 | 30, 45, 90 | 2.5, 5.0 | |
| 2.22 | 0.18 | 2.4 | 30, 45, 90 | 2.5, 5.0 | |
| 3.33 | 0.18 | 3.1 | 30, 45, 90 | 2.5, 5.0 | |
| Total number of tests: 120 | |||||
| Width (m) | Initial Water Height (m) | Fr (-) | Inlet Pipe Diameter (m) | Junction Angle (Degree) | Lateral Flow Proportion (%) |
|---|---|---|---|---|---|
| 3.05 (10′) | 1.22 (4′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′) | 30, 45, 90 | 2.5, 5, 10 |
| 2.13 (7′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′), 1.52 (5′) | 30, 45, 90 | 2.5, 5, 10 | |
| 3.05 (10′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′), 1.52 (5′) | 30, 45, 90 | 2.5, 5, 10 | |
| 7.62 (25′) | 1.22 (4′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′) | 30, 45, 90 | 2.5, 5, 10 |
| 2.13 (7′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′), 1.52 (5′) | 30, 45, 90 | 2.5, 5, 10 | |
| 3.05 (10′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′), 1.52 (5′) | 30, 45, 90 | 2.5, 5, 10 | |
| 15.24 (50′) | 1.22 (4′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′) | 30, 45, 90 | 2.5, 5, 10 |
| 2.13 (7′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′), 1.52 (5′) | 30, 45, 90 | 2.5, 5, 10 | |
| 3.05 (10′) | 0.8, 1.2, 2.0 | 0.46 (1.5′), 0.91 (3′), 1.52 (5′) | 30, 45, 90 | 2.5, 5, 10 | |
| Total number of simulations: 648 | |||||
| Fr (-) | Q Flume (m3/s) | V Flume (m/s) | θ Junc. (Deg.) | 2.5% Lateral Flow | 5% Lateral Flow | ||||
|---|---|---|---|---|---|---|---|---|---|
| q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | ||||
| 0.8 | 0.18 | 1.37 | 90 | 0.0045 | 2.23 | 1.05 | 0.0091 | 4.45 | 1.1 |
| 1 | 0.18 | 1.55 | 90 | 0.0045 | 2.23 | 1.16 | 0.0091 | 4.45 | 1.26 |
| 1.2 | 0.18 | 1.65 | 90 | 0.0045 | 2.23 | 1.46 | 0.0091 | 4.45 | 1.63 |
| 1.6 | 0.18 | 1.86 | 90 | 0.0045 | 2.23 | 1.29 | 0.0091 | 4.45 | 1.57 |
| 2 | 0.18 | 2.10 | 90 | 0.0045 | 2.23 | 1.22 | 0.0091 | 4.45 | 1.74 |
| Fr (-) | Q Flume(m3/s) | V Flume(m/s) | θ Junc. (deg.) | 2.5% Lateral Flow | 5% Lateral Flow | 7.5% Lateral Flow | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | ||||
| 0.72 | 0.1322 | 1.16 | 90 | 0.0034 | 1.65 | 1.14 | 0.0065 | 3.26 | 1.17 | 0.0099 | 4.91 | 1.20 |
| 0.95 | 0.1158 | 1.34 | 90 | 0.0028 | 1.43 | 1.30 | 0.0057 | 2.87 | 1.40 | 0.0088 | 4.30 | 1.48 |
| 1.45 | 0.1368 | 1.89 | 90 | 0.0034 | 1.68 | 1.12 | 0.0068 | 3.38 | 1.58 | 0.0102 | 5.06 | 1.73 |
| 1.74 | 0.1385 | 2.13 | 90 | 0.0034 | 1.71 | 1.13 | 0.0068 | 3.41 | 1.29 | 0.0105 | 5.12 | 1.71 |
| 2.01 | 0.1399 | 2.35 | 90 | 0.0034 | 1.74 | 1.16 | 0.0071 | 3.44 | 1.32 | 0.0105 | 5.18 | 1.26 |
| 2.32 | 0.1294 | 2.53 | 90 | 0.0031 | 1.58 | 1.24 | 0.0065 | 3.20 | 1.29 | 0.0096 | 4.79 | 1.53 |
| 2.8 | 0.1322 | 2.87 | 90 | 0.0034 | 1.65 | 1.20 | 0.0065 | 3.26 | 1.60 | 0.0099 | 4.91 | 1.87 |
| 3.27 | 0.1280 | 3.17 | 90 | 0.0031 | 1.58 | 1.29 | 0.0065 | 3.17 | 1.86 | 0.0096 | 4.75 | 2.50 |
| Fr (-) | Q Flume (m3/s) | V Flume (m/s) | θ Junc. (Deg.) | 2.5% Lateral Flow | 5% Lateral Flow | ||||
|---|---|---|---|---|---|---|---|---|---|
| q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | ||||
| 0.8 | 0.18 | 1.37 | 45 | 0.0045 | 2.23 | 1.03 | 0.0975 | 4.45 | 1.06 |
| 1 | 0.18 | 1.55 | 45 | 0.0045 | 2.23 | 1.14 | 0.0975 | 4.45 | 1.14 |
| 1.2 | 0.18 | 1.65 | 45 | 0.0045 | 2.23 | 1.16 | 0.0975 | 4.45 | 1.2 |
| 1.6 | 0.18 | 1.86 | 45 | 0.0045 | 2.23 | 1.19 | 0.0975 | 4.45 | 1.3 |
| 2 | 0.18 | 2.10 | 45 | 0.0045 | 2.23 | 1.22 | 0.0975 | 4.45 | 1.28 |
| Fr (-) | Q Flume (m3/s) | V Flume (m/s) | θ Junc. (Deg.) | 2.5% Lateral Flow | 5% Lateral Flow | 7.5% Lateral Flow | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | ||||
| 0.72 | 0.1322 | 1.16 | 45 | 0.0034 | 1.65 | 1.12 | 0.0065 | 3.26 | 1.13 | 0.0099 | 4.91 | 1.13 |
| 0.95 | 0.1158 | 1.34 | 45 | 0.0028 | 1.43 | 1.16 | 0.0057 | 2.87 | 1.16 | 0.0088 | 4.30 | 1.15 |
| 1.45 | 0.1368 | 1.89 | 45 | 0.0034 | 1.68 | 1.04 | 0.0068 | 3.38 | 1.16 | 0.0102 | 5.06 | 1.08 |
| 1.74 | 0.1385 | 2.13 | 45 | 0.0034 | 1.71 | 1.19 | 0.0068 | 3.41 | 1.13 | 0.0105 | 5.12 | 1.17 |
| 2.01 | 0.1399 | 2.35 | 45 | 0.0034 | 1.74 | 1.11 | 0.0071 | 3.44 | 1.16 | 0.0105 | 5.18 | 1.21 |
| 2.32 | 0.1294 | 2.53 | 45 | 0.0031 | 1.58 | 1.12 | 0.0065 | 3.20 | 1.12 | 0.0096 | 4.79 | 1.24 |
| 2.8 | 0.1322 | 2.87 | 45 | 0.0034 | 1.65 | 1.40 | 0.0065 | 3.26 | 1.33 | 0.0099 | 4.91 | 1.53 |
| 3.27 | 0.1280 | 3.17 | 45 | 0.0031 | 1.58 | 1.36 | 0.0065 | 3.17 | 1.29 | 0.0096 | 4.75 | 1.36 |
| Fr (-) | Q Flume (m3/s) | V Flume (m/s) | θ Junc. (Deg.) | 2.5% Lateral Flow | 5% Lateral Flow | ||||
|---|---|---|---|---|---|---|---|---|---|
| q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | ||||
| 0.8 | 0.18 | 1.37 | 30 | 0.0045 | 2.23 | 1.03 | 0.009 | 4.45 | 1.03 |
| 1 | 0.18 | 1.55 | 30 | 0.0045 | 2.23 | 1.10 | 0.009 | 4.45 | 1.10 |
| 1.2 | 0.18 | 1.65 | 30 | 0.0045 | 2.23 | 1.12 | 0.009 | 4.45 | 1.12 |
| 1.6 | 0.18 | 1.86 | 30 | 0.0045 | 2.23 | 1.10 | 0.009 | 4.45 | 1.10 |
| 2 | 0.18 | 2.10 | 30 | 0.0045 | 2.23 | 1.11 | 0.009 | 4.45 | 1.11 |
| Fr (-) | Q Flume (m3/s) | V Flume (m/s) | θ Junc. (Deg.) | 2.5% Lateral Flow | 5% Lateral Flow | 7.5% Lateral Flow | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | q Pipe (m3/s) | v Pipe (m/s) | H/H0 | ||||
| 0.72 | 0.1322 | 1.16 | 30 | 0.0034 | 1.65 | 1.13 | 0.0065 | 3.26 | 1.13 | 0.0099 | 4.91 | 1.13 |
| 0.95 | 0.1158 | 1.34 | 30 | 0.0028 | 1.43 | 1.13 | 0.0057 | 2.87 | 1.18 | 0.0088 | 4.30 | 1.18 |
| 1.45 | 0.1368 | 1.89 | 30 | 0.0034 | 1.68 | 1.12 | 0.0068 | 3.38 | 1.17 | 0.0102 | 5.06 | 1.08 |
| 1.74 | 0.1385 | 2.13 | 30 | 0.0034 | 1.71 | 1.19 | 0.0068 | 3.41 | 1.19 | 0.0105 | 5.12 | 1.24 |
| 2.01 | 0.1399 | 2.35 | 30 | 0.0034 | 1.74 | 1.16 | 0.0071 | 3.44 | 1.21 | 0.0105 | 5.18 | 1.21 |
| 2.32 | 0.1294 | 2.53 | 30 | 0.0031 | 1.58 | 1.29 | 0.0065 | 3.20 | 1.29 | 0.0096 | 4.79 | 1.29 |
| 2.8 | 0.1322 | 2.87 | 30 | 0.0034 | 1.65 | 1.40 | 0.0065 | 3.26 | 1.33 | 0.0099 | 4.91 | 1.40 |
| 3.27 | 0.1280 | 3.17 | 30 | 0.0031 | 1.58 | 1.20 | 0.0065 | 3.17 | 1.29 | 0.0096 | 4.75 | 1.27 |
| Mesh Block | Grid Size (cm) |
|---|---|
| 1 | 2 |
| 2 | 1.5 |
| 3 | 1 |
| 4 (Pipe) | 0.7 |
| Froude Number | Nash–Sutcliffe Efficiency |
|---|---|
| 0.8 | 0.87 |
| 2.0 | 0.83 |
| 3.1 | 0.85 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nazari-Sharabian, M.; Karakouzian, M.; Hayes, D. Flow Topology in the Confluence of an Open Channel with Lateral Drainage Pipe. Hydrology 2020, 7, 57. https://doi.org/10.3390/hydrology7030057
Nazari-Sharabian M, Karakouzian M, Hayes D. Flow Topology in the Confluence of an Open Channel with Lateral Drainage Pipe. Hydrology. 2020; 7(3):57. https://doi.org/10.3390/hydrology7030057
Chicago/Turabian StyleNazari-Sharabian, Mohammad, Moses Karakouzian, and Donald Hayes. 2020. "Flow Topology in the Confluence of an Open Channel with Lateral Drainage Pipe" Hydrology 7, no. 3: 57. https://doi.org/10.3390/hydrology7030057
APA StyleNazari-Sharabian, M., Karakouzian, M., & Hayes, D. (2020). Flow Topology in the Confluence of an Open Channel with Lateral Drainage Pipe. Hydrology, 7(3), 57. https://doi.org/10.3390/hydrology7030057







