Nonlinear Effects on the Convergence of Picard and Newton Iteration Methods in the Numerical Solution of One-Dimensional Variably Saturated–Unsaturated Flow Problems

Abstract

Finite element discretization of the pressure head form of the Richards equation leads to a nonlinear model, which yields numerical convergence difficulties. When the numerical solution to this problem has either an extremely sharp moving front, infiltration into dry soil, flow domains containing materials with spatially varying properties, or involves time-dependent boundary conditions, the corrector iteration used in many time integrators can terminate prematurely, which leads to incorrect results. While the Picard and Newton iteration methods can solve this problem through tightening the tolerances provided to the solvers, there is a more efficient approach to overcome the convergence difficulties. Four tests examples are examined, and each test case is solved with five sufficiently small tolerances to demonstrate the effectiveness of convergence. The numerical results illustrate that the methods greatly improve the convergence and stability. Test experiments show that the Newton method is more complex and expensive on a per iteration basis than the Picard method for simulating variably saturated–unsaturated flow in one spatial dimension. Consequently, it is suggested that the resulting local and global mass balance is exact within the minimum specified accuracy.

1. Introduction

Fluid flow through variably saturated–unsaturated porous media is usually described by the classical Richards equation [1]. It is defined by coupling a statement of mass conservation with Darcy’s equation. It is a highly nonlinear partial differential equation that can be represented in three standard forms, depending on whether pressure, moisture, or both are used as dependent variables. For one-dimensional vertical flow, the pressure head-based Richards equation is written as

$$C\left(\Psi \right)\frac{\partial \Psi }{\partial t}=\frac{\partial }{\partial z}\left(K(\Psi )\left(\frac{\partial \Psi }{\partial z}+1\right)\right)$$

(1)

where, Ψ is the pressure head (L), $t$ is time (T), $z$ denotes the vertical distance from reference elevation, which is assumed positive upward (L), $K(\Psi )$ is the hydraulic conductivity ($L{T}^{-1}$), $C\left(\Psi \right)=\frac{d\theta }{d\mathit{\Psi }}$ is the specific fluid capacity (L⁻¹), and $\theta$ is the moisture content.

Numerical schemes for solving Equation (1) on the basis of grid resolution techniques, and/or time discretization procedures including other dynamic approaches for different forms of Richards equation are available. The choices of these techniques greatly influence the computational efficiency, numerical stability, and accuracy of water flow problems. The moisture content of the Richards equation is limited to unsaturated flow problems due to $\theta$ not being a smooth function for layered soils, and discontinuous near saturation. As a result, severe numerical convergence difficulties, numerical oscillations, and stability problems result in the failure of subsurface solvers. Thus, this form may be useful only for homogeneous flow conditions. On the other hand, a pressure head formulation of Richards equation is continuous in both saturated and unsaturated zones, and can be used for homogeneous and non-homogeneous soils. However, numerical approaches based on this form can suffer large mass balance errors [2,3,4]. Small step size coupled with mass lumping effectively ensures the improvement of the mass balance of the pressure head-based Richards equation [2].

Due to the shape of the soil water retention and hydraulic conductivity curves, the Richards equation is highly nonlinear. For the less sharp region of the moisture content or moisture capacity, many iterations are required to achieve a robust and accurate solution of the Richards equation with relatively large tolerance. For the portion of the soil water curve where the profile is very sharp, a much smaller specified accuracy should be used to avoid the numerical errors as well as computational challenge [5]. Therefore, the numerical solution of the Richards equation is very sensitive to the value of the convergence tolerance. An adaptive and heuristics time-stepping scheme [6], a mass-conservative algorithm [2], and a nested-Newton algorithm [7] with small nonlinear tolerance have been successfully applied for different soil properties with different initial and boundary conditions depending on the formulation of the Richards equation. Besides a mining geostatical approach [8] for disordered soil’s structure, a fully analytical model in case of nonstationary of unsaturated flow variables has been introduced [9]. Therefore, the flow problems that involve extremely sharp front in space- and/or time-varying boundary conditions flow into layered soil, making them difficult to solve accurately unless tight tolerance is used.

The highly nonlinear model (1) is solved using common constitutive relations and standard approximation methods such as finite differences [2,3,10], finite elements [2,11,12,13], and finite volumes [12,14,15]. Standard algorithms that employ the numerical solution of sharp front problems with poor accuracy are computationally expensive and lead to less accurate results. The solution of the resulting large nonlinear algebraic systems that arise in implicit numerical discretizations of the Richards equation has been the subject of significant research, and hence, one needs efficient and robust linearization techniques that maintain not only the accuracy of the solution, but also its mass conservation property. Typical linearization methods, such as the Picard, Newton, fast-secant and relaxation methods, as well as non-iterative methods, such as the implicit factored schemes and three-level Lees schemes, have been proposed [4,11,16,17,18].

In the process of linearization, two iterative schemes, Picard and Newton, are characterized by different convergence behavior. The Picard iterative scheme is more popular than the Newton due to its simplicity and satisfactory performance [2]. Theoretically, the Newton method converges one order faster than the Picard method, but under certain flow conditions, the Picard method is more efficient than the Newton method [16]. Generally, the Picard method is less expensive per iteration basis, and preserves the symmetry of the discrete system of equations. However, it suffers from slow convergence, or may diverge for cases of gravity drainage, complex time-varying boundary conditions, strongly nonlinear characteristic equations, and saturated–unsaturated interfaces [16]. The Newton method has better convergence properties, but creates nonsymmetric system matrices and involves the computation of derivatives, which leads to a complex and expensive linearization technique. This study concerns the comprehensive behavior of two linearization methods, Picard and Newton, with tighter accuracy for efficiently solving the Richards equation in saturated–unsaturated porous media based on backward Euler finite difference in time and finite elements in space with mass lumping.

The objectives of this work are: to assess the lack of robustness of solution of the Richards equation when using common solution approaches with very small tolerances, to investigate the effect of different tolerances, and to compare a set of alternative tolerances for a wide range of porous media conditions to test robustness and efficiency with minimum accuracy limit.

2. Numerical Formulation

2.1. Finite Element Model

To develop a finite element approximation of (1), a Galerkin finite element method is used to discretize the spatial domain with linear basis function. Solutions are obtained by solving the discretized Richards equation using a mass-lumping linear Galerkin finite element method, which has been proved to be a mass conservation formulation [2]. The time discretization is carried out with implicit backward Euler finite difference method, and mass lumping is used for the mass accumulation term. Discretization yields a system of nonlinear equations:

$$\mathit{f}\left({\mathit{\Psi }}^{k+1}\right)=\mathit{A}\left({\mathit{\Psi }}^{k+1}\right){\mathit{\Psi }}^{k+1}+\mathit{F}\left({\mathit{\Psi }}^{k+1}\right)\frac{{\mathit{\Psi }}^{k+1}-{\mathit{\Psi }}^k}{∆{\mathrm{t}}^{\mathrm{k}+1}}-\mathit{q}\left(t^{k+1}\right)+\mathit{b}\left({\mathit{\Psi }}^{k+1}\right)=0$$

(2)

where $\mathit{\Psi }$ is the vector of the pressure head at each node, $k$ denotes the time step, and $\mathit{A}$, $\mathit{F}$, $\mathit{b}$ and $\mathit{q}$ are the stiffness matrix, mass matrix, gravitational gradient component, and Darcy’s flux boundary conditions, respectively.

2.2. Linearization Techniques

To obtain a cost-effective solution of the system of nonlinear Equation (2), Picard iterative and a more strongly convergent Newton iterative schemes are employed. The later one is designed especially to avoid the convergence difficulties usually encountered when certain nodes are being desaturated. However, this technique is computationally more expensive and algebraically complex than the Picard scheme.

2.2.1. Newton and Picard Schemes

Letting superscript ($m$) be an iteration level, using (2), the Newton scheme [16] can be written as

$${\mathit{f}}^{\prime }\left({\mathit{\Psi }}^{k+1, \left(m\right)}\right)\mathit{h}=-\mathit{f}\left({\mathit{\Psi }}^{k+1, \left(m\right)}\right)$$

(3)

where $\mathit{h}={\mathit{\Psi }}^{k+1, \left(m+1\right)}-{\mathit{\Psi }}^{k+1, \left(m\right)}$, and the Jacobian for the system is

$$f_{ij}^{\prime }=\lambda A_{ij}+\frac{1}{\mathsf{\Delta }{t}^{k+1}}{F}_{ij}+{{\displaystyle \sum }}_s\frac{\partial A_{is}}{\partial {\psi }_j^{k+1}}{\psi }_s^{k+1}+\frac{1}{\mathsf{\Delta }{t}^{k+1}}{{\displaystyle \sum }}_s\frac{\partial F_{is}}{\partial {\psi }_j^{k+1}}\left({\psi }_s^{k+1}-{\psi }_s^k\right)+\frac{\partial b_i}{\partial {\psi }_j^{k+1}}.$$

The simplest formulation of the Picard scheme [16] of the Richards equation is

$$\left[\mathit{\lambda }\mathit{A}\left({\mathit{\Psi }}^{k+1, \left(m\right)}\right)+\frac{1}{∆t^{k+1}}\mathit{F}\left({\mathit{\Psi }}^{k+1, \left(m\right)}\right)\right]\mathit{h}=-\mathit{f}\left({\mathit{\Psi }}^{k+1, \left(m\right)}\right)$$

(4)

2.3. Characteristic Equations

Solving Richards equation requires constitutive relationships relating the dependent variable pressure head and the nonlinear terms, such as moisture content, moisture capacity, and conductivity. The most commonly used soil characteristic models, van Genuchten [19] and Brooks–Corey [20], are employed in this work, and these models are illustrated below.

2.3.1. Van Genuchten Model

The most frequently used constitutive relationships were derived by van Genuchten [19] and are given by:

$$\theta \left(\psi \right)={\theta }_r+\frac{{\theta }_s-{\theta }_r}{{\left[1+{\left|\alpha \psi \right|}^n\right]}^m}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}\psi \le 0$$

(5a)

$$\theta \left(\psi \right)={\theta }_s\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}\psi >0$$

(5b)

$$K\left(\psi \right)=K_s{\left[\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}\right]}^{\frac{1}{2}}{\left\{1-{\left[1-{\left(\frac{\theta -{\theta }_r}{{\theta }_s-{\theta }_r}\right)}^{\frac{1}{m}}\right]}^m\right\}}^2\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}\psi \le 0$$

(6a)

$$K\left(\psi \right)=K_s\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}\psi >0$$

(6b)

$$c\left(\psi \right)=\alpha mn\frac{{\theta }_s-{\theta }_r}{{\left[1+{\left|\alpha \psi \right|}^n\right]}^{m+1}}{\left|\alpha \psi \right|}^{n-1}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}\psi \le 0$$

(7a)

$$c\left(\psi \right)=0\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\hspace{1em}\psi >0$$

(7b)

where, $m=1-\frac{1}{n}$ is a pore-size distribution index, ${\theta }_s$ is the saturated moisture content, and ${\theta }_r$ is the residual moisture content.

2.3.2. The Brooks-Corey Model

Another common form of the constitutive relationships proposed by Brooks and Corey [20] are given by:

$$\theta \left(\psi \right)={\theta }_r+\left({\theta }_s-{\theta }_r\right){\left(\frac{{\psi }_d}{\psi }\right)}^n\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\psi \le {\psi }_d$$

(8a)

$$\theta \left(\psi \right)={\theta }_s\hspace{1em}\mathrm{if}\hspace{1em}\hspace{1em}\psi >{\psi }_d$$

(8b)

$$K\left(\psi \right)=K_s{\left[\frac{\theta \left(\psi \right)-{\theta }_r}{{\theta }_s-{\theta }_r}\right]}^{3+\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}\hspace{1em}\hspace{1em}\mathrm{if} \psi \le {\psi }_d$$

(9a)

$$K\left(\psi \right)=K_s\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\psi >{\psi }_d$$

(9b)

$$c\left(\psi \right)=n\frac{{\theta }_s-{\theta }_r}{\left|{\psi }_d\right|}{\left(\frac{{\Psi }_d}{\Psi }\right)}^{n+1}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\psi \le {\psi }_d$$

(10a)

$$c\left(\psi \right)=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{if}\hspace{1em}\psi >{\psi }_d$$

(10b)

where ${\psi }_d=-\frac{1}{\alpha }$ is the bubbling or air entry pressure head (L).

2.4. Implementation

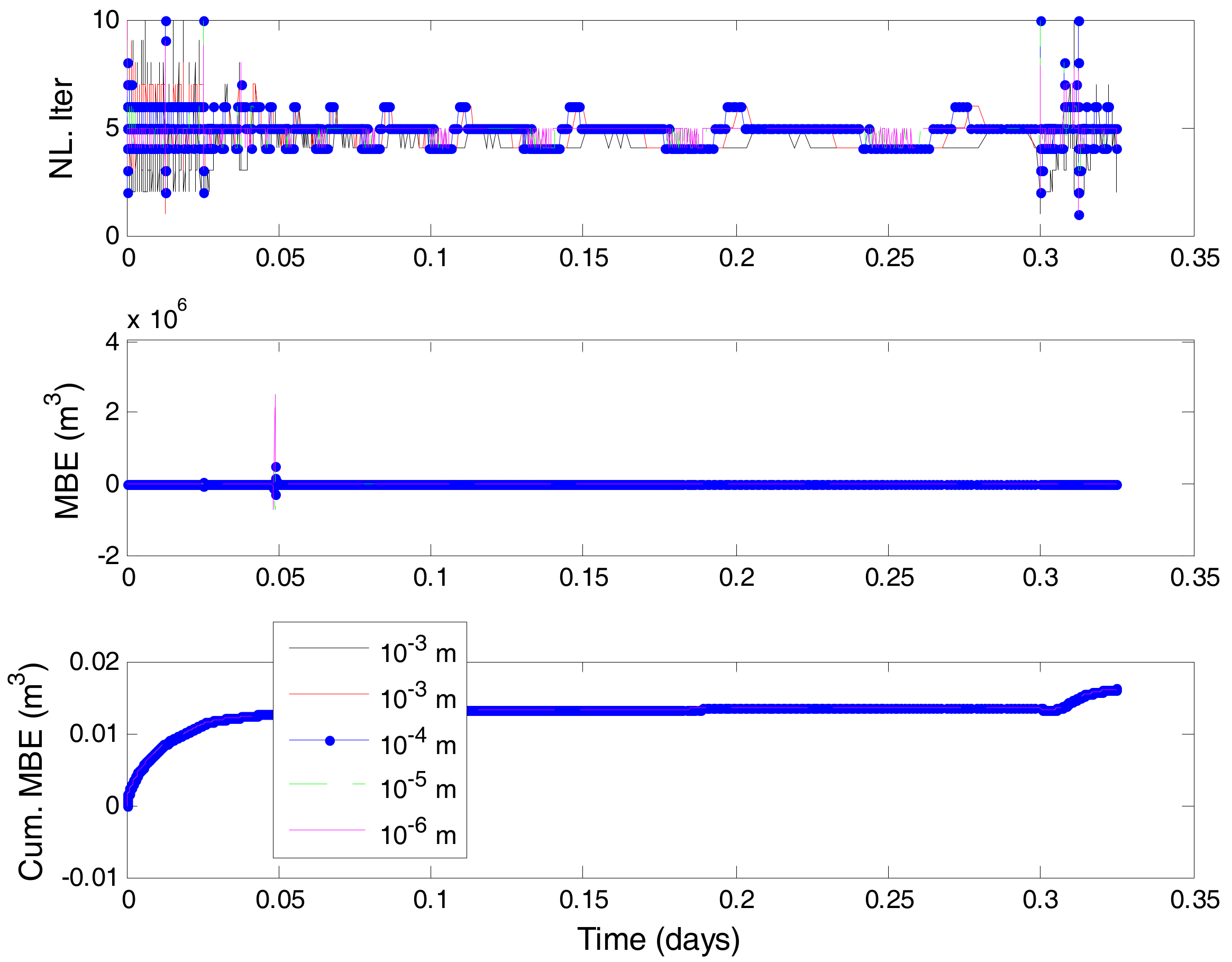
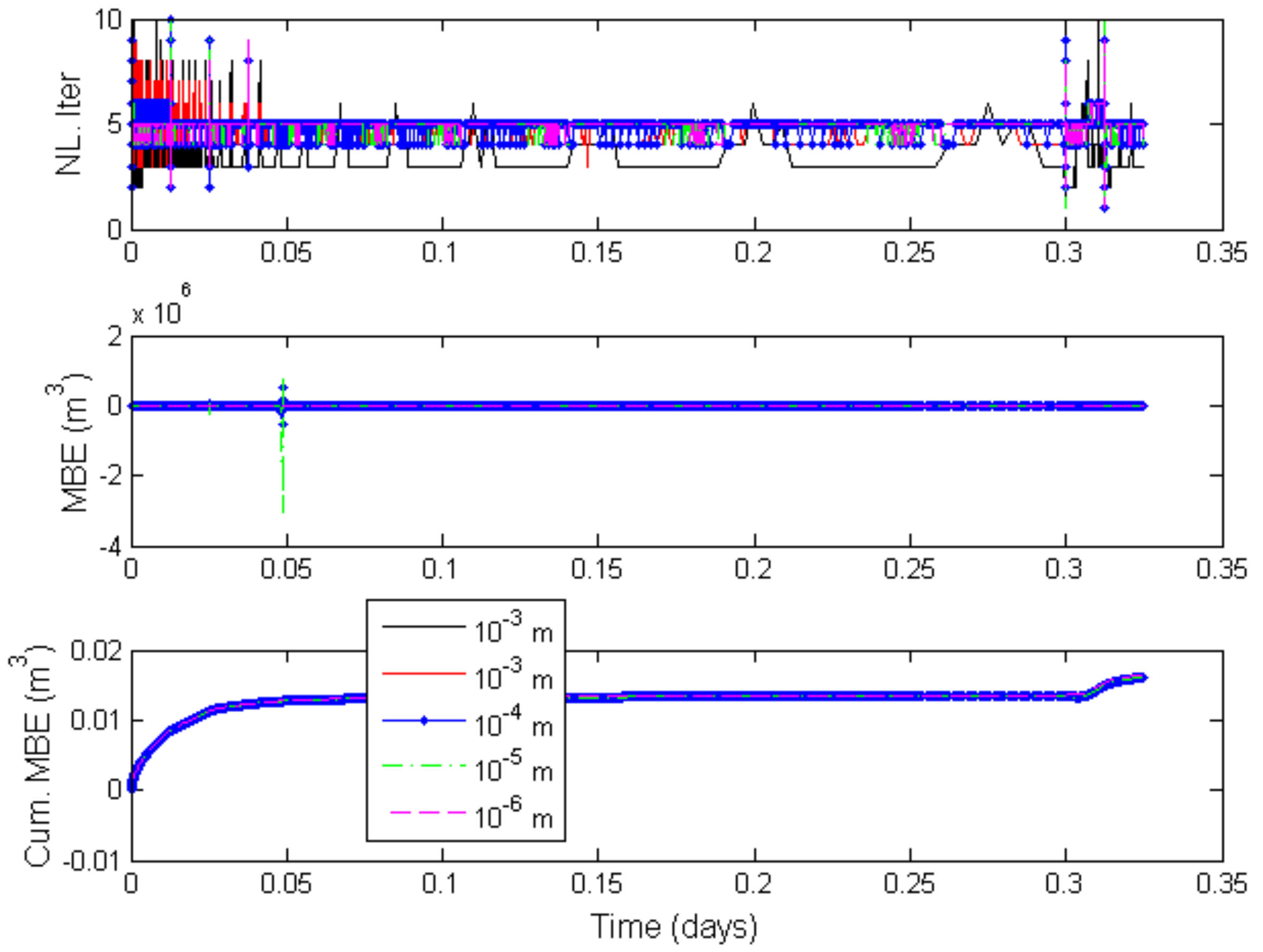
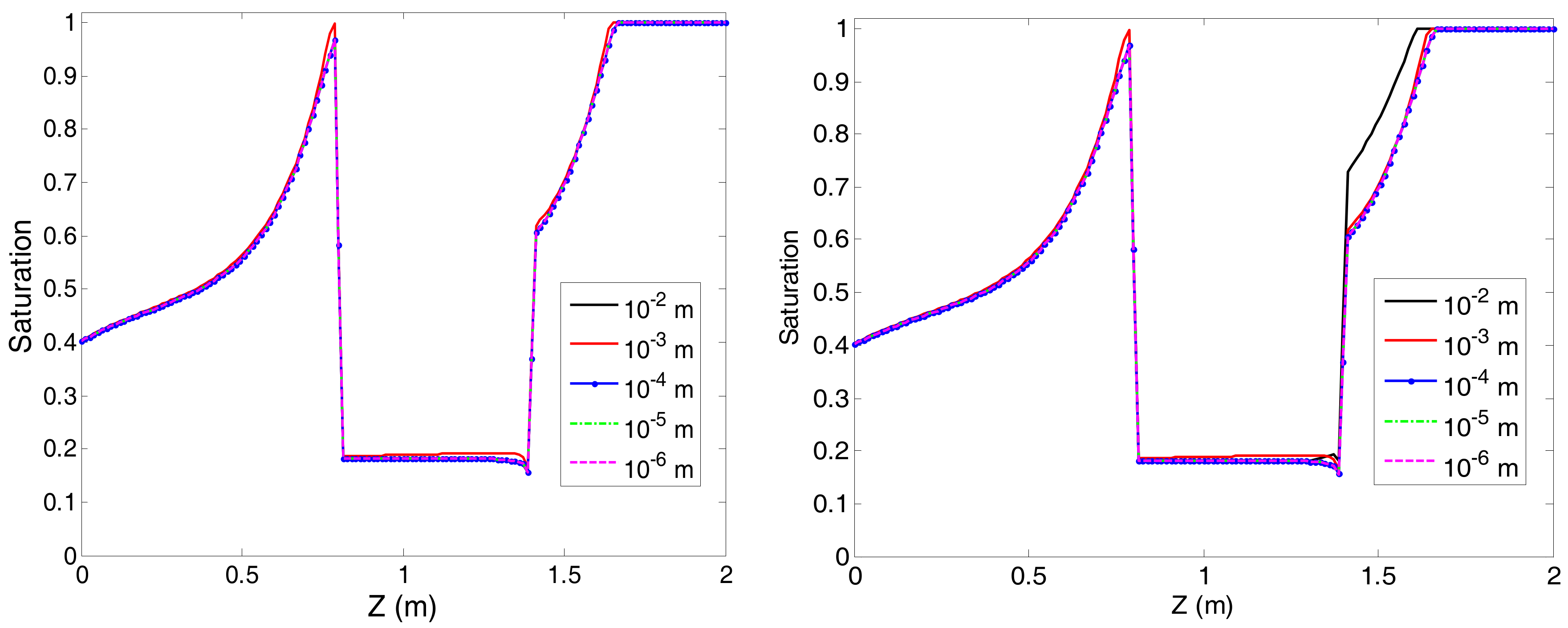
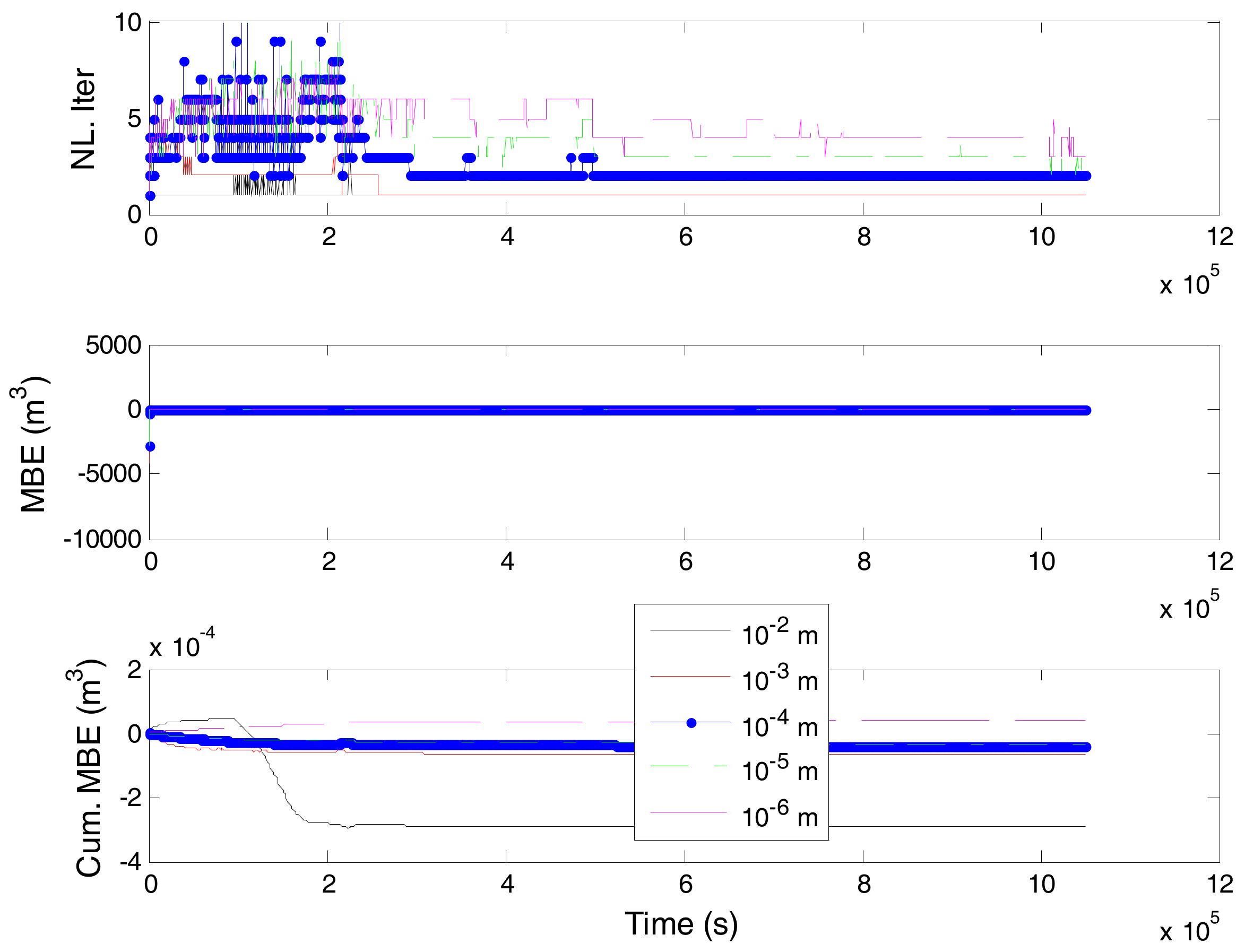
Numerical results were obtained by implementing the Picard and Newton iteration techniques into the computer code CATHY (CATchment Hydrology) [21]. It is a coupled physically-based spatially-distributed model for surface–subsurface simulations. The model simulates the three-dimensional equation for subsurface flow in variably saturated porous media (i.e., Richards equation) using Galerkin finite elements in space, a weighted finite difference scheme in time, and linearization via Newton or Picard iteration. In the Picard and Newton iterative schemes, convergence is achieved when the termination criterion $\parallel {\mathit{\Psi }}^{k+1, \left(m+1\right)}-{\mathit{\Psi }}^{k+1, \left(m\right)}\le Tol\parallel$ is satisfied, where $Tol$ is the specified tolerance/accuracy, and in this work, five sufficiently small enough values (10⁻², 10⁻³, 10⁻⁴, 10⁻⁵ and 10⁻⁶) are used. In all of the runs, the time-step size is adaptively adjusted according to the convergence behavior of the previous nonlinear iteration [16] in order to optimize convergence and CPU efficiency. The simulation begins with a time step size of $∆t_0$, and continues until reach the ending time $T_{max}$. At each time step of the simulation, the current time-step size is increased by a factor of $∆t_{mag}$ (=1.20) to the specified maximum size of $∆t_{max}$ if convergence at the previous iteration is achieved in fewer iteration than $maxi{t}_1$ (=5), but it is left unchanged if convergence requires between $maxi{t}_1$ and $maxi{t}_2$ (=8). When the scheme is not convergent within the iteration $maxi{t}_2$, the time step is decreased by a reduction factor of $∆t_{red}$ (=0.5) to a minimum of $∆t_{min}$. If convergence is not achieved ($maxit$ exceded), the time-step size is repeated (‘back-stepping’) using a reduced time-step size (factor $∆t_{red}$, to a minimum of $∆t_{min}$). The values of the $∆t$s and $maxit$s are chosen. The main advantage of the dynamic time marching is that it avoids undesirable abrupt changes in time step. Linear solvers for large sparse nonsymmetric systems arising from the Newton scheme are generally inefficient, but presently consistent, and efficient conjugate gradient-type algorithms are available for solving such systems. Biconjugate gradient stabilized algorithm (BICGSTAB), minimum residual algorithm (GRAMRB), generalized conjugate residual method (GCRK), and transpose-free quasi-minimal residual algorithm (TFQMR) are reliable, large, sparse nonsysmmetric solvers. Detailed descriptions of the various algorithms can be found in the works Axelsson, Pini et al., van der Vorst, and Freund [22,23,24,25]. The solutions of the linear systems obtained by using BICGSTAB algorithm in modeling flow problems have shown best performance [17]. Another important feature of this solution’s employed algorithms is the use of an analytical differentiation for the evaluation of the gradient of the soil moisture characteristic curves. To measure the accuracy of the solution of the subsurface solver, mass balance error (MBE) is calculated. According to the mass continuity equation, the MBE is defined as the difference between the net amount of water added to the system, and the change in the amount of water stored in the system after a given elapsed time, and it is evaluated by the following formula [2].

$$MB\left(t^{k+1}\right)=\frac{{{\displaystyle \sum }}_{i=1}^E\left({\theta }_i^{k+1}-{\theta }_i^o\right)\left(∆z\right)+\left({\theta }_o^{k+1}-{\theta }_o^o\right)\left(\frac{∆z}{2}\right)+\left({\theta }_E^{k+1}-{\theta }_E^o\right)\left(\frac{∆z}{2}\right)}{{{\displaystyle \sum }}_{j=1}^{k+1}\left(q_o^j-q_N^j\right)\left(∆t\right)}$$

(11)

with $N=E+1$ nodes $\left\{z_0, z_1, z_2, \dots , z_E\right\}$, constant nodal spacing $∆z$ is considered, and $q_o$ and $q_N$ are boundary fluxes calculated from the finite element equations associated with the boundary nodes $z_0$ and $z_N$.

For this study, the simple procedure given above has been proved to be effective and sufficient. All of the numerical simulations were executed on personal machine, Dell INSPIRON 2.5 GHz with 4 GB RAM of intel Core 2 processor.

3. Numerical Results

Four one-dimensional test simulations with different soil characteristics were performed for evaluating the performance of two iterative schemes for five sufficiently small accuracies. The numerical results needed to meet the objective of this work; we focus our attention on the analysis of how much the small tolerance will affect the efficiency, accuracy, and convergence properties of the numerical solution to the Richards equation. However, the performance of the simulations is more difficult to judge, as there are a number of factors that control the efficiency and robustness of the model. Such factors include total central processing unit (CPU), total number of time steps, average nonlinear (NL) iterations (Iter) per time step, cumulative mass balance error (Cum. MBE), the number of backstepping, etc. The most significant parameters, depending on the physical and numerical characteristics of the specific simulations, will be selected to better convey the performance of the Picard and Newton iterative schemes.

3.1. Problem 1

This one-dimensional test problem consists a soil column of 0.3 m length discretized with a fine vertical resolution $∆z$ = 0.0024 m. This test case is a standard test problem [26], and substantially easier than remaining test problems because the domain is much shorter, media is nonuniform, and saturated conditions are not developed. However, it is a common test case and very helpful in clearly illustrating the analysis of nonlinear performance of the proposed methodology. The initial pressure head is −10 m, and constant pressure head boundary conditions are applied at the bottom and top of the soil column; these are −10 m and −0.75 m, respectively. The soil hydraulic properties are described by the van Genuchten model with ${\theta }_s$ = 0.368, ${\theta }_r$ = 0.102, $\alpha$ = 3.35/m, $n$ = 2.0, and $K_s$ = 7.970 m/day. As a result, simulation conditions yield a difficult sharp-front problem.

Computed pressure head profiles for different tolerances of two iterative schemes are presented in Figure 1. Both the constant pressure head and initial condition of this test problem are easily noted. Figure 1 shows that it is very difficult to distinguish the solutions obtained with various tolerances for two iterative schemes, and all of the profiles are very similar to the published results [26,27,28,29]. However, slight numerical oscillations are observed in the bottom of the soil column for the Picard scheme with error tolerance ${10}^{-2}$ m.

The computational performance of this test problem of two linearization techniques can be compared with the results of different tolerances, as shown in

Table 1. Computational performances of the Picard and Newton schemes for various tolerances. MBE: mass balance error; CPU: central processing unit.

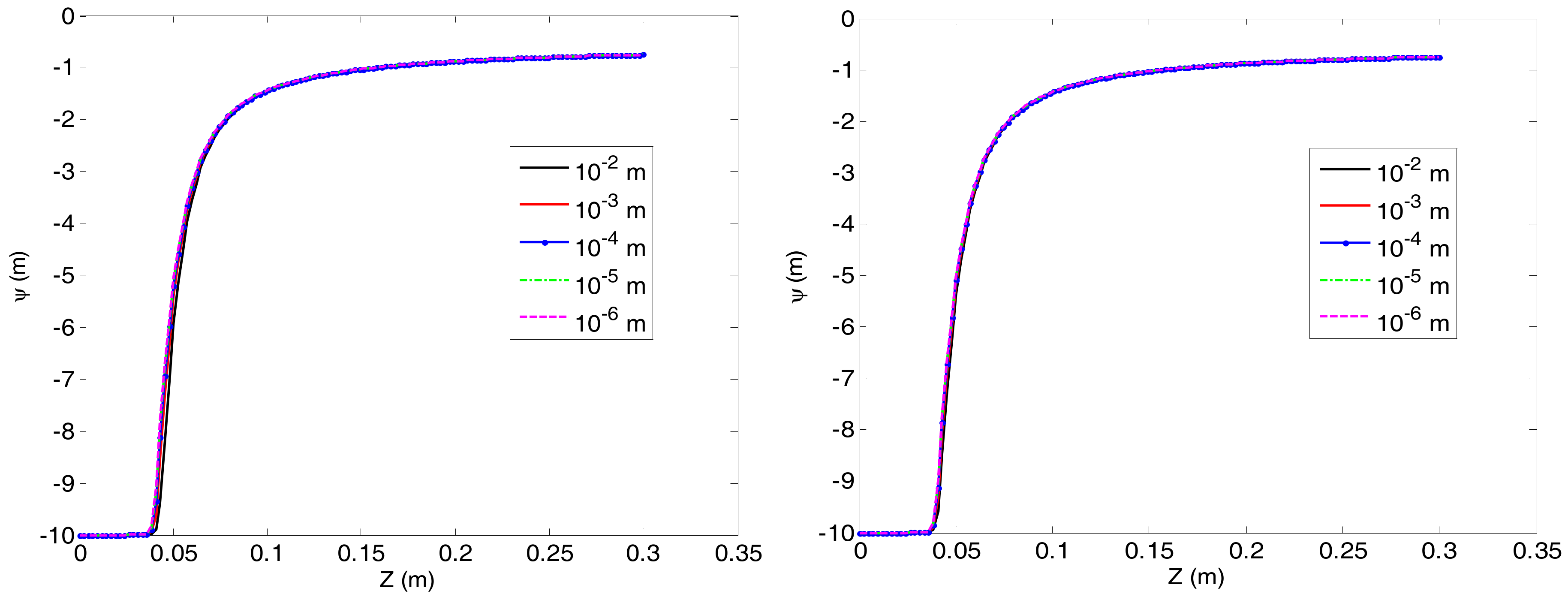
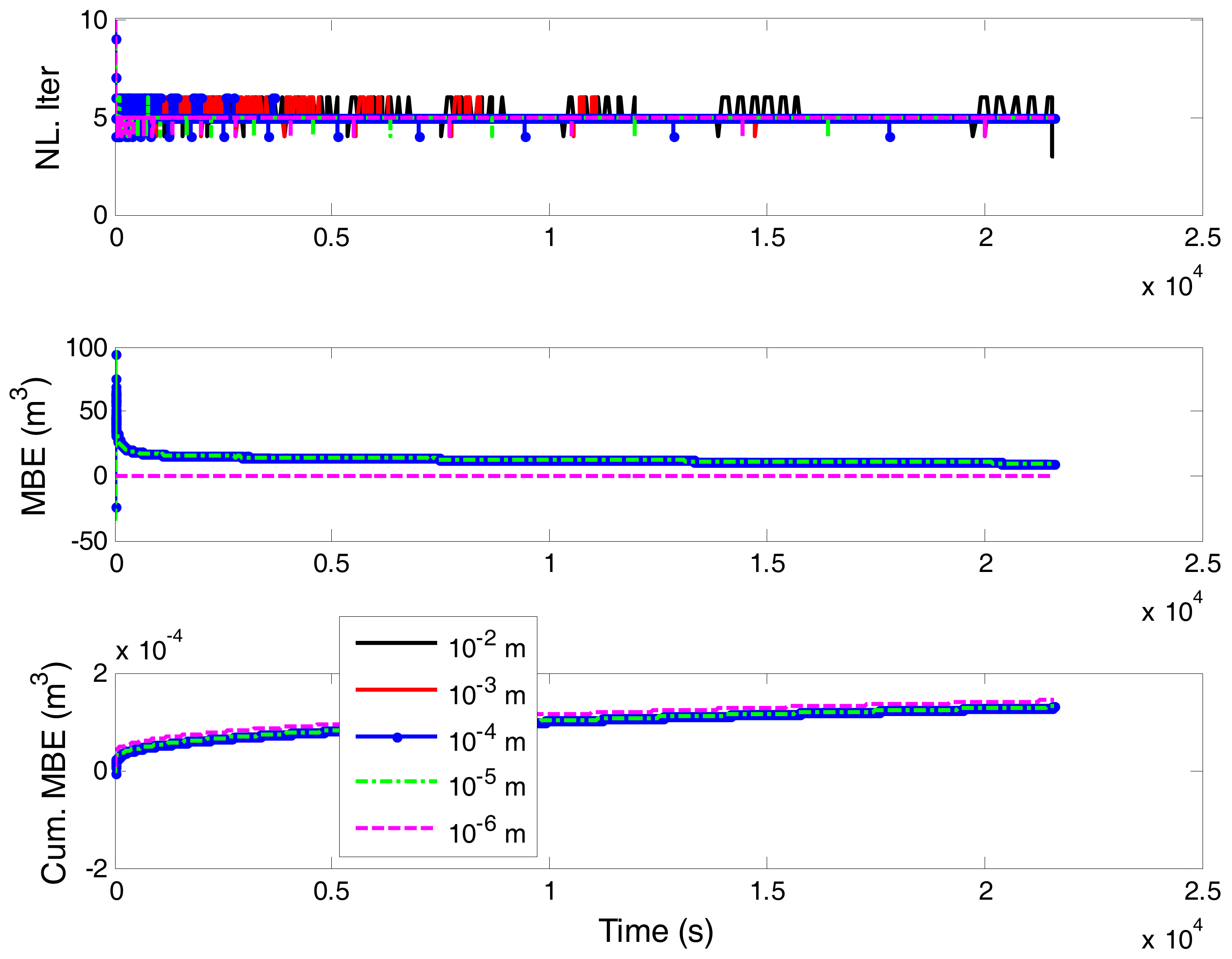
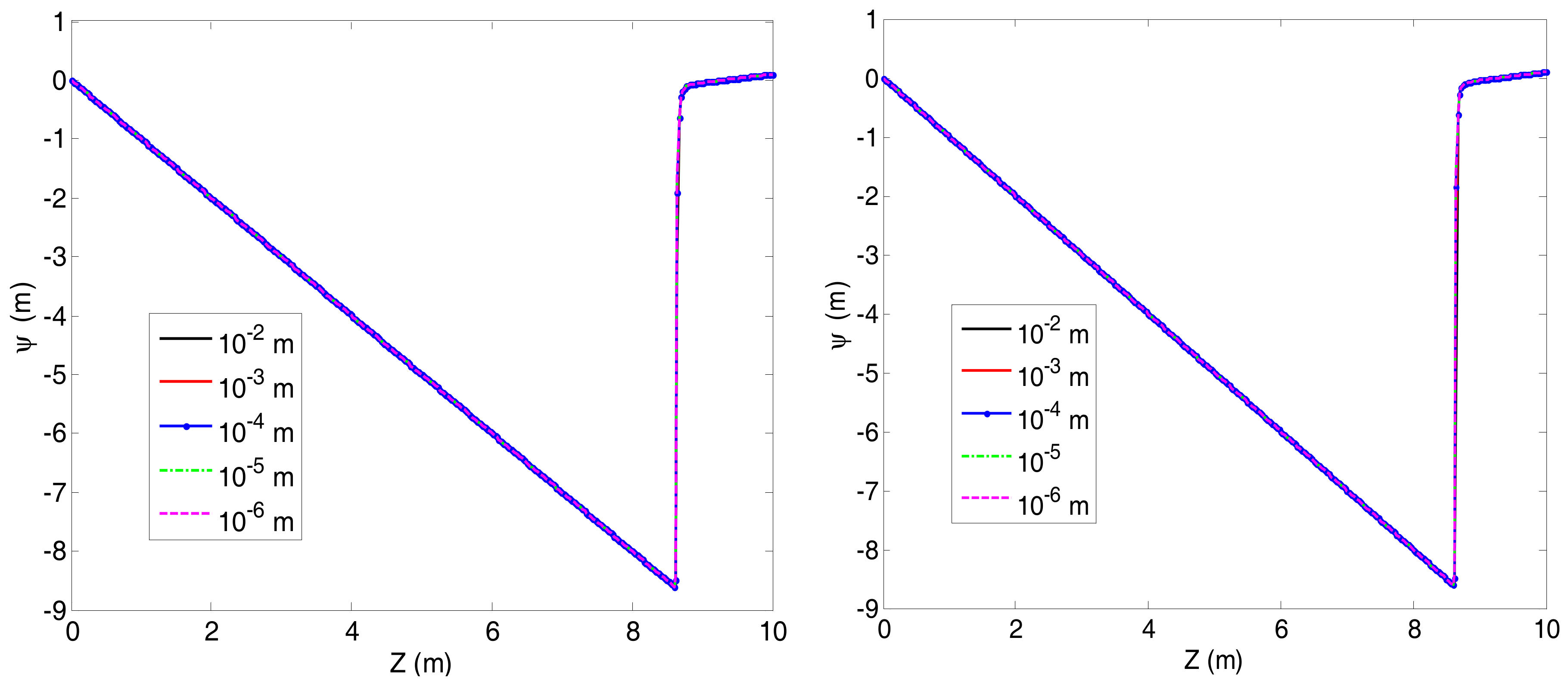
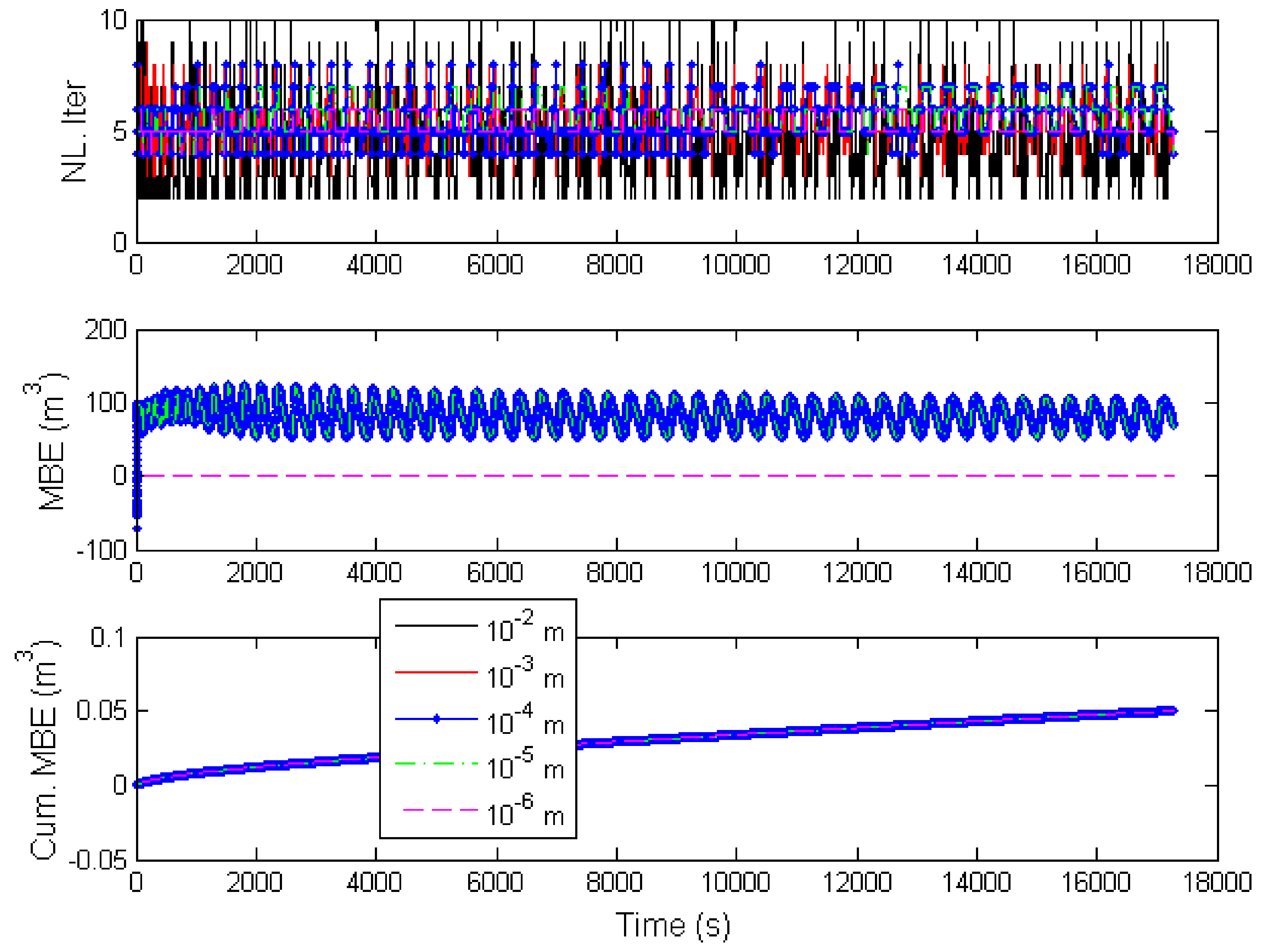
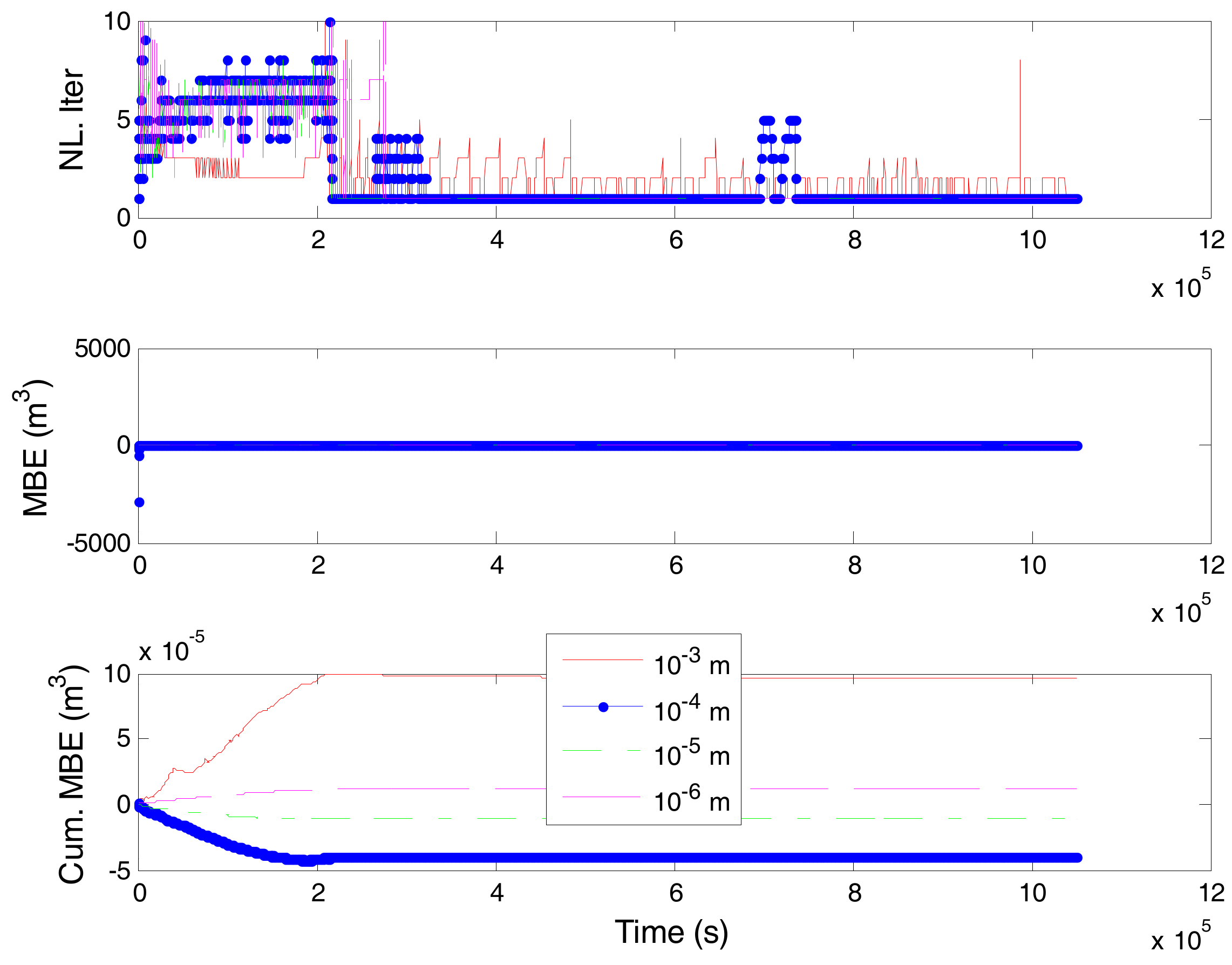
Technique
	Picard					Newton
	Tolerance (m)
	10−2	10−3	10−4	10−5	10−6	10−2	10−3	10−4	10−5	10−6
MBE (m3)	1.439 × 10−4	1.331 × 10−4	1.299 × 10−4	1.295 × 104	1.283 × 10−4	1.403 × 10−4	1.310 × 10−4	1.292 × 104	1.294 × 10−4	1.288 × 10−4
MBE (%)	1.779 × 10	1.653 × 10	1.681 × 10	1.614 × 10	1.601 × 10	1.744 × 10	1.630 × 10	1.610 × 10	1.612 × 10	1.605 × 10
No. of time steps	413	802	1458	2622	4779	859	1673	3216	6130	11,365
Average $∆t$ (s)	5.230 × 10	2.693 × 10	1.481 × 10	8.238	4.520	2.515 × 10	1.291 × 10	6.716	3.524	1.901
NL. Iter/time step	4.99	5.01	5.01	5.02	5.01	4.92	5.24	5.10	5.02	5.01
No. of back steps	1	2	2	3	3	2	3	3	4	4
CPU (s)	162.91	324.28	572.31	1041.50	1881.01	832.13.28	1508.64	2746.24	5171.76	9180.59

. It is clear that the cumulative mass balance errors for all of the runs are very close and remarkably small throughout the entire simulation, confirming the consistency of the schemes and reliability of the accuracies. The measures of other computational efforts used in this study are the total number of time steps and average nonlinear iterations per time step. Usually, these results vary with the size of time steps, because the step sizes are strongly influenced by the convergence of the nonlinear solver. When we reduce the tolerance by a factor of 10⁻¹ m, the number of time steps increases approximately 50–80%. Central processing unit (CPU) time is a common measure, but it is dependent on machine, compiler, program, system load, and algorithm. It is the most meaningful measure for evaluating the relative efficiency for solving the Richards equation, and the results in Table 1 indicate that CPU time is greatly influenced by the reduction of tolerance. For this simple test, the Picard method is characterized by a lower (approximately one-fifth for the same tolerance) computational cost with respect to the Newton technique because of the differences in the per iteration costs of the two approaches, as can be seen in the last row of Table 1. Almost the same number of average nonlinear iterations is required for all of the cases. We note that both the schemes resulted in significantly fewer backstepping occurrences. Convergence behavior and MBE plots for the Picard and Newton schemes are presented in Figure 2 and Figure 3, respectively. The results of the two iterative schemes with tolerance 10⁻³ m are indistinguishable from all of the solutions within the simulation and hence, we can say that it has sufficient error tolerance to achieve an accurate, efficient, and robust solution under such flow conditions.

3.2. Problem 2

This one-dimensional test case concerns a difficult vertical infiltration problem of a 10 m-high soil column. It will be solved, and has already been analyzed in detail by many researchers [26,28,29,30]. This soil column is parameterized by the van Genuchten model with the soil parameters ${\theta }_s=0.301$, ${\theta }_r=0.093$, $\alpha =5.47/\mathrm{m}$, $n=4.264$, and $K_s=5.040 \mathrm{m}/\mathrm{days}$.

Constant head boundary conditions at both the top ($\Psi \left(10,t\right)=0.1$) and bottom ($\Psi \left(0,t\right)=0.0$) boundaries, and a hydrostatic equilibrium initial condition ($\psi \left(z,0\right)=-z$), are applied. These forcing conditions, along with the constitutive relationships, lead to the development of a sharp infiltration front and induce large gradients in the solution. This type of problem provides a rigorous test case for time integrators, and is well suited for the analysis of numerical convergence and efficiency with accuracy. As a result, it is a meaningful test problem to measure the limit of accuracy.

Due to the expense involved in accurate computing, a sufficient number of nodes in a grid is important to approximate the Richards equation. Since our objective is to achieve accurate results with the highest possible tolerance, the dense grid solutions for this test problem were made on a uniform grid of 401 nodes.

The solutions from these dense grid simulations at time T = 17,280 s for the Picard and Newton methods with different tolerances are shown in Figure 4. A sharp infiltration front between the saturated and unsaturated zones and the drained-to-equilibrium initial condition are noted, which are the trademark of this test problem. It is evident from these figures that the same accuracy is obtained for each of the five tolerances, and the results show good agreement with that of the published reports [26,28,29,30].

The results obtained by two iterative techniques with different tolerances are compared in

Table 2. Computational performances of the Picard and Newton schemes for various tolerances.

Technique
	Picard					Newton
	Tolerance (m)
	${10}^{-2}$	${10}^{-3}$	${10}^{-4}$	${10}^{-5}$	${10}^{-6}$	${10}^{-2}$	${10}^{-3}$	${10}^{-4}$	${10}^{-5}$	${10}^{-6}$
MBE (m3)	5.029 × 10−2	5.024 × 10−2	5.022 × 10−2	5.021 × 10−2	5.020 × 10−2	5.037 × 10−2	5.027 × 10−2	5.022 × 10−2	5.020 × 10−2	5.019 × 10−2
MBE (%)	8.282 × 10	8.274 × 10	8.275 × 10	8.274 × 10	8.273 × 10	8.284 × 10	8.279 × 10	8.275 × 10	8.273 × 10	8.272 × 10
No. of time steps	2783	4028	6641	10,053	17,950	1124	2539	7641	17,616	34,975
Average $∆t$ (s)	6.209	4.290	4.745	1.719	9.627 × 10−1	1.537	6.806	2.261	9.809 × 10−1	4.941 × 10−1
NL. Iter/time step	5.24	5.60	5.51	5.67	5.34	5.24	5.56	5.09	5.04	5.07
No. of back steps	360	21	22	22	23	63	29	23	23	23
CPU (s)	4644.83	7057.22	11,467.73	17,767	29,438.61	3754.03	8911.04	23,707.95	53,058.00	10,352.78

and Figure 5 and Figure 6. A low mass balance error is necessary, but is not a sufficient condition to ensure the accuracy of the solution. In other words, accurate solutions ensure a small mass balance error. The MBE results for the two iterative schemes with five tolerances confirm the accurate numerical solutions. Errors are not significantly decreased for all of the runs if the tolerances are decreased, which are almost same for all of the runs performed in this work. For the Picard and Newton runs, the reduction in the magnitude of the tolerance in the nonlinear solver does not significantly affect the overall accuracy of the solution. There are very little differences for the nonlinear iterations per time step. For both the Picard and Newton schemes, approximately 1.5 times and three times more steps are required to converge to the final solution compared with each of the previous head tolerances, respectively. The same inclinations are observed in CPU time for all of the given levels of iteration tolerances, which drastically increases for the convergence of the Newton scheme. The oscillations of nonlinear convergence (Figure 5 and Figure 6) and the number of backsteppings are comparatively very high for the case of 10⁻² m, which can be attributed to a sharp infiltration front produced at top of the soil column. Therefore, as far as the accuracy of the solution of the Richards equation is concerned, 10⁻³ m is enough as a level of tolerance to achieve a reliable and robust solution.

3.3. Problem 3

In order to attain our objective, our present test study consists of one-dimensional vertical infiltration with redistribution in a 5 m soil column [29,30,31]. A vertical discretization of 0.0125 m is used. Constant head boundary condition $\Psi \left(0,t\right)=0.0$ at the bottom of the domain, and a time-dependent boundary condition $\psi \left(10,t\right)=-10\left(1.0-1.01{\mathrm{e}}^{-t}\right)$ at the top of the domain with hydrostatic equilibrium initial conditions $\psi \left(z,0\right)=-z$ are applied. The time-varying boundary condition yields a difficult two-front problem. The van Genuchten model was fitted to the water retention curves, and the soil properties ${\theta }_s=0.301$, ${\theta }_r=0.093$, $\alpha =5.47/\mathrm{m}$, $n=\mathrm{4.264.0}$, and $K_s=5.040\mathrm{m}/\mathrm{days}$ were used.

Comparison of pressure head profiles in the Picard and Newton methods by using all values of the head tolerances are shown in Figure 7. Due to the dynamic boundary conditions at the top of the domain, there is rapid infiltration of water from the surface, followed by a period of redistribution of the water. The simulated results in each of the two schemes with five tolerances closely agree with the previous studies [29,30,31].

A major problem in solving the Richards equation is to maintain good MBE concerning its nonlinear nature, especially for flow involving extremely sharp two-front and rapid infiltration of water from the surface with dynamic boundary conditions. A small mass balance does not guarantee an appropriate numerical solution; for an accurate solution, it is usually required to satisfy the mass conservation property, and the evaluated MBE results presented in

Table 3. Computation performances of the Picard and Newton schemes for various tolerances.

Technique
	Picard					Newton
	Tolerance (m)
	${10}^{-2}$	${10}^{-3}$	${10}^{-4}$	${10}^{-5}$	${10}^{-6}$	${10}^{-2}$	${10}^{-3}$	${10}^{-4}$	${10}^{-5}$	${10}^{-6}$
MBE (m3)	1.643 × 10−2	1.342 × 10−2	1.612 × 10−2	1.611 × 10−2	1.610 × 10−2	1.655 × 10−2	1.342 × 10−2	1.611 × 10−2	1.642 × 10−2	1.610 × 10−2
MBE (%)	9.037 × 10	9.753 × 10	8.871 × 10	8.869 × 10	8.868 × 10	9.120 × 10	9.755 × 10	8.869 × 10	9.047 × 10	8.867 × 10
No. of time steps	3987	3579	7426	11,572	18,681	3333	2865	8954	18,512	34,915
Average $∆t$ (days)	8.151 × 10−5	8.382 × 10−5	4.377 × 10−5	2.809 × 10−5	1.740 × 10−5	9.751 × 10−5	1.047 × 10−4	3.630 × 10−5	1.756 × 10−5	9.308 × 10−6
NL. Iter/time step	2.63	4.37	4.41	4.61	4.84	3.53	4.13	4.45	4.78	4.93
No. of back steps	56	14	53	56	54	48	6	52	54	53
CPU (s)	2914.02	4276.15	8973.47	14,565.64	24,645.02	4821.05	5967.86	20,579.44	43,493.02	83,722.34

attest to this proposition. It can be seen from the computational results for all of the runs that the two iteration methods precisely conserved the mass. Very closed MBE results are obtained for all cases; however, some differences are observed in terms of average nonlinear iterations per time steps, except the case of ${10}^{-2}$ m, it should be noted from Table 3 that both numerical techniques have taken the largest average time step size during the simulation; as a result, the number of iterations becomes smallest for the head tolerance ${10}^{-3}$ m. For this test problem, the Picard and Newton schemes need on average four to five iterations per time step throughout the simulation period for all of the head tolerances. This explains why remarkable differences are not shown by the Picard and Newton schemes in terms of convergence behavior, as we observed on the plots of Figure 8 and Figure 9 (including MBE behavior). The number of backstepping increased dramatically compared with the previous examples due to the strong nonlinear nature of the soil hydraulic properties with time-varying surface boundary conditions. Also, both the Picard and Newton iterative methods for the case of ${10}^{-2}$ m failed to converge several times (56 for Picard and 48 for Newton) during the course of simulation. It can be inferred from these discussions that the head tolerance of ${10}^{-3}$ m bears consistent head distribution profiles, as well as perfect mass conservation nature.

3.4. Problem 4

This case involves vertical drainage through a layered soil from initially saturated conditions. At time $t=0$, the pressure head at the base of the column is reduced from 2 m to 0 m. During the subsequent drainage, a no-flow boundary condition is applied to the top of the column. This problem is considered to be a challenging test for numerical methods, because a sharp discontinuity in the moisture content occurs at the interface between two material layers [7,15,32].

During downward draining, the middle coarse soil tends to restrict drainage from the upper fine soil, and high saturation levels are maintained in the upper fine soil for a considerable period of time. The Brooks–Corey model is used to prescribe the pressure–moisture relationship. The hydraulic properties of the soils are given in

Table 4. Soil hydraulic properties used in Test Problem 4.

Parameters	Soil 1	Soil 2
${\theta }_s$	0.35	0.35
${\theta }_r$	0.07	0.035
$\alpha \left({\mathrm{cm}}^{-1}\right)$	0.0286	0.0667
$n$	1.5	3.0
$K_s \left(\mathrm{cm}/\mathrm{s}\right)$	9.81 × 10−5	9.81 × 10−3

. The soil profile is Soil 1 for 0 < $z$ < 60 cm and 120 cm < $z$ < 200 cm, and Soil 2 for 60 cm < $z$ < 120 cm. A Dirichlet boundary condition is imposed at the base of the bottom boundary.

Simulations are performed by the Picard and Newton methods on a fine mesh of 150 elements with five very small head tolerances. The evolution of saturation distribution in the soil column while drainage occurs is illustrated in Figure 10 for all of the cases of head tolerances at an elapsed time of 1,050,000 s (approximately 12 days). All of the solutions are in excellent agreement with the published results [7,15,32], except the Newton runs for error tolerance ${10}^{-2}$ m. Desaturation takes place at early times in both the middle medium sand and upper fine sand layers, as clearly shown in this plot. A physical implication of the Richards equation, as this figure demonstrates, is that air is freely available to all parts of the water flow system, irrespective of the saturation distribution.

At the intermediate times, desaturation in the upper fine sand layer decelerates significantly, as the middle medium sand keeps desaturating. It is clear from the figure that the base of the middle medium sand is mostly desaturated, and the drying front has begun to move downward into the lower fine sand layer. At later times, desaturation occurs very slowly in the upper fine sand layer. Finally, a new hydrostatic saturation distribution will be formed in the column. A compelling feature of this simulation is that the middle medium sand layer tends to limit drainage from the overlying fine sand. High saturations are presented in the upper fine sand layer for significant periods of time. This test example demonstrates the efficacy of coarser-grained layers as capillary barriers in unsaturated flow.

Numerical simulations for layered soil under vertical drainage are generally much more complicated than those under homogeneous porous media, and require more CPU time with large number of iterations, thus representing a challenging computational task.

Table 5. Computational performances of the Picard and Newton schemes for various tolerances.

Technique
	Picard					Newton
	Tolerance (m)
	${10}^{-2}$	${10}^{-3}$	${10}^{-4}$	${10}^{-5}$	${10}^{-6}$	${10}^{-2}$	${10}^{-3}$	${10}^{-4}$	${10}^{-5}$	${10}^{-6}$
MBE (m3)	−2.961 × 10−4	−6.590 × 10−5	−3.861 × 10−5	−3.174 × 10−5	−1.918 × 10−5	1.718 × 10−4	9.602 × 10−5	−4.012 × 10−5	−1.081 × 10−5	−3.150 × 10−6
MBE (%)	2.263	5.281 × 10−1	3.054 × 10−1	2.513 × 10−1	1.520 × 10−1	−1.075	−7.787 × 10−1	3.172 × 10−1	8.569 × 10−2	2.498 × 10−2
No. of time steps	1109	1147	1565	1962	2623	1,445,671	46,165	385,744	515,932	743,781
Average $∆t$ (s)	9.468 × 102	9.154 × 102	6.709 × 102	5.352 × 102	4.003 × 102	7.263 × 10−1	2.274 × 10	2.722	2.035	1.412
NL. Iter/time step	1.16	1.61	3.78	4.98	5.66	4.75	3.61	3.63	3.67	4.09
No. of back steps	12	28	149	155	202	372,457	11,943	101,364	133,895	163,735
CPU (s)	141.5	359.60	668.23	1070.44	1628.36	539,363.19	62,557.76	378,278.25	403,718.38	531,572.38

compares the computational requirements by the two iterative schemes with five values of head tolerances. Since numerical oscillations occurred in the Newton scheme for ${10}^{-2}$ m, this case will be excluded in the numerical discussion, and not shown in the plot (Figure 11) of convergence and MBEs. Simulations scenarios such as MBE, the total number of iterations used for each simulation, the average nonlinear iterations required for each step for the various simulations, the largest time stepping, and CPU time are included in this table. As shown in the table, the number of iterations for both iterative methods increases with the reduction of head tolerances. A perfect mass balance is guaranteed by the two schemes for all of the numerical experiments. We note here that 1147 and 46,165 steps are required to complete the simulation with head tolerance ${10}^{-3}$ m for the Picard and Newton techniques, respectively. As compared with the Picard method, the Newton scheme required more than 46 times the iterations and 174 times the CPU time for simulating the 12-day drainage event. Furthermore, for the Newton method, the total steps and computational time increase severely with the reduction of tolerance. This is because discontinuity arises across the boundaries between different soil layers, and saturation gradients are steep on each side of the interface. The calculation of three derivative terms in the Jacobian makes the Newton scheme more costly; as a result, the numerical model needs to recompute (backstepping) many times than the current solution. A comparison of the behavior of convergence and MBEs for the Picard and Newton schemes is shown in Figure 11 and Figure 12, respectively. The results are broadly representative, in that for most of the simulations, very little difference was found among the saturation predictions. Moreover, the MBEs usually follow parallel paths. Therefore, to avoid the excessive CPU time without significantly affecting convergence difficulties, one can use ${10}^{-3}$ m of head tolerance.

4. Conclusions

A realistic computational approach is presented that effectively addresses the minimal head tolerance to solve the Richards equation accurately for four difficult test problems in combination with Picard and Newton linearization techniques. The tested examples and computational results presented illustrate clearly that the finite element formulation developed in this work is effective in handling severely nonlinear flow problems, including time-varying boundary conditions, nonhomogeneous soil hydraulic parameters, and an extremely sharp infiltration front in space. Simulations of redistribution, infiltration, and drainage problems in a one-dimensional soil column were used to evaluate the performance of the two schemes. An adaptive time-stepping scheme was incorporated easily in the Newton and Picard iteration techniques. The performance efficiency of the study is compared on the basis of MBE, CPU, the total number of time steps, and the average number of nonlinear iterations required by the algorithm to achieve the convergent solution within the specified tolerance. Accuracy and convergence profiles were generated to demonstrate the behavior of the two iterative techniques over a wide range of head tolerances. The main characteristic of the present formulation is to determine the least value of the head tolerances for the Picard and Newton iterative methods to obtain a stable and accurate solution with perfect mass balance. It has been shown that the schemes are extremely simple to implement, and such a procedure can greatly enhance the convergence properties of the iterative solution process with the head tolerance ${10}^{-3}$ m. The numerical assessment has shown that the Picard scheme requires less CPU time per iteration than the Newton technique, because it needs to evaluate the Jacobian and produces a nonsymmetric coefficient matrix, which requires more computational effort. The procedure implemented in this work is very straightforward, and we believe its simplicity makes it an attractive approach for numerical simulations of variably saturated–unsaturated flow problems, and can easily be extended in more complex flow cases.