Evaluating Country-Scale Irrigation Demand Through Parsimonious Agro-Hydrological Modeling
Abstract
1. Introduction
2. Materials and Methods
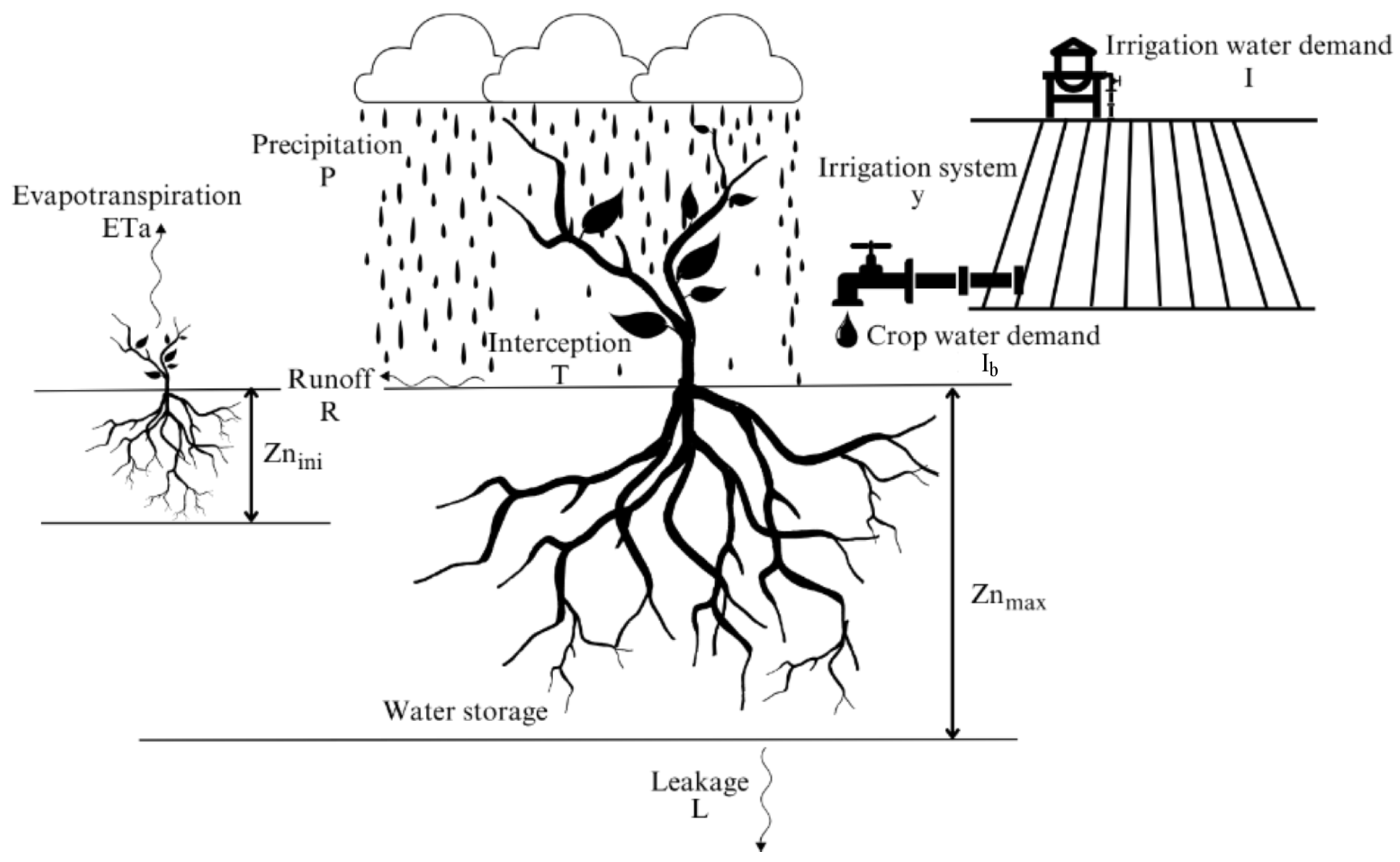
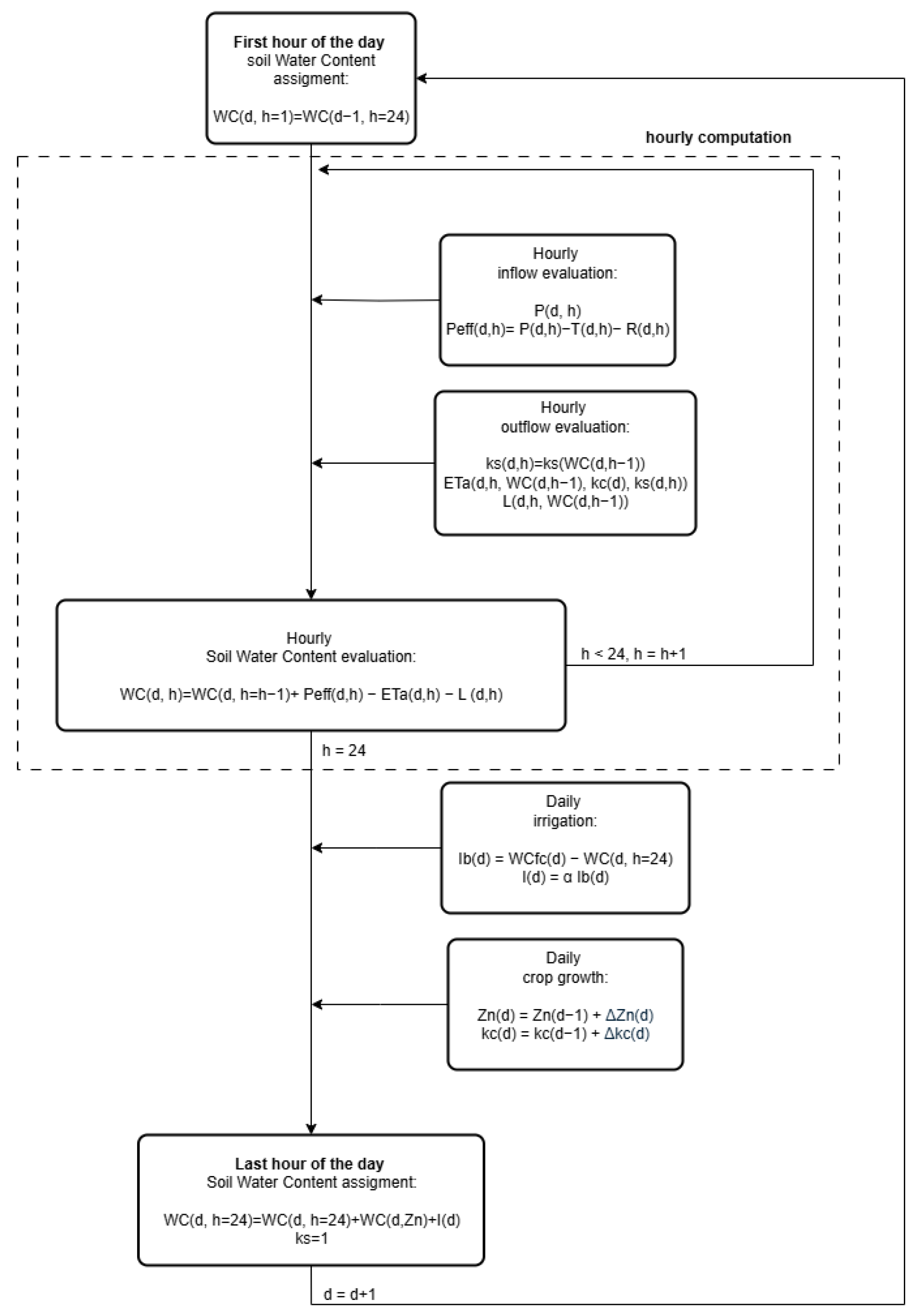
2.1. Model
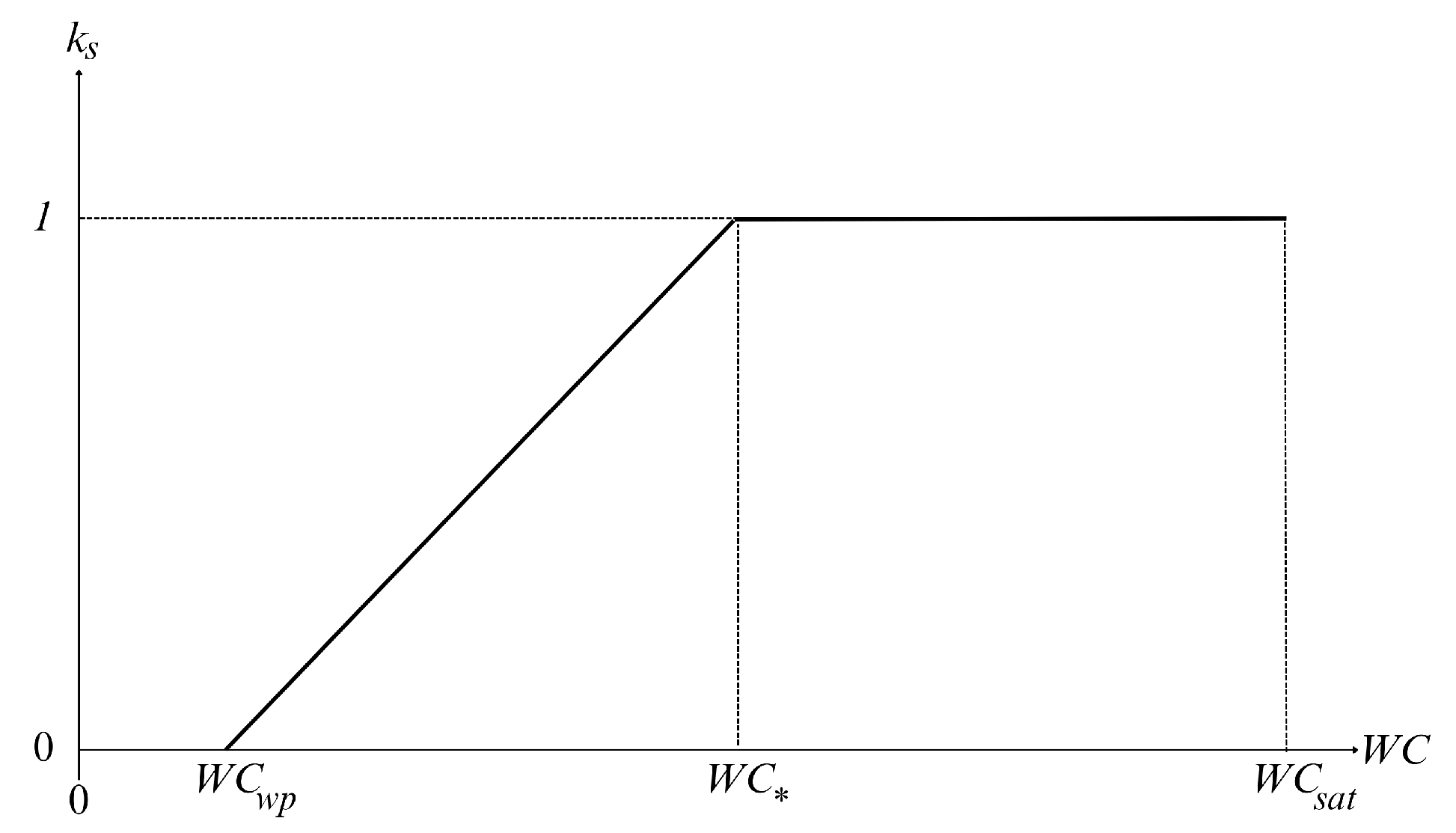
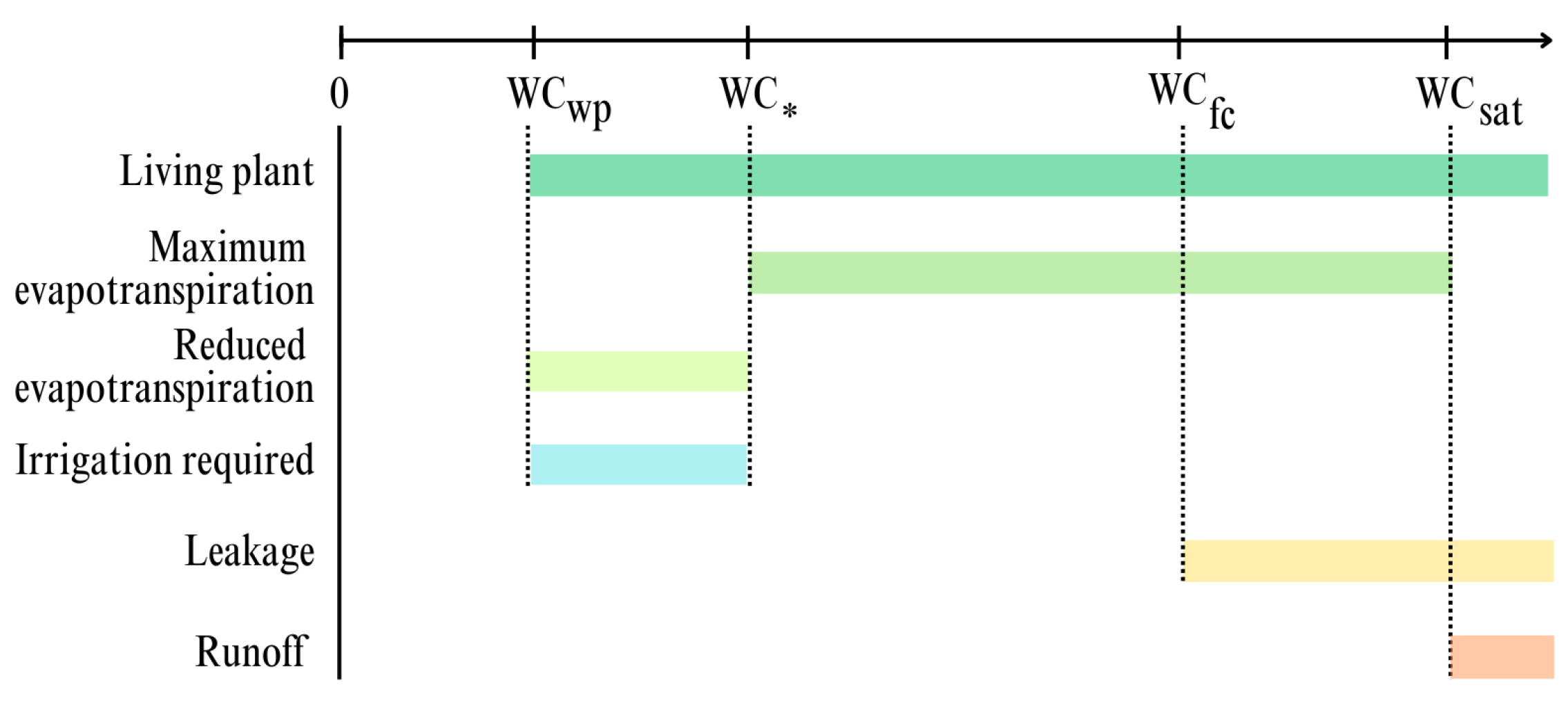
- . It is the at wilting point and sets the minimum water content for plants to survive;
- . It is the at critical condition and is the threshold that controls whether evapotranspiration is at maximum and whether it is necessary to resort to irrigation;
- . It is the at field capacity, and, when goes below , the leakage process ends;
- . It is the at saturation, which controls the surface runoff formation.
2.2. Data
3. Results
3.1. Validation
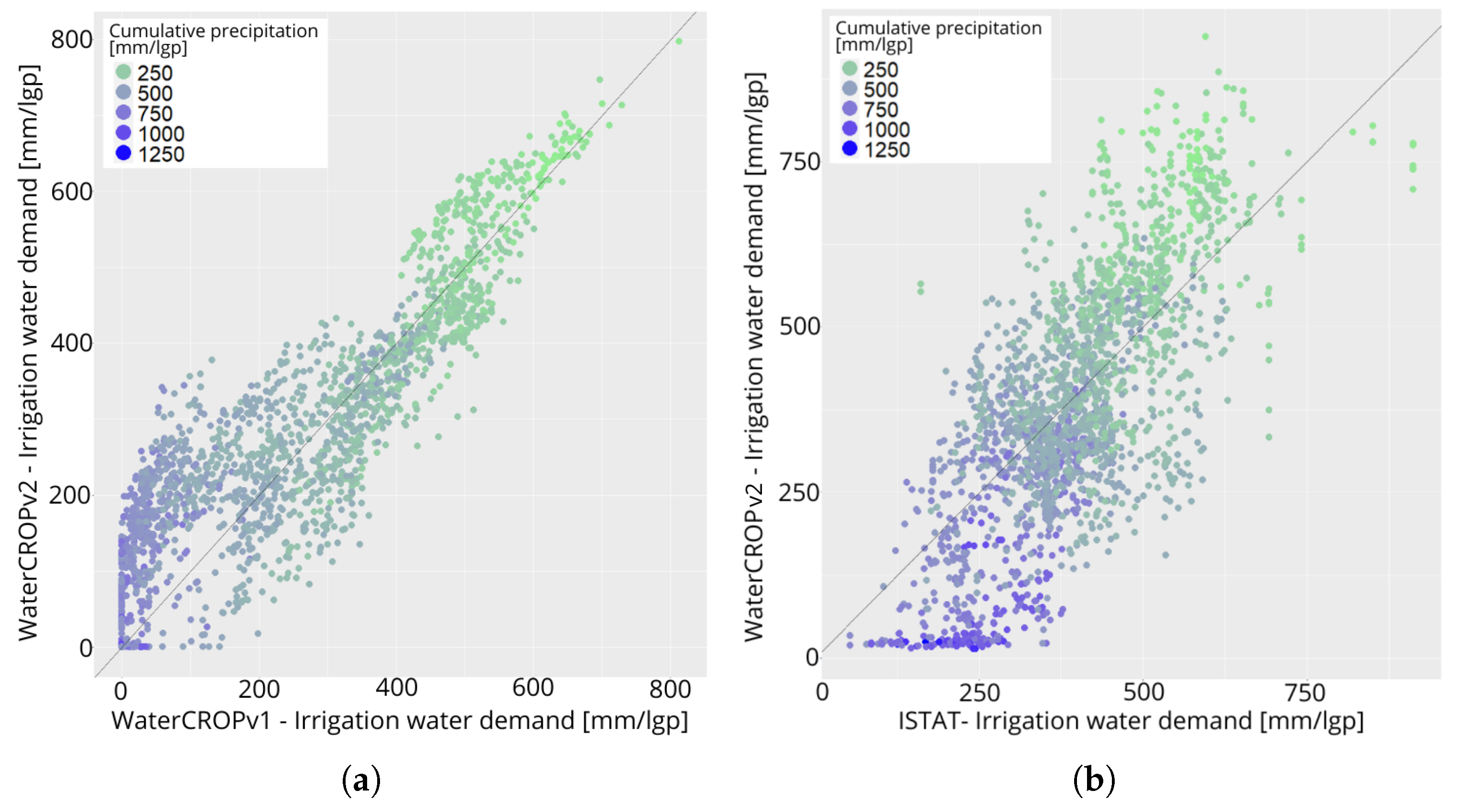
3.1.1. Comparison with Previous Version, WaterCROPv1
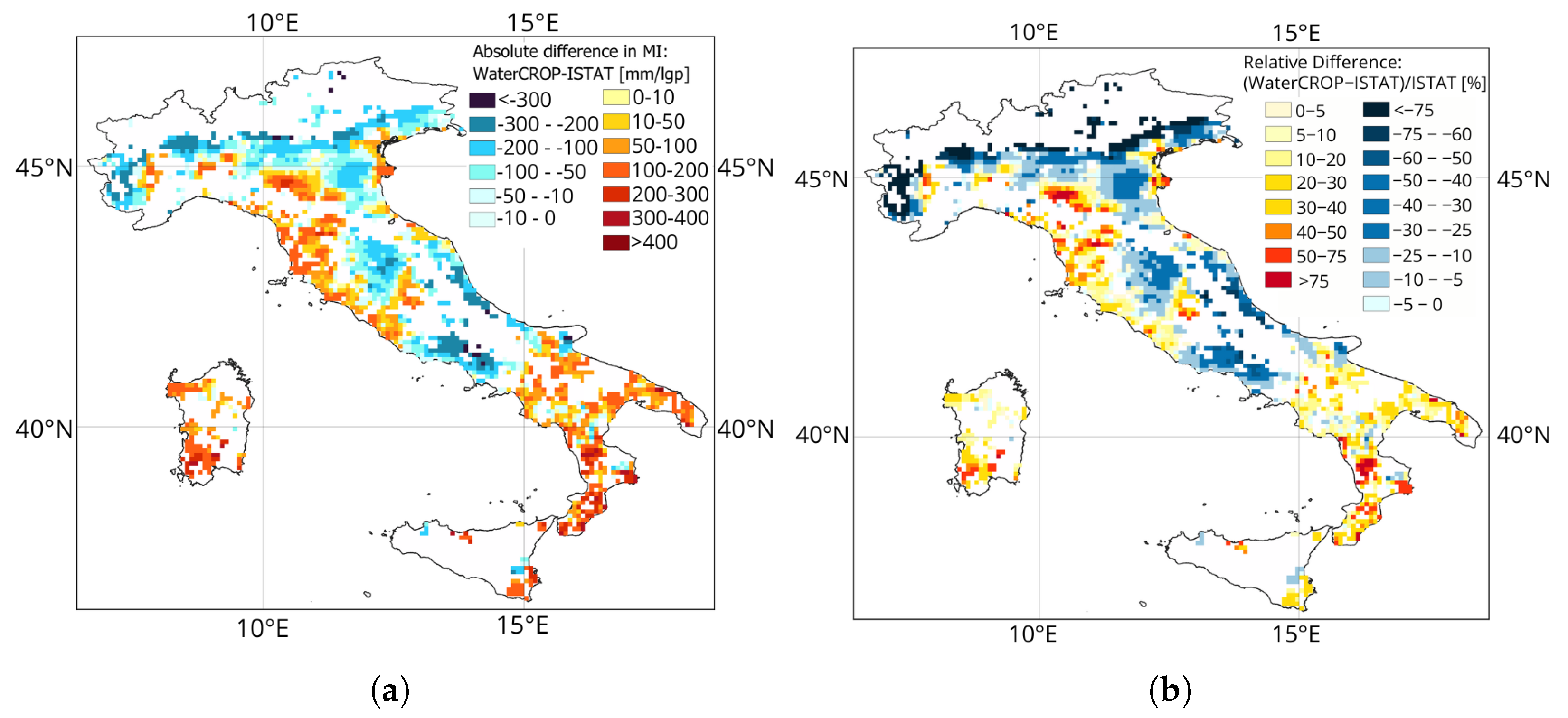
3.1.2. Comparison with Independent Data
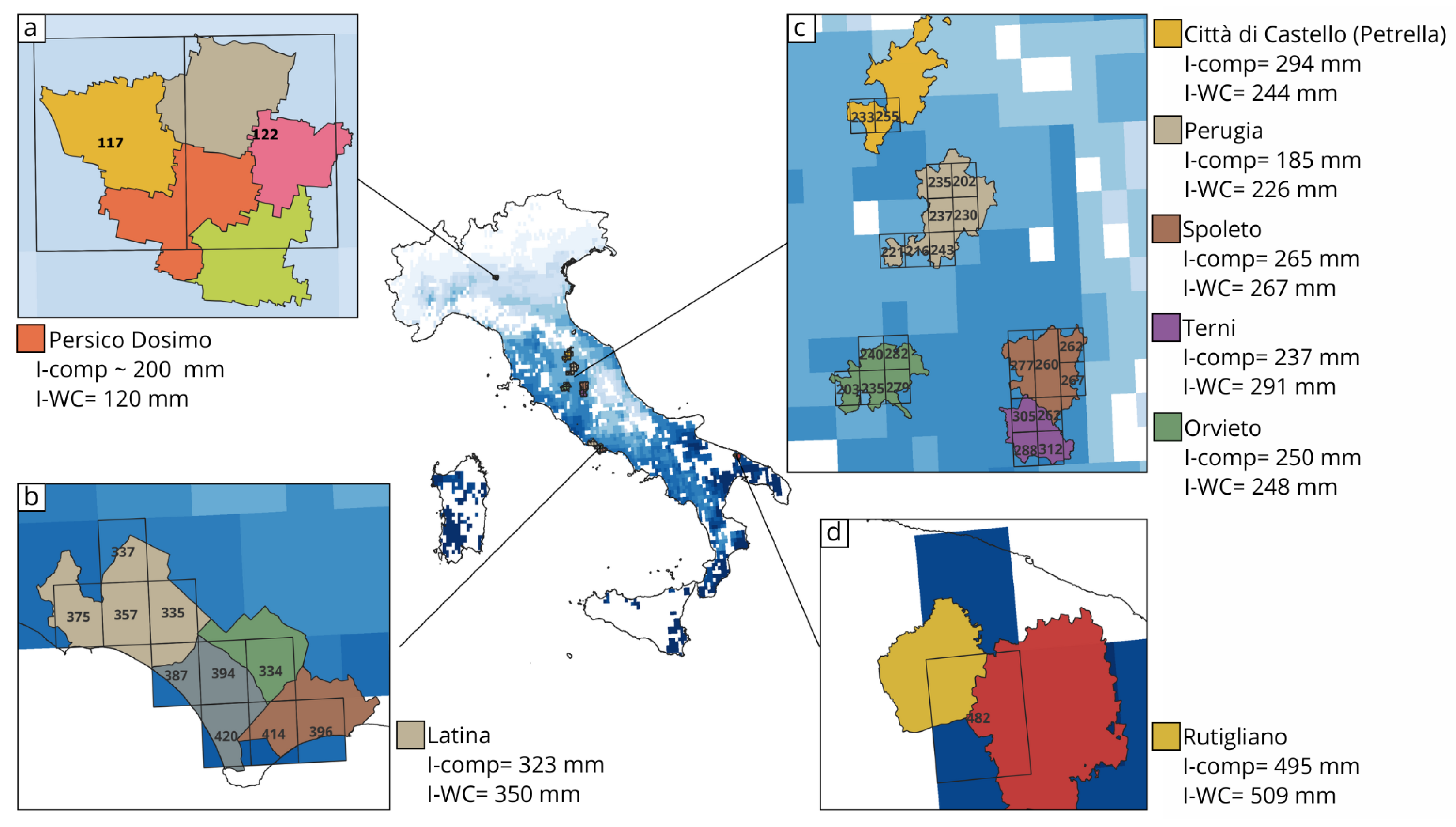
3.1.3. Comparison with Previous Local-Scale Studies
3.2. Examples of Model Application
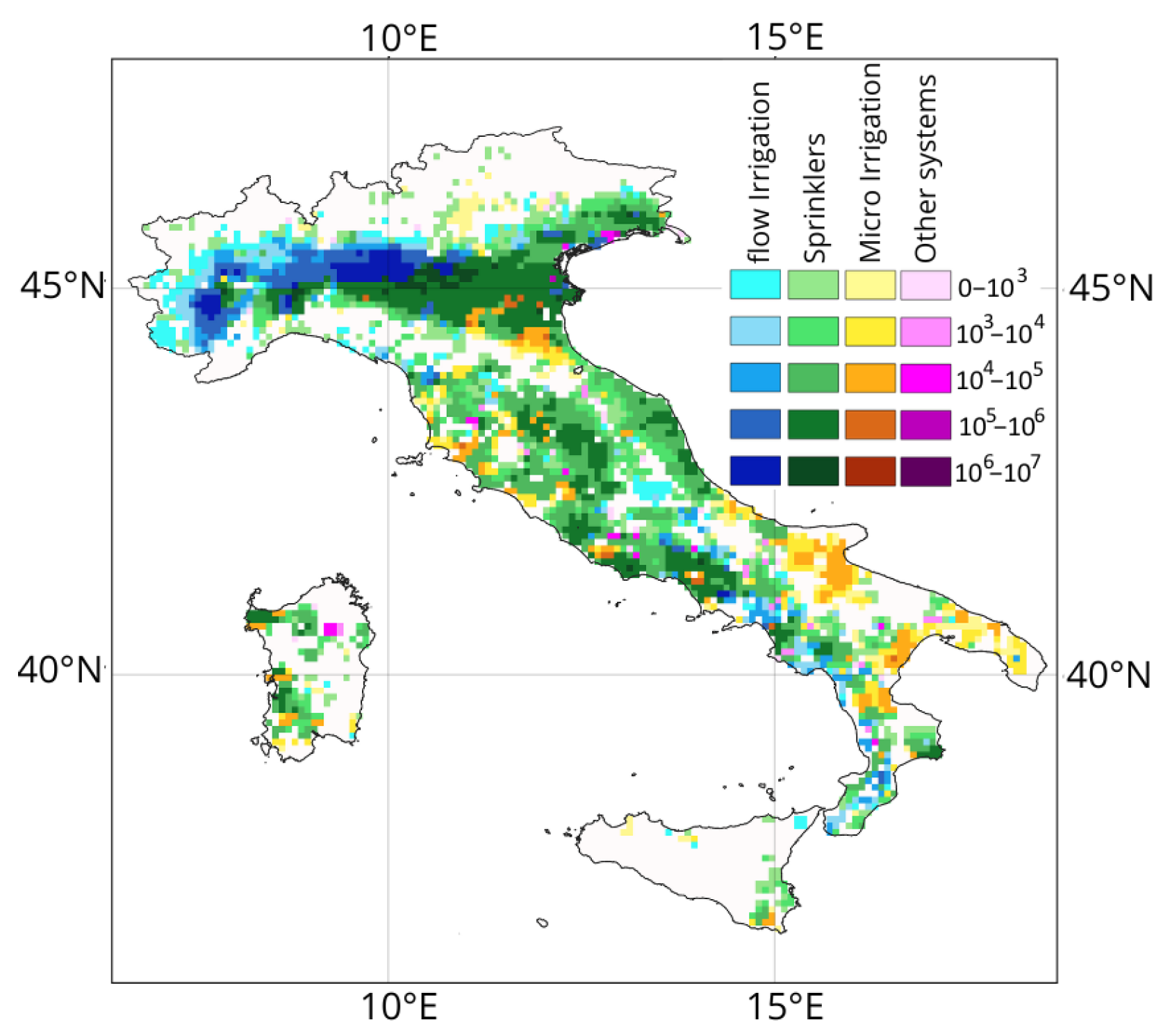
3.2.1. Water Demand Assessment
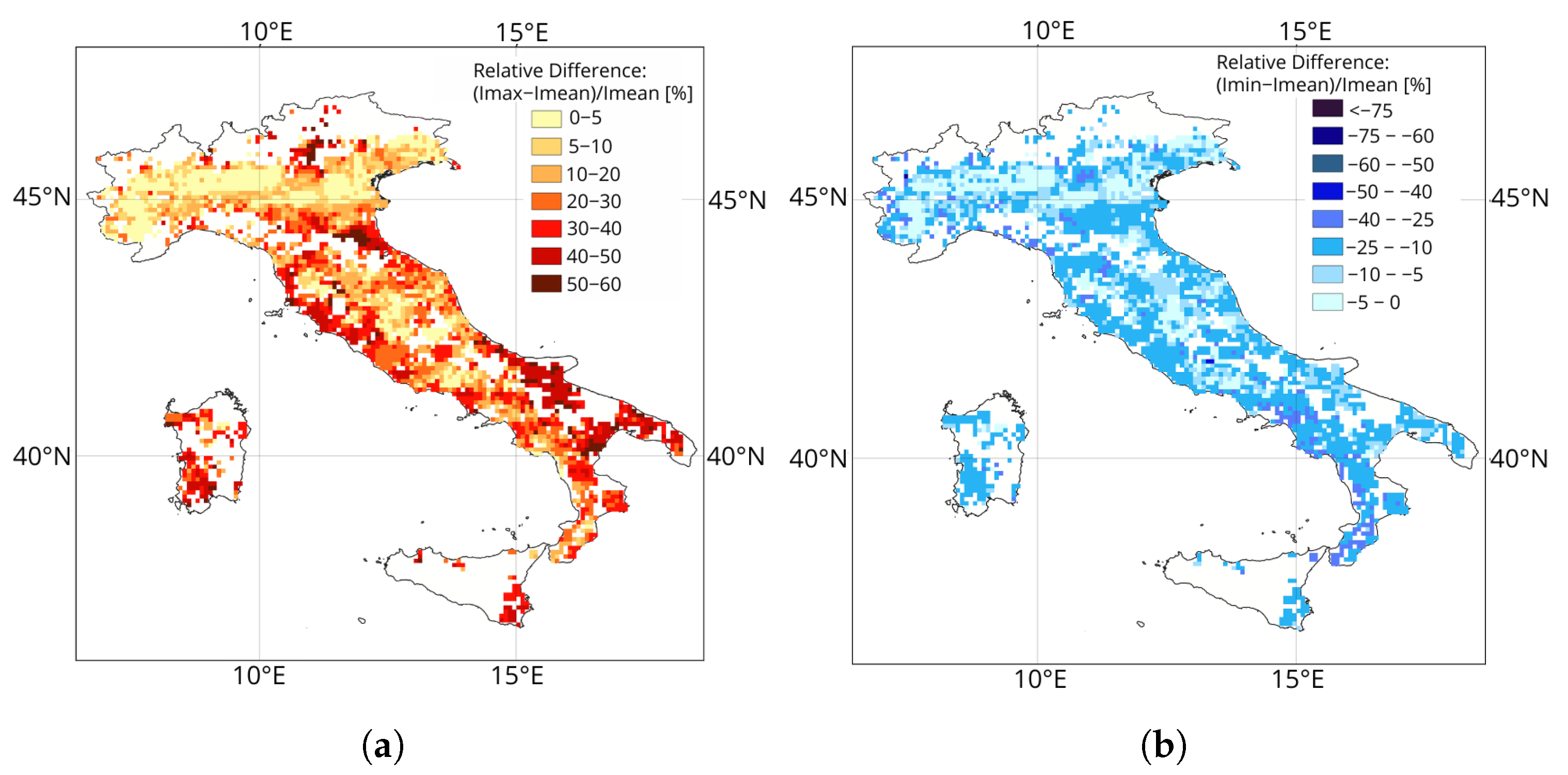
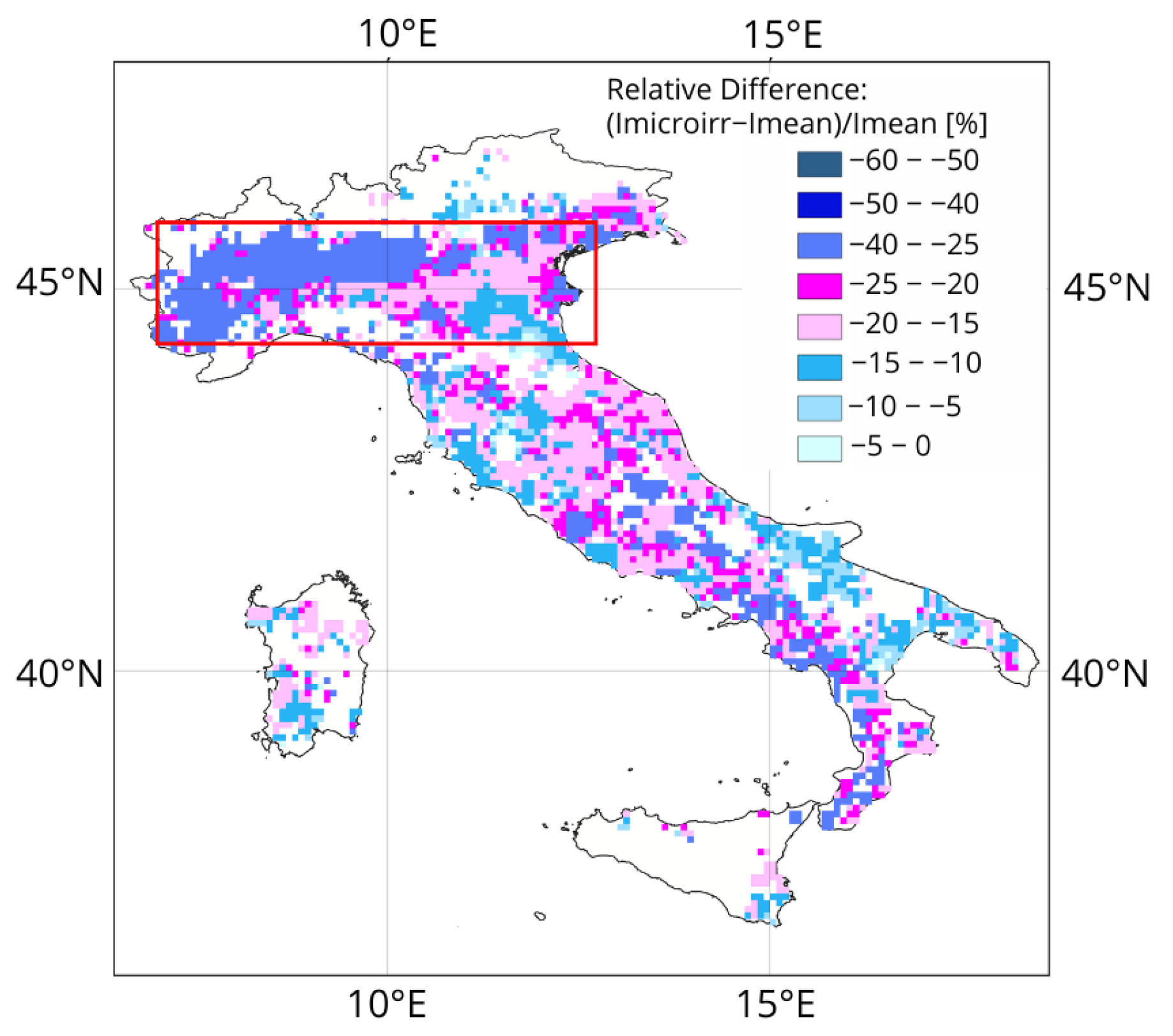
3.2.2. Scenario Analysis
| Irrigation System | Coverage [103·ha] | % | Efficiency |
|---|---|---|---|
| Submersion | 221.0 | 9 | 0.25 |
| Micro-irrigation | 423.0 | 17 | 0.9 |
| Flow and Lateral infiltration | 748.4 | 31 | 0.55 |
| Sprinklers | 958.5 | 40 | 0.75 |
| Other | 68.4 | 3 | 0.7 |
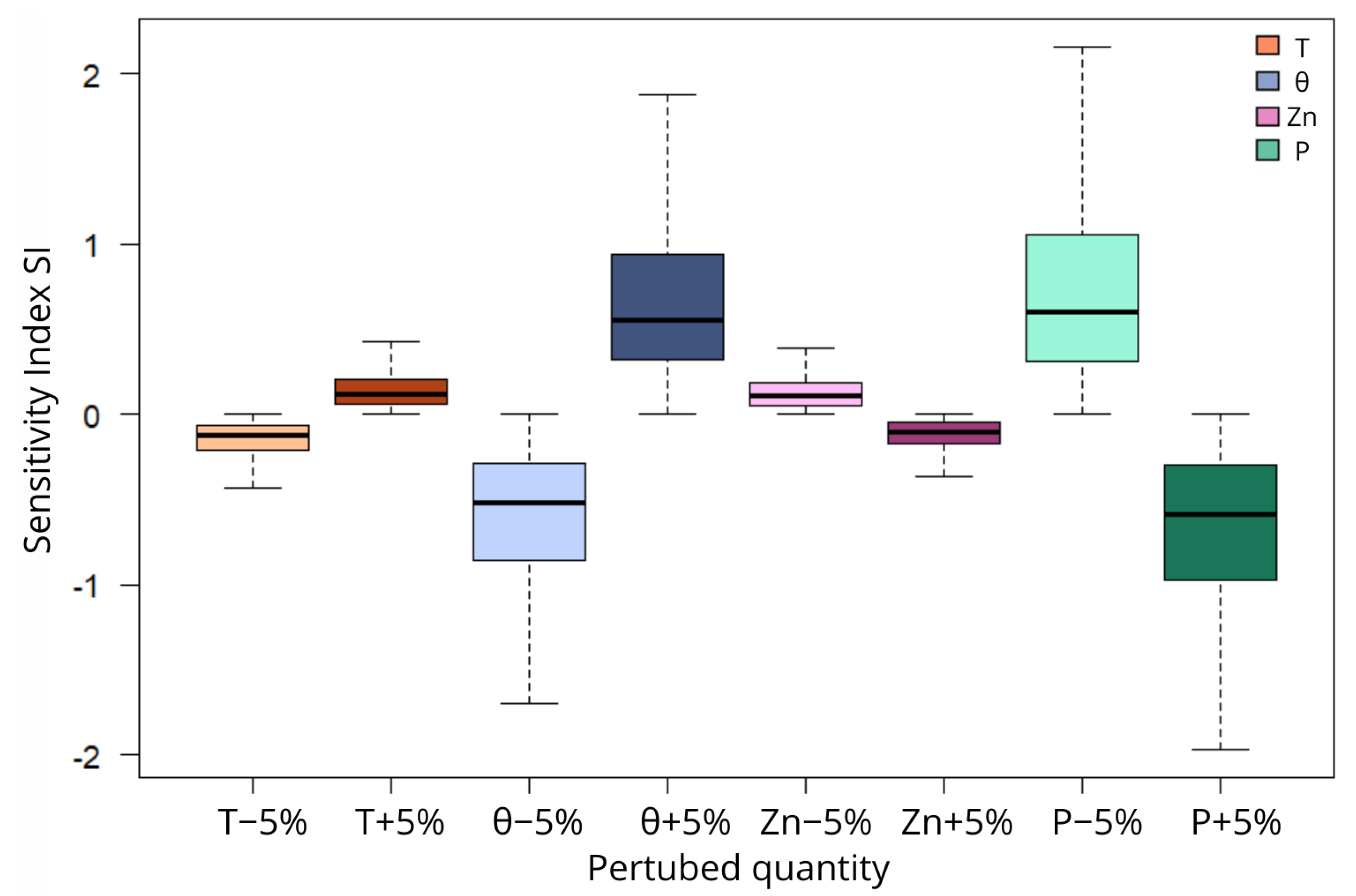
4. Sensitivity Analysis
5. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
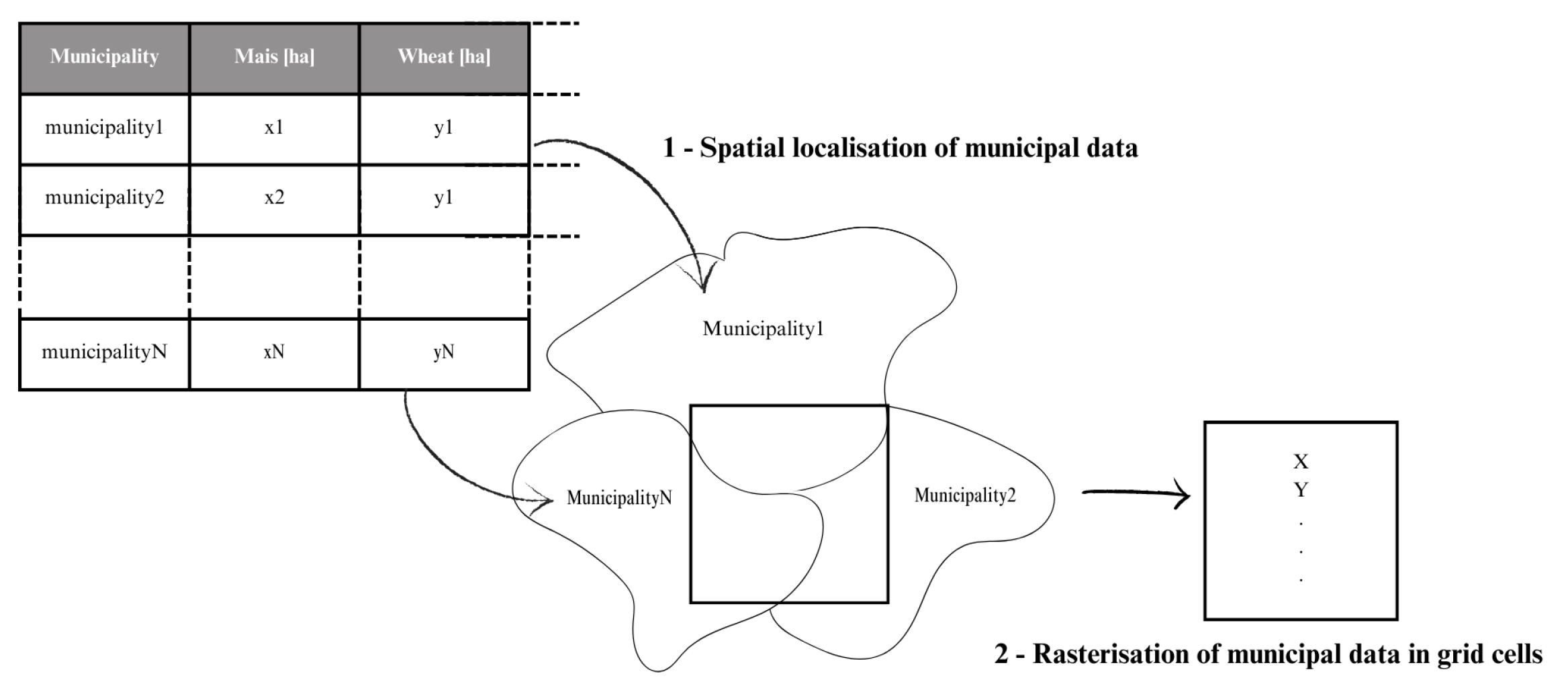
Appendix A. Data Pre-Processing

| Data Type | Variable | Dataset | Temporal Resolution | Spatial Resolution |
|---|---|---|---|---|
| Crop | Potential evapotranspiration | CRU 1 | month | 0.5° |
| p fraction 3 | - | year | 5 arc min | |
| FAO-56 4 | - | - | ||
| Soil | Available water content | Harmonized World 5 Soil Database v1.2 | year | 5 arc min |
| Pedologic characteristics 6 | - | - | - | |
| Soil type | LUCAS 7 | year | 500 m | |
| Climate | Climate zones | PAMDataset 8 | year | 5 arc min |
| Precipitation | ERA5 9 | hour | 0.25° | |
| Irrigation | Cultivated areas | CensimentoAgricoltura2010 2 | year | municipality |
| Irrigated areas | CensimentoAgricoltura2010 2 | year | municipality | |
| Irrigation system | CensimentoAgricoltura2010 2 | year | municipality | |
| Irrigation system efficiency 10 | - | - | - | |
| Municipalities extensions | ConfiniAmministrativi2010 2 | year | municipality |
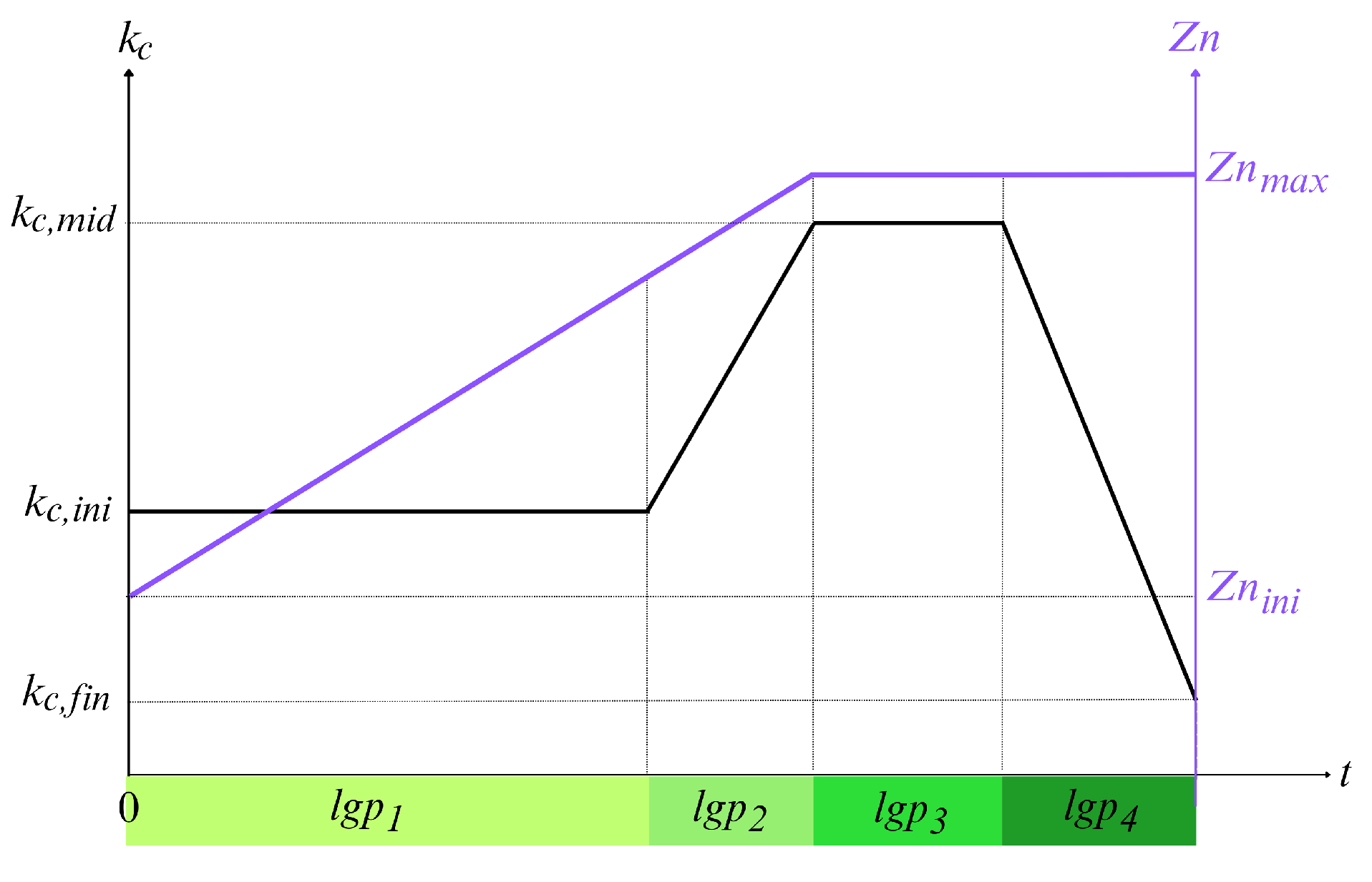
| Znini | Znmax | Dr* | kcini | kcmid | kcend |
|---|---|---|---|---|---|
| 0.3 | rf: 1.7 irr: 1 | 0.55 | 0.3 | 1.2 | 0.5 |
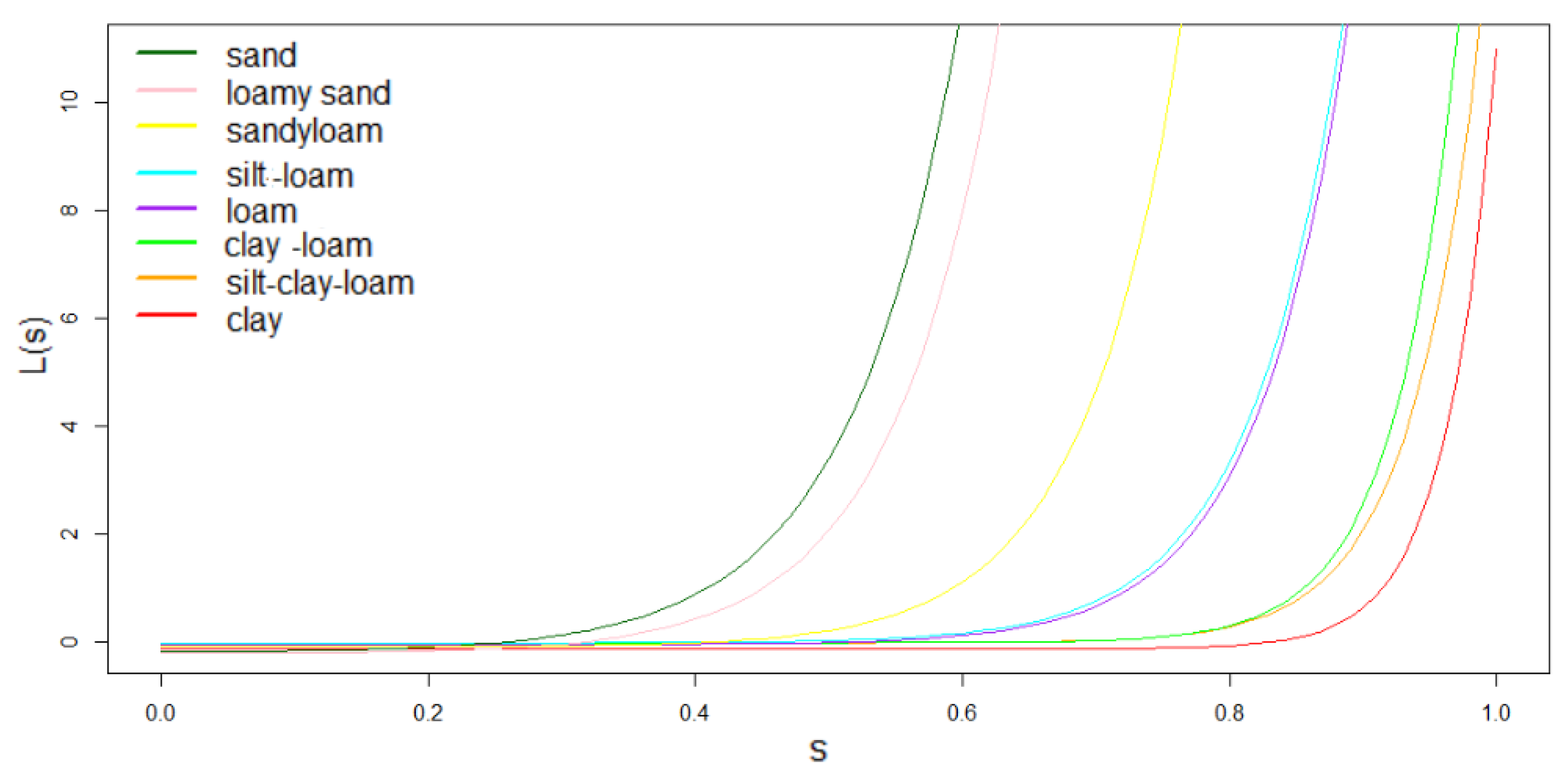
| Soil Class | [mm/h] | b | ||
|---|---|---|---|---|
| Silt–Clay–Loam | 0.0612 | 7.75 | 0.477 | 0.275 |
| Loam | 0.2502 | 5.39 | 0.451 | 0.225 |
| Loam–sand | 5.628 | 4.38 | 0.401 | 0.125 |
Appendix B. Trends of Root Growth and Crop and Stress Coefficient
References
- Rudebeck, T. Introducing Corporate Water Stewardship in the Context of Global Water Governance. In Water Governance—Concepts, Methods, and Practice; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Biswas, A.K.; Tortajada, C. Future Water Governance: Problems and Perspectives. Water Resour. Dev. 2010, 26, 129–139. [Google Scholar] [CrossRef]
- FAO. Water Auditing/Water Governance Analysis—Governance and Policy Support: Methodological Framework; FAO: Rome, Italy, 2024. [Google Scholar] [CrossRef]
- Cherlet, M.; Hutchinson, C.; Reynolds, J.; Hill, J.; Sommer, S.; von Maltitz, G. (Eds.) World Atlas of Desertification—Increasing Production; Publications Office of the European Union: Luxembourg, 2018. [Google Scholar] [CrossRef]
- Wu, B.; Tian, F.; Zhang, M.; Piao, S.; Zeng, H.; Zhu, W.; Liu, J.; Elnashar, A.; Lu, Y. Quantifying global agricultural water appropriation with data derived from earth observations. J. Clean. Prod. 2022, 358, 131891. [Google Scholar] [CrossRef]
- FAO. The State of the World’s Land and Water Resources for Food and Agriculture (SOLAW)—Managing Systems at Risk; Food and Agriculture Organization of the United Nations: Rome, Italy, 2011. [Google Scholar]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food security: The challenge of feeding 9 billion people. Science 2010, 327, 812–818. [Google Scholar] [CrossRef]
- Wallace, J. Increasing agricultural water use efficiency to meet future food production. Agric. Ecosyst. Environ. 2000, 82, 105–119. [Google Scholar] [CrossRef]
- Pfister, S.; Bayer, P.; Koehler, A.; Hellweg, S. Projected water consumption in future global agriculture: Scenarios and related impacts. Sci. Total Environ. 2011, 409, 4206–4216. [Google Scholar] [CrossRef]
- Vogel, E.; Donat, M.G.; Alexander, L.V.; Meinshausen, M.; Ray, D.K.; Karoly, D.; Meinshausen, N.; Frieler, K. The effects of climate extremes on global agricultural yields. Environ. Res. Lett. 2019, 14, 054010. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. Climate change impacts on the hydrological cycle. Ecohydrol. Hydrobiol. 2008, 8, 195–203. [Google Scholar] [CrossRef]
- Stagl, J.; Mayr, E.; Koch, H.; Hattermann, F.; Huang, S. Effects of Climate Change on the Hydrological Cycle in Central and Eastern Europe. In Managing Protected Areas in Central and Eastern Europe Under Climate Change; Rannow, S., Neubert, M., Eds.; Advances in Global Change Research; Springer: Berlin/Heidelberg, Germany, 2014; Volume 58. [Google Scholar] [CrossRef]
- Ma, J.; Zhou, L.; Foltz, G.R.; Qu, X.; Ying, J.; Tokinaga, H.; Mechoso, C.R.; Li, J.; Gu, X. Hydrological cycle changes under global warming and their effects on multiscale climate variability. Ann. N. Y. Acad. Sci. 2020, 1472, 21–48. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, L. The Impacts of Climate Change on the Hydrological Cycle and Water Resource Management. Water 2019, 15, 2342. [Google Scholar] [CrossRef]
- Peters-Lidard, C.D.; Rose, K.C.; Kiang, J.E.; Strobel, M.L.; Anderson, M.L.; Byrd, A.R.; Kolian, M.J.; Brekke, L.D.; Arndt, D.S. Indicators of climate change impacts on the water cycle and water management. Clim. Change 2021, 165, 36. [Google Scholar] [CrossRef]
- Wriedt, G.; der Velde, M.V.; Aloe, A.; Bouraoui, F. Estimating irrigation water requirements in Europe. J. Hydrol. 2009, 373, 527–544. [Google Scholar] [CrossRef]
- Fellmann, T. The assessment of climate change-related vulnerability in the agricultural sector: Reviewing conceptual frameworks. Build. Resil. Adapt. Clim. Change Agric. Sect. 2012, 23, 37. [Google Scholar]
- EUCAP-Network. Agricultural & Rural Inspiration Awards (ARIA); EU CAP Network: Saint-Josse-ten-Noode, Belgium, 2023. [Google Scholar]
- EUCAP-Network. Water Efficiency Benefits Flow from CAP Strategic Plans; EU CAP Network: Saint-Josse-ten-Noode, Belgium, 2024; pp. 1–172. [Google Scholar]
- Hayashi, A.; Akimoto, K.; Tomoda, T.; Kii, M. Global evaluation of the effects of agriculture and water management adaptations on the water-stressed population. Mitig. Adapt. Strateg. Glob. Change 2013, 18, 591–618. [Google Scholar] [CrossRef]
- Pereira, L.S. Agriculture and Food: Challenges and Issues. Water Resour Manag. 2017, 31, 2985–2999. [Google Scholar] [CrossRef]
- Díaz, J.A.R.; Perea, R.G.; Ángel Moreno, M. Modelling and Management of Irrigation System. Water 2020, 12, 697. [Google Scholar] [CrossRef]
- Maton, L.; Leenhardt, D.; Goulard, M.; Bergez, J.E. Assessing the irrigation strategies over a wide geographical area from structural data about farming systems. Agric. Syst. 2005, 86, 293–311. [Google Scholar] [CrossRef]
- Cancela, J.; Cuesta, T.; Neira, X.; Pereira, L. Modelling for Improved Irrigation Water Management in a Temperate Region of Northern Spain. Biosyst. Eng. 2006, 94, 151–163. [Google Scholar] [CrossRef]
- Singh, A. Irrigation Planning and Management Through Optimization Modelling. Water Resour. Manag. 2014, 28, 1–14. [Google Scholar] [CrossRef]
- Olivera-Guerra, L.E.; Laluet, P.; Altés, V.; Ollivier, C.; Pageot, Y.; Paolini, G.; Chavanon, E.; Rivalland, V.; Boulet, G.; Villar, J.M.; et al. Modeling actual water use under different irrigation regimes at district scale: Application to the FAO-56 dual crop coefficient method. Agric. Water Manag. 2023, 278, 108119. [Google Scholar] [CrossRef]
- Salman, M.; García-Vila, M.; Fereres, E.; Raes, D.; Steduto, P. The AquaCrop Model—Enhancing Crop Water Productivity. In Ten Years of Development, Dissemination and Implementation 2009–2019; FAO Water Report; FAO: Rome, Italy, 2021. [Google Scholar] [CrossRef]
- Kroes, J.; van Dam, J.; Bartholomeus, R.; Groenendijk, P.; Heinen, M.; Hendriks, R.; Mulder, H.; Supit, I.; van Walsum, P. SWAP version 4; Theory description and user manual. In Wageningen Environmental Research, Report 2780; Wageningen Environmental Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Jones, J.; Hoogenboom, G.; Porter, C.; Boote, K.; Batchelor, W.; Hunt, L.; Wilkens, P.; Singh, U.; Gijsman, A.; Ritchie, J. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO—Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Allen, R.; Droogers, P.; D’Urso, G.; Steduto, P. Twenty-five years modeling irrigated and drained soils: State of the art. Agric. Water Manag. 2007, 92, 111–125. [Google Scholar] [CrossRef]
- Lazarovitch, N.; Kisekka, I.; Oker, T.E.; Brunetti, G.; Wöhling, T.; Xianyue, L.; Yong, L.; Skaggs, T.H.; Furmanj, A.; Sasidharank, S.; et al. Chapter Two—Modeling of irrigation and related processes with HYDRUS. Adv. Agron. 2023, 181, 79–181. [Google Scholar] [CrossRef]
- Schaphoff, S.; von Bloh, W.; Rammig, A.; Thonicke, K.; Biemans, H.; Forkel, M.; Gerten, D.; Heinke, J.; Jägermeyr, J.; Knauer, J.; et al. LPJmL4—A dynamic global vegetation model with managed land—Part 1: Model description. Geosci. Model Dev. 2018, 11, 1343–1375. [Google Scholar] [CrossRef]
- Hanasaki, N.; Yoshikawa, S.; Pokhrel, Y.; Kanae, S. A global hydrological simulation to specify the sources of water used by humans. Hydrol. Earth Syst. Sci. 2018, 22, 789–817. [Google Scholar] [CrossRef]
- Chiarelli, D.D.; Passera, C.; Rosa, L.; Davis, K.F.; D’Odorico, P.; Rulli, M.C. The green and blue crop water requirement WATNEEDS model and its global gridded outputs. Sci. Data 2020, 7, 273. [Google Scholar] [CrossRef] [PubMed]
- Doell, P.; Siebert, S. Global modeling of irrigation water requirements. Water Resour. Res. 2002, 38, 8-1–8-10. [Google Scholar] [CrossRef]
- Tuninetti, M.; Tamea, S.; D’Odorico, P.; Laio, F.; Ridolfi, L. Global sensitivity of high-resolution estimates of crop water footprint. Water Resour. Res. 2015, 51, 8257–8272. [Google Scholar] [CrossRef]
- Jackson, R.D.; Hatfield, J.L.; Reginato, R.J.; Idso, S.B.; Pinter, P.J.J. Estimation of daily evapotranspiration from one-time-of-day measurements. Agric. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and responce to water stress II. Probabilistic soil moisture dynamics. Adv. Water Res. 2002, 24, 707–723. [Google Scholar] [CrossRef]
- ISTAT. 6th General Agricultural Census: Use of Water Resources for Irrigation Purpuses in Agriculture (6° Censimento Generale dell’Agricoltura: UTILIZZO DELLA RISORSA IDRICA A FINI IRRIGUI IN AGRICOLTURA). STEALTH. 2014. Available online: https://www.istat.it/it/files/2014/11/Utilizzo_risorsa_idrica.pdf (accessed on 12 September 2025).
- Lupia, F.; Vanino, S.; Santis, F.D.; Laruccia, N. A Model-Based Irrigation Water Consumption Estimation at Farm Level; INEA: Vienna, Austria, 2013. [Google Scholar]
- Katerji, N.; Campi, P.; Mastrorilli, M. Productivity, evapotranspiration, and water use efficiency of corn and tomato crops simulated by AquaCrop under contrasting water stress conditions in the Mediterranean region. Agric. Water Manag. 2013, 130, 14–26. [Google Scholar] [CrossRef]
- Bocchiola, D.; Nana, E.; Soncini, A. Impact of climate change scenarios on crop yield and water footprint of maize in the Po valley of Italy. Agric. Water Manag. 2013, 116, 50–61. [Google Scholar] [CrossRef]
- Casa, R.; Rossi, M.; Sappa, G.; Trotta, A. Assessing Crop Water Demand by Remote Sensing and GIS for the Pontina Plain, Central Italy. Water Resour Manag. 2009, 23, 1685–1712. [Google Scholar] [CrossRef]
- Todisco, F.; Vergni, L. Climatic changes in Central Italy and their potential effects on corn water consumption. Agric. For. Meteorol. 2008, 148, 1–11. [Google Scholar] [CrossRef]
- ISPRA. Indicators of Italian Climate in 2020 (Gli Indicatori del Clima in Italia del 2020). 2021. Available online: https://www.isprambiente.gov.it/it/pubblicazioni/stato-dellambiente/rapporto_clima_2020-1.pdf (accessed on 12 September 2025).
- Coppola, E.; Giorgi, F. An assessment of temperature and precipitation change projections over Italy from recent global and regional climate model simulations. Int. J. Climatol. 2010, 30, 11–32. [Google Scholar] [CrossRef]
- MIPAAF. Metodologia di Stima degli Utilizzi e Delle Restituzioni; Technical Report; Ministry of Agriculture, Food Sovereignty and Forestry: Rome, Italy, 2016. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Harris, I.; Osborn, T.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Mekonnen, M.M.; Hoekstra, A.Y. The green, blue and grey water footprint of crops and derived crop products. Hydrol. Earth Syst. Sci. 2011, 15, 1577–1600. [Google Scholar] [CrossRef]
- Fischer, G.; Nachtergaele, F.; Prieler, S.; van Velthuizen, H.; Verelst, L.; Wiberg, D. Global Agro-Ecological Zones Assessment for Agriculture; IIASA: Laxenburg, 2008; Volume 10. [Google Scholar]
- Clapp, R.; Hornberger, G. Empirical Equations for Some Soil Hydraulic Properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef]
- Ballabio, C.; Panagos, P.; Monatanarella, L. Mapping topsoil physical properties at European scale using the LUCAS database. Geoderma 2016, 261, 110–123. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Sabater, J.M.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1940 to present. Copernic. Clim. Change Serv. (C3S) 2023, 10. [Google Scholar] [CrossRef]
- Pereira, L.; Paredes, P.; Melton, F.; Johnson, L.; Wang, T.; López-Urrea, R.; Cancela, J.; Allen, R. Prediction of crop coefficients from fraction of ground cover and height. Background and validation using ground and remote sensing data. Agric. Waer Manag. 2020, 241, 106197. [Google Scholar] [CrossRef]
- Portmann, F.; Siebert, S.; Döll, P. MIRCA2000—Global monthly irrigated and rainfed crop areas around the year 2000: A new high-resolution data set for agricultural and hydrological modeling. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]


| Variable | Description | Unit |
|---|---|---|
| d | Day | day number |
| Dr* | Critical depletion fraction | m |
| ET0 | Potential evapotranspiration | mm/hour |
| ETa | Actual evapotranspiration | mm/hour |
| I | Irrigation | mm/day |
| Ib | Blue water requirement | mm/day |
| Imz | Maize irrigation water demand | mm/day |
| h | Hour | hour |
| H | Time enlapsed since sunrise | hour |
| kc | Crop coefficient | - |
| kc,fin | Crop coefficient at the end of the growing season | - |
| kc,ini | Crop coefficeint at the beginning of the growing season | - |
| kc,mid | Crop coefficient at plant maturity | - |
| ks | Water stress coefficient | - |
| ks,sat | Saturated hydraulic conductivity | m/s |
| L | Leakage | mm/hour |
| lgp | Length of the growing period | days |
| N | Number of hours between sunrise and sunset | hour |
| q | Generic quantity | - |
| P | Precipitation | mm/hour |
| Peff | Effective Precipitation | mm/hour |
| R | Runoff | mm/hour |
| s | Relative soil moisture | - |
| sfc | Relative soil moisture at field capacity | - |
| sr | Sunrise time | hour of day |
| ss | Sunset time | hour of day |
| SIq | Sensitivity Index | - |
| t | time | hour |
| T | Canopy interception | mm/hour |
| Vsoii | Soil volume | m3 |
| WC | Soil water content | m |
| WCfc | Soil water content at field capacity | m |
| WCsat | Soil water content at saturation | m |
| WCth | Soil water content at a chosen water content threshold | m |
| WCwp | Soil water content at wilting point | m |
| WC* | Soil water content at critical point | m |
| y | Irrigation system | - |
| Znini | Sowing depth | m |
| Znmax | Maximum Root depth | m |
| Irrigation inefficiency of the irrigation system | - | |
| Soil-dependent coefficient | - | |
| Volumetric water content at field capacity | m/m | |
| Volumetric water content at saturation | m/m | |
| Volumetric water content at critical point | m/m |
| Variable | Description | Initial Value | Variation | Final Value | National Water Demand Variation | National SIv |
|---|---|---|---|---|---|---|
| Znfin | Maximum rooting depth | 1 m | ± 5% | 1.05/0.95 | −0.83%/+0.84 % | −0.166/+0.168 |
| Relative soil water content at field capacity | 0.275 (silt–clay–loam) | ± 5% | 0.28875/0.26125 | +4.44%/−4.13% | +0.88/−0.826 | |
| 0.225 (loam) | ± 5% | 0.23625/0.21375 | ||||
| 0.125 (loam–sand) | ± 5% | 0.13125/0.118 | ||||
| T | Interception | 0.5 mm | ± 5% | 0.525/0.475 | +1.03%/−1.00% | +0.206/−0.2 |
| P | Precipitation | site- and hour-specific | ± 5% | site- and hour-specific | −5.10%/+5.53 % | −1.02/+1.106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiesa Turiano, N.; Tuninetti, M.; Laio, F.; Ridolfi, L. Evaluating Country-Scale Irrigation Demand Through Parsimonious Agro-Hydrological Modeling. Hydrology 2025, 12, 240. https://doi.org/10.3390/hydrology12090240
Chiesa Turiano N, Tuninetti M, Laio F, Ridolfi L. Evaluating Country-Scale Irrigation Demand Through Parsimonious Agro-Hydrological Modeling. Hydrology. 2025; 12(9):240. https://doi.org/10.3390/hydrology12090240
Chicago/Turabian StyleChiesa Turiano, Nike, Marta Tuninetti, Francesco Laio, and Luca Ridolfi. 2025. "Evaluating Country-Scale Irrigation Demand Through Parsimonious Agro-Hydrological Modeling" Hydrology 12, no. 9: 240. https://doi.org/10.3390/hydrology12090240
APA StyleChiesa Turiano, N., Tuninetti, M., Laio, F., & Ridolfi, L. (2025). Evaluating Country-Scale Irrigation Demand Through Parsimonious Agro-Hydrological Modeling. Hydrology, 12(9), 240. https://doi.org/10.3390/hydrology12090240






