Abstract
The proper development of groundwater resources is very important in many parts of the world. Its planning requires mathematical simulation of groundwater flows. Simulation can be either analytical or numerical. Analytical tools, when available, require fewer computational resources, but they are usually based on more assumptions, at the conceptual level, which restrict their applicability. In this paper, we aim to check the applicability of one-dimensional analytical solutions for groundwater flows through non-homogeneous aquifers, which are bound by two constant head and two impermeable boundaries and bear many zones of different transmissivities. These solutions are based on the stepwise inclusion of neighboring zones to larger ones, with equivalent transmissivity coefficients. We compare analytical results with numerical ones, obtained from a two-dimensional numerical model. We have selected the boundary element method (BEM) for this task. BEM is very versatile in solving steady-state groundwater flow problems, since discretization is restricted to external and internal field boundaries only. This feature fits perfectly with our research, which requires flow velocities at the boundaries only. Our research shows that analytical results can serve as upper and lower limits of total inflow. If the differences between the transmissivities of adjacent zones are small, they can be used in preliminary calculations too.
1. Introduction
Water demand is increasing worldwide, mainly because of population growth and climate change. This trend makes the proper development of groundwater resources even more important. Problems related to aquifer restoration and to control of high groundwater levels should be properly addressed as well.
Dealing with all these problems requires mathematical simulations of the respective groundwater flows. The first step is to construct the conceptual model of the aquifer system with adequate but not excessive detail. The question is “what adequate detail means”, in particular in complex systems, such as aquifers, where rock properties are quite variable (de Marsily et al. [1]). A theoretical background to answer this question was offered by Plato [2] in the 5th century BCE, who stated that our approach to nature is just a plausible account or description.
Then, the conceptual model should be expressed in mathematical terms, in order to allow the prediction of the response of the studied system to natural or man-induced changes. Finally, the mathematical model should be solved analytically or numerically to obtain answers to the questions posed. In all these steps, the assumptions made should be clear.
One decision made at the conceptual level has to do with aquifer homogeneity. In principle, no aquifer is homogeneous [3,4]. The modeling of heterogeneity depends on the available field data and computational resources and on the accuracy sought. In this paper, we deal with confined groundwater flows through non-homogeneous aquifers, which bear many zones of different hydraulic conductivities. Alluvial aquifers can exhibit such a structure, in particular in earthquake-prone areas, where vertical movements of parts of successive horizontal layers may occur along fractures.
The fictitious aquifer used in our study is bound by two constant head and two impermeable boundaries. We aim at checking the efficiency of one-dimensional analytical solutions in calculating flow rates, at least approximately. These solutions are based on stepwise inclusion of neighboring zones to larger ones, with equivalent transmissivity coefficients. Their main advantage is low computational volume. This advantage is very important when simulation models are combined with evolutionary optimization techniques, such as genetic algorithms [5]. Nevertheless, the assumption of one-dimensional flow may severely compromise their accuracy. Hence, accuracy checks are necessary. Following a well-known practice, e.g., [6], we compare analytical results with numerical ones, obtained from a two-dimensional numerical model.
To solve the two-dimensional flow problem numerically, we have selected the boundary element method (BEM). This method is very versatile in solving steady-state groundwater flow problems, since discretization is restricted to external and internal field boundaries only. This feature fits perfectly with our research, which requires the calculation of flow velocities at a restricted number of points. Application of the method is further explained in Section 2.1.
During the comparison of analytical and numerical results, one should keep in mind that numerical results are inherently approximate too.
2. The Groundwater Flow Simulation Models
2.1. Numerical Flow Simulation—A Short Outline of the Boundary Element Method
The BEM, which has been chosen for the numerical simulation of the groundwater flow, is based on the second Green’s formula. As mentioned above, it requires discretization of the external and internal field boundaries only. On these boundaries, the potential, φ, and its derivative, q, along the normal direction n (), are calculated. Based on these, the required values are calculated separately at any point at the interior of the calculation field, without interpolation between values at adjacent nodes.
The method gained popularity in 1970s, when relevant books appeared, e.g., [7]. Since then, BEM has been used extensively to solve problems described mathematically by the Laplace or the Poisson equation. Application areas include acoustics, e.g., Kirkup [8], electromagnetics, e.g., Kleanthous et al. [9], friction, e.g., Xu and Jackson [10], elasticity, etc. They include steady-state groundwater flows, as well. In these flows, φ represents hydraulic heads (expressed in units of length) and q represents their non-dimensional derivatives normal to the respective boundary element. Internal field boundaries may include interfaces between zones of different transmissivities, open fractures, (which allow water to move with large velocities), and healed fractures, which act as thin flow barriers [11]. BEM applications to groundwater flows are numerous. Some of them deal with the estimation of aquifer parameters, e.g., El Harrouni et al. [12], Lesnic et al. [13], Katsifarakis et al. [14], or with complex aquifer features (e.g., Luo et al. [15]). Meanwhile, the method’s efficacy has been improved, and its application field has been extended, e.g., Liu et al. [16], Zabala et al. [17]. Moreover, new books on the method have been authored during the last decade, e.g., Katsikadelis [18] and Gwinner and Stephan [19].
The boundary element code, which is used in this paper, is based on constant boundary elements, in which φ and q values are calculated at the respective nodes (middle points of each element). It has been extensively tested by the authors in previous applications to zoned aquifers and its accuracy was satisfactory. Interfaces between zones are discretized exactly as the outer boundary. The number of boundary elements (or of the respective nodes) on the external boundary is equal to N, while on the interfaces it is equal to M. So, the total number of nodes is N + M. Their numbering is accomplished following the zone pattern: First, all the nodes of zone 1 on its external and internal boundaries are numbered consecutively. Then the remaining nodes of zone 2 are numbered and so on. Data include coordinates of the endpoints of the boundary elements, their type (constant head, impermeable, interface), and the zone(s) to which they belong.
2.2. Analytical Groundwater Flow Simulation
Analytical solutions for groundwater flows are rather few, mostly for one-dimensional or radial flows in homogeneous aquifers, or aquifers to which the method of images can be applied. According to Darcy law, the flow velocity Vx along direction x through a homogeneous porous medium is given as
In Equation (1), K is the hydraulic conductivity (referred also as permeability) of the porous medium and φ is the hydraulic head. Combining Equation (1) with the continuity equation, we get
In Equation (2) QUx is the flow rate through an aquifer cross-section of thickness b and of unit width, and T is the aquifer’s transmissivity, namely T = K∙b.
For heterogenous aquifers consisting of any number of parallel zones with different hydraulic conductivities, equivalent hydraulic conductivity coefficients can be defined, depending on the direction of flow with respect to that of the zones, e.g., Polubarinova- Kochina [20] and Freeze and Cherry [4], who studied layered vertical flows. For flows parallel or perpendicular to the zones, the respective coefficients and are given be Equations (3) and (4):
In Equations (3) and (4), nz is the number of zones, Ki is the hydraulic conductivity of zone i, and di its width. In Equation (3), which holds for flows parallel to the zones, di is measured in the direction perpendicular to the flow (direction y in Figure 1), while in Equation (4), which holds for flows perpendicular to the zones, di is measured in the direction of the flow (direction x in Figure 1). Moreover, d is the sum of all di that are involved in each calculation of mean.
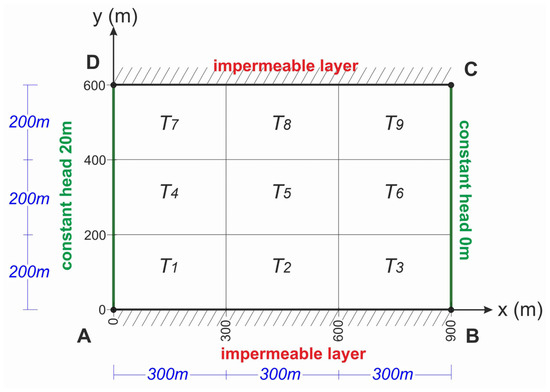
Figure 1.
The fictitious 9-zone aquifer (plan view).
Mathematically, represents the weighted arithmetic mean of Ki, while represents the weighted harmonic mean. In both cases, the widths di serve as weights. It is known that the arithmetic mean of n numbers is larger than the harmonic one of the same numbers, except for the trivial case [21].
Mathematically, vertical flow is not a prerequisite for using the aforementioned means. So, in this paper, we have extended their use to horizontal flows. Moreover, considering horizontal flow through zones of the same thickness (in the vertical direction), similar equations can be written for their transmissivities Ti, as follows:
In general, the introduction of means facilitates calculations and overall conclusions, at the expense of missing details, in our case exact values of hydraulic heads and flow velocities at particular points of the flow field. Our evaluation criterion is whether it allows an accurate calculation of the total flow through a given aquifer or, at least, useful upper and lower bounds of it. To this end, we study the fictitious aquifer, which is described in the following section.
3. The Fictitious Flow Field
Analytical and numerical simulations have been conducted for groundwater flows through the fictitious rectangular aquifer, shown in Figure 1. Its horizontal dimensions are 900 m and 600 m, in the x and y directions, respectively. Boundaries AB and CD are considered impermeable, while DA and BC exhibit constant heads, equal to 20 m and 0 m, respectively, considering that the reference datum coincides with the known surface water level along BC (being higher than the top of the aquifer, to ensure confined flow). It follows that the main flow is parallel to the x-axis (from DA towards BC).
The aquifer bears nine zones of different transmissivities Ti. Their values, for the basic problem configuration, appear in Table 1. The ratio of the largest to the smallest Ti is RT = Tmax/Tmin = 10. Regarding the dimensions of the zones, they are equal to 200 m and 300 m, respectively, as shown in Figure 1.

Table 1.
Zone transmissivities for the basic flow field configuration (in m2/s).
4. Simulation Results
4.1. Analytical Approach
Using Equation (5), namely considering flow parallel to the layers, we derive the following equivalent transmissivity values, for zones (1, 4, 7), (2, 5, 8) and (3, 6, 9):
The respective aquifer is shown in Figure 2. Then, using Equation (6) and the aforementioned values, we derive the overall Teq1 = 0.002024 m2/s.
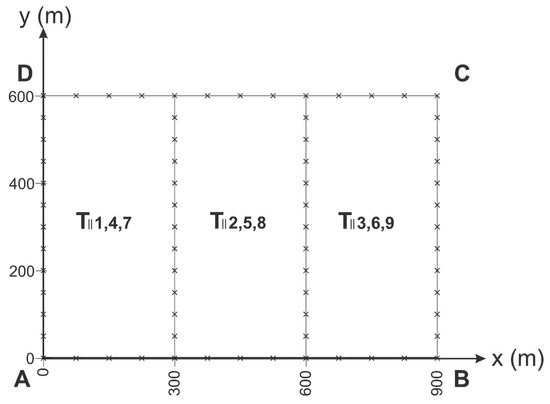
Figure 2.
The fictitious aquifer with three zones parallel to the y-axis and its boundary discretization, used in the numerical solution.
Then, we consider flow perpendicular to the layers first. We use Equation (6) to derive equivalent transmissivity values for zones (1, 2, 3), (4, 5, 6) and (7, 8, 9), and we get:
The respective aquifer is shown in Figure 3. Then, using Equation (5) and the aforementioned values, we derive the overall Teq2 = 0.001316 m2/s. It results that Teq1 is 53.8% larger than Teq2 (as a percentage of Teq2). Their difference is transferred to the calculation of the total incoming flow Qin, which is based on Equation (2). The respective values are: Qin1 = 0.02698 m3/s and Qin2 = 0.01754 m3/s.
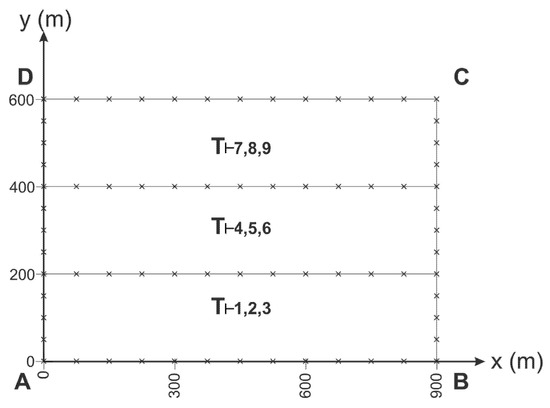
Figure 3.
The fictitious aquifer with three zones parallel to the x-axis and its boundary discretization, used in the numerical solution.
A physical explanation is that by using the equivalent transmissivity for the flow parallel to the layers, we implicitly take care of the perpendicular flow, along the aquifer’s width. So, it seems plausible to end up with larger total inflow values, compared to the other case. This issue is further discussed in Section 4.3.
Then, we repeat our calculations, rearranging the T values along x and y axis. The new configuration is shown in Table 2. Following the same procedure as previously, we end up with the following values: Teq1r = 0.002053 m2/s and Teq2r = 0.001254 m2/s. They result in the following total incoming flows: Qin1r = 0.02737 m3/s and Qin2r = 0.01672 m3/s.

Table 2.
Zone transmissivities for the rearranged flow field configuration (in m2/s).
4.2. Results of the BEM Simulation
To simulate groundwater flow through the aquifer of Figure 1, we have discretized its outer boundary to 48 boundary elements, using 12 on each side. Their length on constant head boundaries (BC and DA) is 50 m, while on impermeable boundaries (AB and CD) their length is 75 m. We have followed a similar pattern for the internal field boundaries (interfaces between zones of different transmissivity), which added 48 boundary elements, raising their total number to 96, as shown in Figure 4. The choice of the number of the boundary elements is briefly discussed in Appendix A.
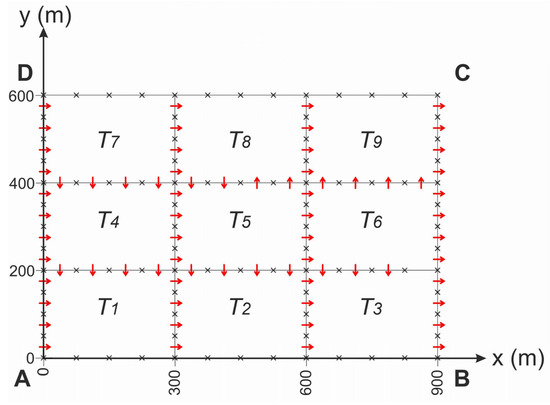
Figure 4.
Boundary discretization of the fictitious 9-zone aquifer. Arrows indicate the flow direction perpendicular to the respective boundary element.
As an initial check we simulated the homogeneous aquifer, using the transmissivity values Teq1 and Teq2. In both cases, the BEM code (using the same discretization as previously on the outer boundary) practically reproduced the Qin values of the analytical solution. This is a strong indication that its accuracy is good.
Then, we simulated the flow through the 9-zone aquifer. The results appear in Table A1. To investigate the accuracy of the results, we have checked if the water balance is observed, in the following way. We calculated, for each zone j, the non-dimensional ratio Prj of the sum of all (incoming and outgoing) flow rates to the sum of ingoing flow rates only. The results appear in Table 3. The largest absolute value is 0.00143. Moreover, PrT (for the aquifer as a whole) is −0.00000013. It can be concluded that there is no indication of inaccuracy.

Table 3.
Results of the accuracy check (non-dimensional Prj flux ratios) for the 9-zone aquifer.
The total flow through the constant head boundary DA is found to be QΒΕ9 = 0.02461 m3/s. The use of so many decimal digits in the results does not imply such a high accuracy. However, it facilitates comparisons and calculation of result precision.
In Figure 4, the arrows show the flow direction at each node, perpendicular to the respective boundary element. It can be seen that the flow along the y-axis is substantial, and that water generally moves from lower transmissivity zones to higher transmissivity ones.
Then, we simulated the flow through the 3-zone aquifers, which are shown in Figure 2 and Figure 3. The total inflows through boundary DA are QΒΕ3Y = 0.02728 m3/s and QΒΕ3X = 0.01788 m3/s, respectively.
We simulated also the 9-zone aquifer with the rearranged transmissivity values, which appear in Table 2. We found that the total flow through the constant head boundary DA is QΒΕ9r = 0.025454 m3/s.
4.3. Comparison of Analytical and Numerical Results
We compare the total inflow values obtained using the one-dimensional analytical model with the numerical ones. We see that for the 9-zone aquifer (and the basic flow field configuration) the following relationship holds:
Qin1 = 0.02698 m3/s > QΒΕ9 = 0.02461 m3/s > Qin2 = 0.01754 m3/s.
The relative errors (or rather discrepancies) between the numerical and the two analytical values are 9.6% and 28.7%, respectively.
A similar relationship holds for the 9-zone aquifer with the rearranged transmissivity values, which are shown in Table 2:
Qin1r = 0.02737 m3/s > QΒΕ9r = 0.02545 m3/s > Qin2r = 0.01672 m3/s.
In this case, the relative errors between the numerical and the two analytical values are 7.5% and 34.3%, respectively.
In both cases, the total inflow, resulting from the numerical solution, lies between the two values, obtained by analytical means. It is much closer, though, to QΒΕ3Y, which takes implicitly into account two-dimensional flow.
Regarding the 3-zone aquifers resulting from the basic field configuration, the numerical results are:
QΒΕ3Y = 0.02728 m3/s and QΒΕ3X = 0.01788 m3/s, for the aquifers of Figure 2 and Figure 3, respectively.
While for the 3-zone aquifers resulting from the transmissivity data of Table 2, the numerical results are:
QΒΕ3Yr = 0.02767 m3/s and QΒΕ3Xr = 0.01704 m3/s, for the aquifers of Figure 2 and Figure 3, respectively.
It can be seen that in both cases the difference between Qin1 and QΒΕ3Y is about 1%, while QΒΕ3X is about 2% larger than Qin2. While a difference of 1% could be attributed to numerical approximations, the additional 1% in the second case is probably due to the assumption of one-dimensional flow, made in the analytical model.
Additional Investigation
The aforementioned differences between QΒΕ9 and Qin1 (9.6% and 7.5%), which cannot be attributed to numerical approximations, deserve further investigation. To this end, we have used a 9-zone aquifer with very pronounced differences between Ti values. The latter are shown in Table 4. In this case, the ratio RT = Tmax/Tmin = 90, much larger than that of the previous case, where RT = 10.

Table 4.
Zone transmissivities for the additional flow field example (in m2/s).
Following the analytical procedure, described in Section 2.2, we find that Qin1L = 0.04596 m3/s and Qin2L = 0.01298 m3/s. Then, using the BEM code, we find that QΒΕ9L = 0.02597 m3/s. Their relationship has the same form as inequalities (7) and (8). Their differences are substantially larger, though, due to the larger differences between the Ti values and to the properties of Pythagorean means:
Qin1L = 0.04596 m3/s > QΒΕ9L = 0.025967 m3/s > Qin2L = 0.01298 m3/s.
The relative errors between the numerical and the two analytical values are 77.0% and 50.1%, respectively.
Moreover, the numerical results for the respective 3-zone aquifers are as follows:
QΒΕ3YL = 0.04647 m3/s and QΒΕ3XL = 0.01323 m3/s, respectively.
The additional results lead us to the following explanation of the differences between Qin1L, QΒΕ9L, and Qin2L: As mentioned above, Qin2L allows for one-dimensional flow only. So, it underestimates the total inflow. On the other hand, Qin1L overestimates total inflow, since it misses the actual tortuous path of least resistance followed by the water. The differences between the numerical and the analytical results increase with the differences between the transmissivities of aquifer zones.
5. Additional Discussion and Conclusions
The basic principle of Hydraulics could be stated as follows: Water flows from high hydraulic head (energy) areas towards low hydraulic head ones, following the path of smallest resistance. As a result, flow tends to skip low transmissivity aquifer zones and to concentrate into high transmissivity ones. So, heterogeneity leads to flow deviation from the direction indicated by the hydraulic head gradient. This effect is more pronounced if the shortest path from higher to lower head areas does not coincide with the highest transmissivity path between them. Its intensity depends on the transmissivity differences between adjacent zones. The numerical results, obtained using the BEM, follow this pattern of two-dimensional flow in the studied heterogeneous aquifers. This is an additional indication of their accuracy.
Regarding the analytical results, they can serve as upper and lower limits of total inflow. If the difference between them is small, they can be used in preliminary calculations, as well. To increase their accuracy, the following intuitive principle in the stepwise construction of the equivalent porous medium can be followed: Take the steps that lead to unification of zones with the smallest possible differences in their T values. This guideline is supported by the increased differences between Qin1 and Qin2, in the case of large Ti differences between aquifer zones. The ratio RT, mentioned in Section 3 and Section 4, could offer an applicability indication.
The analysis presented in this paper for groundwater flows can be extended to conductive heat flows through heterogeneous media, which are mathematically described by similar equations.
Author Contributions
Conceptualization, K.L.K.; methodology, K.L.K.; software, K.L.K. and Y.N.K.; numerical experiments O.K., Y.N.K. and K.L.K.; figure preparation Y.N.K. and O.K.; writing—original draft preparation, K.L.K. and Y.N.K.; writing—review and editing, K.L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new field data were created or analyzed in this study. The theoretical data used are presented in the paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
To simulate the fictitious 9-zone aquifer using the BEM, we have discretized the outer and inner boundaries in 96 elements, setting N = M = 48. Our choice was based on some initial trials, aimed at combining adequate accuracy with low computational volume. First, we used one boundary element at each zone side. Then, we tried two elements per zone side. For this discretization (N = M = 24), we obtained very good results in the accuracy check (max Prj < 0.004). The total flow through boundary DA was equal to 0.02593 m3/s. Then, we used four elements per zone side (N = M = 48). The total flow through DA was quite close to the previous one, while the accuracy check gave excellent results, as mentioned in Section 4.2. So, we concluded that no further refinement was necessary.
Table A1 includes the detailed results of the numerical simulation of the flow through the 9-zone aquifer, for the basic problem configuration (and for N = M = 48). The calculated φ and q values are given per zone.

Table A1.
Values of φ (in m), (non-dimensional) and flow rates through each boundary element (in m3/s) at the external and internal field boundaries of the 9-zone aquifer.
Table A1.
Values of φ (in m), (non-dimensional) and flow rates through each boundary element (in m3/s) at the external and internal field boundaries of the 9-zone aquifer.
| Node | φ (m) | q (-) | Flow Rate (m3/s) |
|---|---|---|---|
| Zone 1 | |||
| 1 (37.5, 0.0) | 19.04 | 0.0000 | 0.0000 |
| 2 (112.5, 0.0) | 16.90 | 0.0000 | 0.0000 |
| 3 (187.5, 0.0) | 14.68 | 0.0000 | 0.0000 |
| 4 (262.5,0.0) | 12.28 | 0.0000 | 0.0000 |
| 5 (300.0, 25.0) | 11.14 | −0.0371 | −0.00186 |
| 6 (300.0, 75.0) | 11.23 | −0.0323 | −0.00162 |
| 7 (300.0, 125.0) | 11.40 | −0.0326 | −0.00163 |
| 8 (300.0, 175.0) | 11.67 | −0.0405 | −0.00203 |
| 9 (262.5, 200.0) | 13.11 | 0.0116 | 0.00087 |
| 10 (187.5, 200.0) | 15.29 | 0.0062 | 0.00047 |
| 11 (112.5, 200.0) | 17.27 | 0.0037 | 0.00028 |
| 12 (37.5, 200.0) | 19.16 | 0.0011 | 0.00008 |
| 13 (0.0, 175.0) | 20.00 | 0.0273 | 0.00137 |
| 14 (0.0, 125.0) | 20.00 | 0.0252 | 0.00126 |
| 15 (0.0, 75.0) | 20.00 | 0.0259 | 0.00130 |
| 16 (0.0, 25.0) | 20.00 | 0.0304 | 0.00152 |
| Zone 2 | |||
| 5 (300.0, 25.0) | 11.14 | 0.0074 | 0.00186 |
| 6 (300.0, 75.0) | 11.23 | 0.0065 | 0.00162 |
| 7 (300.0, 125.0) | 11.40 | 0.0065 | 0.00163 |
| 8 (300.0, 175.0) | 11.67 | 0.0081 | 0.00203 |
| 17 (337.5, 0.0) | 10.88 | 0.0000 | 0.0000 |
| 18 (412.5, 0.0) | 10.19 | 0.0000 | 0.0000 |
| 19 (487.5, 0.0) | 9.35 | 0.0000 | 0.0000 |
| 20 (562.5, 0.0) | 8.36 | 0.0000 | 0.0000 |
| 21 (600.0, 25.0) | 7.86 | −0.0163 | −0.00407 |
| 22 (600.0, 75.0) | 7.92 | −0.0143 | −0.00358 |
| 23 (600.0, 125.0) | 8.04 | −0.0147 | −0.00367 |
| 24 (600.0, 175.0) | 8.23 | −0.0190 | −0.00474 |
| 25 (562.5, 200.0) | 8.95 | 0.0081 | 0.00304 |
| 26 (487.5, 200.0) | 9.83 | 0.0039 | 0.00147 |
| 27 (412.5, 200.0) | 10.70 | 0.0043 | 0.00159 |
| 28 (337.5, 200.0) | 11.56 | 0.0076 | 0.00285 |
| Zone 3 | |||
| 21 (600.0, 25.0) | 7.86 | 0.0272 | 0.00407 |
| 22 (600.0, 75.0) | 7.92 | 0.0239 | 0.00358 |
| 23 (600.0, 125.0) | 8.04 | 0.0245 | 0.00367 |
| 24 (600.0, 175.0) | 8.23 | 0.0316 | 0.00474 |
| 29 (637.5, 0.0) | 6.99 | 0.0000 | 0.0000 |
| 30 (712.5, 0.0) | 5.01 | 0.0000 | 0.0000 |
| 31 (787.5, 0.0) | 2.99 | 0.0000 | 0.0000 |
| 32 (862.5, 0.0) | 0.94 | 0.0000 | 0.0000 |
| 33 (900.0, 25.0) | 0.00 | −0.00298 | −0.00446 |
| 34 (900.0, 75.0) | 0.00 | −0.0258 | −0.00388 |
| 35 (900.0, 125.0) | 0.00 | −0.0259 | −0.00389 |
| 36 (900.0, 175.0) | 0.00 | −0.0300 | −0.00450 |
| 37 (862.5, 200.0) | 0.95 | 0.0000 | 0.00001 |
| 38 (787.5, 200.0) | 3.03 | 0.0001 | 0.00003 |
| 39 (712.5, 200.0) | 5.13 | 0.0005 | 0.00011 |
| 40 (637.5, 200.0) | 7.31 | 0.0023 | 0.00053 |
| Zone 4 | |||
| 9 (262.5, 200.0) | 13.11 | −0.0058 | −0.00087 |
| 10 (187.5, 200.0) | 15.29 | −0.0031 | −0.00047 |
| 11 (112.5, 200.0) | 17.27 | −0.0058 | −0.00028 |
| 12 (37.5, 200.0) | 19.16 | −0.0006 | −0.00008 |
| 41 (300.0, 225.0) | 12.25 | −0.0325 | −0.00325 |
| 42 (300.0, 275.0) | 12.61 | −0.0269 | −0.00269 |
| 43 (300.0, 325.0) | 12.99 | −0.0281 | −0.00281 |
| 44 (300.0, 375.0) | 13.42 | - 0.0442 | −0.00442 |
| 45 (262.5, 400.0) | 15.14 | 0.0254 | 0.00381 |
| 46 (187.5, 400.0) | 16.56 | 0.0085 | 0.00128 |
| 47 (112.5, 400.0) | 17.95 | 0.0044 | 0.00067 |
| 48 (37.5, 400.0) | 19.36 | 0.0012 | 0.00019 |
| 49 (0.0, 375.0) | 20.00 | 0.0210 | 0.00210 |
| 50 (0.0, 325.0) | 20.00 | 0.0202 | 0.00202 |
| 51 (0.0, 275.0) | 20.00 | 0.0216 | 0.00216 |
| 52 (0.0, 225.0) | 20.00 | 0.0265 | 0.00265 |
| Zone 5 | |||
| 25 (562.5, 200.0) | 8.95 | −0.0101 | −0.00304 |
| 26 (487.5, 200.0) | 9.83 | −0.0049 | −0.00147 |
| 27 (412.5, 200.0) | 10.70 | −0.0053 | −0.00159 |
| 28 (337.5, 200.0) | 11.55 | −0.0095 | −0.00285 |
| 41 (300.0, 225.0) | 12.25 | 0.0162 | 0.00325 |
| 42 (300.0, 275.0) | 12.61 | 0.0134 | 0.00269 |
| 43 (300.0, 325.0) | 12.99 | 0.0141 | 0.00281 |
| 44 (300.0, 375.0) | 13.42 | 0.0221 | 0.00442 |
| 53 (600.0, 225.0) | 8.94 | −0.0057 | −0.00114 |
| 54 (600.0, 275.0) | 9.23 | −0.0048 | −0.00097 |
| 55 (600.0, 325.0) | 9.35 | −0.0051 | −0.00102 |
| 56 (600.0, 375.0) | 9.27 | −0.0080 | −0.00159 |
| 57 (562.5, 400.0) | 9.48 | −0.0040 | −0.00120 |
| 58 (487.5, 400.0) | 10.42 | −0.0001 | −0.00004 |
| 59 (412.5, 400.0) | 11.53 | 0.0012 | 0.00035 |
| 60 (337.5, 400.0) | 12.88 | 0.0046 | 0.00138 |
| Zone 6 | |||
| 37 (862.5, 200.0) | 0.95 | −0.0001 | −0.00001 |
| 38 (787.5, 200.0) | 3.03 | −0.0008 | −0.00003 |
| 39 (712.5, 200.0) | 5.13 | −0.0028 | −0.00011 |
| 40 (637.5, 200.0) | 7.31 | −0.0141 | −0.00053 |
| 53 (600.0, 225.0) | 8.94 | 0.0458 | 0.00114 |
| 54 (600.0, 275.0) | 9.23 | 0.0386 | 0.00097 |
| 55 (600.0, 325.0) | 9.35 | 0.0409 | 0.00102 |
| 56 (600.0, 375.0) | 9.27 | 0.0636 | 0.00159 |
| 61 (900.0, 225.0) | 0.00 | −0.0301 | −0.00075 |
| 62 (900.0, 275.0) | 0.00 | −0.0261 | −0.00065 |
| 63 (900.0, 325.0) | 0.00 | −0.0258 | −0.00064 |
| 64 (900.0, 375.0) | 0.00 | −0.0288 | −0.00072 |
| 65 (862.5, 400.0) | 0.89 | −0.0007 | −0.00003 |
| 66 (787.5, 400.0) | 2.87 | −0.0026 | −0.00010 |
| 67 (712.5, 400.0) | 4.89 | −0.0058 | −0.00022 |
| 68 (637.5, 400.0) | 7.06 | −0.0253 | −0.00095 |
| Zone 7 | |||
| 45 (262.5, 400.0) | 15.14 | −0.0169 | −0.00381 |
| 46 (187.5, 400.0) | 16.56 | −0.0057 | −0.00128 |
| 47 (112.5, 400.0) | 17.95 | −0.0030 | −0.00067 |
| 48 (37.5, 400.0) | 19.36 | −0.0008 | −0.00019 |
| 69 (300.0, 425.0) | 15.14 | −0.0095 | −0.00143 |
| 70 (300.0, 475.0) | 15.73 | −0.0063 | −0.00094 |
| 71 (300.0, 525.0) | 16.08 | −0.0060 | −0.00091 |
| 72 (300.0, 575.0) | 16.24 | −0.0069 | −0.00103 |
| 73 (262.5, 600.0) | 16.51 | 0.0000 | 0.0000 |
| 74 (187.5, 600.0) | 17.30 | 0.0000 | 0.0000 |
| 75 (112.5, 600.0) | 18.32 | 0.0000 | 0.0000 |
| 76 (37.5, 600.0) | 19.46 | 0.0000 | 0.0000 |
| 77 (0.0, 575.0) | 20.00 | 0.0171 | 0.00256 |
| 78 (0.0, 525.0) | 20.00 | 0.0153 | 0.00229 |
| 79 (0.0, 475.0) | 20.00 | 0.0160 | 0.00240 |
| 80 (0.0, 425.0) | 20.00 | 0.0199 | 0.00299 |
| Zone 8 | |||
| 57 (562.5, 400.0) | 9.48 | 0.0319 | 0.00120 |
| 58 (487.5, 400.0) | 10.42 | 0.0011 | 0.00004 |
| 59 (412.5, 400.0) | 11.53 | −0.0093 | −0.00035 |
| 60 (337.5, 400.0) | 12.88 | −0.0368 | −0.00138 |
| 69 (300.0, 425.0) | 15.14 | 0.0572 | 0.00143 |
| 70 (300.0, 475.0) | 15.73 | 0.0376 | 0.00094 |
| 71 (300.0, 525.0) | 16.08 | 0.0362 | 0.00091 |
| 72 (300.0, 575.0) | 16.24 | 0.0413 | 0.00103 |
| 81 (600.0, 425.0) | 7.57 | −0.0484 | −0.00121 |
| 82 (600.0, 475.0) | 7.03 | −0.0335 | −0.00084 |
| 83 (600.0, 525.0) | 6.74 | −0.0329 | −0.00082 |
| 84 (600.0, 575.0) | 6.60 | −0.0380 | −0.00095 |
| 85 (562.5, 600.0) | 7.75 | 0.0000 | 0.0000 |
| 86 (487.5, 600.0) | 10.14 | 0.0000 | 0.0000 |
| 87 (412.5, 600.0) | 12.46 | 0.0000 | 0.0000 |
| 88 (337.5, 600.0) | 14.99 | 0.0000 | 0.0000 |
| Zone 9 | |||
| 65 (862.5, 400.0) | 0.89 | 0.0003 | 0.00003 |
| 66 (787.5, 400.0) | 2.87 | 0.0013 | 0.00010 |
| 67 (712.5, 400.0) | 4.89 | 0.0029 | 0.00022 |
| 68 (637.5, 400.0) | 7.06 | 0.0127 | 0.00095 |
| 81 (600.0, 425.0) | 7.57 | 0.0242 | 0.00121 |
| 82 (600.0, 475.0) | 7.03 | 0.0167 | 0.00084 |
| 83 (600.0, 525.0) | 6.74 | 0.0165 | 0.00082 |
| 84 (600.0, 575.0) | 6.60 | 0.0190 | 0.00095 |
| 89 (900.0, 425.0) | 0.00 | −0.0282 | −0.00141 |
| 90 (900.0, 475.0) | 0.00 | −0.0238 | −0.00119 |
| 91 (900.0, 525.0) | 0.00 | −0.0234 | −0.00117 |
| 92 (900.0, 575.0) | 0.00 | −0.027 | −0.00133 |
| 93 (862.5, 600.0) | 0.84 | 0.0000 | 0.0000 |
| 94 (787.5, 600.0) | 2.66 | 0.0000 | 0.0000 |
| 95 (712.5, 600.0) | 4.39 | 0.0000 | 0.0000 |
| 96 (637.5, 600.0) | 5.96 | 0.0000 | 0.0000 |
References
- de Marsily, G.; Delay, F.; Teles, V.; Schafmeister, M.T. Some current methods to represent the heterogeneity of natural media in hydrogeology. Hydrogeol. J. 1998, 6, 115–130. [Google Scholar] [CrossRef]
- Plato. Timaeus, 360 BC. Available online: https://scaife.perseus.org/reader/urn:cts:greekLit:tlg0059.tlg031.perseus-eng2:29 (accessed on 1 July 2025).
- Bear, J. Hydraulics of Groundwater; Dover Publications: Mineola, NY, USA, 1979. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall. Inc.: Englewood Cliffs, NJ, USA, 1979; pp. 30–34. [Google Scholar]
- Katsifarakis, K.L.; Petala, Z. Combining genetic algorithms and boundary elements to optimize coastal aquifers’ management. J. Hydrol. 2006, 327, 200–207. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N.; Tsihrintzis, V.A. Analytical Solutions and Simulation Approaches for Double Permeability Aquifers. Water Resour. Manag. 2009, 23, 395–415. [Google Scholar] [CrossRef]
- Brebbia, C.A. The Boundary Element Method for Engineers; Pentech Press: London, UK, 1978. [Google Scholar]
- Kirkup, S. The Boundary Element Method in Acoustics: A Survey. Appl. Sci. 2019, 9, 1642. [Google Scholar] [CrossRef]
- Kleanthous, A.; Baran, A.J.; Betcke, T.; Hewett, D.P.; Westbrook, C.D. An application of the boundary element method (BEM) to the calculation of the single-scattering properties of very complex ice crystals in the microwave and sub-millimetre regions of the electromagnetic spectrum. J. Quant. Spectrosc. Radiat. Transf. 2024, 312, 108793. [Google Scholar] [CrossRef]
- Xu, Y.; Jackson, R.L. Boundary element method (BEM) applied to the rough surface contact vs. BEM in computational mechanics. Friction 2019, 7, 359–371. [Google Scholar] [CrossRef]
- Katsifarakis, K.L. Boundary conditions for mathematical model of flows through fractured rocks. Adv. Water Resour. 1994, 17, 265–267. [Google Scholar] [CrossRef]
- El Harrouni, K.; Ouazar, D.; Walters, G.A.; Cheng, A.H.-D. Groundwater optimization and parameter estimation by genetic algorithm and dual reciprocity boundary element method. Eng. Anal. Bound. Elem. 1996, 18, 287–296. [Google Scholar] [CrossRef]
- Lesnic, D.; Elliott, L.; Ingham, D.B. A boundary element method for the determination of the transmissivity of a heterogeneous aquifer in groundwater flow systems. Eng. Anal. Bound. Elem. 1998, 21, 223–234. [Google Scholar] [CrossRef]
- Katsifarakis, K.L.; Karpouzos, D.K.; Theodossiou, N. Combined use of BEM and genetic algorithms in groundwater flow and mass transport problems. Eng. Anal. Bound. Elem. 1999, 23, 555–565. [Google Scholar] [CrossRef]
- Luo, W.; Wang, J.; Wang, L.; Zhou, Y. An alternative BEM for simulating the flow behavior of a leaky confined fractured aquifer with the use of the semianalytical approach. Water Resour. Res. 2020, 56, e2019WR026581. [Google Scholar] [CrossRef]
- Liu, Y.J.; Mukherjee, S.; Nishimura, N.; Schanz, M.; Ye, W.; Sutradhar, A.; Pan, E.; Dumont, N.A.; Frangi, A.; Saez, A. Recent Advances and Emerging Applications of the Boundary Element Method. ASME. Appl. Mech. Rev. 2011, 64, 030802. [Google Scholar] [CrossRef]
- Zabala, I.; Henriques, J.C.C.; Kelly, T.E.; Ricci, P.P.; Blanco, J.M. Post-processing techniques to improve the results of hydrodynamic Boundary Element Method solvers. Ocean Eng. 2024, 295, 116913. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. The Boundary Element Method for Engineers and Scientists. Theory and Applications, 2nd ed.; Elsevier: London, UK, 2016. [Google Scholar]
- Gwinner, J.; Stephan, E.P. Advanced Boundary Element Methods. Treatment of Boundary Value, Transmission and Contact Problems; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Polubarinova-Kochina, P.Y. Theory of Groundwater Movement; Roger De Wiest, J.M., Translator; Princeton University Press: Princeton, NJ, USA, 1962; Chapter 8. [Google Scholar]
- Chakrabarty, D. Extended Inequality Satisfied by Pythagorean Classical Means. Partn. Univ. Int. Innov. J. 2024, 2, 13–18. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).