Effect of Storm Event Duration on the Indices of Concentration Discharge Hysteresis
Abstract
1. Introduction
2. Materials and Methods
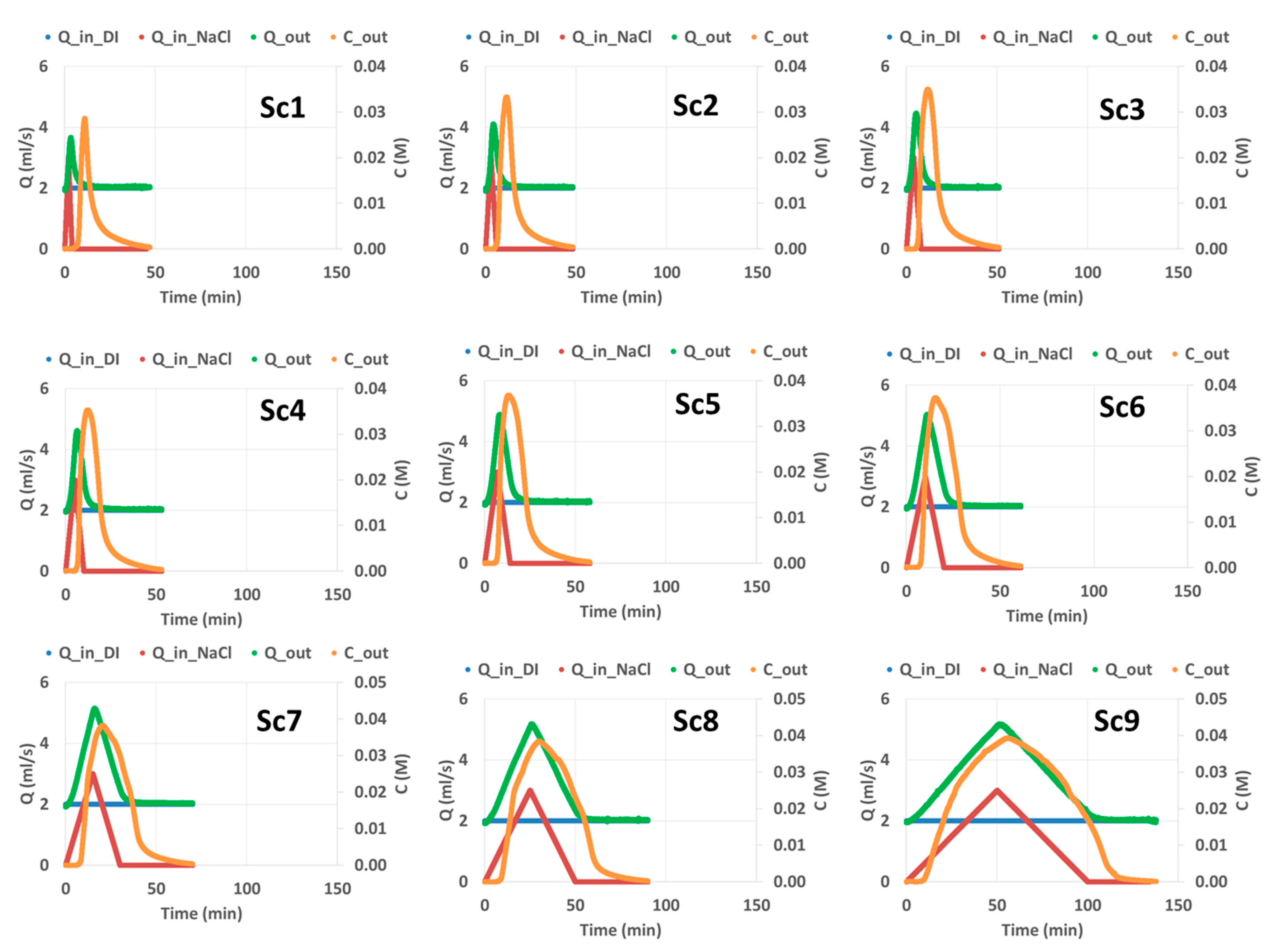
2.1. Experimental Setup
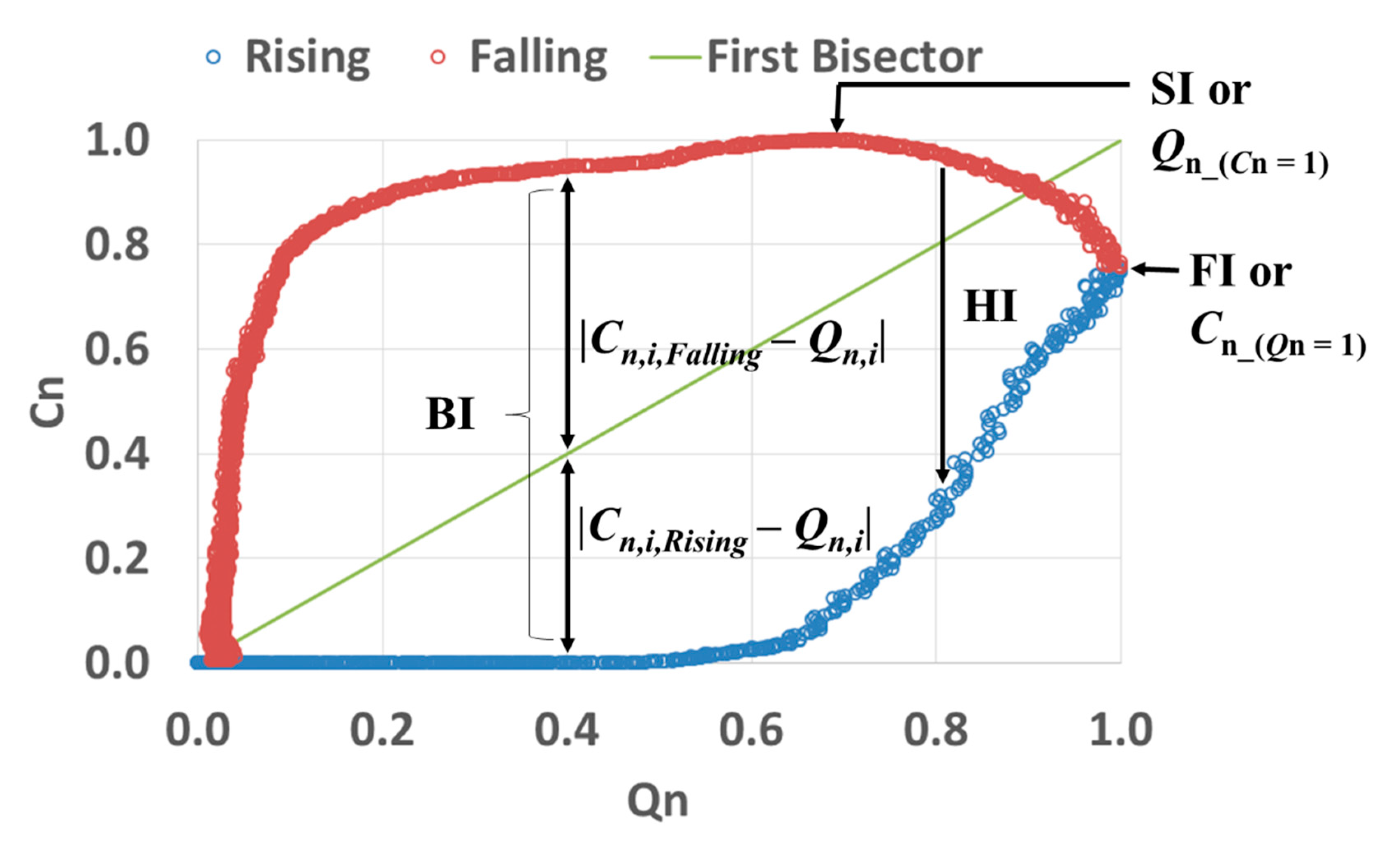
2.2. Hysteresis Indices
- The ‘saturation index’ SI (Figure 2) is obtained by calculating the value of Qn that corresponds to the maximum of concentration (Cn = 1). The resulting index Qn_(Cn=1) is SI.
- The ‘bisector index’ (BI) is based on the mean absolute distance between the first bisector and both rising and falling limbs of the hysteresis according to the following:
3. Results
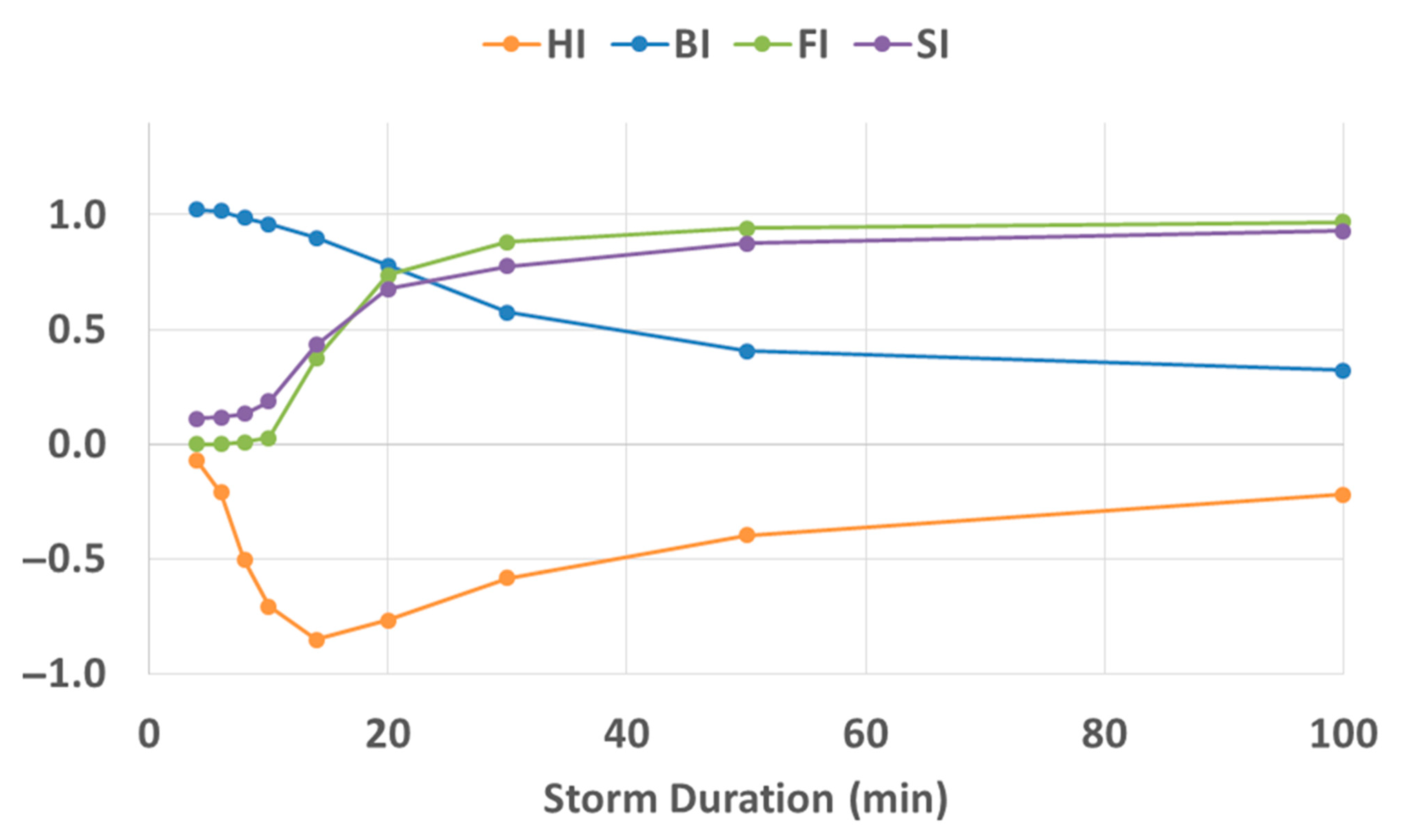
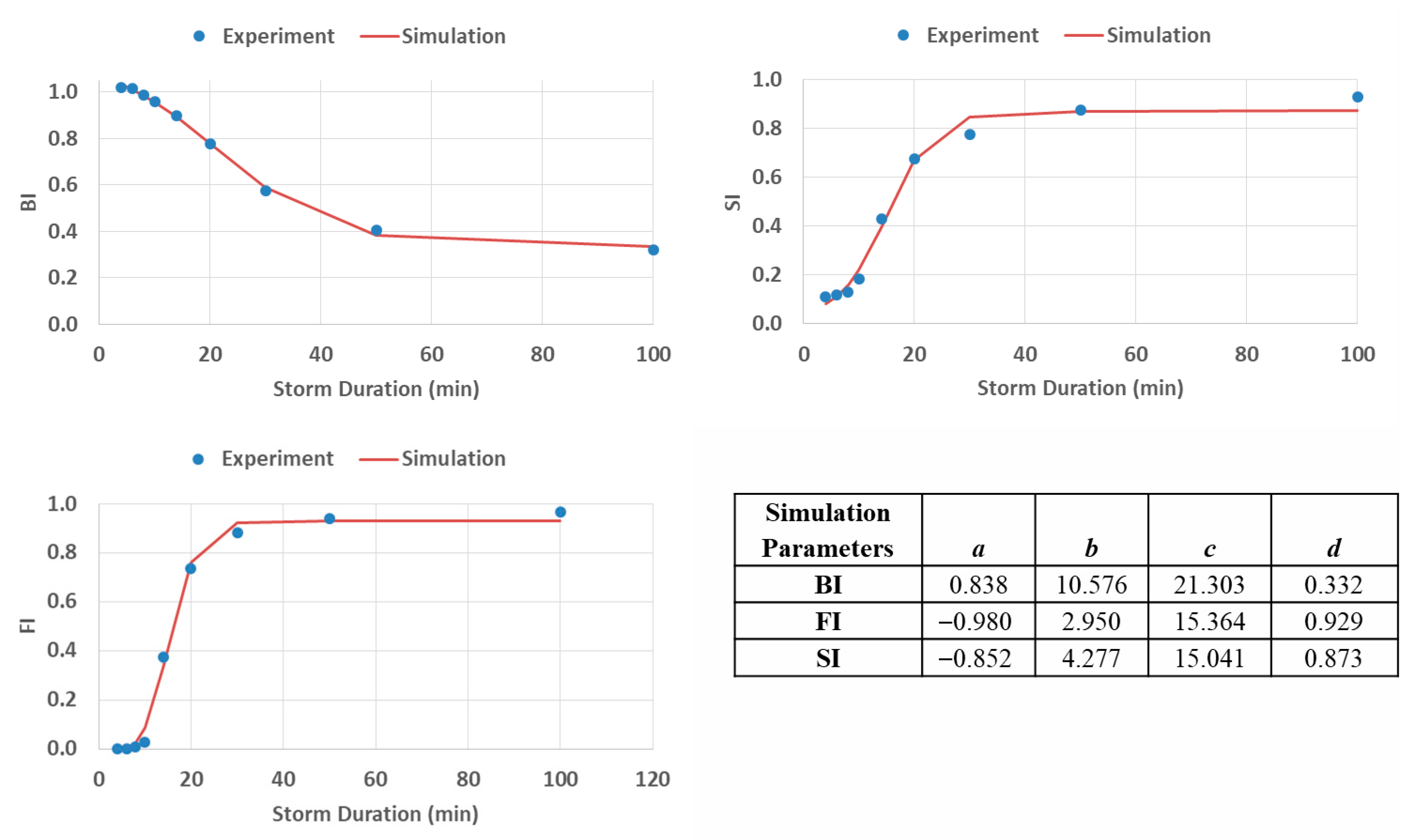
- The HI index does not follow a monotonic mathematical function: HI decreases until it reaches a minimum (−0.847) around 14 min, then it increases asymptotically towards 0.
- FI and SI follow a monotonic increase from 0 to 1.
- BI follows a monotonic decrease from 1 to 0.
4. Discussion
4.1. Platform Models
4.2. Concentration–Discharge (C/Q) Hysteresis
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Evans, C.; Davies, T.D. Causes of concentration/discharge hysteresis and its potential as a tool for analysis of episode hydrochemistry. Water Resour. Res. 1998, 34, 129–137. [Google Scholar] [CrossRef]
- Evans, C.; Davies, T.D.; Murdoch, P.S. Component flow processes at four streams in the Catskill Mountains, New York, analysed using episodic concentration/discharge relationships. Hydrol. Process. 1999, 13, 563–575. [Google Scholar] [CrossRef]
- Rose, S. Comparative solute–discharge hysteresis analysis for an urbanized and a ‘control basin’ in the Georgia (USA) Piedmont. J. Hydrol. 2003, 284, 45–56. [Google Scholar] [CrossRef]
- Fournier, M.; Massei, N.; Bakalowicz, M.; Dussart-Baptista, L.; Rodet, J.; Dupont, J.P. Using turbidity dynamics and geochemical variability as a tool for understanding the behavior and vulnerability of a karst aquifer. Hydrogeol. J. 2007, 15, 689–704. [Google Scholar] [CrossRef]
- Butturini, A.; Alvarez, M.; Bernal, S.; Vazquez, E.; Sabater, F. Diversity and temporal sequences of forms of DOC and NO3− discharge responses in an intermittent stream: Predictable or random succession? J. Geophys. Res. 2008, 113, G03016. [Google Scholar] [CrossRef]
- Toran, L.; Reisch, C.E. Using stormwater hysteresis to characterize karst spring discharge. Groundwater 2013, 51, 575–587. [Google Scholar] [CrossRef]
- Sherriff, S.C.; Rowan, J.S.; Fenton, O.; Jordan, P.; Melland, A.R.; Mellander, P.E.; Ó hUallacháin, D. Storm Event Suspended Sediment-Discharge Hysteresis and Controls in Agricultural Watersheds: Implications for Watershed Scale Sediment Management. Environ. Sci. Technol. 2016, 50, 1769–1778. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, X.; Zhang, Z.; Soulsby, C. Using hysteretic behaviour and hydrograph classification to identify hydrological function across the “hillslope–depression–stream” continuum in a karst catchment. Hydrol. Process. 2020, 34, 3464–3480. [Google Scholar] [CrossRef]
- Heathwaite, A.L.; Bieroza, M. Fingerprinting hydrological and biogeochemical drivers of freshwater quality. Hydrol. Process. 2020, 2021, e13973. [Google Scholar] [CrossRef]
- Le Mesnil, M.; Charlier, J.B.; Moussa, R.; Caballero, Y. Investigating flood processes in karst catchments by combining concentration-discharge relationship analysis and lateral flow simulation. J. Hydrol. 2022, 605, 127358. [Google Scholar] [CrossRef]
- Floury, P.; Bouchez, J.; Druhan, J.L.; Gaillardet, J.; Blanchouin, A.; Gayer, E.; Ansart, P. Linking dynamic water storage and subsurface geochemical structure using high-frequency concentration-discharge records. Water Resour. Res. 2024, 60, e2022WR033999. [Google Scholar] [CrossRef]
- Malutta, S.; Kobiyama, M.; Chaffe, P.L.B.; Bonumá, N.B. Hysteresis analysis to quantify and qualify the sediment dynamics: State of the art. Water Sci. Technol. 2020, 81, 2471–2487. [Google Scholar] [CrossRef]
- Liu, W.; Birgand, F.; Tian, S.; Chen, C. Event-scale hysteresis metrics to reveal processes and mechanisms controlling constituent export from watersheds: A review. Water Res. 2021, 200, 117254. [Google Scholar] [CrossRef] [PubMed]
- Chanat, J.G.; Rice, K.C.; Hornberger, G.M. Consistency of patterns in concentration-discharge plots. Water Resour. Res. 2002, 38, 1147. [Google Scholar] [CrossRef]
- Husic, A.; Fox, J.F.; Clare, E.; Mahoney, T.; Zarnaghsh, A. Nitrate hysteresis as a tool for revealing storm-event dynamics and improving water quality model performance. Water Resour. Res. 2023, 59, e2022WR033180. [Google Scholar] [CrossRef]
- Vaughan, M.C.H.; Bowden, W.B.; Shanley, J.B.; Vermilyea, A.; Sleeper, R.; Gold, A.J.; Pradhanang, S.M.; Inamdar, S.P.; Levia, D.F.; Andres, A.S.; et al. High-frequency dissolved organic carbon and nitrate measurements reveal differences in storm hysteresis and loading in relation to land cover and seasonality. Water Resour. Res. 2017, 53, 5345–5363. [Google Scholar] [CrossRef]
- Rose, L.A.; Karwan, D.L.; Godsey, S.E. Concentration–discharge relationships describe solute and sediment mobilization, reaction, and transport at event and longer timescales. Hydrol. Process. 2018, 32, 2829–2844. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Lin, J.; Yin, W.; Shi, Y.Y.; Wang, L.; Xiao, H.B.; Zhong, Z.M.; Jiang, H.; Shi, Z.H. Hysteresis analysis reveals dissolved carbon concentration—Discharge relationships during and between storm events. Water Res. 2022, 226, 119220. [Google Scholar] [CrossRef]
- Zhu, M.; Yu, X.; Li, Z.; Xu, X.; Ye, Z. Quantifying and interpreting the hysteresis patterns of monthly sediment concentration and water discharge in karst watersheds. J. Hydrol. 2023, 618, 129179. [Google Scholar] [CrossRef]
- Yu, B.; Shi, Z.; Zhang, Y. Linking hydrological and landscape characteristics to suspended sediment-discharge hysteresis in Wudinghe River Basin on the Loess Plateau, China. Catena 2023, 228, 107169. [Google Scholar] [CrossRef]
- Senatore, A.; Corrente, G.A.; Argento, E.L.; Castagna, J.; Micieli, M.; Mendicino, G.; Beneduci, A.; Botter, G. Seasonal and storm event-based dynamics of Dissolved Organic carbon (DOC) concentration in a Mediterranean headwater catchment. Water Resour. Res. 2023, 59, e2022WR034397. [Google Scholar] [CrossRef]
- Knapp, J.L.A.; von Freyberg, J.; Studer, B.; Kiewiet, L.; Kirchner, J.W. Concentration–discharge relationships vary among hydrological events, reflecting differences in event characteristics. Hydrol. Earth Syst. Sci. 2020, 24, 2561–2576. [Google Scholar] [CrossRef]
- Peña, P.; Pesántez, J.; Birkel, C.; Mosquera, G.; Arízaga-Idrovo, V.; Mora, E.; Crespo, P. How do storm characteristics influence concentration-discharge hysteresis in a high-elevation tropical ecosystem? J. Hydrol. 2023, 619, 129345. [Google Scholar] [CrossRef]
- Lloyd, C.E.M.; Freer, J.E.; Johnes, P.J.; Collins, A.L. Technical Note: Testing an improved index for analysing storm discharge–concentration hysteresis. Hydrol. Earth Syst. Sci. 2016, 20, 625–632. [Google Scholar] [CrossRef]
- Majdalani, S.; Delestre, O.; Moussa, R. Experimental investigation of loop rating curve on a small 3D printed laboratory channel. J. Hydrol. 2023, 623, 129741. [Google Scholar] [CrossRef]
- Majdalani, S.; Moussa, R.; Chazarin, J.P. A novel platform to evaluate the dampening of water and solute transport in an experimental channel under unsteady flow conditions. Hydrol. Process. 2020, 34, 956–971. [Google Scholar] [CrossRef]
- Majdalani, S.; Chazarin, J.P.; Moussa, R. A new water level measurement method combining infrared sensors and floats for applications on laboratory scale channel under unsteady flow regime. Sensors 2019, 19, 1511. [Google Scholar] [CrossRef]


| Storm Duration (min) | Scenario | HI | BI | FI | SI |
|---|---|---|---|---|---|
| 4 | Sc1 | −0.099 | 1.02 | 0.00008 | 0.111 |
| 6 | Sc2 | −0.265 | 1.02 | 0.0002 | 0.117 |
| 8 | Sc3 | −0.547 | 0.99 | 0.008 | 0.130 |
| 10 | Sc4 | −0.739 | 0.96 | 0.027 | 0.185 |
| 14 | Sc5 | −0.847 | 0.90 | 0.372 | 0.431 |
| 20 | Sc6 | −0.754 | 0.78 | 0.736 | 0.676 |
| 30 | Sc7 | −0.562 | 0.57 | 0.881 | 0.775 |
| 50 | Sc8 | −0.366 | 0.40 | 0.941 | 0.876 |
| 100 | Sc9 | −0.191 | 0.32 | 0.967 | 0.930 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majdalani, S. Effect of Storm Event Duration on the Indices of Concentration Discharge Hysteresis. Hydrology 2025, 12, 221. https://doi.org/10.3390/hydrology12080221
Majdalani S. Effect of Storm Event Duration on the Indices of Concentration Discharge Hysteresis. Hydrology. 2025; 12(8):221. https://doi.org/10.3390/hydrology12080221
Chicago/Turabian StyleMajdalani, Samer. 2025. "Effect of Storm Event Duration on the Indices of Concentration Discharge Hysteresis" Hydrology 12, no. 8: 221. https://doi.org/10.3390/hydrology12080221
APA StyleMajdalani, S. (2025). Effect of Storm Event Duration on the Indices of Concentration Discharge Hysteresis. Hydrology, 12(8), 221. https://doi.org/10.3390/hydrology12080221






