Method for Establishing Heavy Rainfall Equations Based on Regional Characteristics: Transformation of Maximum Daily Precipitation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Proposed Method
2.2.1. Maximum Daily Precipitation Depth Associated with a Return Period (hday,T)
2.2.2. Coefficients to Transform Daily Rainfall ()
2.3. Method’s Application and Assessment
2.3.1. Establishing for Brazil
2.3.2. Assessment
3. Results and Discussion
3.1. for Brazil
3.2. Application of TMDP
3.2.1. hday,T Values
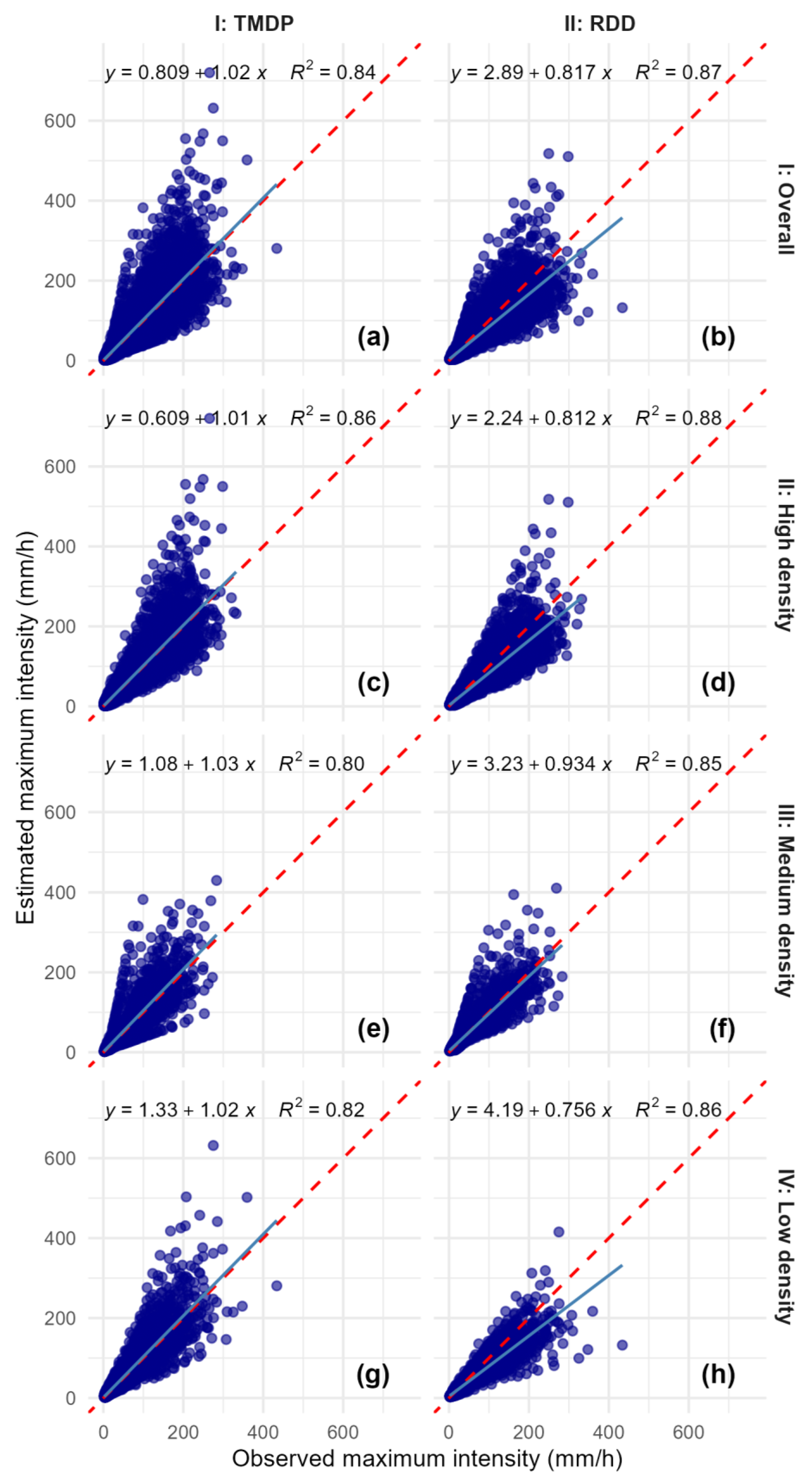
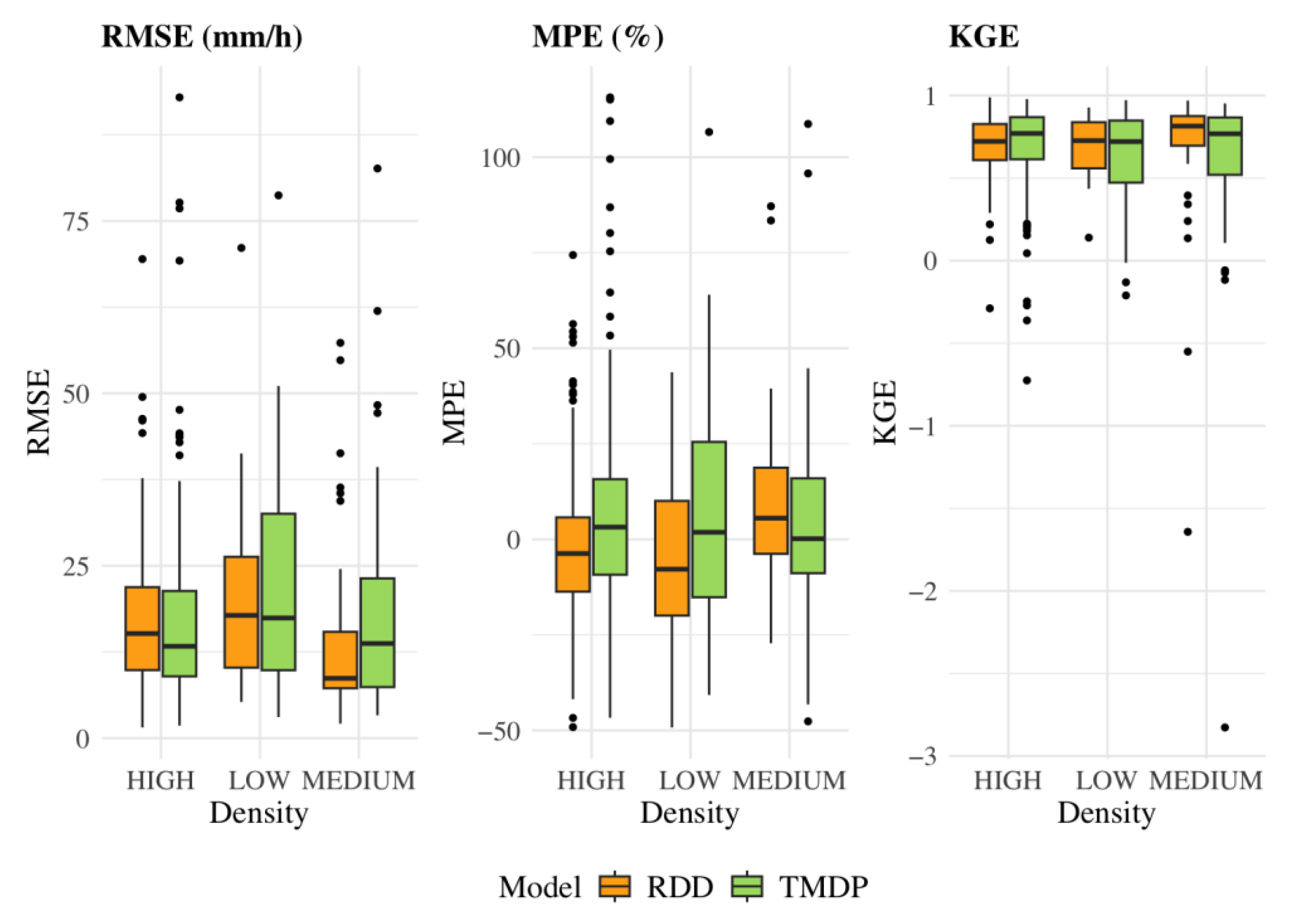
3.2.2. TMDP and RDD Performances
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moura Cardoso do Vale, T.; Helena Constantino Spyrides, M.; De Melo Barbosa Andrade, L.; Guedes Bezerra, B.; Evangelista da Silva, P. Subsistence Agriculture Productivity and Climate Extreme Events. Atmosphere 2020, 11, 1287. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y.; Li, K.; Zhang, Z.; Chen, C. Gully Internal Erosion Triggered by a Prolonged Heavy Rainfall Event in the Tableland Region of China’s Loess Plateau. Int. Soil Water Conserv. Res. 2023, 11, 610–621. [Google Scholar] [CrossRef]
- Chhetri, T.B.; Dhital, Y.P.; Tandong, Y.; Devkota, L.P.; Dawadi, B. Observations of Heavy Rainfall and Extreme Flood Events over Banke-Bardiya Districts of Nepal in 2016–2017. Prog. Disaster Sci. 2020, 6, 100074. [Google Scholar] [CrossRef]
- Ma, S.; Shao, X.; Xu, C. Landslides Triggered by the 2016 Heavy Rainfall Event in Sanming, Fujian Province: Distribution Pattern Analysis and Spatio-Temporal Susceptibility Assessment. Remote Sens. 2023, 15, 2738. [Google Scholar] [CrossRef]
- Prokop, P.; Wiejaczka, Ł.; Sarkar, S.; Bryndal, T.; Bucała-Hrabia, A.; Kroczak, R.; Soja, R.; Płaczkowska, E. Morphological and Sedimentological Responses of Small Stream Channels to Extreme Rainfall and Land Use in the Darjeeling Himalayas. CATENA 2020, 188, 104444. [Google Scholar] [CrossRef]
- Fekete, A.; Sandholz, S. Here Comes the Flood, but Not Failure? Lessons to Learn after the Heavy Rain and Pluvial Floods in Germany 2021. Water 2021, 13, 3016. [Google Scholar] [CrossRef]
- Martel, J.-L.; Brissette, F.P.; Lucas-Picher, P.; Troin, M.; Arsenault, R. Climate Change and Rainfall Intensity–Duration–Frequency Curves: Overview of Science and Guidelines for Adaptation. J. Hydrol. Eng. 2021, 26, 03121001. [Google Scholar] [CrossRef]
- Yang, Z.; Burn, D.H. Automatic Feature Selection and Weighting for the Formation of Homogeneous Groups for Regional IDF Estimation. J. Hydrol. 2019, 575, 292–307. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A Mathematical Framework for Studying Rainfall Intensity-Duration-Frequency Relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guide to Hydrological Practices: Hydrology from Measurement to Hydrological Information (WMO-No. 168); World Meteorological Organization: Geneva, Switzerland, 2008; ISBN 978-92-63-10168-6. [Google Scholar]
- Torres, I.P.; Cecílio, R.A.; de Almeida, L.T.; Abreu, M.C.; da Silva, D.D.; Zanetti, S.S.; Xavier, A.C. Rainfall Intensity–Duration–Frequency Curves Dataset for Brazil. Data 2025, 10, 17. [Google Scholar] [CrossRef]
- COMPANHIA DE TECNOLOGIA DE SANEAMENTO AMBIENTAL. Drenagem Urbana: Manual de Projeto, 3rd ed.; CETESB: São Paulo, Brazil, 1986.
- Carvalho Abreu, M.; Thebit de Almeida, L.; Bernardes Silva, F.; de Souza Fraga, M.; Bastos Lyra, G.; Souza, A.; da Silva, D.D.; Avelino Cecílio, R. Disaggregation Coefficients for Obtaining Rainfall Intensity-Duration-Frequency Curves: Concepts, Models, Errors and Trends in Minas Gerais, Brazil. Urban Water J. 2023, 20, 1647–1660. [Google Scholar] [CrossRef]
- Passos, J.B.d.M.C.; da Silva, D.D.; Lima, R.P.C. Daily Rainfall Disaggregation Coefficients for the Doce River Basin, Brazil: Regional Applicability and the Return Period Influence. Eng. Agrícola 2021, 41, 223–234. [Google Scholar] [CrossRef]
- de Bodas Terassi, P.M.; Pontes, P.R.M.; Xavier, A.C.F.; Cavalcante, R.B.L.; de Oliveira Serrão, E.A.; Sobral, B.S.; de Oliveira-Júnior, J.F.; de Melo, A.M.Q.; Baratto, J. A Comprehensive Analysis of Regional Disaggregation Coefficients and Intensity-Duration-Frequency Curves for the Itacaiúnas Watershed in the Eastern Brazilian Amazon. Theor. Appl. Climatol. 2023, 154, 863–880. [Google Scholar] [CrossRef]
- Abreu, M.C.; Cecílio, R.A.; Pruski, F.F.; de Almeida, L.T.; dos Santos, G.R.; Zanetti, S.S.; Pereira, S.B.; Silva, D.D. Daily Rainfall Disaggregation to Estimate the Intensity-Duration-Frequency Relationship in Minas Gerais State, Brazil. Braz. Arch. Biol. Technol. 2022, 65, e20210694. [Google Scholar] [CrossRef]
- Damé, R.d.C.F.; Teixeira-Gandra, C.F.A.; Villela, F.A.; dos Santos, J.P.; Winkler, A.S. Analysis of the Relationship Intensity, Duration, Frequency of Disaggregated Daily Rainfall in Southern Rio Grande Do Sul, Brazil. Eng. Agrícola 2014, 34, 660–670. [Google Scholar] [CrossRef][Green Version]
- Back, Á.J.; Pola, A.C. Relações Entre Precipitações Intensas de Diferentes Durações de Videira, Santa Catarina. Tecnol. e Ambient. 2016, 22, 125–135. [Google Scholar] [CrossRef]
- Dorneles, V.R.; Damé, R.d.C.F.; Teixeira-Gandra, C.F.A.; Méllo, L.B.; Ramirez, M.A.A.; Manke, E.B. Intensity-Duration-Frequency Relationships of Rainfall through the Technique of Disaggregation of Daily Rainfall. Rev. Bras. Eng. Agrícola e Ambient. 2019, 23, 506–510. [Google Scholar] [CrossRef]
- dos Anjos, R.S.; Nóbrega, R.S.; de Araújo, F.E.; Rocha Filho, G.B. Spacial Distribution of Rain Types in Pernambuco with the Usage of Remote Sensing. J. Hyperspectr. Remote Sens. 2016, 6, 154–163. [Google Scholar] [CrossRef]
- Szwed, M. Variability of Precipitation in Poland under Climate Change. Theor. Appl. Climatol. 2019, 135, 1003–1015. [Google Scholar] [CrossRef]
- Abreu, M.C.; Cecílio, R.A.; Pruski, F.F.; dos Santos, G.R.; De Almeida, L.T.; Zanetti, S.S. Critérios Para Escolha de Distribuições de Probabilidades Em Estudos de Eventos Extremos de Precipitação. Rev. Bras. Meteorol. 2018, 33, 601–613. [Google Scholar] [CrossRef]
- de Mello, C.R.; Viola, M.R.; de Mello, J.M.; Silva, A.M. Continuidade Espacial de Chuvas Intensas No Estado de Minas Gerais. Ciência e Agrotecnol. 2008, 32, 532–539. [Google Scholar]
- Back, Á.J.; Henn, A.; Oliveira, J.L.R. Heavy Rainfall Equations for Santa Catarina, Brazil. Rev. Bras. Ciência do Solo 2011, 35, 2127–2134. [Google Scholar] [CrossRef]
- Denardin, J.E.; Freitas, P.L. de Características Fundamentais Da Chuva No Brasil. Pesqui. Agropecuária Bras. 1982, 10, 1409–1416. [Google Scholar]
- Fendrich, R. Chuvas Intensas Para Obras de Drenagem (No Estado Do Paraná), 1st ed.; Champagnat: Curitiba, Brazil, 1998. [Google Scholar]
- Freitas, A.J.; da Silva, D.D.; Pruski, F.F.; Pinto, F.A.; Pereira, S.B.; Gomes Filho, R.R.; Teixeira, A.F.; Baena, L.G.N.; Mello, L.T.A.; Novaes, L.F.d. Equações de Chuvas Intensas No Estado de Minas Gerais, 1st ed.; Companhia de Saneamento de Minas Gerais: Belo Horizonte, Brazil, 2001. [Google Scholar]
- da Silva, D.D.; Pinto, F.R.L.; Pruski, F.F.; Pinto, F.A. Estimativa e Espacialização Dos Parâmetros Da Equação de Intensidade-Duração-Freqüência Da Precipitação Para o Rio de Janeiro e o Espírito Santo. Eng. Agrícola 1999, 19, 11–21. [Google Scholar]
- da Silva, D.D.; Gomes Filho, R.R.; Pruski, F.F.; Pereira, S.B.; Novaes, L.F. de Chuvas Intensas No Estado Da Bahia. Rev. Bras. Eng. Agrícola e Ambient. 2002, 6, 362–367. [Google Scholar] [CrossRef]
- da Silva, D.D.; Pereira, S.B.; Pruski, F.F.; Gomes Filho, R.R.; Lana, Â.M.Q.; Baena, L.G.N. Equações de Intensidade-Duração-Freqüência Da Precipitação Pluvial Para o Estado de Tocantins. Eng. na Agric. 2003, 11, 7–14. [Google Scholar]
- Agência Nacional de Águas Sistema de Informação Hidrológicas—Hidroweb. Available online: https://www.snirh.gov.br/hidroweb/ (accessed on 3 February 2020).
- Zambrano-Bigiarini, M. hydroGOF: Goodness-of-Fit Functions for Comparison of Simulated and Observed Hydrological Time Series; R Package Version 0.3-10. 2017. Available online: https://cran.r-project.org/ (accessed on 28 August 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Junqueira Júnior, J.A.; de Mello, C.R.; Alves, G.J. Eventos Extremos de Precipitação No Alto Rio Grande, MG: Análise Probabilística. Rev. Bras. Eng. Agrícola e Ambient. 2015, 19, 301–308. [Google Scholar] [CrossRef]
- Lima, A.O.; Lyra, G.B.; Abreu, M.C.; Oliveira-Júnior, J.F.; Zeri, M.; Cunha-Zeri, G. Extreme Rainfall Events over Rio de Janeiro State, Brazil: Characterization Using Probability Distribution Functions and Clustering Analysis. Atmos. Res. 2021, 247, 105221. [Google Scholar] [CrossRef]
- Silva, C.B.; Oliveira, L.F.C. Relação Intensidade-Duração-Frequência de Chuvas Extremas Na Região Nordeste Do Brasil. Rev. Bras. Climatol. 2017, 20, 267–283. [Google Scholar] [CrossRef]
- Martins, F.B.; Gonzaga, G.; dos Santos, D.F.; Reboita, M.S. Classificação Climática de Köppen e de Thornthwaite Para Minas Gerais: Cenário Atual e Projeções Futuras. Rev. Bras. Climatol. 2018, 1, 129–156. [Google Scholar] [CrossRef]
- Reboita, M.S.; Rodrigues, M.; Silva, L.F.; Alves, M.A. Aspectos Climáticos Do Estado de Minas Gerais. Rev. Bras. Climatol. 2015, 17, 209–229. [Google Scholar] [CrossRef]
- Back, Á.J. Alternative Model of Intense Rainfall Equation Obtained from Daily Rainfall Disaggregation. RBRH 2020, 25, e2. [Google Scholar] [CrossRef]
- Marengo, J.; Valverde, M.; Obregon, G. Observed and Projected Changes in Rainfall Extremes in the Metropolitan Area of São Paulo. Clim. Res. 2013, 57, 61–72. [Google Scholar] [CrossRef]
- Vemado, F.; Pereira Filho, A.J. Severe Weather Caused by Heat Island and Sea Breeze Effects in the Metropolitan Area of São Paulo, Brazil. Adv. Meteorol. 2016, 2016, 8364134. [Google Scholar] [CrossRef]
- Dalagnol, R.; Gramcianinov, C.B.; Crespo, N.M.; Luiz, R.; Chiquetto, J.B.; Marques, M.T.A.; Neto, G.D.; de Abreu, R.C.; Li, S.; Lott, F.C.; et al. Extreme Rainfall and Its Impacts in the Brazilian Minas Gerais State in January 2020: Can We Blame Climate Change? Clim. Resil. Sustain. 2022, 1, e15. [Google Scholar] [CrossRef]
- Sanches, F.; Verdum, R.; Fisch, G.; Gass, S.L.B.; Rocha, V.M. Extreme Rainfall Events in the Southwest of Rio Grande Do Sul (Brazil) and Its Association with the Sandization Process. Am. J. Clim. Chang. 2019, 08, 441–453. [Google Scholar] [CrossRef]
- Pousa, R.; Costa, M.H.; Pimenta, F.M.; Fontes, V.C.; de Brito, V.F.A.; Castro, M. Climate Change and Intense Irrigation Growth in Western Bahia, Brazil: The Urgent Need for Hydroclimatic Monitoring. Water 2019, 11, 933. [Google Scholar] [CrossRef]
- Silva Dias, M.A.F.; Dias, J.; Carvalho, L.M.V.; Freitas, E.D.; Silva Dias, P.L. Changes in Extreme Daily Rainfall for São Paulo, Brazil. Clim. Change 2013, 116, 705–722. [Google Scholar] [CrossRef]
- Back, Á.J.; Oliveira, J.L.R.; Henn, A. Relações Entre Precipitações Intensas de Diferentes Durações Para Desagregação Da Chuva Diária Em Santa Catarina. Rev. Bras. Eng. Agrícola e Ambient. 2012, 16, 391–398. [Google Scholar] [CrossRef][Green Version]
- Manke, E.B.; Teixeira-Gandra, C.F.A.; Damé, R.d.C.F.; Nunes, A.B.; Neta, M.C.C.C.; Karsburg, R.M. Seasonal Intensity-Duration-Frequency Relationships for Pelotas, Rio Grande Do Sul, Brazil. Rev. Bras. Eng. Agrícola e Ambient. 2022, 26, 85–90. [Google Scholar] [CrossRef]
- Goyal, M.K.; Shivam, G.; Sarma, A.K. Spatial Homogeneity of Extreme Precipitation Indices Using Fuzzy Clustering over Northeast India. Nat. Hazards 2019, 98, 559–574. [Google Scholar] [CrossRef]

| 24 h/1 d | 12 h/24 h | 10 h/24 h | 8 h/24 h | 6 h/24 h | 4 h/24 h | 2 h/24 h | 1 h/24 h | 50 min/1 h | 40 min/1 h | 30 min/1 h | 20 min/30 min | 10 min/30 min | 5 min/30 min |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.14 | 0.85 | 0.82 | 0.78 | 0.72 | 0.54 | 0.48 | 0.42 | 0.74 | 0.91 | 0.81 | 0.7 | 0.54 | 0.34 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Almeida, L.T.; Cecílio, R.A.; Abreu, M.C.; Torres, I.P. Method for Establishing Heavy Rainfall Equations Based on Regional Characteristics: Transformation of Maximum Daily Precipitation. Hydrology 2025, 12, 211. https://doi.org/10.3390/hydrology12080211
de Almeida LT, Cecílio RA, Abreu MC, Torres IP. Method for Establishing Heavy Rainfall Equations Based on Regional Characteristics: Transformation of Maximum Daily Precipitation. Hydrology. 2025; 12(8):211. https://doi.org/10.3390/hydrology12080211
Chicago/Turabian Stylede Almeida, Laura Thebit, Roberto Avelino Cecílio, Marcel Carvalho Abreu, and Ivana Patente Torres. 2025. "Method for Establishing Heavy Rainfall Equations Based on Regional Characteristics: Transformation of Maximum Daily Precipitation" Hydrology 12, no. 8: 211. https://doi.org/10.3390/hydrology12080211
APA Stylede Almeida, L. T., Cecílio, R. A., Abreu, M. C., & Torres, I. P. (2025). Method for Establishing Heavy Rainfall Equations Based on Regional Characteristics: Transformation of Maximum Daily Precipitation. Hydrology, 12(8), 211. https://doi.org/10.3390/hydrology12080211







