Seasonal Freshwater Inflows in Cochin Backwater Estuary Inferred from Stable Isotopes and Machine Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sample Collection and Analysis
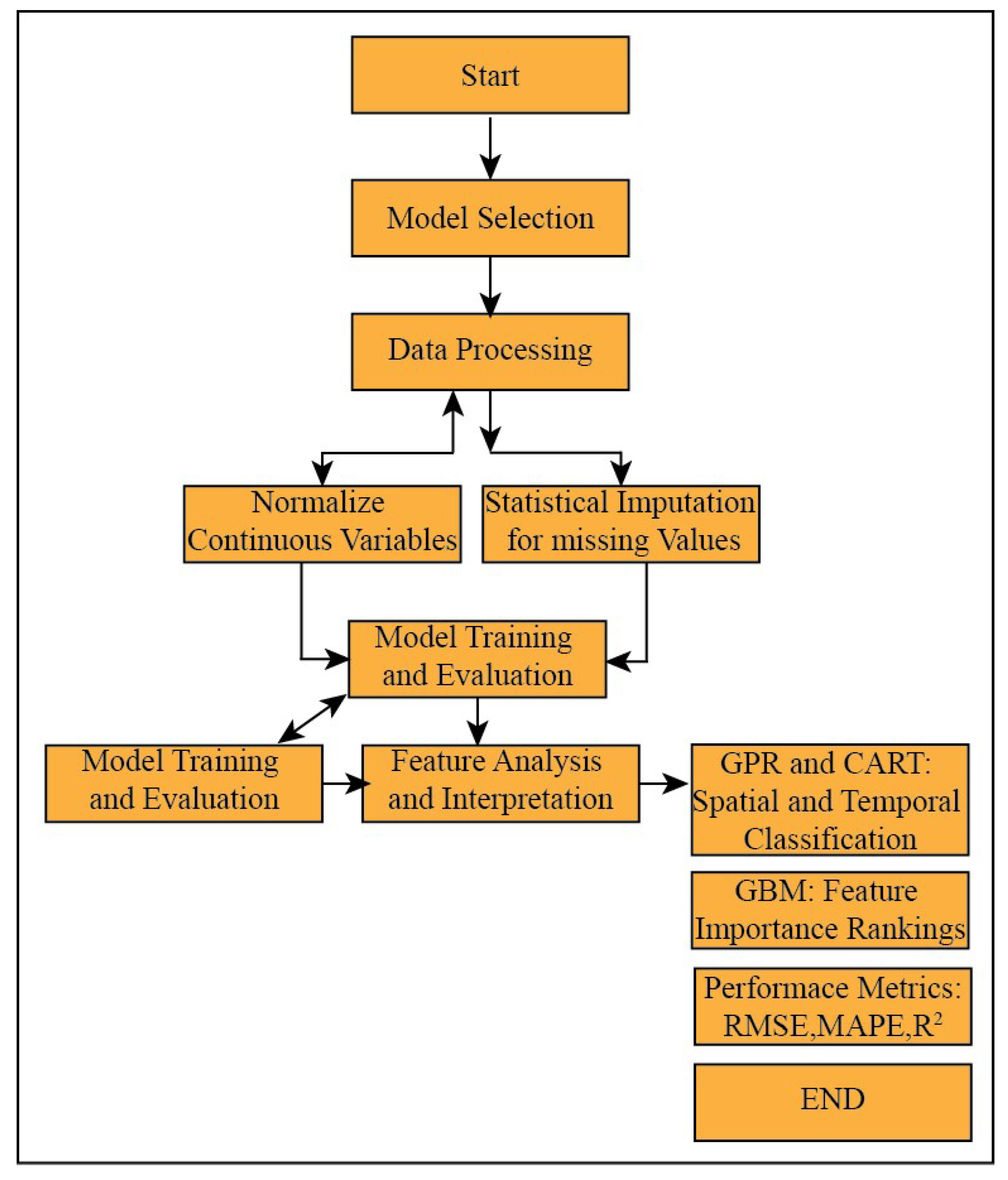
2.3. ML Methodology
- Conventional Models: K-Nearest Neighbor (KNN), Random Forest (RF), and Sup-port Vector Machine (SVM) were chosen as they have been previously applied in stable isotope modeling studies and serve as established benchmarks [20].
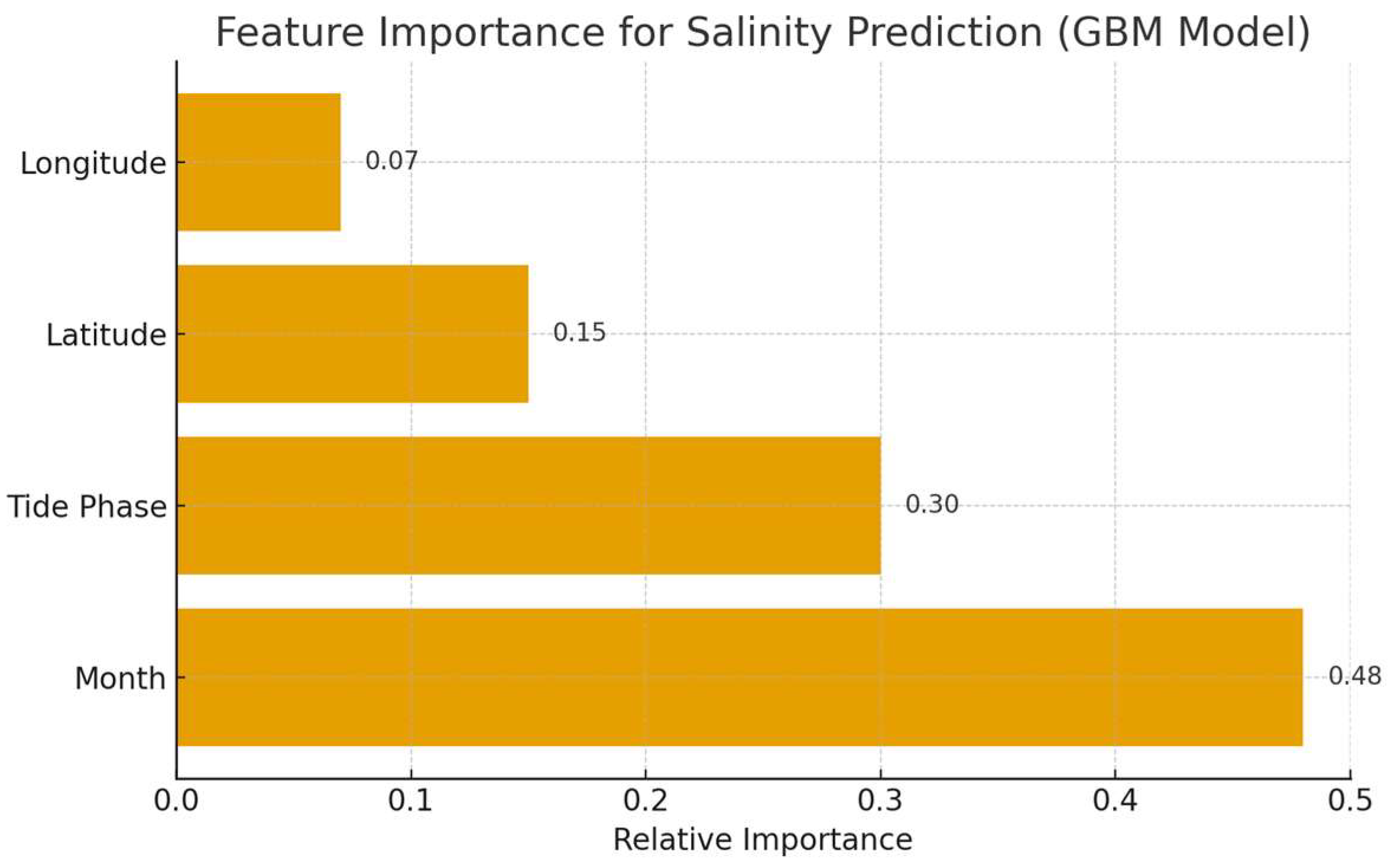
- Advanced Tree-Based Models: Gradient Boosting Machine (GBM) and Classification and Regression Tree (CART) were selected for their ability to capture complex non-linear interactions and provide insights into feature importance, which is crucial for understanding the environmental drivers.
- Other Advanced Models: Gaussian Process Regression (GPR) was included for its strength in quantifying prediction uncertainty. Extreme Learning Machines (ELMs) and Radial Basis Function Networks (RBNNs) were tested for their efficiency and effectiveness in modeling spatial gradients and patterns with potentially limited data.
3. Results
3.1. Seasonal Variations in δ18O and Salinity
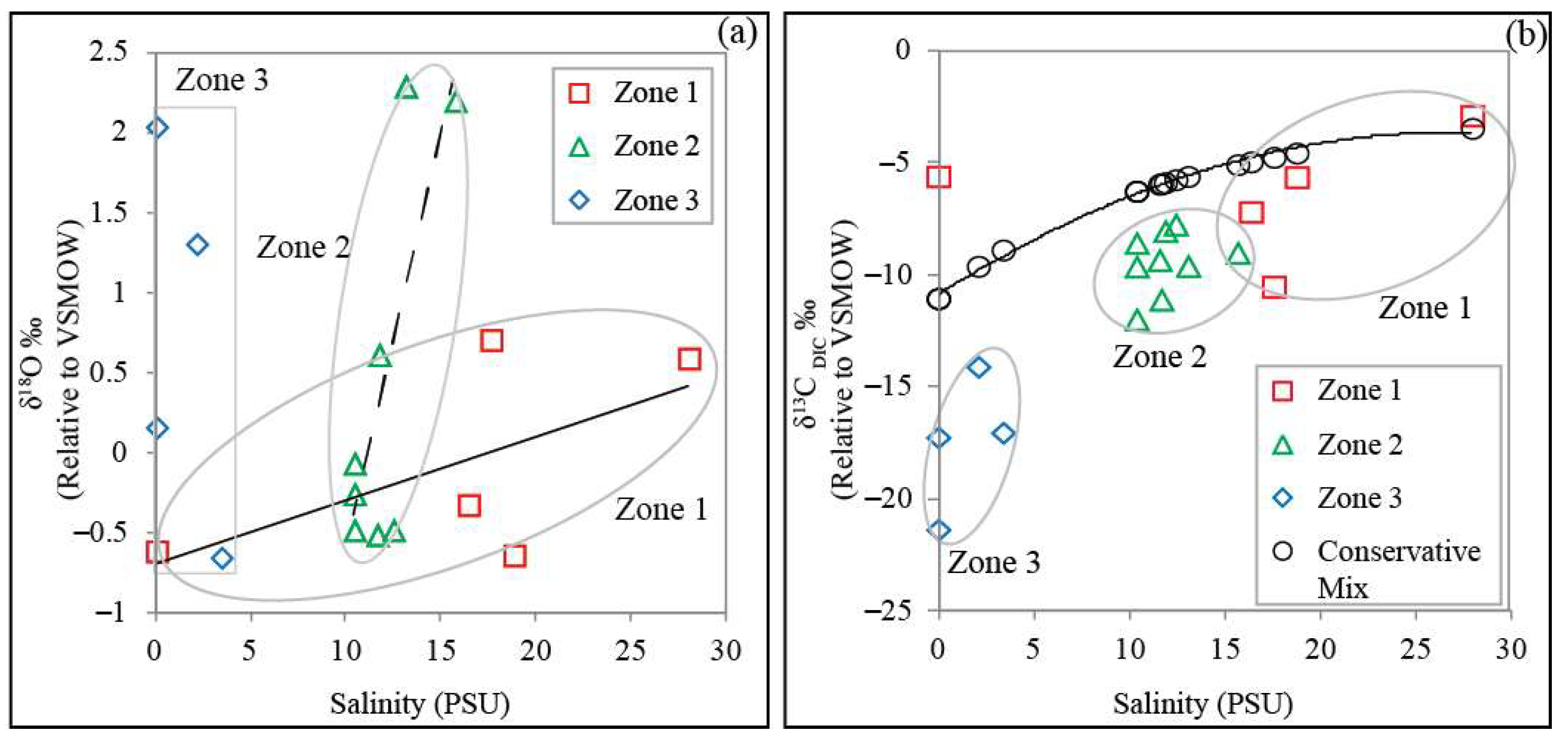
3.2. Spatial Variations in δ18O, δ13C, and Salinity
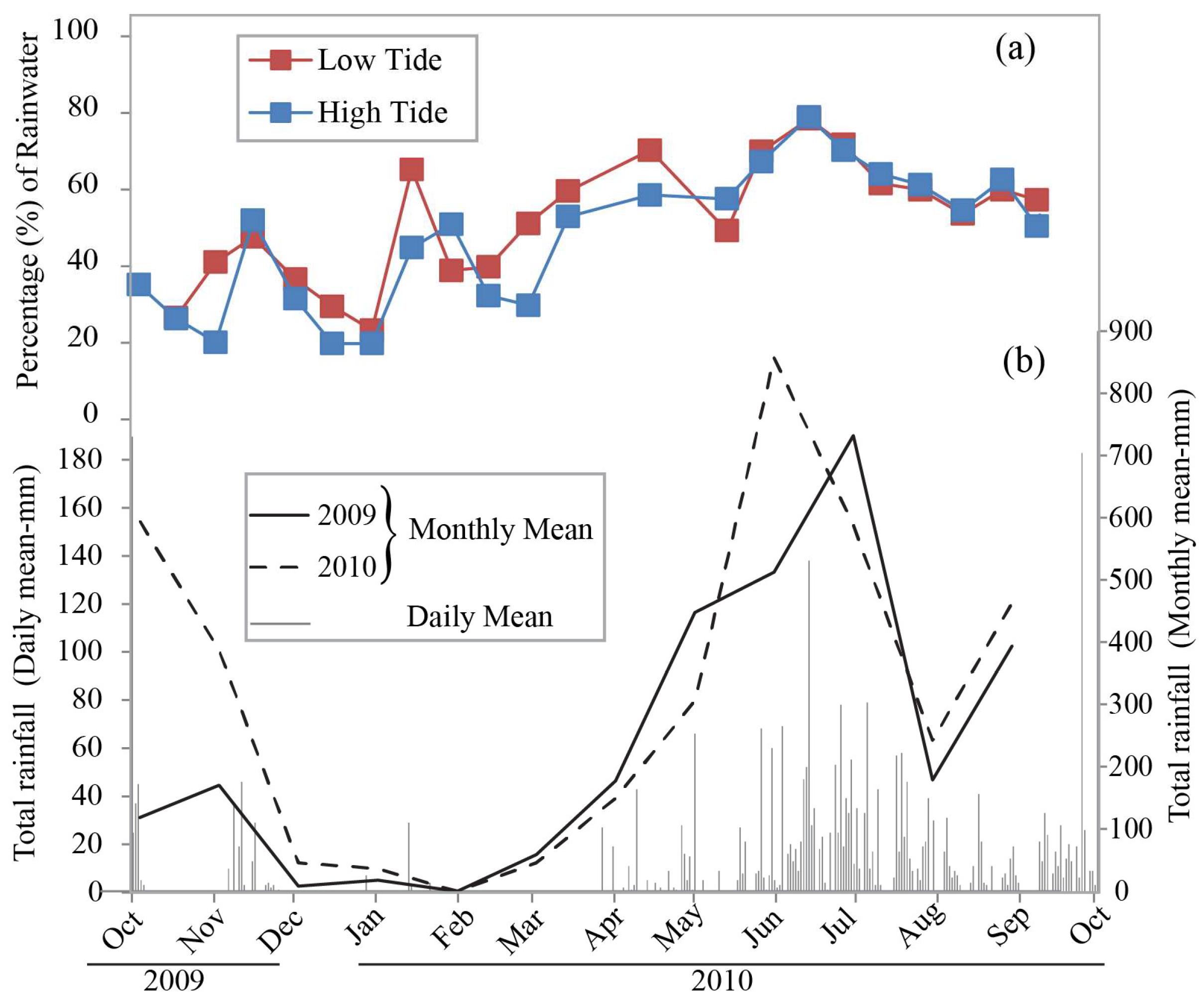
3.3. Freshwater Flux in Comparison with Seasonal Rainfall
3.4. Performance Metrics for ML Models
4. Discussion
4.1. Seasonal and Spatial Variations in δ18O and Salinity
4.2. δ18O and δ13C Relationship with Salinity
4.3. δ18O–δD Relationship of CBW Estuary
4.4. Carbon Dynamics Using Salinity and δ13CDIC
4.5. Evaluating ML Models for Salinity and Stable Isotopic Prediction
- Severe Overfitting: Flexible models, in an attempt to find a pattern, likely learned the random noise within the training data. This results in a model that is perfectly tuned to the training set but has no predictive power on unseen data.
- Unsuitable Model Architecture: The complex and potentially discontinuous nature of δ13C dynamics may require more specialized model architectures than those tested. The ‘step-function’ discontinuities introduced by biological fractionation are particularly challenging for standard regression algorithms.
- Hyperparameter Tuning Failure: In a low-signal environment, the Bayesian optimization process is susceptible to finding a ‘fluke’ set of hyperparameters that perform well on the validation set by chance but fail to capture any generalizable relationship, leading to the observed poor performance on the final test set.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CBW | Cochin Backwater |
| DIC | Dissolved Inorganic Carbon |
| PM | Premonsoon |
| SWM | Southwest Monsoon |
| NEM | Northeast Monsoon |
| HT | High Tide |
| LT | Low Tide |
| NBS19 | National Bureau of Standards-19 |
| HDPE | High-Density Polyethylene |
| ML | Machine Learning |
| ANN | Artificial Neural Network |
| ANFIS | Adaptive Neuro-Fuzzy Inference System |
| SVM | Support Vector Machine |
| RBNN | Radial Function Based Neural Network |
| RF | Random Forest |
| KNN | K-Nearest Neighbor |
| GBM | Gradient Boosting Machine |
| GPR | Gaussian Process Regression |
| CART | Classification and Regression Tree |
| ELM | Extreme Learning Machine |
| RMSE | Root Mean Square Error |
| MAPE | Mean Absolute Percentage Error |
References
- Day, J.W., Jr.; Kemp, W.M.; Yáñez-Arancibia, A.; Crump, B.C. (Eds.) Estuarine Ecology; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Dittmar, T.; Lara, R.J. Driving forces behind nutrient and organic matter dynamics in a mangrove tidal creek in North Brazil. Estuar. Coast. Shelf Sci. 2001, 52, 249–259. [Google Scholar] [CrossRef]
- Cloern, J.E.; Jassby, A.D. Patterns and scales of phytoplankton variability in estuarine–coastal ecosystems. Estuaries Coasts 2010, 33, 230–241. [Google Scholar]
- Vijith, V.; Sundar, D.; Shetye, S.R. Time-dependence of salinity in monsoonal estuaries. Estuar. Coast. Shelf Sci. 2009, 85, 601–608. [Google Scholar] [CrossRef]
- Qasim, S.; Gopinathan, C. Tidal cycle and the environmental features of Cochin Backwater (a tropical estuary). Proc. Indian Acad. Sci. Sect. A Part 3 Math. Sci. 1969, 69, 336–348. [Google Scholar]
- Haldar, R.; Khosa, R.; Gosain, A.K. Impact of Anthropogenic Interventions on the Vembanad Lake System. In Water Resources and Environmental Engineering I; Rathinasamy, M., Chandramouli, S., Phanindra, K., Mahesh, U., Eds.; Springer: Singapore, 2019. [Google Scholar]
- Kulk, G.; George, G.; Abdulaziz, A.; Menon, N.; Theenathayalan, V.; Jayaram, C.; Brewin, R.J.; Sathyendranath, S. Effect of Reduced Anthropogenic Activities on Water Quality in Lake Vembanad, India. Remote Sens. 2020, 13, 1631. [Google Scholar] [CrossRef]
- Pranav, P.; Roy, R.; Jayaram, C.; D’Costa, P.M.; Choudhury, S.B.; Menon, N.N.; Nagamani, P.; Sathyendranath, S.; Abdulaziz, A.; Sai, M.S.; et al. Seasonality in carbon chemistry of Cochin backwaters. Reg. Stud. Mar. Sci. 2021, 46, 101893. [Google Scholar] [CrossRef]
- Shivaprasad, A.; Vinita, J.; Revichandran, C.; Reny, P.D.; Deepak, M.P.; Muraleedharan, K.R.; Naveen Kumar, K.R. Seasonal stratification and property distributions in a tropical estuary (Cochin estuary, west coast, India). Hydrol. Earth Syst. Sci. 2013, 17, 187–199. [Google Scholar] [CrossRef]
- Balachandran, K.K.; Joseph, T.; Nair, K.K.C.; Nair, M.; Joseph, P.S. The Complex Estuarine Formation of Six Rivers (Cochin Backwaters System on West Coast of India)—Sources and Distribution of Trace Metals and Nutrients. 2002. Available online: https://drs.nio.org/drs/handle/2264/1340 (accessed on 30 August 2025).
- Sankaranarayanan, V.N.; Qasim, S.Z. Nutrients of the Cochin Backwater in relation to environmental characteristics. Mar. Biol. 1969, 2, 236–247. [Google Scholar] [CrossRef]
- Aneesh, T.D.; Srinivas, R.; Singh, A.T.; Resmi, T.R.; Nair, A.M.; Redkar, B.L. Stable water isotope signatures of dual monsoon precipitation: A case study of Greater Cochin region, south-west coast of India. J. Earth Syst. Sci. 2019, 128, 210. [Google Scholar] [CrossRef]
- Ghosh, P.; Chakrabarti, R.; Bhattacharya, S.K. Short- and long-term temporal variations in salinity and the oxygen, carbon and hydrogen isotopic compositions of the Hooghly Estuary water, India. Chem. Geol. 2013, 335, 118–127. [Google Scholar] [CrossRef]
- Nasir, U.P.; Harikumar, P.S. Hydrochemical and isotopic investigation of a tropical wetland system in the Indian sub-continent. Environ. Earth Sci. 2012, 66, 111–119. [Google Scholar]
- Bhavya, P.S.; Kumar, S.; Gupta, G.V.M.; Sudharma, K.V.; Sudheesh, V.; Dhanya, K.R. Carbon isotopic composition of suspended particulate matter and dissolved inorganic carbon in the Cochin estuary during post-monsoon. Curr. Sci. 2016, 110, 1539–1543. [Google Scholar]
- Raymond, P.A.; Bauer, J.E.; Caraco, N.F.; Cole, J.J.; Longworth, B.; Petsch, S.T. Controls on the variability of organic matter and dissolved inorganic carbon ages in northeast US rivers. Mar. Chem. 2004, 92, 353–366. [Google Scholar] [CrossRef]
- Bouillon, S.; Borges, A.V.; Castañeda-Moya, E.; Diele, K.; Dittmar, T.; Duke, N.C.; Kristensen, E.; Lee, S.Y.; Marchand, C.; Middelburg, J.J.; et al. Mangrove production and carbon sinks: A revision of global budget estimates. Glob. Biogeochem. Cycles 2008, 22, GB2013. [Google Scholar] [CrossRef]
- Ghosh, P.; Ramdas, L.; Banerjee, Y.; Thamizharasan, S.; Banerjee, S. Seasonal freshwater flux estimation using mollusc from the tropical Mandovi Zuari estuary, Goa, India. J. Earth Syst. Sci. 2021, 130, 107. [Google Scholar] [CrossRef]
- Bhavya, P.S.; Kumar, S.; Gupta, G.V.M.; Sudharma, K.V.; Sudheesh, V. Spatio-temporal variation in δ13C-DIC of a tropical eutrophic estuary (Cochin estuary, India) and adjacent Arabian Sea. Cont. Shelf Res. 2018, 153, 75–85. [Google Scholar] [CrossRef]
- Astray, G.; Soto, B.; Barreiro, E.; Gálvez, J.F.; Mejuto, J.C. Machine learning applied to the oxygen-18 isotopic composition, salinity and temperature/potential temperature in the Mediterranean Sea. Mathematics 2021, 9, 2523. [Google Scholar] [CrossRef]
- Cemek, B.; Arslan, H.; Küçüktopcu, E.; Simsek, H. Comparative analysis of machine learning techniques for estimating groundwater deuterium and oxygen-18 isotopes. Stoch. Environ. Res. Risk Assess. 2022, 36, 4271–4285. [Google Scholar] [CrossRef]
- Noori, N.; Kalin, L.; Isik, S. Water quality prediction using SWAT-ANN coupled approach. J. Hydrol. 2020, 590, 125220. [Google Scholar] [CrossRef]
- Ly, Q.V.; Nguyen, X.C.; Lê, N.C.; Truong, T.D.; Hoang, T.H.T.; Park, T.J.; Maqbool, T.; Pyo, J.-C.; Cho, K.H.; Lee, K.-S.; et al. Application of machine learning for eutrophication analysis and algal bloom prediction in an urban river: A 10-year study of the Han River, South Korea. Sci. Total Environ. 2021, 797, 149040. [Google Scholar]
- Samalavičius, V.; Gadeikienė, S.; Žaržojus, G.; Gadeikis, S.; Lekstutytė, I. Oxygen-18 prediction using machine learning in the Baltic Artesian Basin groundwater. Stoch. Environ. Res. Risk Assess. 2024, 39, 765–787. [Google Scholar] [CrossRef]
- Albuquerque, L.G.; de Oliveira Roque, F.; Valente-Neto, F.; Koroiva, R.; Buss, D.F.; Baptista, D.F.; Hepp, L.U.; Kuhlmann, M.L.; Sundar, S.; Covich, A.P.; et al. Large-scale prediction of tropical stream water quality using Rough Sets Theory. Ecol. Inform. 2021, 61, 101226. [Google Scholar] [CrossRef]
- Al Sudani, Z.A.; Salem, G.S.A. Evaporation rate prediction using advanced machine learning models: A comparative study. Adv. Meteorol. 2022, 2022, 1433835. [Google Scholar] [CrossRef]
- Dagher, D.H. Assessment of using machine and deep learning applications in surface water quantity and quality predictions: A review. J. Water Resour. Geosci. 2024, 3, 18–48. [Google Scholar]
- Van Binh, D. Reconstructing Daily Discharge in a Megadelta Using Machine Learning Techniques. Water Resour. Res. 2022, 58, e2021WR031048. [Google Scholar] [CrossRef]
- Downing, B.D.; Bergamaschi, B.A.; Kendall, C.; Kraus, T.E.C.; Dennis, K.J.; Carter, J.A.; von Dessonneck, T.S. Using Continuous Underway Isotope Measurements to Map Water Residence Time in Hydrodynamically Complex Tidal Environments. Environ. Sci. Technol. 2016, 50, 13387–13396. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Jani, R.A.; Ramesh, R. Spatiotemporal variations of the δ18O-salinity relation in the northern Indian Ocean. Deep Sea Res. Part I Oceanogr. Res. Pap. 2010, 57, 1422–1431. [Google Scholar] [CrossRef]
- Deshpande, R.D.; Muraleedharan, P.M.; Singh, R.L.; Kumar, B.; Rao, M.S.; Dave, M.; Sivakumar, K.U.; Gupta, S.K. Spatio-temporal distributions of δ18O, δD and salinity in the Arabian Sea: Identifying processes and controls. Mar. Chem. 2013, 157, 144–161. [Google Scholar] [CrossRef]
- Rasheed, K.; Joseph, K.A.; Balchand, A.N. Impacts of harbour dredging on the coastal shoreline features around Cochin. In Proceedings of the International Conference on Coastal Change, Bordeaux, France, 10–16 February 1995; pp. 943–948. [Google Scholar]
- Epstein, S.; Mayeda, T. Variation of O18 content of waters from natural sources. Geochim. Cosmochim. Acta 1953, 4, 213–227. [Google Scholar] [CrossRef]
- Rangarajan, R.; Ghosh, P. Role of water contamination within the GC column of a GasBench II peripheral on the reproducibility of 18O/16O ratios in water samples. Isot. Environ. Health Stud. 2011, 47, 498–511. [Google Scholar] [CrossRef]
- Assayag, N.; Rivé, K.; Ader, M.; Jézéquel, D.; Agrinier, P. Improved method for isotopic and quantitative analysis of dissolved inorganic carbon in natural water samples. Rapid Commun. Mass Spectrom. 2006, 20, 2243–2251. [Google Scholar] [CrossRef]
- Rangarajan, R.; Pathak, P.; Banerjee, S.; Ghosh, P. Floating boat method for carbonate stable isotopic ratio determination in a GasBench II peripheral. Rapid Commun. Mass Spectrom. 2021, 35, e9115. [Google Scholar]
- Lekshmy, P.R.; Midhun, M.; Ramesh, R.; Jani, R.A. 18O depletion in monsoon rain relates to large-scale organized convection rather than the amount of rainfall. Sci. Rep. 2014, 4, 5661. [Google Scholar] [CrossRef]
- Rahul, P.; Ghosh, P. Long term observations on stable isotope ratios in rainwater samples from twin stations over Southern India; identifying the role of amount effect, moisture source and rainout during the dual monsoons. Clim. Dyn. 2019, 52, 6893–6907. [Google Scholar] [CrossRef]
- Hameed, A.S.; Resmi, T.R.; Suraj, S.; Warrier, C.U.; Sudheesh, M.; Deshpande, R.D. Isotopic characterization and mass balance reveals groundwater recharge pattern in Chaliyar river basin, Kerala, India. J. Hydrol. Reg. Stud. 2015, 4, 48–58. [Google Scholar] [CrossRef]
- Warrier, C.U.; Babu, M.P.; Manjula, P.; Velayudhan, K.T.; Hameed, A.S.; Vasu, K. Isotopic characterization of dual monsoon precipitation—Evidence from Kerala, India. Curr. Sci. 2010, 99, 1487–1495. [Google Scholar]
- Seena, G.; Muraleedharan, K.R.; Revichandran, C.; Abdul Azeez, S.; John, S. Seasonal spreading and transport of buoyant plumes in the shelf off Kochi, southwest coast of India—A modeling approach. Sci. Rep. 2019, 9, 19956. [Google Scholar] [CrossRef] [PubMed]
- Torgersen, T. Isotopic composition of river runoff on the US East Coast: Evaluation of stable isotope versus salinity plots for coastal water mass identification. J. Geophys. Res. Ocean 1979, 84, 3773–3775. [Google Scholar] [CrossRef]
- Fairbanks, R.G.; Sverdlove, M.; Free, R.; Wiebe, P.H.; Bé, A.W. Vertical distribution and isotopic fractionation of living planktonic foraminifera from the Panama B—Asin. Nature 1982, 298, 841. [Google Scholar] [CrossRef]
- Khim, B.-K.; Park, B.-K.; Yoon, H.-I. Oxygen isotopic compositions of seawater in the Maxwell Bay of King George Island, west Antarctica. Geosci. J. 1997, 1, 115. [Google Scholar] [CrossRef]
- Samanta, S.; Dalai, T.K.; Tiwari, S.K.; Rai, S.K. Quantification of source contributions to the water budgets of the Ganga (Hooghly) River estuary, India. Mar. Chem. 2018, 207, 42–54. [Google Scholar] [CrossRef]
- Kaushal, R.; Ghosh, P.; Geilmann, H. Fingerprinting environmental conditions and related stress using stable isotopic composition of rice (Oryza sativa L.) grain organic matter. Ecol. Indic. 2016, 61, 941–951. [Google Scholar] [CrossRef]
- Nagarathinam, A.; Retnamma, J.; Loganathan, J.; Singaram, P.; Madam, S.M.K.; Jose, A.K.; Subramanian, P.R. Implications of an extensive salt water barrage on the distribution of black clam in a tropical estuarine system, Southwest coast of India. Oceanologia 2021, 63, 343–355. [Google Scholar] [CrossRef]

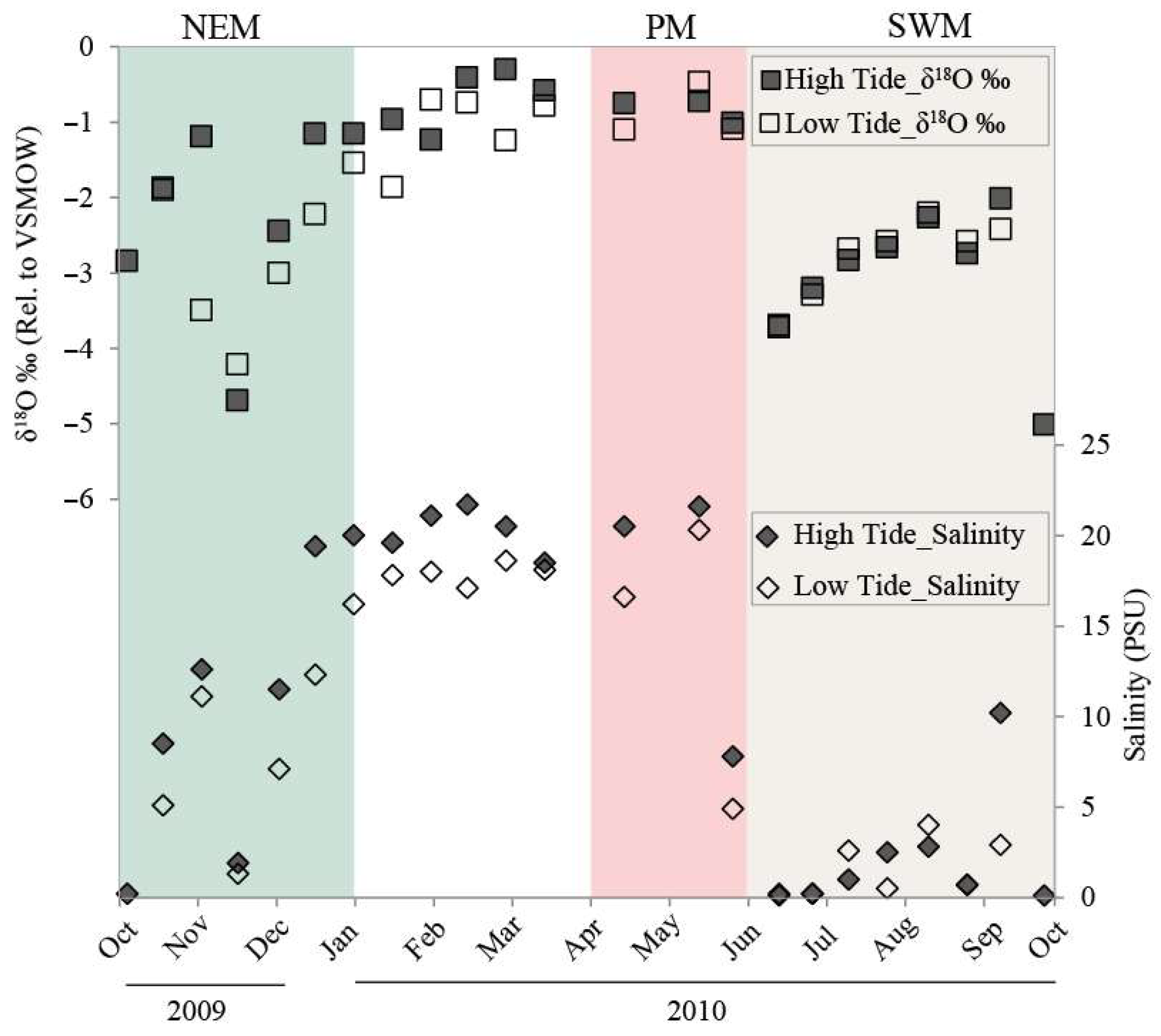


| Date of Sample Collection | Seasons | δ18OVSMOW (‰) | Salinity | ||
|---|---|---|---|---|---|
| High Tide | Low Tide | High Tide | Low Tide | ||
| 4-October | Northeast Monsoon | −2.84 | 0.2 | ||
| 18-October | −1.87 | −1.9 | 8.5 | 5.1 | |
| 2-November | −1.19 | −3.49 | 12.6 | 11.1 | |
| 16-November | −4.69 | −4.21 | 1.9 | 1.3 | |
| 2-December | −2.44 | −3 | 11.5 | 7.1 | |
| 16-December | −1.15 | −2.22 | 19.4 | 12.3 | |
| 31-December | −1.15 | −1.54 | 20 | 16.2 | |
| 15-January | −0.96 | −1.86 | 19.6 | 17.8 | |
| 30-January | −1.23 | −0.7 | 21.1 | 18 | |
| 13-February | Premonsoon | −0.41 | −0.74 | 21.7 | 17.1 |
| 28-February | −0.3 | −1.24 | 20.5 | 18.6 | |
| 15-March | −0.58 | −0.78 | 18.5 | 18.1 | |
| 15-April | −0.75 | −1.1 | 20.5 | 16.6 | |
| 14-May | −0.72 | −0.47 | 21.6 | 20.3 | |
| 27-May | −1.01 | −1.09 | 7.8 | 4.9 | |
| 14-June | Southwest Monsoon | −3.72 | −3.69 | 0.2 | 0.1 |
| 27-June | −3.2 | −3.29 | 0.2 | 0.2 | |
| 11-July | −2.83 | −2.68 | 1 | 2.6 | |
| 26-July | −2.66 | −2.58 | 2.5 | 0.5 | |
| 11-August | −2.26 | −2.2 | 2.8 | 4 | |
| 26-August | −2.74 | −2.58 | 0.7 | 0.7 | |
| 8-September | −2.01 | −2.42 | 10.2 | 2.9 | |
| 25-September | −5.01 | 0.1 | |||
| Sl. No | Location | Lat (oN) | Long (oE) | Salinity (PSU) | δ18O (‰ VSMOW) | δ13CDIC (‰ VPDB) |
|---|---|---|---|---|---|---|
| 1 | Thevara ferry | 9.926 | 76.304 | 0.10 | 0.42 | −5.60 |
| 2 | Panangad | 9.883 | 76.331 | 18.80 | 0.54 | −5.64 |
| 3 | Arror | 9.882 | 76.307 | 17.60 | 0.89 | −10.52 |
| 4 | Kudapuram (Eramallor) | 9.829 | 76.320 | 15.70 | NA | −9.01 |
| 5 | Kodamthuruthu (Kuthiathodu) | 9.803 | 76.326 | 13.10 | 2.49 | −9.60 |
| 6 | Thykkatusherry | 9.773 | 76.331 | 11.70 | 3.31 | −11.10 |
| 7A | Vyalar | 9.718 | 76.345 | 10.40 | 1.52 | −9.62 |
| 7B | Vyalar | 9.718 | 76.350 | 10.40 | 0.43 | −8.58 |
| 8 | Punnamada | 9.508 | 76.353 | 2.10 | 0.50 | −14.09 |
| 9 | Aaryad | 9.544 | 76.353 | 0.10 | 1.76 | −17.23 |
| 10 | Pallathuserry | 9.563 | 76.356 | 0.10 | 0.53 | −21.34 |
| 11 | Muhamma | 9.604 | 76.362 | 3.40 | 1.23 | −17.03 |
| 12 | Thalayazham (Puthanpalam) | 9.692 | 76.413 | 10.40 | 2.00 | −11.97 |
| 13 | Vaikom | 9.749 | 76.389 | 11.60 | 3.06 | −9.33 |
| 14 | Kulasekaramagalam (Mekara) | 9.799 | 76.379 | 11.90 | 0.78 | −8.04 |
| 15 | Punnakkaveli (South Paravoor) | 9.855 | 76.379 | 12.45 | 2.45 | −7.74 |
| 16 | Chavakakadavuamera (Udayamperoor) | 9.894 | 76.363 | 16.40 | 1.59 | −7.20 |
| 17 | Fort Kochi | 9.968 | 76.244 | 28.00 | −1.75 | −2.90 |
| Feature Name | Role | Type | Unit/Description | Preprocessing Steps |
|---|---|---|---|---|
| Latitude | Predictor | Continuous | Degrees North (°N) | Normalized to a range using Min–Max scaling |
| Longitude | Predictor | Continuous | Degrees East (°E) | Normalized to a range using Min–Max scaling |
| Month | Predictor | Continuous | Numerical representation of the month (1 = January, …, 12 = December). | Normalized to a range using Min–Max scaling |
| Tide Phase | Predictor | Categorical | The tidal state during sampling (‘High Tide’ or ‘Low Tide’). | Converted to a binary numerical format: High Tide = 1, Low Tide = 0 |
| Salinity | Target | Continuous | Practical Salinity Units (PSU) | Normalized to a range using Min–Max scaling |
| δ18O | Target | Continuous | Isotopic ratio relative to Vienna Standard Mean Ocean Water (‰ VSMOW). | Normalized to a range using Min–Max scaling. The single missing value from the spatial dataset was imputed via Gaussian Process Regression, using salinity as a covariance kernel |
| δ13C | Target | Continuous | Isotopic ratio relative to Vienna Pee Dee Belemnite (‰ VPDB). | Normalized to a range using Min–Max scaling |
| Model | Target | RMSE | R2 | MAPE (%) | T-Test (p-Value) |
|---|---|---|---|---|---|
| GBM | Salinity | 0.0993 | 0.9563 | N/A | <0.001 |
| GPR | δ18O | 0.6298 | −5.7860 | N/A | 0.045 |
| CART | δ13C | 0.3449 | −2.0460 | N/A | 0.089 |
| ELM | δ18O | 0.9187 | −13.440 | N/A | 0.103 |
| ELM | δ13C | 0.7626 | −13.890 | N/A | 0.097 |
| RBNN | δ18O | 0.2869 | −0.4080 | N/A | <0.001 |
| RBNN | δ13C | 0.2626 | −0.7660 | N/A | <0.001 |
| RF | δ18O | 0.2101 | 0.2451 | 36.19 | <0.001 |
| RF | δ13C | 0.2489 | −0.5869 | 34.90 | 0.032 |
| SVM | δ18O | 0.2500 | −0.0695 | 39.16 | 0.071 |
| SVM | δ13C | 0.2556 | −0.6722 | 25.88 | 0.089 |
| KNN | δ18O | 0.1703 | 0.5039 | 29.87 | <0.001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
K., P.; Rangarajan, R.; Thabit, F.; Ghosh, P.; Rahman, H. Seasonal Freshwater Inflows in Cochin Backwater Estuary Inferred from Stable Isotopes and Machine Learning. Hydrology 2025, 12, 277. https://doi.org/10.3390/hydrology12110277
K. P, Rangarajan R, Thabit F, Ghosh P, Rahman H. Seasonal Freshwater Inflows in Cochin Backwater Estuary Inferred from Stable Isotopes and Machine Learning. Hydrology. 2025; 12(11):277. https://doi.org/10.3390/hydrology12110277
Chicago/Turabian StyleK., Prasanna, Ravi Rangarajan, Fursan Thabit, Prosenjit Ghosh, and Habeeb Rahman. 2025. "Seasonal Freshwater Inflows in Cochin Backwater Estuary Inferred from Stable Isotopes and Machine Learning" Hydrology 12, no. 11: 277. https://doi.org/10.3390/hydrology12110277
APA StyleK., P., Rangarajan, R., Thabit, F., Ghosh, P., & Rahman, H. (2025). Seasonal Freshwater Inflows in Cochin Backwater Estuary Inferred from Stable Isotopes and Machine Learning. Hydrology, 12(11), 277. https://doi.org/10.3390/hydrology12110277







