Improving Soil Water Simulation in Semi-Arid Agriculture: A Comparative Evaluation of Water Retention Curves and Inverse Modeling Using HYDRUS-1D
Abstract
1. Introduction
2. Materials and Methods
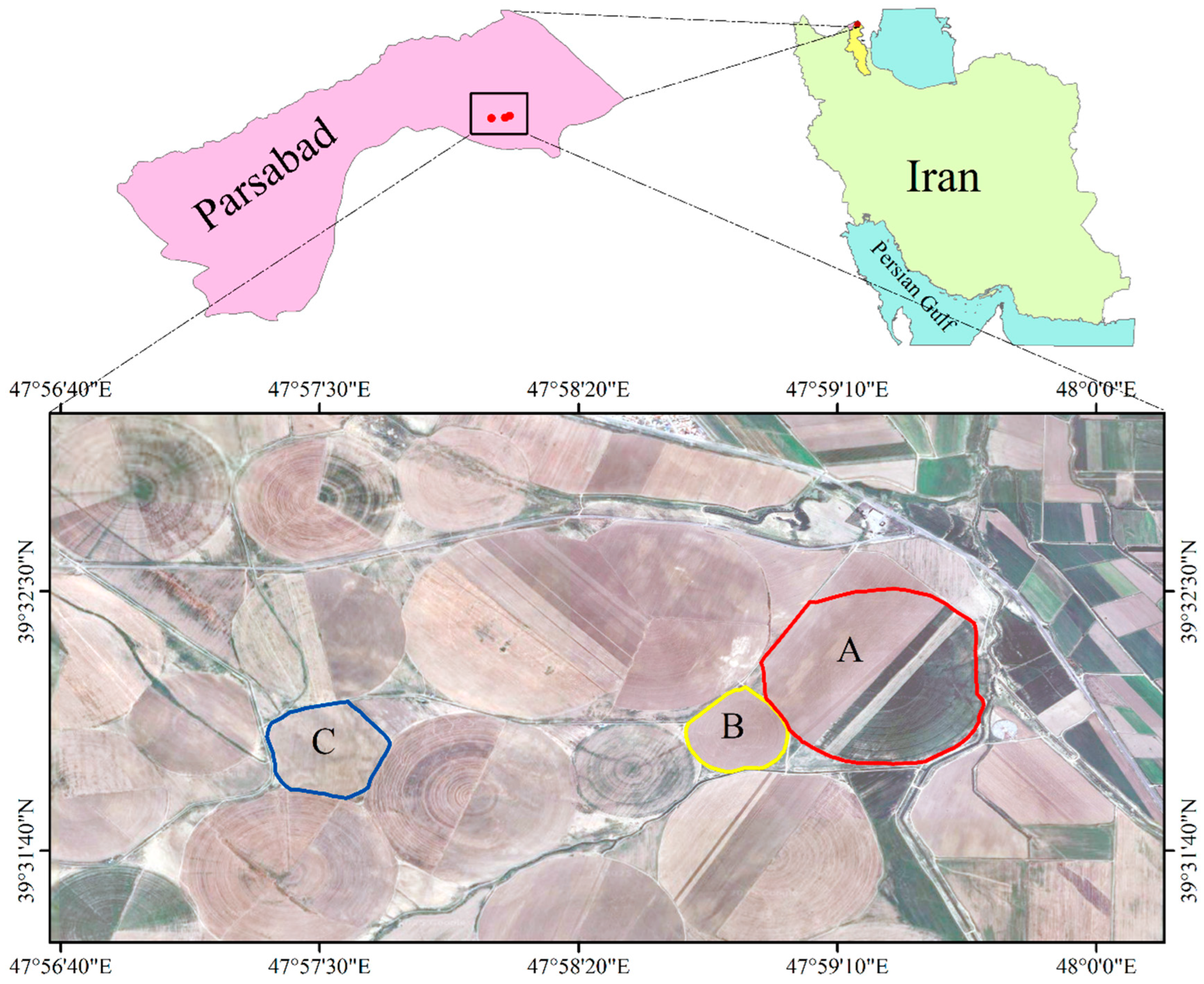
2.1. Study Area
2.2. Field Studies
2.3. Laboratory Analyses
2.4. Numerical Modeling
2.4.1. One-Dimensional Richards Equation
2.4.2. Drying Branch of the SWRC
2.4.3. Wetting Branch of the SWRC
2.4.4. Inverse Modeling
2.5. Statistical Evaluation
3. Results and Discussion
3.1. Climatic Conditions During the Study Period
3.2. Physical and Chemical Properties of Soil and Irrigation Water
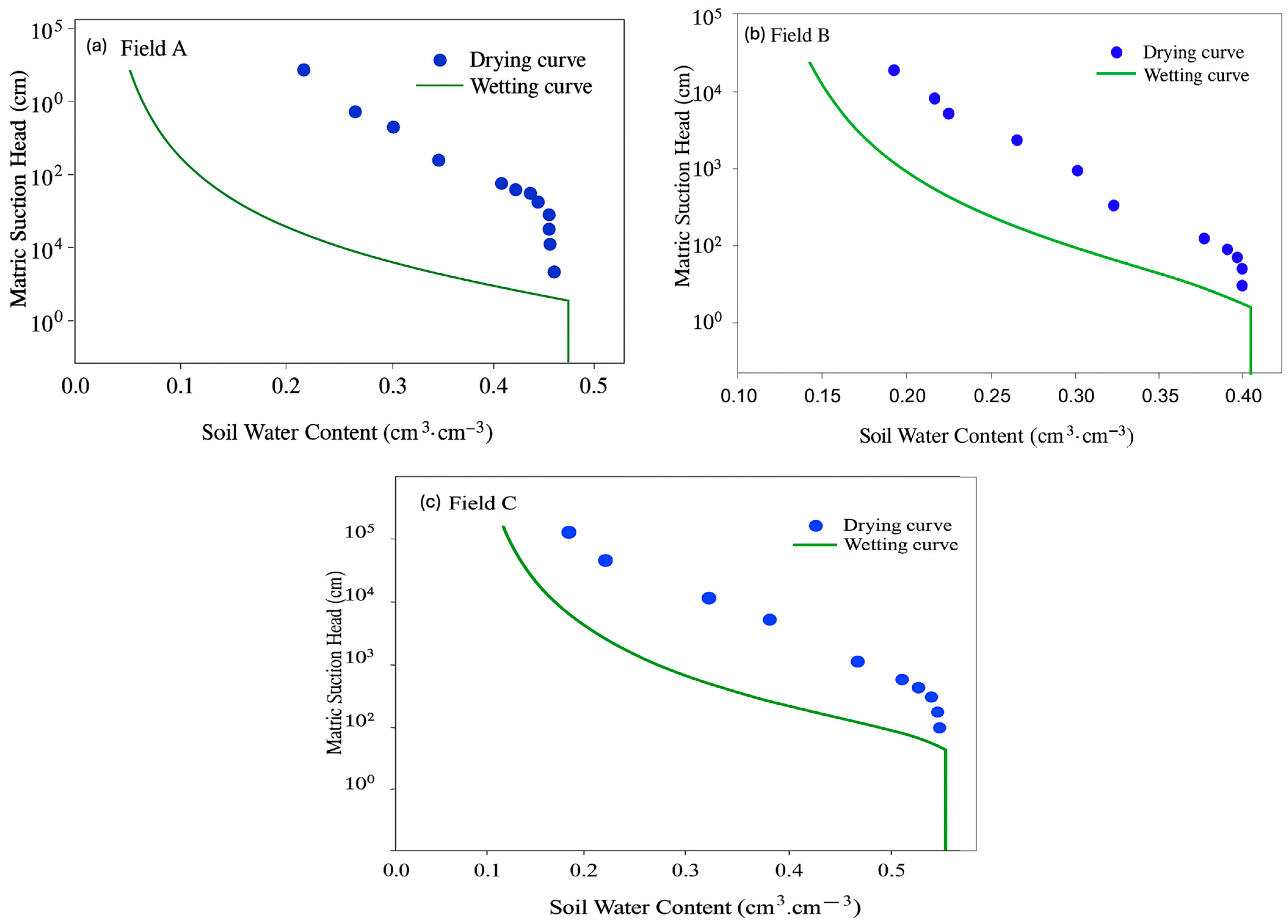
3.3. Drying and Wetting Branches of the SWRC
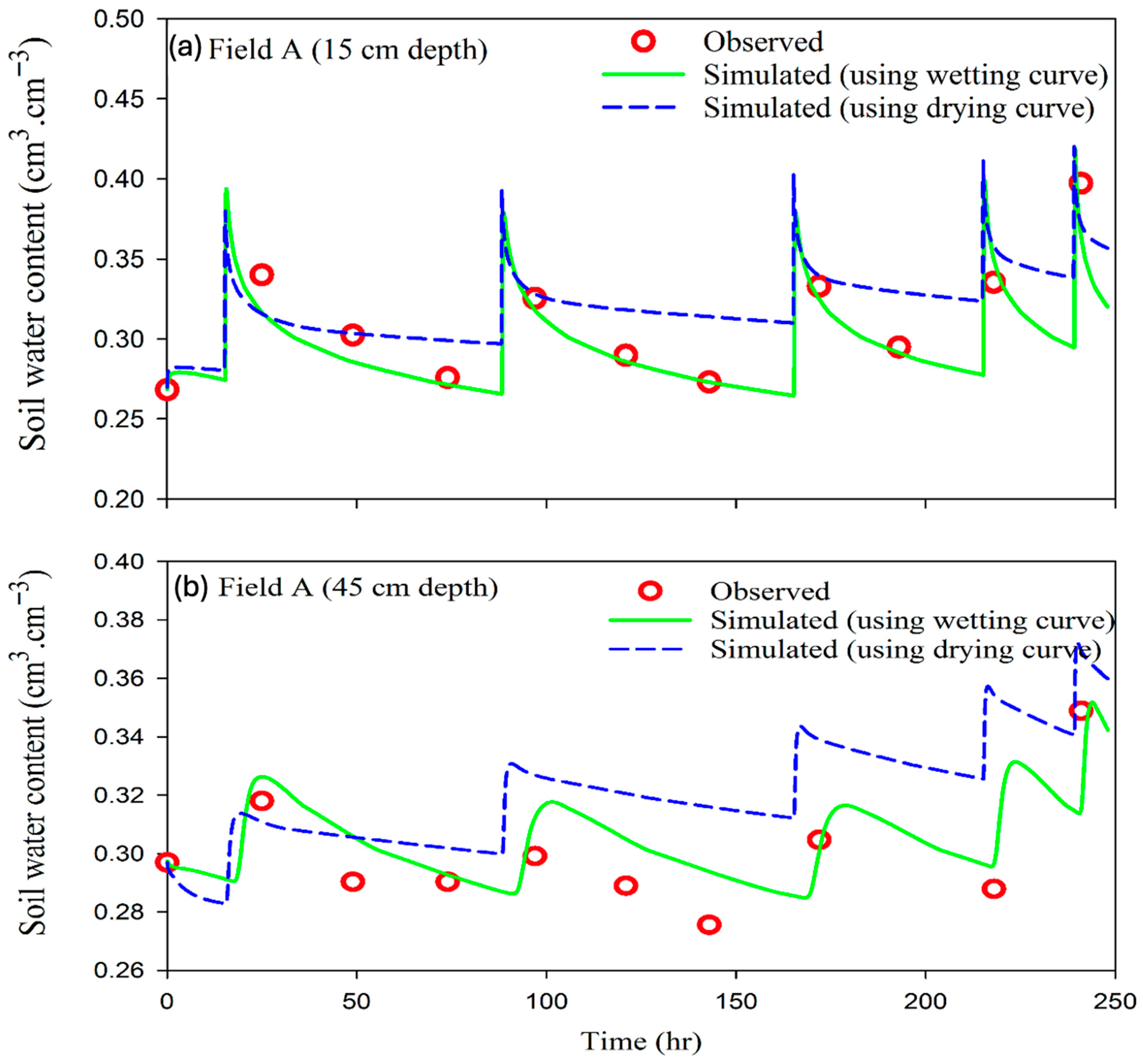
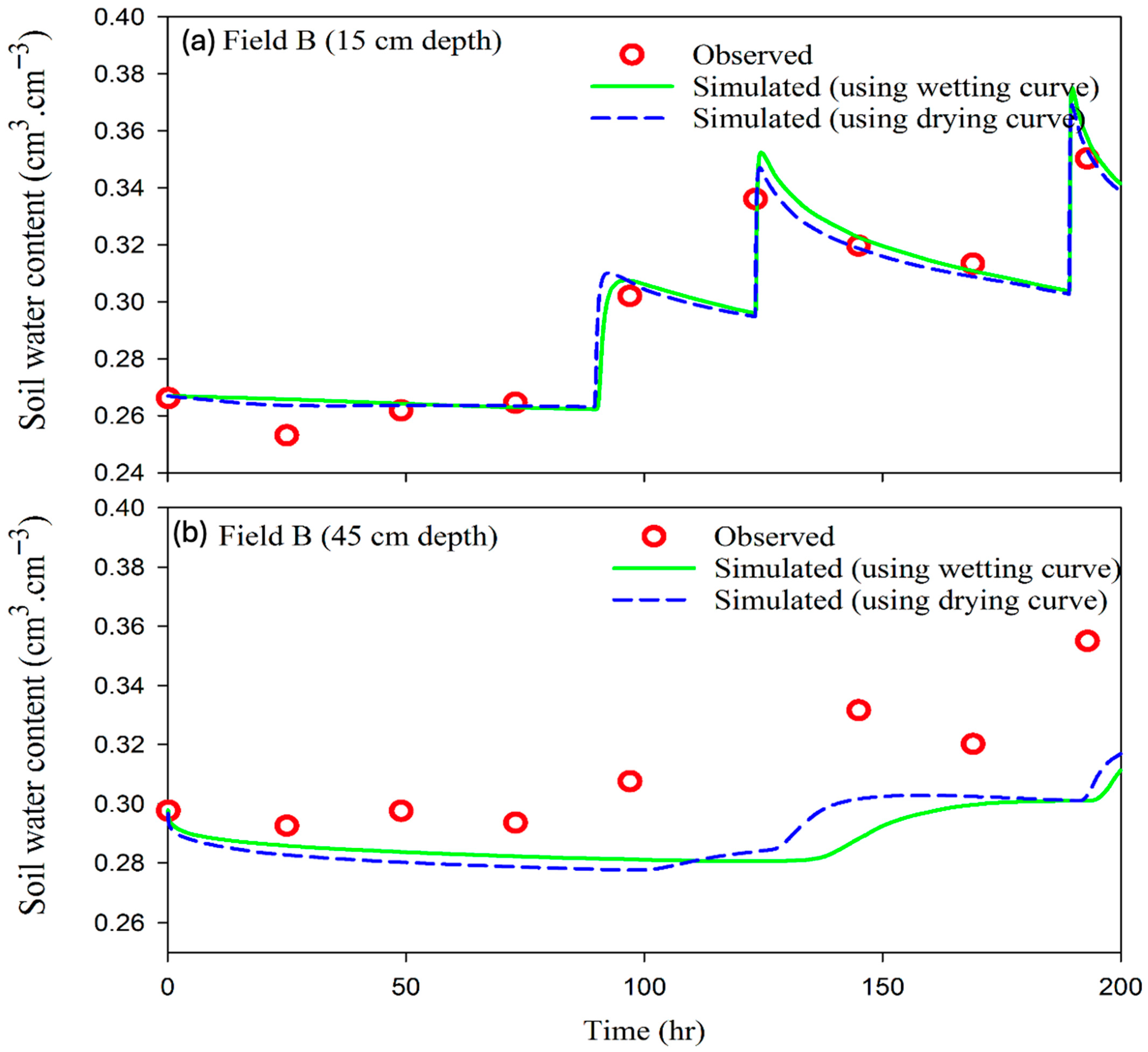
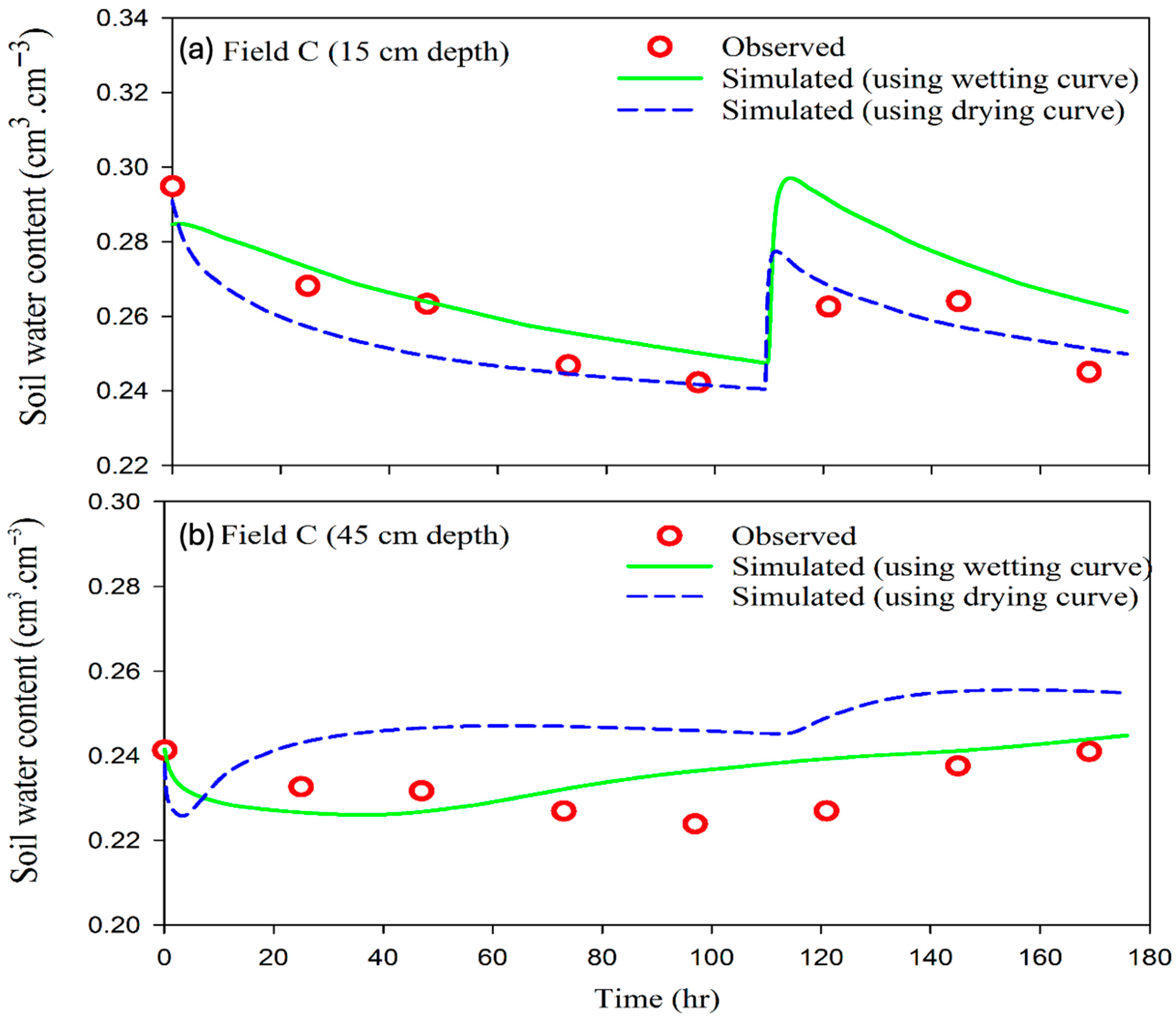
3.4. Soil Water Content Simulations Using the Drying and Wetting Branches of SWRC
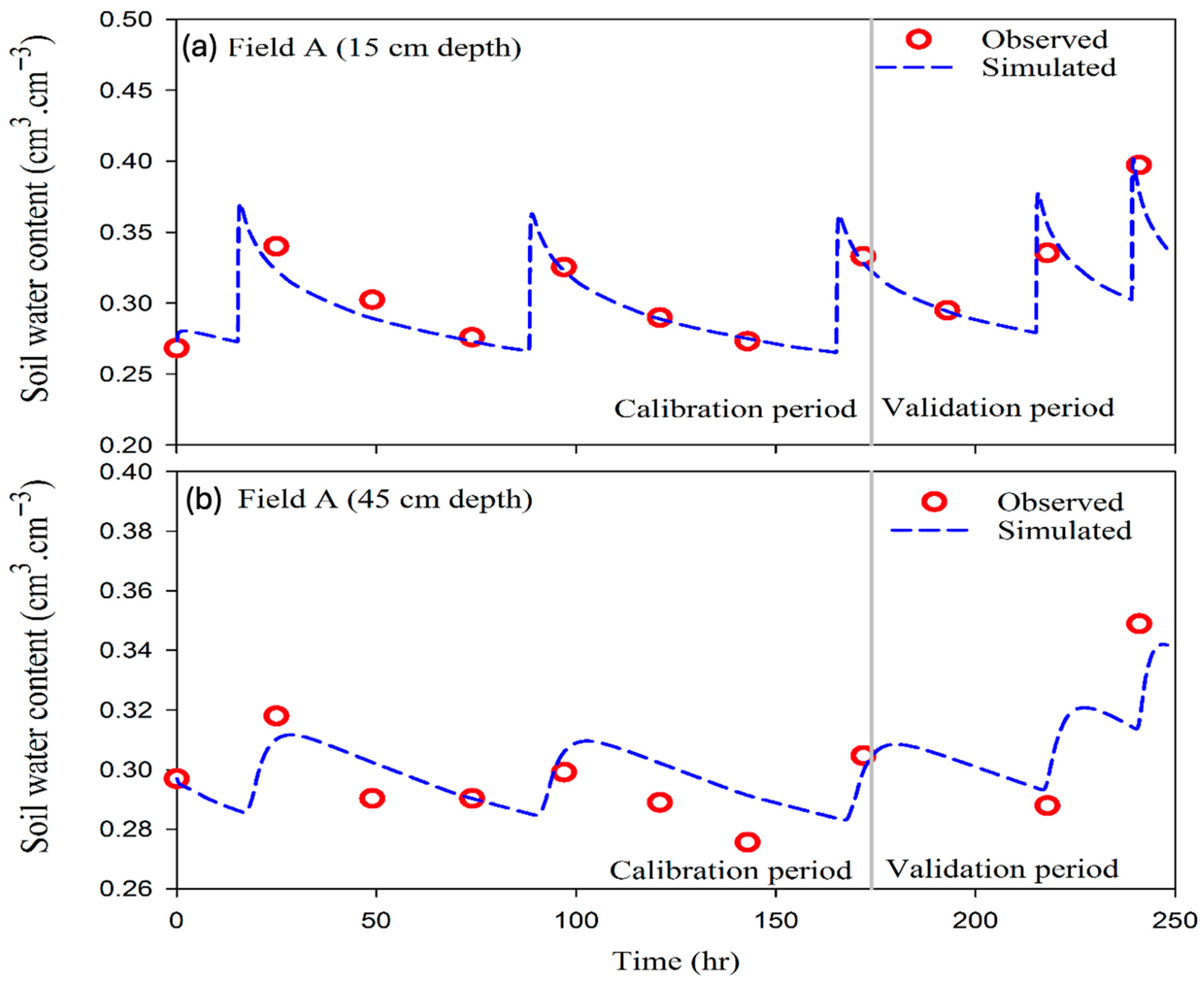
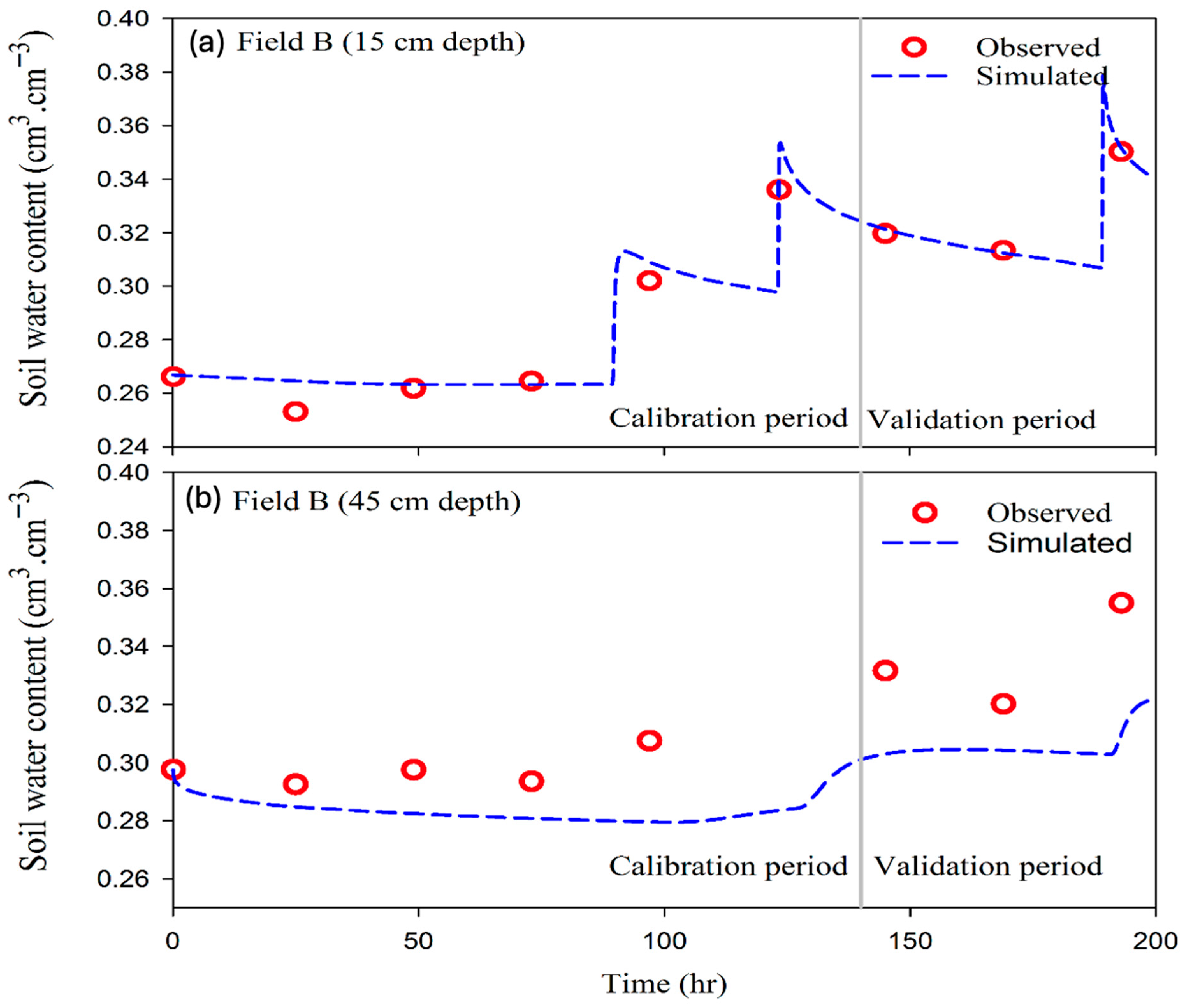
3.5. Soil Water Content Simulation Using the Inverse Modeling Approach
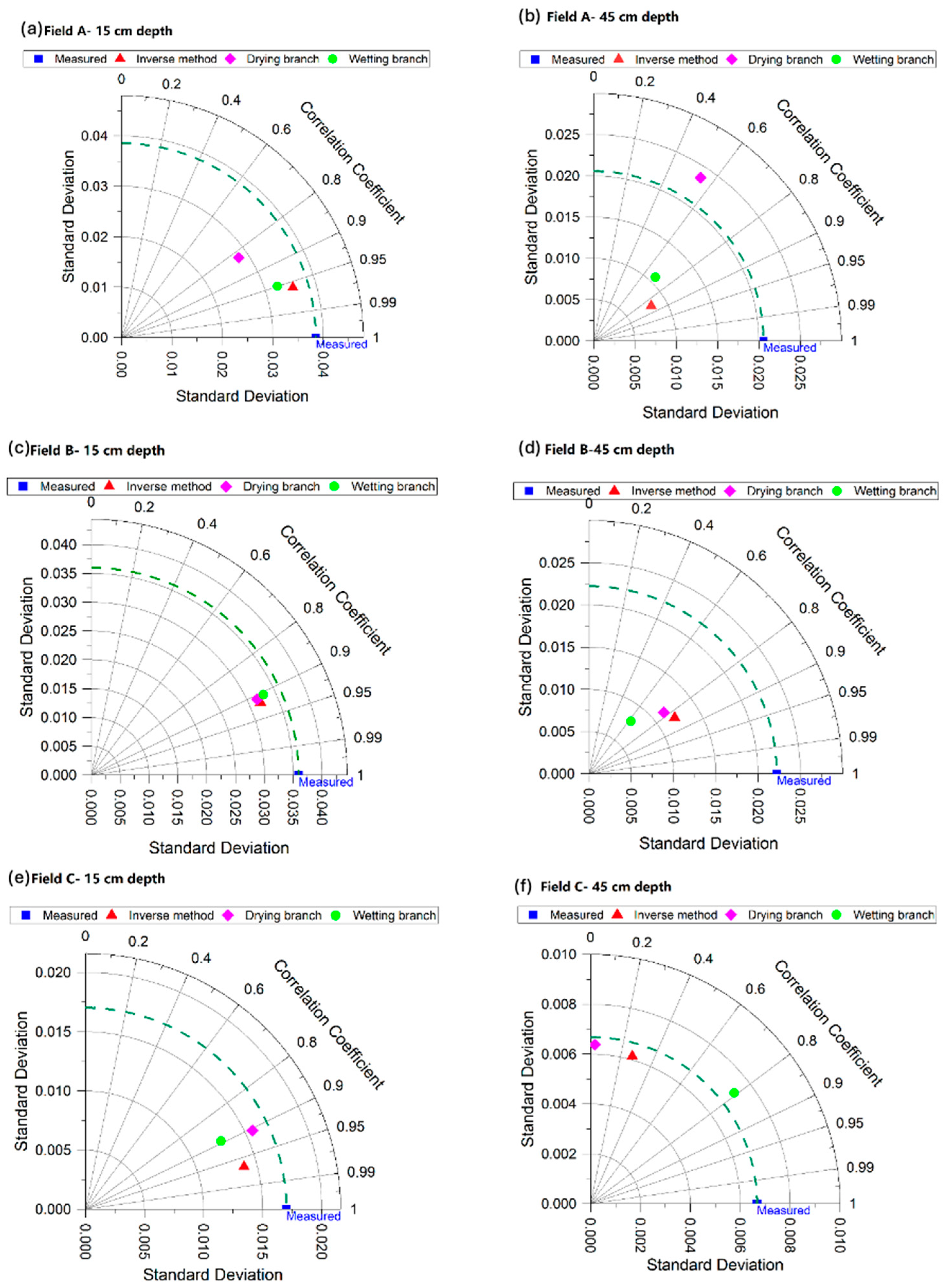
3.6. Comparison Evaluation Using Taylor Diagrams
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lou, B.; Hu, Y.; Li, T.; Liu, Q.; Wang, J.; Dong, X.; Tian, L.; Zhang, X.; Bian, W.; Liu, T. Assessment of saline water irrigation on biomass and quality of alfalfa: A sustainable agriculture perspective. Agric. Water Manag. 2025, 314, 109504. [Google Scholar] [CrossRef]
- Muhammed, H.H.; Anlauf, R.; Daum, D. Estimation of Hydraulic Properties of Growing Media from Numerical Inversion of Mini Disk Infiltrometer Data. Hydrology 2025, 12, 100. [Google Scholar] [CrossRef]
- Li, J.; Jiao, X.; Jiang, H.; Song, J.; Chen, L. Optimization of irrigation scheduling for maize in an arid oasis based on simulation–optimization model. Agronomy 2020, 10, 935. [Google Scholar] [CrossRef]
- Šimůnek, J.; Hopmans, J.W. 1.7 parameter optimization and nonlinear fitting. Methods Soil Anal. Part 4 Phys. Methods 2002, 5, 139–157. [Google Scholar] [CrossRef]
- Twarakavi, N.K.C.; Šimůnek, J.; Seo, S. Evaluating interactions between groundwater and vadose zone using the HYDRUS-based flow package for MODFLOW. Vadose Zone J. 2008, 7, 757–768. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Šimůnek, J.; Shi, H.; Chen, N.; Hu, Q. Quantifying water and salt movement in a soil-plant system of a corn field using HYDRUS (2D/3D) and the stable isotope method. Agric. Water Manag. 2023, 288, 108492. [Google Scholar] [CrossRef]
- Xu, C.; Zeng, W.-Z.; Wu, J.-W.; Huang, J.-S. Effects of different irrigation strategies on soil water, salt, and nitrate nitrogen transport. Ecol. Chem. Eng. 2015, 22, 589. [Google Scholar] [CrossRef]
- Arbat Pujolràs, G.; Cufí Aregay, S.; Duran i Ros, M.; Pinsach i Boada, J.; Puig Bargués, J.; Pujol Planella, J.; Ramírez de Cartagena Bisbe, F. Modeling Approaches for Determining Dripline Depth and Irrigation Frequency of Subsurface Drip Irrigated Rice on Different Soil Textures. Water 2020, 12, 1724. [Google Scholar] [CrossRef]
- Raoof, M.; Akbari Baseri, Z.; Rasoulzadeh, A.; Azizi Mobaser, J. Sensitivity analysis of Hydrus software to input data in simulating water movement and root uptake of grass as a reference plant. Water Soil Manag. Model. 2022, 2, 94–107. [Google Scholar] [CrossRef]
- Kim, D.H.; Kim, J.; Kwon, S.H.; Jung, K.-Y.; Lee, S.H. Simulation of soil water movement in upland soils under sprinkler and spray hose irrigation using HYDRUS-1D. J. Biosyst. Eng. 2022, 47, 448–457. [Google Scholar] [CrossRef]
- Feng, Z.; Miao, Q.; Shi, H.; Feng, W.; Li, X.; Yan, J.; Liu, M.; Sun, W.; Dai, L.; Liu, J. Simulation of water balance and irrigation strategy of typical sand-layered farmland in the Hetao Irrigation District, China. Agric. Water Manag. 2023, 280, 108236. [Google Scholar] [CrossRef]
- Etminan, S.; Jalali, V.; Mahmodabadi, M.; Khashei-Siuki, A.; Pourreza Bilondi, M. Assessing the hydraulic parameter’s uncertainty of the HYDRUS model using DREAM method. Water Soil Manag. Model. 2022, 3, 1–15. [Google Scholar] [CrossRef]
- Nouri, A.; Sadraddini, A.A.; Samadianfard, S.; Mikaeili, F. Simulation of moisture distribution in different soil textures under a point source using the moment analysis method. Water Soil Manag. Modeling 2024, 4, 167–182. [Google Scholar] [CrossRef]
- Elliott, J. Evaluating Parameter Fitting and Model Design for Unsaturated Processes in Peatlands; University of Waterloo: Waterloo, ON, Canada, 2019. [Google Scholar]
- Rasoulzadeh, A.; Sepaskhah, A. Advanced Topics in Soil Water Physics; University of Mohaghegh Ardabili: Ardabil, Iran, 2021; ISBN 978-622-7258-86-8. [Google Scholar]
- Singh, A.; Verdi, A. Estimating the soil water retention curve by the HYPROP-WP4C system, HYPROP-based PCNN-PTF and inverse modeling using HYDRUS-1D. J. Hydrol. 2024, 639, 131657. [Google Scholar] [CrossRef]
- Shani, U.; Hanks, R.; Bresler, E.; Oliveira, C. Field method for estimating hydraulic conductivity and matric potential-water content relations. Soil Sci. Soc. Am. J. 1987, 51, 298–302. [Google Scholar] [CrossRef]
- Scott, P.; Farquhar, G.; Kouwen, N. Hysteretic Effects on Net Infiltration. In Advances in Infiltration; American Society of Agricultural Engineers Publication: St. Joseph, MI, USA, 1983; pp. 163–170. [Google Scholar]
- Kool, J.; Parker, J.C. Development and evaluation of closed-form expressions for hysteretic soil hydraulic properties. Water Resour. Res. 1987, 23, 105–114. [Google Scholar] [CrossRef]
- Varsa, E.; Chong, S.; Abolaji, J.; Farquhar, D.; Olsen, F. Effect of deep tillage on soil physical characteristics and corn (Zea mays L.) root growth and production. Soil Tillage Res. 1997, 43, 219–228. [Google Scholar] [CrossRef]
- Bandyopadhyay, K.; Aggarwal, P.; Chakraborty, D.; Pradhan, S.; Garg, R.N.; Singh, R. Practical Manual on Measurement of Soil Physical Properties; Division of Agricultural Physics, Indian Agricultural Research Institute: New Delhi, India, 2012; Volume 62. [Google Scholar]
- Jabro, J.D.; Stevens, W.B.; Iversen, W.M. Comparing two methods for measuring soil bulk density and moisture content. Open J. Soil Sci. 2020, 10, 233–243. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, Y.; Li, X.; Liu, L.; Lu, Y.; Ren, T. Measuring soil particle density using water pycnometer: Influencing factors, errors, and correction. Soil Sci. Soc. Am. J. 2025, 89, e70073. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Bezaatpour, J.; Mobaser, J.A.; Fernández-Gálvez, J. Performance of a set of soil water retention models for fitting soil water retention data covering all textural classes. Land 2024, 13, 487. [Google Scholar] [CrossRef]
- Feddes, R.; Kowalik, P.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1978. [Google Scholar]
- Wesseling, J. Steady State Moisture Flow Theory; Program Description; User Manual; Report; The Winand Staring Centre: Wageningen, The Netherlands, 1991; Volume 37. [Google Scholar]
- Rasoulzadeh, A.; Homapoor Ghoorabjiri, M. Comparing hydraulic properties of different forest floors. Hydrol. Process. 2014, 28, 5122–5130. [Google Scholar] [CrossRef]
- Rasoulzadeh, A.; Yaghoubi, A. Inverse modeling approach for determining soil hydraulic properties as affected by application of cattle manure. Int. J. Agric. Biol. Eng. 2014, 7, 27–35. [Google Scholar] [CrossRef]
- Autovino, D.; Bagarello, V.; Caltabellotta, G.; Fusco, M.; Iovino, M. Determining saturated hydraulic conductivity of a repacked loam soil by the simplified falling-head technique: Impact of sieving duration and scraping of exposed surfaces. Soil Water Res. 2024, 19, 210–217. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15, 1–25. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.; Leij, F.; Yates, S. The RETC Code for Quantifying the Hydraulic Functions of Unsaturated Soils; Robert S. Kerr Environmental Research Laboratory, Office of Research and Development, US Environmental Protection Agency: Ada, OK, USA, 1992. [Google Scholar]
- Wooding, R. Steady infiltration from a shallow circular pond. Water Resour. Res. 1968, 4, 1259–1273. [Google Scholar] [CrossRef]
- Brooks, R.; Corey, A. Hydraulic Properties of Porous Media. Hydrology Paper No. 3; Civil Engineering Department, Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Li, M.-F.; Tang, X.-P.; Wu, W.; Liu, H.-B. General models for estimating daily global solar radiation for different solar radiation zones in mainland China. Energy Convers. Manag. 2013, 70, 139–148. [Google Scholar] [CrossRef]
- Zakizadeh Abkenar, F.; Rasoulzadeh, A. Functional evaluation of Pedotransfer functions for simulation of soil profile drainage. Irrig. Drain. 2019, 68, 573–587. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Water Quality for Agriculture; Food and Agriculture Organization of the United Nations Rome: Rome, Italy, 1985; Volume 29. [Google Scholar]
- Abdoli, S.; Rahmati, M.; Ahmadi, H.; Kamali, B.; Groh, J.; Vereecken, H. Interplay of soil moisture memory and soil hysteresis. Authorea Prepr. 2024. [Google Scholar] [CrossRef]
- Yu, J.; Wu, Y.; Xu, L.; Peng, J.; Chen, G.; Shen, X.; Lan, R.; Zhao, C.; Zhangzhong, L. Evaluating the Hydrus-1D model optimized by remote sensing data for soil moisture simulations in the maize root zone. Remote Sens. 2022, 14, 6079. [Google Scholar] [CrossRef]
- Chen, M.; Willgoose, G.R.; Saco, P.M. Spatial prediction of temporal soil moisture dynamics using HYDRUS-1D. Hydrol. Process. 2014, 28, 171–185. [Google Scholar] [CrossRef]
- Dexter, A.; Czyż, E.; Richard, G.; Reszkowska, A. A user-friendly water retention function that takes account of the textural and structural pore spaces in soil. Geoderma 2008, 143, 243–253. [Google Scholar] [CrossRef]
- Etminan, S.; Mahmoodabadi, M.; Khashei Siuki, A.; Pourreza Bilondi, M. Investigating the effect of optimizing soil hydraulic parameters with inverse and parametric solution methods in increasing the accuracy of water movement simulation with HYDRUS. Appl. Soil Res. 2021, 9, 15–30. [Google Scholar]
- Ritter, A.; Hupet, F.; Muñoz-Carpena, R.; Lambot, S.; Vanclooster, M. Using inverse methods for estimating soil hydraulic properties from field data as an alternative to direct methods. Agric. Water Manag. 2003, 59, 77–96. [Google Scholar] [CrossRef]
- Scharnagl, B.; Vrugt, J.; Vereecken, H.; Herbst, M. Inverse modelling of in situ soil water dynamics: Investigating the effect of different prior distributions of the soil hydraulic parameters. Hydrol. Earth Syst. Sci. 2011, 15, 3043–3059. [Google Scholar] [CrossRef]


| Date | Wind Speed (m s−1) | Max T (°C) | Min T (°C) | Humidity (%) | Sunshine (h) | Rn (MJ m−2 d−1) |
|---|---|---|---|---|---|---|
| 12 August 2024 | 4.35 | 24.8 | 15.0 | 62 | 8.9 | 8.87 |
| 13 August 2024 | 3.44 | 24.0 | 12.4 | 66 | 7.2 | 8.54 |
| 14 August 2024 | 3.44 | 27.3 | 10.1 | 61 | 11.2 | 9.97 |
| 15 August 2024 | 4.53 | 22.8 | 13.4 | 87 | 3.2 | 7.19 |
| 16 August 2024 | 5.25 | 22.8 | 15.2 | 89 | 4.2 | 7.44 |
| 17 August 2024 | 5.8 | 22.1 | 11.3 | 78 | 10.4 | 9.76 |
| 18 August 2024 | 2.45 | 20.6 | 7.4 | 95 | 1.3 | 6.68 |
| 19 August 2024 | 2.54 | 24.6 | 13.7 | 86 | 4.9 | 7.72 |
| 20 August 2024 | 2.99 | 25.6 | 11.3 | 83 | 9.6 | 9.43 |
| 21 August 2024 | 2.54 | 27.5 | 10.4 | 80 | 10.0 | 9.57 |
| 22 August 2024 | 3.44 | 30.0 | 8.1 | 59 | 11.1 | 10.03 |
| 23 August 2024 | 3.53 | 32.0 | 12.4 | 63 | 11.7 | 9.8 |
| Field | Soil Depth (cm) | Soil Texture | EC (dS m−1) | Soil pH | (g cm−3) | (g cm−3) | Porosity (-) |
|---|---|---|---|---|---|---|---|
| A | 0–30 | Silty Clay Loam | 2.27 | 7.26 | 2.57 | 1.40 | 0.45 |
| 30–60 | Silty Clay Loam | 2.00 | 7.32 | 2.61 | 1.47 | 0.44 | |
| B | 0–30 | Silty Clay | 1.26 | 6.88 | 2.54 | 1.46 | 0.42 |
| 30–60 | Silty Clay | 1.70 | 7.46 | 2.64 | 1.53 | 0.42 | |
| C | 0–30 | Silty Clay | 2.20 | 7.09 | 2.75 | 1.23 | 0.55 |
| 30–60 | Silty Clay | 1.00 | 6.58 | 2.73 | 1.24 | 0.55 |
| Method | Parameter | Field A | Field B | Field C |
|---|---|---|---|---|
| Pressure plate method (van Genuchten model) | θr | 0.151 | 0.189 | 0.000 † |
| θs | 0.460 | 0.430 | 0.550 | |
| α (1 cm−1) | 0.014 | 0.031 | 0.007 | |
| n | 1.304 | 1.436 | 1.191 | |
| Ks (cm h−1) | 27.4 | 18.6 | 10.92 | |
| Shani method (Brooks–Corey model) | θr | 0.077 | 0.154 | 0.117 |
| θs | 0.460 | 0.430 | 0.550 | |
| α (1 cm−1) | 0.835 | 0.766 | 0.560 | |
| λ | 0.283 | 0.244 | 0.334 | |
| Ks (cm h−1) | 36.4 | 21.2 | 19.8 |
| Field | Depth (cm) | RMSE (cm3 cm−3) | MAE (cm3 cm−3) | NRMSE (%) |
|---|---|---|---|---|
| A | 15 | 0.023 | 0.019 | 7.48 |
| 45 | 0.031 | 0.026 | 10.46 | |
| B | 15 | 0.014 | 0.008 | 4.86 |
| 45 | 0.026 | 0.022 | 8.36 | |
| C | 15 | 0.008 | 0.006 | 2.90 |
| 45 | 0.017 | 0.016 | 7.21 |
| Location | Depth (cm) | RMSE (cm3 cm−3) | MAE (cm3 cm−3) | NRMSE (%) |
|---|---|---|---|---|
| A | 15 | 0.014 | 0.010 | 4.61 |
| 45 | 0.015 | 0.012 | 5.05 | |
| B | 15 | 0.014 | 0.008 | 4.87 |
| 45 | 0.028 | 0.022 | 8.97 | |
| C | 15 | 0.014 | 0.011 | 5.36 |
| 45 | 0.007 | 0.006 | 3.10 |
| Estimated Parameters | Field A | Field B | Field C | |||
|---|---|---|---|---|---|---|
| Value | SE | Value | SE | Value | SE | |
| θr | 0.013 | 0.132 | 0.087 | 0.182 | 0.021 | 0.297 |
| θs | 0.49 | 0.089 | 0.432 | 0.056 | 0.399 | 0.139 |
| α (1 cm−1) | 0.055 | 0.042 | 0.013 | 0.027 | 0.05 | 0.088 |
| n | 1.41 | 0.185 | 1.117 | 0.117 | 1.258 | 0.147 |
| Ks (cm h−1) | 7.825 | 11.476 | 3 | 4.822 | ||
| Field A | Field B | Field C | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θr | θs | α | n | Ks | θr | θs | α | n | θr | θs | α | n | Ks | |
| θr | 1.00 | 1.00 | 1.00 | |||||||||||
| θs | 0.11 | 1.00 | 0.39 | 1.00 | −0.85 | 1.00 | ||||||||
| α | 0.47 | 0.06 | 1.00 | 0.32 | −0.63 | 1.00 | 0.89 | −0.88 | 1.00 | |||||
| n | 0.67 | 0.40 | −0.22 | 1.00 | 0.88 | 0.45 | 0.28 | 1.00 | 0.15 | 0.33 | −0.14 | 1.00 | ||
| Ks | 0.22 | 0.61 | 0.73 | −0.17 | 1.00 | 0.65 | −0.74 | 0.76 | −0.47 | 1.00 | ||||
| Field | Depth (cm) | RMSE (cm3 cm−3) | MAE (cm3 cm−3) | NRMSE (%) |
|---|---|---|---|---|
| A | 15 | 0.011 | 0.008 | 3.47 |
| 45 | 0.014 | 0.010 | 4.52 | |
| B | 15 | 0.013 | 0.006 | 4.39 |
| 45 | 0.023 | 0.019 | 7.40 | |
| C | 15 | 0.006 | 0.005 | 2.29 |
| 45 | 0.009 | 0.007 | 3.74 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasoulzadeh, A.; Kohan, M.R.; Amirzadeh, A.; Heydari, M.; Mobaser, J.A.; Raoof, M.; Moghadam, J.R.; Fernández-Gálvez, J. Improving Soil Water Simulation in Semi-Arid Agriculture: A Comparative Evaluation of Water Retention Curves and Inverse Modeling Using HYDRUS-1D. Hydrology 2025, 12, 273. https://doi.org/10.3390/hydrology12100273
Rasoulzadeh A, Kohan MR, Amirzadeh A, Heydari M, Mobaser JA, Raoof M, Moghadam JR, Fernández-Gálvez J. Improving Soil Water Simulation in Semi-Arid Agriculture: A Comparative Evaluation of Water Retention Curves and Inverse Modeling Using HYDRUS-1D. Hydrology. 2025; 12(10):273. https://doi.org/10.3390/hydrology12100273
Chicago/Turabian StyleRasoulzadeh, Ali, Mohammad Reza Kohan, Arash Amirzadeh, Mahsa Heydari, Javanshir Azizi Mobaser, Majid Raoof, Javad Ramezani Moghadam, and Jesús Fernández-Gálvez. 2025. "Improving Soil Water Simulation in Semi-Arid Agriculture: A Comparative Evaluation of Water Retention Curves and Inverse Modeling Using HYDRUS-1D" Hydrology 12, no. 10: 273. https://doi.org/10.3390/hydrology12100273
APA StyleRasoulzadeh, A., Kohan, M. R., Amirzadeh, A., Heydari, M., Mobaser, J. A., Raoof, M., Moghadam, J. R., & Fernández-Gálvez, J. (2025). Improving Soil Water Simulation in Semi-Arid Agriculture: A Comparative Evaluation of Water Retention Curves and Inverse Modeling Using HYDRUS-1D. Hydrology, 12(10), 273. https://doi.org/10.3390/hydrology12100273






