Seasonal Design Floods Estimated by Stationary and Nonstationary Flood Frequency Analysis Methods for Three Gorges Reservoir
Abstract
Highlights
- The whole flood season of TGR is divided into four sub-periods based on seasonal rainy pattern variation characteristics.
- Seasonal design floods are estimated using stationary and nonstationary frequency analysis methods.
- Nonstationary seasonal 1000-year design floods of TGR have reduced by about 20% in the transition period.
- Flood control water level could rise from 145 m to 157 m, which can generate 2.288 billion kW h more hydropower.
Abstract
1. Introduction
2. Study Basin and Materials
2.1. Large-Scale Reservoir Groups in the Upper Yangtze River
2.2. Three Gorges Reservoir (TGR)
2.3. Data
3. Methodology
3.1. Flood Seasonal Division Methods
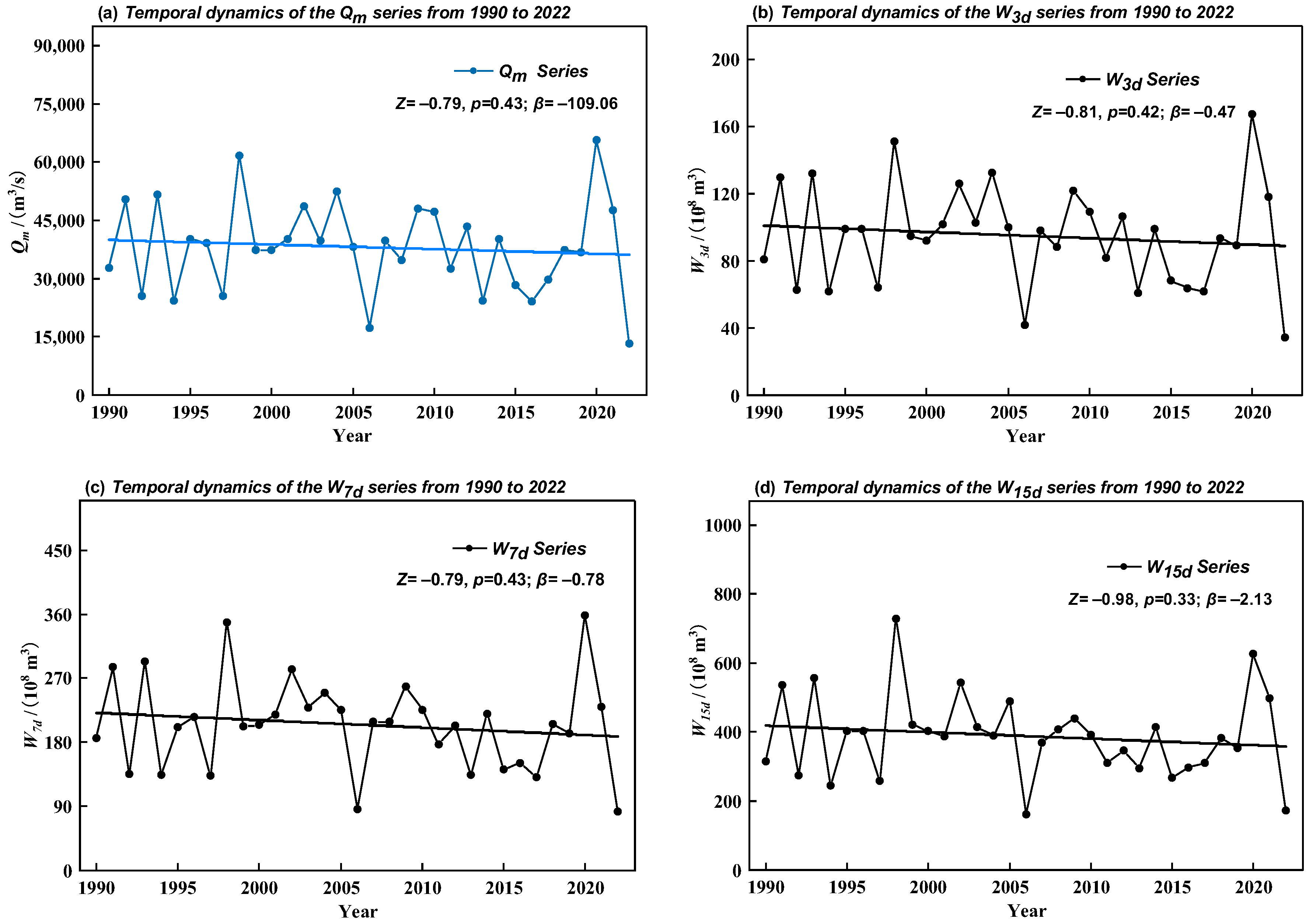
3.2. Detecting Temporal Dynamics of Flow Data Series
3.3. Flood Frequency Analysis Method in China
3.4. Nonstationary Flood Frequency Analysis Method
3.4.1. Time-Varying P-III Distribution
3.4.2. Time-Varying P-III Distribution Curve Fitting Method
4. Seasonal Design Flood Estimation Results
4.1. Flood Seasonal Division for TGR
4.2. Stationary Seasonal Flood Frequency Analysis Results
4.3. Nonstationary Flood Frequency Analysis Results
4.4. Derive Seasonal Design Flood Hydrograph and Flood Limited/Control Water Level
4.5. Hydropower Benefit Analysis
5. Discussion
6. Conclusions
- (1)
- The whole flood season of TGR can be divided into four periods, i.e., the reservoir drawdown period (1 May to 20 June), the Meiyu flood period (21 June to 31 July), the transition period (1 August to 10 September), and the Autumn Rain refill period (11 September to 30 October).
- (2)
- The time-varying P-III curve fitting method was employed to estimate the seasonal design floods in the transition period. Compared to the original design values, 1000-year seasonal design peak discharge and 15-day flood volume are reduced by 22.9% and 14.3%, respectively.
- (3)
- Nonstationary seasonal FCWL could be raised up from 145 m to 157 m while maintaining unchanged flood control standards, which can generate 2.288 billion kW·h more hydropower (or increase 16.57%) in the transition period from 1 August to 10 September.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jain, S.K.; Shilpa, L.S.; Rani, D.; Sudheer, K.P. State-of-the-art review: Operation of multi-purpose reservoirs during flood season. J. Hydrol. 2023, 618, 129165. [Google Scholar] [CrossRef]
- Mohammadi, P.; Ebrahimi, K.; Bazrafshan, J. Flood frequency analysis under nonstationary modeling in the Gorganrood River basin, Iran. J. Hydrol. Eng. 2023, 28, 05023004. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Liu, K.; Cheng, L.; Cai, X. Theory and practice of basin-wide floodwater utilization: Typical implementing measures in China. J. Hydrol. 2024, 628, 130520. [Google Scholar] [CrossRef]
- He, S.; Li, B.; Li, Q.; Zheng, H.; Chen, Y. Refining hydropower operation by dynamic control of cascade reservoir water levels with flood season segmentation. Energy 2025, 314, 134156. [Google Scholar] [CrossRef]
- Cunnane, C. Statistical Distribution for Flood Frequency Analysis; Operational Hydrology Report, WMO, No.718; WMO: Geneva, Switzerland, 1989. [Google Scholar]
- Huang, K.; Ye, L.; Chen, L.; Wang, Q.; Dai, L.; Zhou, J.; Singh, V.P.; Huang, M.; Zhang, J. Risk analysis of flood control reservoir operation considering multiple uncertainties. J. Hydrol. 2018, 565, 672–684. [Google Scholar] [CrossRef]
- Milly, P.C.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Zhao, G.; Bates, P.; Neal, J. The impact of dams on design floods in the conterminous US. Water Resour. Res. 2020, 56, e2019WR025380. [Google Scholar] [CrossRef]
- Ouyang, S.; Zhou, J.; Li, C.; Liao, X.; Wang, H. Optimal design for flood limit water level of cascade reservoirs. Water Resour. Manag. 2015, 29, 445–457. [Google Scholar] [CrossRef]
- MWR (Ministry of Water Resources of China). Specification for Calculating Design Flood of Water Resources and Hydropower Projects; China Water & Power Press: Beijing, China, 2006. (In Chinese) [Google Scholar]
- Alfieri, L.; Dottori, F.; Salamon, P.; Wu, H.; Feyen, L. Global modeling of seasonal mortality rates from river floods. Earth Future 2020, 8, e2020EF001541. [Google Scholar] [CrossRef]
- Wang, X.; Guo, S.; Zhong, S.; Wang, M.; Xiang, X. Flood season division using statistical analysis methods and verifying by regional rainy characteristics. Water 2024, 16, 3677. [Google Scholar] [CrossRef]
- Jiang, M.; Qiao, C.; Lu, F.; Zhu, K.; Zhu, C. The impact of reservoirs with seasonal flood limit water level on the frequency of downstream floods. J. Hydrol. 2024, 644, 132009. [Google Scholar] [CrossRef]
- Ray, L.K.; Goel, N.K. Flood frequency analysis of Narmada River basin in India under nonstationary condition. J. Hydrol. Eng. 2019, 24, 05019018. [Google Scholar] [CrossRef]
- Li, W.; Xiong, L.; Zhou, Y.; Yin, J.; Li, R.; Chen, J.; Liu, D. Nonstationary seasonal design flood estimation: Exploring mixed copulas for the nonmonotonic dependence between peak discharge and timing. J. Hydrol. Eng. 2024, 29, 04023046. [Google Scholar] [CrossRef]
- Li, R.; Xiong, L.; Zha, X.; Xiong, B.; Liu, H.; Chen, J.; Zeng, L.; Li, W. Impacts of climate and reservoirs on the downstream design flood hydrograph: A case study of Yichang Station. Nat. Hazards 2022, 113, 1803–1831. [Google Scholar] [CrossRef]
- Falter, D.; Dung, N.V.; Vorogushyn, S.; Schröter, K.; Hundecha, Y.; Kreibich, H.; Apel, F.; Merz, B. Continuous, large-scale simulation model for flood risk assessments: Proof-of-concept. J. Flood Risk Manag. 2016, 9, 3–21. [Google Scholar] [CrossRef]
- Nazari, R.; Vasiliadis, H.; Karimi, M.; Fahad, M.G.R.; Simon, S.; Zhang, T.; Sun, Q.; Peters, R. Hydrodynamic study of the impact of extreme Flooding events on wastewater treatment plants considering total water level. Nat. Hazards Rev. 2022, 23, 04021056. [Google Scholar] [CrossRef]
- Xu, Z.; Mo, L.; Zhou, J.; Zhang, X. Optimal dispatching rules of hydropower reservoir in flood season considering flood resources utilization: A case study of Three Gorges Reservoir in China. J. Clean. Prod. 2023, 388, 135975. [Google Scholar] [CrossRef]
- Liu, P.; Li, L.; Guo, S.; Xiong, L.; Zhang, W.; Zhang, J.; Xu, C.Y. Optimal design of seasonal flood limited water levels and its application for the Three Gorges Reservoir. J. Hydrol. 2015, 527, 1045–1053. [Google Scholar] [CrossRef]
- Hu, Y.; Cao, Z.; Chen, Y.; Hu, J.; Guo, J.; Liang, Z. Nonstationary multi-site design flood estimation and application to design flood regional composition analysis. J. Hydrol. 2024, 638, 131538. [Google Scholar] [CrossRef]
- Black, A.R.; Werritty, A. Seasonality of flooding: A case study of North Britain. J. Hydrol. 1997, 195, 1–25. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Ouarda, T.B.M.J.; Bobée, B. Determination of flood seasonality from hydrological records. Hydrol. Sci. J. 2004, 49, 11. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Guo, S.; Fang, B.; Liu, P. A new method for identification of flood seasons using directional statistics. Hydrol. Sci. J. 2013, 58, 28–40. [Google Scholar] [CrossRef]
- Liu, P.; Guo, S.; Xiong, L.; Chen, L. Flood season segmentation based on the probability change-point analysis technique. Hydrol. Sci. J. 2010, 55, 540–554. [Google Scholar] [CrossRef]
- Xiong, F.; Guo, S.; Chen, L.; Chang, F.J.; Zhong, Y.; Liu, P. Identification of flood seasonality using an entropy-based method. Stoch. Environ. Res. Risk Assess. 2018, 32, 3021–3035. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Shi, X.; Ding, Y. Large-scale topography of China: A factor for the seasonal progression of the Meiyu rainband? J. Geophys. Res. Atmos. 2010, 115, 2009JD012444. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Z.; Zhou, B.; Li, Y.; Tang, H.; Xiang, B. Trends in autumn rain of West China from 1961 to 2014. Theor. Appl. Climatol. 2019, 135, 533–544. [Google Scholar] [CrossRef]
- Mann, H. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.; Gibbons, J. Rank Correlation Methods, 5th ed.; Griffin: London, UK, 1990. [Google Scholar]
- Xiao, Y.; Guo, S.; Liu, P.; Yan, B.; Chen, L. Design flood hydrograph based on multicharacteristic synthesis index method. J. Hydrol. Eng. 2009, 14, 1359–1364. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Mitosek, H.T. Nonstationary approach to at-site flood frequency modelling. III. Flood analysis of Polish Rivers. J. Hydrol. 2001, 248, 152–167. [Google Scholar] [CrossRef]
- Rigby, R.; Stasinopoulos, D. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C Appl. Stat. 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Cui, H.; Jiang, S.; Gao, B.; Ren, L.; Xiao, W.; Wang, M.; Ren, M.; Xu, C.Y. On method of regional non-stationary flood frequency analysis under the influence of large reservoir group and climate change. J. Hydrol. 2023, 618, 129255. [Google Scholar] [CrossRef]
- Xie, Y.; Guo, S.; Zhong, S.; Wang, X.; Tian, J.; Liang, Z. A novel time-varying P-III distribution curve fitting model to estimate design floods in Three Gorges Reservoir operation period. Hydrology 2024, 11, 203. [Google Scholar] [CrossRef]
- Gao, S.; Liu, P.; Pan, Z.; Ming, B.; Guo, S.; Cheng, L.; Wang, J. Incorporating reservoir impacts into flood frequency distribution functions. J. Hydrol. 2019, 568, 234–246. [Google Scholar] [CrossRef]
- Zhou, Y.; Guo, S. Risk analysis for flood control operation of seasonal flood-limited water level incorporating inflow forecasting error. Hydrol. Sci. J. 2014, 59, 1006–1019. [Google Scholar] [CrossRef]
- Xiong, B.; Xiong, L.; Guo, S.; Xu, C.Y.; Xia, J.; Zhong, Y.; Yang, H. Nonstationary frequency analysis of censored data: A case study of the floods in the Yangtze River from 1470 to 2017. Water Resour. Res. 2020, 56, e2020WR027112. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Feluch, W. Nonstationary approach to at-site flood frequency modelling I. Maximum likelihood estimation. J. Hydrol. 2001, 248, 123–142. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kaczmarek, Z. Non-Stationary Approach to at-Site Flood Frequency Modelling II. Weighted Least Squares Estimation. J. Hydrol. 2001, 248, 143–151. [Google Scholar] [CrossRef]
- Xiong, F.; Guo, S.; Liu, P.; Xu, C.Y.; Zhong, Y.; Yin, J.; He, S. A general framework of design flood estimation for cascade reservoirs in operation period. J. Hydrol. 2019, 577, 124003. [Google Scholar] [CrossRef]
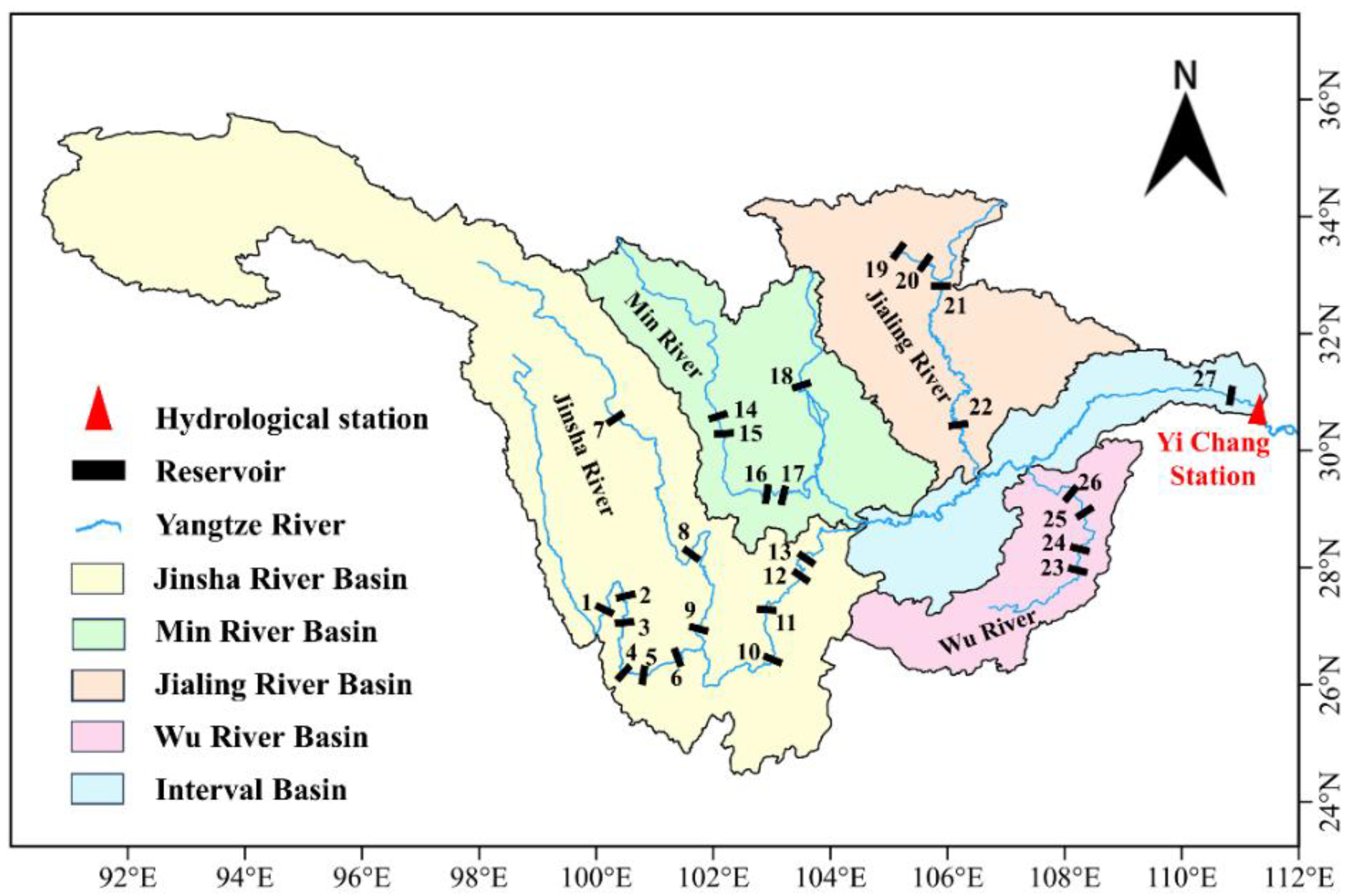


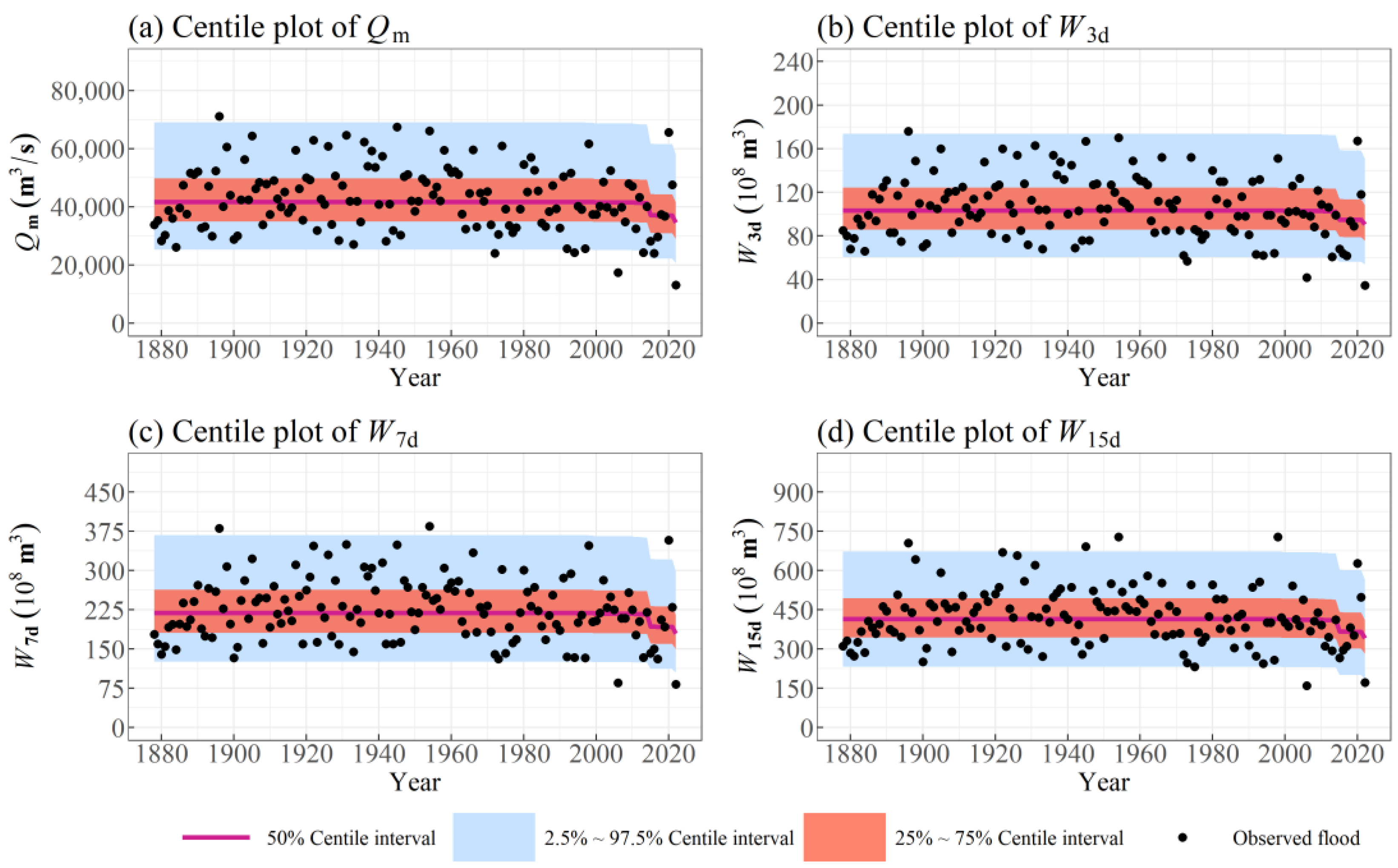


| Basin | Reservoir Name | Reservoir Number | Catchment Area (104 km2) | Flood Prevention Storage Capacity (108 m3) | Operation Year |
|---|---|---|---|---|---|
| Jinsha River | Liyuan | 1 | 22.00 | 1.73 | 2016 |
| Ahai | 2 | 23.54 | 2.15 | 2014 | |
| Jinanqiao | 3 | 23.74 | 1.58 | 2012 | |
| Longkaikou | 4 | 24.00 | 1.26 | 2014 | |
| Ludila | 5 | 24.73 | 5.64 | 2014 | |
| Guanyinyan | 6 | 25.65 | 2.53 | 2016 | |
| Lianghekou | 7 | 6.57 | 20.0 | 2022 | |
| Jinping-Ⅰ | 8 | 10.26 | 16.0 | 2014 | |
| Ertan | 9 | 11.64 | 9.00 | 1999 | |
| Wudongde | 10 | 40.61 | 24.4 | 2021 | |
| Baihetan | 11 | 43.03 | 75.0 | 2022 | |
| Xiluodu | 12 | 45.44 | 46.5 | 2014 | |
| Xiangjiaba | 13 | 45.88 | 9.03 | 2014 | |
| Min River | Houziyan | 14 | 5.40 | 0.68 | 2017 |
| Changheba | 15 | 5.67 | 0.36 | 2017 | |
| Dagangshan | 16 | 6.27 | 0.82 | 2015 | |
| Pubugou | 17 | 6.85 | 7.30 | 2010 | |
| Zipingpu | 18 | 2.27 | 1.67 | 2006 | |
| Jialing River | Bikou | 19 | 2.60 | 1.03 | 1997 |
| Baozhusi | 20 | 2.84 | 2.80 | 1998 | |
| Tingzikou | 21 | 6.11 | 14.4 | 2014 | |
| Caojie | 22 | 15.61 | 1.99 | 2011 | |
| Wu River | Goupitan | 23 | 4.33 | 2.00 | 2009 |
| Silin | 24 | 4.86 | 1.84 | 2010 | |
| Shatuo | 25 | 5.45 | 2.09 | 2013 | |
| Pengshui | 26 | 6.90 | 2.32 | 2009 | |
| Yangtze River | TGR | 27 | 100.0 | 221.5 | 2003 |
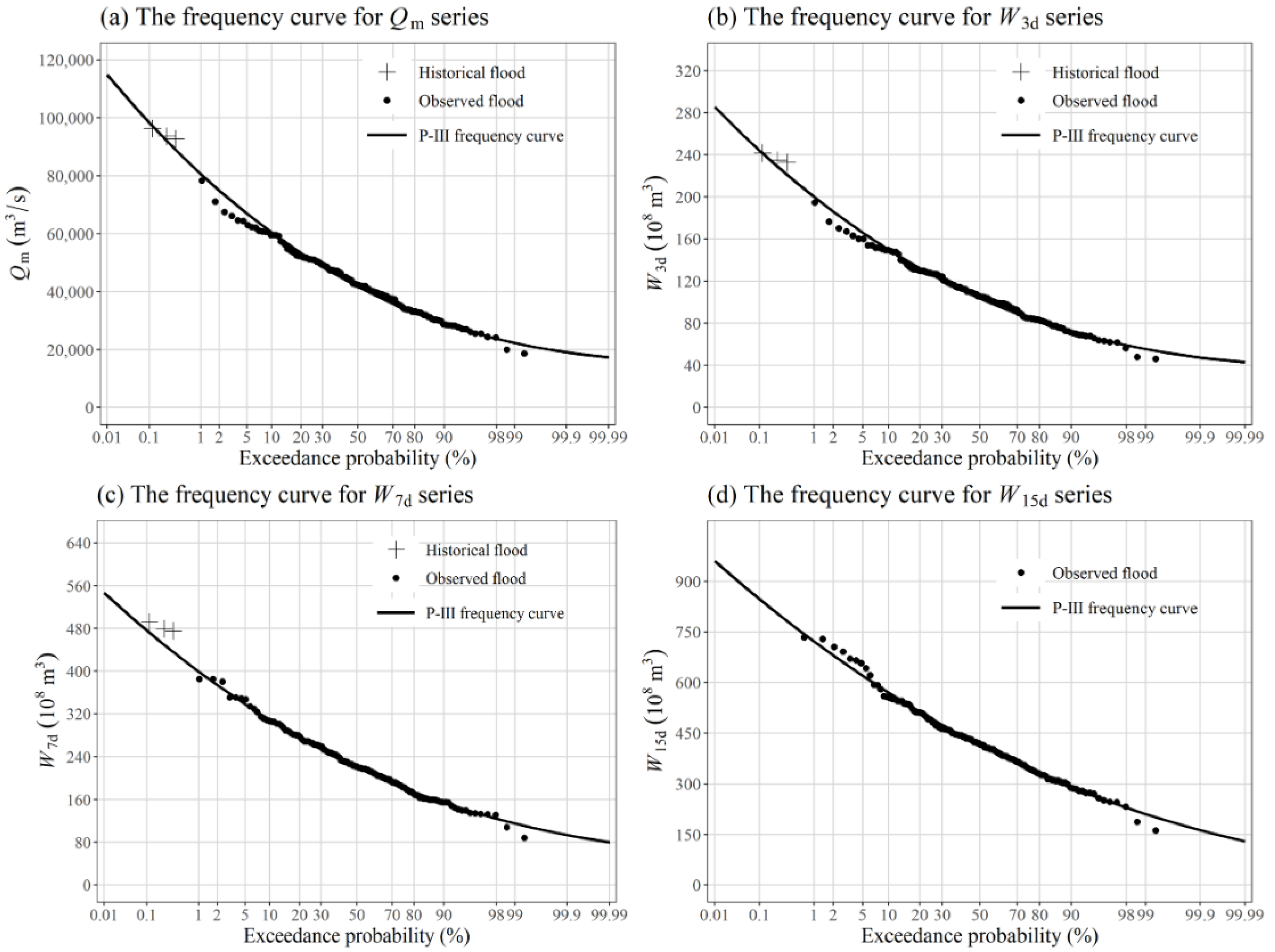
| Flood Series | Mean | Cv | Cs/Cv | Design Frequency | |||
|---|---|---|---|---|---|---|---|
| 0.1% | 1% | 2% | 5% | ||||
| Qm (m3/s) | 52,000 | 0.21 | 4 | 98,800 | 83,900 | 78,800 | 72,300 |
| W3d (108 m3) | 130.0 | 0.21 | 4 | 247.0 | 209.3 | 197.5 | 180.7 |
| W7d (108 m3) | 275.0 | 0.19 | 3.5 | 486.8 | 420.8 | 399.9 | 368.5 |
| W15d (108 m3) | 524.0 | 0.19 | 3.0 | 911.8 | 796.5 | 757.5 | 702.2 |
| Year | Qm (m3/s) | W3d (108 m3) | W7d (108 m3) | W15d (108 m3) |
|---|---|---|---|---|
| 1153 | 92,800 (1) | 232.7 (1) | 475.3 (1) | / |
| 1227 | 96,300 (2) | 241.6 (2) | 492.5 (2) | / |
| 1560 | 93,600 (3) | 234.8 (3) | 479.2 (3) | / |
| Flood Series | Mean | Cv | Cs/Cv | Design Frequency | |||
|---|---|---|---|---|---|---|---|
| 0.10% | 1% | 2% | 5% | ||||
| Qm (m3/s) | 43,500 | 0.29 | 3.0 | 98,300 | 80,600 | 74,900 | 66,900 |
| W3d (108 m3) | 108 | 0.29 | 3.0 | 244 | 200 | 186 | 166 |
| W7d (108 m3) | 227 | 0.27 | 2.5 | 477 | 400 | 374 | 338 |
| W15d (108 m3) | 424 | 0.26 | 2.0 | 847 | 722 | 680 | 620 |
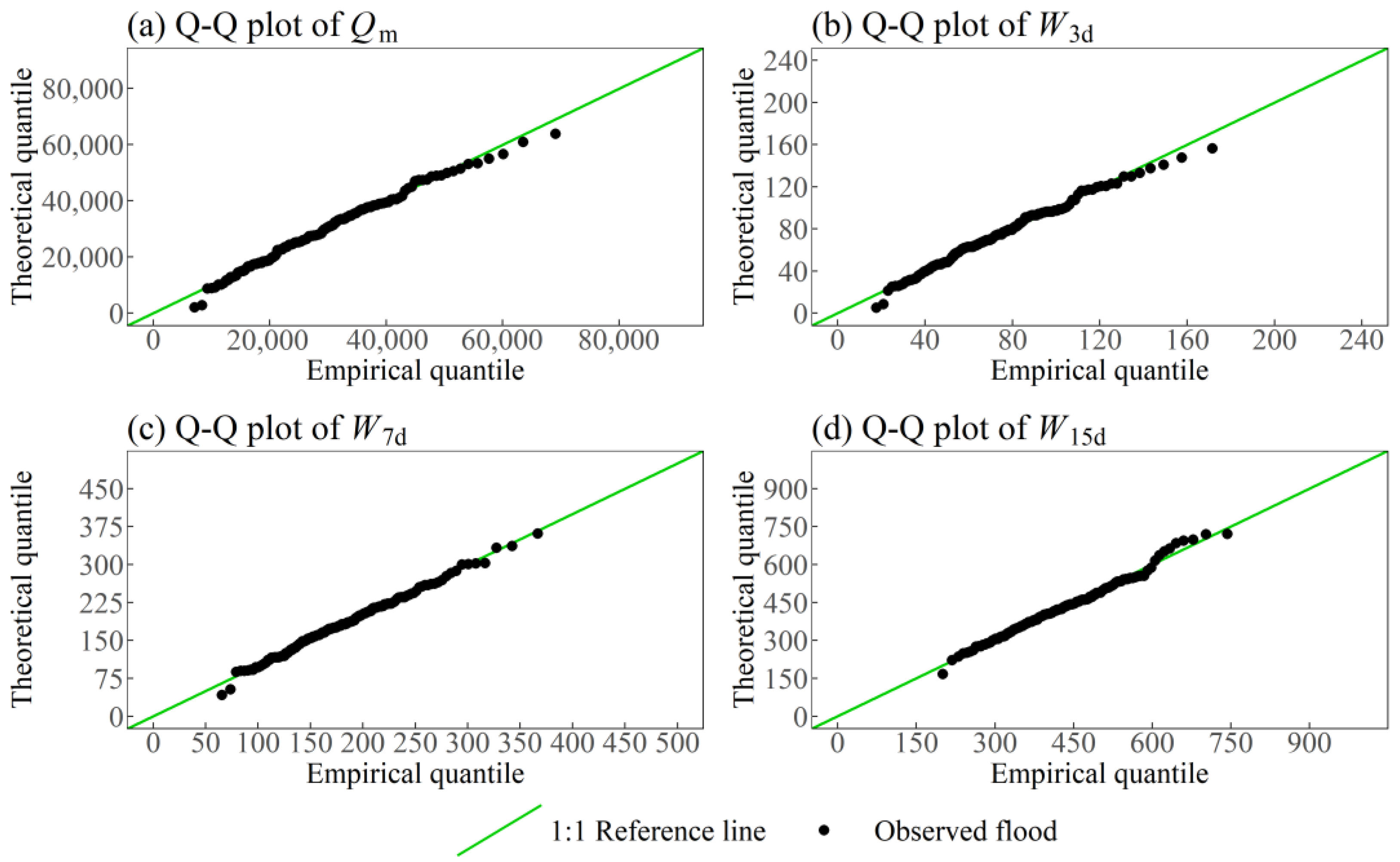
| Flood Series | Estimated Parameters | K-S Test | SSD | AIC | ||||
|---|---|---|---|---|---|---|---|---|
| Qm | 12,963.62 | −56,767.90 | 4231.56 | −12,844.30 | 7.14 | 0.97 | 1.94 × 108 | 2034.90 |
| W3d | 27.95 | −30.79 | 10.86 | −32.74 | 7.27 | 0.70 | 1.37 × 103 | 319.88 |
| W7d | 47.22 | −85.45 | 21.76 | −89.90 | 8.22 | 0.94 | 2.58 × 103 | 418.90 |
| W15d | −5.06 | −310.71 | 29.72 | −81.25 | 14.45 | 0.90 | 1.47 × 104 | 684.20 |
| Flood Variables | Statistical Parameters | Design Frequency | ||||
|---|---|---|---|---|---|---|
| Mean | Cv | Cs | 0.10% | 1% | 5% | |
| Qm (m3/s) | 35,800 | 0.27 | 0.75 | 75,800 (−22.9%) | 63,200 (−21.6%) | 53,300 (−20.3%) |
| W3d (108 m3) | 94 | 0.27 | 0.74 | 198 (−18.9%) | 165 (−17.5%) | 139 (−16.3%) |
| W7d (108 m3) | 186 | 0.27 | 0.70 | 389 (−18.4%) | 325 (−18.8%) | 276 (−18.3%) |
| W15d (108 m3) | 351 | 0.28 | 0.53 | 726 (−14.3%) | 615 (−14.8%) | 525 (−15.3%) |
| Design Scheme | FLWL/FCWL (m) | Hydropower (Billion kW h) | Increase Rate |
|---|---|---|---|
| Stationary annual design | 145 | 13.807 | / |
| Stationary seasonal design | 149 | 14.762 | 6.92% |
| Nonstationary seasonal design | 157 | 16.095 | 16.57% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, B.; Guo, S.; Zhong, S.; Wang, X.; Li, N. Seasonal Design Floods Estimated by Stationary and Nonstationary Flood Frequency Analysis Methods for Three Gorges Reservoir. Hydrology 2025, 12, 258. https://doi.org/10.3390/hydrology12100258
Sun B, Guo S, Zhong S, Wang X, Li N. Seasonal Design Floods Estimated by Stationary and Nonstationary Flood Frequency Analysis Methods for Three Gorges Reservoir. Hydrology. 2025; 12(10):258. https://doi.org/10.3390/hydrology12100258
Chicago/Turabian StyleSun, Bokai, Shenglian Guo, Sirui Zhong, Xiaoya Wang, and Na Li. 2025. "Seasonal Design Floods Estimated by Stationary and Nonstationary Flood Frequency Analysis Methods for Three Gorges Reservoir" Hydrology 12, no. 10: 258. https://doi.org/10.3390/hydrology12100258
APA StyleSun, B., Guo, S., Zhong, S., Wang, X., & Li, N. (2025). Seasonal Design Floods Estimated by Stationary and Nonstationary Flood Frequency Analysis Methods for Three Gorges Reservoir. Hydrology, 12(10), 258. https://doi.org/10.3390/hydrology12100258







