Exploring Seasonality Indices for Low-Flow Analysis on Tibagi Watershed (Brazil)
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Materials
2.3. Seasonality Indices
3. Results and Discussion
3.1. Seasonality Ratio
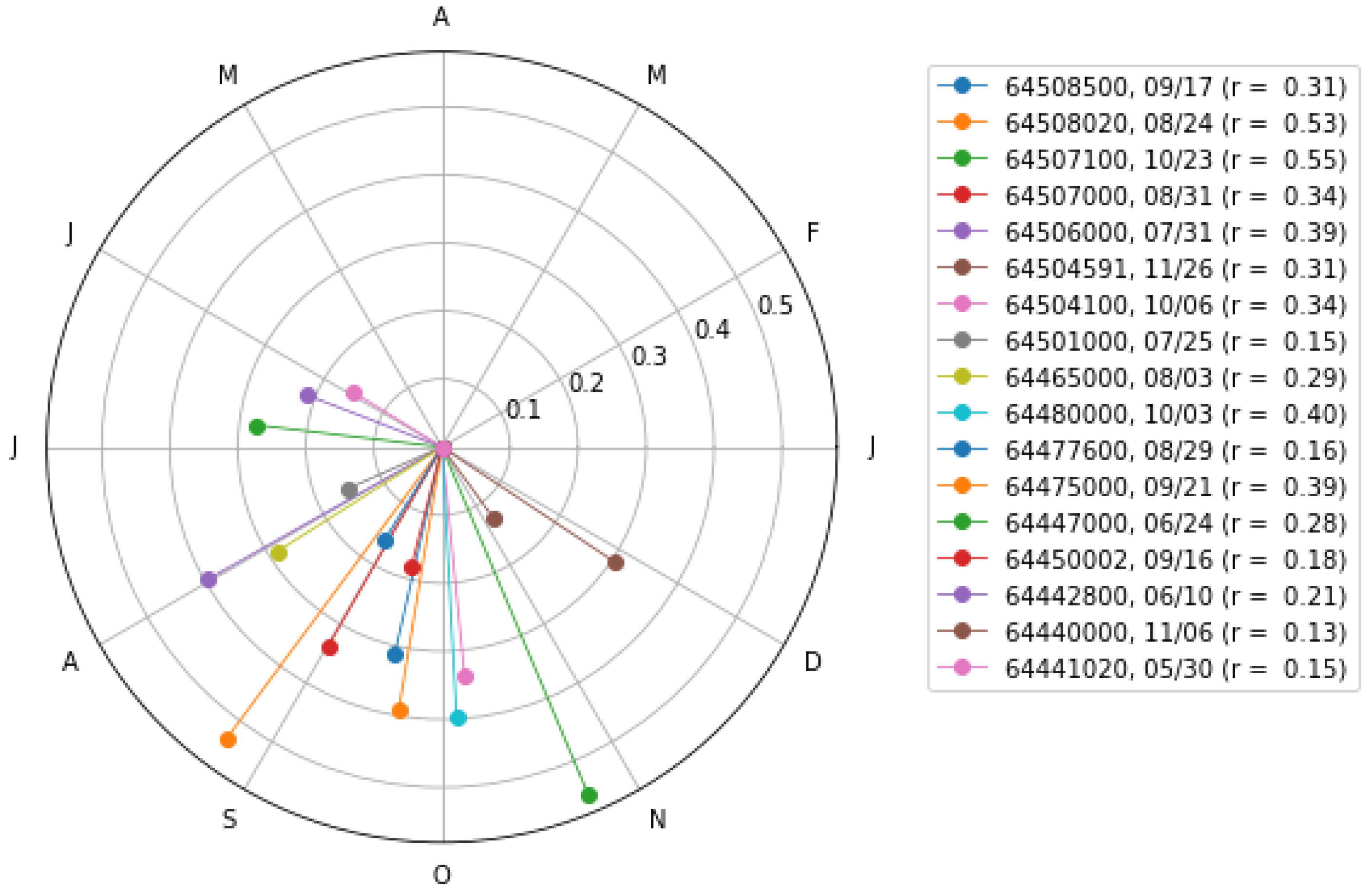
3.2. Seasonality Index
3.3. Seasonality Histogram
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Smahtin, V.U. Low flow hydrology: A review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Chagas, V.B.; Chaffe, P.L.; Bloschl, G. Regional low flow hydrology: Model development and evaluation. Water Resour. Res. 2024, 60, e2023WR035063. [Google Scholar] [CrossRef]
- Schreiber, P.; Demuth, S. Regionalization of low flows in southwest Germany. Hydrol. Sci. J. 1997, 42, 845–858. [Google Scholar] [CrossRef]
- Vezza, P.; Rosso, M.; Viglione, A.; Claps, P. Low flows regionalization in north-western Italy. Water Resour. Manag. 2010, 24, 4049–4074. [Google Scholar] [CrossRef]
- Pruski, F.F.; Braga, C.C.; Nascimento, A.D.; Ramos, M.M. Low-flow estimates in regions of extrapolation of the regionalization equations: A new concept. Eng. Agric. 2015, 35, 808–816. [Google Scholar] [CrossRef]
- Cupak, A.; Kaczor, G. Determination of seasonal indices for the regionalization of low flows in the upper Vistula River Basin. Water 2023, 15, 246. [Google Scholar] [CrossRef]
- Serrano, L.D.O.; Ribeiro, R.B.; Borges, A.C.; Pruski, F.F. Low-Flow Seasonality and Effects on Water Availability throughout the River Network. Water Resour. Manag. 2020, 34, 1289–1304. [Google Scholar] [CrossRef]
- ANA. Conjuntura dos Recursos Hídricos no Brasil 2021: Informe Anual; ANA: Brasília, Brazil, 2021. [Google Scholar]
- Burn, D.H.; Zrinji, Z.; Kowalchuk, M. Regionalization of catchments for regional flood frequency analysis. J. Hydrol. Eng. 1997, 2, 76–82. [Google Scholar] [CrossRef]
- Young, A.; Round, C.; Gustard, A. Spatial and temporal variations in the occurrence of low flow events in the UK. Hydrol. Earth Syst. Sci. 2000, 4, 35–45. [Google Scholar] [CrossRef]
- Laaha, G. Modelling summer and winter droughts as a basis for estimating river low flows. In FRIEND 2002—Regional Hydrology: Bridging the Gap Between Research and Practice; van Lanen, H.A.J., Demuth, S., Eds.; IAHS Publication No. 274; IAHS Press: Wallingford, UK, 2002; pp. 289–295. [Google Scholar]
- Laaha, G.; Bloschl, G. Seasonality indices for regionalizing low flows. Hydrol. Process. Int. J. 2006, 20, 3851–3878. [Google Scholar] [CrossRef]
- Beskow, S.; Mello, C.R.; Faria, L.C.; Fernandes, M.M.; Viola, M.R. Índices de sazonalidade para regionalização hidrológica de vazões de estiagem no Rio Grande do Sul. Rev. Bras. Eng. Agric. Ambient. 2014, 18, 748–754. [Google Scholar] [CrossRef]
- Euclides, H.P.; Ferreira, P.A.; Filho, R.F. Critério de outorga sazonal para a agricultura irrigada no estado de Minas Gerais–estudo de caso. Rev. Item–Irrig. Tecnol. Mod. 2006, 71/72, 42–50. [Google Scholar]
- Silva, D.D.D.; Marques, F.A.; Lemos, A.F. Flexibilidade das vazões mínimas de referência com a adoção do período trimestral. Rev. Eng. Agric. 2011, 19, 244–254. [Google Scholar] [CrossRef]
- Bof, L.H.N.; Silva, D.D.; Mello, C.R.; Viola, M.R. Analysis of appropriate timescales for water diversion permits in Brazil. Environ. Manag. 2013, 51, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Silva, B.M.B.d.; Silva, D.D.d.; Moreira, M.C. Influência da sazonalidade das vazões nos critérios de outorga de uso da água: Estudo de caso da bacia do rio Paraopeba. Rev. Ambiente Água 2015, 10, 623–634. [Google Scholar]
- Ribeiro, T.B.; Santos, P.C.P.; Pires, G.V.; Brito, A.O. Estimativa das vazões mínimas de referência (Q7,10, Q95 e Q90) anuais e semestrais para a bacia do rio Branco. In Proceedings of the XXII Simpósio Brasileiro de Recursos Hídricos, Florianópolis, Brazil, 26 November–1 December 2017. [Google Scholar]
- Arai, F.K.; Santos, L.G.; Silva, M.R.; Paz, A.R. Seasonality and criteria for concession of water in the Ivinhema basin. Res. Soc. Dev. 2020, 9, e1969108391. [Google Scholar] [CrossRef]
- Moreira, H.S.; Silva, D.D.; Prado, R.B.; Moreira, M.C. Cenários de disponibilidade hídrica para concessão de outorga: Estudo de caso da bacia Vertentes do Rio Grande, estados de Minas Gerais e São Paulo, Brasil. Rev. Bras. Gestão Ambient. Susten. 2020, 7, 341–350. [Google Scholar] [CrossRef]
- Macedo, A.S.A.D.; Stinghen, C.M.; Mannich, M. Vazões de referência sazonal e sua aplicação na outorga de recursos hídricos. Rev. Gestão Água Am. Lat. 2024, 21, e21. [Google Scholar] [CrossRef]
- Mannich, M.; Stinghen, C.M. Diagnóstico de outorgas de captação e lançamento de efluentes no Paraná e impactos dos usos insignificantes. Rev. Gestão Água Am. Lat. 2019, 16, e10. [Google Scholar] [CrossRef]
- CNRH. Resolução CNRH Nº 140, de 21 de Março de 2012. In Estabelece Critérios Gerais para Outorga de Lançamento de Efluentes com fins de Diluição em Corpos de Água Superficiais; Publicada no D.O.U. em 22/08/2012; CNRH: Brasília, Brazil, 2012. [Google Scholar]
- CNRH. Resolução CNRH Nº 141, de 10 de Julho de 2012. In Estabelece Critérios e Diretrizes para Implementação dos Instrumentos de Outorga de Direito de uso de Recursos Hídricos e de Enquadramento dos corpos de Água em Classes, Segundo os usos Preponderantes da Água, em rios Intermitentes e Efêmeros, e dá Outras Providências; Publicada no D.O.U. em 24/08/2012; CNRH: Brasília, Brazil, 2012. [Google Scholar]
- ANA. Outorga com Gestão de Garantia e Prioridade (OGP)—Uma Proposta para Maximização do uso da Água. 2022. Available online: https://participacao-social.ana.gov.br/api/files/Parecer_Tecnico_3_2022_SRE-1675339471836.pdf (accessed on 22 March 2024).
- Dinerstein, E.; Olson, D.; Joshi, A.; Vynne, C.; Burgess, N.D.; Wikramanayake, E.; Hahn, N.; Palminteri, S.; Hedao, P. An ecoregion-based approach to protecting half the terrestrial realm. BioScience 2017, 67, 534–545. [Google Scholar] [CrossRef]
- Olson, D.M.; Dinerstein, E.; Wikramanayake, E.D.; Burgess, N.D.; Powell, G.V.; Underwood, E.C.; D’Amico, J.A.; Itoua, I.; Strand, H.E.; Morrison, J.C.; et al. Terrestrial ecoregions of the world: A new map of life on earth: A new global map of terrestrial ecoregions provides an innovative tool for conserving biodiversity. BioScience 2001, 51, 933–938. [Google Scholar] [CrossRef]
- ANA. Comitê da Bacia Hidrográfica Rio Paranapanema—CBHRP. Plano Integrado de Recursos Hídricos da Unidade de Gestão de Recursos Hídricos Paranapanema; ANA/CBHRP: Brasília, Brazil, 2016. [Google Scholar]
- Porras, E.A.A.; Santos, J.G.; Borges, M.A.; Pereira, L.C.; Souza, L.T. Modelo de estimativa de cargas de fósforo como auxílio na gestão da bacia hidrográfica do rio Tibagi. In Proceedings of the XXIV Simpósio Brasileiro de Recursos Hídricos, Porto Alegre, Brasil, 21–26 November 2021; pp. 1–9. Available online: https://anais.abrhidro.org.br/job.php?Job=13605 (accessed on 14 April 2023).
- Hidroweb—Sistema de Informações Hidrológicas. 2023. Available online: https://www.snirh.gov.br/hidroweb/download (accessed on 17 July 2023).
- INPE. TOPODATA: Banco de dados Geomorfológicos do Brasil. 2011. Available online: http://www.dsr.inpe.br/topodata/data/geotiff/?C=N;O=D (accessed on 25 July 2023).
- SUDERHSA. Manual Técnico de Outorgas, Revision 01; Superintendência de Desenvolvimento de Recursos Hídricos e Saneamento Ambiental—DEOF: Paraná, Brazil, 2006. Available online: https://www.iat.pr.gov.br/sites/agua-terra/arquivos_restritos/files/documento/2020-10/manual_outorgas_suderhsa_2006.pdf (accessed on 7 January 2025).
- Nery, J.T.; Vargas, W.M.; Martins, M. Caracterização da precipitação no estado do Paraná. Rev. Bras. Agrometeorol. 1996, 4, 81–89. [Google Scholar]
- Floriancic, M.G.; Berghuijs, W.R.; Molnar, P.; Kirchner, J.W. Seasonality and drivers of low flows across Europe and the United States. Water Resour. Res. 2021, 57, e2019WR026928. [Google Scholar] [CrossRef]
- Parolin, M.; Volkmer-Ribeiro, C.; Leandrini, J.A. Abordagem Ambiental Interdisciplinar em Bacias Hidrográficas no Estado do Paraná; Editora da Fecilcam: Campo Mourão, Brazil, 2010. [Google Scholar]
- Nitsche, P.R.; Caramori, P.H.; Ricce, W.S.; Pinto, L.F.D. Atlas Climático do Estado do Paraná; IAPAR: Londrina, Brazil, 2019. [Google Scholar]
- Salton, F.G.; Morais, H.; Lohmann, M. Períodos secos no estado do Paraná. Rev. Bras. Meteorol. 2021, 36, 295–303. [Google Scholar] [CrossRef]
- Mastrotheodoros, T.; Pappas, C.; Molnar, P.; Burlando, P.; Manoli, G.; Parajka, J.; Rigon, R.; Szeles, B.; Bottazzi, M.; Hadjidoukas, P.; et al. More green and less blue water in the Alps during warmer summers. Nat. Clim. Change 2020, 10, 155–161. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Lehner, I.; Gurtz, J.; Teuling, A.J.; Lang, H.; Moser, U.; Grebner, D.; Menzel, L.; Schroff, K.; Vitvar, T.; et al. Swiss prealpine Rietholzbach research catchment and lysimeter: 32 year time series and 2003 drought event. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Teuling, A.J.; Van Loon, A.F.; Seneviratne, S.I.; Lehner, I.; Aubinet, M.; Heinesch, B.; Bernhofer, C.; Grünwald, T.; Prasse, H.; Spank, U. Evapotranspiration amplifies European summer drought. Geophys. Res. Lett. 2013, 40, 2071–2075. [Google Scholar] [CrossRef]
- Costa, A.B.F.D.; Santos, J.R.D.; Ferreira, L.C.; Alves, P.S.; Silva, M.E.A. Análise climatológica de dias consecutivos sem chuva no estado do Paraná. In Proceedings of the III Simpósio Internacional de Climatologia, Sociedade Brasileira de Meteorologia, Canela, Brazil, 18–21 October 2009. [Google Scholar]
- Fritzsons, E.; Vieira, M.L.; Amorim, R.; Franz, G.C.; Dias, G.A.R. Análise da pluviometria para definição de zonas homogêneas no estado do Paraná. RA’E GA—O Espaço Geogr. Anal. 2011, 23, 555–572. [Google Scholar]
- Wrege, M.S.; Steinmetz, S.; Reisser, C.; Almeida, I.R. Risco de deficiência hídrica na cultura do milho no estado do Paraná. Pesqui. Agropecu. Bras. 1999, 34, 1119–1124. [Google Scholar] [CrossRef]
- Vanhoni, F.; Mendonça, F. O clima do litoral do estado do Paraná. Rev. Bras. Climatol. 2008, 3, 49–63. [Google Scholar] [CrossRef]
- Mendonça, F.; Danni-Oliveira, I.M. Climatologia: Noções Básicas e Climas do Brasil; Oficina de Textos: São Paulo, Brazil, 2017. [Google Scholar]
- Van der Ent, R.J.; Savenije, H.H.; Schaefli, B.; Steele-Dunne, S.C. Origin and fate of atmospheric moisture over continents. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Stinghen, C.M.; Carvalho, J.M.; Mannich, M. Aplicação de indicador de estresse hídrico na bacia do rio Tibagi para a identificação de bacias críticas quanto ao uso dos recursos hídricos. Revista Gestão Água Am. Lat. 2022, 19, 2022. [Google Scholar] [CrossRef]
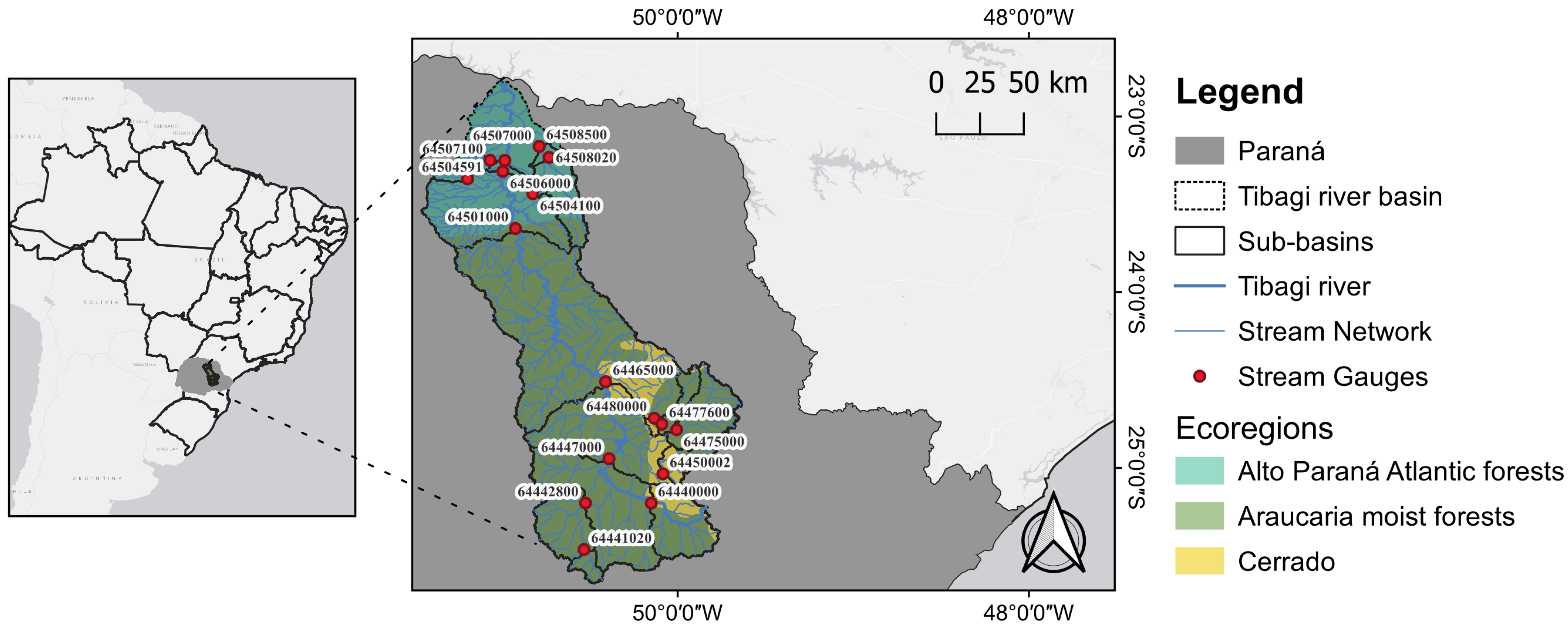
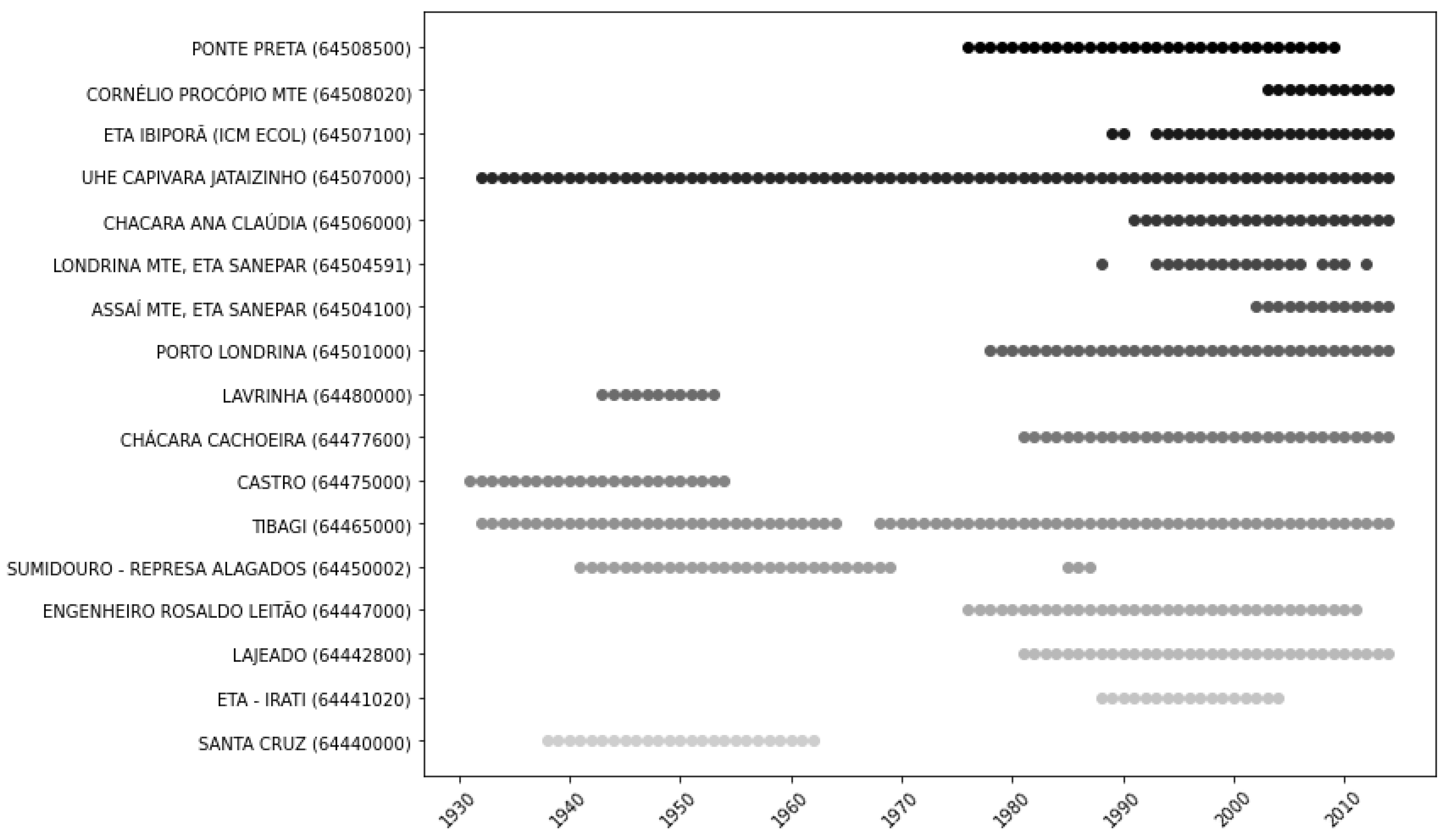

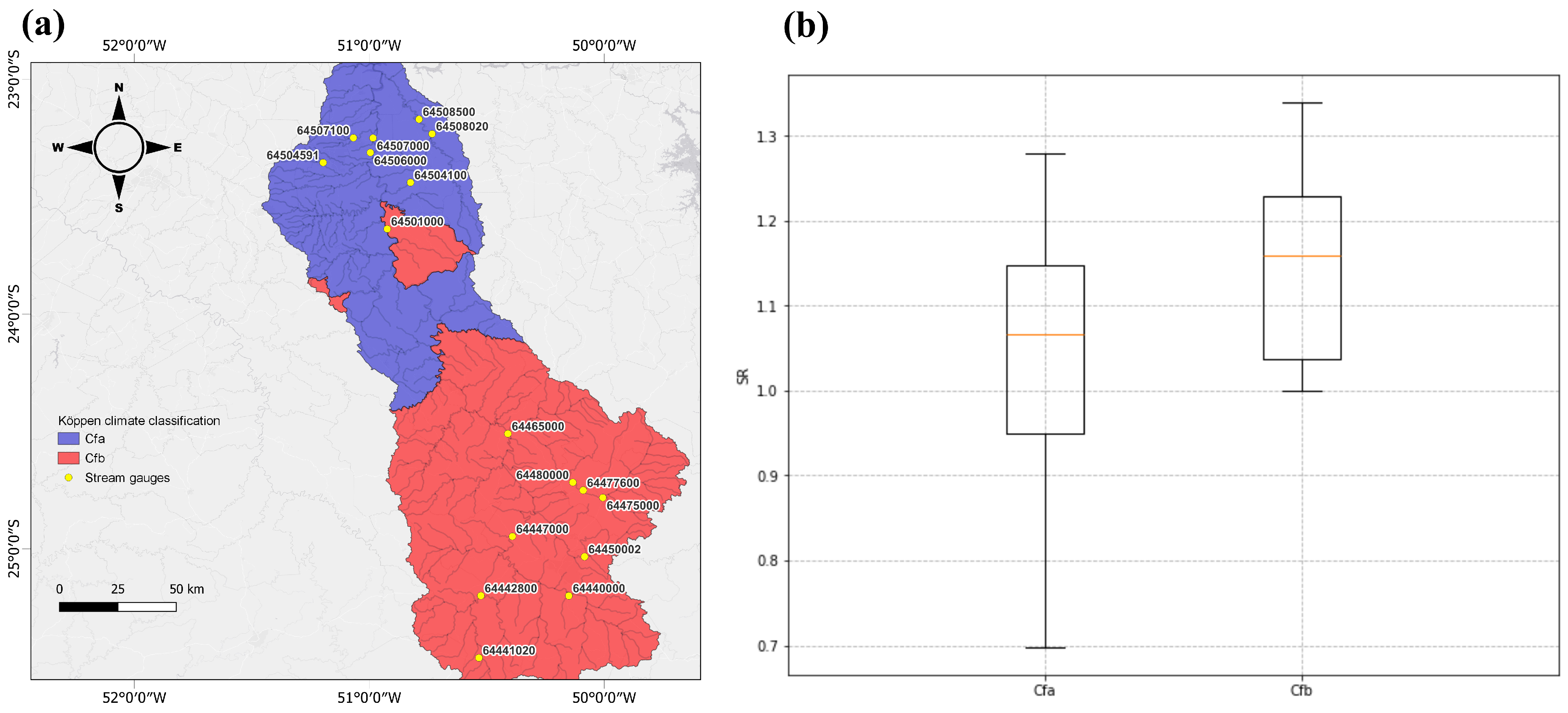
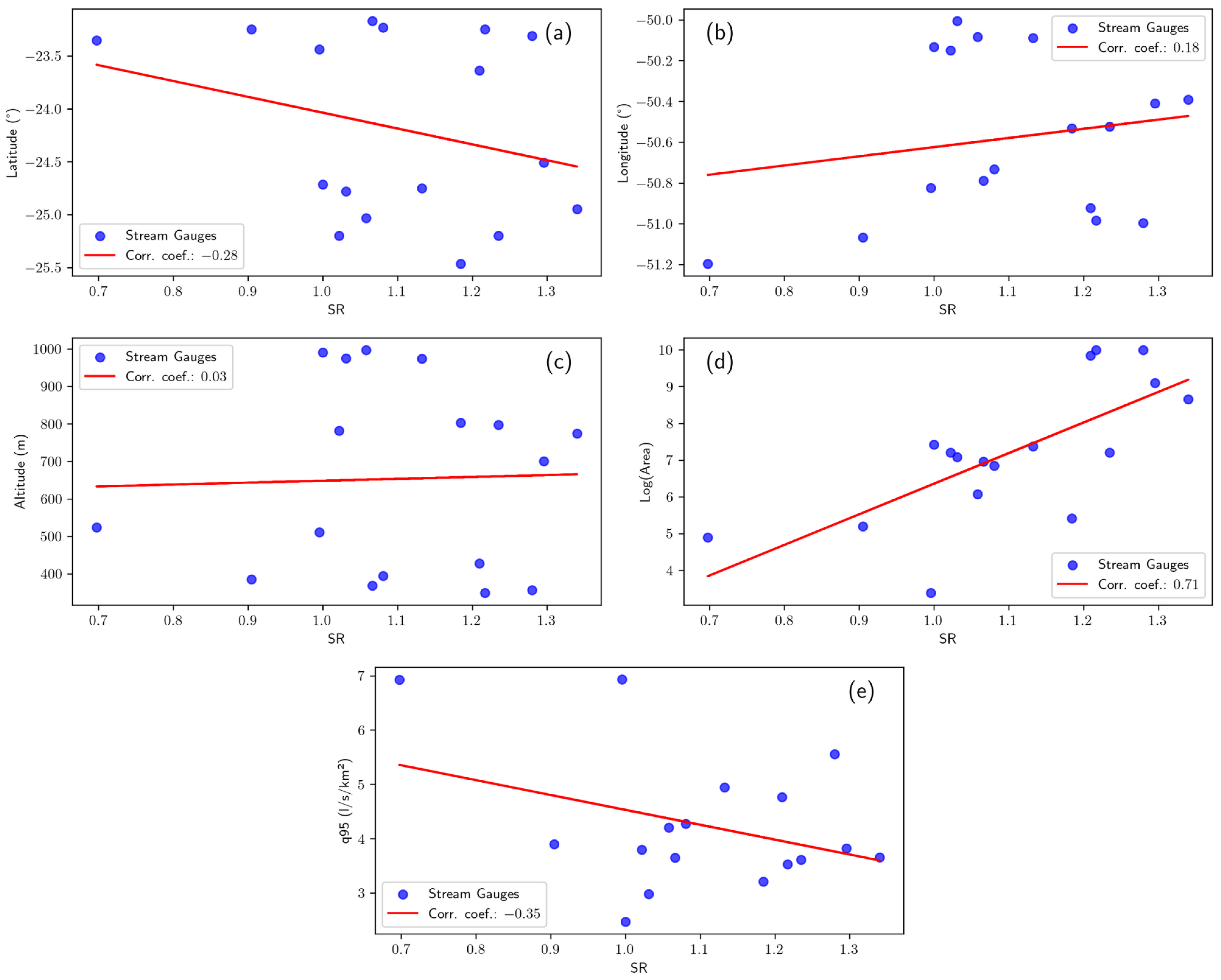
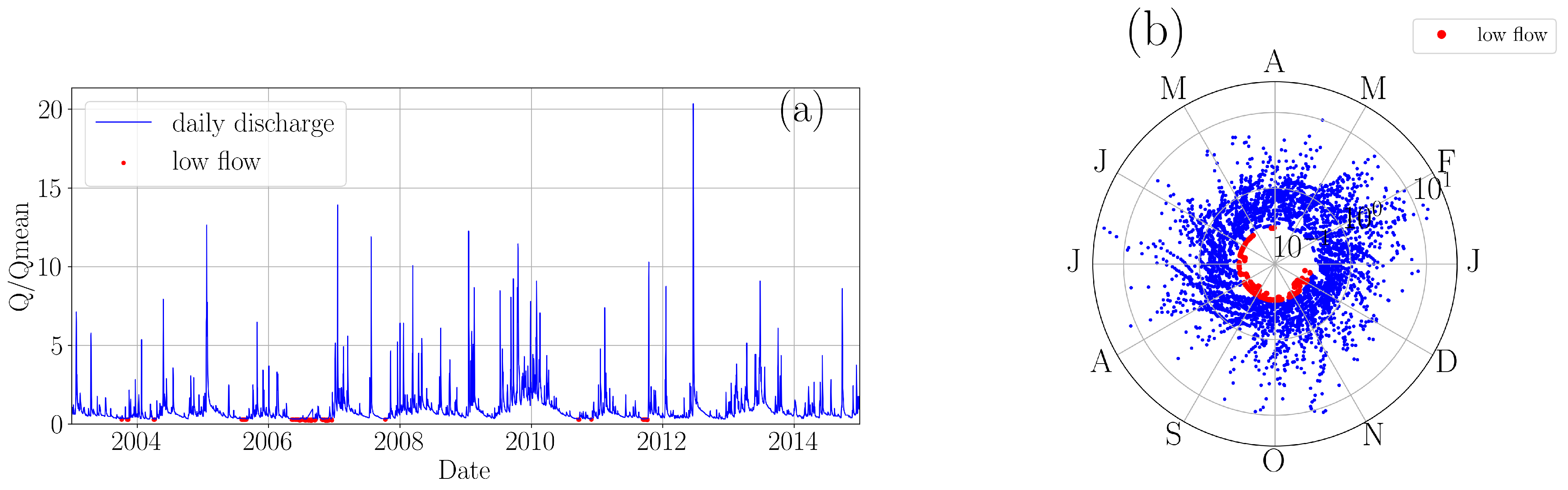


| Gauge (ID) | Longitude (°) | Latitude (°) | Area () | () | () | () | Altitude (m) |
|---|---|---|---|---|---|---|---|
| 64508500 | −50.788 | −23.170 | 1049 | 3.831 | 3.733 | 3.980 | 368.5 |
| 64508020 | −50.733 | −23.232 | 942 | 4.026 | 4.026 | 4.350 | 394.3 |
| 64507100 | −51.068 | −23.249 | 181 | 0.706 | 0.746 | 0.675 | 384.8 |
| 64507000 | −50.984 | −23.250 | 21,938 | 77.356 | 71.467 | 86.953 | 349.5 |
| 64506000 | −50.995 | −23.312 | 21,826 | 121.306 | 108.200 | 138.466 | 356.6 |
| 64504591 | −51.196 | −23.354 | 134 | 0.928 | 1.124 | 0.784 | 524.1 |
| 64504100 | −50.824 | −23.439 | 29.7 | 0.206 | 0.207 | 0.206 | 510.8 |
| 64501000 | −50.923 | −23.637 | 18,758 | 89.401 | 83.944 | 101.538 | 427.8 |
| 64465000 | −50.410 | −24.509 | 1665 | 34.104 | 30.831 | 39.945 | 700.3 |
| 64480000 | −50.133 | −24.717 | 1593 | 4.110 | 4.110 | 4.110 | 990.6 |
| 64477600 | −50.089 | −24.750 | 1190 | 7.880 | 7.337 | 8.309 | 973.9 |
| 64475000 | −50.006 | −24.782 | 8929 | 3.550 | 3.550 | 3.660 | 974.7 |
| 64447000 | −50.391 | −24.947 | 433 | 20.941 | 18.786 | 25.174 | 774.8 |
| 64450002 | −50.083 | −25.033 | 5731 | 1.820 | 1.720 | 1.820 | 997.3 |
| 64442800 | −50.525 | −25.199 | 1342 | 4.850 | 4.521 | 5.583 | 797.1 |
| 64440000 | −50.150 | −25.200 | 225 | 5.100 | 4.990 | 5.100 | 781.6 |
| 64441020 | −50.533 | −25.464 | 1344 | 0.722 | 0.673 | 0.797 | 803.2 |
| Gauges | r | D | Mean Day (mm/dd) |
|---|---|---|---|
| 64508500 | 0.31 | 260.7 | 09/17 |
| 64508020 | 0.53 | 236.8 | 08/24 |
| 64507100 | 0.55 | 296.9 | 10/23 |
| 64507000 | 0.34 | 243.6 | 08/31 |
| 64506000 | 0.39 | 212.4 | 07/31 |
| 64504591 | 0.31 | 330.9 | 11/26 |
| 64504100 | 0.34 | 279.5 | 10/06 |
| 64501000 | 0.15 | 206.6 | 07/25 |
| 64465000 | 0.29 | 215.3 | 08/03 |
| 64480000 | 0.40 | 276.9 | 10/03 |
| 64477600 | 0.16 | 241.6 | 08/29 |
| 64475000 | 0.39 | 264.3 | 09/21 |
| 64447000 | 0.28 | 175.7 | 06/24 |
| 64450002 | 0.18 | 259.2 | 09/16 |
| 64442800 | 0.21 | 161.2 | 06/10 |
| 64440000 | 0.13 | 310.2 | 11/06 |
| 64441020 | 0.15 | 150.2 | 05/30 |
| Mean Day | Occurrence (%) |
|---|---|
| 28 August–27 September | 29.4% |
| 27 September–27 October | 17.6% |
| 30 May–29 June | 17.6% |
| 29 July–28 August | 17.6% |
| 27 October–26 November | 11.8% |
| 29 June–29 July | 5.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Macedo, A.S.d.A.D.; Männich, M. Exploring Seasonality Indices for Low-Flow Analysis on Tibagi Watershed (Brazil). Hydrology 2025, 12, 19. https://doi.org/10.3390/hydrology12010019
de Macedo ASdAD, Männich M. Exploring Seasonality Indices for Low-Flow Analysis on Tibagi Watershed (Brazil). Hydrology. 2025; 12(1):19. https://doi.org/10.3390/hydrology12010019
Chicago/Turabian Stylede Macedo, Alexandre Sokoloski de Azevedo Delduque, and Michael Männich. 2025. "Exploring Seasonality Indices for Low-Flow Analysis on Tibagi Watershed (Brazil)" Hydrology 12, no. 1: 19. https://doi.org/10.3390/hydrology12010019
APA Stylede Macedo, A. S. d. A. D., & Männich, M. (2025). Exploring Seasonality Indices for Low-Flow Analysis on Tibagi Watershed (Brazil). Hydrology, 12(1), 19. https://doi.org/10.3390/hydrology12010019






