Agricultural Drought Model Based on Machine Learning Cubist Algorithm and Its Evaluation
Abstract
1. Introduction
2. Materials and Methods
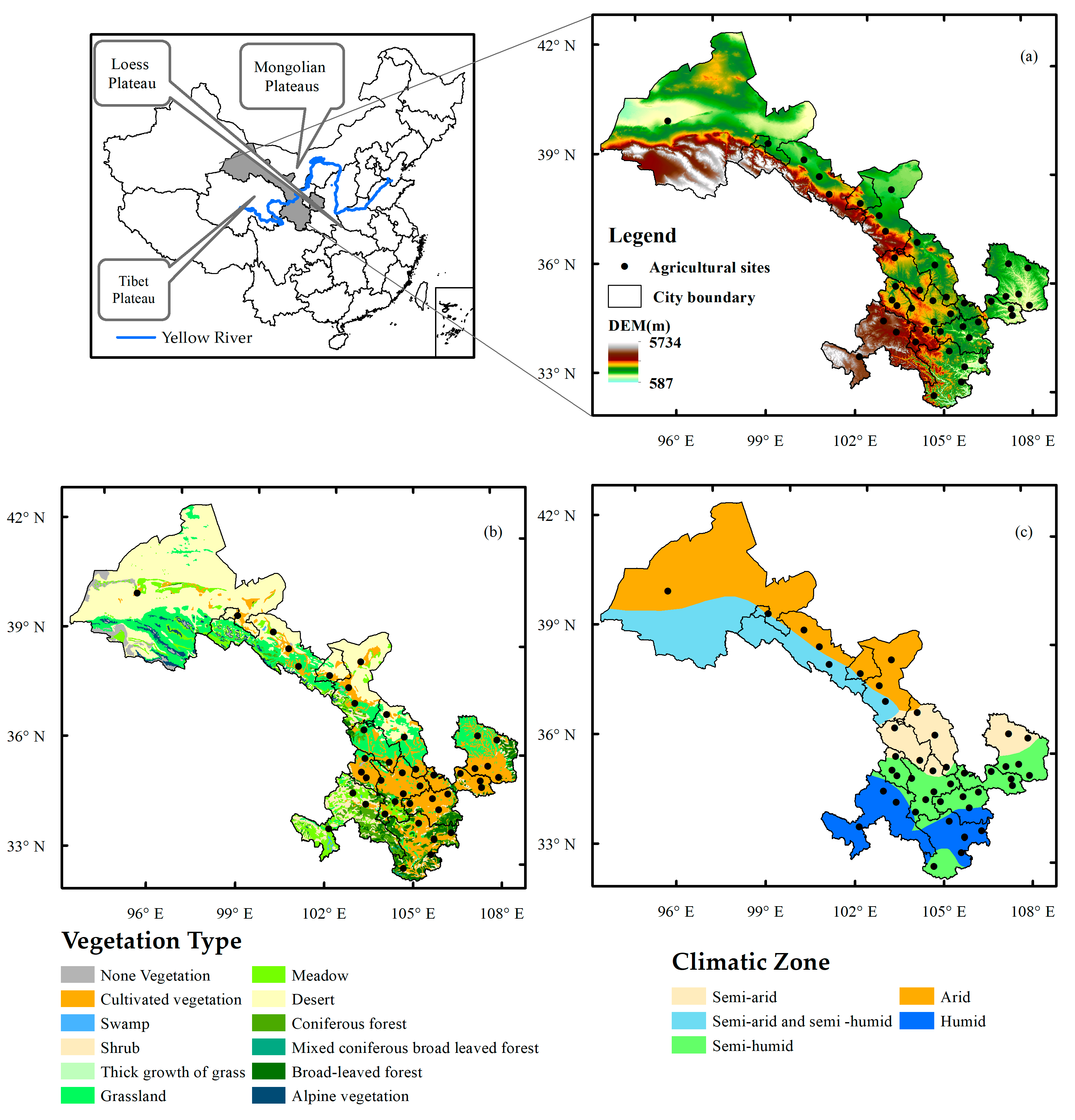
2.1. Study Area
2.2. Dataset Descriptions
2.2.1. Relative Soil Moisture
2.2.2. Meteorological Data
2.2.3. Remote Sensing Data
2.2.4. Land Surface Model Data
2.2.5. Environmental Data
2.3. Method
2.3.1. CART Algorithm
2.3.2. Random Forest Algorithm
2.3.3. Cubist Algorithm
2.3.4. Evaluation Method
3. Results
3.1. Construction of Comprehensive Model
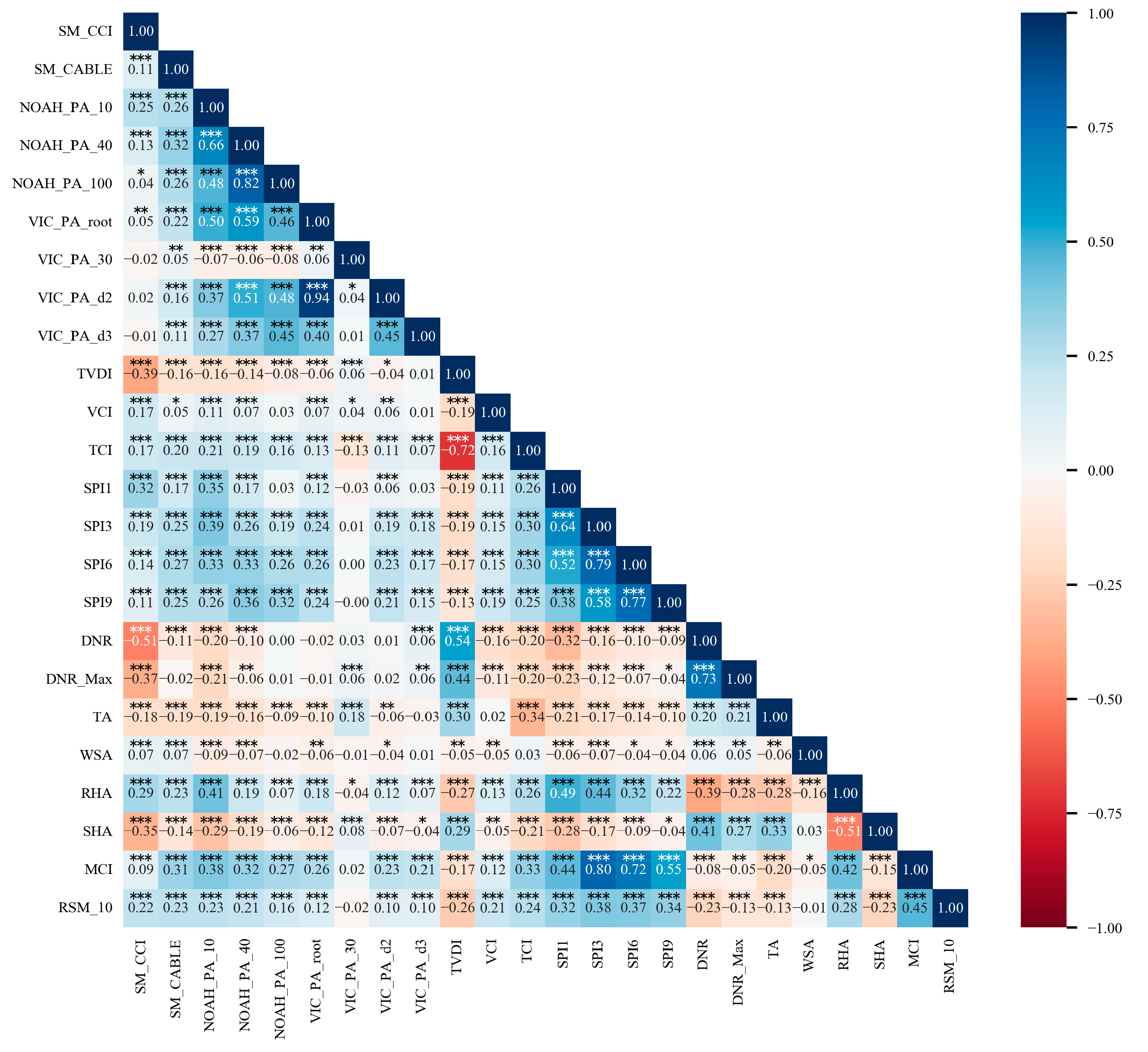
3.1.1. Correlation between Multi-Source Drought Indexes
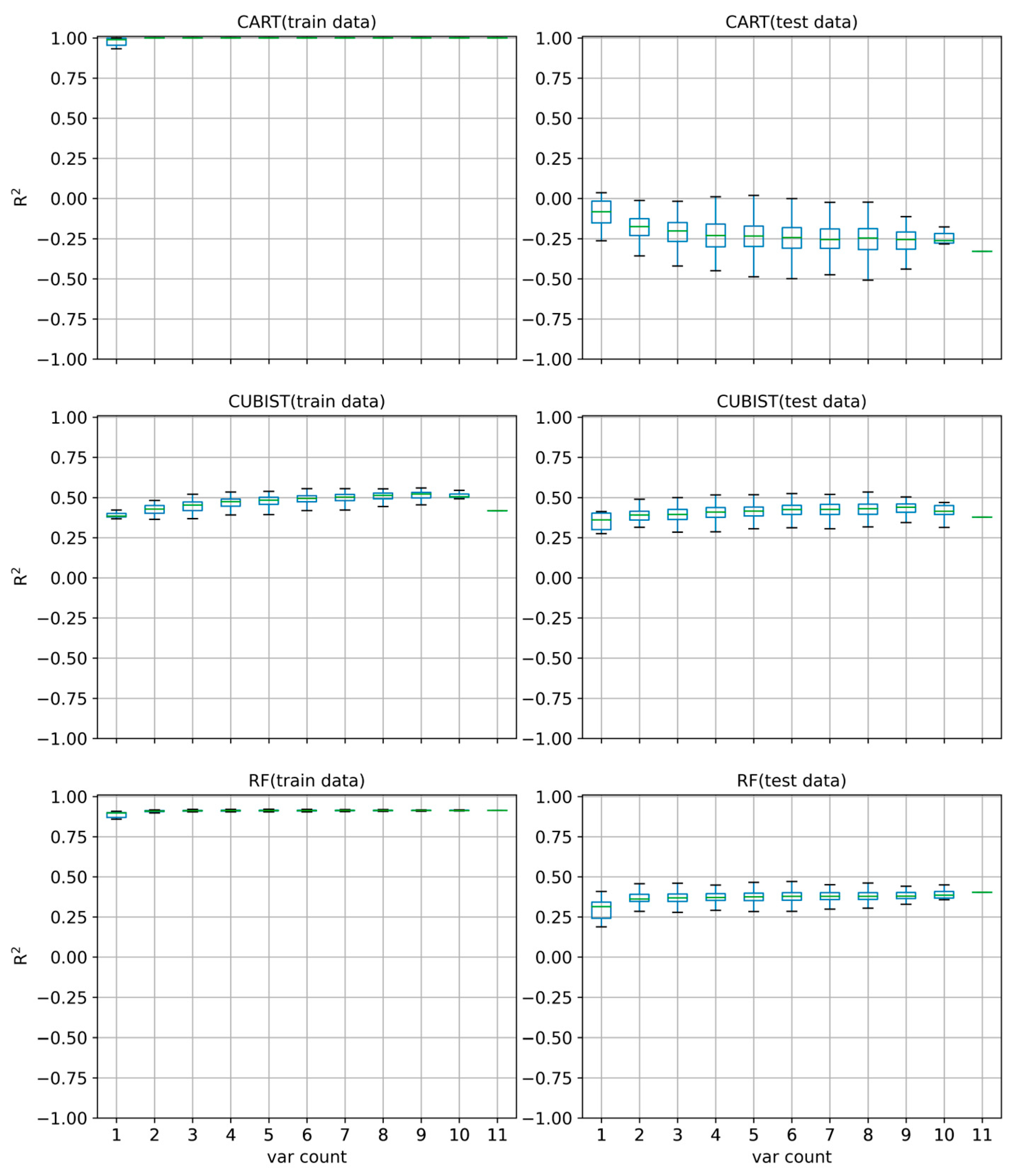
3.1.2. Selection of Algorithm
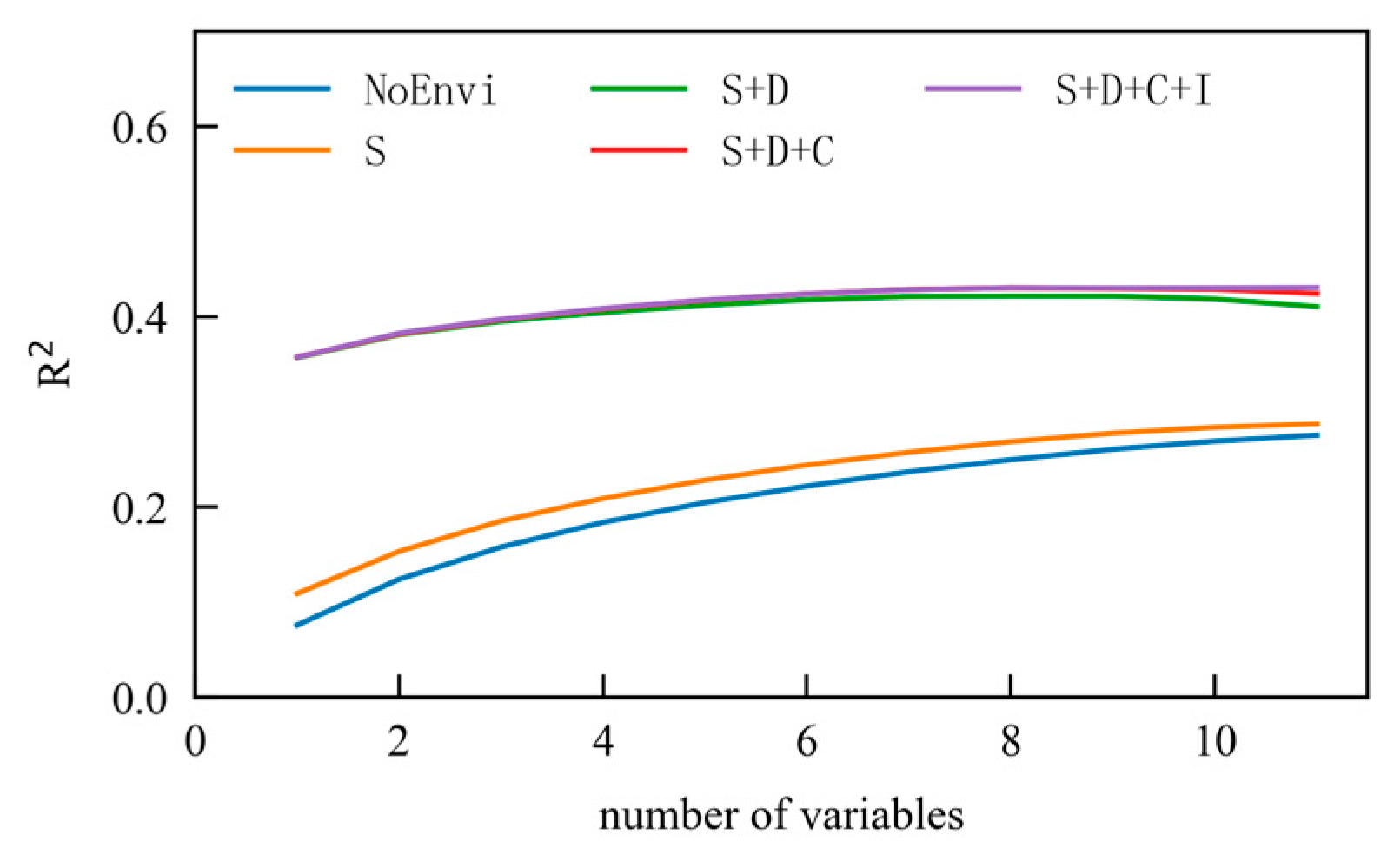
3.1.3. Selection of Environmental Factors
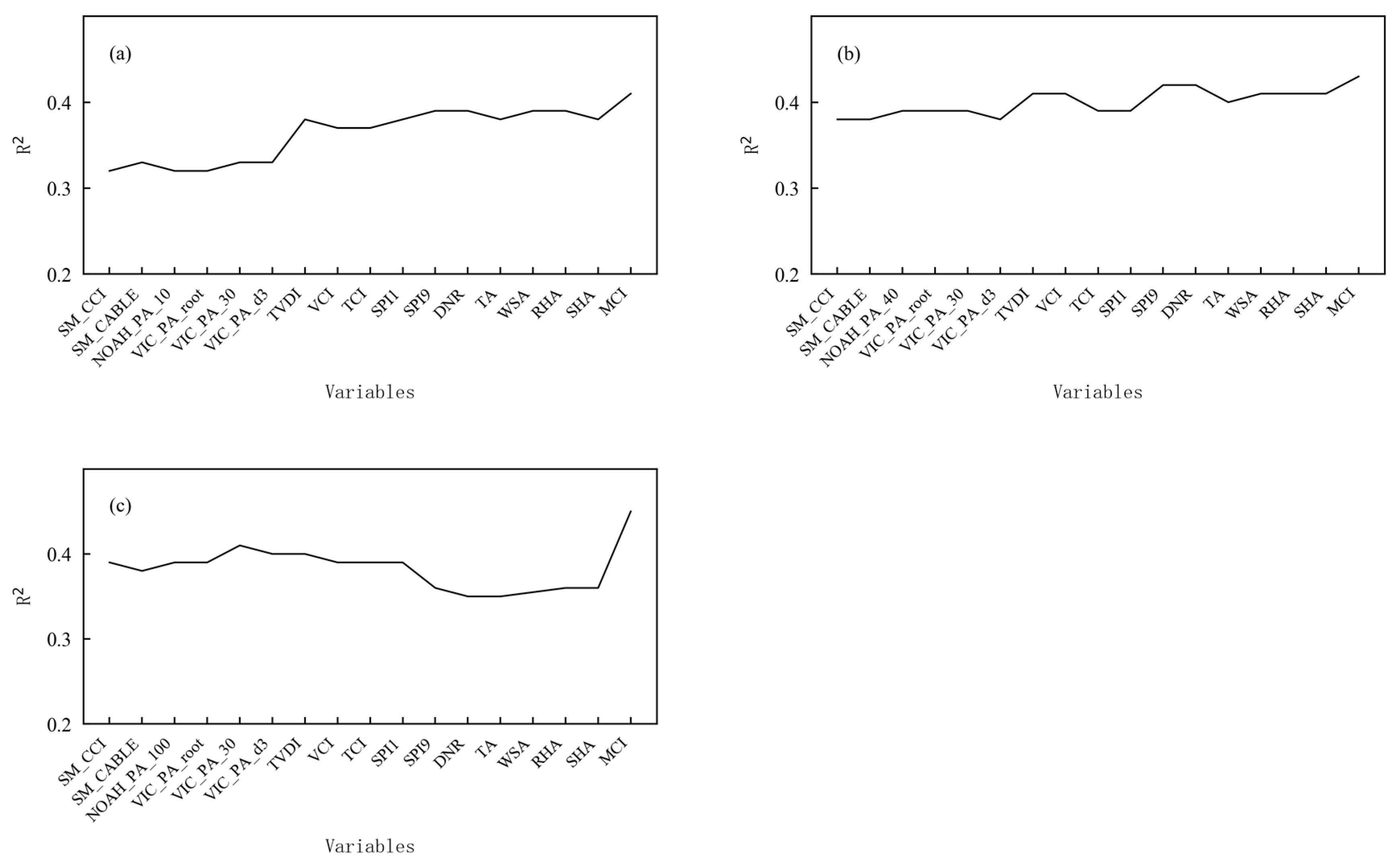
3.1.4. Selection of Variables
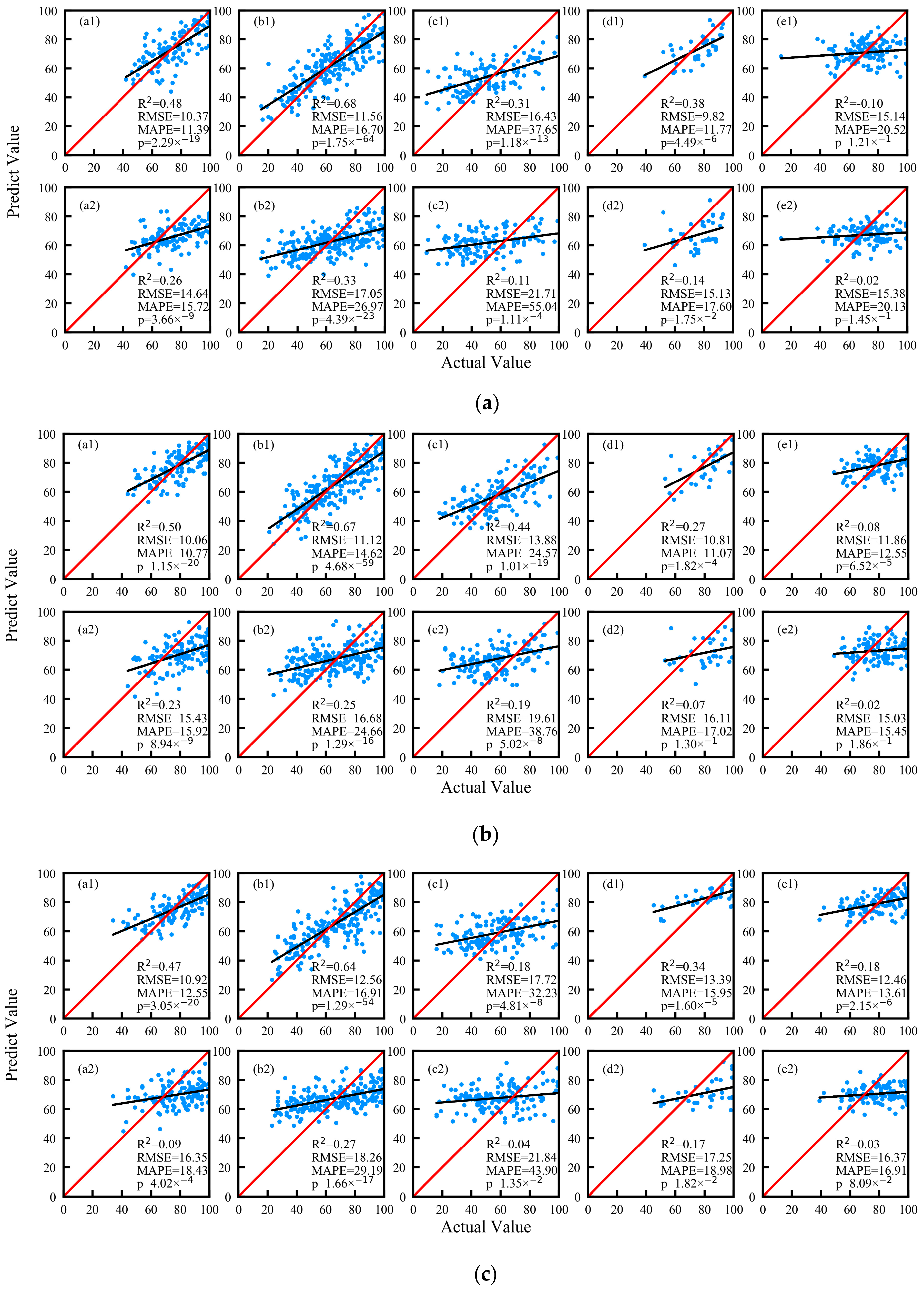
3.2. Evaluation of the Comprehensive Model
3.2.1. Comprehensive Evaluation
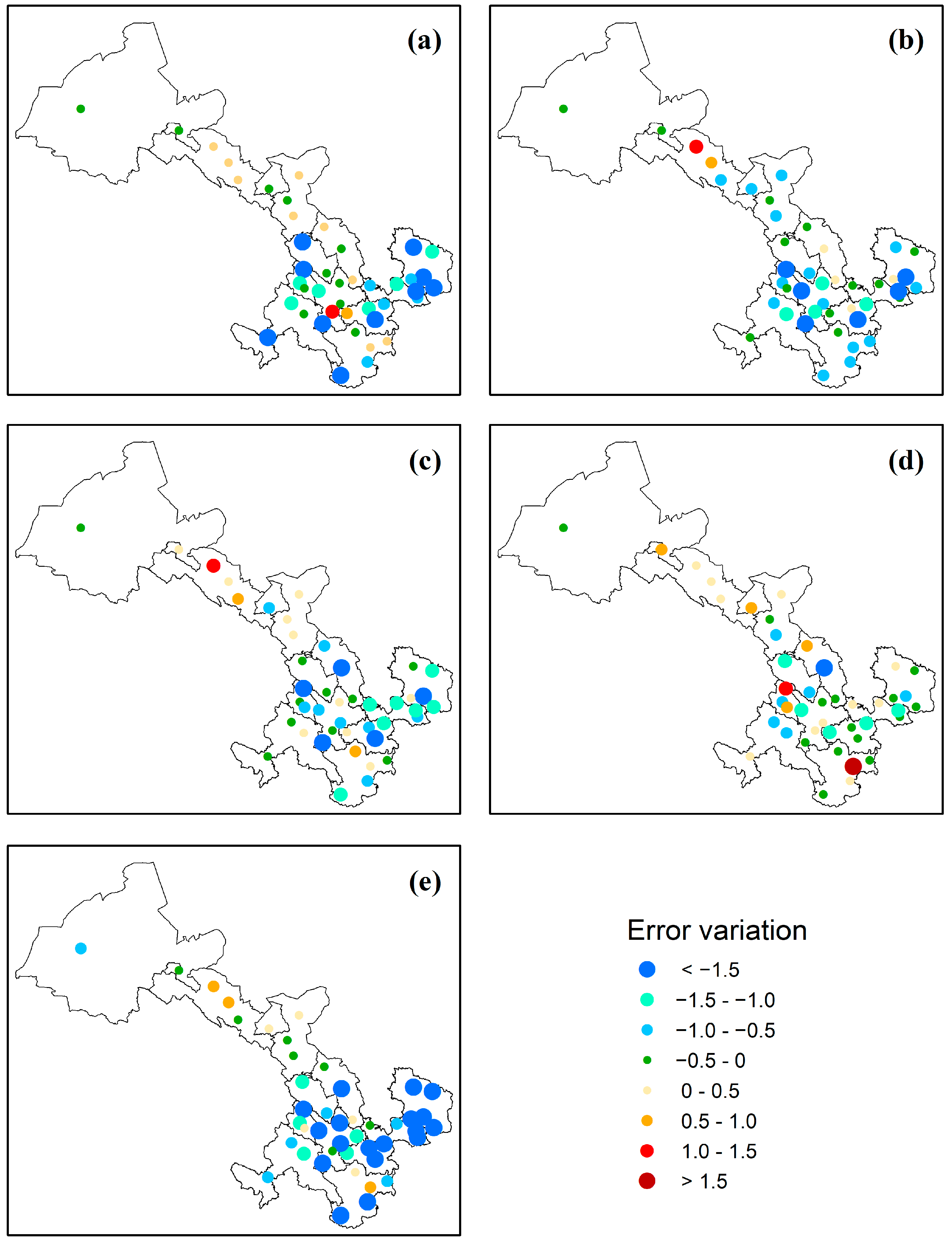
3.2.2. Evaluation of the Impact of Environmental Factors on the Model
3.2.3. Evaluation of the Impact of Meteorological Factors on Comprehensive Models
3.3. Application of the Comprehensive Model
4. Discussion
5. Conclusions
- (1)
- Among the comprehensive models constructed by the Cubist algorithm, the model at 20 cm depth has the highest accuracy, followed by the models at 10 cm and 50 cm depths. The validation R2 of the comprehensive model at 10 cm, 20 cm, and 50 cm depth is 0.56, 0.57, and 0.54, and the RMSE is 13.1, 12.8, and 13.2, respectively. The MAPEs are about 20.3%, 18.6%, and 18.6%, respectively. The accuracy of the comprehensive model has been significantly improved compared to the single-variable model. The RMSE and MAPE of the comprehensive model has decreased by about 26% and 28% compared to the best MCI model, on average, at the 10 cm, 20 cm, and 50 cm depths.
- (2)
- The fitting accuracy of the comprehensive model in humid areas and semi-humid areas, as well as semi-arid and semi-humid areas, is significantly higher than that in arid and semi-arid areas. In humid areas, semi-humid areas, semi-arid and semi-humid areas, semi-arid areas, and arid areas, the average validation R2 of the comprehensive model at 10 cm, 20 cm, and 50 cm depth is 0.48, 0.66, 0.31, 0.33, and 0.16, respectively. The average RMSE is 10.5, 11.7, 16, 11.3, and 13.2, and MAPEs are about 11.6%, 16.1%, 31.5%, 12.9%, and 16.5%, respectively.
- (3)
- Environmental factors play a crucial role in improving the accuracy of comprehensive models, with a greater impact than increasing the number of drought indicators. Considering that the DEM, climate zone, season alone can averagely reduce the error by about 20%, 7.5%, and 2.5%, respectively, and considering that all three factors can averagely reduce the error by about 25%. Compared to environmental factors, meteorological factors have a slightly weaker effect on improving the accuracy of comprehensive models. The consideration of meteorological factors, such as precipitation, WS, and SH, averagely reduce the error by about 6.5%.
- (4)
- The lack of irrigation, soil property, and evapotranspiration data, especially the lack of evapotranspiration data, may be an important reason for the low fitting accuracy of the comprehensive model in the arid and semi-arid areas of Hexi. In the future, efforts will be made to introduce water content information, such as irrigation, soil properties, and evapotranspiration data, into the comprehensive model, in order to improve the soil moisture-monitoring ability in the Hexi region.
- (5)
- Classification is another major task of machine learning algorithms, which can directly obtain drought levels and may improve the accuracy of drought levels. In the future, it will be necessary to compare the results of machine learning regression algorithms and classification algorithms to improve the accuracy of drought levels, especially in the division of drought levels in semi-arid and arid areas. In addition, the “boundary phenomenon” exists due to climate zone, and climate zone is based on multiple indicators, such as precipitation, dryness, temperature, and accumulated temperature [24]. Therefore, in addition to improving the fitting accuracy of regression models or the accuracy of classification models, using zoning indicators instead of climate zone may improve this situation. However, further research is needed to discover the impact of these factors on the comprehensive model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, N.; Wang, X. Advances and Developing Opportunities in Remote Sensing of Drought. J. Arid. Meteorol. 2015, 33, 1–18. [Google Scholar]
- Liu, H.; Wang, F.; Zhang, T. Evaluation applicability of CLDAS and GLDAS soil moisture for the Loess Plateau. Agric. Res. Arid. Areas 2018, 36, 270–276. [Google Scholar]
- Kowalczyk, E.A.; Wang, Y.P.; Law, R.M.; Davies, H.L.; McGregor, J.L.; Abramowitz, G. CSIRO Atmosphere Biosphere Land Exchange Model for Use in Climate Models and as an Offline Model; CSIRO Marine and Atmospheric Technical Report; Commonwealth Scientific and Industrial Research Organisation: Canberra, Australia, 2006; pp. 1–37. [Google Scholar]
- Yang, X.; Yang, Q. Research on meteorological drought severity model for Loess Plateau in Gansu. J. Nat. Disasters 2007, 16, 30–36. [Google Scholar]
- Zhang, L.; Zhang, Q.; Zhang, H.; Yue, P.; Li, H.; Wang, J.; Zhao, F.; Wang, Y.; Wang, J. Environmental factors driving evapotranspiration over a grassland in a transitional climate zone in China. Meteorol. Appl. 2022, 29, e2066. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, Y.; Cao, X.; Liu, W. On Some Problems of Arid Climate System of Northwest China. J. Desert Res. 2000, 20, 357–362. [Google Scholar]
- Yang, S.; Liu, C. Remote sensing calculation of soil moisture and analysis of water cycle process in the Yellow River Basin. Sci. China Ser. E Technol. Sci. 2004, 34, 1–12. [Google Scholar] [CrossRef]
- Zhou, S.; Williams, A.; Lintner, B.; Berg, A.; Zhang, Y.; Keenan, T.; Cook, B.; Hagemann, S.; Seneviratne, S.; Gentine, P. Soil moisture–atmosphere feedbacks mitigate declining water availability in drylands. Nat. Clim. Chang. 2021, 11, 38–44. [Google Scholar] [CrossRef]
- Brown, J.; Wardlow, B.; Tadesse, T.; Hayes, M.; Reed, B. The Vegetation Drought Response Index (VegDRI): A New Integrated Approach for Monitoring Drought Stress in Vegetation. GISci. Remote Sens. 2008, 45, 16–46. [Google Scholar] [CrossRef]
- Sánchez, N.; González-Zamora, Á.; Piles, M.; Martínez-Fernández, J. A New Soil Moisture Agricultural Drought Index (SMADI) Integrating MODIS and SMOS Products: A Case of Study over the Iberian Peninsula. Remote Sens. 2016, 8, 287. [Google Scholar] [CrossRef]
- Sun, P.; Zhang, Q.; Wen, Q.; Singh, V.; Shi, P. Multisource data based integrated agricultural drought monitoring in the Huai River basin, China. J. Geophys. Res. Atmos. 2017, 122, 10751–10772. [Google Scholar] [CrossRef]
- Ji, T.; Li, G.; Yang, H.; Liu, R.; He, T. Comprehensive drought index as an indicator for use in drought monitoring integrating multi-source remote sensing data: A case study covering the Sichuan-Chongqing region. Int. J. Remote Sens. 2018, 39, 786–809. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, X.; Liu, X.; Pan, Y. Research on agriculture drought monitoring method of Henan Province with multi-sources data. Remote Sens. Land Resour. 2018, 30, 180–186. [Google Scholar]
- Bijaber, N.; El Hadani, D.; Saidi, M.; Svoboda, M.D.; Wardlow, B.D.; Hain, C.R.; Poulsen, C.C.; Yessef, M.; Rochdi, A. Developing a Remotely Sensed Drought Monitoring Indicator for Morocco. Geosciences 2018, 8, 55. [Google Scholar] [CrossRef] [PubMed]
- Meng, L.; Dong, T.; Zhang, W. Drought monitoring using an Integrated Drought Condition Index (IDCI) derived from multi-sensor remote sensing data. Nat. Hazards 2016, 80, 1135–1152. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, N.; Li, J.; Chen, Z. Multi-sensor integrated framework and index for agricultural drought monitoring. Remote Sens. Environ. 2017, 188, 141–163. [Google Scholar] [CrossRef]
- Peng, X.; Wang, Q.; Yuan, C.; Lin, K. Review of research on data mining in application of meteorological forecasting. J. Arid. Meteorol. 2015, 33, 19–27. [Google Scholar]
- Han, J.; Mao, K.; Xu, T.; Guo, J.; Zuo, Z.; Gao, C. A Soil Moisture Estimation Framework Based on the CART Algorithm and Its Application in China. J. Hydrol. 2018, 563, 65–75. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, S.; Bai, Y.; Huang, A.; Zhang, J. SPEI Simulation for Monitoring Drought Based Machine Learning Integrating Multi-Source Remote Sensing Data in Shandong. Chin. J. Agrometeorol. 2021, 42, 230–242. [Google Scholar]
- Shen, R.; Huang, A.; Li, B.; Guo, J. Construction of a drought monitoring model using deep learning based on multi-source remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 48–57. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C.; Olshen, R. Classification and Regression Trees; Chapman and Hall: New York, NY, USA, 1984. [Google Scholar]
- Demisse, G.; Tadesse, T.; Bayissa, Y.; Atnatu, S.; Argaw, M.; Nedaw, D. Vegetation condition prediction for drought monitoring in pastoralist areas: A case study in Ethiopia. Int. J. Remote Sens. 2018, 39, 4599–4615. [Google Scholar] [CrossRef]
- Nam, H.; Tadesse, T.; Wardlow, B.; Hayes, M.; Svoboda, M.; Hong, E.; Pachepsky, Y.; Jang, M. Developing the vegetation drought response index for South Korea (VegDRI-SKorea) to assess the vegetation condition during drought events. Int. J. Remote Sens. 2018, 39, 1548–1574. [Google Scholar] [CrossRef]
- Bao, W. Gansu Climate; China Meteorological Press: Beijing, China, 2018; 283p. [Google Scholar]
- Deng, Z.; Xie, J.; Liu, X.; Yin, D. The Characteristics and Development and Utilization of Climate Resources in Gansu Province. J. Arid. Meteorol. 1998, 16, 16–19. [Google Scholar]
- GB/T20481-2006; Classification of Meteorological Drought. National Climate Center: Beijing, China, 2006; pp. 1–17.
- Kogan, F. Remote sensing of weather impacts on vegetation in non-homogeneous areas. Int. J. Remote Sens. 1990, 11, 1405–1419. [Google Scholar] [CrossRef]
- Kogan, F. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature—Vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Mcnally, A.; Shukla, S.; Arsenault, K.; Wang, S.; Peters-Lidard, C.D.; Verdin, J.P. Evaluating ESA CCI soil moisture in East Africa. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 96–109. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; An, R.; Quaye-Ballard, J.; Zhang, L.; Wang, Z. Evaluation of the European Space Agency Climate Change Initiative Soil Moisture Product over China Using Variance Reduction Factor. J. Am. Water Resour. Assoc. 2016, 52, 1524–1535. [Google Scholar] [CrossRef]
- Xu, W. Educational Statistics, 2nd ed.; Nanjing Normal University Press: Nanjing, China, 2007. [Google Scholar]
- Li, Y.; Zhang, L.; Zhang, H.; Pu, X. Drought Monitoring Based on CABLE Land Surface Model and Its Effect Examination of Typical Drought Events. Plateau Meteorol. 2015, 34, 1005–1018. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, L. Drought Monitoring Technique Based on Land Surface Model and the Study of its Application Effects in China. Ph.D. Thesis, Lanzhou University, Lanzhou, China, 2016. [Google Scholar]
- Deng, H.; Lu, Y.; Wang, Y.; Chen, X.; Liu, Q. Assessment of Actual Evapotranspiration in the Minjiang River Basin Based on the GLDAS-Noah Model. Sci. Geogr. Sin. 2022, 42, 548–556. [Google Scholar]
- Liu, P.; Song, H.; Bao, W.; Li, J. Applicability Evaluation of CLDAS and GLDAS Soil Temperature Data in Shaanxi Province. Meteorol. Sci. Technol. 2021, 49, 604–611. [Google Scholar]
- Breiman, L. Random Forests. Machine Learning. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- Data Mining with Cubist. Available online: http://www.rulequest.com/cubist-info.html (accessed on 4 April 2022).
- Ma, Y.; Sun, D.; Zhang, R.; Xu, J.; Wang, X. Analysis of driving factors for spatiotemporal variation of reference crop evapotranspiration in Gansu Province. Chin. Agric. Meteorol. 2022, 43, 881–892. [Google Scholar]
- Zhang, L.; Sha, S.; Zhang, Q.; Zhao, F.; Zhao, J.; Li, H.; Wang, S.; Wang, J.; Hu, Y.; Han, H. Investigating the Coupling Relationship between Soil Moisture and Evaporative Fraction over China’s Transitional Climate Zone. Hydrology 2023, 10, 221. [Google Scholar] [CrossRef]


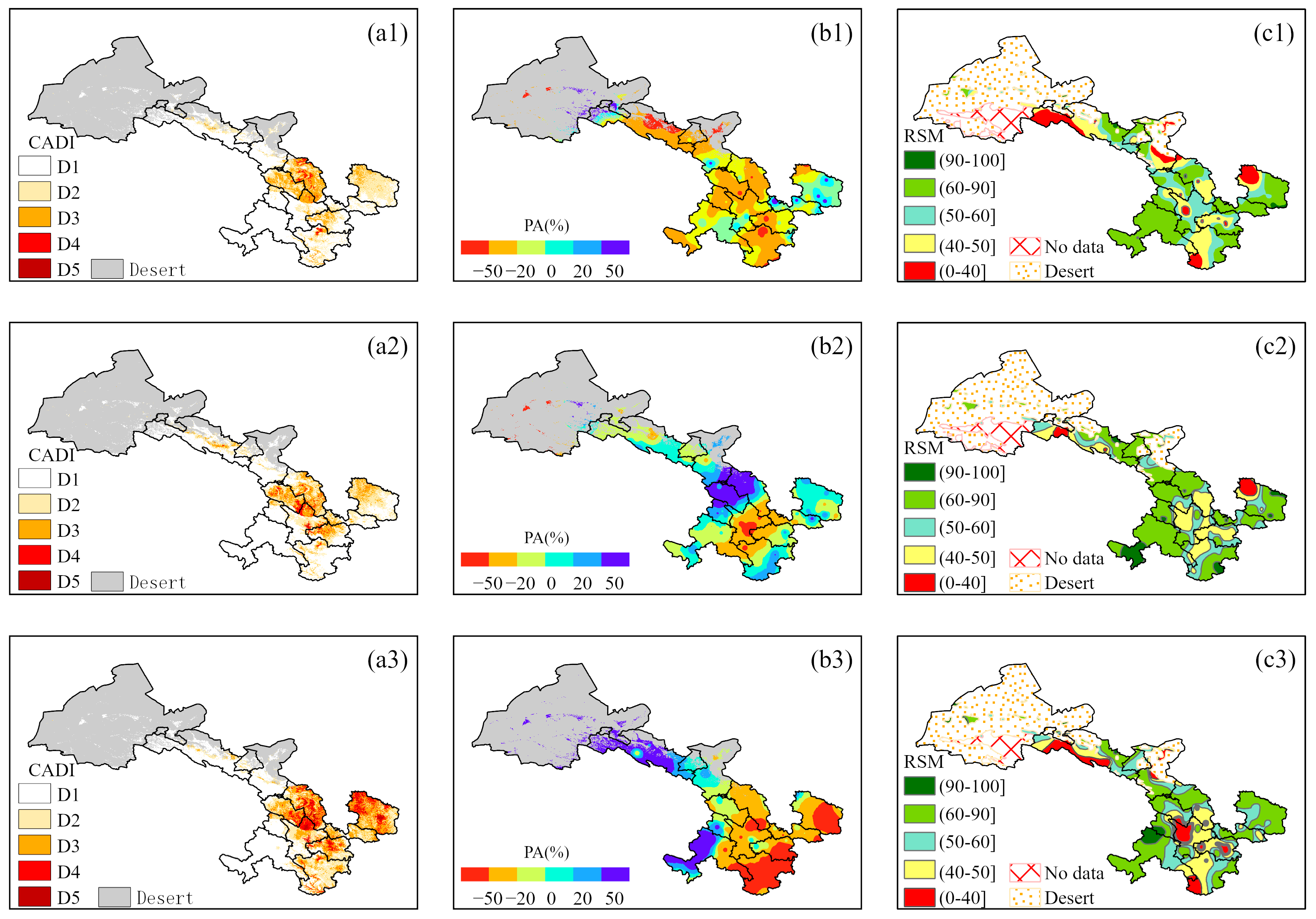
| Agricultural Drought Grade | Classification |
|---|---|
| None drought D1 | 60% < RSM |
| Light drought D2 | 50% < RSM ≤ 60% |
| Moderate drought D3 | 40% < RSM ≤ 50% |
| Severe drought D4 | 30% < RSM ≤ 40% |
| Extreme drought D5 | RSM ≤ 30% |
| Depth | Variables |
|---|---|
| 10 cm | MCI, TVDI, SPI1, SPI9, SM_CABLE, WSA |
| 20 cm | NOAH_10_40 cm_PA, TVDI, SPI9, WSA, SHA, MCI |
| 50 cm | NOAH_40_100 cm_PA, VIC_PA_30, MCI |
| Depth | Training Data Set | Test Data Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sample Size | R2 | p-Value | RMSE | MAPE | Sample Size | R2 | p-Value | RMSE | MAPE | |
| 10 cm | 2636 | 0.71 | 0 | 10.19 | 15.24 | 659 | 0.56 | 2.19 × 10−118 | 13.10 | 20.33 |
| 20 cm | 2621 | 0.75 | 0 | 9.44 | 12.72 | 656 | 0.57 | 1.88 × 10−124 | 12.77 | 18.57 |
| 50 cm | 2687 | 0.67 | 0 | 11.31 | 15.81 | 672 | 0.54 | 1.07 × 10−116 | 13.23 | 18.62 |
| Depth | Error Variation of Season | Error Variation of DEM | Error Variation of Climate Zone | Error Variation of Three Factors | ||||
|---|---|---|---|---|---|---|---|---|
| Absolute Value | Relative Value | Absolute Value | Relative Value | Absolute Value | Relative Value | Absolute Value | Relative Value | |
| 10 cm | −0.4 | −3% | −2.4 | −14.3 | −1 | −5.7% | −3.2 | −22% |
| 20 cm | −0.4 | −3% | −2.8 | −18% | −1.2 | −7.6% | −3.7 | −26% |
| 50 cm | −0.2 | −1.3% | −3.2 | −20% | −1.5 | 9% | −4.2 | −26% |
| Algorithm | Depth | Training Data Set | Test Data Set | ||||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | MAPE | R2 | RMSE | MAPE | ||
| multiple regression | 10 cm | 0.27 | 16.24 | 25.73 | 0.28 | 16.74 | 27.64 |
| 20 cm | 0.26 | 16.15 | 23.04 | 0.25 | 16.93 | 26.16 | |
| 50 cm | 0.17 | 17.86 | 27.22 | 0.15 | 18.06 | 26.89 | |
| Cubist | 10 cm | 0.65 | 11.28 | 17.24 | 0.47 | 14.29 | 22.94 |
| 20 cm | 0.68 | 10.61 | 14.25 | 0.50 | 13.85 | 20.15 | |
| 50 cm | 0.57 | 12.79 | 18.18 | 0.45 | 14.55 | 21 | |
| Variables | Rules | Models |
|---|---|---|
| DEM | 86 | 87 |
| MCI | 41 | 93 |
| TVDI | 12 | 82 |
| SPI1 | 6 | 68 |
| SPI9 | 4 | 59 |
| SM_CABLE | 2 | 45 |
| WSA | 1 | 29 |
| Depth | MCI | SPI1 | SPI9 | WS | SH | Considering All | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | r (%) | a | r(%) | a | r (%) | a | r (%) | a | r(%) | a | r (%) | |
| 10 cm | −0.8 | −6.7 | −0.7 | −5.6 | −0.5 | −4.1 | −0.2 | −1.48 | - | - | −1.27 | −10.6 |
| 20 cm | −0.7 | −6.5 | - | - | −0.3 | −2.8 | −0.01 | −0.25 | −0.13 | −1 | −0.51 | −2.9 |
| 50 cm | −0.7 | −5.9 | - | - | - | - | - | - | - | - | −0.7 | −5.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sha, S.; Wang, L.; Hu, D.; Ren, Y.; Wang, X.; Zhang, L. Agricultural Drought Model Based on Machine Learning Cubist Algorithm and Its Evaluation. Hydrology 2024, 11, 100. https://doi.org/10.3390/hydrology11070100
Sha S, Wang L, Hu D, Ren Y, Wang X, Zhang L. Agricultural Drought Model Based on Machine Learning Cubist Algorithm and Its Evaluation. Hydrology. 2024; 11(7):100. https://doi.org/10.3390/hydrology11070100
Chicago/Turabian StyleSha, Sha, Lijuan Wang, Die Hu, Yulong Ren, Xiaoping Wang, and Liang Zhang. 2024. "Agricultural Drought Model Based on Machine Learning Cubist Algorithm and Its Evaluation" Hydrology 11, no. 7: 100. https://doi.org/10.3390/hydrology11070100
APA StyleSha, S., Wang, L., Hu, D., Ren, Y., Wang, X., & Zhang, L. (2024). Agricultural Drought Model Based on Machine Learning Cubist Algorithm and Its Evaluation. Hydrology, 11(7), 100. https://doi.org/10.3390/hydrology11070100







