A Spatiotemporal Assessment of the Precipitation Variability and Pattern and an Evaluation of the Predictive Reliability of Global Climate Models over Bihar
Abstract
1. Introduction
2. Study Area, Materials, and Methods
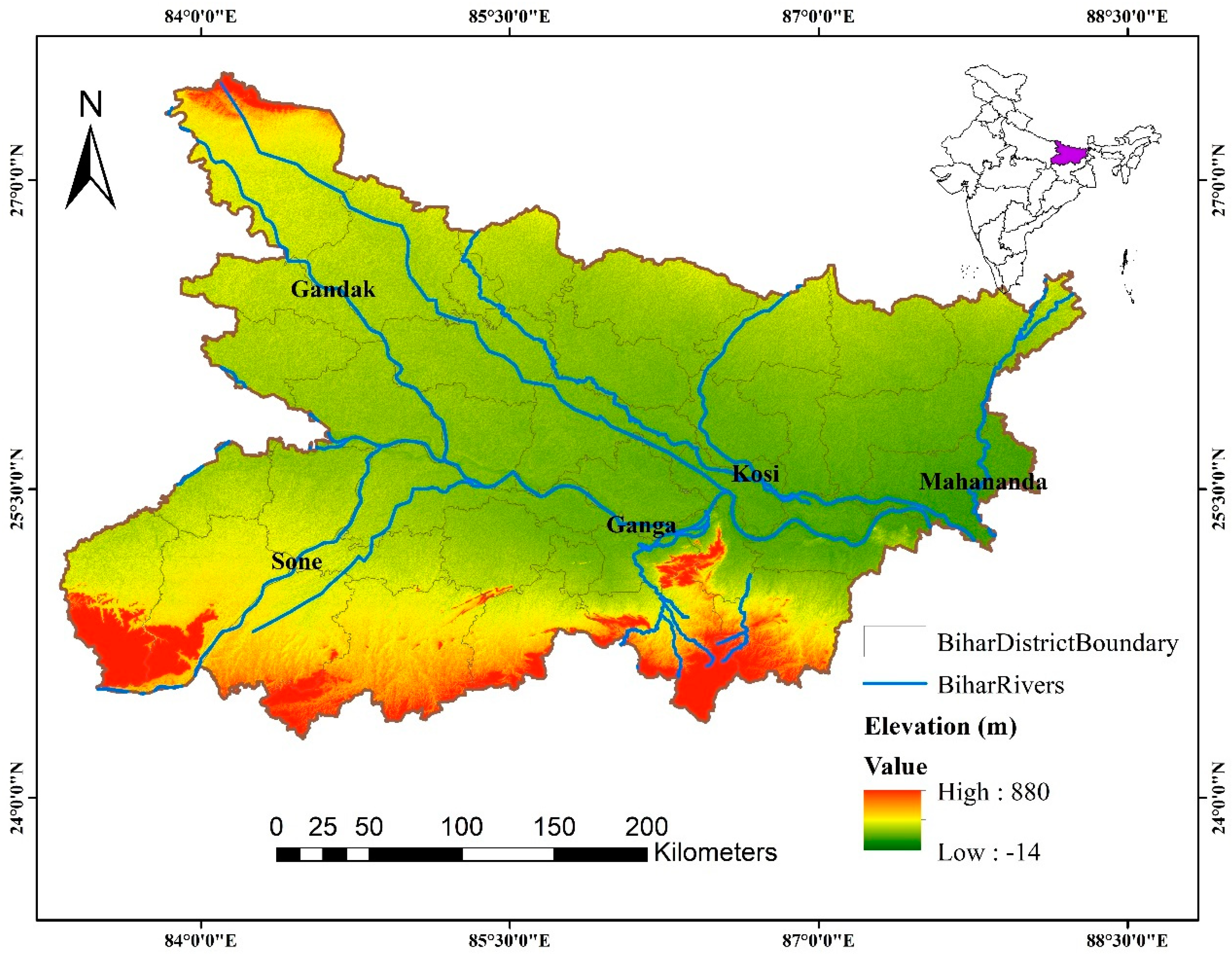
2.1. Study Area
2.2. Precipitation Data
2.3. Global Climate Models
2.4. Shared Socioeconomic Pathways
2.5. Methodology
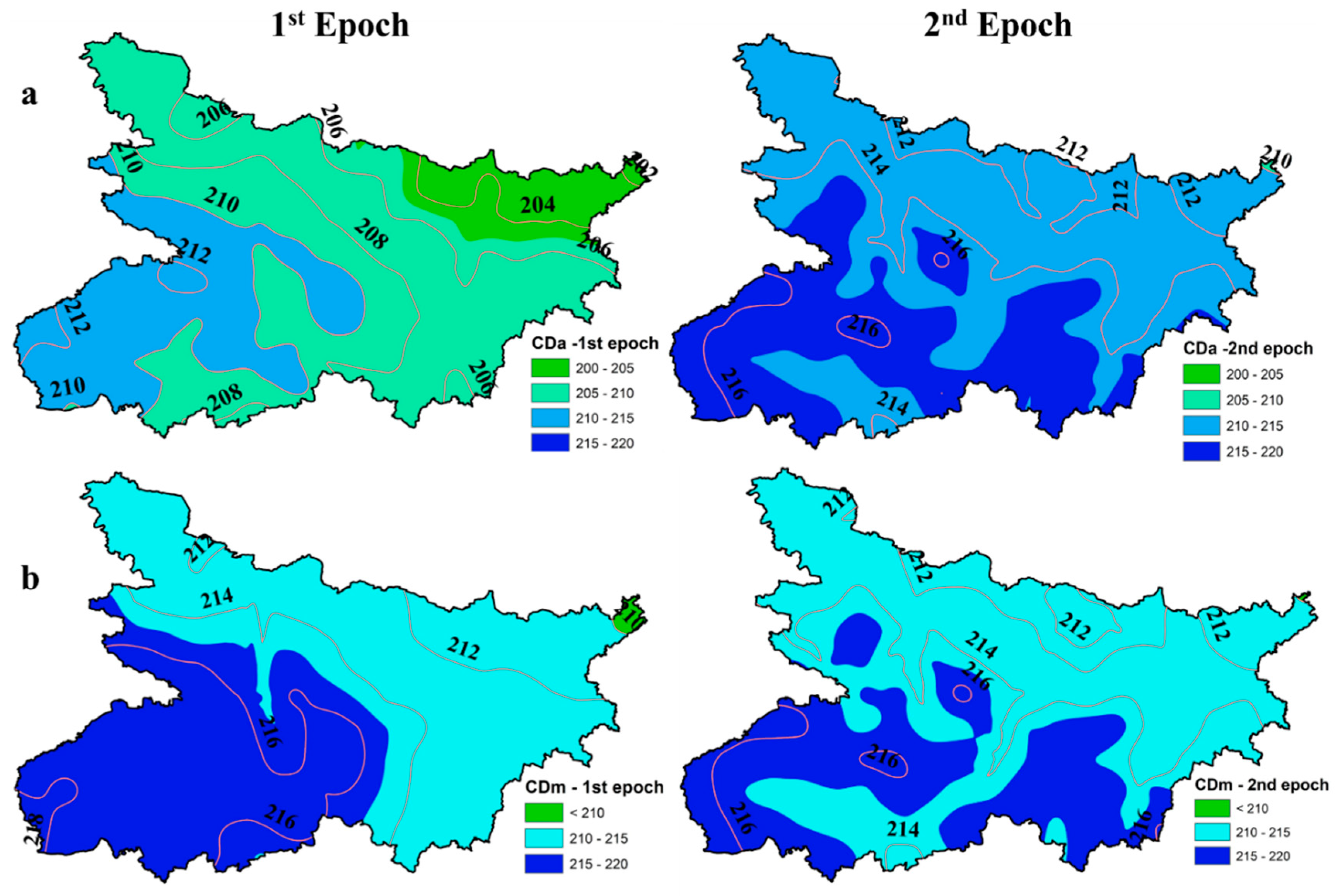
2.5.1. Centroidal Day (CD)
2.5.2. Modified Mann–Kendall Trend Test and Sen’s Slope Estimator
2.5.3. Extreme Event Analysis
2.5.4. Bayesian Model Averaging
3. Results
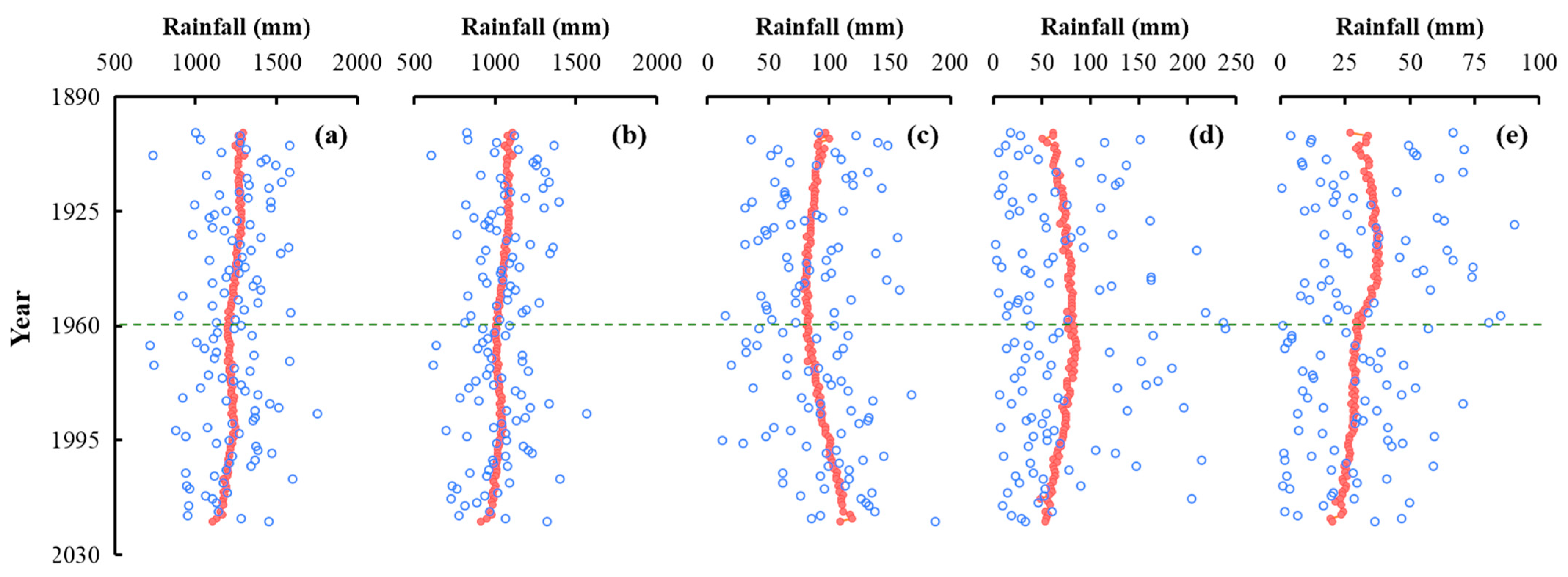
3.1. Change Point Detection
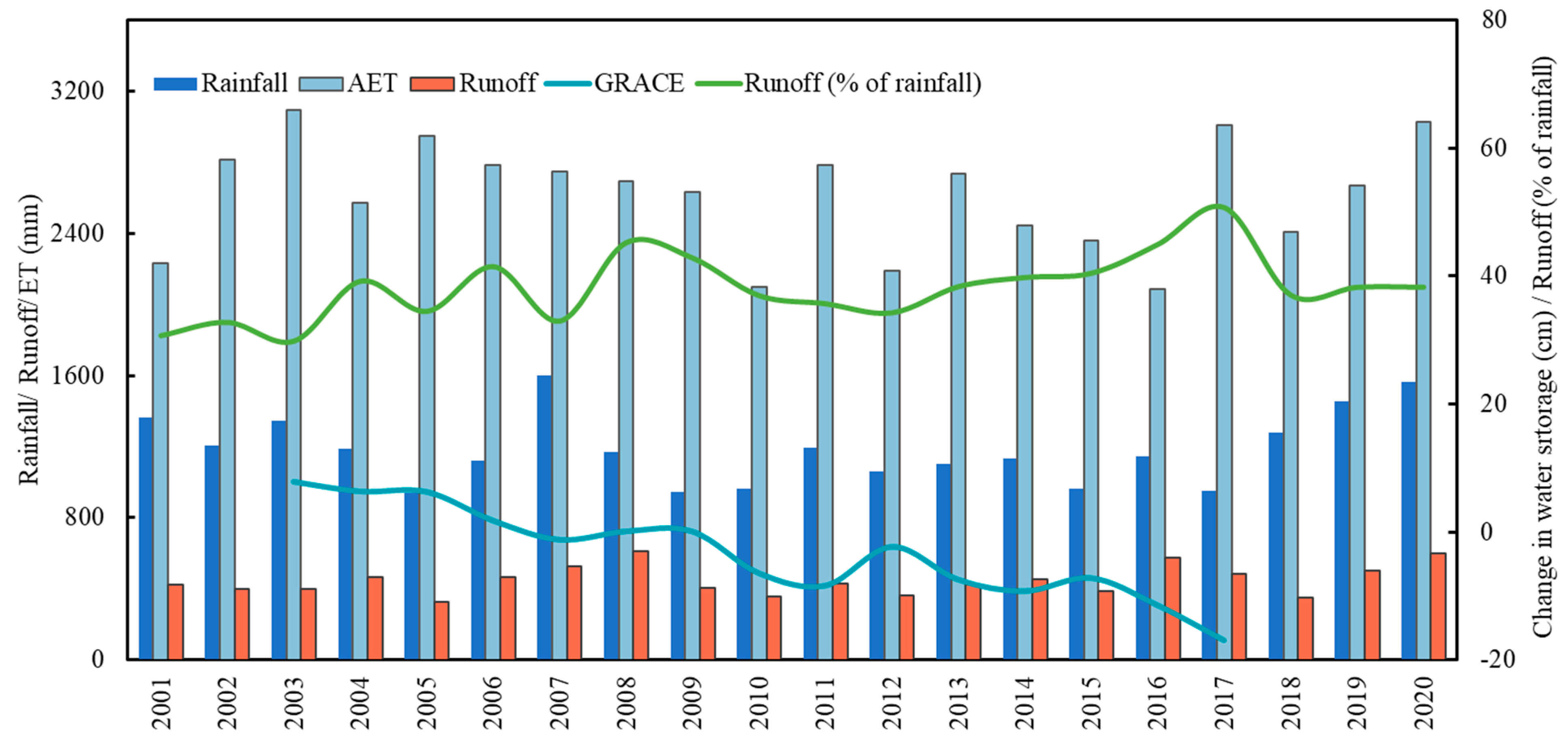
3.2. Overview of Rainfall in the Two Epochs
3.3. Shift in Annual and Monsoonal Rainfall
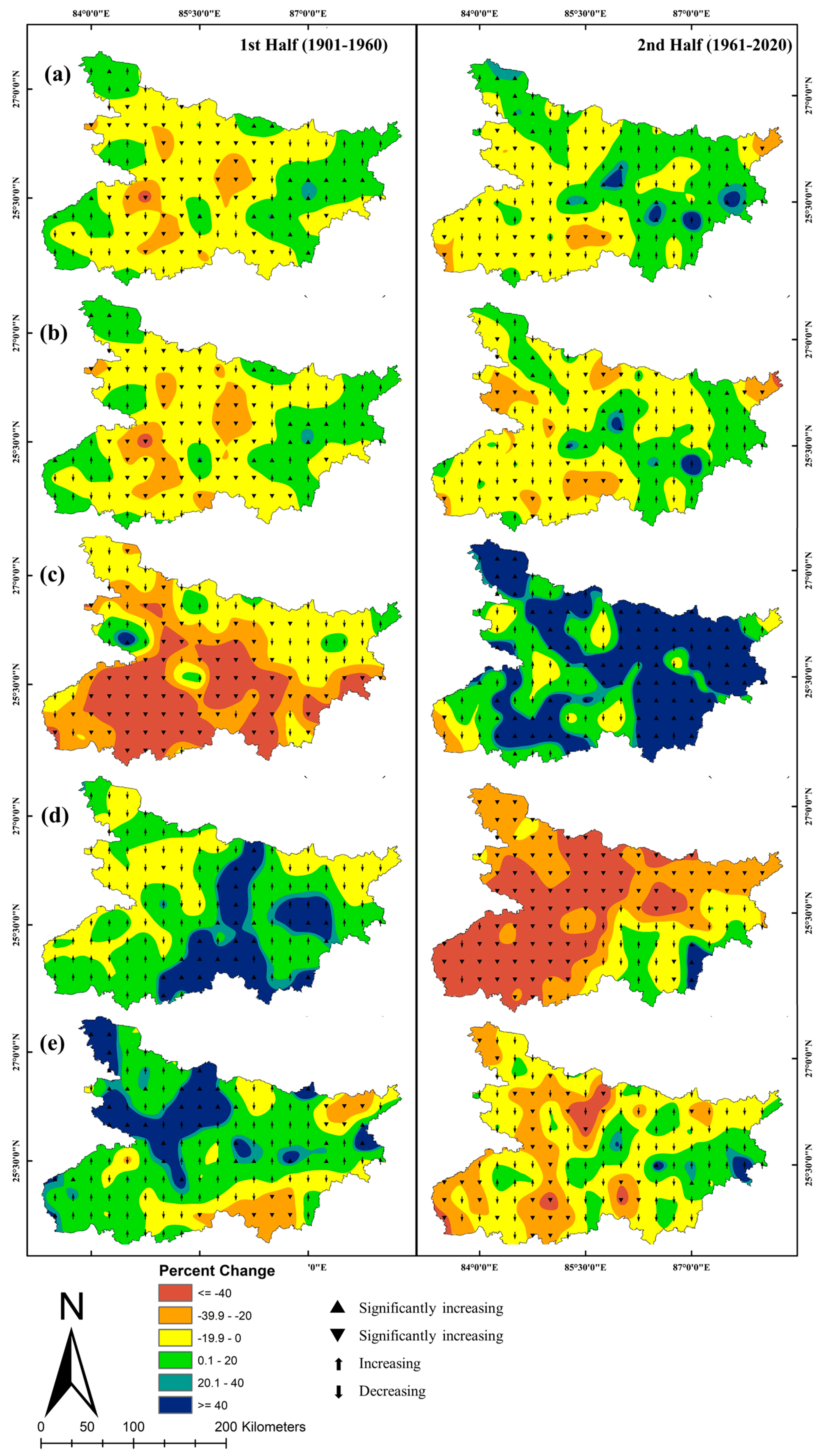
3.4. Trends in Annual and Seasonal Rainfall
3.5. Trends in Extreme Rainfall Events and Rainfall Intensity
3.6. Changes in Regions with Homogeneous Rainfall
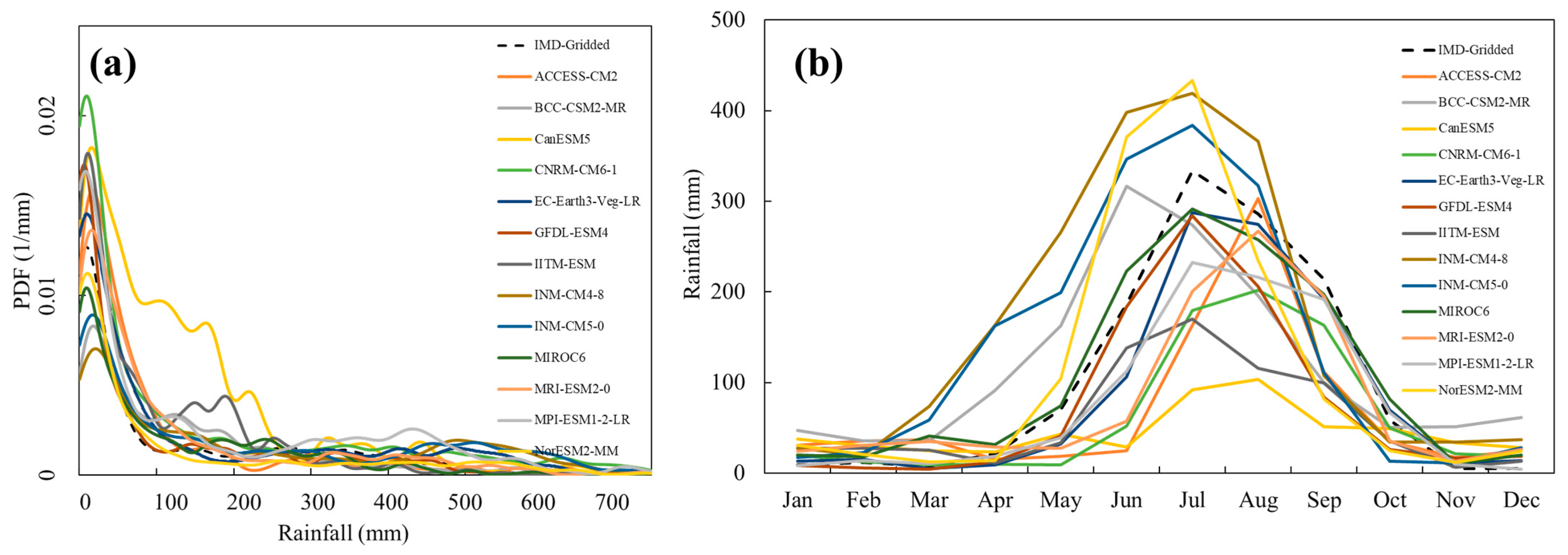
3.7. Comparison of GCMs with IMD Precipitation
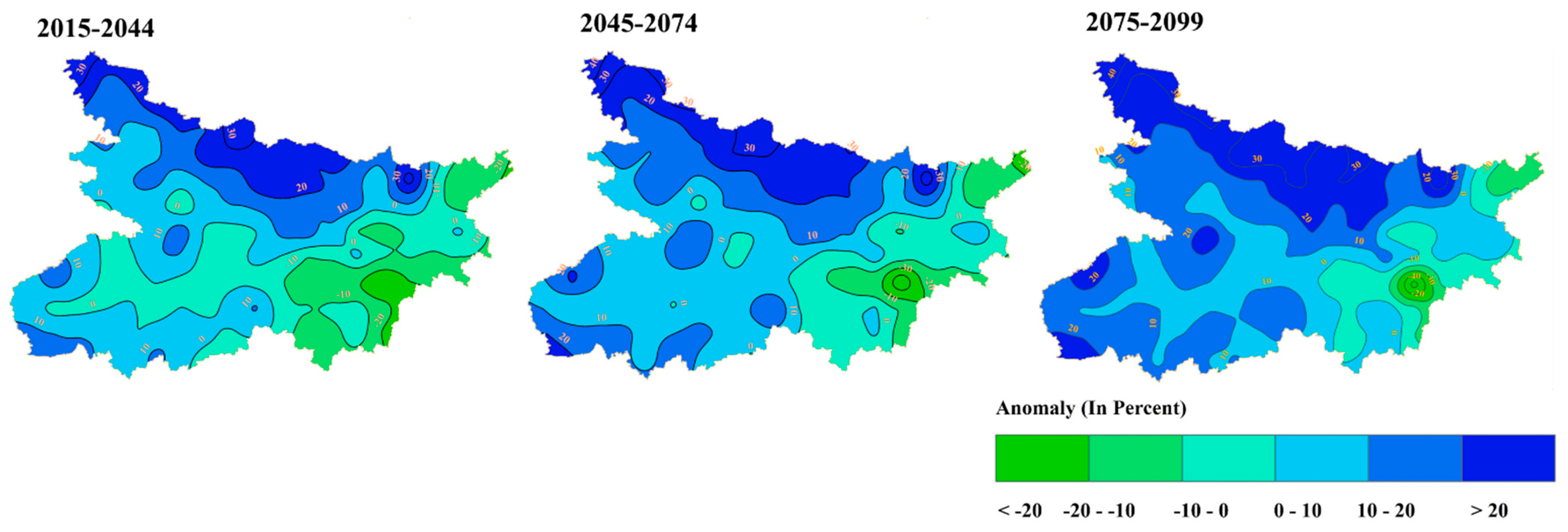
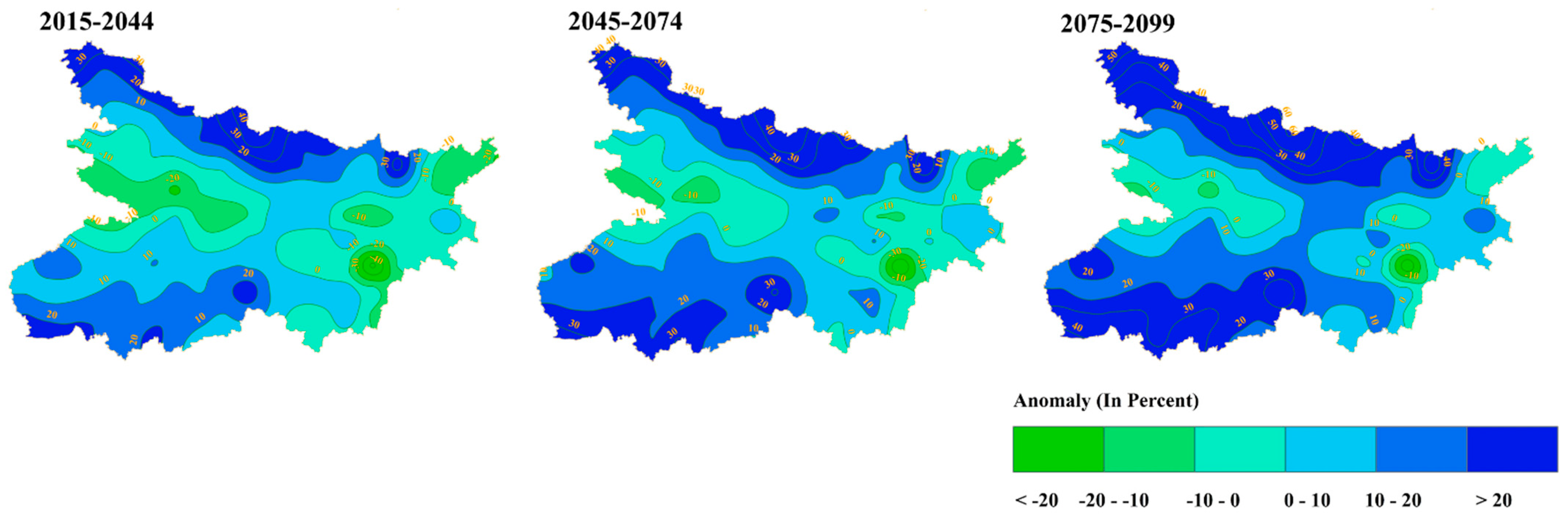
3.8. Bayesian Multi-Model Ensemble for Future Prediction
4. Discussion
- An evident change in precipitation trend was observed around the year 1960. There is a clear shift in the trend of southwest monsoons over the region, as evidenced by the rainfall variability during the different seasons pre- and post-1960. The nature of the pre-monsoon and post-monsoon seasons has flipped over the area in recent years.
- The nature of annual rainfall has completely changed between the two epochs, as evident by CDann.
- An increase in dry days has increased in monsoonal rainfall intensity. The frequency and intensity of extreme rainfall increased in the second epoch. Overall, the state experienced an increase in extreme rainfall of 60.6 mm/day (25.59%). Further, an increase in higher intensity (rainfall > 20 mm/day) areas is seen in north Bihar, while south Bihar sees an increase in low intensity (rainfall < 10 mm/day) areas.
- There is a marked variability in the state as one goes from east to west in terms of homogeneity (defined by clusters) and hydrological extremes as one goes from north to south. This leaves Bihar in a unique position, with an imminent need to combat the climate variability-induced risk to water resources for sustainable development.
- EC-Earth3-Veg-LR, MIROC6 and MPI-ESM1-2-LR are the best-performing models for the region. A Bayesian multi-model ensemble suggests that south Bihar will receive low rainfall for the duration of 2015–2045, hence increasing the drought risk.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Islam, T.; Rico-Ramirez, M.A.; Han, D.; Srivastava, P.K.; Ishak, A.M. Performance evaluation of the TRMM precipitation estimation using ground-based radars from the GPM validation network. J. Atmos. Sol.-Terr. Phys. 2012, 77, 194–208. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Meshram, C.; Singh, S.K.; Srivastava, P.K.; Islam, T. Precipitation trend analysis of Sindh River basin, India, from 102-year record (1901–2002). Atmos. Sci. Lett. 2016, 17, 71–77. [Google Scholar] [CrossRef]
- Srivastava, P.K.; Han, D.; Rico-Ramirez, M.A.; Islam, T. Sensitivity and uncertainty analysis of mesoscale model downscaled hydro-meteorological variables for discharge prediction. Hydrol. Process. 2014, 28, 4419–4432. [Google Scholar] [CrossRef]
- Res, C.; Trenberth, K.E. Changes in precipitation with climate change. Clim. Res. 2011, 47, 123–138. [Google Scholar] [CrossRef]
- Ashok, K.; Guan, Z.; Saji, N.H.; Yamagata, T. Individual and combined influences of ENSO and the Indian Ocean Dipole on the Indian summer monsoon. J. Clim. 2004, 17, 3141–3155. [Google Scholar] [CrossRef]
- Torrence, C.; Webster, P.J. Interdecadal changes in the ENSO-monsoon system. J. Clim. 1999, 12 Pt 2, 2679–2690. [Google Scholar] [CrossRef]
- Dash, S.K.; Jenamani, R.K.; Kalsi, S.R.; Panda, S.K. Some evidence of climate change in twentieth-century India. Clim. Chang. 2007, 85, 299–321. [Google Scholar] [CrossRef]
- Mondal, A.; Khare, D.; Kundu, S. Spatial and temporal analysis of rainfall and temperature trend of India. Theor. Appl. Climatol. 2015, 122, 143–158. [Google Scholar] [CrossRef]
- Dash, S.K.; Kulkarni, M.A.; Mohanty, U.C.; Prasad, K. Changes in the characteristics of rain events in India. J. Geophys. Res. Atmos. 2009, 114, 1–12. [Google Scholar] [CrossRef]
- Guhathakurta, P.; Rajeevan, M.; Sikka, D.R.; Tyagi, A. Observed changes in southwest monsoon rainfall over India during 1901–2011. Int. J. Climatol. 2015, 35, 1881–1898. [Google Scholar] [CrossRef]
- Gnanaseelan, C.; Mujumdar, M.; Kulkarni, A.; Chakraborty, S.; Sciences, E. Assessment of Climate Change over the Indian Region; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Naidu, C.V.; Srinivasa Rao, B.R.; Bhaskar Rao, D.V. Climatic trends and periodicities of annual rainfall over India. Meteorol. Appl. 1999, 6, 395–404. [Google Scholar] [CrossRef]
- Zhang, L.; Zhou, T. An assessment of monsoon precipitation changes during 1901–2001. Clim. Dyn. 2011, 37, 279–296. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers: A Report of Working Group I of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- Guhathakurta Pulak Khedikar, S.; Menon, P.; Prasad, A.K.; Sable, S.T.; Advani, S.C. Climate Research and Services Observed Rainfall Variability and Changes over Assam State. IMD Annu. Rep. 2020, 16, 28. [Google Scholar]
- Praveen, B.; Talukdar, S.; Shahfahad Mahato, S.; Mondal, J.; Sharma, P.; Islam AR, M.T.; Rahman, A. Analyzing trend and forecasting of rainfall changes in India using non-parametrical and machine learning approaches. Sci. Rep. 2020, 10, 10342. [Google Scholar] [CrossRef]
- Warwade, P.; Tiwari, S.; Ranjan, S.; Chandniha, S.K.; Adamowski, J. Spatio-temporal variation of rainfall over Bihar State, India. J. Water Land Dev. 2018, 36, 183–187. [Google Scholar] [CrossRef]
- Zakwan, M.; Ara, Z. Statistical analysis of rainfall in Bihar. Sustain. Water Resour. Manag. 2019, 5, 1781–1789. [Google Scholar] [CrossRef]
- NITI Aayog. Composite Water Mangement Index. 2019; pp. 11–13. Available online: http://niti.gov.in/writereaddata/files/new_initiatives/presentation-on-CWMI.pdf (accessed on 23 June 2023).
- Tesfaye, K.; Aggarwal, P.K.; Mequanint, F.; Shirsath, P.B.; Stirling, C.M.; Khatri-Chhetri, A.; Rahut, D.B. Climate variability and change in Bihar, India: Challenges and opportunities for sustainable crop production. Sustainability 2017, 9, 1998. [Google Scholar] [CrossRef]
- Rashiq, A.; Prakash, O. Assessment of Spatio-temporal variability of climate in the lower Gangetic alluvial plain. Environ. Monit. Assess. 2023, 195, 945. [Google Scholar] [CrossRef] [PubMed]
- Bommaraboyina, P.R.; Daniel, J.; Abbhishek, K. Book Review: Climate Change and Agriculture in India: Impact and Adaptations. Front. Clim. 2020, 2, 576004. [Google Scholar] [CrossRef]
- NRSC. Flood Hazard Atlas–Bihar; NRSC: Hyderabad, India, 2020; p. 137.
- Saharia, M.; Jain, A.; Baishya, R.R.; Haobam, S.; Sreejith, O.P.; Pai, D.S.; Rafieeinasab, A. India flood inventory: Creation of a multi-source national geospatial database to facilitate comprehensive flood research. Nat. Hazards 2021, 108, 619–633. [Google Scholar] [CrossRef]
- Bhatt, C.M.; Srinivasa Rao, G.; Manjushree, P.; Bhanumurthy, V. Space based disaster management of 2008 Kosi floods, North Bihar, India. J. Indian Soc. Remote Sens. 2010, 38, 99–108. [Google Scholar] [CrossRef]
- Kumar, S.; Roshni, T.; Kumar, A.; Jayakumar, D. GIS-Based Drought Assessment in Climate Change Context: A Case Study for Sone Command, Bihar. J. Inst. Eng. Ser. A 2021, 102, 199–213. [Google Scholar] [CrossRef]
- Sinha, R.; Bapalu, G.V.; Singh, L.K.; Rath, B. Flood risk analysis in the Kosi river basin, north Bihar using multi-parametric approach of Analytical Hierarchy Process (AHP). J. Indian Soc. Remote Sens. 2008, 36, 335–349. [Google Scholar] [CrossRef]
- Tripathi, G.; Parida, B.R.; Pandey, A.C. Spatio-temporal rainfall variability and flood prognosis analysis using satellite data over North Bihar during the August 2017 flood event. Hydrology 2019, 6, 38. [Google Scholar] [CrossRef]
- Brakenridge, G.R. Global Active Archive of Large Flood Events. In Dartmouth Flood Observatory; University of Colorado: Boulder, CO, USA, 2016; Available online: http://floodobservatory.colorado.edu/Archives/ (accessed on 23 June 2023).
- Yaduvanshi, A.; Srivastava, P.K.; Pandey, A.C. Integrating TRMM and MODIS satellite with socioeconomic vulnerability for monitoring drought risk over a tropical region of India. Phys. Chem. Earth 2015, 83–84, 14–27. [Google Scholar] [CrossRef]
- Krishna Kumar, K.; Rupa Kumar, K.; Ashrit, R.G.; Deshpande, N.R.; Hansen, J.W. Climate impacts on Indian agriculture. Int. J. Climatol. 2004, 24, 1375–1393. [Google Scholar] [CrossRef]
- Khanal, A.R.; Mishra, A.K. Enhancing food security: Food crop portfolio choice in response to climatic risk in India. Glob. Food Secur. 2017, 12, 22–30. [Google Scholar] [CrossRef]
- Sharma, A.; Maharana, P.; Sahoo, S.; Sharma, P. Environmental change and groundwater variability in South Bihar, India. Groundw. Sustain. Dev. 2022, 19, 100846. [Google Scholar] [CrossRef]
- Sen, S. Climate variability and migration in Bihar: An empirical analysis. Int. J. Disaster Risk Reduct. 2024, 103, 104301. [Google Scholar] [CrossRef]
- Das, L.; Bhowmick, S.; Meher, J.K.; Mahdi, S.S. CMIP5 based past and future climate change scenarios over South Bihar, India. J. Earth Syst. Sci. 2023, 132, 8. [Google Scholar] [CrossRef]
- Jha, R.K.; Kalita, P.K.; Cooke, R.A. Assessment of climatic parameters for future climate change in a major agricultural state in India. Climate 2021, 9, 111. [Google Scholar] [CrossRef]
- Kumar, S.; Roshni, T.; Kahya, E.; Ghorbani, M.A. Climate change projections of rainfall and its impact on the cropland suitability for rice and wheat crops in the Sone river command, Bihar. Theor. Appl. Climatol. 2020, 142, 433–451. [Google Scholar] [CrossRef]
- IWMI. Chapter 1: Present Scenario and Need for Index Based Flood Insurance in Bihar. In Index Based Flood Insurance (IBFI); IWMI: New Delhi, India, 2018. [Google Scholar]
- GoI. SDG India Index & Dashboard 2020–21 Report. In Partnerships in the Decade of Action; Niti Aayog: New Delhi, India, 2021; p. 348. Available online: https://niti.gov.in/writereaddata/files/SDG_3.0_Final_04.03.2021_Web_Spreads.pdf (accessed on 1 June 2023).
- Pai, D.S.; Sridhar, L.; Rajeevan, M.; Sreejith, O.P.; Satbhai, N.S.; Mukhopadhyay, B. Development of a new high spatial resolution (0.25° × 0.25°) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region. Mausam 2014, 65, 1–18. [Google Scholar] [CrossRef]
- Riahi, K.; van Vuuren, D.P.; Kriegler, E.; Edmonds, J.; O’Neill, B.C.; Fujimori, S.; Bauer, N.; Calvin, K.; Dellink, R.; Fricko, O.; et al. The Shared Socioeconomic Pathways and their energy, land use, and greenhouse gas emissions implications: An overview. Glob. Environ. Chang. 2017, 42, 153–168. [Google Scholar] [CrossRef]
- Hamed, K.; Rao, R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. Eng. 1998, 213, 346–360. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 2013, 37–41. [Google Scholar] [CrossRef]
- Salam, A.; Anwer, E.; Alam, S. Agriculture and the Economy of Bihar. Int. J. Sci. Res. Publ. 2013, 3, 1–19. [Google Scholar]



| Sl. No. | GCM | Institution, Country | Resolution |
|---|---|---|---|
| 1 | ACCESS-CM2 | Australian Community Climate and Earth System Simulator, Australia | 1.9° × 1.3° |
| 2 | BCC-CSM2-MR | Beijing Climate Center, China | 1.1° × 1.1° |
| 3 | CanESM5 | Canadian Centre for Climate Modelling and Analysis, Canada | 2.8° × 2.8° |
| 4 | CNRM-CM6-1 | National Centre for Meteorologic Research, France | 1.4° × 1.4° |
| 5 | EC-Earth3-Veg-LR | Europe | 0.7° × 0.7° |
| 6 | GFDL-ESM4 | Geophysical Fluid Dynamics Laboratory, USA | 1.3° × 1.0° |
| 7 | IITM-ESM | Indian Institute of Tropical Meteorology | 1.91° × 1.87° |
| 8 | INM-CM4-8 | Marchuk Institute of Numerical Mathematics, Russia | 2.0° × 1.5° |
| 9 | INM-CM5-0 | 2.0° × 1.5° | |
| 10 | MIROC6 | The University of Tokyo, National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology, Japan | 1.4° × 1.4° |
| 11 | MPI-ESM1-2-LR | Max Plank Institute, Germany | 1.9° × 1.9° |
| 12 | MRI-ESM2-0 | Meteorological Research Institute, Japan | 1.1° × 1.1° |
| 13 | NorESM2-MM | Norwegian Meteorological Institute, Norway | 0.94° × 1.25° |
| Global Climate Models | Std. Dev. | MAE | RMSE | P-Bias | |
|---|---|---|---|---|---|
| 1 | ACCESS-CM2 | 96.94 | 66.99 | 105.37 | −32.54 |
| 2 | BCC-CSM2-MR | 124.50 | 81.36 | 121.11 | 17.47 |
| 3 | CanESM5 | 46.91 | 83.74 | 130.93 | −55.05 |
| 4 | CNRM-CM6-1 | 84.46 | 62.11 | 99.70 | −38.33 |
| 5 | EC-Earth3-Veg-LR | 109.24 | 46.11 | 73.74 | −14.97 |
| 6 | GFDL-ESM4 | 104.29 | 53.12 | 87.5 | −26.29 |
| 7 | IITM-ESM | 67.35 | 62.95 | 102.63 | −41.86 |
| 8 | INM-CM4-8 | 156.73 | 93.37 | 125.29 | 60.78 |
| 9 | INM-CM5-0 | 142.44 | 74.71 | 105.01 | 38.07 |
| 10 | MIROC6 | 117.99 | 52.20 | 79.74 | 4.51 |
| 11 | MPI-ESM1-2-LR | 91.59 | 47.78 | 78.52 | −23.58 |
| 12 | MRI-ESM2-0 | 100.19 | 57.75 | 88.98 | −22.4 |
| 13 | NorESM2-MM | 160.07 | 69.99 | 113.34 | 12.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashiq, A.; Kumar, V.; Prakash, O. A Spatiotemporal Assessment of the Precipitation Variability and Pattern and an Evaluation of the Predictive Reliability of Global Climate Models over Bihar. Hydrology 2024, 11, 50. https://doi.org/10.3390/hydrology11040050
Rashiq A, Kumar V, Prakash O. A Spatiotemporal Assessment of the Precipitation Variability and Pattern and an Evaluation of the Predictive Reliability of Global Climate Models over Bihar. Hydrology. 2024; 11(4):50. https://doi.org/10.3390/hydrology11040050
Chicago/Turabian StyleRashiq, Ahmad, Vishwajeet Kumar, and Om Prakash. 2024. "A Spatiotemporal Assessment of the Precipitation Variability and Pattern and an Evaluation of the Predictive Reliability of Global Climate Models over Bihar" Hydrology 11, no. 4: 50. https://doi.org/10.3390/hydrology11040050
APA StyleRashiq, A., Kumar, V., & Prakash, O. (2024). A Spatiotemporal Assessment of the Precipitation Variability and Pattern and an Evaluation of the Predictive Reliability of Global Climate Models over Bihar. Hydrology, 11(4), 50. https://doi.org/10.3390/hydrology11040050






