Evaluation of Baseflow Modeling with BlueM.Sim for Long-Term Hydrological Studies in the German Low Mountain Range of Hesse, Germany
Abstract
:1. Introduction
- -
- How does BlueM perform in the long-term continuous simulation of baseflow, as it has not been previously used for this purpose?
- -
- While it is likely that the physically based soil moisture simulation will outperform the constant discharge rate with monthly factors, is there any potential for the simpler approach to be used as part of the Hessian guideline and, potentially, the nationwide guideline?
2. Materials and Methods
2.1. Study Site
2.2. Data Availability
2.3. Methods
2.4. BlueM.Sim—Hydrological Simulation
2.5. BlueM.Opt—Calibration and Validation
2.5.1. Objective Functions
2.5.2. Calibration and Validation Datasets
2.5.3. Model Setup and Calibration Scheme
3. Results
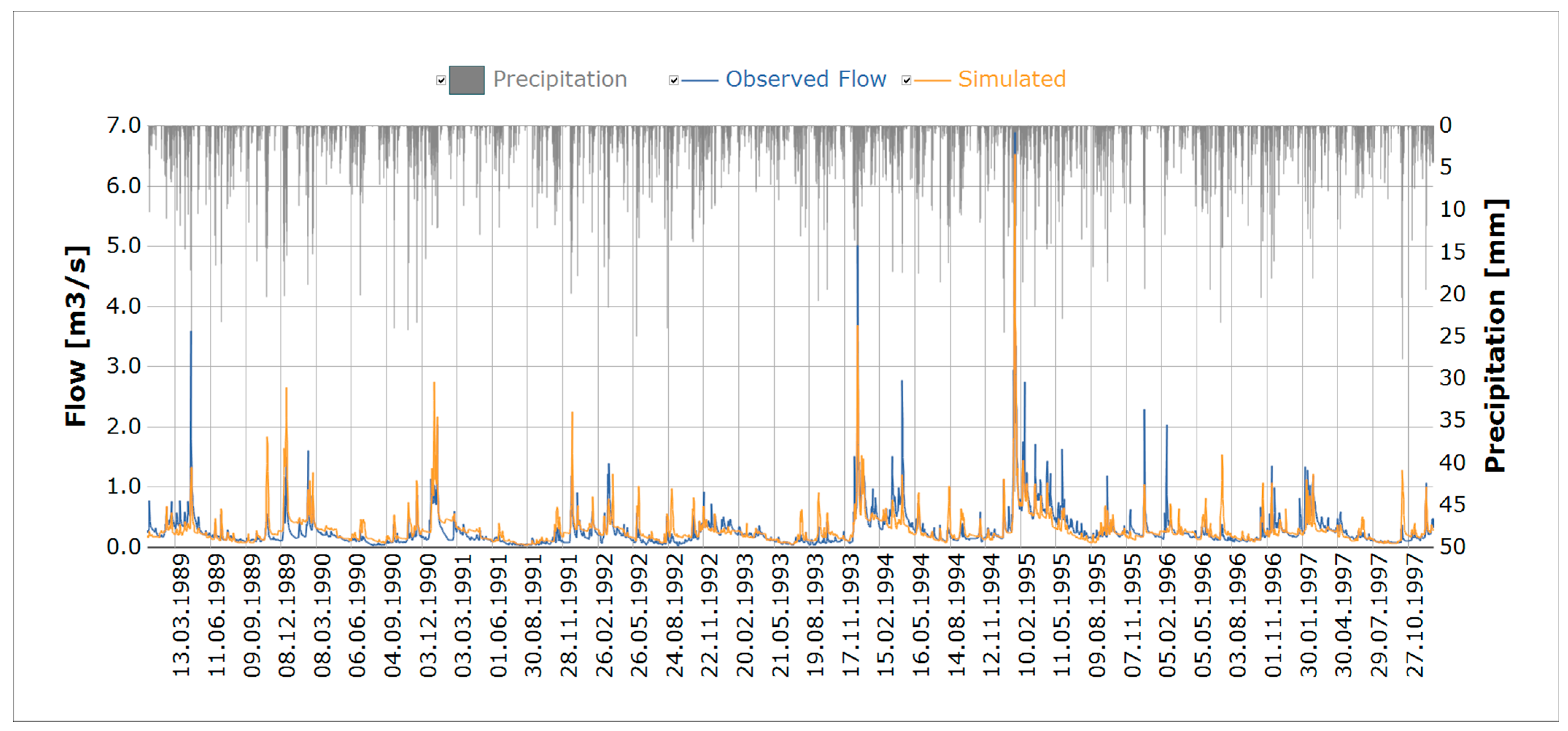
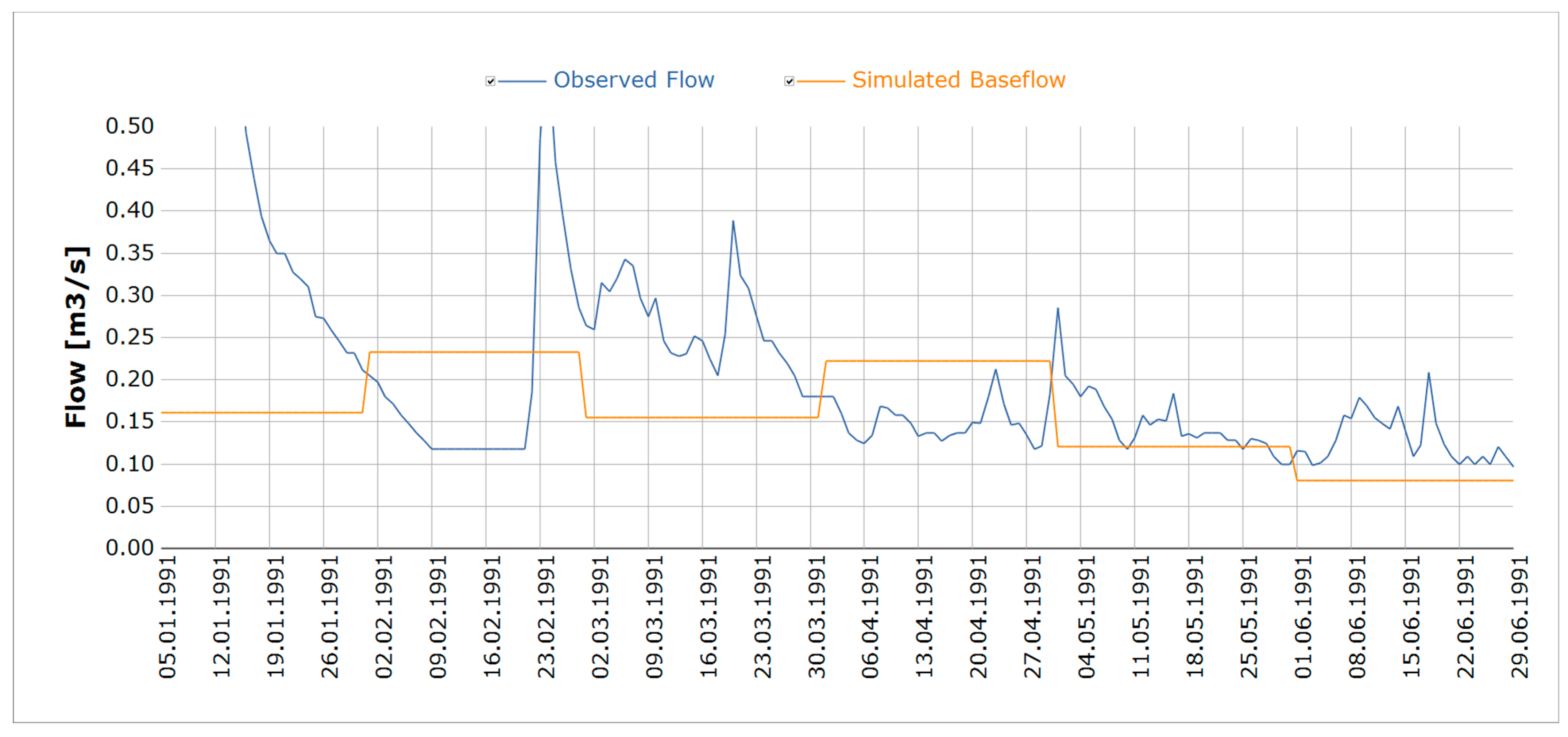
3.1. Precipitation Data Analysis and Baseflow Separation
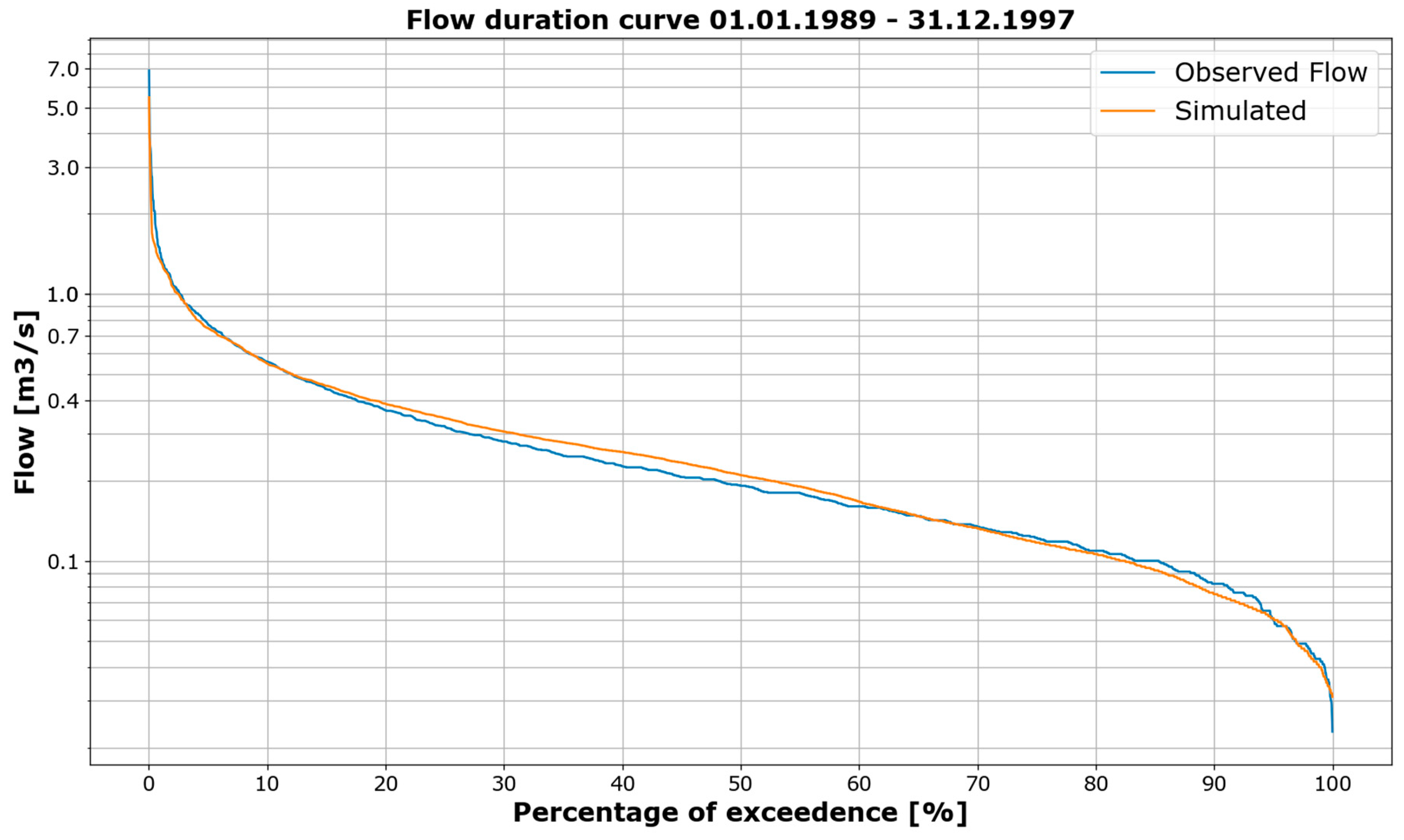
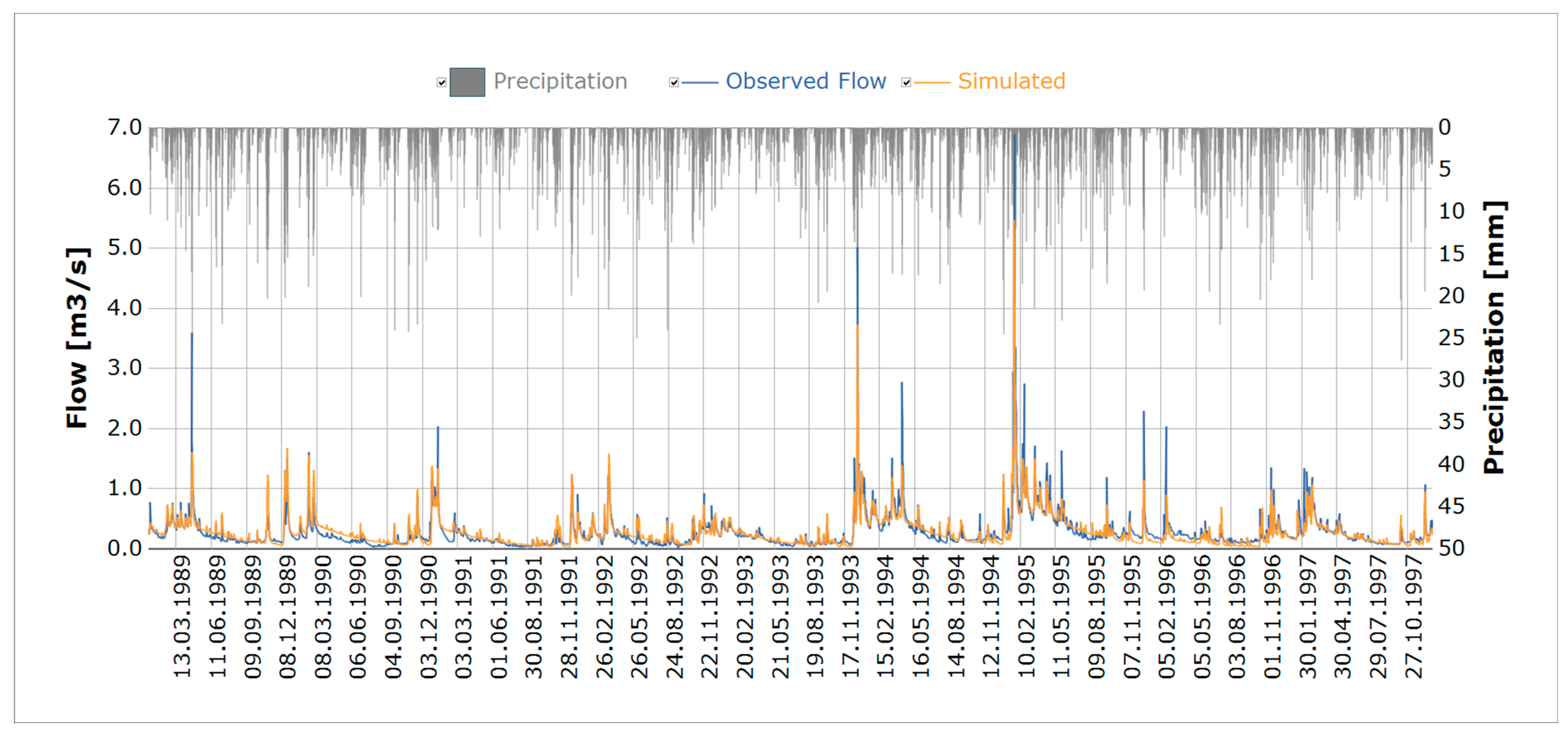
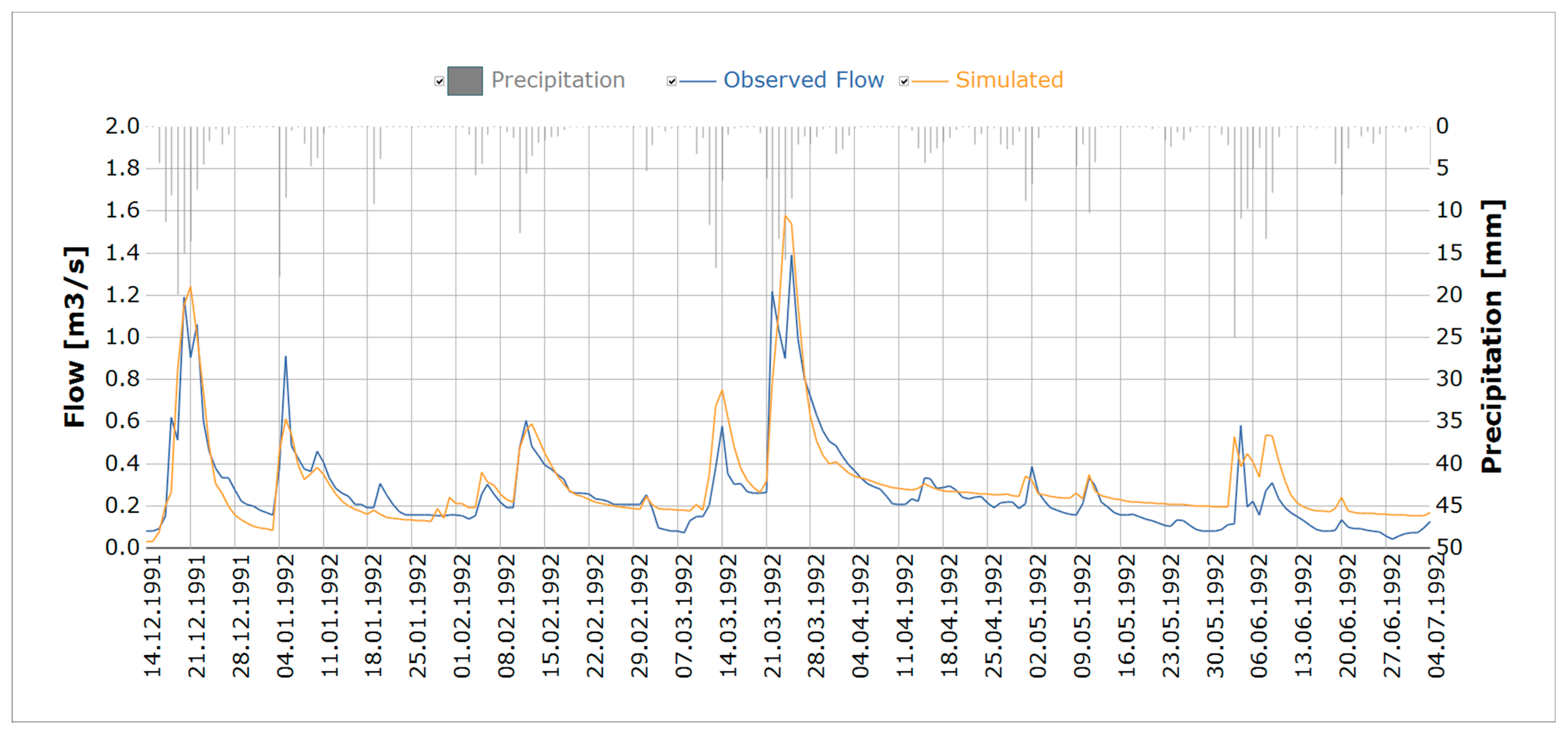
3.2. Calibration of FA
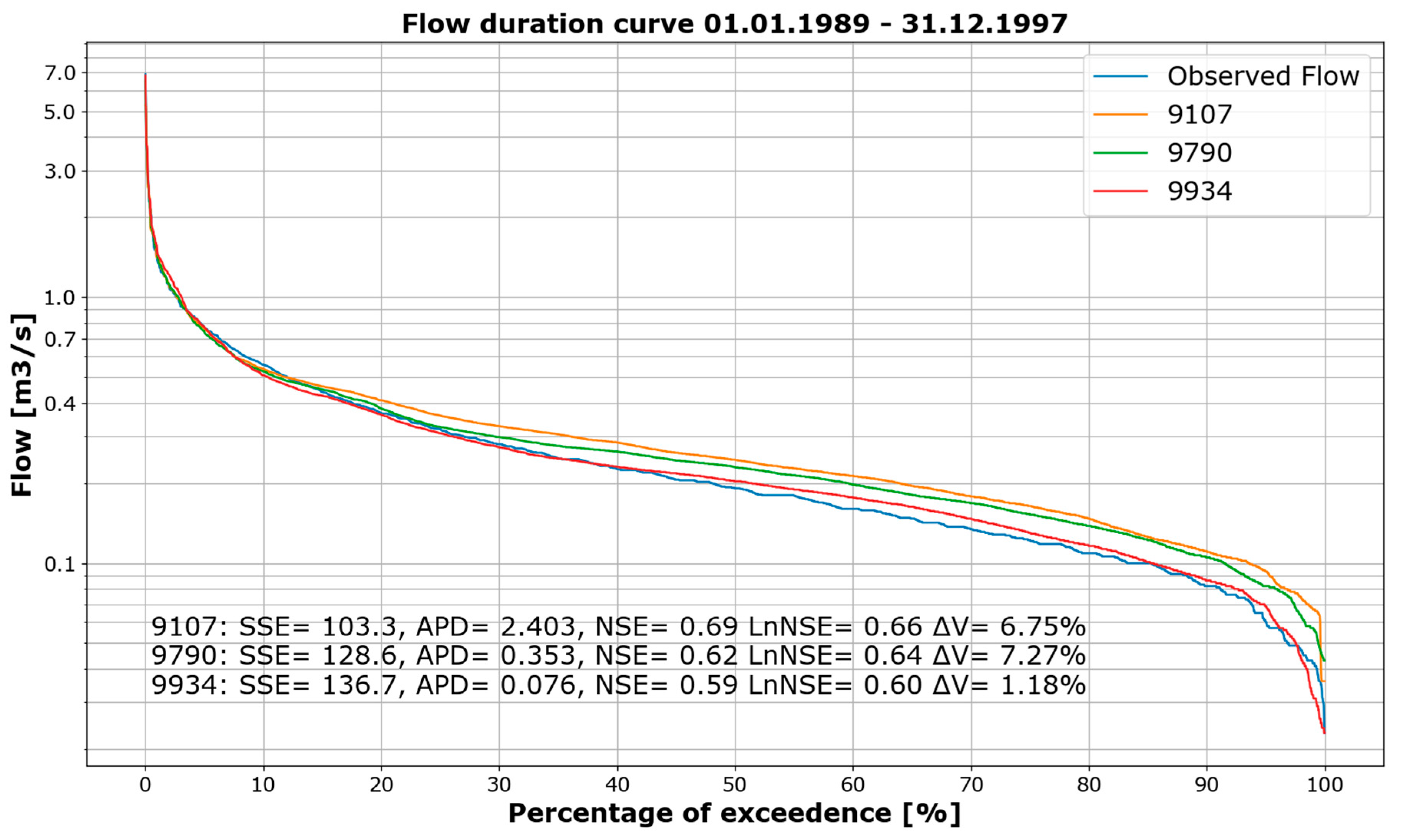
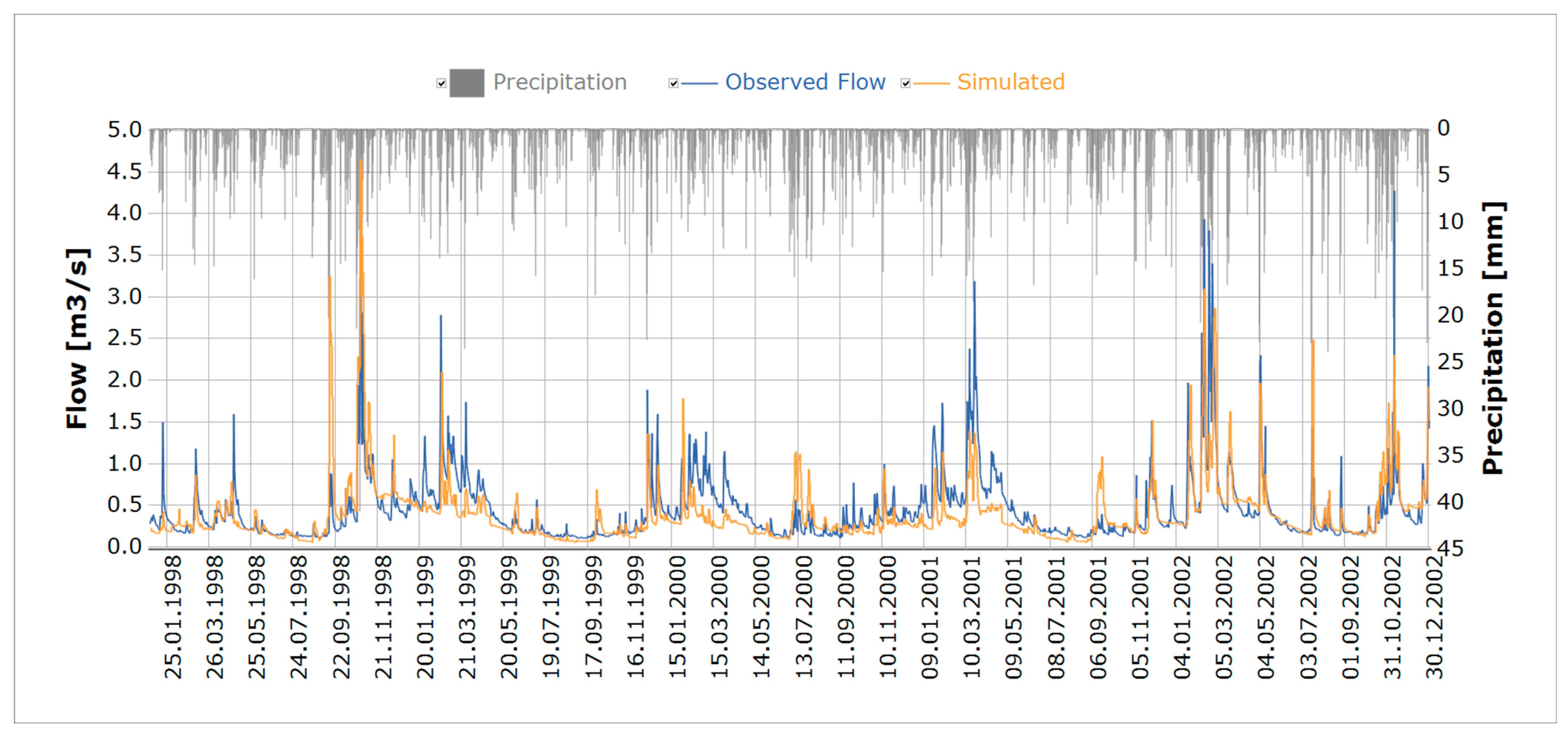
3.3. Validation of FA
3.4. Comparison of Calibration and Validation Results of FA
3.5. Calibration of SMA
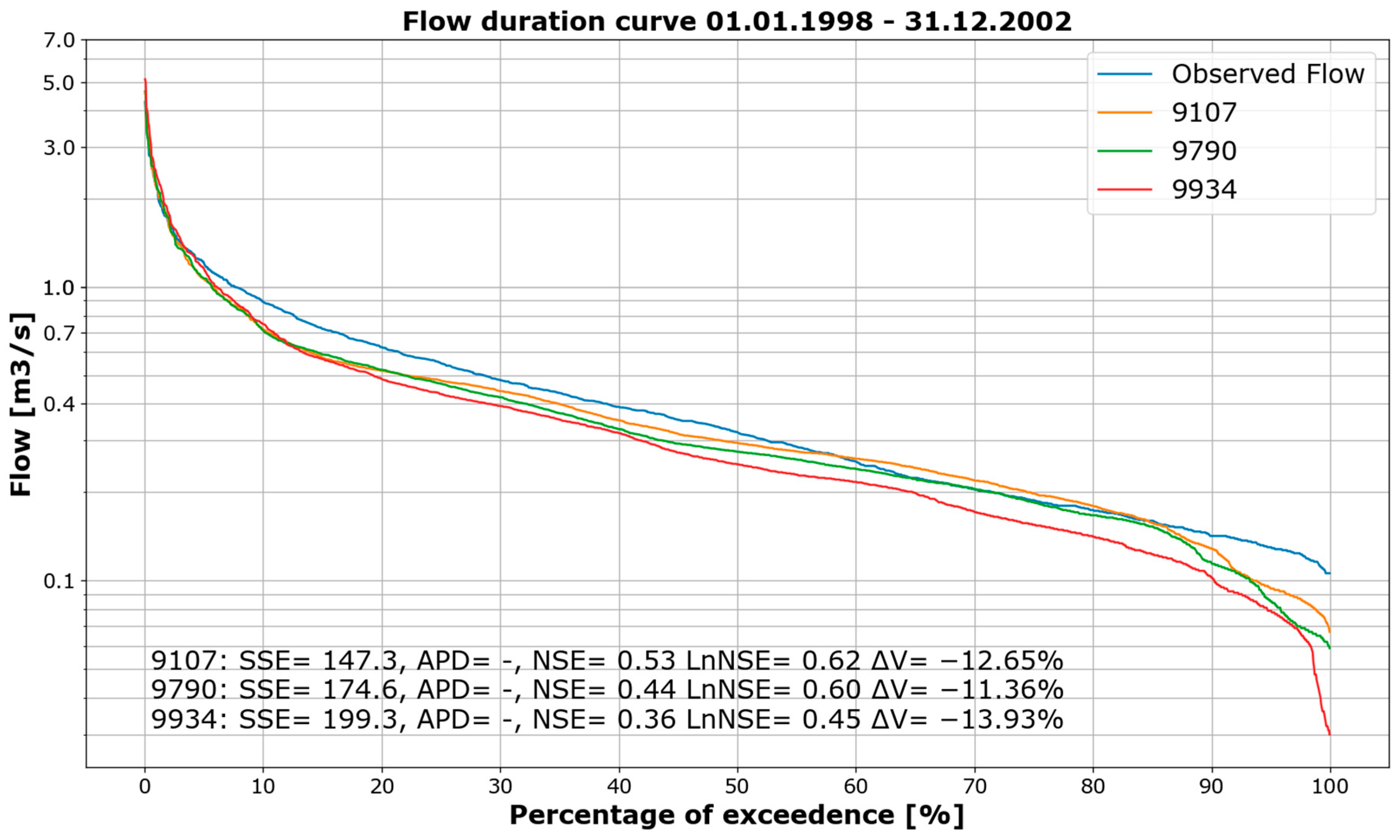
3.6. Validation of SMA
3.7. Comparison of Calibration and Validation of SMA
4. Discussion
- -
- NSE (0.62, 0.44): satisfactory, unsatisfactory;
- -
- LnNSE (0.64, 0.60): satisfactory, satisfactory;
- -
- ∆V (7.27%, −11.36%): very good, good;
- -
- APD (5%, 8%): very good, very good;
- -
- SSE (128.6 (m3/s)2, 175.6 (m3/s)2): no rating.
- -
- NSE (0.78, 0.75): very good, good/very good;
- -
- LnNSE (0.72, 0.78): good, very good;
- -
- ∆V (0.79%, −2.95%): very good, very good;
- -
- APD (15%, 15%): good, good;
- -
- SSE (73.58 (m3/s)2, 78.13 (m3/s)2): no rating.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smakhtin, V.U. Low Flow Hydrology: A Review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Meyer, R.; Schädler, B.; Viviroli, D.; Weingartner, R. Die Rolle Des Basisabflusses Bei Der Modellierung von Niedrigwasserprozessen in Klimaimpaktstudien. Hydrol. Wasserbewirtsch. 2011, 55, 244–257. [Google Scholar]
- Piggott, A.R.; Moin, S.; Southam, C. A Revised Approach to the UKIH Method for the Calculation of Baseflow/Une Approche Améliorée de La Méthode de l’UKIH Pour Le Calcul de l’écoulement de Base. Hydrol. Sci. J. 2005, 50, 911–920. [Google Scholar] [CrossRef]
- Price, K. Effects of Watershed Topography, Soils, Land Use and Climate on Baseflow Hydrology in Humid Regions: A Review. Prog. Physcial Geogr. 2011, 35, 465–492. [Google Scholar] [CrossRef]
- Stoelzle, M.; Weiler, M.; Stahl, K.; Morhard, A.; Schuetz, T. Is There a Superior Conceptual Groundwater Model Structure for Baseflow Simulation? Hydrol. Process 2015, 29, 1301–1313. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Schilling, K.E. Increasing Streamflow and Baseflow in Mississippi River since the 1940 s: Effect of Land Use Change. J. Hydrol. 2006, 324, 412–422. [Google Scholar] [CrossRef]
- Huang, X.D.; Shi, Z.H.; Fang, N.F.; Li, X. Influences of Land Use Change on Baseflow in Mountainous Watersheds. Forests 2016, 7, 16. [Google Scholar] [CrossRef]
- Huang, X.D.; Wang, D.; Han, P.P.; Wang, W.C.; Li, Q.J.; Zhang, X.L.; Ma, M.W.; Li, B.J.; Han, S.J. Spatial Patterns in Baseflow Mean Response Time across a Watershed in the Loess Plateau: Linkage with Land-Use Types. For. Sci. 2020, 66, 382–391. [Google Scholar] [CrossRef]
- Zomlot, Z.; Verbeiren, B.; Huysmans, M.; Batelaan, O. Spatial Distribution of Groundwater Recharge and Base Flow: Assessment of Controlling Factors. J. Hydrol. Reg. Stud. 2015, 4, 349–368. [Google Scholar] [CrossRef]
- Götzinger, J.; Barthel, R.; Jagelke, J.; Bárdossy, A. The Role of Groundwater Recharge and Baseflow in Integrated Models. In Proceedings of the Groundwater–Surface Water Interaction: Process Understanding, Conceptualization and Modelling (Proceedings of Symposium HS1002 at IUGG2007), Perugia, Italy, 11–13 July 2007; IAHS Publication: Perugia, Italy, 2008; pp. 103–109. [Google Scholar]
- Partington, D.; Brunner, P.; Simmons, C.T.; Werner, A.D.; Therrien, R.; Maier, H.R.; Dandy, G.C. Evaluation of Outputs from Automated Baseflow Separation Methods against Simulated Baseflow from a Physically Based, Surface Water-Groundwater Flow Model. J. Hydrol. 2012, 458–459, 28–39. [Google Scholar] [CrossRef]
- KLIWA. KLIWA-Kurzbericht Das Jahr 2018 Im Zeichen Des Klimawandels? Arbeitskreis KLIWA. 2019. Available online: https://www.kliwa.de/_download/Rueckblick2018.pdf (accessed on 20 April 2020).
- Kopp, B.; Baumeister, C.; Gudera, T.; Hergesell, M.; Kampf, J.; Morhard, A.; Neumann, J. Entwicklung von Bodenwasserhaushalt und Grund-Wasserneubildung in Baden-Württemberg, Bayern, Rheinland-Pfalz und Hessen von 1951 Bis 2015. Hydrol. Wasserbewirtsch. 2018, 62, 62–76. [Google Scholar] [CrossRef]
- KLIWA Niedrigwasser in Süddeutschland. Analysen, Szenarien Und Handlungsempfehlungen; Arbeitskreis KLIWA; Verlagspublikation: Baden, Germany, 2018; pp. 1–96. ISBN 978-3-88251-399-8. [Google Scholar]
- Hellwig, J.; Stahl, K. An Assessment of Trends and Potential Future Changes in Groundwater-Baseflow Drought Based on Catchment Response Times. Hydrol. Earth Syst. Sci. 2018, 22, 6209–6224. [Google Scholar] [CrossRef]
- Grosser, P.F.; Schmalz, B. Low Flow and Drought in a German Low Mountain Range Basin. Water 2021, 13, 316. [Google Scholar] [CrossRef]
- Grosser, P.F.; Schmalz, B. Projecting Hydroclimatic Extremes: Climate Change Impacts on Drought in a German Low Mountain Range Catchment. Atmosphere 2023, 14, 1203. [Google Scholar] [CrossRef]
- Bach, M.; Fröhlich, F.; Heusch, S.; Hübner, C.; Muschalla, D.; Reußner, F.; Ostrowski, M. BlueM—A free software package for integrated river basin management. In Forum für Hydrologie und Wasserbewirtschaftung; Fachgemeinschaft Hydrologisch Wissenschaften in der DWA: Kiel, Germany, 2009; Volume Heft 26.09, pp. 109–115. ISBN 978-3-94108-954-9. [Google Scholar]
- Feldmann, A.D. Hydrologic Modelling System HEC-HMS—Technical Reference Manual; US Army Corps of Engineers: Davis, CA, USA, 2000.
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modeling and Assessment Part I: Model Development1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Bergström, S. The HBV Model. In Computer Models of Watershed Hydrology; Water Resources Publications: Highlands Ranch, CO, USA, 1995; pp. 443–476. [Google Scholar]
- Hughes, J.D.; Langevin, C.D.; Banta, E.R. Documentation for the MODFLOW 6 Framework. Tech. Methods 2017. [Google Scholar] [CrossRef]
- Chapman, T. A Comparison of Algorithms for Stream Flow Recession and Baseflow Separation. Hydrol. Process 1999, 13, 701–714. [Google Scholar] [CrossRef]
- Fenicia, F.; Savenije, H.H.G.; Matgen, P.; Pfister, L. Hydrology and Earth System Sciences Is the Groundwater Reservoir Linear? Learning from Data in Hydrological Modelling. Hydrol. Earth Syst. Sci. 2006, 10, 139–150. [Google Scholar] [CrossRef]
- Wittenberg, H. Baseflow Recession and Recharge as Nonlinear Storage Processes. Hydrol. Process 1999, 13, 715–726. [Google Scholar] [CrossRef]
- Maneta, M.P.; Soulsby, C.; Kuppel, S.; Tetzlaff, D. Conceptualizing Catchment Storage Dynamics and Nonlinearities. Hydrol. Process 2018, 32, 3299–3303. [Google Scholar] [CrossRef]
- Rezaei-Sadr, H. Flood Hydrograph Simulation in Ungaged Basins: Modeling Linear–Nonlinear Storage-Discharge Relationships in a Semiarid Mountain Region. Phys. Geogr. 2019, 40, 52–70. [Google Scholar] [CrossRef]
- Cheng, S.; Cheng, L.; Liu, P.; Zhang, L.; Xu, C.; Xiong, L.; Xia, J. Evaluation of Baseflow Modelling Structure in Monthly Water Balance Models Using 443 Australian Catchments. J. Hydrol. 2020, 591, 125572. [Google Scholar] [CrossRef]
- Dittmann, R.; Froehlich, F.; Pohl, R.; Ostrowski, M. Optimum Multi-Objective Reservoir Operation with Emphasis on Flood Control and Ecology. Nat. Hazards Earth Syst. Sci. 2009, 9, 1973–1980. [Google Scholar] [CrossRef]
- Lohr, H.; Rebscher, A.; Abdelwahab, N.; Richter, S.; Froehlich, F.; Dissevelt, W.; Klopsch, H. Klimaszenarien Zur Optimierung Eines Talsperren-Betriebsplans. Wasserwirtschaft 2023, 113, 106–109. [Google Scholar] [CrossRef]
- Muschalla, D. Optimization of Integrated Urban Wastewater Systems Using Multi-Objective Evolution Strategies. Urban Water J. 2008, 5, 59–67. [Google Scholar] [CrossRef]
- Heusch, S.; Ostrowski, M. Model Predictive Control with SWMM. J. Water Manag. Model. 2011, 19, 237–247. [Google Scholar] [CrossRef]
- Bach, M.; Ostrowski, M. Analysis of Intensively Used Catchments Based on Integrated Modelling. J. Hydrol. 2013, 485, 148–161. [Google Scholar] [CrossRef]
- Moussa, A.M.A. Dynamic Operation Rules of Multi-Purpose Reservoir for Better Flood Management. Alex. Eng. J. 2018, 57, 1665–1679. [Google Scholar] [CrossRef]
- Wolf, S.; Stenger, D.; Steudtner, F.; Esser, V.; Lehmkuhl, F.; Schüttrumpf, H. Modeling Anthropogenic Affected Sediment Transport in a Mid-Sized European River Catchment–Extension of the Sediment Rating Curve Equation. Model. Earth Syst. Environ. 2023, 9, 3815–3835. [Google Scholar] [CrossRef]
- HMUELV. Leitfaden Zum Erkennen Ökologisch Kritischer Gewässerbelastungen Durch Abwassereinleitungen; HMUELV: Wiesbaden, Germany, 2012. [Google Scholar]
- HLNUG. Dokumentation Des Schmutzfrachtmodells SMUSI—Version 6.1; HLNUG: Wiesbaden, Germany, 2012. [Google Scholar]
- DWA/BWK. Merkblatt DWA-M 102-3—Grundsätze Zur Bewirtschaftung Und Behandlung von Regenwetterabflüssen Zur Ein-Leitung in Oberflächengewässer—Teil 3: Immissionsbezogene Bewertungen Und Regelungen; DWA/BWK: Lüneburg, Germany, 2021; ISBN 978-3-96862-137-1. [Google Scholar]
- Braud, I.; Fletcher, T.D.; Andrieu, H. Hydrology of Peri-Urban Catchments: Processes and Modelling. J. Hydrol. 2013, 485, 1–4. [Google Scholar] [CrossRef]
- Schmalz, B.; Kruse, M. Impact of Land Use on Stream Water Quality in the German Low Mountain Range Basin Gersprenz. Landsc. Online 2019, 72, 72. [Google Scholar] [CrossRef]
- Kissel, M.; Schmalz, B. Comparison of Baseflow Separation Methods in the German Low Mountain Range. Water 2020, 12, 1740. [Google Scholar] [CrossRef]
- HLNUG. Grundwasser in Hessen, Heft 2: Hydrogeologie von Hessen—Odenwald Und Sprendlinger Horst; HLNUG: Wiesbaden, Germany, 2017. [Google Scholar]
- DWD Rain and Climate Data, Deutscher Wetterdienst. Available online: https://opendata.dwd.de/climate_environment/CDC/observations_germany/climate/daily/more_precip/historical/ (accessed on 13 October 2019).
- HLNUG Daily Mean Flow Data for Gaging Station Groß-Bieberau2 (No. 24761005) Time Period 1974–2019 2019.
- HLNUG Hydrological Yearbook of Gaging Station Groß-Bieberau 2 (No. 24761005). Available online: http://www.hlnug.de/static/pegel/wiskiweb2/stations/24761005/berichte/Jahrbuchseiten/24761005_Q2017_Gross-Bieberau2.pdf (accessed on 22 April 2020).
- EEA Copernicus Land Monitoring Service—Corine Land Cover; Copernicus Publications: Göttingen, Germany, 2019.
- HVBG ATKIS (Amtliches Topographisch—Kartographisches Informationssystem; Authorative Topographic-Cartographic Information System) 2017.
- HLNUG Produktdokumentation Bodenflächendaten 1:50.000 Hessen. Available online: https://www.hlnug.de/themen/boden/information/bodenflaechenkataster-und-kartenwerke/bfd50 (accessed on 12 April 2019).
- Thiessen, A.H. Precipitation Averages for Large Areas. Mon. Weather. Rev. 1911, 39, 1082–1089. [Google Scholar] [CrossRef]
- Brandt, T. Modell Zur Abflussgangliniensimulation Unter Besonderer Berücksichtigung Des Grundwasserbürtigen Abflusses; TH Darmstadt: Darmstadt, Germany, 1979; Volume 24. [Google Scholar]
- Kille, K. Das Verfahren MoMNQ, Ein Beitrag Zur Berechnung Der Mittleren Langjährigen Grundwasserneubildung Mit Hilfe Der Monatlichen Niedrigwasserabflüsse. Z. Dtsch. Geol. Ges. 1970, 120, 89–95. [Google Scholar] [CrossRef]
- Demuth, S. Untersuchung Zum Niedrigwasser in West-Europa; Freiburger Schriften zur Hydrologie; Institut für Hydrologie der Universität Freiburg im Breisgau: Freiburg im Breisgau, Germany, 1993; Volume 1. [Google Scholar]
- Eckhardt, K. How to Construct Recursive Digital Filters for Baseflow Separation. Hydrol. Process 2005, 19, 507–515. [Google Scholar] [CrossRef]
- Zaiß, H. Simulation Ereignisspezifischer Einflüsse Des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen Kleiner Einzugsgebiete Mit Niederschlag-Abfluß-Modellen; Institut für Wasserbau: Darmstadt, Germany, 1989; Volume 42. [Google Scholar]
- USDA. National Engineering Handbook, Section 4, Hydrology; U.S. Deptartment of Agriculture: Washington, DC, USA, 1954.
- Rosemann, H.J.; Vederal, J. Das Kalinin-Miljukov Verfahren Zur Berechnung Des Ablaufs Von Hochwasserwellen; Landesstelle für Gewässerkunde, München. Schriftenreihe: Bavaria, Germany, 1970. [Google Scholar]
- Ostrowski, M.W. Einœ Beitrag Zur Kontinuierlichen Simulation Der Wasserbilanz; Institut für Wasserbau und Wasserwirtschaft der RWTH: Aachen, Germany, 1982; Volume 42. [Google Scholar]
- Bach, M. Integrierte Modellierung Für Einzugsgebiete Mit Komplexer Nutzung. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2011. [Google Scholar]
- Schwefel, H.P. Numerical Optimization of Computer Models; Interdisciplinary Systems Research; Wiley: Hoboken, NJ, USA, 1981; ISBN 978-0-47109-988-8. [Google Scholar]
- Schwefel, H.-P. Numerische Optimierung von Computer-Modellen Mittels Der Evolutionsstrategie. In Numerische Optimierung von Computer-Modellen Mittels der Evolutionsstrategie; Springer: Basel, Switzerland, 1977. [Google Scholar] [CrossRef]
- Rechenberg, I.; Aviation, G.; Britain, M.; Establishment, R.A. Cybernetic Solution Path of an Experimental Problem by Ingo Rechenberg; RAE-LT-1122; Royal Aircraft Establishment: Farnborough, UK, 1965. [Google Scholar]
- Rechenberg, I. Evolutionsstrategie: Optimierung Technischer Systeme Nach Prinzipien Der Biologischen Evolution; Problemata (Stuttgart); Frommann-Holzboog: Stuttgart, Germany, 1973; ISBN 978-3-77280-374-1. [Google Scholar]
- Muschalla, D. Evolutionäre Multikriterielle Optimierung Komplexer Wasserwirtschaftlicher Systeme. Ph.D. Thesis, Technische Universität Darmstadt, Darmstadt, Germany, 2006. [Google Scholar]
- Schwefel, H.-P.P. Evolution and Optimum Seeking: The Sixth Generation; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1993; ISBN 0-47-157148-2. [Google Scholar]
- Muschalla, D.; Schneider, S.; Schröter, K.; Gamerith, V.; Gruber, G. Sewer Modelling Based on Highly Distributed Calibration Data Sets and Multi-Objective Auto-Calibration Schemes. Water Sci. Technol. 2008, 57, 1547–1554. [Google Scholar] [CrossRef] [PubMed]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Vogel, R.M.; Fennessey, N.M. Flow Duration Curves II: A Review of Applications in Water Resources Planning1. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 1029–1039. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Bach, A. Analyse von Niederschlagsdaten Aus Der Satellitenfernerkundung in Der Hydrologischen Modellierung Am Beispiel Des Fischbach-Einzugsgebietes. Master’s Thesis, Technische Universität Darmstadt, Institut für Wasserbau und Wasserwirtschaft, Darmstadt, Germany, 2018. [Google Scholar]
- Amarjargal, S. Entwicklung Einer Methode Zur Ableitung Hydrologischer Elementarflächen Für Das Fischbach-Einzugsgebiet. Bachelor’s Thesis, Technische Universität Darmstadt, Institut für Wasserbau und Wasserwirtschaft, Darmstadt, Germany, 2019. [Google Scholar]
- Reifschläger, K. Optimierung Eines Niederschlag-Abfluss-Modells Durch Erweiterung Des Auf Elementarflächen Basierenden Physikali-Schen Bodenfeuchteansatzes. Master’s Thesis, Technische Universität Darmstadt, Institut für Wasserbau und Wasserwirtschaft, Darmstadt, Germany, 2019. [Google Scholar]
- Sponagel, H. Ad-hoc-Arbeitsgruppe Boden der Staatlichen Geologischen Dienste und der Bundesanstalt für Geowissenschaften und Rohstoffe. In Bodenkundliche Kartieranleitung: Mit 41 Abbildungen, 103 Tabellen Und 31 Listen; Schweizerbart: Stuttgart, Germany, 2005; ISBN 978-3-51095-920-4. [Google Scholar]
- Knauf, D. Die Berechnung Des Abflusses Aus Einer Schneedecke. Schriftenreihe Dtsch. Verb. Wasserwirtsch. Kult. 1980, 46, 95–135. [Google Scholar]
- Climate Service Center Verfahren Nach HAUDE (1954). Available online: https://www.climate-service-center.de/products_and_publications/publications/detail/063341/index.php.de#a2 (accessed on 2 November 2020).
- Arnold, J.; Moriasi, D.; Gassman, P.; Abbaspour, K.; White, M.; Raghavan; Srinivasan; Santhi, C.; Harmel, D.; Griensven, A.; et al. SWAT: Model Use, Calibration, and Validation. Trans. ASABE 2012, 55, 1249–1260. [Google Scholar] [CrossRef]
- Schreiber, P.; Demuth, S. Regionalization of Low Flows in Southwest Germany. Hydrol. Sci. J. 1997, 42, 845–858. [Google Scholar] [CrossRef]
- Eckhardt, K.; Haverkamp, S.; Fohrer, N.; Frede, H.G. SWAT-G, a Version of SWAT99.2 Modified for Application to Low Mountain Range Catchments. Phys. Chem. Earth Parts A/B/C 2002, 27, 641–644. [Google Scholar] [CrossRef]
- Pfannerstill, M.; Guse, B.; Fohrer, N. A Multi-Storage Groundwater Concept for the SWAT Model to Emphasize Nonlinear Groundwater Dynamics in Lowland Catchments. Hydrol. Process 2014, 28, 5599–5612. [Google Scholar] [CrossRef]
- Luo, Y.; Arnold, J.; Allen, P.; Chen, X. Baseflow Simulation Using SWAT Model in an Inland River Basin in Tianshan Mountains, Northwest China. Hydrol. Earth Syst. Sci. 2012, 16, 1259–1267. [Google Scholar] [CrossRef]
- Dariane, A.B.; Javadianzadeh, M.M.; James, L.D. Developing an Efficient Auto-Calibration Algorithm for HEC-HMS Program. Water Resour. Manag. 2016, 30, 1923–1937. [Google Scholar] [CrossRef]
- Awa Agathe Ouédraogo, W.; Messo Raude, J.; Mwangi Gathenya, J.; Assani, A.; Kinnard, C.; Mesfioui, M. Continuous Modeling of the Mkurumudzi River Catchment in Kenya Using the HEC-HMS Conceptual Model: Calibration, Validation, Model Performance Evaluation and Sensitivity Analysis. Hydrology 2018, 5, 44. [Google Scholar] [CrossRef]
- Parra, V.; Arumí, J.L.; Muñoz, E. Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water 2019, 11, 1506. [Google Scholar] [CrossRef]
- Chathuranika, I.M.; Gunathilake, M.B.; Baddewela, P.K.; Sachinthanie, E.; Babel, M.S.; Shrestha, S.; Jha, M.K.; Rathnayake, U.S. Comparison of Two Hydrological Models, HEC-HMS and SWAT in Runoff Estimation: Application to Huai Bang Sai Tropical Watershed, Thailand. Fluids 2022, 7, 267. [Google Scholar] [CrossRef]
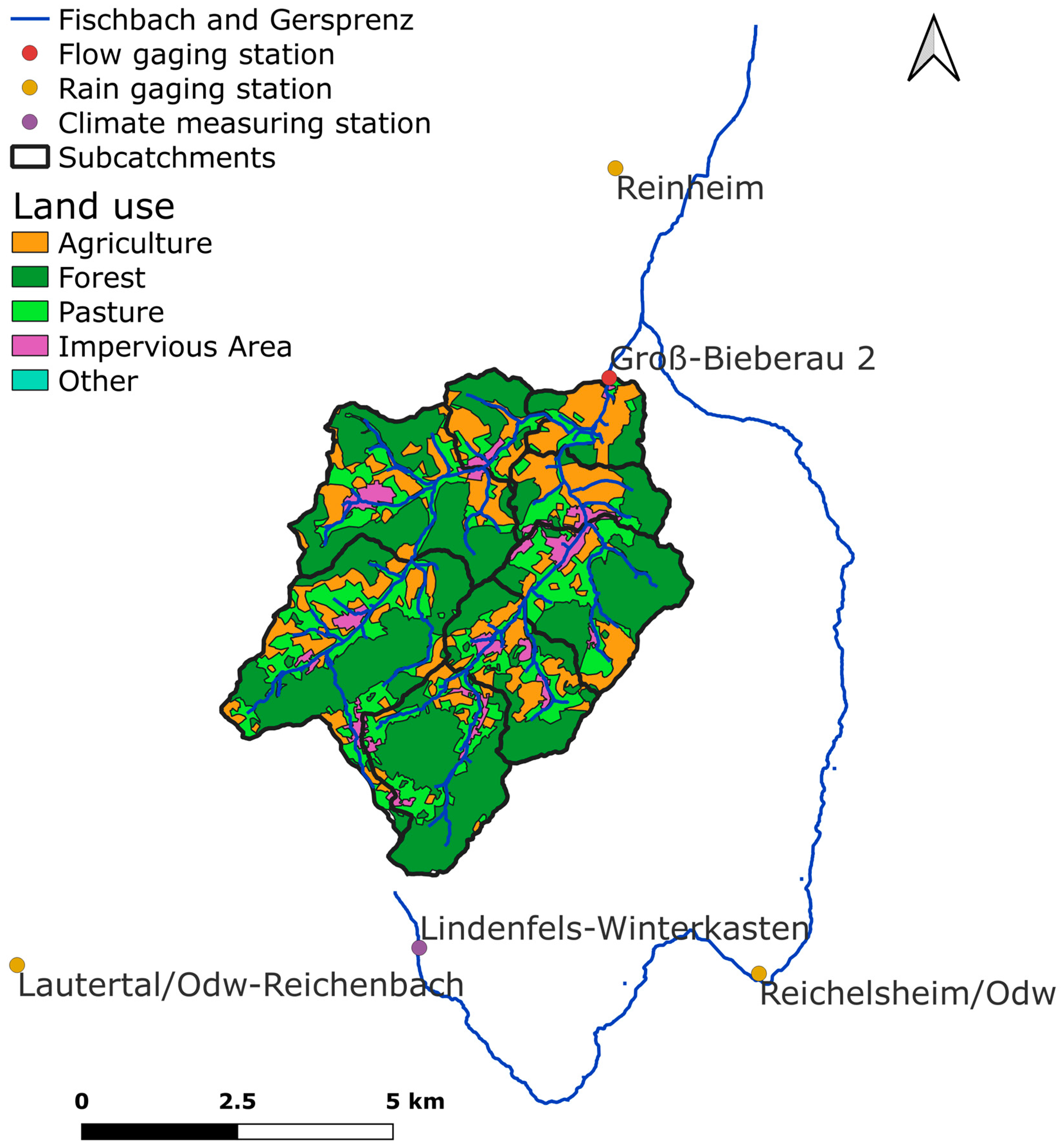
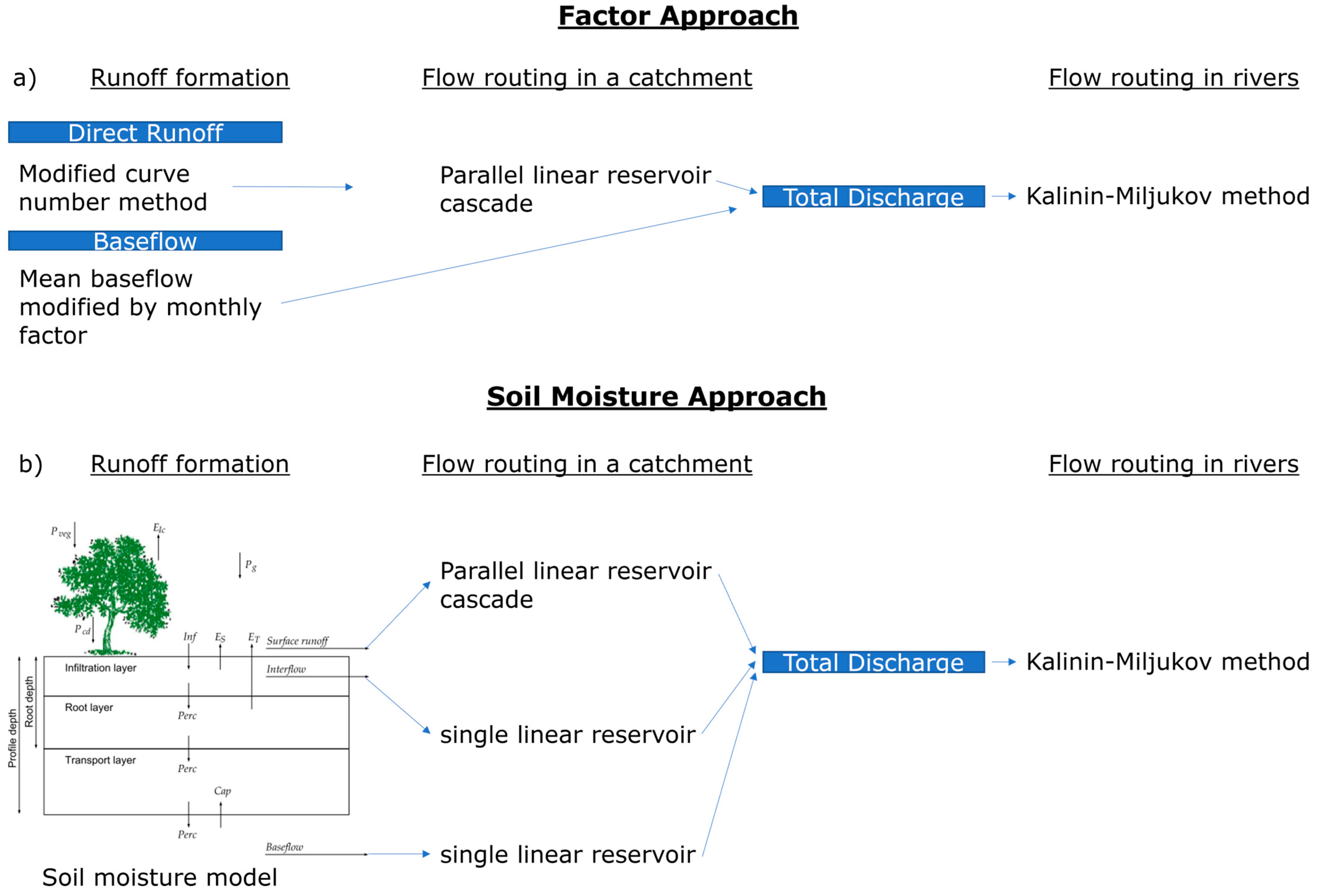

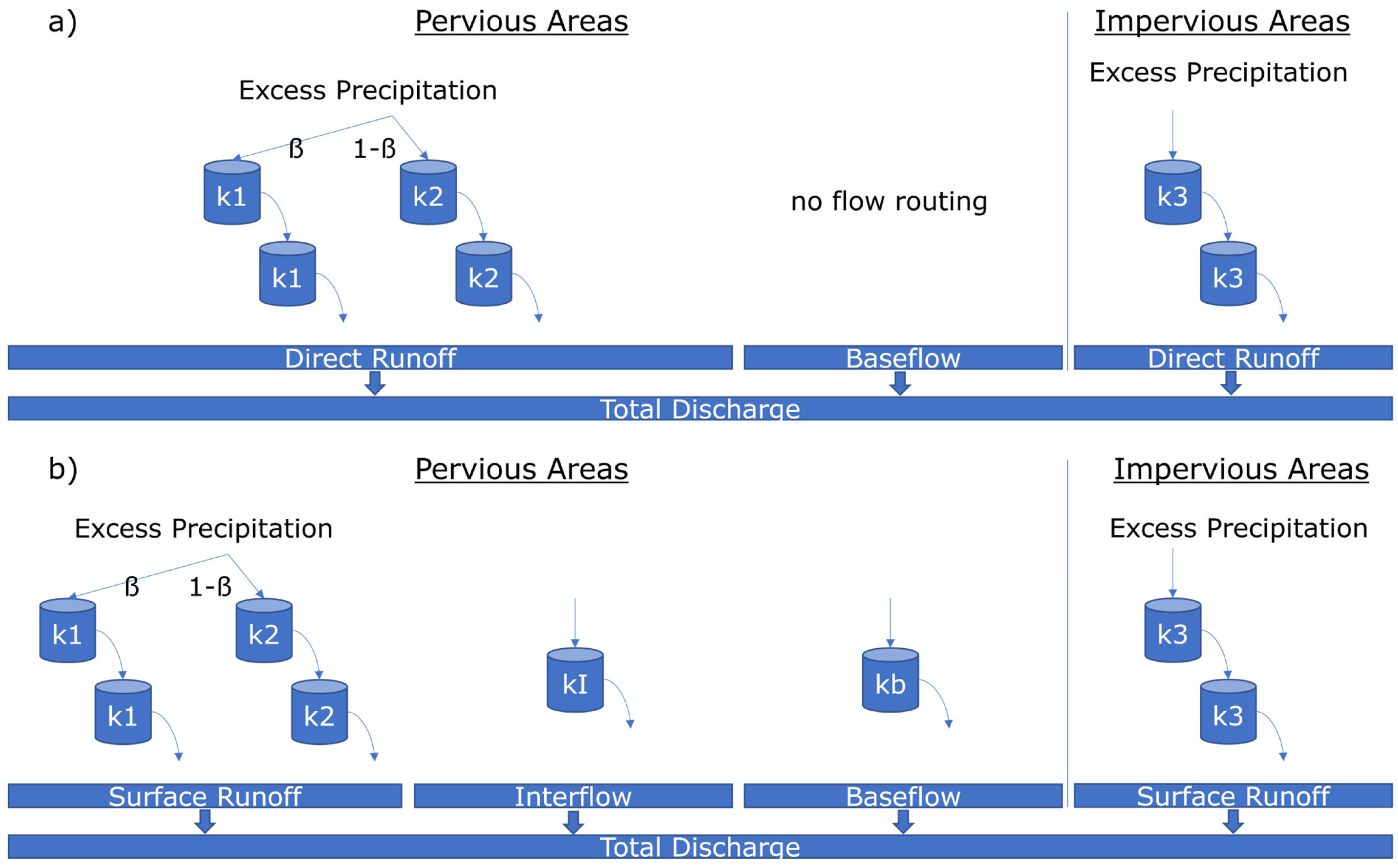

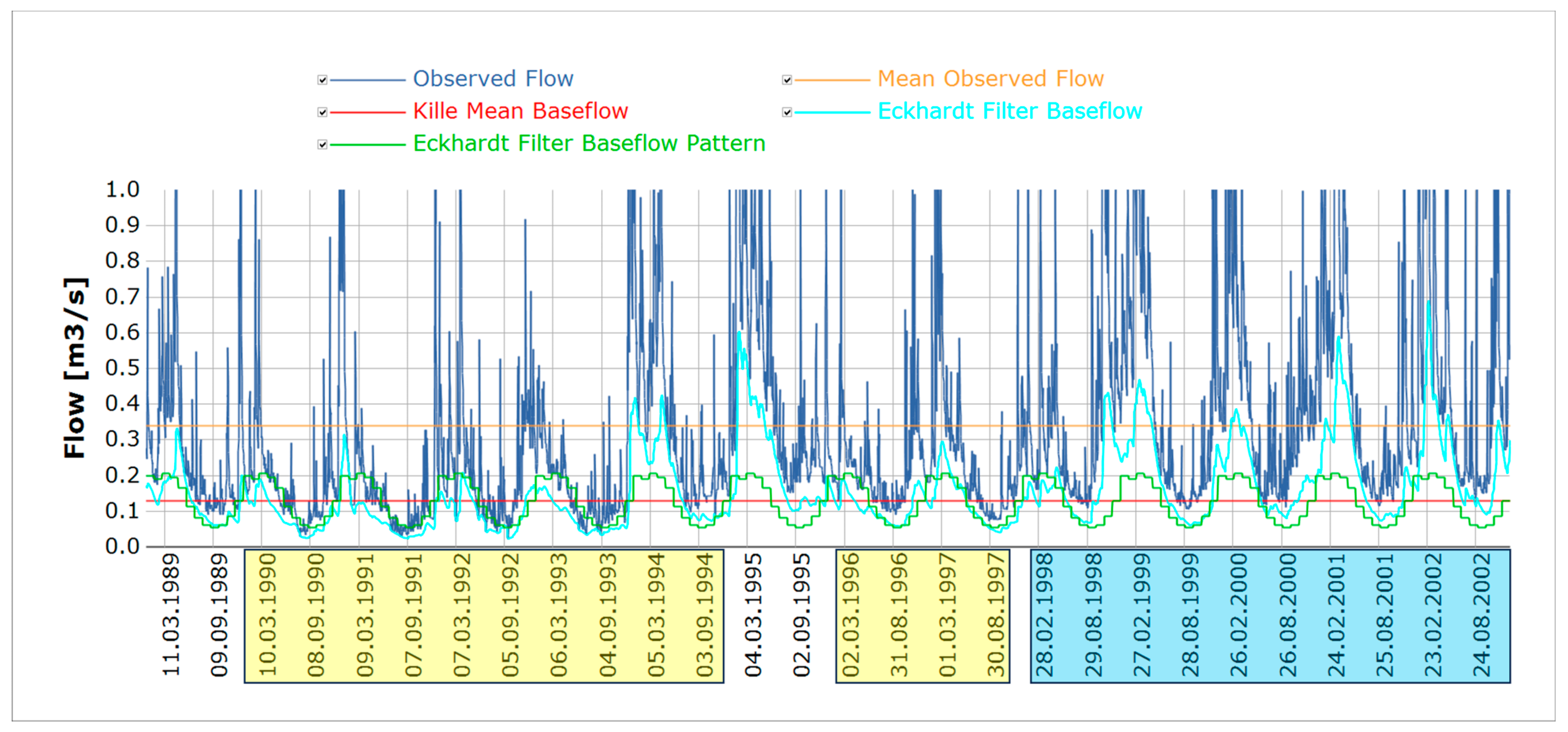

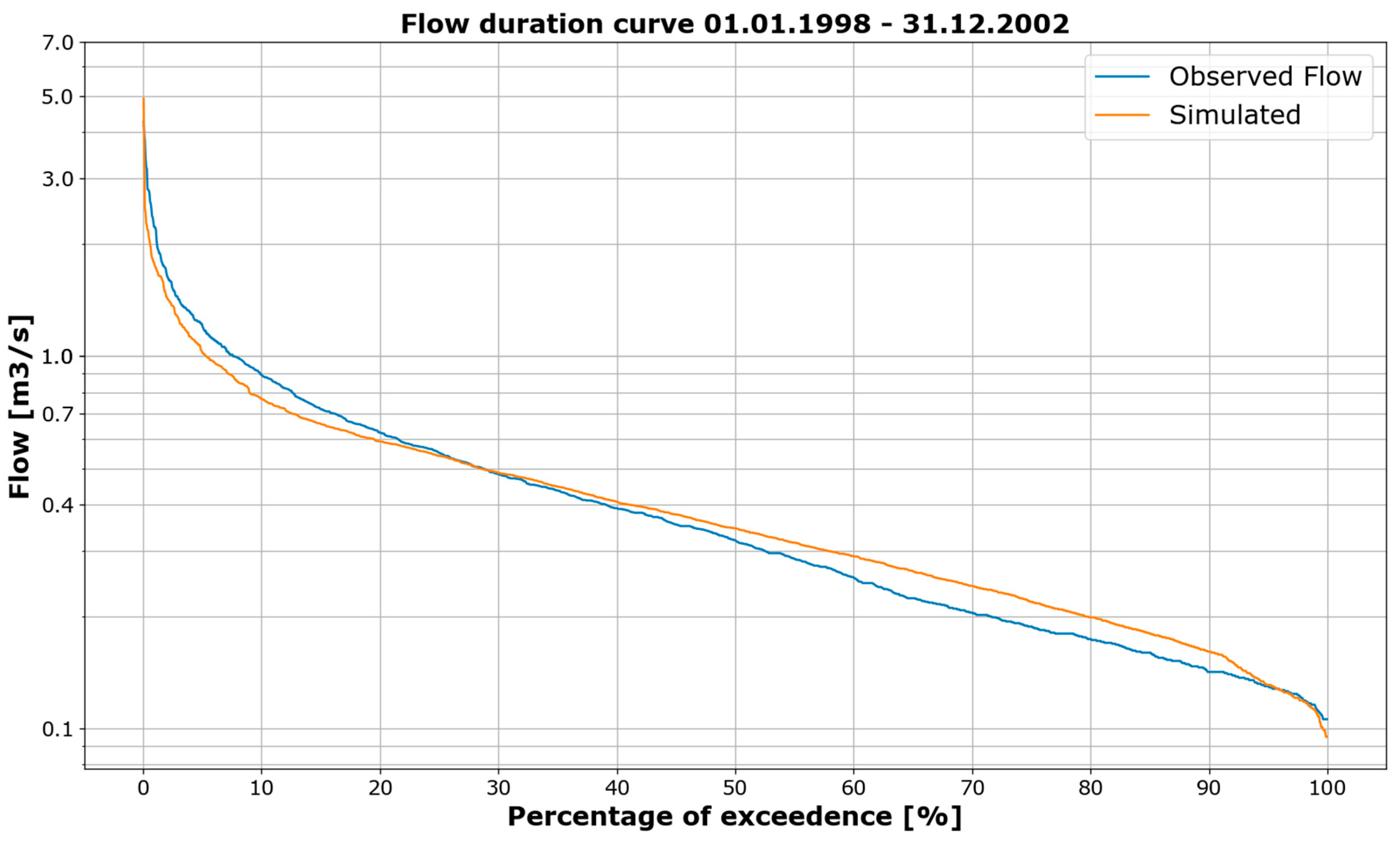
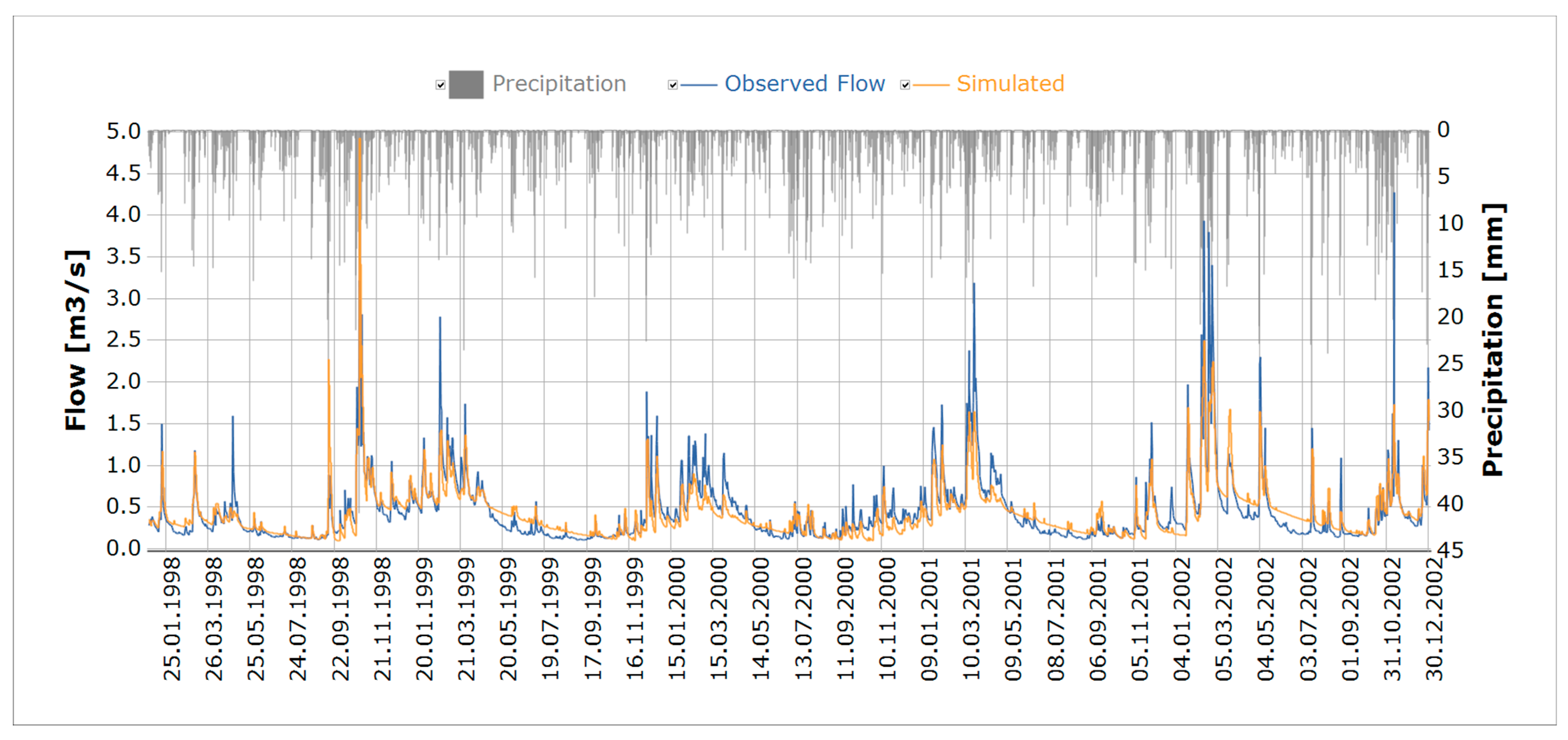
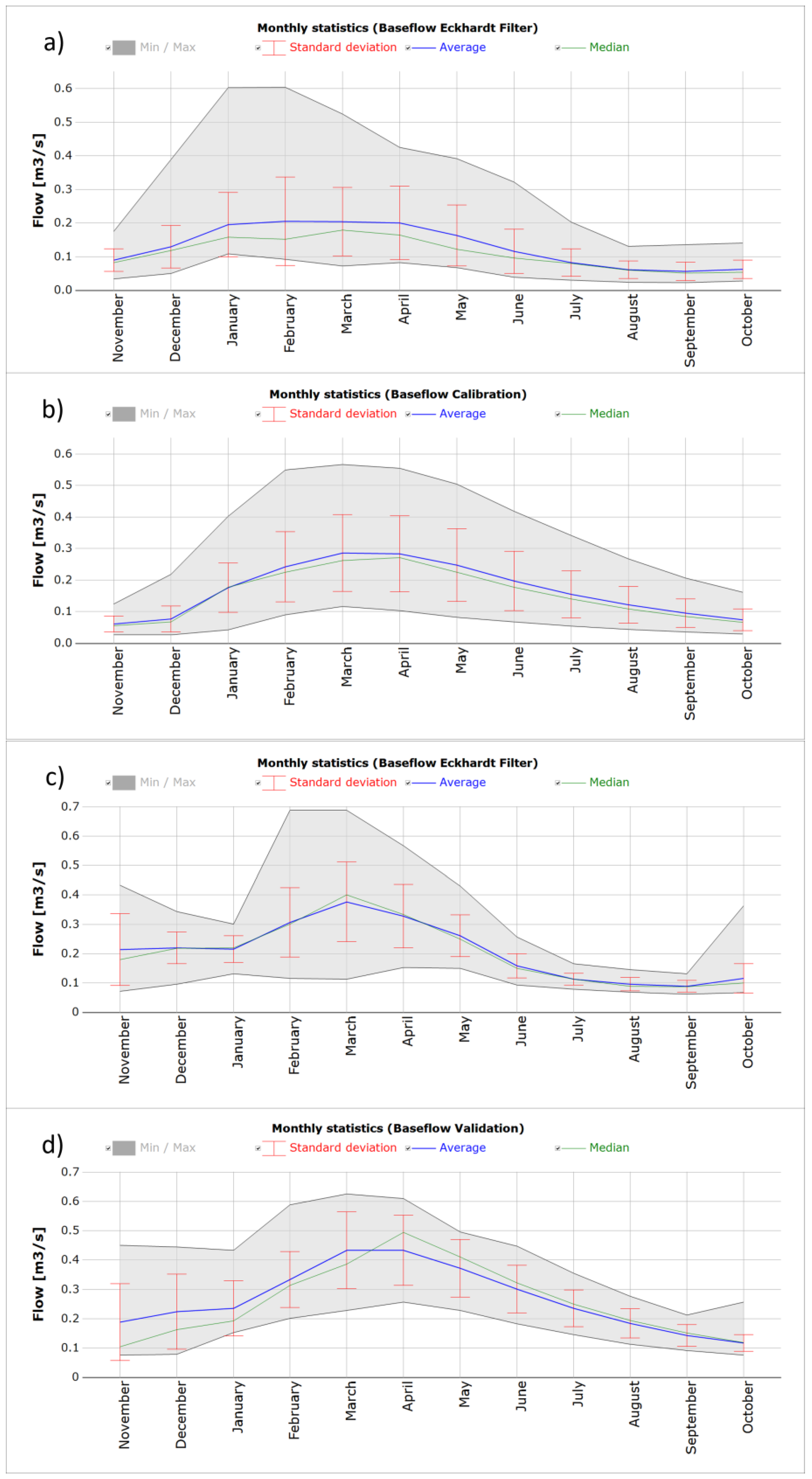
| Station | Type | Resolution | Unit | Start | End | Gaps |
|---|---|---|---|---|---|---|
| Lautertal/Odw-Reichenbach | precipitation | daily | mm/d | 1983 | - | |
| Reichelsheim | precipitation | daily | mm/d | 1951 | - | 2003–2007 |
| Reinheim | precipitation | daily | mm/d | 1951 | - | February 2003 |
| Groß-Bieberau 2 | flow | daily | m3/s | 1974 | - | |
| Lindenfels- Winterkasten | temperature | daily | °C | 1973 | 2005 |
| Parameter | Starting Value | Variation Range | Calibrated Solution | |
|---|---|---|---|---|
| Mean * (Range) | Mean * (Range) | |||
| FA | Baseflow Qb | 4.7 L/(s km2) | 3.0–5.6 L/(s km2) | 3.5 L/(s km2) |
| Monthly factors fi | See Figure 5 | 0.2–2.0 | See Figure 5 | |
| CN | 71.5 (64–84) | 50–90 | 58.1 (52–68) | |
| k1 | 3.5 h | 1.0–3.5 h | 2.3 h (1.5–3.1 h) | |
| k2 | 12 h | 4.0–12.0 h | 8.6 h (4.4–11.3) | |
| ß | 0.28 (0.25–0.30) | 0.1–0.7 | 0.30 (0.10–0.59) | |
| Nonlinear exponent, nlin | 0.85 | 0.7–1.0 | 0.81 (0.70–0.99) | |
| Snow formation temperature Ts ** | 0.0 °C | 0.0–5.0 °C | 1.7 °C (0.4–4.0 °C) | |
| New snow density NSD ** | 11.0% | 5.0–20.0% | 10.0% (5.9–16.8%) | |
| Threshold density TD ** and *** | 40.0% | 35.0–45.0% | 39.8% (36.7–44.8%) | |
| Melting rate MR ** | 1.8 mm/(°C d) | 1.4–2.2 mm/(°C d) | 1.7 (1.5–2.2) | |
| Insolation and soil warmth melting rate MRIS ** | 4.2 mm/d | 3.8–4.6 mm/d | 4.1 (3.8–4.4) | |
| SMA | Fraction of impervious areas | 10.0% | 10.0–100.0% | 11.5% |
| CN pervious areas | 10 | 1–100 | 26.7 | |
| k_baseflow | 500 | 500–3500 h | 2737 h | |
| k_interflow | 2 | 1–96 h | 16 h | |
| Hydraulic conductivity kf **** | 9.3 mm/h (3–41) | 0.8–67.0 mm/h | 11.3 mm/h (1–36) | |
| Maximum infiltration rate m_I **** | 18.4 mm/h (6–82) | 1.6–134 mm/h | 23.8 mm/h (5–75) | |
| Field capacity fc **** | 350 mm/m (250–390) | 230–450 mm/m | 359.4 mm/m (255–434) | |
| Total pore volume tpv **** | 433 mm/m (420–450) | 310–540 mm/m | 443.9 mm/m (374–515) | |
| Wilting point w **** | 159 mm/m (70–270) | 60–280 mm/m | 160.4 mm/m (64–260) | |
| Potential Evapotranspiration ETP | 600 mm/a | 580–750 mm/a | 666 mm/a (586–741) | |
| Agriculture ETP scaling factor a_f | 0.24 | 0.11–0.50 | 0.24 (0.15–0.37) | |
| Forest ETP scaling factor f_f | 0.16 | 0.00–0.52 | 0.23 (0.04–0.43) | |
| Pastures ETP scaling factor p_f | 0.21 | 0.20–0.39 | 0.28 (0.22–0.34) | |
| Snow formation temperature Ts ** | 0.0 °C | 0.0–5.0 °C | 0.3 °C | |
| New snow density NSD ** | 11.0% | 5.0–20.0 % | 11.6% | |
| Threshold density TD ** and *** | 40.0% | 35.0–45.0 % | 44.3% | |
| Melting rate MR ** | 1.8 mm/(°C d) | 1.4–2.2 mm/(°C d) | 2.1 mm/(°C d) | |
| Insolation and soil warmth melting rate MRIS ** | 4.2 mm/d | 3.8–4.6 mm/d | 4.4 mm/d |
| GOFC | Mean | Range | Solution 9790 |
|---|---|---|---|
| SSE | 122.48 (m3/s)2 | 103.30–187.90 (m3/s)2 | 128.60 (m3/s)2 |
| APD | 1.02 m3/s | 0.00–2.49 m3/s | 0.35 m3/s |
| NSE | 0.64 | 0.44–0.69 | 0.62 |
| LnNSE | 0.60 | 0.39–0.66 | 0.64 |
| ∆V | 5.51% | −6.03–19.26% | 7.27% |
| GOFC | Solution 9790 |
|---|---|
| SSE | 175.60 (m3/s)2 |
| APD | +0.37 m3/s |
| NSE | 0.44 |
| LnNSE | 0.60 |
| ∆V | −11.36% |
| Parameter | Values Compiled by [71] | Mean Value [42] | Mean Calibration Period | Mean Validation Period | Unit |
|---|---|---|---|---|---|
| Precipitation | 850–950 | 981 | 799 | 985 | mm/a |
| Total runoff | 327 | 327 | 265 | 350 | mm/a |
| Direct runoff | 159 | 159 | 159 | 244 | mm/a |
| Groundwater recharge (baseflow) | 168 | 168 | 106 | 106 | mm/a |
| GOFC | Mean | Range | Solution 3468 |
|---|---|---|---|
| SSE | 77.34 (m3/s)2 | 69.03–108.02 (m3/s)2 | 73.58 (m3/s)2 |
| APD | 1.72 m3/s | 0.00–3.56 m3/s | 1.03 m3/s |
| NSE | 0.76 | 0.56–0.80 | 0.78 |
| LnNSE | 0.73 | 0.59–0.76 | 0.72 |
| ∆V | 3.77% | 0.42–11.29% | 0.79% |
| GOFC | Solution 3468 |
|---|---|
| SSE | 78.13 (m3/s)2 |
| APD | 0.65 m3/s |
| NSE | 0.75 |
| LnNSE | 0.78 |
| ∆V | −2.95% |
| Parameter | Values Compiled by [71] | Mean Value [42] ** | Calibration Mean | Validation Mean | Unit |
|---|---|---|---|---|---|
| Precipitation | 850–950 | 981 | 799 | 985 | mm/a |
| Potential evapotranspiration | 542–612 * | - | 740 | 740 | mm/a |
| Actual evapotranspiration | 432–450 * | 654 | 577 | 611 | mm/a |
| Total runoff | 327 | 327 | 239 | 368 | mm/a |
| Direct runoff | 159 | 159 | 91 | 133 | mm/a |
| Surface runoff | - | - | 17 | 22 | mm/a |
| Interflow | - | - | 75 | 115 | mm/a |
| Groundwater recharge (baseflow) | 168 | 168 | 148 | 235 | mm/a |
| Study | Model | Region | Year | NSE (Calibration/Validation) | LnNSE (Calibration/Validation) |
|---|---|---|---|---|---|
| This study | BlueM.Sim (FA, SMA) | FIS, German Low Mountain range | 1989–2002 | FA: 0.62/0.44 SMA: 0.78/0.75 | FA: 0.64/0.60 SMA: 0.72/0.78 |
| Eckhardt et al. (2002) [77] * | SWAT-G | Lahn-Dill-Bergland, German Low Mountain range | 1991–1993 | 0.76 | - |
| Stoelzle et al. (2015) [5] * | GWN-BW (case: setup 2PA, weight BQ and input GR are reported here) | Baden-Württemberg, e.g., hard-rock aquifers of the Black Forest, Germany | 1971–2008 | - | 0.7 < log NSE < 0.8 |
| Pfannerstill et al. (2013) [78] * | SWAT (three reservoirs for baseflow) | Kielstau catchment, lowland, Northern Germany | 1997–2010 | 0.67/0.72 | |
| Luo et al. (2012) [79] * | SWAT | Manas River basin, Tianshan Mountains, Northwest China | 1961–1999 | One lin. reservoir: 0.68/0.62 Two parallel lin. reservoirs: 0.76/0.69 | - |
| Dariane et al. (2016) [80] | HEC-HMS (calibration case using genetic algorithm reported here) | Mehraban subbasin of the Ajichai Basin, northwestern Iran | 1999–2006 | 0.76/0.54 | A low-flow weighted NSE is only reported for the validation: 0.64 |
| Ouédraogo et al. (2018) [81] | HEC-HMS | Mkurumudzi River Catchment, Kenya | 1988–1995 | 0.8/0.65 | |
| Parra et al. (2019) [82] * | HBV Two reservoirs for baseflow | Three of eight watersheds with fractured hard-rock aquifers in south-central Chile | 2000–2006 | 0.81, 0.81, 0.91 /0.72, 0.82, 0.92 for the three catchments, respectively | |
| Chathuranika et al. (2022) [83] | SWAT HEC-HMS | Huai Bang Sai Watershed, Thailand | 2007–2014 | SWAT: 0.78/0.77 HEC-HMS: 0.84/0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kissel, M.; Bach, M.; Schmalz, B. Evaluation of Baseflow Modeling with BlueM.Sim for Long-Term Hydrological Studies in the German Low Mountain Range of Hesse, Germany. Hydrology 2023, 10, 222. https://doi.org/10.3390/hydrology10120222
Kissel M, Bach M, Schmalz B. Evaluation of Baseflow Modeling with BlueM.Sim for Long-Term Hydrological Studies in the German Low Mountain Range of Hesse, Germany. Hydrology. 2023; 10(12):222. https://doi.org/10.3390/hydrology10120222
Chicago/Turabian StyleKissel, Michael, Michael Bach, and Britta Schmalz. 2023. "Evaluation of Baseflow Modeling with BlueM.Sim for Long-Term Hydrological Studies in the German Low Mountain Range of Hesse, Germany" Hydrology 10, no. 12: 222. https://doi.org/10.3390/hydrology10120222
APA StyleKissel, M., Bach, M., & Schmalz, B. (2023). Evaluation of Baseflow Modeling with BlueM.Sim for Long-Term Hydrological Studies in the German Low Mountain Range of Hesse, Germany. Hydrology, 10(12), 222. https://doi.org/10.3390/hydrology10120222






